Open Access Article
Open Access ArticleStrength of bacterial adhesion on nanostructured surfaces quantified by substrate morphometry†
Christian
Spengler
 a,
Friederike
Nolle
a,
Johannes
Mischo
a,
Thomas
Faidt
a,
Friederike
Nolle
a,
Johannes
Mischo
a,
Thomas
Faidt
 a,
Samuel
Grandthyll
a,
Nicolas
Thewes
a,
Marcus
Koch
b,
Frank
Müller
a,
Samuel
Grandthyll
a,
Nicolas
Thewes
a,
Marcus
Koch
b,
Frank
Müller
 a,
Markus
Bischoff
a,
Markus
Bischoff
 c,
Michael Andreas
Klatt‡
c,
Michael Andreas
Klatt‡
 d and
Karin
Jacobs
d and
Karin
Jacobs
 *a
*a
aDepartment of Experimental Physics, Saarland University, Campus E2 9, 66123 Saarbrücken, Germany. E-mail: k.jacobs@physik.uni-saarland.de; Fax: +49 (0)681 302 71700; Tel: +49 (0)681 302 71777
bINM – Leibniz Institute for New Materials, Campus D2 2, 66123 Saarbrücken, Germany
cInstitute of Medical Microbiology and Hygiene, Saarland University, 66421 Homburg/Saar, Germany
dInstitute of Stochastics, Karlsruhe Institute of Technology, 76131 Karlsruhe, Germany
First published on 4th October 2019
Abstract
Microbial adhesion and the subsequent formation of resilient biofilms at surfaces are decisively influenced by substrate properties, such as the topography. To date, studies that quantitatively link surface topography and bacterial adhesion are scarce, as both are not straightforward to quantify. To fill this gap, surface morphometry combined with single-cell force spectroscopy was performed on surfaces with irregular topographies on the nano-scale. As surfaces, hydrophobized silicon wafers were used that were etched to exhibit surface structures in the same size range as the bacterial cell wall molecules. The surface structures were characterized by a detailed morphometric analysis based on Minkowski functionals revealing both qualitatively similar features and quantitatively different extensions. We find that as the size of the nanostructures increases, the adhesion forces decrease in a way that can be quantified by the area of the surface that is available for the tethering of cell wall molecules. In addition, we observe a bactericidal effect, which is more pronounced on substrates with taller structures but does not influence adhesion. Our results can be used for a targeted development of 3D-structured materials for/against bio-adhesion. Moreover, the morphometric analysis can serve as a future gold standard for characterizing a broad spectrum of material structures.
Introduction
Bacterial biofilms can cause serious problems in many medical, biological and industrial applications.1–3 Once formed, they are chemically and mechanically robust and therefore very difficult to remove.4,5 A promising approach in biofilm prevention is to inhibit the first step of its formation, which is the adhesion of bacterial cells to surfaces. An important substrate property for the adhesion of bacterial cells is the surface topography, which has therefore been addressed in numerous studies,6–9 especially in the prevention of bio-fouling, a subject of ongoing discussion.8–10 However, in the literature no universal approach to quantify bacterial adhesion on nanostructured surfaces can be found since previous studies mostly feature two main drawbacks: lack of (i) quantitative adhesion force determination and (ii) detailed surface characterization.(i) Bacterial adhesion on structured surfaces has often been examined in adsorption experiments by immersing the structured surfaces in bacterial suspensions.11–15 Although this approach is intuitive and mimics the natural situation of bacterial colonization quite accurately, the results from different labs are hard to compare since too many parameters are involved that cannot be controlled accurately. For example, the processes of obtaining the number of adhering cells may differ: in some cases, the sample is first dried and then coated with gold in order to count the bacteria later in electron microscopy images11,12 or by conductance microbiology.13 It is also difficult to describe the rinsing of loosely bound cells and the removal of adsorbed cells for plating or counting in all parameters. These problems can be overcome by quantitative measurements of actual bacterial adhesion forces (the force required to detach the cell from the surface) under controlled conditions. Hence, we used single-cell force spectroscopy (SCFS), a well-established method for quantitative adhesion force measurements of living bacterial cells.16–26
(ii) Many studies have used different types of topographically (regularly27–32 or randomly11–15,33–36) structured surfaces without a detailed morphological characterization. There are a number of parameters to describe surface morphologies:37,38 for example, the average roughness or the root mean square (RMS) roughness are very descriptive parameters that are, therefore, often used in bacterial adhesion studies. Other measures, such as the skewness or the kurtosis of the surface, are less intuitive, but give additional information about the surface geometry.35,36 However, all these parameters are local shape descriptors that are insensitive to global features because they do not distinguish between arbitrary permutations of the positions of different heights. Therefore, these parameters do not fully characterize the surface morphologies, which makes it difficult to compare the results of different studies. One way to overcome these problems in describing the topography are the so-called Minkowski functionals that we therefore used in our study.39
Minkowski functionals are comprehensive and efficient shape descriptors from integral geometry40 that contain, put simply, the complete additive – and hence robust – shape information (according to Hadwiger's theorem).41 Since they are versatile geometric measures, they have already been widely used in statistical physics and pattern analysis (see ref. 42–48 and references therein). There, an integral geometry-based analysis using the Minkowski functionals has been termed morphometry.48 With this method, height data of nanostructured surfaces can be analysed using three-dimensional Minkowski functionals or the level sets at different heights using two-dimensional Minkowski functionals (for explanatory figures, see the ESI†).
In 2D, the Minkowski functionals of a domain can be intuitively interpreted as its area, perimeter, and Euler characteristic. The latter is a topological constant, which is given for a compact body by its number of components minus its number of holes.
In this study, we used Staphylococcus aureus (S. aureus), a Gram-positive, biofilm-forming bacterium that is a frequent cause of severe infections,49 and measured the adhesion forces of single cells to nanostructured surfaces (see Fig. 1 for an about-to-scale sketch) that are characterized by their Minkowski functionals and show how the strength of bacterial adhesion can be quantified with the help of these functionals. We focus on nanostructures since the radius of the contact area of bacteria like S. aureus to flat surfaces is only in the range of some hundred nanometers.50
 | ||
| Fig. 1 Bacterial cell adhering to a partially smooth and nanostructured surface (represented by real AFM data). | ||
Results and discussion
Surface morphometry
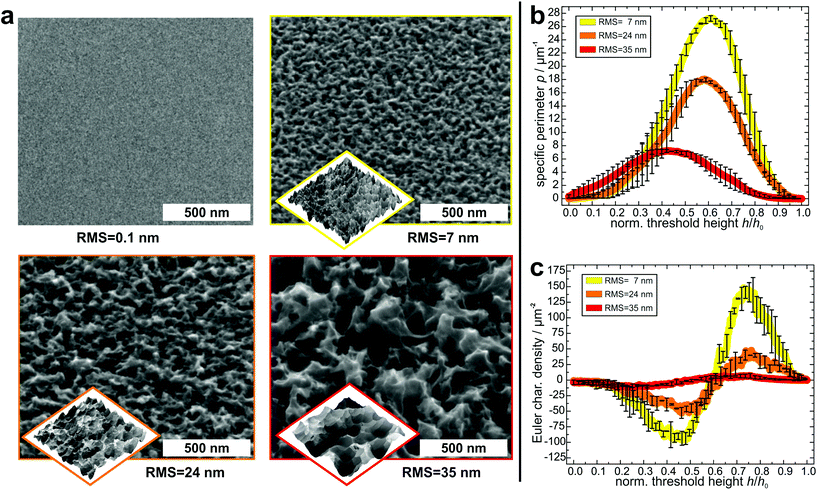
In order to create suitable substrates for the quantification of the influence of surface nanostructures on bacterial adhesion, we etched clean silicon wafers in a mixture of fluoric acid, hydrogen peroxide and water for different periods of time (90 s, 180 s, 360 s).51 Beforehand, the surfaces were covered with small gold clusters as catalysts for the etching process. These clusters were applied by physical vapor deposition52 and afterwards removed by immersing the wafers in aqua regia. Then, the wafers were rendered hydrophobic because strong bacterial adhesion is governed by hydrophobic interaction.53,54 This was achieved by covering them with a self-assembling monolayer of silanes according to a standard recipe55 (the quality of the silane monolayer was checked by contact angle measurements and AFM experiments in quantitative nanomechanical mapping; for details, see the ESI†). As shown in Fig. 2a, on the formerly smooth surfaces, etching created characteristic nanostructures, whose lateral and vertical dimensions increased with increasing etching time. The structures feature sharp edges on all surfaces and their shape seems similar in general.To characterize the surface structures in a quantitative way, the hydrophobized substrates were imaged by atomic force microscopy (AFM) at different positions with high aspect ratio tips. Before further analysis, the surface was reconstructed by unfolding the recorded image and the tip geometry. As a simple parameter – and for comparison to other studies – the RMS roughness of each surface was determined (and was used as label for the different surfaces). Its value increases with increasing etching time: 7 ± 1 nm for the 90 s etched surface, 24 ± 1 nm for the 180 s etched surface, and 35 ± 1 nm for the 360 s etched surface.
For a more detailed characterization, the Minkowski functionals of all AFM images were calculated and averaged over different positions on each surface47 (for a visual explanation of the Minkowski functionals of level sets, see Fig. S2 in the ESI†).45,46 Since the maximum height range of the samples varies, the functionals were normalized to their respective maximum height value. In Fig. 2b and c, the specific perimeter and the Euler characteristic density are plotted in dependence of this normalized threshold height (absolute values and data of surface area are given in Fig. S3 in the ESI†). For all surfaces, both functionals have similar shapes, with only their extents varying: the specific perimeter features a very smooth shape with a single maximum for all substrates. The position of the maximum differs slightly between the different substrates (for an explanation, see Fig. S6 in the ESI†). The Euler characteristic density has, in every case, for low threshold heights, a minimum with negative values and at larger heights, a maximum with positive values. Due to the different RMS values, the peaks and dips, especially for the surface with an RMS value of 35 nm occur at different values of normalized threshold height. The Minkowski functionals thus characterize quantitative differences between the surfaces. These differences pertain mainly to the absolute values of the specific perimeter and Euler characteristic density: both quantities have the highest values for the surface with 7 nm RMS roughness, lower values for the surface with 24 nm RMS roughness and the lowest values for the surface with 35 nm RMS roughness. This means that the lateral dimensions of the etched structures are smaller for the surfaces that were etched for shorter times.
Overall, the Minkowski analysis confirms the morphological similarity between the surfaces, allowing for a systematic investigation of the influence of differently sized nanostructures on bacterial adhesion. Whether the differences are due to statistical fluctuations, pixelization errors, or physically relevant qualitative differences between the surfaces, is beyond the scope of this study and not relevant for our further analysis.
Moreover, these analyses show that all etched surfaces feature a sub-micron topography with dimensions in the same range as the radius of the bacterial contact area, which is about 150–300 nm.50
Bacterial adhesion is known to be affected not only by surface chemistry, but also by the subsurface of a material through long-ranging van der Waals forces.57 Hence, to exclude potential influences originating from differences in surface and subsurface composition, XPS measurements of all substrates were performed before silanization, showing that the roughened surfaces oxidize immediately after etching. Since this surface oxide layer has the same thickness as the oxide layers of the unetched substrates (XPS spectra are given in Fig. S1 in the ESI†), all surfaces used can be considered chemically identical.
Effect of the nanostructure on bacterial adhesion
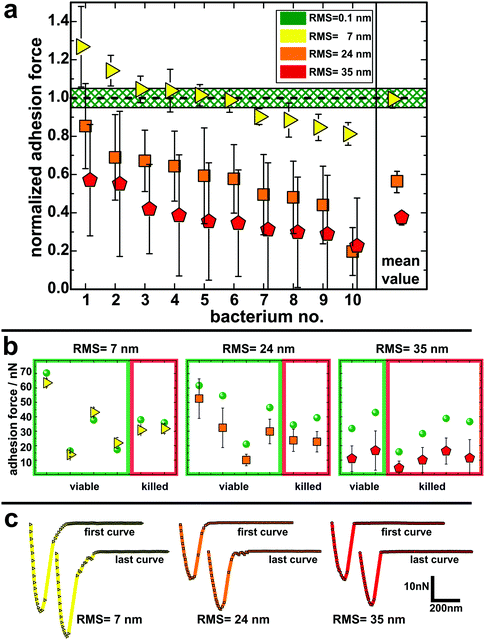
To quantify the impact of the nano-topography on the adhesive strength of bacteria, we performed single-cell force spectroscopy measurements on each etched surface and on a smooth surface as a reference. Thereto, a single viable S. aureus cell was immobilized on a tipless cantilever and force–distance curves were recorded in buffer at room temperature.53,54,58 From these curves the so-called adhesion force, i.e. the maximum force needed to detach the cell from the surface, was calculated.Fig. 3 shows the mean adhesion forces of all tested cells on each type of surface. Of note, adhesion forces of S. aureus on hydrophobic surfaces are very cell-individual, i.e. they can differ markedly between different cells.50 Therefore, for each cell, its mean adhesion force determined on the smooth surface was normalized to 1.0 and its adhesion force on the etched surface was adjusted accordingly (non-normalized values are given in Fig. 3b and Fig. S5 in the ESI†). On the surface with 7 nm RMS roughness (yellow triangles in Fig. 3a), adhesion forces range from 80–130% of the forces recorded on the smooth surface with a mean value matching the adhesion force on the smooth surface. On the surface with 24 nm RMS roughness (orange squares in Fig. 3a), cells feature adhesion forces between 30% and 90% of the ones observed on the smooth surface with a mean value of 56(6)%.§ Adhesion forces on the roughest surface (red pentagons in Fig. 3a) vary between 25% and 60% of the forces recorded on the smooth surface. The mean value on the roughest surface is 38(4)% of the value determined on the smooth surface.
The results of the adhesion force measurements can be interpreted in such a way that the contact between a cell and a surface is mediated primarily by cell wall macromolecules tethering to the substrate53,54 and thus the adhesive strength of a single cell is determined by the total number of such tethering macromolecules. A recent study indicated that these macromolecules in the S. aureus cell wall can extend by approximately 50 nm due to thermal fluctuations, a length hereinafter referred to as ‘tether length’.54 The value of 50 nm for the tether length is confirmed by the snap-in separations obtained from the force–displacement curves of our adhesion experiments (for data, see Fig. S7 in the ESI†). Based on this, Fig. 4 a sketches our proposed molecular picture of bacterial adhesion to nanostructured surfaces: on the smooth silicon surface, a high number or even all surface macromolecules within a certain area, called the contact area,50 tether to the surface, and thus adhesion is strongest. Then, with increasing roughness, more and more cell wall macromolecules can no longer reach the surface via thermal fluctuations resulting in a smaller number of tethered molecules. This means that the rougher the surface, the lower the bacterial adhesion force.
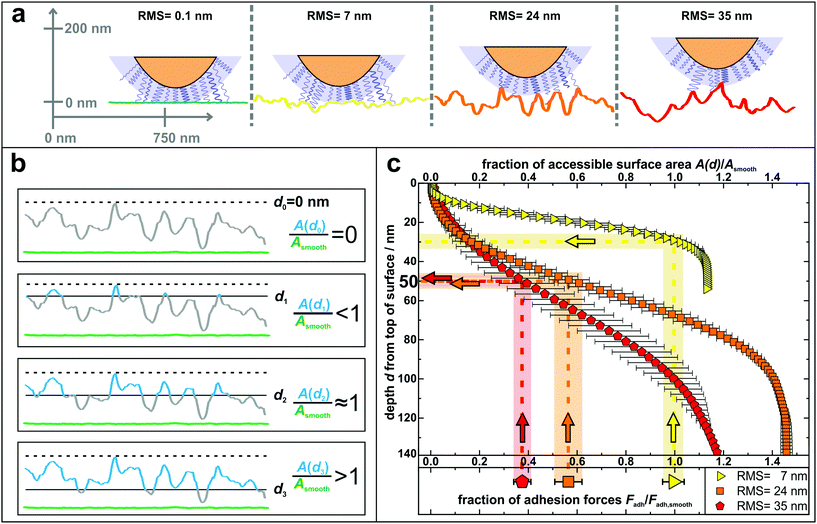 | ||
| Fig. 4 (a) Sketch to illustrate the adhesion of S. aureus mediated by macromolecular tethering on different nanostructured surfaces: the bigger the surface structures, the lower is the number of macromolecules that are able to reach the substrate. Notably, only few molecules are drawn on the cell wall, whereas their density is in reality much higher, as symbolized by the blue shaded layer. All surfaces are represented by real AFM scan lines. (b) Visual explanation of the data shown in part c: accessible surface area (blue lines) of a nanostructured substrate compared to the surface area of a smooth substrate (green lines) for four exemplary depth values d0–d3. (c) Depth d from top of the surface and corresponding fraction of accessible surface area of all nanostructured substrates compared to the total surface area of a smooth substrate. The light-colored vertical rectangles show the relative decrease of adhesion forces on the nanostructured surfaces (the center line of each rectangle indicates the mean value of adhesion forces and the width corresponds to the error of the mean from Fig. 3). The horizontal rectangles indicate the corresponding depth in which this fraction of surface area is accessible. | ||
In other words, on the nanostructured surfaces, in a certain depth d of the sample (measured from the highest point downwards), only a certain fraction of the total area of the smooth surface is accessible by tethering molecules as visualized in Fig. 4b: for some depth values, e.g. d1, the accessible surface area (blue line in Fig. 4b) is smaller than the area of a smooth wafer (green scan line in Fig. 4b). Then, at a certain depth (d2) the accessible surface area is approximately equal to the area of a smooth wafer, while for larger depth values, e.g. d3, the nanostructured substrate offers more surface area than a smooth wafer. These data are quantitatively shown in Fig. 4c: the accessible surface area of each nanostructured substrate is plotted as a function of the depth from the top of the surface, whereby the data are normalized to the surface area of a smooth wafer as explained in Fig. 4b.
These curves can be used to explain the adhesion forces on nanostructured substrates in a quantitative way: assuming that the primary reason for reduced adhesion is the reduced accessible surface area, for each curve, this ratio of surface areas equals the ratio of reduced adhesion forces from Fig. 3 (vertical rectangles in Fig. 4c). Thus, the latter can be associated with a corresponding depth that is accessible from the typical top of the surface, whose measurement is described in Fig. S8 in the ESI† (horizontal rectangles in Fig. 4c).
The plot shows that on the surface with 7 nm RMS roughness, after about 30 nm from top, the accessible surface area is already at 100% and all cell wall macromolecules (with an average tether length of 50 nm) responsible for adhesion can reach the surface and, therefore, the adhesive strength is the same as on the smooth wafer. Some cells even show a stronger adhesion than on the smooth surface, which can be explained, besides by statistical fluctuations, by the fact that the total surface area on the nanostructured substrate is – for distances from the top greater than 30 nm – larger than on the smooth wafer. Hence, cell wall macromolecules with tether lengths of 50 nm can ‘find’ even more binding sites resulting in stronger adhesion.59,60 For the surfaces with 24 nm and 35 nm RMS roughness, the ratios of surface areas that correspond to the reduced adhesion forces of 56(6)% and 38(4)% are both accessible in a depth of 45–55 nm. This depth perfectly matches the S. aureus tether length of 50 nm, a fact that strongly supports our hypothesis that the reason for reduced adhesion forces is primarily caused by the reduced accessible surface area.
The quantitative influence of surface roughness on the adhesion of S. aureus cells can probably be transferred to other (Gram-positive) bacteria (see Fig. S9 in the ESI† for experiments with Staphylococcus carnosus). However, it should be mentioned that the exact range of surface roughness that best prevents adhesion depends on the average tether length of the cell wall macromolecules and in part on the contact area. Both quantities may vary for different species. In addition, care should be taken when transferring our results to surfaces where other effects, such as surface deformations due to rather flexible structures (see Fig. S10 in the ESI†), may dominate the adhesive behaviour of bacteria. The same might be true for the bactericidal properties of our substrates which are described below.
Since other studies have reported bactericidal effects of surfaces with structures similar to those of our substrates,61–64 it was of particular interest for us to determine the impact of the nano-topography on the viability of the cells used in our study. Therefore, we performed live/dead staining for some of the cells after adhesion measurements. In doing so, we also checked if there is a correlation between the measured adhesion of particular cells and their viability after the experiment. It shows that the fraction of dead cells increases with increasing size of surface structures: on the smooth silicon, none of the tested cells were killed. On the surfaces with 7 nm and 24 nm RMS roughness, one third of the tested cells were killed and on the roughest surface, two thirds of the tested cells were found dead after measurements. Interestingly, no correlation between the adhesion force (or the change in adhesion force) and the viability of the corresponding cell can be observed in adhesion force measurements (Fig. 3b). Accordingly, the characteristic shape of the force–distance curves did not change in the course of several measurements with cells that were found to be dead at the end of the experiment (Fig. 3c). Hence, it seems that, surprisingly, the viability of a cell does not influence its adhesive strength – at least not for the time scales (approximately one hour) and the conditions of our experiments and for the used surfaces.
In the literature, the bactericidal properties of structured surfaces are usually attributed to the penetration or intrusion and subsequent stretching of the bacterial cell wall by ‘spiky’ features on the substrate.61–64 On the one hand, our experiments suggest that the size of these features on the roughest surface is generally most effective for killing because the fraction of dead cells is the largest on this substrates. On the other hand, cell death on a certain surface seems to depend on the particular cell respectively its locally varying cell wall properties at the contact area.65 For some cells, the layer of cell wall molecules may be (locally) very dense and/or thick and therefore so ‘strong’ that it prevents the spiky structures from deeply intruding the cell wall. Other cells, in contrast, may have a less dense and/or thinner rather ‘weak’ macromolecular layer and can, therefore, be penetrated by the spiky structures. Interestingly, the adhesion force of an individual cell is not correlated to its viability after adhesion force measurement (see Fig. 3b). Therefore, we can conclude that a more ‘robust’ macromolecular layer is not necessarily a more ‘adhesive’ layer. Notably, we determined the viability only for a limited number of cells. Hence, to give a general statement about the bactericidal effect of our nanostructured surfaces, the number of these measurements should be increased and additional experiments (for example, in a flow chamber setup) should be performed.
Conclusions
In summary, we have shown that surface morphometry is quantitatively related to the strength of bacterial adhesion on surfaces with a nano-scaled topography. Our single-cell force spectroscopy measurements on etched silicon surfaces revealed that the adhesion force of S. aureus cells to nanostructured substrates decreases with increasing size of surface structures. The most important outcome is that a detailed characterization by Minkowski functionals allows a direct correlation between surface nanostructures and bacterial adhesion forces: since the adhesive strength is determined by the number of cell wall macromolecules tethering to the surface, the reduced accessible surface area on the nanostructured substrates for cell wall molecules with average tether lengths of 50 nm matches the reduced mean adhesion forces on the nano-topographies remarkably well. Quantifying the variances of tether lengths, surface areas and adhesion forces and determining whether they are also related to each other is an interesting question for future research.In addition, we have shown that the nanostructure of our substrates influences the viability of bacteria after contact: similar to the adhesive strength, the percentage of viable cells on the nanostructured surfaces decreases with increasing surface roughness while the adhesive strength of individual cells is not influenced by their viability.
Our results can be of importance in industry and medicine since nanostructured surfaces are increasingly used in various applications (for example, as materials for bioreactors or prosthetics).2,3 For scenarios, in which bacterial adhesion is unwanted, our results can provide suggestions regarding surface topography: while molecularly smooth surfaces or those with structures larger than the cells display a favorable adhesion ground for bacteria, this property is markedly reduced on surfaces that feature structures in the same size range as the macromolecules of the bacterial cell wall. At the same time, this size range also seems to be effective for killing cells by contact with these structures. Furthermore, our study shows the strong potential of surface characterization using Minkowksi functionals since this method provides universal morphological information allowing, for example, a precise comparison of different surfaces.
Materials and methods
Silicon wafers
Silicon wafers in (100) orientation with a resistivity of 10–20 Ω cm were purchased from Siltronic (Burghausen, Germany). They feature a native silicon oxide layer with a thickness of 1.7(2) nm as determined by ellipsometry.66 The wafers are by default polished to an RMS roughness of 0.09(2) nm as determined by AFM.66Preparation of the nanostructured surfaces
In a first step, silicon surfaces were covered with a gold layer of a nominal film thickness of 2 nm which was determined with a quartz crystal microbalance by physical vapor deposition. As is known, this procedure does not result in a continuous gold film, but in gold clusters of sub-micron size.52 Subsequently, following a recipe by Koynov et al.,51 the gold-covered silicon was etched by immersing the wafers in a mixture of fluoric acid (HF, 40%), hydrogen peroxide (H2O2, 35%) and water for 90 s, 180 s and 360 s, respectively. Residues from the etching solution were removed by extensively rinsing the etched wafers in ultra-pure water. After etching, the gold clusters were removed by immersing the wafers in aqua regia (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mixture of HNO3 (65%) and HCl (37%)) for 25 min. Afterwards, the wafers were rinsed again with ultra-pure water to remove possible leftovers of the acid. X-ray photoelectron spectroscopy (XPS) confirmed that no gold was present on the surface after this treatment (an XPS overview spectrum is given in Fig. S1a†). To render the wafers hydrophobic, they were covered with a self-assembling monolayer of silanes according to a standard recipe.55 Right before every set of experiments with bacteria, all surfaces were cleaned in ultrasonic baths of ethanol and acetone for 3 min each. After cleaning, the surfaces were dried under a stream of pure nitrogen.
3 mixture of HNO3 (65%) and HCl (37%)) for 25 min. Afterwards, the wafers were rinsed again with ultra-pure water to remove possible leftovers of the acid. X-ray photoelectron spectroscopy (XPS) confirmed that no gold was present on the surface after this treatment (an XPS overview spectrum is given in Fig. S1a†). To render the wafers hydrophobic, they were covered with a self-assembling monolayer of silanes according to a standard recipe.55 Right before every set of experiments with bacteria, all surfaces were cleaned in ultrasonic baths of ethanol and acetone for 3 min each. After cleaning, the surfaces were dried under a stream of pure nitrogen.
Bacteria
For this study, cells of the S. aureus strain SA113 were used. Bacteria from a deep-frozen stock solution were grown on a blood agar plate for 2.5 days at 37 °C. Such a plate was used for two weeks at the maximum. For the experiments, one colony from the plate was transferred into 5 ml of sterile tryptic soy broth (TSB) and cultured for 16 h at 37 °C under agitation (150 rpm). From this culture, 40 μl were transferred into 4 ml of fresh TSB and cultured once more for 2.5 h at 37 °C and 150 rpm. Finally, 1 ml was taken from this culture and washed three times by centrifuging for 3 min at 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000g, replacing the supernatant by 1 ml of fresh phosphate buffered saline (PBS, pH 7.3) and thoroughly vortexing. This procedure results in a bacterial suspension with an optical density at 600 nm (OD600) of 0.2–0.3.
000g, replacing the supernatant by 1 ml of fresh phosphate buffered saline (PBS, pH 7.3) and thoroughly vortexing. This procedure results in a bacterial suspension with an optical density at 600 nm (OD600) of 0.2–0.3.
Viability measurements
To check the viability of the cells, the BacLight assay purchased from Molecular Probes, Eugene, USA was used. It consists of Syto 9 and propidium iodide. After excitation, the Syto 9 stain emits green light when bound to nucleic acids in bacteria. In contrast, propidium iodide, which can only enter the porous cell wall of dead bacterial cells, emits red light and causes a reduction of the binding between the Syto 9 stain and the bacterial nucleic acids. Hence, after staining a bacterial solution with the BacLight mixture and illuminating it with white light, viable cells glow green and dead cells red. After adhesion measurements, we placed the used cantilever including the immobilized cell in a drop (1 ml) of the staining assay. To achieve best results, the stain was left to act on the cell for 10 min in the dark. Thereafter, its residues were removed by carefully replacing the drop by fresh PBS for three times. Care was taken that the cantilever with the cell never was completely dry. Then, the cell on the cantilever was observed by fluorescence microscopy.Force–distance measurements
We recorded force–distance curves on a Bioscope Catalyst (Bruker-Nano, Santa Barbara, USA) with single viable bacterial cells immobilized on a tipless cantilever (MLCT-0, Bruker-Nano) with nominal spring constants of 0.01 N m−1 and 0.3 N m−1. A detailed description of how the cells were attached to the cantilevers can be found in the paper by Thewes et al.,67 in short: tipless cantilevers were cleaned in an air-plasma and afterwards covered with a thin layer of dopamine by immersing them in a solution of 4 mg ml−1 dopamine hydrochloride in TRIS/HCL-buffer for one hour. The cantilevers were then cleaned in ultrapure water and dried in a clean room environment. The cantilevers’ spring constant and deflection sensitivity were calibrated before each set of measurements. To pick up a single cell, a very dilute bacterial suspension was placed on a Petri dish that was observed with an inverse optical microscope equipped with a micromanipulator. The calibrated cantilever is then connected to the micromanipulator and approached from above to the sedimented bacterial cells in the Petri dish. In a final step, the cantilever is carefully lowered onto a single cell and gently pressed onto it so that the cell adheres to the cantilever. This bacterial probe is afterwards carefully inserted in the microscope without drying out the cell.For every force–distance curve, the approach and retraction distance was 800 nm with a retraction velocity of 800 nm s−1. The force trigger, i.e. the force with which the cell is pressed onto the surface, was set to 300 pN which does hardly deform the cell or change its contact area50,68 (for a more detailed discussion of the chosen force trigger, see the ESI†). Curves were recorded with 0 s surface delay time which corresponds to a ‘real’ contact time below 0.5 s.53,58 For each individual cell, 100 force–distance curves were recorded on the smooth as well as on a nanostructured surface in a rectangular pattern with a distance of 1 μm between each curve. To exclude that probing the smooth/nanostructured surfaces might alter the adhesive behaviour of the bacterial cell, the first 50 curves were recorded on the smooth surface and the next 50 were recorded on the nanostructured surface. Then, again, the smooth surface and afterwards the nanostructured surface was probed by 50 curves each. By comparing the adhesion of each set of curves on the smooth/nanostructured surface, it was ensured that the adhesion behavior was not changed during the recording of several force–distance curves on the different surfaces (as it was also seen before on smooth silicon53,68).
AFM surface topography measurements
The surface topography was measured in tapping mode with an Icon FastscanBio (Bruker-Nano, Santa Barbara, USA) in air using high aspect ratio tips (HAR1-200-10, Bruker-Nano) with a nominal spring constant of 42 N m−1 in soft tapping mode with an image resolution of 1024 × 1024 pixels. The scan area was 1 μm × 1 μm for the 90 s and 180 s etched substrates. The 360 s etched surface fluctuates strongly and so do its geometrical properties. To reduce the statistical error, we scanned a larger observation window of 3 μm × 3 μm. Systematic effects of the lower physical resolution on the total surface area should be less than 3%, as estimated from the other surface when we artificially reduced the resolution. The resolution in z-direction was below 0.5 nm. From these images, the AFM tip shape was determined and the real surface was reconstructed by deconvoluting the recorded image and the tip geometry using the software Gwyddion. For every type of surface, several AFM images were recorded and analyzed, providing average values and standard deviations for RMS roughnesses and Minkowski functionals.Minkowski analysis
The level sets of the AFM images and their three-dimensional triangulations were analyzed using Minkowski functionals. In the latter case, the triangulation was constructed using the ‘Advancing Front Surface Reconstruction’ from CGAL.56 Using the 3D Minkowski software Karambola,47 the surface area was computed as a function of the height. More precisely, as a function of the difference in height to the maximal peak within the observation window, the surface area was computed for all those triangles whose lowest vertex was above this threshold. In the first case, the AFM images were converted into pixelated gray scale maps and then into black-and-white images via thresholding. A pixel whose height is above a threshold h turns white, all others become black. The three two-dimensional Minkowski functionals of the white domains were then computed as a function of the threshold height h using the software Papaya.46 To reduce the pixelization errors, a standard marching square algorithm was applied.45 Edge effects from the observation window were avoided by using minus-sampling boundary conditions (the outermost pixels were used for the boundary conditions). To avoid dependencies on lateral dimensions of the AFM scans so-called densities of Minkowski functionals are used, i.e. the functionals are rescaled by the size of the observation window.Electronmicroscopy measurements
For the scanning electron microscopy (SEM) measurements, a FEI (Hilsboro, USA) Quanta 400 FEG SEM in high vacuum mode was used. Secondary electron images were collected at 10 kV and 15 kV accelerating voltage under different tilting angles.Author contributions
C.S., N.T., M.B., K.J. designed research. C.S., F.N., J.M. performed AFM and viability measurements. S.G., F.M. performed XPS measurements. M.K. performed REM measurements. M.A.K. performed Minkowski analyses. C.S., F.N., J.M., T.F., S.G., F.M., M.A.K. analyzed data. C.S., M.B., M.A.K., K.J. wrote the manuscript with the help of all other authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Günter Marchand (Mitranz Mikrotechnologie-Transferzentrum, Saarland University) for etching the substrates. Work was funded by the German Research Foundation (DFG) within the framework of the Collaborative Research Center SFB 1027 (project B2). M. A. K. acknowledges support of the DFG through the research group ‘Geometry and Physics of Spatial Random Systems’ (GPSRS) under grants number HU1874/3-2, and LA965/6-2.Notes and references
- J. W. Costerton and L. Montanaro, Int. J. Artif. Organs, 2007, 30, 757–763 CrossRef CAS PubMed.
- D. Neut, H. C. van der Mei, S. K. Bulstra and H. J. Busscher, Acta Orthop., 2007, 78, 299–308 CrossRef PubMed.
- J. A. Callow and M. E. Callow, Nat. Commun., 2011, 2, 244 CrossRef PubMed.
- O. Lieleg, M. Caldara, R. Baumgärtel and K. Ribbeck, Soft Matter, 2011, 7, 3307–3314 RSC.
- C. S. Laspidou, L. A. Spyrou and N. Aravas, Math. Biosci., 2014, 251, 11–15 CrossRef CAS PubMed.
- K. Anselme, P. Davidson, A. M. Popa, M. Giazzon, M. Liley and L. Ploux, Acta Biomater., 2010, 6, 3824–3846 CrossRef CAS PubMed.
- L. Rizzello, B. Sorce, S. Sabella, G. Vecchio, A. Galeone, V. Brunetti, R. Cingolani and P. P. Pompa, ACS Nano, 2011, 5, 1865–1876 CrossRef CAS PubMed.
- Y. Lu, S. Sathasivam, J. Song, C. R. Crick, C. J. Carmalt and I. P. Parkin, Science, 2015, 347, 1132–1135 CrossRef CAS PubMed.
- D. P. Linklater, M. De Volder, V. A. Baulin, M. Werner, S. Jessl, M. Golozar, L. Maggini, S. Rubanov, E. Hanssen, S. Juodkazis and E. P. Ivanova, ACS Nano, 2018, 12, 6657–6667 CrossRef CAS PubMed.
- J. Li, K. Zhang, L. Ruan, S. F. Chin, N. Wickramasinghe, H. Liu, V. Ravikumar, J. Ren, H. Duan and L. Yang, et al. , Nano Lett., 2018, 18, 4180–4187 CrossRef CAS PubMed.
- E. P. Ivanova, V. K. Truong, J. Y. Wang and C. C. Berndt, Langmuir, 2010, 26, 1973–1982 CrossRef CAS PubMed.
- V. K. Truong, S. Rundell, R. Lapovok and Y. Estrin, Appl. Microbiol. Biotechnol., 2009, 83, 925–937 CrossRef CAS PubMed.
- S. H. Flint, J. D. Brooks and P. J. Bremer, J. Food Eng., 2000, 43, 235–242 CrossRef.
- L. C. Hsu, J. Fang and D. A. Borca, Appl. Environ. Microbiol., 2013, 79, 2703 CrossRef CAS PubMed.
- S. D. Puckett, E. Taylor, T. Raimondo and T. J. Webster, Biomaterials, 2010, 31, 706–713 CrossRef CAS PubMed.
- S. Kang and M. Elimelech, Langmuir, 2009, 25, 9656–9659 CrossRef CAS PubMed.
- S. El-Kirat-Chatel, A. Beaussart, C. D. Boyd, G. A. O'Toole and Y. F. Dufrêne, ACS Chem. Biol., 2013, 9, 485–494 CrossRef PubMed.
- A. Beaussart, S. El-Kirat-Chatel, P. Herman, D. Alsteens, J. Mahillon, P. Hols and Y. F. Dufrêne, Biophys. J., 2013, 104, 1886–1892 CrossRef CAS PubMed.
- A. Beaussart, S. El-Kirat-Chatel, R. M. A. Sullan, D. Alsteens, P. Herman, S. Derclaye and Y. F. Dufrêne, Nat. Protoc., 2014, 9, 1049 CrossRef CAS PubMed.
- A. Beaussart, M. Abellán-Flos, S. El-Kirat-Chatel, S. P. Vincent and Y. F. Dufrêne, Nano Lett., 2016, 16, 1299–1307 CrossRef CAS PubMed.
- C. Formosa-Dague, C. Feuillie, A. Beaussart, S. Derclaye, S. Kucharíková, I. Lasa, P. Van Dijck and Y. F. Dufrêne, ACS Nano, 2016, 10, 3443–3452 CrossRef CAS PubMed.
- C. Formosa-Dague, Z.-H. Fu, C. Feuillie, S. Derclaye, T. J. Foster, J. A. Geoghegan and Y. F. Dufrêne, Nanoscale Horiz., 2016, 1, 298–303 RSC.
- C. Spengler, N. Thewes, F. Nolle, T. Faidt, N. Umanskaya, M. Hannig, M. Bischoff and K. Jacobs, J. Mol. Recognit., 2017, 30, e2615 CrossRef PubMed.
- Y. F. Dufrêne, ACS Nano, 2017, 11, 19–22 CrossRef PubMed.
- T. D. Becke, S. Ness, R. Gürster, A. F. Schilling, A.-M. di Guilmi, S. Sudhop, M. Hilleringmann and H. Clausen-Schaumann, ACS Nano, 2018, 12, 549–558 CrossRef CAS PubMed.
- C. Feuillie, C. Valotteau, L. Makart, A. Gillis, J. Mahillon and Y. F. Dufrêne, Nano Lett., 2018, 18, 5821–5826 CrossRef CAS PubMed.
- T. R. Scheuerman, A. K. Camper and M. A. Hamilton, J. Colloid Interface Sci., 1998, 208, 23–33 CrossRef CAS PubMed.
- A. I. Hochbaum and J. Aizenberg, Nano Lett., 2010, 10, 3717–3721 CrossRef CAS PubMed.
- C. Díaz, P. L. Schilardi and R. C. Salvarezza, Langmuir, 2007, 23, 11206–11210 CrossRef PubMed.
- D. Perera-Costa, J. M. Bruque, M. L. González-Martín, A. C. Gómez-García and V. Vadillo-Rodríguez, Langmuir, 2014, 30, 4633–4641 CrossRef CAS PubMed.
- N. Lu, W. Zhang, Y. Weng, X. Chen, Y. Cheng and P. Zhou, Food Control, 2016, 68, 344–351 CrossRef CAS.
- K. K. Sakimoto, C. Liu, J. Lim and P. Yang, Nano Lett., 2014, 14, 5471–5476 CrossRef CAS PubMed.
- Y. Wu, J. P. Zitelli, K. S. TenHuisen, X. Yu and M. R. Libera, Biomaterials, 2011, 32, 951–960 CrossRef CAS PubMed.
- V. K. Truong, V. Pham and A. Medvedev, Appl. Microbiol. Biotechnol., 2015, 99, 6831–6840 CrossRef CAS PubMed.
- E. P. Ivanova, V. K. Truong, H. K. Webb and V. A. Baulin, Sci. Rep., 2011, 1, 165 CrossRef PubMed.
- A. V. Singh, V. Vyas, R. Patil, V. Sharma and P. E. Scopelliti, PLoS One, 2011, 6, e25029 CrossRef CAS PubMed.
- E. Gadelmawla, M. Koura, T. Maksoud, I. Elewa and H. Soliman, J. Mater. Process. Technol., 2002, 123, 133–145 CrossRef.
- R. J. Crawford, H. K. Webb, V. K. Truong, J. Hasan and E. P. Ivanova, Adv. Colloid Interface Sci., 2012, 179, 142–149 CrossRef PubMed.
- G. E. Schröder-Turk, W. Mickel, S. C. Kapfer, M. A. Klatt, F. M. Schaller, M. J. F. Hoffmann, N. Kleppmann, P. Armstrong, A. Inayat, D. Hug, M. Reichelsdorfer, W. Peukert, W. Schwieger and K. Mecke, Adv. Mater., 2011, 23, 2535–2553 CrossRef PubMed.
- R. Schneider and W. Weil, Stochastic and Integral Geometry (Probability and Its Applications), Springer, Berlin, 2008 Search PubMed.
- H. Hadwiger, Vorlesungen über Inhalt, Oberfläche und Isoperimetrie, Springer, Berlin, 1957 Search PubMed.
- M. A. Klatt, G. E. Schröder-Turk and K. Mecke, Med. Phys., 2017, 44, 3663–3675 CrossRef CAS PubMed.
- K. Mecke, Int. J. Mod. Phys. B, 1998, 12, 861–899 CrossRef.
- K. Jacobs, R. Seemann and K. Mecke, Statistical Physics and Spatial Statistics, Springer, 2000, 72–91 Search PubMed.
- H. Mantz, K. Jacobs and K. Mecke, J. Stat. Mech.: Theory Exp., 2008, 12, P12015 CrossRef.
- G. E. Schröder-Turk, S. Kapfer, B. Breidenbach, C. Beisbart and K. Mecke, J. Microsc., 2010, 238, 57–74 CrossRef PubMed.
- G. E. Schröder-Turk, W. Mickel, S. C. Kapfer, F. M. Schaller, B. Breidenbach, D. Hug and K. Mecke, New J. Phys., 2013, 15, 083028 CrossRef.
- D. Göring, M. A. Klatt, C. Stegmann and K. Mecke, Astron. Astrophys., 2013, 555, A38 CrossRef.
- F. D. Lowy, N. Engl. J. Med., 1998, 339, 520–532 CrossRef CAS PubMed.
- C. Spengler, N. Thewes, P. Jung, M. Bischoff and K. Jacobs, Nanoscale, 2017, 9, 10084–10093 RSC.
- S. Koynov, M. S. Brandt and M. Stutzmann, Appl. Phys. Lett., 2006, 88, 203107 CrossRef.
- I. Doron-Mor, Z. Barkay, N. Filip-Granit, A. Vaskevich and I. Rubinstein, Chem. Mater., 2004, 16, 3476–3483 CrossRef CAS.
- N. Thewes, P. Loskill, P. Jung, H. Peisker, M. Bischoff, M. Herrmann and K. Jacobs, Beilstein J. Nanotechnol., 2014, 5, 1501–1512 CrossRef PubMed.
- N. Thewes, A. Thewes, P. Loskill, H. Peisker, M. Bischoff, M. Herrmann, L. Santen and K. Jacobs, Soft Matter, 2015, 11, 8913–8919 RSC.
- M. Lessel, O. Bäumchen, M. Klos, H. Hähl, R. Fetzer, M. Paulus, R. Seemann and K. Jacobs, Surf. Interface Anal., 2015, 47, 557–564 CrossRef CAS.
- T. K. F. Da and D. Cohen-Steiner, CGAL User and Reference Manual, CGAL Editorial Board, 4.12 edn, 2018 Search PubMed.
- P. Loskill, H. Hähl, N. Thewes, C. T. Kreis, M. Bischoff, M. Herrmann and K. Jacobs, Langmuir, 2012, 28, 7242–7248 CrossRef CAS PubMed.
- A. Beaussart, P. Herman and S. El, Nanoscale, 2013, 5, 10894–10900 RSC.
- R. D. Boyd, J. Verran, M. V. Jones and M. Bhakoo, Langmuir, 2002, 18, 2343–2346 CrossRef CAS.
- K. A. Whitehead, D. Rogers, J. Colligon, C. Wright and J. Verran, Colloids Surf., B, 2006, 51, 44–53 CrossRef CAS PubMed.
- E. P. Ivanova, J. Hasan, H. K. Webb and V. K. Truong, Small, 2012, 8, 2489–2494 CrossRef CAS PubMed.
- E. P. Ivanova, J. Hasan, H. K. Webb, G. Gervinskas, S. Juodkazis, V. K. Truong, A. H. Wu, R. N. Lamb, V. A. Baulin, G. S. Watson, J. A. Watson, D. E. Mainwaring and R. J. Crawford, Nat. Commun., 2013, 4, 2838 CrossRef PubMed.
- S. Pogodin, J. Hasan, V. A. Baulin, H. K. Webb and V. K. Truong, Biophys. J., 2013, 104, 835–840 CrossRef CAS PubMed.
- C. M. Bhadra, V. K. Truong, V. Pham and M. Al Kobaisi, Sci. Rep., 2015, 5, 16817 CrossRef CAS PubMed.
- J. M. Monteiro, P. B. Fernandes, F. Vaz, A. R. Pereira, A. C. Tavares, M. T. Ferreira, P. M. Pereira, H. Veiga, E. Kuru and M. S. VanNieuwenhze, et al. , Nat. Commun., 2015, 6, 8055 CrossRef CAS PubMed.
- M. Bellion, L. Santen, H. Mantz, H. Hähl, A. Quinn, A. Nagel, C. Gilow, C. Weitenberg and Y. Schmitt, J. Phys.: Condens. Matter, 2008, 20, 404226 CrossRef.
- N. Thewes, P. Loskill, C. Spengler, S. Hümbert, M. Bischoff and K. Jacobs, Eur. Phys. J. E: Soft Matter Biol. Phys., 2015, 38, 140 CrossRef PubMed.
- P. Loskill, P. M. Pereira, P. Jung, M. Bischoff, M. Herrmann, M. G. Pinho and K. Jacobs, Biophys. J., 2014, 107, 1082–1089 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/C9NR04375F |
| ‡ Present address: Department of Physics, Princeton University, Jadwin Hall, Princeton, NJ 08544-0001, USA. |
| § Values in brackets indicate the standard error of the mean. |
| This journal is © The Royal Society of Chemistry 2019 |