Imaging dopant distribution across complete phase transformation by TEM and upconversion emission

Abstract

Correlating dopant distribution to its optical response represents a complex challenge for nanomaterials science. Differentiating the “true” clustering nature from dopant pairs formed in statistical distribution complicates even more the elucidation of doping–functionality relationship. The present study associates lanthanide dopant distribution, including all significant events (enrichment, depletion and surface segregation), to its optical response in upconversion (UPC) at the ensemble and single-nanoparticle level. A small deviation from the Er nominal concentration of a few percent is able to induce clear differences in Er UPC emission color, intensity, excited-state dynamics and ultimately, UPC mechanisms, across tetragonal to monoclinic phase transformation in rationally designed Er doped ZrO₂ nanoparticles. Rare evidence of a heterogeneous dopant distribution leading to the coexistence of two polymorphs in a single nanoparticle is revealed by Z- and phase contrast transmission electron microscopy (TEM). Despite their spatial proximity, Er in the two polymorphs are spectroscopically isolated, i.e. they do not communicate by energy transfer. Segregated Er, which is well imaged in TEM, is absent in UPC, while the minor phase content overlooked by X-ray diffraction and TEM is revealed by UPC. The outstanding sensitivity of combined TEM and UPC emission to subtle deviations from uniform doping in the diluted concentration regime renders such an approach relevant for various functional oxides supporting lanthanide dopants as emitters.

---

1. Introduction

Among the factors contributing to the low upconversion (UPC) luminescence efficiency of lanthanide based nanoparticles, control over the lanthanide dopant distribution is considered a challenging task.^1–4 A uniform lanthanide distribution minimizes concentration quenching, thereby greatly enhancing the optical functionality of the UPC nanoparticles. However, despite the progress made in the last decade towards optimizing the UPC emission yield,⁵ only a few studies have considered the luminescence–dopant distribution correlations. Until recently, lanthanide dopants were considered to be statistically distributed in lanthanide-based UPC hosts on the basis of the similar physical–chemical properties of the dopant and host cations. Synchrotron radiation X-ray photoelectron spectroscopy (SXPS) along with X-ray powder diffractometry (XRD), transmission electron microscopy (TEM), and energy-dispersive X-ray (EDX) spectroscopy, coupled with plasma atomic emission spectrometry and single-particle optical microscopy evidenced nonrandom lanthanide distribution in NaGdF₄ down to the single-nanoparticle level.^6,7 Antibunching experiments on sub-10 nm Er,Yb-doped β-NaYF₄ have also shown fewer lanthanide species near the surface than expected for a statistical distribution.⁸ By the use of SXPS a radial gradient distribution of Yb from the core to the surface of the β-NaYF₄ nanoparticles was also established.⁹ The effects of non-uniform doping of Yb and Ho codoped core–shell β-NaYF₄ on UPC emission shape and brightness when considering specific applications were detailed recently.¹⁰ To date, advanced TEM techniques have become indispensable for the characterization of UPC nanoparticles¹¹ as they provide outstanding information regarding the 3D maps of dopant distribution,^1,3 cation intermixing¹² or the density of defects at the core–shell and shell–shell interfaces.¹³

Different from studies that are predominantly focused on sophisticated, core–shell NaYF₄ upconversion architectures, here we investigate the distribution of a lanthanide dopant in a non-lanthanide based host, phase-changing oxide. As a case in point, we selected ZrO₂ which is known as a suitable host for luminescent lanthanide ions with relevancy for various optical and biological applications.^14,15 The lanthanide dopant concentration and distribution control not only the emission properties but also the structural phase via charge-compensation-induced oxygen vacancies, which is a key feature of zirconia technological applications.¹⁶ When stabilized with the optically inert rare-earth Y, the tetragonal/cubic Y doped ZrO₂ (YSZ) turns into one of the most important materials for electrolytes in solid oxide fuel cells;¹⁷ however, the mechanisms of dopant distribution even for this apparently simple oxide are still not fully clarified.¹⁸ The direct observation of Y segregation at the atomic-scale was only recently observed by the use of atomic-resolution scanning transmission electron microscopy with ultrahigh-sensitive energy-dispersive EDX.¹⁹ Besides, though the tetragonal-to-monoclinic phase transformation is technologically exploited for ZrO₂ based ceramics or heterogeneous catalysis applications,²⁰ its transformation kinetics at the atomic level remains controversial.²¹

As a dopant, the Er lanthanide plays a dual role in the activation of UPC emission as well as in the stabilization of the tetragonal phase of ZrO₂. The spatial distribution, crystallographic phase location and insertion mode of Er dopants in the ZrO₂ lattice are described by high-angle annular scanning transmission electron microscopy (HAADF–STEM), EDX spectroscopy, EDX tomography and integrated differential phase-contrast (iDPC)–STEM (ref. 1, 3 and 22–24). Combination of TEM and upconversion emission as a probe tool for dopant distribution has not been reported to the authors’ knowledge. The optical signatures characteristic of Er in the tetragonal and monoclinic domains are identified under precise spectral/phase-selective excitation into Er absorption at around 975 nm. Rare evidence of a heterogeneous (enriched/depleted) distribution leading to the coexistence of tetragonal/monoclinic polymorphs in a single nanoparticle is revealed by STEM–HAADF and integrated differential phase-contrast (iDPC)–STEM). This rarely observed configuration allowed us to test the manifestation of an inter-polymorph energy transfer by the use of two spectroscopic rulers.

The paper is organized as follows. We first describe the synthesis approach of the Er–ZrO₂ nanoparticle series. From the materials side, the challenge was to obtain Er doped ZrO₂ nanoparticles spanning a complete tetragonal to monoclinic phase transition while keeping constant both the nominal concentration of the Er dopant (in the diluted regime of a few %) and the annealing temperature. We then present an in-depth TEM characterization in terms of Er enrichment, depletion and surface segregation. The experimental approach used in the upconversion investigations is based on phase selective excitation, additional Er and Eu doped ZrO₂ samples used as reference and local probe series, and clear identification of the variable parameters. Having thus defined the accurate phase selective excitation conditions, we correlate subtle deviations from the Er nominal distribution to its upconversion emission response in the tetragonal and monoclinic domains across full phase transformation. We conclude by exemplifying the possible relevancy of the described approach for other functional oxides, such as diluted semiconductor oxides.

To the authors’ knowledge, this is the first study that correlates the dopant distribution in the diluted concentration regime comprising all significant events (enrichment, depletion and surface segregation) to its optical response in upconversion across a full crystallographic phase transformation.

2. Results and discussion

2.1. Synthesis approach

Impurity doping is known as an effective tool to control the crystallographic phase, sizes and shapes.²⁵ Here, the Er dopant plays the dual role of stabilizer of the tetragonal phase and upconversion luminescent activator. The general goal was to obtain a series of Er doped ZrO₂, spanning the complete tetragonal to monoclinic phase transition without changing the dopant concentration or the annealing temperature. To this aim, we selected monovalent Li as the codopant anticipating its role as a phase modifier^25–27 and potential enhancer for the upconversion emission.² First, 3% Er–ZrO₂ was synthesized by the citrate complexation method, which is a facile and reproducible route for obtaining homogeneous doped ZrO₂ solid solutions.²⁸ The Er concentration of 3% was selected at the minimum value required for tetragonal phase stabilization.¹⁶ Then, Li with the concentration varying from a few % up to 20% was added post-synthesis to the preformed 3% Er–ZrO₂ by wet impregnation and the resulting samples were subjected to calcination in air at the same temperature of 750 °C using identical heating and cooling rates (see the Experimental details in the ESI†). The annealing temperature was limited to 750 °C to account for Li volatility²⁹ while inducing similar crystallization effects across all samples investigated at a reasonable level of particle agglomeration. Of these various Li concentrations, values at 0, 5, 10 and 15% were selected with the highest amount leading to complete tetragonal to monoclinic phase transformation. The crystallite sizes, phase content and lattice constants obtained by standard XRD analysis are summarized in Fig. 1 (see also Fig. S1 and the associated text in the ESI†).

Fig. 1 XRD patterns, crystallite sizes, phase content and lattice constants of 3Er,Li–ZrO₂ samples. t, tm, mt and m labelling refer to pure tetragonal (3Er,0Li), mixed phase with either the major (3Er,5Li) or minor tetragonal phase (3Er,10Li) and pure monoclinic (3Er,15Li).

The Li-free, 3Er sample is fully stabilized in the tetragonal phase, and 5% and 10% Li addition generates tetragonal/monoclinic mixed samples (53/47 and 36/64, respectively) while 15% Li addition induces a pure monoclinic phase. Throughout the text, the four samples are also labelled as t, tm, mt and m (Fig. 1). The crystallite sizes of tetragonal particles increase from ca. 10 (0Li) to 16 nm (10Li) while those of the monoclinic particles increase from 24 (5Li) to 31 (15Li). All samples have a similar small surface area of only a few m² g⁻¹ which is characteristic of the citrate complexation route used in synthesis.²⁸ The ionic radius of Li is rather close to that of Zr, 0.92 Å compared to 1.004 Å, in the eight-fold coordination of the tetragonal phase (to the best of our knowledge, ionic radius for the seven-fold coordination of the monoclinic phase is not available, Table S1†). Though a clear distinction cannot be made between substitutional and interstitial doping mechanisms, Li apparently enters the zirconia lattice, as no Li phase impurity, such as Li₂ZrO₃,³⁰ is evidenced irrespective of the amount of Li. We have thus designated Er,Li codoped ZrO₂ nanoparticles prepared from the same batch of 3% Er–ZrO₂ where Li drives the tetragonal to monoclinic full transformation transition by post-synthesis wet impregnation; to the best of our knowledge, a similar approach for inducing a complete phase transition in doped oxide nanoparticles by varying exclusively the concentration of the additional dopant has not been reported.

2.2. TEM analysis: Er enrichment/depletion and segregation across a complete phase transition. Evidence for the coexistence of two polymorphs in a single nanoparticle

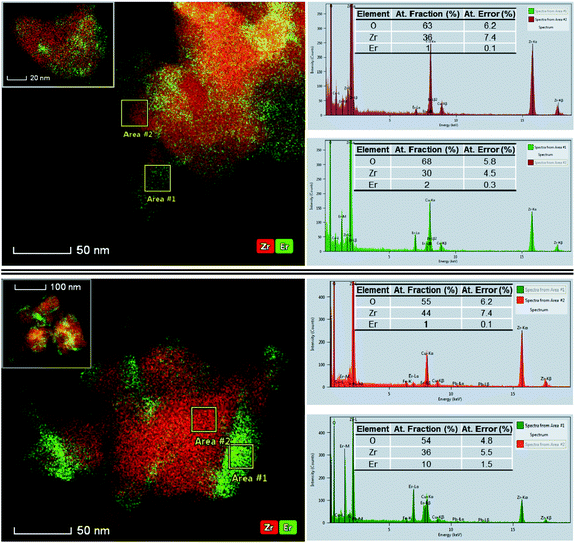
To analyze the Er distribution across the 3Er,Li–ZrO₂ series, we employed a Thermo Fisher Scientific Themis Z microscope equipped with a Schottky field-emission electron gun operating at 300 kV and with both probe and image aberration correctors. HAADF–STEM imaging shows that as a general feature, all four sample nanoparticles form mild agglomerates that have particle sizes varying from 10 to 80 nm and a heterogeneous morphology and contain defects (Fig. S2†). STEM and EDX spectroscopy mapping of Li-free, 3Er–ZrO₂ (pure tetragonal structure based on XRD, Fig. 1) shows a rather homogenous distribution of Er in a tetragonal zirconia lattice (images not included). Li addition induces an inhomogeneous Er distribution likely towards the grain surface, with the substitutional mechanism (Er substituting for Zr host cations) being directly confirmed by atomic-resolution HAADF–STEM (Fig. S3†). Compared to standard TEM, STEM operated in the HAADF mode is very sensitive to the atomic number (Z) contrast, scaling roughly proportional to the square of the atomic numbers, Z.^31,32 One Er (Z = 68) atom will thus appear roughly 2.5 times brighter than the Zr atom (Z = 40) that it is expected to substitute for, which highlights the sensitivity of TEM for detecting single dopant atoms.

The comparison of the EDX mapping images of the samples with the lowest and highest Li contents, Er,5Li–ZrO₂ and Er,15Li–ZrO₂, respectively, illustrated in Fig. 2 evidences that the former sample is slightly depleted in Er in two selected areas of interest (with local concentrations of 1 and 2%, both of which are below the nominal Er concentration of 3%).

Fig. 2 EDX mapping of small agglomerates of Er,5Li–ZrO₂ (top) and Er,15Li–ZrO₂ (bottom) evidencing moderately (5% Li, 53% tetragonal and 47% monoclinic by XRD) to strongly (15% Li, pure monoclinic by XRD) inhomogeneous Er distribution, respectively. The trend is confirmed by the EDX mapping of additional small agglomerates of Er,5Li–ZrO₂ and Er,15Li–ZrO₂ illustrated as insets.

The areas depleted in Er were indexed as the monoclinic phase after the measurement of the interatomic spacings in the atomic-resolution HAADF–STEM images (Fig. S4 and S5†). The end series sample, 3Er,15Li–ZrO₂ (pure monoclinic based on XRD, Fig. 1), shows local concentrations that vary as large as one order of magnitude (1 and 10%). Fig. 2 and the EDX tomography results in Fig. S6† show that Er-rich regions tend to concentrate at the nanocrystal surfaces (ESI video†), leaving the monoclinic domains with an Er concentration of approximately 1%. The trend is verified by measurements with several agglomerates, with additional images included in the insets in Fig. 2.

The indexing of the atomic-resolution STEM images indicated mainly the monoclinic phase for all Li-containing samples, in contradiction with XRD data which indicate significant tetragonal phase contents of ca. 53 and 36% for the 3Er,5Li sample and the 3Er,10Li sample, respectively (Fig. 1). This discrepancy is probably due to the TEM sample preparation and particle screening during characterization, since only the small domains are suitable for atomic-resolution imaging and crystallographic indexing.³³ Although no pure tetragonal nanoparticles could be identified by TEM characterization, an example of a monoclinic nanoparticle with Er-enriched tetragonal phase “caps” was fully characterized by simultaneous STEM–HAADF (Fig. 3a) and atomic-resolution integrated differential phase contrast (iDPC)–STEM²⁴ (Fig. 3b). Since with STEM–ADF the square of the electrostatic potential is imaged, the resulting contrast ratio between Zr and O is roughly the square of their atomic numbers (Z), 40/8 ≈ 25.^31,32 On the other hand, with iDPC–STEM the electrostatic potential itself is imaged which is roughly linear in Z as 5. While the dynamic range of the detector is large enough to accommodate a factor of 25, achieving the necessary signal to noise ratio is challenging being bypassed in iDPC–STEM.²⁴ In this way, the combination of iDPC–STEM with EDX mapping (Fig. 3c, see also Fig. S4†) enabled the unambiguous assignment of the Er-depleted and Er-enriched regions to monoclinic and tetragonal structures. The two structural phases originate from the same fluorite (CaF₂) structure:³⁴ in the monoclinic phase, Zr is seven-fold coordinated with different Zr–O bonds in C₁, low local symmetry, while in the tetragonal phase, Zr assumes an eight-fold coordination with two types of Zr–O bonds in a higher, D_2d local symmetry.³⁵ As shown in Fig. 1, the cell parameters of monoclinic ZrO₂ exceed those of the tetragonal polymorph with a significant volume expansion of ca. 4% relative to the tetragonal lattice (see also Fig. S1†). As also illustrated in Fig. S1,† with the increase of the Li concentration, opposing shifts of tetragonal and monoclinic peaks were measured, though no definite trend was evidenced.

Fig. 3 Coexistence of monoclinic (Er-depleted) and tetragonal (Er-enriched) polymorphs in a single nanocrystal of 3Er,10Li–ZrO₂ revealed by (a) STEM–HAADF and (b) atomic-resolution integrated differential phase contrast (iDPC)–STEM imaging. (c) EDX mapping. Also included in (b) are the schemes of tetragonal and monoclinic lattice structures.

When both phases contact each other directly, the tetragonal phase likely compresses the monoclinic phase while the monoclinic one will expand the tetragonal one in the capping configuration illustrated in Fig. 3 and Fig. S4.† A similar cap-like configuration was evidenced by high-resolution TEM in non-doped nanocrystalline ZnS, where pure wurtzite particles could not be separately distinguished but observed only as caps on the sphalerite polymorph.³⁶ The STEM–HAADF and atomic-resolution iDPC–STEM images in Fig. 3a and b represent rare^37,38 evidence of polymorph coexistence in a ZrO₂ nanocrystal and to the best of the authors’ knowledge, this is the first such example for rare-earth doped ZrO₂. Considering that all the 3Er,Li series samples were obtained by impregnating the same batch of preformed 3% Er–ZrO₂ with Li at concentrations of 0, 5, 10 and 15% and subjected to identical thermal treatment, as well as the XRD and TEM data illustrated in Fig. 1–3, it is conceivable to conclude that the tetragonal-to-monoclinic phase transformation is due to Li-induced non-uniform Er distribution. The mechanisms of tetragonal/cubic phase stabilization in ZrO₂ by trivalent rare-earth ions are well established, being attributed to the generation of oxygen vacancies adjacent (nearest neighbor) to the Zr cations (or the next nearest neighbor to the trivalent stabilizer).³⁴ Er-depleted (<3%) zirconia nanograins are less stable and more likely to undergo transformation due to the reduced number of oxygen vacancies and these act as preferential nucleation sites for the transition from the tetragonal to the more thermodynamically stable monoclinic phase.¹⁶ Size (ionic radii of Er exceed by ca. 20% of those of Zr in both tetragonal and monoclinic coordination, Table S1†), and charge mismatches with the host Zr cation and, especially, the oxygen vacancies induced by Li probably drive Er segregation to positively charged interfaces where the amount of oxygen vacancies is significant.^39,40 The influence of Li doping on the phase structure of upconversion hosts was recently reported for NaYF₄ ^25,41 where for the Li content above 40%, the phase changed from hexagonal to cubic. The reasoning in this case was that due to the steric effect, Y could not coordinate with F ligands with the same coordination number as without Li doping, driving thus the phase transition.⁴¹ The EDX mapping in Fig. 3c illustrates the enrichment of Er ions and depletion of O²⁻ ions in the tetragonal cap regions, considering that the depletion of O²⁻ ions is equivalent to the accumulation of oxygen vacancies.⁴² Although the visualization of EDX mapping displayed in Fig. 3c seems to show that the Er mapping contrast exhibits uniform distribution in either the monoclinic or tetragonal phase, when analyzed in 3D (see the ESI video and Fig. S6†) it clearly indicates the surface segregation of the Er dopant.

Nevertheless, the distribution of oxygen vacancies is expected to be even more complex⁴⁰ due to the coexistence of aliovalent Er³⁺/Li⁺ metals. Dedicated studies will need to elucidate the actual location of the Li light element (Z = 3) in the ZrO₂ lattice, exploiting, for example, Li strong electron energy loss spectra (EELS) signals in STEM–EELS imaging.⁴³

2.3. Experimental design for the analysis of upconversion emission: phase selectivity, reference series and variable parameters

To correlate the non-uniform Er doping effects determined by TEM to the UPC emission of the Er dopant, a strict separation of the phase contributions to UPC emission across the 3Er,Li series should be first established. Cw excitation at 975 nm (corresponding to the ⁴I_15/2–⁴I_11/2 absorption transition) leads to the well-known Er emissions in green at 560 nm and red and 680 nm, related to the ²H_11/2, ⁴S_3/2–⁴I_15/2 and ⁴F_9/2–⁴I_15/2 transitions, respectively (Fig. 4a). The UPC emission intensity, which is observable by the naked eye reaches its maximum at 5% Li, with only a modest enhancement of ×2–2.5 times relative to Li free 3Er–ZrO₂. The emission color evolves from yellow-green (3Er,0Li) to pure green (3Er,15Li). To separate the Er absorptions responsible for the tetragonal and monoclinic type emissions, we measured the UPC excitation spectra monitoring the red emission at 680 nm (0, 5, 10Li) and green emission at 560 nm (5, 10 and 15Li) (see details in the ESI†) when scanning the Er absorption profile in the 940 to 1000 nm range. The UPC excitation spectra illustrated in Fig. 4b and c show that cw excitation at 975 nm (spectral line width of 5 nm) leads inherently to a superposition of emission characteristic of the two phases in the mixed phase samples. In contrast, narrow laser excitation at 952 and 982 nm, provided by ns OPO laser with a spectral line width of 0.5 nm, allows the tetragonal and monoclinic like upconversion emission, respectively, to be spectrally “fingerprinted”.

Fig. 4 (a) Evolution of the non-selective UPC emission (cw laser diode excitation at 975 nm) and UPC excitation spectra (b, c) across the 3Er,Li series. The emission was monitored at 680 nm (0, 5 and 10Li) (b) and 560 nm (5, 10 and 15Li), (c) using a short delay of 10 μs and wide gate of 3 ms. Next to (a) are included the digital images taken under ambient light conditions and a schematic representation of phase transformation across 3Er,Li series that considers both TEM data (see text above) and phase selective UPC (see text below).

With the phase selective excitation conditions being accurately determined, we identified the variable parameters that influence the phase selective UPC emission properties (such as shape, intensity and excited state dynamics). The emission shape is described by the well-known red-to-green emission ratio (R/G), which corresponds to the intensity ratio of the 680 nm- and 560 nm-based emissions. R/G reflects the balance between the radiative and nonradiative transition probabilities of Er and is quite sensitive to the Er concentration,⁴⁴ crystallite/particle size,⁴⁵ local symmetry,⁴⁶ morphology⁴⁷ or particle aggregation.⁴⁸ To understand in detail how the Er concentration influences the UPC emission shape/color, intensity and excited-state dynamics, we synthesized an additional Li-free Er series, with the Er concentration intentionally varied from 1 to 10%, covering the extreme local concentrations observed by TEM (Fig. 2). The 3–10% Er samples were fully stabilized in the tetragonal phase following annealing at 750 °C, displayed a small crystallite size (7.2–9.7 nm) and were used as tetragonal reference samples. The 1% Er–ZrO₂ sample transformed into a full monoclinic phase following annealing at 1000 °C (crystallite size of 20 nm) and was used as a monoclinic reference sample. Structural and elemental analyses for this reference series are summarized in Fig. S8 and Table S2.† A further set of experiments was performed to check the possibility of local symmetry distortion by the Li codopant. To this aim, we have synthesized a new Eu based series, 3Eu, xLi (x = 0, 5, 10 and 15%) where Eu luminescence is exploited as a local probe.^49,50 The XRD patterns of the 3Eu, Li series follow the same trend as that of the 3Er,Li series, in terms of crystallite size and phase content, confirming the reproducibility of the used synthesis route (data not included). As shown in Fig. S7,† the luminescence of Eu coincides with the well-known fingerprint emissions in tetragonal or monoclinic ZrO₂ ^51,52 or is composed of a superposition of these, which confirms that Li destabilizes the tetragonal phase without modifying the local symmetry around Er.^51,52 The heterogeneous morphology and aggregation level observed by TEM (Fig. S2†) did not significantly differ across 3Er,Li series and therefore was disregarded as a variable parameter. Since all samples (both Er,Li and reference series) have a similar surface area of only a few m² g⁻¹ the surface effect (surface Er experiences enhanced interaction with defects, surface states and impurities compared to core Er⁵³) was neglected. Finally, considering the sensitivity of R/G to pump power excitation density⁵⁴ and excitation wavelength⁴⁴ all phase selective measurements across tetragonal and monoclinic domains were performed under similar conditions. The setup is centered on a tunable laser that outputs ∼5 ns pulses at the 10 Hz repetition rate with an average energy density of ca. 40 mJ cm⁻². All emission/excitation spectra and decays represent the average of three up to five measurements (see the ESI†).

2.4. Correlating dopant distribution events (enrichment, depletion and segregation) with the upconversion emission (shape, intensity and excited-state dynamics)

2.4.1. Correlating TEM data and upconversion emission in the tetragonal domains. As discussed previously, the tetragonal domains could not be separated by TEM, as these apparently coexist with the monoclinic ones in the “capping” configuration illustrated in Fig. 3. Since the nominal Er concentration is constant across the entire 3Er,Li series while TEM analysis demonstrated a dilution of Er concentration in the monoclinic domains with Li addition (Fig. 2), Er enrichment with Li addition is anticipated to occur in the tetragonal domains and confirmed by the UPC measurements discussed below. Fig. 5 blue panel illustrates the evolution of R/G, UPC emission spectra and intensity with Li addition under tetragonal phase selective excitation at 952 nm. The R/G was also determined from the UPC emission spectra measured using broad excitation from 950 to 990 nm, with the “tetragonal” region defined by the rectangle in Fig. 5a blue panel. The R/G evidently increases with Li addition, with a maximum increase of ∼2.5 times measured for the 3Er, 10Li sample compared to that of the Li-free sample (Fig. 5a–c blue panel). The maximum UPC emission intensity is measured for the 3Er,5Li sample; further addition of Li (3Er,10Li) reduces the intensity by a factor of 4, below that measured with the Li free 3Er sample (Fig. 5d blue panel). We assume that the inclusion of pure tetragonal 3Er,0Li in the dependencies illustrated in Fig. 5c and d blue panel does not introduce the crystallite size as a variable (tetragonal crystallite size of ∼10 nm for the Li free sample compared to 15–16 nm for the 3Er,5Li and 3Er,10Li) as a smaller particle size usually induces higher R/G and reduced intensity compared to bigger particles.⁴⁵ The increase of R/G with the Er concentration is well-documented in the literature being assigned to shortening of the distance between Er ions, which facilitates the cross-relaxation processes (e.g., ⁴I_13/2–⁴I_15/2 ↔ ⁴I_11/2–⁴F_9/2 and ⁴I_11/2–⁴F_9/2 ↔ ⁴F_7/2–⁴F_9/2) leading thus to enhanced red emission.^44,55,56

Fig. 5 Blue panel: Evolution of the phase-selective UPC emission shape and intensity across tetragonal domains of 3Er,Li series. (a) Excitation wavelength dependency of the red to green emission ratio (R/G) around 952 nm. (b) UPC emission spectra. Digital images visualize the corresponding color and intensity changes. (c) R/G and (d) UPC emission intensity. Yellow panel: Evolution of the UPC emission shape and intensity across the tetragonal reference series: (a) UPC emission spectra; (b) R/G and (c) UPC emission intensity. Note: The dependencies in (c) were obtained by data interpolation.

In addition to the UPC emission shape, the UPC emission dynamics is also a strong indicator of Er distribution effects. As shown in Fig. 6 blue panel, the UPC emission decay of the 3Er,10Li sample is clearly faster than the decay of the 3Er,5Li sample, with the average lifetime of 0.19 ms compared to 0.3 ms, respectively (all emission decays were monitored at 680 nm, corresponding to the red emitting ⁴F_9/2 level). All UPC decays are non-exponential as a result of the complex superposition of various populating/depopulating energy transfer processes of red and green emitting levels.^57,58 The average PL lifetimes (τ_avg) used as a figure of merit were estimated by integrating the area of the experimental decay curves via the equation

where the radiative and nonradiative relaxation rates (K_r and K_nr)/lifetimes are linked to the quantum yield (QY) as . Usually, the relative contributions of the radiative and nonradiative relaxation pathways cannot be separated without the estimation of the quantum yield.⁵⁹ However, the correspondence between the UPC decays/lifetimes (Fig. 6a blue panel) and intensity (Fig. 5d blue panel), both diminished in the 3Er,10Li relative to that in the 3Er,5Li sample, suggests that the nonradiative relaxation rate of 3Er,10Li is enhanced. The dependency of UPC emission dynamics on the Er concentration is confirmed with the tetragonal reference series (Fig. 6a yellow panel) as the average lifetimes of the red level at 680 nm decrease from ∼0.14 ms (3% Er) to 0.04 ms (10% Er), see also Table S3.† Besides the UPC emission shape, intensity and dynamics, the dopant distribution determines the channels⁶⁰ or nature of UPC mechanism populating the emitting levels, where ground state absorption is followed by excited state absorption (GSA/ESA) or energy transfer (ETU).⁴⁴Fig. 6b blue panel compares the emission dynamics measured downconversion (DC, excitation at 380 nm) and UPC excitation at 952 nm.

Fig. 6 Blue panel: Evolution of the phase-selective UPC emission dynamics across tetragonal domains of 3Er,Li series. (a) Comparison between UPC emission decays of 3Er,5Li–ZrO₂ and 3Er,10Li–ZrO₂; (b) comparison between the emission decays measured under upconversion and downconversion (DC) excitation. Yellow panel: Tetragonal reference series: (a) comparison between the emission decays measured under UPC and downconversion (DC, at 380 nm) excitation; (b) schematic representation of energy levels and mechanisms involved in the “tetragonal” UPC emission. All the emission decays were measured at 680 nm corresponding to the red emitting ⁴F_9/2 level.

The obvious prolonging of the UPC decays compared to those under DC excitation in the tetragonal 3Er,Li domains points to a major contribution of the Er–Er energy transfer (ETU) relative to the ground state absorption followed by the excited state absorption (GSA/ESA). It should be noted that, due to the lack in phase selectivity in DC excitation, the DC decays of the mixed phase ZrO₂ are artificially shortened due to the superposition of tetragonal and monoclinic decays. The effect is grounded in the parity-forbidden nature of lanthanide f–f transitions known as the Laporte selection rule:^61,62 Er in the low symmetry (C₁) monoclinic sites displays an enhanced radiative transition probability (that is, shorter radiative lifetimes) compared to Er in the higher (D_2d) tetragonal sites.⁶³ As such, the “true” downconversion decays should approach more the upconversion decays than is the case illustrated in Fig. 6b blue panel.

The data above show how slight Er enrichment in the tetragonal domains (above the nominal value of 3%) which is equivalent to shorter Er–Er distances (below that of 10.4 Å, estimated under the very rough approximation of an ideal, uniform Er distribution, see the ESI†) is reflected in UPC emission properties. As a result of enhanced cross-relaxations, R/G increases, the UPC emission intensity increases and then decreases above a certain value of Er enrichment and UPC decays accelerate, with all three dependencies following closely those of the tetragonal reference series (Fig. 5 and 6 yellow panel). The efficiencies of the energy transfers that either enhance or quench the UPC emission increase with the Er concentration typically with a r⁻⁶ dependency on the average distance Er–Er (in the common Förster dipole–dipole interaction mechanism⁶⁴). The interplay of gain via “good” and loss by “bad” energy transfers limits the optimum Er concentration in the tetragonal reference series to 7% at an average Er–Er distance of 7.93 Å. Above this concentration value (i.e. at 10% Er), the cross-relaxation is so efficient that it leads to an intensity drop by 70% while the R/G continues to increase by 50% relative to 7% Er (Fig. 5b and c yellow panel). For the 3Er,Li series, the optimum Er enrichment is measured with the 3Er,5Li sample. Further Er enrichment induced by the Li content in the 3Er,10Li sample leads to strong concentration quenching with a resulting emission intensity falling even below that of the Li free, 3Er sample, despite that the crystallite size of the latter sample is smaller by a factor of almost two (10 nm relative to 16 nm).

Er enrichment in the tetragonal domains is also responsible for the progressive broadening of the UPC emission spectra with Li. The UPC emission spectra of 3Er,5(10)Li are broader by roughly 3–4 nm than those of the Li free sample (Fig. S9†), although the reverse trend would be expected⁶⁵ based on the particle size considerations. The observed Er–Er clustering in the tetragonal domains are therefore of a “true” clustering nature, which differs from that of Er–Er pairs formed in a statistical distribution, usually characterized by distinct absorption and emission lines.^66,67 The more common chemical clustering is reported in the literature, especially for the well investigated Er,Yb codoped yttrium fluoride nanoparticles.⁶⁸ Finally, the observation of a weak but discernible tetragonal UPC emission (R/G of around 2.15) in the 3Er,15Li (that is purely monoclinic by XRD, Fig. 1) is highlighted with “*” in Fig. 5b and c blue panel. This result confirms the outstanding sensitivity of the UPC emission to the presence of a subtle amount of “impurity” domains that remain unrevealed by XRD (instrumental sensitivity of a few %) or TEM (limited sampling volume). Considering the TEM data and upconversion emission results, a schematic representation of Er distribution across the 3Er,Li series is attempted in Fig. 4.

2.4.2. Interaction between “tetragonal Er” and “monoclinic Er” in a single nanoparticle. The spatial closeness of Er in the tetragonal and monoclinic polymorphs coexisting in a single nanoparticle (Fig. 3), together with their strongly overlapping characteristic emission and absorption spectra, may facilitate an interpolymorph Förster energy transfer.⁶⁴ Beyond relevancy for fundamental knowledge, such an energy transfer would alter the trends of UPC emission properties determined across tetragonal and monoclinic domains due to the loss in phase selectivity. We analyzed two spectroscopic rulers for the energy transfer, the excitation spectra and the emission decays.

The UPC excitation spectra monitoring the red emission (Fig. 4b) (which is largely predominant for the tetragonal Er, see also Fig. 5a and b blue panel) show some interference from the monoclinic absorption features (Fig. 4c). This observation suggests the presence of an energy transfer from monoclinic Er to tetragonal Er in the donor–acceptor scheme, respectively. However, as discussed later in Section 2.4.3, the contribution from the relatively weaker red emission characteristic of the monoclinic phase in the same spectral range (ca. 625–700 nm), (Fig. 7b) cannot be totally neglected. Next, the acceleration of UPC emission decays of tetragonal Er with Li addition (Fig. 6 blue panel) that is responsible for Er dilution in the monoclinic domains (Fig. 2) discards the possibility of an energy transfer from tetragonal Er to monoclinic Er. Conversely, as shown in Section 2.4.3, the possibility of an energy transfer from monoclinic Er to tetragonal Er is negligible based on the evolution of Er UPC decays in the monoclinic domains (Fig. 7c). On the other side, the coexistence of two polymorphs in a single nanoparticle can lead to the appearance of new luminescence lines, as found for coexisting (undoped) wurtzite and zinc blende domains in a single nanoparticle.⁶⁹ In our case, due to large strains accompanying the tetragonal to structural transformation, the local atomic environment may be no longer monoclinic in the vicinity of the boundary.⁷⁰ As such, new Er emission lines that cannot be related to either the monoclinic or tetragonal phase can form. Such a possibility was checked in a further set of experiments using Eu as the luminescent probe. The comparison between Eu luminescence in the mixed phase samples 3Eu, 5Li and 3Eu, 10Li and the physical mixtures of pure tetragonal and monoclinic Eu–ZrO₂ (percentage factors of 53/47 and 36/64, respectively, similar to phase contents listed in Fig. 1, data not shown) discarded the presence of additional luminescence lines. In conclusion, “tetragonal Er” and “monoclinic Er” do not interact by energy transfer nor do they induce additional luminescence lines, distinct from those measured with pure tetragonal and monoclinic nanoparticles.

Fig. 7 Evolution of the phase-selective UPC emission shape and dynamics across monoclinic domains of 3Er,Li series. (a) Excitation wavelength dependency of the red to green emission ratio (R/G) around 982 nm; (b) UPC emission spectra. Also included is the UPC spectrum of the reference monoclinic sample. Digital images in (b) visualize the corresponding color and intensity changes; (c) comparison between the UPC emission decays of 3Er,5Li–ZrO₂ and 3Er,10Li–ZrO₂. (d) Comparison between the emission decays of 3Er,15Li–ZrO₂ under UPC and downconversion (DC, at 380 nm) excitation. All the emission decays were measured at 560 nm corresponding to the green emitting ⁴S_3/2 level. Schematic representation of energy levels and mechanisms involved in “monoclinic” UPC emission.

2.4.3. Correlating TEM data and upconversion emission in the monoclinic domains. The EDX mapping evidenced areas depleted in Er, with local concentrations of 1 and 2% in the 3Er,5Li and 1% in 3Er,15Li indexed as the monoclinic phase in the atomic-resolution HAADF–STEM images (Fig. 2). Since the nominal Er concentration of 3% represents the minimum value required for the tetragonal phase stabilization, a small reduction in the amount of oxygen vacancies due to Er depletion is enough to phase revert the tetragonal domains to the more thermodynamically stable monoclinic phase.^16,34 The R/G characteristic of Er UPC emission in the monoclinic domains is strongly sub unitary (Fig. 7a) with a predominant green emission characteristic of the ⁴S_3/2 level also confirmed by the emission spectrum of the monoclinic reference sample (1% Er–ZrO₂) in Fig. 7b.

With the increase of the Li concentration from 5% to 10% and 15%, R/G decreased from 0.26 to 0.19 and 0.08 respectively, sustaining a dilution of Er in the monoclinic sites in agreement with TEM observations (Fig. 2). The UPC intensity decreased with Li addition, from 1 (5% Li) to 0.7 (10% Li) and 0.12 (15% Li). This trend is further supported by the slightly longer UPC decay at 560 nm of 3Er,10Li than that of 3Er,5Li (average lifetimes of 0.034 ms compared to 0.026 ms), Fig. 7c. The ⁴S_3/2 level is known to be subjected to more efficient cross-relaxation than the ⁴F_9/2 level, due to the near perfect energy matching of the involved intermediary levels (for example, via⁴S_3/2, ⁴I_15/2–⁴I_13/2, ⁴I_11/2 ^71,72). Since with Li addition, the Er UPC decays in the monoclinic domains are slightly lengthened, while the Er local concentration in the tetragonal domains is enhanced, this confirms further the absence of the energy transfer from monoclinic Er to tetragonal Er in a potential donor–acceptor scheme.

In the pure monoclinic 3Er,15Li–ZrO₂, HAADF–STEM and EDX mapping tomography (Fig. 2b, Fig. S6 and ESI video†) identified local Er concentrations that varied by one order of magnitude (1 and 10 at%) in the monoclinic domains and surface regions, respectively.

As shown in Fig. 7d, the almost perfect superposition of the emission decays under DC (excitation at 380 nm) and UPC excitation converging to an average lifetime of 0.032 ms confirms the population of the ⁴S_3/2 level exclusively by ground-state absorption followed by excited state absorption (GSA/ESA), (see also scheme in Fig. 7d).⁴⁴ At a concentration level of around 1%, the average Er–Er distance at 15.05 Å (again, estimated under very rough approximation of an ideal, uniform Er distribution, ESI†) is too large to induce an effective energy transfer that is apparently still observable for 5 and 10% Li (as speculated from the “lifting” effect of decay tails represented in Fig. S10†). The data above show how slight Er dilution from the nominal concentration, (basically the Er concentration is fluctuating around 1–2%) triggers measurable changes in the UPC emission shape, intensity and dynamics.

2.4.4. Surface segregated dopants are silent in upconversion. Though EDX mapping identified segregation areas where the Er local concentration was as high as 10% (Fig. 3), within the instrumental detection limit of XRD (few %), the presence of a segregated Er oxide phase (Er₂O₃, Er–Li–O compounds or possible Er₂Zr₂O₇ ¹⁹) could not be detected (Fig. 1). Concerning the optical response, the emission of surface-segregated Er species is expected to be shape distinct (broader) and shorter lived compared to that of Er in the monoclinic lattice sites, as a result of strong luminescence-quenching processes induced by cross-relaxation and/or energy migration to surface defects.^2,7 We have checked this by time-gated single photon UPC measurements⁷³ using a short delay (ca. 1 μs) along with a small gate (up to few tens of μs) that favor the detection of minor, short-lived species across the 975 to 990 nm excitation range (Fig. 7a), see also details in the ESI.† The resulting emission shape and kinetics well resembled that of the monoclinic type characteristic of the 3Er,15Li sample and therefore, we conclude that segregated Er is silent in upconversion.

2.4.5. Relevance of combinatorial TEM and upconversion emission characterization for other functional oxides. Although the demonstration has been performed with a single material, the approach can be scalable across a wide range of functional oxides supporting the lanthanide emitter as the dopant. More broadly, with the support of advanced TEM techniques, the outstanding sensitivity of the Er upconversion emission shape, intensity and kinetics to subtle deviations of a few percent from the nominal concentration (itself in the diluted regime), promotes this lanthanide as an excellent luminescent probe for dopant distribution. An example at hand is the widely used electrolyte yttrium stabilized ZrO₂, YSZ^19,74 for which Z-contrast imaging is not suitable to identify the distribution of Y (ΔZ relative to Zr equals 1).⁷⁵ As such, Er can be used as a strain equivalent (similar ionic radii of 1.004 to 1.019 Å) but high Z (ΔZ = 28) and luminescent substitute for the optically inert Y. Other examples include the effects of trivalent doping concentration and distribution on the still debated kinetics mechanism of the anatase to rutile transition of TiO₂ ⁷⁶ or especially, the dopant distribution effects in the diluted magnetic semiconducting oxides.⁷⁷ Among these, anatase TiO₂, ZnO, and SnO₂ allow substitutional doping with Er lanthanide, at least in the diluted regime,^78–80 that can be further used as a luminescent, high Z substitute for 3d transition metal dopants.

3. Conclusions

We integrated advanced TEM techniques and phase selective UPC emission to successfully resolve the dopant distribution across a complete phase transformation at the ensemble and single nanoparticle level. The optical signatures of Er characteristic of these structural phases were identified under precise spectral/phase-selective excitation. Small deviations from doping uniformity could be assigned to clear changes in the Er UPC emission (shape, intensity and excited-state dynamics) across tetragonal to monoclinic phase transformation. Rare evidence of a heterogeneous (Er enriched/Er depleted) distribution leading to the coexistence of two polymorphs in a single nanoparticle is revealed by phase and Z contrast TEM while the absence of the energy transfer between Er of the two polymorphs was confirmed by UPC emission measurements. Collectively, our findings reveal the outstanding potential of combining advanced TEM and UPC emission for imaging subtle deviations from uniform doping in a large variety of functional nanomaterials.

Author contributions

CT, DS and SL conceived and designed the experiments. CC and MF performed the synthesis and characterised the samples. DA and CC contributed equally. DA performed the luminescence measurements and analysed the data. CT, DS and SL co-wrote the paper.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

DA, CC and CT acknowledge CNCS-UEFISCDI through project PN-III-P4-ID-PCE-2016-0305, contract PCE 67/2017 for the financial support. MF acknowledges the Romanian Ministry of Research and Innovation through the Core Program PN18-110201 and project PN-III-P4-ID-PCE-2016-0692 for the partial financial support.

Notes and references

1. E. Chan, E. Levy and B. Cohen, Adv. Mater., 2015, 27, 5753–5761.
2. S. Han, R. Deng, X. Xie and X. Liu, Angew. Chem., Int. Ed., 2014, 53, 11702–11715.
3. S. Wen, J. Zhou, K. Zheng, A. Bednarkiewicz, X. Liu and D. Jin, Nat. Commun., 2018, 9, 2415.
4. S. Fischer, N. Bronstein, J. Swabeck, E. Chan and A. Alivisatos, Nano Lett., 2016, 16, 7241–7247.
5. S. Wilhelm, ACS Nano, 2017, 11, 10644–10653.
6. C. Dong, J. Pichaandi, T. Regier and F. van Veggel, J. Phys. Chem. C, 2011, 115, 15950–15958.
7. X. Li, R. Wang, F. Zhang and D. Zhao, Nano Lett., 2014, 14, 3634–3639.
8. D. Gargas, E. Chan, A. Ostrowski, S. Aloni, M. Altoe, E. Barnard, B. Sanii, J. Urban, D. Milliron, B. Cohen and P. Schuck, Nat. Nanotechnol., 2014, 9, 300–305.
9. X. Xu, C. Clarke, C. Ma, G. Casillas, M. Das, M. Guan, D. Liu, L. Wang, A. Tadich, Y. Du, C. Ton-That and D. Jin, Nanoscale, 2017, 9, 7719–7726.
10. A. Pilch, C. Wurth, M. Kaiser, D. Wawrzynczyk, M. Kurnatowska, S. Arabasz, K. Prorok, M. Samoc, W. Strek, U. Resch-Genger and A. Bednarkiewicz, Small, 2017, 13, 1701635.
11. D. Hudry, I. A. Howard, R. Popescu, D. Gerthsen and B. S. Richards, Adv. Mater., 2019, 1900623.
12. D. Hudry, D. Busko, R. Popescu, D. Gerthsen, A. Abeykoon, C. Kubel, T. Bergfeldt and B. Richards, Chem. Mater., 2017, 29, 9238–9246.
13. J. Xu, D. Tu, W. Zheng, X. Shang, P. Huang, Y. Cheng, Y. Wang and X. Chen, Adv. Sci., 2018, 5, 1800766.
14. Q. Ma, J. Wang, Z. Li, X. Lv, L. Liang and Q. Yuan, Small, 2019, 1804969.
15. H. Xiang and Y. Chen, Small, 2019, 15, 1805339.
16. J. Chevalier, L. Gremillard, A. Virkar and D. Clarke, J. Am. Ceram. Soc., 2009, 92, 1901–1920.
17. Y. Kim, T. Holme, T. Gur and F. Prinz, Adv. Funct. Mater., 2011, 21, 4684–4690.
18. X. Guo and R. Waser, Prog. Mater. Sci., 2006, 51, 151–210.
19. B. Feng, T. Yokoi, A. Kumamoto, M. Yoshiya, Y. Ikuhara and N. Shibata, Nat. Commun., 2016, 7, 11079.
20. P. Kelly and L. Rose, Prog. Mater. Sci., 2002, 47, 463–557.
21. S. Guan, X. Zhang and Z. Liu, J. Am. Chem. Soc., 2015, 137, 8010–8013.
22. K. Abel, J. Boyer, C. Andrei and F. van Veggel, J. Phys. Chem. Lett., 2011, 2, 185–189.
23. W. Bian, Y. Lin, T. Wang, X. Yu, J. Qiu, M. Zhou, H. Luo, S. Yu and X. Xu, ACS Nano, 2018, 12, 3623–3628.
24. I. Lazic, E. Bosch and S. Lazar, Ultramicroscopy, 2016, 160, 265–280.
25. D. Chen and Y. Wang, Nanoscale, 2013, 5, 4621–4637.
26. J. Xiong, C. Jiao, M. Han, W. Yi, J. Ma, C. Yan, W. Cai and H. Cheng, RSC Adv., 2016, 6, 106555–106562.
27. L. Liu, C. Li, Y. Chen, X. Zhang, L. Li and Y. Wang, Mater. Lett., 2012, 79, 75–77.
28. M. Alifanti, B. Baps, N. Blangenois, J. Naud, P. Grange and B. Delmon, Chem. Mater., 2003, 15, 395–403.
29. S. Korf, J. Roos, N. Debruijn, J. Vanommen and J. Ross, Appl. Catal., 1990, 58, 131–146.
30. S. Wang, K. Murata, T. Hayakawa, S. Hamakawa and K. Suzuki, Chem. Commun., 1999, 103–104.
31. A. Howie, J. Microsc., 1979, 117, 11–23.
32. T. Mizoguchi, S. Findlay, A. Masuno, Y. Saito, K. Yamaguchi, H. Inoue and Y. Ikuhara, ACS Nano, 2013, 7, 5058–5063.
33. A. Weibel, R. Bouchet, F. Boulc'h and P. Knauth, Chem. Mater., 2005, 17, 2378–2385.
34. P. Li, I. Chen and J. Pwnnrhahn, J. Am. Ceram. Soc., 1994, 77, 118–128.
35. C. Howard, R. Hill and B. Reichert, Acta Crystallogr., Sect. B: Struct. Sci., 1988, 44, 116–120.
36. F. Huang and J. Banfield, J. Am. Chem. Soc., 2005, 127, 4523–4529.
37. R. Nitsche, M. Rodewald, G. Skandan, H. Fuess and H. Hahn, Nanostruct. Mater., 1996, 7, 535–546.
38. T. I. Mitsuhashi, M. Ichihara and U. Tatsuke, J. Am. Ceram. Soc., 1974, 57, 97–101.
39. W. Lee, J. Han, Y. Chen, Z. Cai and B. Yildiz, J. Am. Chem. Soc., 2013, 135, 7909–7925.
40. H. Lee, F. Prinz and W. Cai, Acta Mater., 2013, 61, 3872–3887.
41. Q. Dou and Y. Zhang, Langmuir, 2011, 27, 13236–13241.
42. W. Lee, H. Jung, M. Lee, Y. Kim, J. Park, R. Sinclair and F. Prinz, Adv. Funct. Mater., 2012, 22, 965–971.
43. A. Gunawan, K. Mkhoyan, A. Wills, M. Thomas and D. Norris, Nano Lett., 2011, 11, 5553–5557.
44. F. Auzel, Chem. Rev., 2004, 104, 139–173.
45. J. Zhao, Z. Lu, Y. Yin, C. Mcrae, J. Piper, J. Dawes, D. Jin and E. Goldys, Nanoscale, 2013, 5, 944–952.
46. H. Dong, L. D. Sun, Y. F. Wang, J. Ke, R. Si, J. W. Xiao, G. M. Lyu, S. Shi and C. H. Yan, J. Am. Chem. Soc., 2015, 137, 6569–6576.
47. H. Dong, L. Sun, Y. Wang, J. Ke, R. Si, J. Xiao, G. Lyu, S. Shi and C. Yan, J. Am. Chem. Soc., 2015, 137, 6569–6576.
48. F. Gonell, A. M. P. Botas, C. D. S. Brites, P. Amorós, L. D. Carlos, B. Julián-López and R. A. S. Ferreira, Nanoscale Adv., 2019, 1, 2537–2545.
49. P. A. Tanner, Chem. Soc. Rev., 2013, 42, 5090–5101.
50. C. Tiseanu, V. Parvulescu, D. Avram, B. Cojocaru, M. Boutonnet and M. Sanchez-Dominguez, Phys. Chem. Chem. Phys., 2014, 16, 703–710.
51. L. Chen, Y. Liu and Y. Li, J. Alloys Compd., 2004, 381, 266–271.
52. C. Tiseanu, B. Cojocaru, V. Parvulescu, M. Sanchez-Dominguez, P. Primus and M. Boutonnet, Phys. Chem. Chem. Phys., 2012, 14, 12970–12981.
53. A. Podhorodecki, M. Banski, A. Noculak, B. Sojka, G. Pawlik and J. Misiewicz, Nanoscale, 2013, 5, 429–436.
54. A. Nadort, J. Zhao and E. Goldys, Nanoscale, 2016, 8, 13099–13130.
55. L. Yan, B. Zhou, N. Song, X. Liu, J. Huang, T. Wang, L. Tao and Q. Zhang, Nanoscale, 2018, 10, 17949–17957.
56. M. Soares, T. Holz, F. Oliveira, F. Costa and T. Monteiro, RSC Adv., 2015, 5, 20138–20147.
57. J. Bergstrand, Q. Liu, B. Huang, X. Peng, C. Würth, U. Resch-Genger, Q. Zhan, J. Widengren, H. Ågren and H. Liu, Nanoscale, 2019, 11, 4959–4969.
58. P. May and M. Berry, Methods Appl. Fluoresc., 2019, 7, 023001.
59. C. Wurth, S. Fischer, B. Grauel, A. Alivisatos and U. Resch-Genger, J. Am. Chem. Soc., 2018, 140, 4922–4928.
60. L. Sun, L. Li, R. Gao, K. Tang, L. Fu, X. Ai and J. Zhang, Phys. Chem. Chem. Phys., 2018, 20, 17141–17147.
61. G. S. Ofelt, J. Chem. Phys., 1962, 37, 511.
62. B. R. Judd, Phys. Rev., 1962, 127, 750.
63. G. Teufer, Acta Crystallogr., 1962, 15, 1187–1187.
64. T. Förster, Naturwissenschaften, 1946, 33, 166–175.
65. B. Tissue, Chem. Mater., 1998, 10, 2837–2845.
66. L. Agazzi, K. Worhoff and M. Pollnau, J. Phys. Chem. C, 2013, 117, 6759–6776.
67. V. Lupei, A. Lupei, S. Georgescu, T. Taira, Y. Sato and A. Ikesue, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 092102.
68. A. Noculak, A. Podhorodecki, G. Pawlik, M. Banski and J. Misiewicz, Nanoscale, 2015, 7, 13784–13792.
69. D. Denzler, M. Olschewski and K. Sattler, J. Appl. Phys., 1998, 84, 2841–2845.
70. M. Chen, J. Thomas, A. Natarajan and A. Van der Ven, Phys. Rev. B, 2016, 94, 054108.
71. E. De la Rosa-Cruz, L. Diaz-Torres, R. Rodriguez-Rojas, M. Meneses-Nava, O. Barbosa-Garcia and P. Salas, Appl. Phys. Lett., 2003, 83, 4903–4905.
72. F. Liu, E. Ma, D. Chen, Y. Yu and Y. Wang, J. Phys. Chem. B, 2006, 110, 20843–20846.
73. M. Florea, D. Avram, V. A. Maraloiu, B. Cojocaru and C. Tiseanu, Nanoscale, 2018, 10, 18043–18054.
74. J. An, A. Koh, J. Park, R. Sinclair, T. Gur and F. Prinz, J. Phys. Chem. Lett., 2013, 4, 1156–1160.
75. B. Feng, R. Ishikawa, A. Kumamoto, N. Shibata and Y. Ikuhara, Nano Lett., 2019, 19, 2162–2168.
76. S. Zhu, S. Xie and Z. Liu, J. Am. Chem. Soc., 2015, 137, 11532–11539.
77. S. Ogale, Adv. Mater., 2010, 22, 3125–3155.
78. S. Obregon, A. Kubacka, M. Fernandez-Garcia and G. Colon, J. Catal., 2013, 299, 298–306.
79. J. Kong, H. Zhu, R. Li, W. Luo and X. Chen, Opt. Lett., 2009, 34, 1873–1875.
80. X. Wang, X. Kong, Y. Yu, Y. Sun and H. Zhang, J. Phys. Chem. C, 2007, 111, 15119–15124.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9nr04345d

‡ These authors contributed equally.

---