Open Access Article
Open Access ArticleAligned carbon nanotube morphogenesis predicts physical properties of their polymer nanocomposites†
Bharath
Natarajan‡§
 ab,
Itai Y.
Stein§
ab,
Itai Y.
Stein§
 cd,
Noa
Lachman
cd,
Noa
Lachman
 ce,
Namiko
Yamamoto
ce,
Namiko
Yamamoto
 cf,
Douglas S.
Jacobs
d,
Renu
Sharma
cf,
Douglas S.
Jacobs
d,
Renu
Sharma
 g,
J. Alexander
Liddle
g,
J. Alexander
Liddle
 *g and
Brian L.
Wardle
*g and
Brian L.
Wardle
 *c
*c
aCenter for Nanoscale Science and Technology, National Institute of Standards and Technology, Gaithersburg, Maryland 20899, USA
bCorporate Strategic Research, ExxonMobil Research and Engineering, Annandale, NJ 08801, USA
cDepartment of Aeronautics and Astronautics, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA. E-mail: wardle@mit.edu
dDepartment of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA
eDepartment of Materials Science and Engineering, Tel Aviv University, Tel Aviv 6997801, Israel
fDepartment of Aerospace Engineering, The Pennsylvania State University, University Park, Pennsylvania 16802, USA
gPhysical Measurement Laboratory, National Institute of Standards and Technology, Gaithersburg, Maryland 20899, USA. E-mail: james.liddle@nist.gov
First published on 17th June 2019
Abstract
Carbon nanostructure (CNS) based polymer nanocomposites (PNCs) are of interest due to the superior properties of the CNS themselves, scale effects, and the ability to transfer these properties anisotropically to the bulk material. However, measurements of physical properties of such materials are not in agreement with theoretical predictions. Recently, the ability to characterize the 3D morphology of such PNCs at the nanoscale has been significantly improved, with rich, quantitative data extracted from tomographic transmission electron microscopy (TEM). In this work, we use new, nanoscale quantitative 3D morphological information and stochastic modeling to re-interpret experimental measurements of continuous aligned carbon nanotube (A-CNT) PNC properties as a function of A-CNT packing/volume fraction. The 3D tortuosity calculated from tomographic reconstructions and its evolution with volume fraction is used to develop a novel definition of waviness that incorporates the stochastic nature of CNT growth. The importance of using randomly wavy CNTs to model these materials is validated by agreement between simulated and previously-measured PNC elastic moduli. Secondary morphological descriptors such as CNT–CNT junction density and inter-junction distances are measured for transport property predictions. The scaling of the junction density with CNT volume fraction is observed to be non-linear, and this non-linearity is identified as the primary reason behind the previously unexplained scaling of aligned-CNT PNC longitudinal thermal conductivity. By contrast, the measured electrical conductivity scales linearly with volume fraction as it is relatively insensitive to junction density beyond percolation. This result verifies prior hypotheses that electrical conduction in such fully percolated and continuous CNT systems is dominated by the bulk resistivity of the CNTs themselves. This combination of electron tomographic data and stochastic simulations is a powerful method for establishing a predictive capability for nanocomposite structure–property relations, making it an essential aid in understanding and tailoring the next-generation of advanced composites.
1. Introduction
Carbon nanostructures (CNSs), when paired with a polymeric matrix, offer a hybrid material system that can be tailored for many high-value applications in addition to being sustainable,1–6 where both components could be derived from naturally occurring precursors.7,8 For example, epoxy systems reinforced with CNSs, such as graphene,9,10 graphene nano-platelets (GNPs)10 and carbon nanotubes (CNTs),11 were recently shown to have scale-dependent electrical, thermal, and mechanical properties, making them leading candidates for use in applications such as electronic skin, pressure sensors, and protective films.12,13 However, the orders of magnitude discrepancies between physical properties forecasted by well-established theoretical models and the experimentally observed material behavior means that the engineering design tools necessary for the commercial application of these next-generation materials are lacking. Although previous studies have shown that the mechanical, thermal, and electrical properties of CNS reinforced polymeric systems are sometimes adequately described using constant intrinsic CNS properties with, e.g., a rule-of-mixtures approach, such a simplification may not be appropriate when the CNS morphology is altered due to packing evolution. See Fig. 1A–C for plots illustrating property and property prediction results for CNTs, graphene, and GNPs at a variety of volume fractions, which indicate that constant values for the elastic modulus and thermal and electrical conductivities do not yield accurate performance projections when utilized in conjunction with rule of mixtures (Fig. 1A and B) and percolation theory (Fig. 1C). These gaps between predicted and measured material performance also stem from the complete omission or overly simplistic description of the inherent morphology of these materials, particularly how the morphology may evolve with volume fraction (Vf).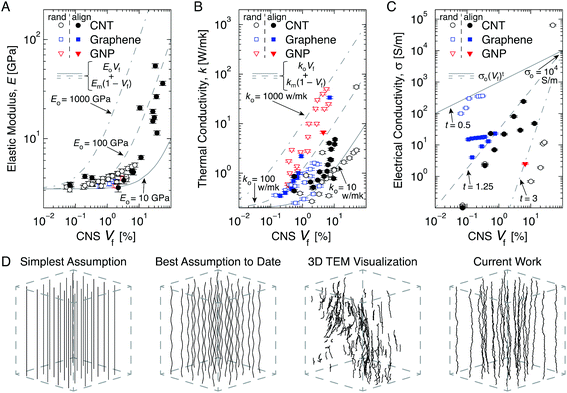 | ||
| Fig. 1 Measured properties of epoxy-based nanocomposites with randomly dispersed or aligned carbon nanotubes (CNTs) and other prevalent carbon nanostructures (CNSs), i.e., graphene and graphene nano-platelets (GNPs) and morphology assumptions in property prediction tools for A-PNCs: (A) Elastic modulus (E) scaling with CNS volume fraction (Vf) for random and aligned CNTs,14–25 graphene,26 and GNPs.27 Fitting with a rule-of-mixtures equation shown in the legend demonstrates that high Vf aligned CNTs exhibit the highest effective CNS modulus, Eo. (B) Thermal conductivity (k) as a function of CNS Vf for random and aligned CNTs,28–32 graphene,33–37 and GNPs.27,31–33,38,39 Fitting with a rule-of-mixtures equation in the legend demonstrates that graphene and GNPs exhibit the highest effective CNS thermal conductivity, ko, while the best overall thermal conductivity k is measured for the highest Vf CNT nanocomposite. (C) Electrical conductivity (σ) as a function of CNS Vf for random and aligned CNTs,30,40–42 graphene,27,43,44 and GNPs.38 Fitting with the power-law equation shown in the legend indicates that although CNT and graphene composites can reach similar σ, since their effective CNS electrical conductivity, σo, is of similar magnitude, their percolation exponent (t) can vary significantly. (A)–(C) demonstrate that although CNT-based polymer nanocomposites could exhibit the best mechanical and transport properties of all the CNSs, precise morphological descriptors are needed to avoid orders of magnitude over- or under-prediction of resultant physical properties. (D) Illustrations of the two commonly assumed morphologies of A-PNCs in comparison to the three-dimensional reconstruction and the morphology generated according to such reconstructions using the current simulation framework. | ||
Recent work on three-dimensional morphological quantification45,46 and modeling of CNS reinforced polymers47,48 has shown that a significant amount of stochastically-varying local curvature is exhibited by the CNSs present in the polymer matrix.45 These works also show that such structural randomness leads to the formation of a large number of van der Waals dominated junctions that may contribute to the mechanical and transport properties of such architectures. However, the formation of such junctions cannot be natively described by the assumptions that dominate previous theoretical frameworks, which primarily include simple functional forms, whereas stochastic descriptions are more representative of the kinetic and diffusive processes by which CNSs are synthesized,5,49e.g., CNTs via chemical vapor deposition.50 See Fig. 1D for an illustration of the simple morphological assumptions previously used to model an exemplary aligned CNT system, in addition to the visualized three-dimensional CNT topology and the stochastic descriptions used herein. Further, while the number of junctions formed in CNS architectures is strongly dependent on the CNS volume fraction, very little is currently known about how the junction density evolves with CNS packing proximity (i.e., Vf).
3D descriptions of CNS morphologies in nanocomposites have recently been provided using quantitative electron tomography45,46 and small angle X-ray scattering.50 Specifically, we have developed an electron tomographic approach that permits the extraction and quantification of the 3D arrangement of aligned CNT forests embedded in a polymeric matrix (Fig. S1†).45 Morphological metrics describing the network structure such as alignment, proximity, junction density, and waviness may be obtained from the resultant digitized reconstructions with nanometer resolution. Since aligned CNTs exhibit the best combination of mechanical, thermal, and electrical properties among the previously studied CNS reinforced polymer systems (see Fig. 1A),17,29,42 and were also the subject of our recent experimental and computational work on their three-dimensional morphology, this system was selected to be the focus of the current study.
Here, we use newly available morphogenesis (evolution of morphology with increasing Vf) data from electron tomography and stochastic simulations, to develop more representative mechanical, thermal, and electrical property prediction tools for aligned CNT polymer nanocomposites (A-PNCs) in directions that are both parallel and transverse to the CNT primary axis. Firstly, using the tortuosity measured by 3D TEM, we introduce a new 3D stochastic definition of waviness, which is found to provide the best match to previously-measured modulus data. We then establish the scaling of the CNT–CNT junction density with CNT Vf. This scaling is used to shed light on the dependence of transport properties on CNT network structure and its evolution with Vf. We believe that the structure–property correlations established here will provide valuable insights into many other past and future results from studies of similar nanocomposites and aligned CNT structures. More broadly, the findings reported herein are expected to be generalizable to other CNS-PNC systems with well characterized 3D morphology.
2. Results and discussion
The aligned-CNT (A-CNT) polymer nanocomposites in all the previous studies cited here17,29,42 were fabricated identically. Multiwalled carbon nanotube (MWCNT, (7.65 ± 0.87) nm in diameter, (mean ± one standard deviation)) forests were grown by thermal chemical vapor deposition. The volume fraction of these MWCNTs in the as-grown forest was estimated to be ≈1%. The CNT forests were then released from the substrate, densified perpendicular to the growth direction to various Vfs, impregnated with an epoxy matrix via capillary action and cured appropriately (Fig. S1e†). Further details of the A-PNC fabrication process are described elsewhere.17,29,42 At all volume fractions, the epoxy matrix is not measured to have been modified by the presence of the A-CNTs, as studied via wide-angle X-ray scattering (WAXS)51 and differential scattering calorimetry (DSC).52 This is a critical and useful assumption in this work as many polymers, particularly thermoplastics, have strong process-nanostructure interactions causing the polymer morphology and crystallization degree to alter, among other effects.53–55 Statistically representative 3D reconstructions of A-CNTs in the A-PNCs of ex situ Vfs of 1.00%, 5.00%, 6.00% and 11.70%, estimated from the change in volume of the forests before epoxy infiltration, were obtained using electron tomography as described earlier (Fig. S1a–d†).45 The reconstructions were quantified to obtain pertinent morphological data via 3D image analysis.45 This morphological data (Vf, CNT proximity and waviness/tortuosity) is required to build analytical models of the A-PNCs for stochastic simulations.Our imaging method enables, for the first time, the accurate measurement of A-CNT Vf in the nanocomposites (nominally the in situ Vf), among other quantitative features.45 Comparing the ex situ and in situ Vfs we observe that polymer impregnation into the porous A-CNT forest causes it to expand laterally (normal to the alignment axis), resulting in a lower Vf than that estimated post densification (in situ Vfs of (0.44 ± 0.01) %, (2.58 ± 0.25) %, (4.04 ± 0.19) %, (6.89 ± 0.43) %, ex situ Vfs of 1.00%, 5.00%, 6.00% and 11.70%, respectively). From the plot of in situ composite Vfversus the ex situ Vf of the densified starting material (Fig. S1f†), we find that a corrective factor of 0.59 can be applied to all the Vf values reported earlier,17,29,42 which did not account for the polymer-induced expansion. The inter-CNT spacings or CNT proximity (Γ) is the second morphological factor and can be readily calculated from the tomography data (Fig. S2†). With increased Vf we observe a non-linear reduction in Γ, which is in excellent agreement with the trends observed in the data obtained from SEM images of as-grown densified CNT arrays (Fig. S2†).56 As suggested by Stein et al., the mean spacings take the form:
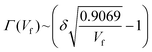 | (1) |
3D tortuosity of the CNTs, the third morphological factor, is key to stochastic simulations of morphology and can also be quantified from our tomography data. From the skeletonized 3D volumes of the 4 different Vf A-PNCs studied (ex situ Vfs of 1.00%, 5.00%, 6.00% and 11.70%), we extract tube arc length (l) to Euclidean distance (d) ratios i.e., tortuosity (l/d), for tube segments in the tomographic volume whose lengths are at least 10 times larger than the diameter of the CNTs (7.65 nm) (Fig. S3a†). The segments have to be at least of this length in order for us to extract a meaningful, representative waviness. We observe the 3D tortuosity to decrease with increasing Vf, suggesting a straightening of CNTs due to increased confinement (Fig. S3b†). However, the tortuosity measured here does not explicitly capture the nature or functional form of waviness, which is also an essential morphological descriptor. The waviness of CNTs has been previously described using simple sinusoidal and helical functions that neglect the stochastic nature of CNT growth.57,58 Here, we employ our novel definition of waviness, which provides a more realistic representation CNT morphology in the form of a “random” helical function. The usual waviness ratio (w) is a scalar measure of waviness that is typically defined as the amplitude over the wavelength of the chosen waviness function. For the random helical definition this ratio is modified by a pre-factor as described in other work.47,59 Depending on the assumed geometry (i.e. sinusoidal/helical/randomly helical), the 3D tortuosity for a given w will vary drastically. The tortuosity versus w plot in Fig. 2B shows how the tortuosity may be converted to an analytical/deterministic waviness (i.e. w) and vice versa.48 Using the 3D morphology data, we first consider the elastic modulus of the A-PNCs.
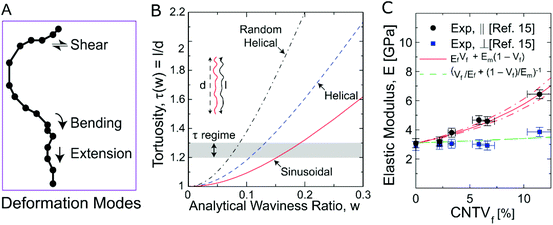 | ||
| Fig. 2 Deformation modes, morphological descriptors, and modulus modeling: (A) Illustration of the dominant physical mechanisms for CNT mechanical response. (B) Plot of tortuosity versus the analytical waviness ratio (w) for sinusoidal, helical and random helical formulations of waviness.48 The shaded region represents the range of tortuosity (τ) values calculated from tomography data. (C) Elastic modulus (E) of A-PNCs in the longitudinal (||, parallel to CNT alignment) and transverse (⊥, perpendicular to CNT alignment) directions, and the respective model predictions, as a function of the in situ CNT volume fraction Vf and accounting for morphology evolution. E scaling for A-PNCs shows that higher Vf mediated waviness reduction leads to significant enhancement in the E previously measured17 in the parallel (||) direction, whereas the perpendicular (⊥) direction sees little benefit with higher Vf. | ||
2.1 Mechanical properties
The axial and transverse/lateral elastic moduli of these A-PNCs measured by Handlin et al.17 are plotted as a function of Vf in Fig. 2C. The in situ Vfs shown here are corrected for volumetric expansion during polymer infiltration (previously-reported ex situ Vf × 0.59). Despite the correction, the measured elastic moduli are found to be an order of magnitude smaller than expected based on simple rule-of-mixtures calculations (see Fig. 1A). For example, at 12.00 vol% CNTs, the expected composite modulus is ≈60.0 GPa for a conservative CNT modulus of ≈500 GPa. However, the measured value is 6.4 GPa. In prior work it has been demonstrated that CNT waviness is the primary cause of this reduction.17,57 Indeed, pre-straining of CNT films to reduce waviness has been found to yield significantly higher elastic modulus values.21 Reciprocally, the modulus of the reinforcing CNT phase (Eo) i.e., the contribution of the CNT to the modulus of the nanocomposite, may be thought of as reducing with increasing waviness. It is possible to calculate the CNT reinforcement modulus, Eo, and its evolution as a function of waviness using our simulations,47 where each CNT is represented as a series of discrete nodes (Fig. 2A and Fig. S4a†). To apply the appropriate waviness to the CNTs, the displacement of each node relative to the node that precedes it in the x–y plane, is evaluated using the amplitude and wavelength. Stochastic waviness is achieved by using 2 Gaussian distributions to independently evaluate displacements in the lateral directions (x–y). Looking in the axial direction (z) we observe that this is essentially a two-dimensional random walk of a helically wavy CNT (Fig. S4a†). Our simulations are run on large ensembles of these CNTs (Fig. 1D and Fig. S4a†), at the requisite Vfs, to get a statistically representative reinforcement modulus for the system. The simulated data for the random helical system is shown in the plot of reinforcement modulus (Ef) versus waviness ratio in Fig. S4b,† where we observe Ef to decrease with increasing waviness. We note that larger ratios between the CNT (Y) and matrix moduli (Em) result in larger reductions in Ef (Fig. S4b†).Most prior studies have employed a constant waviness ratio to fit moduli measured over a range of Vfs, which leads to a strong under- or over-estimation of the elastic modulus depending on the Vf at which the waviness was measured. Since waviness changes with the Vf![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45,60 – decreasing at higher Vfs due to increased crowding – a careful study of the evolution of waviness with CNT packing is essential to interpret the complex dependence of the modulus on Vf. Using the measured trend in waviness with Vf (Fig. S3†), we generate sinusoidal, helical and randomly helical CNT morphologies at the Vfs studied by Handlin et al.17 The reinforcement modulus of these CNTs (Ef) at various Vfs is measured using our simulation technique47 and inserted into the rule-of-mixtures formula (EA-PNC = Vf × Ef + (1 − Vf) × EMatrix) to estimate the composite elastic modulus. From Fig. S5,† we note that, despite accounting for the change in waviness with Vf, the sinusoidal and helical assumptions strongly underestimate the A-PNC properties. This indicates that such simplistic definitions of waviness are inadequate in describing the mechanical performance of these systems (see discussion in Fig. S5†). Remarkably, the random helical definition, which is the first to account for the stochastic CNT morphology, provides the best match to the measured nanocomposite modulus (Fig. 2B and Fig. S5†). This result strongly supports the need to explicitly consider the stochastic nature of CNT morphology, and its evolution with increased crowding.
45,60 – decreasing at higher Vfs due to increased crowding – a careful study of the evolution of waviness with CNT packing is essential to interpret the complex dependence of the modulus on Vf. Using the measured trend in waviness with Vf (Fig. S3†), we generate sinusoidal, helical and randomly helical CNT morphologies at the Vfs studied by Handlin et al.17 The reinforcement modulus of these CNTs (Ef) at various Vfs is measured using our simulation technique47 and inserted into the rule-of-mixtures formula (EA-PNC = Vf × Ef + (1 − Vf) × EMatrix) to estimate the composite elastic modulus. From Fig. S5,† we note that, despite accounting for the change in waviness with Vf, the sinusoidal and helical assumptions strongly underestimate the A-PNC properties. This indicates that such simplistic definitions of waviness are inadequate in describing the mechanical performance of these systems (see discussion in Fig. S5†). Remarkably, the random helical definition, which is the first to account for the stochastic CNT morphology, provides the best match to the measured nanocomposite modulus (Fig. 2B and Fig. S5†). This result strongly supports the need to explicitly consider the stochastic nature of CNT morphology, and its evolution with increased crowding.
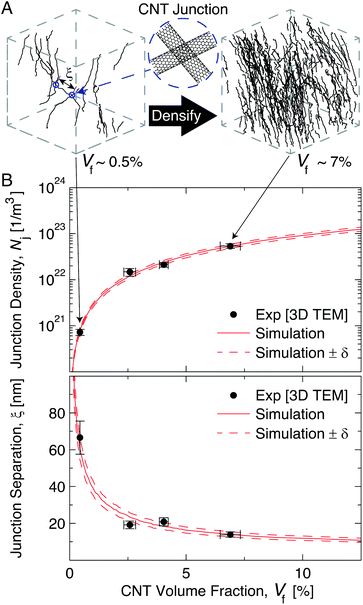
We note that the model CNT ensembles generated using the 3 primary structural descriptors (Vf, proximity and waviness/tortuosity) obtained by tomography, also show agreement with secondary or derivative structural features such as CNT–CNT junction density (NJ) and the average distance between nearest contact points (ξ) (Fig. 3). This agreement further validates the random helical formulation developed herein. We obtain NJ (m−3) by skeletonizing the reconstructed 3D volumes (Fig. S1 and S6†) and tallying the number of CNT–CNT contacts i.e., branches in the skeletonized structures (Fig. 3A).61 We find that, as the CNTs are brought closer, the short range van der Waals attractions cause them to cluster,45 causing a non-linear increase in NJ, best fit by a power law equation, NJ (m−3) = 3 × 1021Vf1.5. NJ increases by nearly two orders of magnitude ((7.24 ± 1.13) × 1020 m−3 to ((5.38 ± 0.63) × 1022 m−3) for an order of magnitude increase in in situ Vf ((0.44 ± 0.01) % to (6.89 ± 0.43) %) (Fig. 3B). We note that these experimentally measured NJ values are in good agreement (in the order of magnitude, ∼1022 m−3) with earlier computational calculations of NJ in CNT films.62 However, these calculations predict a quadratic dependence of NJ on Vf whereas our data shows NJ ∼ Vf1.5. That said, the earlier work simplistically assumed that CNTs are rigid rod-like objects, whereas they are only stiff along the local plane of the CNT wall, and rather overall compliant due to shear and bending modes (see Fig. 2A).62,63 On the other hand, here we have real estimates from high quality tomography data. The average distance between nearest contact points (ξ) may also be readily calculated from NJ using:62
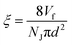 | (2) |
We now turn our attention to the transport properties (thermal and electrical conductivity) of the A-PNCs utilizing the junction density and distance quantification discussed above.
2.2 Thermal properties
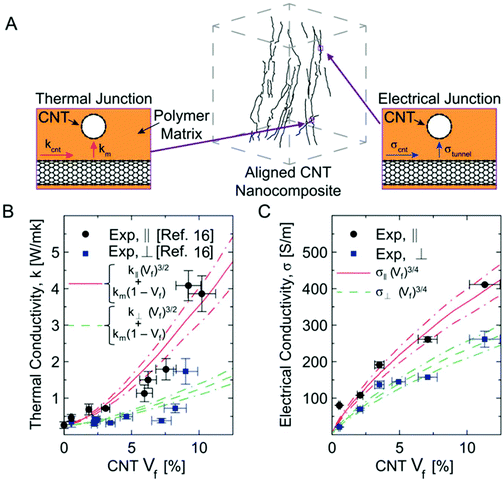
A-PNCs have been proposed as candidate materials for thermal interfaces and thermoelectric power devices, owing to the excellent thermal properties of CNTs.66,67 These composites have been found to possess some of the highest thermal conductivities, in particular compared to randomly-oriented CNT dispersions.29 However, Marconnet et al.,29 like many others before,68,69 observed the axial thermal conductivity of the CNT arrays and resultant nanocomposites to fall far short of what would be expected from a pristine CNT with a modest thermal conductivity of 1000 W m−1 K−1 (Fig. 4B).70 They also found the axial composite thermal conductivity to increase non-linearly with increased Vf, indicating that the simple model of parallel CNTs conducting heat within the matrix is unsupported. Additionally, they observed the anisotropy to increase at higher CNT Vfi.e., the axial thermal conductivity increased more rapidly than the transverse thermal conductivity with increased Vf. In the absence of any variation in the intrinsic CNT properties with densification (invariant ID/IG ratios ∼0.7 and diameter), the authors speculated that the reduced thermal conductivity, as well as most of the non-linearity, is caused by the interaction between CNTs and between the CNT and the polymer. They also suggested that any model explaining the dependence of thermal conductivity on CNT Vf should include the Vf effect on other morphological factors. Our recent imaging methodology facilitates this investigation.45We plot the thermal conductivity values (k) reported in Marconnet et al. against the corresponding corrected, or in situ Vfs, (Fig. 4B).29 We find that the best approximation to the trend in the corrected data is given by (k − km) = (115 ± 17) (W m−1 K−1) Vf1.56, as opposed to (k − km) = 73 (W m−1 K−1) Vf1.72, suggested in the original paper (Fig. S7a†).29 The increase in the prefactor in this relationship suggests a stronger contribution of the CNTs to conduction than originally calculated.29 While the power-law dependence might appear similar to percolation behavior, we note that such scaling at the high CNT loadings investigated here has been found to be due to network characteristics dominated by CNT–CNT contact resistance.63 Marconnet et al. speculated, in accordance with previous findings, that the upward concave trend in the data was indicative that the number density of CNT–CNT contacts (NJ) was increasing (although the nature of this increase was then unclear). Now that CNT–CNT contact density can be quantified, it appears that the scaling of NJ with Vf (NJ ∼ Vf1.50) in our tomography data (Fig. 4C) is identical to the thermal conductivity power law behavior (k ∼ Vf1.50) in the corrected property data, which validates the original interpretation of the data. Additionally, in the plot of the thermal conductivity enhancement versus the estimated NJ for the corrected Vfs in Marconnet et al., we observe a close-to-linear dependence (discounting the clear outlier indicated by red data point in Fig. S7b†). Indeed, the CNT networks, growing and interconnecting with the increased Vf, act as “heat pipes” throughout the composite, thus increasing thermal conductivity as their cross-sectional area contribution to the nanocomposite increases with Vf.
From our tomography data we are able to provide the first quantitative support to hypotheses linking morphological changes and the non-linear increase in thermal conductivity in aligned CNT composites. While it is possible for other sources of non-linearity to exist (see details in ESI, Fig. S8 and S9†), the 3D data reveals that the primary source of non-linearity is the non-linearly increasing density of CNT–CNT contacts with Vf. A natural conclusion from this newly exposed data is that, contrary to the original interpretation, in order to increase the thermal conductivity in a realistic system, with imperfect alignment and continuity, the number of CNT–CNT contacts needs to be maximized, as it provides more axial pathways for phonon transport. These findings further emphasize the importance of network visualization, and allow for better understanding of the origin and limitations on A-PNC thermal conductivity.
2.3 Electrical properties
The excellent axial electrical properties of CNTs make aligned CNT structures and their composites ideal candidates for flexible conductors, tactile displays and sensors.5,71–76 We briefly discuss previously unpublished electrical conductivity data in light of the new tomography results. Re-plotting the electrical conductivity (σ) versus the correct in situ Vfs (Fig. 4C), reveals a stronger contribution of CNTs to conduction than originally presumed. However, unlike in the case of thermal conductivity, which scales linearly with NJ (i.e., k ∼ Vf3/2), the electrical conductivities are found to exhibit a weak (NJ)0.5 scaling (i.e., σ ∼ Vf3/4). Such scaling of electrical conductivity with NJ was recently reported for nanowire networks,77,78 and previous studies on continuous aligned CNT composites have reported similar σ scaling with Vf that is approximately linear in nature.22,24,79,80 This observation is in contrast with the percolation-like scaling of (σ ∼ Vf2) commonly observed in randomly dispersed CNT composites.81 This is because A-PNCs are always beyond percolation axially as the CNTs are continuous. Further, the data also shows the same to be true transversely. Keblinski et al. suggest that this linear scaling at volume fractions well above percolation may be due to the bulk resistivity dominated conduction, as opposed to contact resistance based conduction (seen with thermal transport in continuous composites and electrical transport in randomly dispersed CNT composites).63 In such electrical conduction, the non-linear increase in the contact density does not play a significant role since the conduction is dependent on the concentration of bulk conductors, i.e., the number of parallel pathways between the electrodes, which is proportional to the Vf.63 The additional CNT–CNT junctions do not play a significant role in conduction. These results indicate that the various relevant physical properties of A-PNCs are sensitive to the evolution of morphological features to varying degrees. Our novel characterization of the scaling of properties with changing structure provides a basis for the optimization and design of multifunctional A-PNC properties.3. Conclusions
Using the newly-acquired high-resolution 3D imaging to re-visit previous experimental results has allowed for better understanding of A-CNT based PNC behavior. Previous interpretations have been strongly validated in some cases, and significantly modified in others, based on the new nano-scale, quantitative, morphological data. All the properties considered (thermal, electrical, mechanical) depend to varying degrees on Vf, and the 3D data corrects the prior ex situ assessments (based on densified volume considerations) to in situ ones. CNT waviness, strongly dependent on Vf, is a significant factor in reducing observed modulus trends compared to moduli predicted by simulations and computational modeling work elsewhere.47,59 Most importantly, the stochastic nature of CNT morphology must be accounted for in modeling the mechanical properties. CNT–CNT network connections (and the continuous CNT length between connections) play a dominant role in thermal transport; and since they increase non-linearly with CNT Vf, thermal conductivity should, and indeed does seem to follow this trend. The electrical conductivity, on the other hand, is found to weakly scale with junction density, thereby suggesting that electron conduction in A-CNT nanocomposites well beyond percolation is volume-resistivity dominated, rather than by the increased participation of CNT junctions. These understandings, made possible only due to the new 3D data, can now make PNC tailoring smarter, and more efficient.Disclaimer
Certain commercial equipment, instruments, software, or materials are identified in order to specify the experimental procedure adequately. Such identification is not intended to imply recommendation or endorsement by the National Institute of Standards and Technology, nor is it intended to imply that the materials or equipment identified are necessarily the best available for the purpose.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by ANSYS, Airbus, Embraer, Lockheed Martin, Saab AB, Saertex, and Teijin Carbon America through MIT's Nano-Engineered Composite aerospace STructures (NECST) Consortium and was carried out in part through the use of MIT's Microsystems Technology Laboratories. Research (for B. Natarajan) was supported by a Cooperative Research Agreement (CRA) between the University of Maryland and the National Institute of Standards and Technology (NIST) (grant 70NANB10H193). I. Stein was supported (in part) by the Department of Defense (DoD) through the National Defense Science & Engineering Graduate Fellowship (NDSEG) Program. B. Wardle and I. Stein acknowledge partial support from the National Aeronautics and Space Administration (NASA) Space Technology Research Institute (STRI) for Ultra-Strong Composites by Computational Design (US-COMP), grant number NNX17AJ32G, and from the U.S. Office of Naval Research under grant/contract number N00014-13-1-0213. We acknowledge Dr Thomas Lam (NIST) for useful discussions.Notes and references
- N. Domun, H. Hadavinia, T. Zhang, T. Sainsbury, G. H. Liaghat and S. Vahid, Nanoscale, 2015, 7, 10294–10329 RSC.
- A. Alam, Y. Zhang, H.-C. Kuan, S.-H. Lee and J. Ma, Prog. Polym. Sci., 2018, 77, 1–18 CrossRef CAS.
- V. Schroeder, S. Savagatrup, M. He, S. Lin and T. M. Swager, Chem. Rev., 2019, 119, 599–663 CrossRef CAS PubMed.
- J. Kim, M. S. Choi, K. H. Shin, M. Kota, Y. Kang, S. Lee, J. Y. Lee and H. S. Park, Adv. Mater., 2019, 1803444 CrossRef PubMed.
- R. Rao, C. L. Pint, A. E. Islam, R. S. Weatherup, S. Hofmann, E. R. Meshot, F. Wu, C. Zhou, N. Dee, P. B. Amama, J. Carpena-Nuñez, W. Shi, D. L. Plata, E. S. Penev, B. I. Yakobson, P. B. Balbuena, C. Bichara, D. N. Futaba, S. Noda, H. Shin, K. S. Kim, B. Simard, F. Mirri, M. Pasquali, F. Fornasiero, E. I. Kauppinen, M. Arnold, B. A. Cola, P. Nikolaev, S. Arepalli, H.-M. Cheng, D. N. Zakharov, E. A. Stach, J. Zhang, F. Wei, M. Terrones, D. B. Geohegan, B. Maruyama, S. Maruyama, Y. Li, W. W. Adams and A. J. Hart, ACS Nano, 2018, 12, 11756–11784 CrossRef CAS PubMed.
- I. A. Kinloch, J. Suhr, J. Lou, R. J. Young and P. M. Ajayan, Science, 2018, 362, 547 LP–553 CrossRef PubMed.
- V. Kuzmenko, O. Naboka, M. Haque, H. Staaf, G. Göransson, P. Gatenholm and P. Enoksson, Energy, 2015, 90, 1490–1496 CrossRef CAS.
- T. Ramanathan, A. A. Abdala, S. Stankovich, D. A. Dikin, M. Herrera-Alonso, R. D. Piner, D. H. Adamson, H. C. Schniepp, X. Chen, R. S. Ruoff, S. T. Nguyen, I. A. Aksay, R. K. Prud'Homme and L. C. Brinson, Nat. Nanotechnol., 2008, 3, 327–331 CrossRef CAS PubMed.
- H. Kim, A. A. Abdala and C. W. Macosko, Macromolecules, 2010, 43, 6515–6530 CrossRef CAS.
- K. Hu, D. D. Kulkarni, I. Choi and V. V. Tsukruk, Prog. Polym. Sci., 2014, 39, 1934–1972 CrossRef CAS.
- M. Moniruzzaman and K. I. Winey, Macromolecules, 2006, 39, 5194–5205 CrossRef CAS.
- M. F. L. De Volder, S. H. Tawfick, R. H. Baughman and A. J. Hart, Science, 2013, 339, 535–539 CrossRef CAS PubMed.
- S. K. Kumar, B. C. Benicewicz, R. A. Vaia and K. I. Winey, Macromolecules, 2017, 50, 714–731 CrossRef CAS.
- Y. Breton, G. Désarmot, J. P. Salvetat, S. Delpeux, C. Sinturel, F. Béguin and S. Bonnamy, Carbon, 2004, 42, 1027–1030 CrossRef CAS.
- M. Omidi, H. Rokni D. T., A. S. Milani, R. J. Seethaler and R. Arasteh, Carbon, 2010, 48, 3218–3228 CrossRef CAS.
- M. Li, Z. Wang, Q. Liu, S. Wang, Y. Gu, Y. Li and Z. Zhang, Polym. Compos., 2017, 38, 588–596 CrossRef CAS.
- D. Handlin, I. Y. Stein, R. Guzman de Villoria, H. Cebeci, E. M. Parsons, S. Socrate, S. Scotti and B. L. Wardle, J. Appl. Phys., 2013, 114, 224310 CrossRef.
- A. Montazeri, J. Javadpour, A. Khavandi, A. Tcharkhtchi and A. Mohajeri, Mater. Des., 2010, 31, 4202–4208 CrossRef CAS.
- M. R. Ayatollahi, S. Shadlou and M. M. Shokrieh, Mater. Des., 2011, 32, 2115–2124 CrossRef CAS.
- S. U. Khan, J. R. Pothnis and J.-K. Kim, Composites, Part A, 2013, 49, 26–34 CrossRef CAS.
- P. D. Bradford, X. Wang, H. Zhao, J.-P. Maria, Q. Jia and Y. T. Zhu, Compos. Sci. Technol., 2010, 70, 1980–1985 CrossRef CAS.
- Q. F. Cheng, J. P. Wang, J. J. Wen, C. H. Liu, K. L. Jiang, Q. Q. Li and S. S. Fan, Carbon, 2010, 48, 260–266 CrossRef CAS.
- T. H. Nam, K. Goto, H. Nakayama, K. Oshima, V. Premalal, Y. Shimamura, Y. Inoue, K. Naito and S. Kobayashi, Composites, Part A, 2014, 64, 194–202 CrossRef CAS.
- M. Mecklenburg, D. Mizushima, N. Ohtake, W. Bauhofer, B. Fiedler and K. Schulte, Carbon, 2015, 91, 275–290 CrossRef CAS.
- A. Mikhalchan, T. Gspann and A. Windle, J. Mater. Sci., 2016, 51, 10005–10025 CrossRef CAS.
- C. E. Corcione, F. Freuli and A. Maffezzoli, Polym. Eng. Sci., 2013, 53, 531–539 CrossRef CAS.
- F. Wang, L. T. Drzal, Y. Qin and Z. Huang, J. Mater. Sci., 2015, 50, 1082–1093 CrossRef CAS.
- J. Yang, S. Waltermire, Y. Chen, A. A. Zinn, T. T. Xu and D. Li, Appl. Phys. Lett., 2010, 96, 023109 CrossRef.
- A. M. Marconnet, N. Yamamoto, M. A. Panzer, B. L. Wardle and K. E. Goodson, ACS Nano, 2011, 5, 4818–4825 CrossRef CAS PubMed.
- J. G. Park, Q. Cheng, J. Lu, J. Bao, S. Li, Y. Tian, Z. Liang, C. Zhang and B. Wang, Carbon, 2012, 50, 2083–2090 CrossRef CAS.
- A. Yu, P. Ramesh, M. E. Itkis, E. Bekyarova and R. C. Haddon, J. Phys. Chem. C, 2007, 111, 7565–7569 CrossRef CAS.
- X. Huang, C. Zhi and P. Jiang, J. Phys. Chem. C, 2012, 116, 23812–23820 CrossRef.
- X. Shen, Z. Wang, Y. Wu, X. Liu, Y.-B. He and J.-K. Kim, Nano Lett., 2016, 16, 3585–3593 CrossRef CAS PubMed.
- C.-C. Teng, C.-C. M. Ma, C.-H. Lu, S.-Y. Yang, S.-H. Lee, M.-C. Hsiao, M.-Y. Yen, K.-C. Chiou and T.-M. Lee, Carbon, 2011, 49, 5107–5116 CrossRef CAS.
- Q. Li, Y. Guo, W. Li, S. Qiu, C. Zhu, X. Wei, M. Chen, C. Liu, S. Liao, Y. Gong, A. K. Mishra and L. Liu, Chem. Mater., 2014, 26, 4459–4465 CrossRef CAS.
- G. Lian, C.-C. Tuan, L. Li, S. Jiao, Q. Wang, K.-S. Moon, D. Cui and C.-P. Wong, Chem. Mater., 2016, 28, 6096–6104 CrossRef CAS.
- Z. Liu, D. Shen, J. Yu, W. Dai, C. Li, S. Du, N. Jiang, H. Li and C.-T. Lin, RSC Adv., 2016, 6, 22364–22369 RSC.
- X. Tian, M. E. Itkis, E. B. Bekyarova and R. C. Haddon, Sci. Rep., 2013, 3, 1710 CrossRef.
- H. Yan, Y. Tang, W. Long and Y. Li, J. Mater. Sci., 2014, 49, 5256–5264 CrossRef CAS.
- I. D. Rosca and S. V. Hoa, Carbon, 2009, 47, 1958–1968 CrossRef CAS.
- Q.-P. Feng, J.-P. Yang, S.-Y. Fu and Y.-W. Mai, Carbon, 2010, 48, 2057–2062 CrossRef CAS.
- H. Cebeci, R. Guzman de Villoria, A. J. Hart and B. L. Wardle, Compos. Sci. Technol., 2009, 69, 2649–2656 CrossRef CAS.
- J. Jia, X. Sun, X. Lin, X. Shen, Y.-W. Mai and J.-K. Kim, ACS Nano, 2014, 8, 5774–5783 CrossRef CAS PubMed.
- X. Liu, X. Sun, Z. Wang, X. Shen, Y. Wu and J.-K. Kim, ACS Appl. Mater. Interfaces, 2015, 7, 21455–21464 CrossRef CAS PubMed.
- B. Natarajan, N. Lachman, T. Lam, D. Jacobs, C. Long, M. Zhao, B. L. Wardle, R. Sharma and J. A. Liddle, ACS Nano, 2015, 9, 6050–6058 CrossRef CAS PubMed.
- K. Gnanasekaran, C. Grimaldi, G. With and H. Friedrich, Adv. Funct. Mater., 2019, 29, 1807901 CrossRef.
- I. Y. Stein and B. L. Wardle, Nanotechnology, 2016, 27, 035701 CrossRef PubMed.
- I. Y. Stein and B. L. Wardle, Phys. Chem. Chem. Phys., 2016, 18, 694–699 RSC.
- M. Bedewy and M. Abdulhafez, in Nanotube Superfiber Materials, Elsevier, 2019, pp. 31–64 Search PubMed.
- E. R. Meshot, D. W. Zwissler, N. Bui, T. R. Kuykendall, C. Wang, A. Hexemer, K. J. J. Wu and F. Fornasiero, ACS Nano, 2017, 11, 5405–5416 CrossRef CAS PubMed.
- B. L. Wardle, D. S. Saito, E. J. García, A. J. Hart, R. Guzman de Villoria and E. A. Verploegen, Adv. Mater., 2008, 20, 2707–2714 CrossRef CAS PubMed.
- S. S. Wicks, PhD thesis, Massachusetts Institute of Technology, 2014.
- J. L. Gair, R. H. Lambeth, D. P. Cole, D. L. Lidston, I. Y. Stein, E. Kalfon-Cohen, A. J. Hsieh, H. A. Bruck, M. L. Bundy and B. L. Wardle, Compos. Sci. Technol., 2018, 166, 115–124 CrossRef CAS.
- D. Roy, A. P. Kotula, B. Natarajan, J. W. Gilman, D. M. Fox and K. B. Migler, Polymer, 2018, 153, 70–77 CrossRef CAS.
- J. N. Coleman, M. Cadek, K. P. Ryan, A. Fonseca, J. B. Nagy, W. J. Blau and M. S. Ferreira, Polymer, 2006, 47, 8556–8561 CrossRef CAS.
- I. Y. Stein and B. L. Wardle, Phys. Chem. Chem. Phys., 2013, 15, 4033 RSC.
- F. T. Fisher, R. D. Bradshaw and L. C. Brinson, Appl. Phys. Lett., 2002, 80, 4647–4649 CrossRef CAS.
- U. Vainio, T. I. W. Schnoor, S. Koyiloth Vayalil, K. Schulte, M. Müller and E. T. Lilleodden, J. Phys. Chem. C, 2014, 118, 9507–9513 CrossRef CAS.
- I. Y. Stein, D. J. Lewis and B. L. Wardle, Nanoscale, 2015, 7, 19426–19431 RSC.
- H. Cebeci, I. Y. Stein and B. L. Wardle, Appl. Phys. Lett., 2014, 104, 023117 CrossRef.
- I. Arganda-Carreras, R. Fernández-González, A. Muñoz-Barrutia and C. Ortiz-De-Solorzano, Microsc. Res. Tech., 2010, 73, 1019–1029 CrossRef PubMed.
- P. E. Lyons, S. De, F. Blighe, V. Nicolosi, L. F. C. Pereira, M. S. Ferreira and J. N. Coleman, J. Appl. Phys., 2008, 104, 044302 CrossRef.
- P. Keblinski and F. Cleri, Phys. Rev. B: Condens. Matter, 2004, 69, 184201 CrossRef.
- C. F. Schmidt, M. Baermann, G. Isenberg and E. Sackmann, Macromolecules, 1989, 22, 3638–3649 CrossRef CAS.
- B. Natarajan, N. D. Orloff, R. Ashkar, S. Doshi, K. Twedt, A. Krishnamurthy, C. Davis, A. M. Forster, E. Thostenson, J. Obrzut, R. Sharma and J. A. Liddle, Carbon, 2016, 108, 381–393 CrossRef CAS.
- H. Huang, C. H. Liu, Y. Wu and S. Fan, Adv. Mater., 2005, 17, 1652–1656 CrossRef CAS.
- F. Rivadulla, C. Mateo-Mateo and M. A. Correa-Duarte, J. Am. Chem. Soc., 2010, 132, 3751–3755 CrossRef CAS PubMed.
- Z. Han and A. Fina, Prog. Polym. Sci., 2011, 36, 914–944 CrossRef CAS.
- A. M. Marconnet, M. A. Panzer and K. E. Goodson, Rev. Mod. Phys., 2013, 85, 1295–1326 CrossRef CAS.
- M. Fujii, X. Zhang, H. Q. Xie, H. Ago, K. Takahashi, T. Ikuta, H. Abe and T. Shimizu, Phys. Rev. Lett., 2005, 95, 065502 CrossRef PubMed.
- H. Peng, J. Am. Chem. Soc., 2008, 130, 42–43 CrossRef CAS PubMed.
- Y. J. Jung, S. Kar, S. Talapatra, C. Soldano, G. Viswanathan, X. Li, Z. Yao, F. S. Ou, A. Avadhanula, R. Vajtai, S. Curran, O. Nalamasu and P. M. Ajayan, Nano Lett., 2006, 6, 413–418 CrossRef CAS PubMed.
- L. Liu, W. Ma and Z. Zhang, Small, 2011, 7, 1504–1520 CrossRef CAS PubMed.
- M. Endo, M. S. Strano and P. M. Ajayan, Potential applications of carbon nanotubes, in Carbon nanotubes: Topics in Applied Physics, ed. A. Jorio, G. Dresselhaus and M. S. Dresselhaus, Springer, Berlin, 2008, vol. 111, pp. 13–61 Search PubMed.
- J. Lee, I. Y. Stein, S. S. Kessler and B. L. Wardle, ACS Appl. Mater. Interfaces, 2015, 7, 8900–8905 CrossRef CAS PubMed.
- D. Janas and K. K. Koziol, Nanoscale, 2014, 6, 3037 RSC.
- A. Kumar and G. U. Kulkarni, J. Appl. Phys., 2016, 119, 015102 CrossRef.
- R. Gupta, A. Kumar, S. Sadasivam, S. Walia, G. U. Kulkarni, T. S. Fisher and A. Marconnet, ACS Appl. Mater. Interfaces, 2017, 9, 13703–13712 CrossRef CAS PubMed.
- W. Liu, X. Zhang, G. Xu, P. D. Bradford, X. Wang, H. Zhao, Y. Zhang, Q. Jia, F.-G. Yuan, Q. Li, Y. Qiu and Y. Zhu, Carbon, 2011, 49, 4786–4791 CrossRef CAS.
- X. Wang, P. D. Bradford, W. Liu, H. Zhao, Y. Inoue, J.-P. Maria, Q. Li, F.-G. Yuan and Y. Zhu, Compos. Sci. Technol., 2011, 71, 1677–1683 CrossRef CAS.
- W. Bauhofer and J. Z. Kovacs, Compos. Sci. Technol., 2009, 69, 1486–1498 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9nr03317c |
| ‡ This work was primarily done while at the Center for Nanoscale Science and Technology, National Institute of Standards and Technology, Gaithersburg, Maryland 20899, USA. |
| § These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2019 |