Spontaneous in-flight assembly of magnetic nanoparticles into macroscopic chains

Abstract

Knowing the interactions controlling aggregation processes in magnetic nanoparticles is of strong interest in preventing or promoting nanoparticles’ aggregation at wish for different applications. Dipolar magnetic interactions, proportional to the particle volume, are identified as the key driving force behind the formation of macroscopic aggregates for particle sizes above about 20 nm. However, aggregates’ shape and size are also strongly influenced by topological ordering. 1-D macroscopic chains of several micrometer lengths are obtained with cube-shaped magnetic nanoparticles prepared by the gas-aggregation technique. Using an analytical model and molecular dynamics simulations, the energy landscape of interacting cube-shaped magnetic nanoparticles is analysed revealing unintuitive dependence of the force acting on particles with the displacement and explaining pathways leading to their assembly into long linear chains. The mechanical behaviour and magnetic structure of the chains are studied by a combination of atomic and magnetic force measurements, and computer simulation. The results demonstrate that [111] magnetic anisotropy of the cube-shaped nanoparticles strongly influences chain assembly features.

---

1 Introduction

Magnetic nanoparticles (NPs), nanocomposites, and artificial array materials hold a special place in many areas of technology, not only because of their distinct properties, resulting from their discrete nature and high surface to volume ratios, but also because they can be used as functional building blocks for the design and development of new devices.^1–4 Nowadays, different technological fields, such as catalysis,^5,6 storage devices,^7,8 or biomedicine,⁹ have gained strong industrial and economical relevance boosting research activities in these areas. Each of these applications has different requirements regarding shape, size and degree of particles’ aggregation, and therefore, knowing the interactions controlling aggregation processes is of strong interest for preventing or promoting nanoparticles’ aggregation at wish for different applications. The growing activity in this field has also stimulated the development of methods for the production of NPs and clusters with precise control of size, shape, and composition. In this regard, gas aggregation sources,^10–12 which allow obtaining core/shell structured nanoparticles^6,10 easily, were recently modified to achieve also high production rates¹³ as in the case of wet chemistry synthesis techniques. Nevertheless, these latter methods have limitations in terms of the simplicity of the process, typically involving several processing steps, surface contamination and size distribution. In contrast, gas-phase techniques, operating in a controlled atmosphere, present a way for the fabrication and manipulation of magnetic particles with well-defined composition and a narrow size distribution. Fabrication of magnetic NPs with cuboidal geometry is of particular interest due to their higher surface to volume ratios, high packing density, and high surface adhesion due to atomically flat touching faces. These features are of high interest for applications in fields as diverse as catalysis,⁵ high-density magnetic storage devices,⁸ or tailored superlattices.^14,15 In addition, single domain magnetic configurations are mandatory for applications requiring hard magnetic behaviour, such as hard disk drives⁷ or permanent magnets.¹⁶ The magnetic configuration of constitutive single domain elements in these applications is not determined solely by the magnetic material bulk properties (Fe, Co, etc.). Gatel et al.¹⁷ theoretically and experimentally analysed the magnetic configuration dependence on iron cube size. They showed a surprising transition between single-domain [001] and [111] (vortex) states with an increasing dimension of iron nanocubes from 25 to 27 nm. In turn, magnetic anisotropy changes the way particles assemble.^18–22 In consequence, for sub-25 nm magnetic NPs in suspension, the dominant interaction changes from anisotropic, long-range, and oriented dipole–dipole coupling to the van der Waals short-range surface coupling.^23,24 The potential of magnetic nanocubes to form mesoscopic structures with different geometries is enormous.²⁵ For example, at an air–liquid interface, large monolayers assembled by 9 nm magnetic cubes were created,^14,26 whereas, in the same study, 13 nm NPs formed helices in the presence of a magnetic field.¹⁴

Here, we report on the spontaneous self-assembly of magnetic nanoparticles into macroscopic chains. We show that dipolar interactions, proportional to the particle volume, are the key driving force behind the formation of macroscopic aggregates for particle sizes above about 20 nm; however, aggregates’ shape and size are strongly influenced by topological ordering. 1-D macroscopic chains of several μm lengths are obtained with 25 nm magnetic iron/iron-oxide cube-shaped magnetic nanoparticles fabricated by using a modified gas-aggregation technique, which allows particles to assemble in flight without the influence of the medium. Self-assembled chains represent an excellent paradigmatic system to explore the self-assembly process of individual particles and a unique model system to study the behaviour of complex agglomerates without dumping of the medium (i.e., only conservative interparticle forces are present) at the nano- and mesoscale ranges. Since magnetic cores and shells may have different magnetic anisotropies, a detailed characterisation of the NPs is required for understanding the magnetic structure of the nanocubes. We have used an exact analytical theory to predict the energetically favourable configurations. Our results reveal a complex energy landscape leading to non-intuitive force distance characteristics. Then, to validate the developed model, a series of magnetic and atomic force microscopy measurements and computer simulations were performed. Applying both techniques simultaneously, the processes governing self-assembly of magnetic cubes into single-stranded chains are unveiled.

2 Methods

2.1 Experiment

Arrays of core/shell NPs (see Fig. 1) were prepared in a home-built cluster source connected to a vacuum system with base pressure in the low 10⁻⁶ Torr. More details on the synthesis procedure are given in ESI.† A 1 inch diameter DC magnetron with a Fe target (99.95% purity) was operated typically at 50 W. During deposition, the flux of argon was fixed at 80 sccm, and the measured pressures were in the low 10⁻³ Torr. Si wafers were used as substrates, except for the samples aimed for transmission electron microscopy (TEM) imaging that were deposited on carbon-coated grids.

Fig. 1 Magnetic assembly of nanocubes in a single strand. (a) SEM and (b) TEM images of the micrometre long single-stranded core/shell iron NP chain. (c) TEM image of a chain segment.

The particle-size characterisation was determined by scanning electron microscopy (SEM) using a QUANTA FEI 200 FEG-ESEM microscope. TEM, HRTEM and scanning TEM (STEM) in the high angle annular dark field (HAADF) mode were used to study the crystallinity, morphology, size, and dispersion of the samples. TEM images were obtained using a JEOL JEM 1210 transmission electron microscope operating at 120 kV. HRTEM and STEM images were acquired in a FEI Tecnai F20 microscope operating at 200 kV. Digital diffraction patterns (DDP) of power spectra were obtained from selected regions in the micrographs. No electron-beam-induced changes were observed in any of the analyzed particles.²⁷ Energy dispersive X-ray (EDS) spectra were acquired using an EDAX super ultrathin window (SUTW) X-ray detector.

Micro-Raman spectra were obtained by using a Jobin–Yvon T64000 monochromator with a liquid nitrogen cooled charge-coupled detector. The excitation light was a 514.5 nm line from an Ar-ion laser. The incident and scattered beams were focused by an Olympus microscope using a ×50 objective to give a spot size of ca. 2 μm. Unpolarised Raman spectra were measured due to the polycrystalline nature of the samples.

MFM measurements were performed with an MFP-3D Asylum Research microscope using ASYMFM-HC probes with CoPt/FePt (30 nm) coating. In MFM the phase shift near the cantilever resonance was used to map stray fields by measuring in the amplitude modulation AFM (AM-AFM) mode and keeping the cantilever at a constant height (57 nm) from the surface. Variable field module (VFM2) from Asylum Research, which was a special holder with a rotating permanent magnet, was used to apply a magnetic field of up to 1 T in the in-plane direction.

2.2 Analytical theory and molecular dynamics simulations

We combine two modelling techniques to extract information on the mechanical response of a free-standing chain: (i) We utilise an exact analytical model to obtain a stray magnetic field from a single cubic magnetic domain and calculate the interaction energy of the two cubes,²⁸ as shown in Fig. 3. (ii) The mechanical properties of the magnetic chains are explored using cubes consisting of elements as suggested by John et al. (coarse-grained cube structure) and Zhang et al. (magnetic dipole approximation).^24,29–31 Analytical calculations for uniformly magnetised cubes and simulations assumed monodisperse perfect cubes. Two systems were considered: one with magnetisation orientated in the [001] crystallographic direction, and the other with magnetisation along the [111] direction.

The John et al.²⁹ and Zhang et al.³⁰ models are modified in two ways: first, instead of only one central dipole, 9 were used (cf. illustration in Fig. S5†). In this way, we have reproduced the potential energy profile of the two cubes calculated analytically (see comparison in Fig. S6†). Also, additional dipoles take into account the interaction of the touching corners of the cubes, which is important for the stability of the chain under extension (see ESI Movies†). If we analyse a case of extreme extension, the magnetic energy of two [111] magnetised cubes with aligned magnetisation touching on the corner, which comes from the two adjacent corner cubes 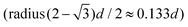, is two times larger than the energy stemming from the interaction between the central cubes (radius d/2), i.e., 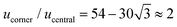. And second, an additional 24 spheres were placed inside of the cube edges in order to make a smooth surface and avoid pinning during mechanical manipulation. The geometrical contact between two cubes is simulated using the WCA potential for the spheres (truncated and shifted Lennard-Jones potential, elsewhere called also soft-sphere model) (see ESI).†

We study the mechanical behaviour of the model system by means of molecular dynamics computer simulations: the cubes are represented by the WCA potential and carry nine-point dipoles as described in Fig. S5.† This model was the basis for zero temperature molecular dynamics simulation. The simulations of the breaking of the chains were performed by different forces exerted on the chain ends. Molecular dynamics was used to study mechanical manipulation of the free-standing chain composed of magnetic cubes. The total force was the conservative force of inter-particle interactions, i.e., contact WCA potential of 33 (overlapping) spheres and 9 dipoles. The dipolar interactions were treated with cut-off at r_cut/d = 8 (cf. ref. 24), and a non-periodic simulation box was used. The constituent spheres within the cube were moved as rigid body data structures in every time step. The rotational degrees of freedom are also governed by the equations of motion for torque and angular velocity of the spheres. The total force and torque on each cluster representing one cube are computed as the sum of the forces and torques on its constituent particles at each time step. The dipole orientation is accordingly rotated with the cube as a single entity. The rotation was implemented by creating internal data structures for each rigid body and performing time integration on these data structures.^32,33 The mass of the cuboid corresponded to a 25 nm iron cube and was distributed over constitutive dipolar particles. MD step was t = 4 ps and the total length of the MD simulation 400 ns.

3 Arrays of core/shell iron nanocubes and their magnetic properties

3.1 One-step synthesis by gas-aggregation and magnetron sputtering

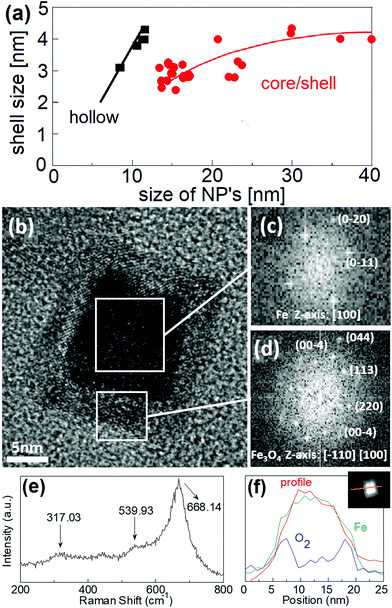
NPs used in this work were prepared by a combination of magnetron sputtering and gas-aggregation techniques.^6,10 Sputtered Fe atoms are cooled down in the cluster source and then aggregate by collisions with flowing Ar gas at room temperature (see Fig. S1† for a schematic of the cluster gun setup in ESI†). Differential pumping drags the clusters through a small nozzle into the deposition chamber. The gas is flowing through the 3 mm slit at the rate of 80 cm³ min⁻¹, i.e., with a speed 0.14 m s⁻¹. The kinetic energy of the particle due to the surrounding gas flow is around 10 meV. Clusters are therefore softly deposited onto a sample holder at room temperature, thus retaining their original shape.⁶ Mean NP size can be controlled by careful selection of the deposition conditions (sputtering power, travelling distances, chamber pressure, and Ar gas flow rates).¹⁰ The travel distance affects the size of the particles. Actually, the smaller travelling distance results in reduced particle size as observed in ESI.† The particles under 12 nm have a hollow magnetite shell structure (cf. Fig. 2a and ESI).† This appears as a consequence of the Kirkendall effect, i.e., somewhat faster diffusion of iron towards the shell than oxygen atoms inwards. As a result, iron from the centre of the cluster diffuses towards the oxygen-rich shell leaving a void space inside the cube. We should note that in any case, natural oxidation makes it difficult to stabilise pure iron NPs after preparation.³⁴ Previous reports showed that an oxygen-rich atmosphere in the deposition chamber during processing leads to the formation of Fe/Fe oxide clusters.³⁵ In our case, the oxygen partial pressure (medium-vacuum conditions) in addition to the Ar atmosphere warrants reactive sputtering; thus, a chemical reaction occurs leading to the formation of iron oxide shells before clusters are deposited on the substrate.

Fig. 2 Shell size as a function of the NP grain size obtained from different TEM images (a). Below 12 nm, the NPs show a hollow structure; above this size, they show a core/shell configuration. Lines are a guide to the eyes. High-resolution Z-contrast TEM image of a Fe/Fe oxide core/shell NP (b). The large areas marked by the full lines are used for the identification of (c) the Fe core and (d) the Fe oxide shell. (e) Raman spectrum confirming the presence of Fe₃O₄ in the shell. (f) EDX line profile analysis of one single NP making evident the core/shell structure.

In the present work, for a 5 cm travel distance, a large number of shell only particles were obtained with an average particle size of about 8 nm. Meanwhile, for an 8 cm travel distance, an increase of the average particle size to 15 nm is observed at the expense of the number of generated particles (see Fig. S2).† In addition, particles produced in the latter case were mainly of a core/shell structure (see Fig. 2a). Further increase of the travel distance resulted in a small increase in the particle size: for a 11 cm travel distance, the average size was 16 nm, while for 13 cm, the average size was 17 nm. When the oxidation process is dominated by the Cabrera–Mott-like mechanism, initial oxidation rapidly develops a 4 nm-thick oxide shell around the Fe core. A similar effect has been observed in the synthesis of iron core/shell cubes from solution,³⁶ where a partial oxidation promoted the formation of core/shell nanostructures with an iron core trapped inside the oxide shell. Following this procedure, single crystalline iron NPs covered by a crystalline Fe₃O₄ shell can be fabricated. For small enough NPs, i.e. below about 9–10 nm, the Cabrera–Mott like oxidation mechanism produces hollows. In contrast, for particles above 12 nm, a core/shell structure is obtained (see Fig. S3).† This evolution can be clearly observed in Fig. 2a. To promote spontaneous self-assembly, stronger interactions between core/shell magnetic cubes are required, i.e., a strongly magnetised iron core is necessary. Therefore, nanocube dimensions should be larger than 12 nm in order to have a core/shell structure with a strongly magnetised core.

3.2 Composition of magnetic cubes

A detailed characterization of the chemical composition of the NPs is required in order to understand the magnetic structure of the cubes, due to the different magnetic anisotropies of the core and shell parts. The synthesis of single crystalline iron NPs, ideally covered by a crystalline Fe₃O₄ (magnetite) shell, has been proposed as a promising way to improve chemical stability and preserve a substantial iron core.^37,38 Pure iron NPs are unstable when brought to ambient conditions transforming into iron/iron-oxide core/shell structured NPs.

A high-resolution Z-contrast TEM image is shown in Fig. 2b. A well-defined square shape of the particle with a sharply defined 4 nm shell can be appreciated. The reflections of the power spectrum pattern (see Fig. 2c and d) obtained by TEM can be indexed using the corresponding reflections of cubic Fe for the core and the spinel structure for the shell. Since TEM and electron diffraction techniques cannot distinguish between the different oxide phases, Raman spectroscopy was used to identify them. Different bands in the Raman spectrum correspond to specific frequency vibration modes, allowing distinguishing different oxide phases. In particular, maghemite differs from magnetite because it contains no divalent iron species. Due to the fact that the ionic radius of Fe(II) is larger than that of Fe(III), Fe(II)–O bonds are longer and weaker than Fe(III)–O bonds; this shifts up the vibration frequency in the Raman spectrum, and hence, Raman analysis allows distinguishing between these two phases. In the Raman spectrum displayed in Fig. 2e, the main band centred at 668 cm⁻¹ and the weaker peaks at ca. 539 and 317 cm⁻¹ have been assigned to A_1g, T_2g, and E_g vibrational modes of magnetite, respectively.³⁹ EDX line profile analysis of one single particle shows the absence of oxygen at the core and the progressive increase at the surface (Fig. 2f), thus giving further support for the idea of core/shell nanostructures of Fe/Fe₃O₄.

3.3 Self-assembled chains of magnetic cubes

The NPs are synthesised with different sizes and directly deposited on various substrates in a controlled atmosphere. The presence of pure metallic iron is important since it promotes higher magnetisation value and, therefore, better functionality compared to iron–nickel alloys or iron-oxide particles. Far from “being weak”, dipolar magnetism plays a leading role in stabilising the structural order in the arrangements of NPs in one dimensional structures. During assembly into chains, the particles move and self-assemble in flight without the influence of the medium. Previously, dipolar chains were associated with ground states of [001] magnetic easy axis, whereas those with [111] oriented magnetic easy axis were expected to adopt square lattice structures, i.e., to form clusters.^14,19,26 Mehdizadeh Taheri et al.²⁶ reported magnetic chains of iron cubes with a core/shell structure featuring fully touching faces of the cubes and synthesised at 0.02 vol% concentration. The chains reported here are created in a controllable way in an even more diluted system.

The magnetic dipolar attraction of particles above 25 nm is strong enough to form long single stranded chains, while for particles less than 25 nm, only individual particles and clusters are detected (see Fig. 1). Individual particles are not observed, which implies that the growth of chains is completed before being deposited on the substrate. Therefore, the substrate does not influence chain formation. The emergence of chains is actually driven by interplay of the geometrical contact between two cubes and the magnetic dipolar interaction. It is worth mentioning that both contact and dipolar interaction are anisotropic. The nanometer-sized iron cubes display a fixed and permanent magnetic dipole moment that is strong enough to form single strand chains.

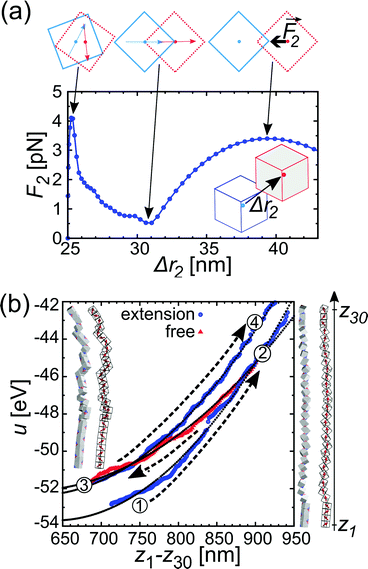
The chain morphology provides an insight into the particle magnetic anisotropy. The magnetic moment of magnetically anisotropic materials tends to align with an easy axis, which is an energetically favourable direction of spontaneous magnetisation. Actually, the direction of the easy axis of the magnetic cube can be controlled by the core to shell ratio. There are indeed two possible magnetic easy axes: one governed by the magnetite shell lying in the [111] direction and the other governed by the iron core along the [001] direction.^17,37,40 Since hollow, i.e., magnetite shell-only, cubes have dimensions below 12 nm, dipolar interactions are small and therefore no chains are formed along the [111] orientation. It is evident that the direction of the net magnetic orientation relative to the cube geometry changes the structure of the observed chains (see Fig. 3a and b). For chains of nanocubes, the assembly mechanism drives the particles to adopt structures that create a head–tail configuration, very much like chains of magnetic beads. In the case of [001] direction, this leads to deep central minimum of magnetic potential energy with respect to the lateral movement of the magnetic particles and consequently to quite stiff configuration (cf., ESI Movie 1†). On the contrary, when the magnetisation is along the principal axis, i.e., [111] direction, the structure becomes more flexible (cf., ESI Movie 2†). The configuration with minimal energy has a zig-zag dipole vector placement (cf., the top left panel where particles are placed in face-to-face configuration in Fig. 3b) of the magnetic cubes, and the system can extend to a head–tail configuration by relative rotation of the cubes (cf., also ref. 24). The relative rotation is taking place along the bottom of the circular valley shown in Fig. 3b. The valley is denoted as a white circle and is tilted towards the centre of mass (c.m.) of the bottom particle. The highest point of the valley is when the c.m. of the upper particle is above the edge corner of the particle below. This corresponds to head–tail placement of the dipoles. Head–tail configuration of dipoles shows about a 20% energy increase along the valley. At the minimum energy point (zig-zag configuration), the distance between their centres of mass Δr₂ is equal to the cube size Δr₂ = d. At the furthest point of the circular minimum valley (i.e., when c.m. of one particle is above the corner of the other), the centres of mass of the particles are 22% further apart than at global minimum (as shown in Fig. 4, 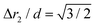, i.e., Δr₂ = 30.6 nm for 25 nm particles).

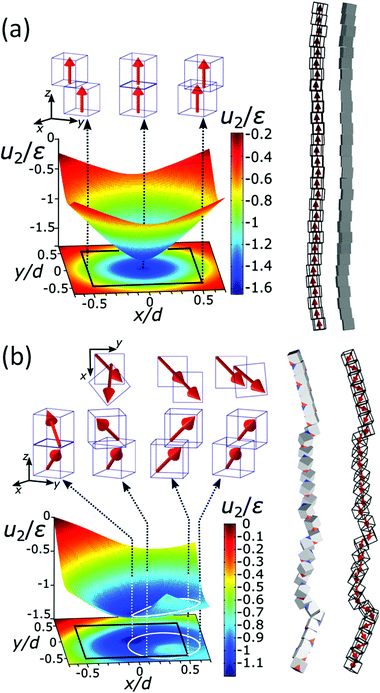Fig. 3 The energy landscape obtained analytically and a schematic view of the chain of the particles for [001] (a) and [111] (b) easy magnetisation axis directions. Interaction energy per particle u₂ for pure iron particles is scaled with the reference interaction energy ε = 25 eV (see also Fig. S4†). The contour of the bottom cube is shown with the black solid line in the energy diagrams. The white solid line circle in the energy diagram for the [111] magnetisation direction represents the bottom of the circular potential valley. Three representative configurations with [001] magnetisation directions are shown with side views in the upper panels of (a). From left to right: centre of mass (c.m.) of one particle in the middle of the edge of the other, one particle on top of the other, and c.m. of one particle on the corner of the other. Four representative configurations with [111] magnetisation are shown with top and side views. The configurations are shown in the upper panels of (b), from left to right: (i) zig-zag configuration, where the particles are above each other with the surfaces placed face-to-face (the zig-zag configuration is the most stable one), (ii) c.m. of the upper particle is at the edge of the contour of the lower particle, (iii) head–tail configuration when the upper particle's c.m. is at the edge of the bottom particle and (iv) the so-called unstable configuration, when c.m. of the upper particle is furthermost from the contour of the bottom.

Fig. 4 Calculated magnetic force and energy evolution under extension. (a) Restoring force dependence on the centre of the mass distance between two 25 nm iron particles as one of the particles follows a minimal energy path and is obtained using an analytical model. (b) Energy per particle dependence on the length of the chain during repeated extension of the chain consisting of 30 iron cubes of 25 nm. Circles (blue) show energy evolution with the distance of its ends and triangles (red) evolution when the chain ends are free and the chain contracts. The extension/free chain retraction results are obtained from simulation. Dashed arrows show the direction of extension/contraction and numbers 1–4 sequence. Black lines are parabolas interpolated through the simulated data.

Fig. 4a gives the calculated dependence of the magnetic restoring force on the distance between the centres of mass of the two particles. We see that there are two maximums of the force (roughly equal in size). The first peak, which is very narrow, locks particles in a zig-zag position while the second broad peak keeps the chain connected. The reason for the existence of the first narrow maximum is that particles have first to move laterally in order to come out of the zig-zag position (see also Fig. 2b). The shape of the magnetic potential energy valley further enhances the flexibility of the whole structure. The contour of the potential valley crosses the edge of the bottom cube, and a large part of it lies outside of the contour of the bottom cube. In this area, the two-particle system becomes unstable. This means that one cube can flip over the edge of the other cube and change in the other equivalent position on the different side of the cube (see ESI Movie 3†). This is also a local minimum of the restoring force (cf., Δr₂ = 30 nm) (Fig. 4a). Also, during extension, cubes can partially detach when they are in a head–tail configuration, i.e., stay only attached by the corner-to-corner contact, i.e., at 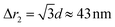. In the corner-to-corner configuration, the parts of the chain have a large rotational freedom. This is also a configuration from which we observe that the chain finally detaches (breaks). Still, the local maximum of the force is at roughly Δr₂ ≈39 nm, and at this point, particles are still overlapping.

The response of the chain of magnetic cubes to strain is shown in Fig. 4b. We observe that the chain is extending and contracting quasi-elastically (see ESI Movie 4†). The energy u follows a parabolic curve, and the elastic force acting on the ends of the chain increases linearly with the extension of the chain. The estimated elastic coefficient of the chain is 0.21 ± 0.05 meV nm⁻². The elastic extension of the chain continues up to the point where the maximal force per particle approaches roughly 3 pN (see Fig. 4a) at roughly Δr₂ = 40 nm. It is also observed that there is a pinning of the parts of the chain in an energetically less favourable configuration, and as a result, the energy depends on the history of the mechanical manipulation.

3.4 Magnetic configuration of the chains

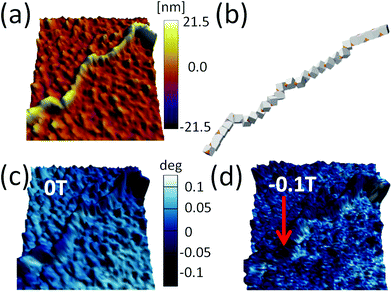
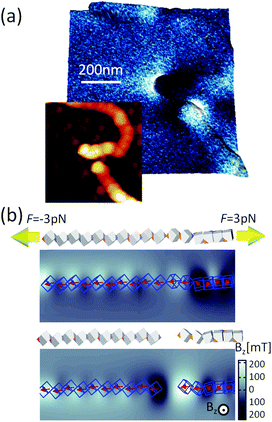
Our results demonstrate that dipole–dipole interactions, with the resulting magnetic moment pointing along the chain, are the origin of the chain formation. It is important to note, however, that particles in the chain spontaneously turn their magnetisation in the presence of other magnetic particles to minimise their own energy. Still, the spontaneous magnetic moment of particles has to be along their easy magnetic axis, i.e., [111] direction^17,40 relative to cube geometry. When an externally applied magnetic field is stronger than the magnetic field of the particles itself, the magnetisation starts to align itself with the external field independent of easy axis direction. Therefore, an estimation of the dipole interaction can be obtained by applying the magnetic field perpendicular to the chain and measuring the field necessary to rotate their magnetic moment out of the chain direction.

In Fig. 5, we show the magnetisation dependence of individual cubes of a representative part of a chain on the external magnetic field. The stray magnetic field generated by the chain is small when no external magnetic field is initially applied (cf. AFM topography and MFM^41,42 measurement in Fig. 5a and c, respectively). A computer generated configuration with similar morphology as in the experiment is also shown in Fig. 5b. The magnetic field necessary to rotate the magnetisation direction of the cubes is larger than 0.1 T (cf., no significant difference between Fig. 5c and d). The small differences in the two figures are a consequence of local reorientation of magnetisation due to the applied field. Still the field is not strong enough to determine magnetisation of all particles.

Fig. 5 (a) Topography image of part of the chain of iron/iron oxide core/shell magnetic cube. (b) Chain of magnetic cubes with [111] magnetisation obtained by computer simulation (see text). (c) MFM image of the chain before the magnetic field is applied, and (d) under 0.1 T in-plane magnetic field. The direction of the magnetic field is indicated by the red arrow.

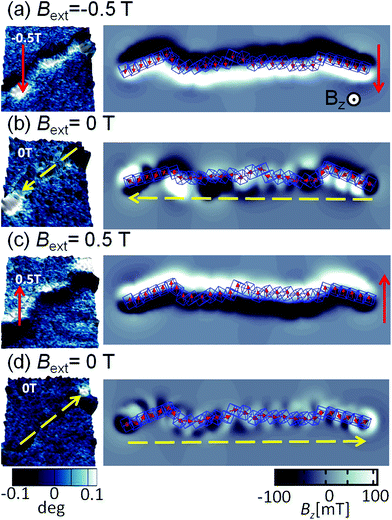
A sequence of MFM measurements at magnetic field −0.5 T, 0 T, 0.5 T, and 0 T is depicted in Fig. 6. In order to study magnetisation reversal in an external magnetic field, a field larger than that necessary to rotate the magnetisation direction of the cubes was applied. It is found that at −0.5 T, the magnetisation of the chain is completely aligned along the external field direction (see Fig. 6a). Therefore, we can conclude that the local magnetic field generated by cubes in the chain is less than 0.5 T. In fact, the analytical results for uniformly magnetised iron cubes give 0.35 T in the centre of the neighbouring cube placed face-to-face in a zig-zag configuration and 0.15 T in the head–tail configuration (see ESI†). Initially, a −0.5 T external magnetic field was applied to magnetise the chain in one direction and then the external magnetic field was turned off so that a spontaneous reordering of magnetisation can take place. No remanence is found when the external field is set back to zero, as observed in Fig. 6a and b. The magnetisation direction, after the external field is switched off, is along the chain backbone. The magnetisation orientation is determined by the previously applied external magnetic field, as it can be observed at the corners in Fig. 6b. In the next step, a 0.5 T external field is applied in the opposite direction. As one would expect, after the magnetic field is switched off, the resulting configuration shows that the pole north and south of the individual cubes and the chain as whole have interchanged their positions. The visualisation of the sequence obtained from the computer simulation is shown in the right panels of Fig. 6.

Fig. 6 Magnetic images of the chain of cubes. MFM images on left panels correspond to different magnetic fields applied in the following sequence (a) −0.5 T, (b) 0 T, (c) 0.5 T, and (d) 0 T. The direction of the applied magnetic field is indicated by a full line (red) and arrow, and magnetisation direction of the chain is indicated by dashed (yellow) arrow. The sequence of the changes of the magnetic field follows the order of the figures from the top (first) to the bottom (last). The visualisation of the magnetic field in the normal direction to the plane corresponding to the different magnetic configurations obtained from computer simulation is shown in the right panels.

The magnetic configuration of a broken chain is also shown in Fig. 7a. The MFM images illustrate that one end corresponds to the a north pole and other end to a south pole (the north and south poles are differentiated in the figure as light and dark contrasts), which is indicative of the magnetic moment aligned along the chain. This can be compared with the simulation results in Fig. 7e; the snapshots just before and after chain break-up are shown as well as the magnetic field perpendicular to the substrate plane. A constant force of 3 pN was applied on the terminal cubes. The initial configuration was a zig-zag magnetisation configuration where cubes are in face-by-face contact, seen on the right side of the panel in Fig. 7b. The transitions between these phases create the stray field. When the chain is finally broken, we observe at the two ends the stray field pointing up and down, similar to Fig. 7a.

Fig. 7 Mechanical manipulation of the chain composed of magnetic nanocubes. (a) Topography and MFM image of a broken chain segment. (b) Force required to break the chain and the calculated magnetic field in the orthogonal direction of the plane.

4 Conclusions

We have shown that a combination of magnetron sputtering and gas aggregation techniques represents a powerful tool to generate complex structures of magnetic NPs in a single step fabrication process. Single-stranded micrometer-long chains made up of 25 nm magnetic nanocubes are obtained by spontaneous self-assembly. The morphology of these chains is remarkably different from those of spheres or fabricated in suspension, i.e., they are long and single-stranded. It is found that dipolar magnetism is the driving force boosting chain formation and its structure reveals a tendency to keep connected under major degrees of structural strain in the process of formation and deposition. Using an exact analytical model and numerical simulations, we have estimated the magnetic energy scales governing the process. The low-kinetic energy of the particles inside the magnetron vacuum chamber and strong dipolar magnetic interaction between individual particles are responsible for agglomeration of the particles at very low volume fractions. The competition between anisotropic interactions and shape offers various pathways for self-assembly, each with exciting possibilities. Here, we have discussed self-assembly of 25 nm magnetic core/shell nanocubes with [111] magnetisation. Since anisotropies of iron and iron-oxide are different, i.e., [001] and [111], respectively, the overall anisotropy of the cubes can be selected through different core/shell ratios controlled by gas-aggregation process parameters. As a general frame, the present results demonstrate that the cluster gun technique can go beyond fabrication of single particles into controlled and reproducible self-assembly of NPs as they form.

Conflicts of interest

There are no conflicts to declare.

Author contributions

Ll.B. and Z.K. designed the work. A.A. prepared the samples. V.F. and L.L-M. performed the SPM experiments, J.O. the TEM measurements, and N.M. the Raman experiments. I.S. developed the theory and performed the computations. C.G. verified the material parameters. I.S. and C.G. wrote the manuscript with the participation of Ll.B. and Z.K. A.P. and B.M. participated in the discussion of the results and the final version of the paper.

Acknowledgements

The authors acknowledge the financial support from European Commission H2020 project DAFNEOX (Grant No. 645658). I. S. and Z. K. acknowledge the support of Ministry of Education, Science, and Technological Development of Republic of Serbia – projects ON171017 and III45018. Financial support from Spanish Ministry of Economy and Competitiveness through the Severo Ochoa Programme for Centres of Excellence in R&D (SEV-2015-0496), RTI2018-099960-B-I00, and MAT2015-71664-R, co-financed by the European Regional Development Fund, is gratefully acknowledged. I.S. and C.G. acknowledge the financial support received from Proyecto CONICYT PIA/Basal FB 0821 and CONICYT MEC80170122. A.P., V.F. and Z.K. thank Senzor-INFIZ (Serbia) for the cooperation provided during their respective secondments. Numerical calculations were run on the PARADOX supercomputing facility at the Scientific Computing Laboratory of the Institute of Physics Belgrade.

References

1. A. Fernández-Pacheco, R. Streubel, O. Fruchart, R. Hertel, P. Fischer and R. P. Cowburn, Nat. Commun., 2017, 8, 15756.
2. R. Streubel, P. Fischer, F. Kronast, V. P. Kravchuk, D. D. Sheka, Y. Gaididei, O. G. Schmidt and D. Makarov, J. Phys. D: Appl. Phys., 2016, 49, 363001.
3. L. Wu, A. Mendoza-Garcia, Q. Li and S. Sun, Chem. Rev., 2016, 116, 10473–10512.
4. E. Bellido, N. Domingo, I. Ojea-Jiménez and D. Ruiz-Molina, Small, 2012, 8, 1465–1491.
5. C. Dey, A. Chaudhuri, A. Ghosh and M. M. Goswami, ChemCatChem, 2017, 9, 1953–1959.
6. L. Balcells, C. Martínez-Boubeta, J. Cisneros-Fernández, K. Simeonidis, B. Bozzo, J. Oró-Sole, N. Bagués, J. Arbiol, N. Mestres and B. Martínez, ACS Appl. Mater. Interfaces, 2016, 8, 28599–28606.
7. N. Liakakos, T. Blon, C. Achkar, V. Vilar, B. Cormary, R. P. Tan, O. Benamara, G. Chaboussant, F. Ott, B. Warot-Fonrose, E. Snoeck, B. Chaudret, K. Soulantica and M. Respaud, Nano Lett., 2014, 14, 3481–3486.
8. L. Wu, P.-O. Jubert, D. Berman, W. Imaino, A. Nelson, H. Zhu, S. Zhang and S. Sun, Nano Lett., 2014, 14, 3395–3399.
9. E. Myrovali, N. Maniotis, A. Makridis, A. Terzopoulou, V. Ntomprougkidis, K. Simeonidis, D. Sakellari, O. Kalogirou, T. Samaras, R. Salikhov, M. Spasova, M. Farle, U. Wiedwald and M. Angelakeris, Sci. Rep., 2016, 6, 37934.
10. D. Llamosa, M. Ruano, L. Martinez, A. Mayoral, E. Roman, M. Garcia-Hernandez and Y. Huttel, Nanoscale, 2014, 6, 13483–13486.
11. H. Haberland, M. Karrais and M. Mall, Zeitschrift für Physik D Atoms, Molecules and Clusters, 1991, vol. 20, pp. 413–415.
12. M. Mery, N. Orellana, C. A. Acevedo, S. Oyarzun, F. Araneda, G. Herrera, D. Aliaga, W. Creixell, T. Corrales and C. Romero, Materials, 2018, 11, 2574.
13. L. Martínez, K. Lauwaet, G. Santoro, J. Sobrado, R. Peláez, V. J. Herrero, I. Tanarro, G. Ellis, J. Cernicharo, C. Joblin, Y. Huttel and J. Martin Gago, Sci. Rep., 2018, 8, 7250.
14. G. Singh, H. Chan, A. Baskin, E. Gelman, N. Repnin, P. Král and R. Klajn, Science, 2014, 345, 1254132.
15. B. Bian, G. Chen, Q. Zheng, J. Du, H. Lu, J. P. Liu, Y. Hu and Z. Zhang, Small, 2018, 14, 1801184.
16. K. Gandha, K. Elkins, N. Poudyal, X. Liu and J. P. Liu, Sci. Rep., 2014, 4, 5345.
17. C. Gatel, F. J. Bonilla, A. Meffre, E. Snoeck, B. Warot-Fonrose, B. Chaudret, L.-M. Lacroix and T. Blon, Nano Lett., 2015, 15, 6952–6957.
18. L. Rossi, J. G. Donaldson, J.-M. Meijer, A. V. Petukhov, D. Kleckner, S. S. Kantorovich, W. T. M. Irvine, A. P. Philipse and S. Sacanna, Soft Matter, 2018, 14, 1080–1087.
19. J. G. Donaldson and S. S. Kantorovich, Nanoscale, 2015, 7, 3217–3228.
20. R. Messina and I. Stanković, Physica A: Statistical Mechanics and its Applications, 2017, vol. 466, pp. 10–20.
21. R. Messina, L. A. Khalil and I. Stanković, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 011202.
22. I. Stankovic, M. Dasic, J. A. Otalora and C. García, Nanoscale, 2019, 11, 2521–2535.
23. A. Baskin, W.-Y. Lo and P. Král, ACS Nano, 2012, 6, 6083–6090.
24. A. Satoh, Modeling of magnetic particle suspensions for simulations, CRC Press, 2017.
25. F. Mazuel, S. Mathieu, R. Di Corato, J.-C. Bacri, T. Meylheuc, T. Pellegrino, M. Reffay and C. Wilhelm, Small, 2017, 13, 1701274.
26. S. Mehdizadeh Taheri, M. Michaelis, T. Friedrich, B. Förster, M. Drechsler, F. M. Römer, P. Bösecke, T. Narayanan, B. Weber, I. Rehberg, S. Rosenfeldt and S. Förster, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 14484–14489.
27. D. A. J. Herman, S. Cheong, M. J. Banholzer and R. D. Tilley, Chem. Commun., 2013, 49, 6203–6205.
28. R. Engel-Herbert and T. Hesjedal, J. Appl. Phys., 2005, 97, 074504.
29. B. S. John, A. Stroock and F. A. Escobedo, J. Chem. Phys., 2004, 120, 9383–9389.
30. X. Zhang, Z. Zhang and S. C. Glotzer, J. Phys. Chem. C, 2007, 111, 4132–4137.
31. D. Luo, C. Yan and T. Wang, Small, 2015, 11, 5984–6008.
32. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
33. H. Kamberaj, R. J. Low and M. P. Neal, J. Chem. Phys., 2005, 122, 224114.
34. A. Pratt, L. Lari, O. Hovorka, A. Shah, C. Woffinden, S. P. Tear, C. Binns and R. Kröger, Nat. Mater., 2014, 13, 26.
35. Y. Qiang, J. Antony, A. Sharma, J. Nutting, D. Sikes and D. Meyer, J. Nanopart. Res., 2006, 8, 489–496.
36. A. Shavel, B. Rodríguez-González, M. Spasova, M. Farle and L. Liz-Marzán, Adv. Funct. Mater., 2007, 17, 3870–3876.
37. K. Leistner, M. Yang, C. Damm, S. Oswald, A. Petr, V. Kataev, K. Nielsch and K. L. Kavanagh, Nanoscale, 2017, 9, 5315–5322.
38. S. Peng, C. Wang, J. Xie and S. Sun, J. Am. Chem. Soc., 2006, 128, 10676–10677.
39. O. N. Shebanova and P. Lazor, J. Solid State Chem., 2003, 174, 424–430.
40. C. Moya, A. M. Abdelgawad, N. Nambiar and S. A. Majetich, J. Phys. D: Appl. Phys., 2017, 50, 325003.
41. S. Schreiber, M. Savla, D. V. Pelekhov, D. F. Iscru, C. Marginean Selcu, P. Chris Hammel and G. Agarwal, Small, 2008, 4, 270–278.
42. S. Sievers, K.-F. Braun, D. Eberbeck, S. Gustafsson, E. Olsson, H. W. Schumacher and U. Siegner, Small, 2012, 8, 2675–2679.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/C9NR02314C

---