Cross-conjugation increases the conductance of meta-connected fluorenones

Abstract

Charge transport is strongly suppressed by destructive quantum interference (DQI) in meta-connected 1,1′-biphenyl-containing molecules, resulting in low electrical conductance. Surprisingly, we have found that DQI is almost entirely overcome by adding a bridging carbonyl, to yield a cross-conjugated fluorenone. This contrasts with other π-systems, such as para-connected anthraquinone, where cross-conjugation results in low conductance.

---

Understanding charge transport through single molecules is essential for the development of single-molecule electronic devices.¹ Studies of single molecules trapped between two metallic electrodes demonstrate that many factors affect charge transport through a molecular device, including the nature of the anchor groups, the molecular length, the nature of spacers and the electronic structures of the aromatic subunits.² Other key factors are molecular conformation, the energy gap between the highest occupied and the lowest unoccupied molecular orbitals (the HOMO–LUMO gap),³ the alignment of this gap to the Fermi level of the metal electrodes and the coordination geometry at the metal–molecule contacts. Recent studies have also revealed that changing the connectivity of electrodes to phenyl rings from para to meta reduces the electrical conductance, because it switches the π system from constructive quantum interference (CQI) to destructive quantum interference (DQI).⁴ Here we examine how this transition from CQI to DQI can be controlled by placing bridging moieties across the biphenyl core.⁵ Previous studies have shown that para-connected cross-conjugated anthraquinone-based molecules have a significantly lower conductance compared to their fully conjugated counterparts⁶ and that para-connected fluorenones exhibit CQI in the HOMO–LUMO gap.⁷ Here we present the first experimental study of the single-molecule electrical conductance of a meta-connected cross-conjugated core. We demonstrate that the DQI of the meta-connected biphenyl core is alleviated in meta-connected cross-conjugated fluorenone, leading to a high conductance, which is comparable with para-connected fluorenone. These experiments support a recent prediction that cross conjugation increases the conductance of meta-connected anthraquinone.⁸

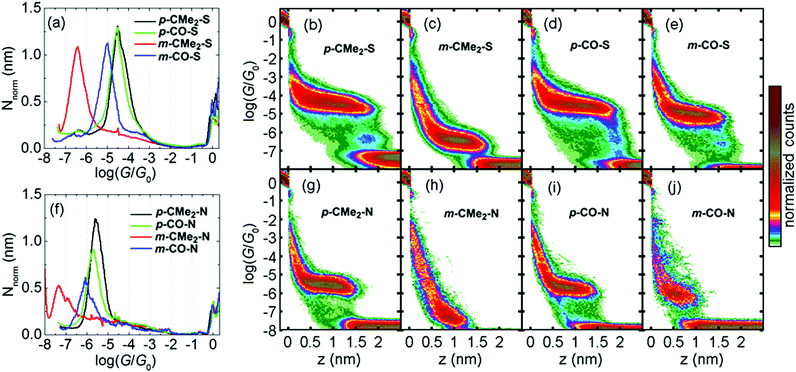
We compared the single-molecule conductance of eight compounds with the molecular structures illustrated in Fig. 1: fluorenes p-CMe₂-S, m-CMe₂-S, p-CMe₂-N and m-CMe₂-N, and fluorenones p-CO-S, m-CO-S, p-CO-N and m-CO-N. The synthesis and chemical characterization of these compounds are reported in the ESI.† Molecules with suffixes p- and m- are referred to as para- and meta-connected respectively, which reflects the connectivity of the acetylene linkers to their biphenyl cores in the absence of bridging moieties. Scanning tunneling microscopy-break junction (STM-BJ) measurement of these eight compounds are summarized in Fig. 2, which shows the low-bias conductance of each compound at fixed applied bias voltage of 0.2 V. For the meta-connected m-CMe₂-N we had to increase the bias to 0.8 V in order to resolve the full conductance distribution due to its very low conductance. We performed thousands of open-close cycles on each sample and focused on the opening stage of the measurement. For more details about the sample preparation and the measurement methodology, see the ESI.† The precise number and percentage of molecular junctions observed in each case is given in the caption to Fig. 2.

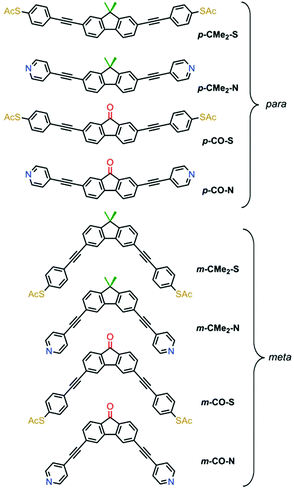Fig. 1 Chemical structures of the eight compounds investigated. The biphenyl core is common throughout; fluorenones have a carbonyl bridge (red) and fluorenes have a –CMe₂ bridge (green).

Fig. 2 (a/f) 1D conductance histograms for thiol/pyridyls-terminated compounds respectively. (b–e/g–j) log(G/G₀)–z 2D histograms generated from all plateau-containing traces for thiol/pyridyl terminated compounds. N_junc = 6486 (68%) (p-CMe₂-S), 6180 (49%) (m-CMe₂-S), 4881 (52%) (p-CO-S), 2318 (30%) (m-CO-S), 1600 (40%) (p-CMe₂-N), 579 (39%) (m-CMe₂-N), 1517 (17%) (p-CO-N), 310 (9%) (m-CO-N).

We processed the data by first separating the molecular junctions from the pure-tunneling junctions (containing no molecule) using an algorithm which searches for plateaus (details in the ESI†). The resulting 1D and 2D ‘molecular-junction’ histograms from this procedure are shown in Fig. 2 (examples of selected conductance–distance, G–z, traces for each compound are shown in Fig. S4.1†).§ Histograms of the ‘tunneling-only’ traces are shown in Fig. S4.2.† The 1D histograms are normalized according to the procedure described in ref. 9 allowing facile comparison of the average length of the plateau region for each compound (i.e. from the point where the plateau begins). To extract a conductance for each compound, we fit a single Gaussian curve to each 1D histogram and extract the peak position. A summary of the low-bias conductance values is presented in Table 1.

Table 1 Measured low-bias single molecule conductance values and junction length data. The values in parentheses are the FWHM. The Au–Au distance is the calculated separation between two gold atoms attached to the two terminal S/N atoms of the extended molecules, from the calculated molecular geometry. The DFT-predicted HOMO–LUMO gaps (obtained from Table S1 of the ESI)

Molecule	Measured low-bias conductance (log(G/G0))	Measured 95^th percentile (L95) + 0.4 nm	Theoretical Au–Au distance (nm)	DFT-predicted HOMO–LUMO gaps (eV)
p-CMe 2 -S	−4.5 (0.9)	2.6	2.5	2.13
m-CMe 2 -S	−6.4 (0.8)	2.4	2.2	2.63
p-CO-S	−4.6 (0.8)	2.6	2.5	1.65
m-CO-S	−5.0 (0.8)	2.3	2.2	1.81
p-CMe 2 -N	−5.6 (0.7)	2.2	2.4	2.30
m-CMe 2 -N	−7.4 (0.6)	1.9	1.8	2.95
p-CO-N	−5.7 (0.6)	2.2	2.4	1.96
m-CO-N	−6.1 (0.7)	1.7	1.8	2.08

---

The most surprising outcome of the STM-BJ measurements is that for the meta-compounds with both thiol and pyridyl anchor groups, replacing the CMe₂ bridge by a C=O leads to a dramatic increase in conductance by approximately a factor 30. The same replacement in the para-compounds has a negligible effect (both p-CO compounds actually appear to be fractionally lower in conductance than their p-CMe₂ counterparts). This agrees with our previous results on para-connected OPE3 molecules, where different substituents on the central phenyl ring have little influence on electrical conductance.^4d,10 Viewed another way, switching from para to meta connectivity when the bridge is CMe₂ causes the conductance to drop two orders of magnitude. In contrast, when the bridge is C=O, the same operation causes the conductance to drop by only a factor 2–3. This behavior is remarkable, because from a valence-bond perspective, each terminal S/N atom is formally cross-conjugated via the carbonyl group, as noted for similar structures by Estrada et al. and Homnick et al.,¹¹ and therefore no direct alternating single/double bond path exists for meta-connectivity.

The junction length distributions (shown in Fig. S4.3,† with mean values from Gaussian fits quoted in Table 1) confirm that we measure fully-stretched junctions at the upper extreme of the distribution. After correcting for the initial jump-out-of-contact (JOC) by adding 0.4 nm to the raw junction lengths (L), we find very good agreement between the calculated Au–Au distance (for gold atoms attached to the terminal S/N atoms) and the 95th percentile length (L₉₅). We find that the longest plateaus for thiol-terminated junctions tend to exceed the predicted maximum value by 1–2 Å, whereas the pyridyls tend to be shorter than this value by 1–2 Å. This behavior agrees with our previous observations, which for thiols¹² is a result of the strength of the Au–S bond which produces more significant deformation of the electrodes compared with weaker binding groups like pyridyl. For both para fluorene and fluorenone compounds with the same anchor group, the break-off histograms almost coincide (Fig. S4.3†). In contrast, for the meta compounds, the histograms for m-CO compounds are noticeably centred towards lower values compared to the m-CMe₂ counterparts, indicating plateaus are on average 1–2 Å shorter. This indicates that conjugation slightly affects junction binding strength.

Comparison between the thiol and the pyridyl anchor groups reveals that for any given backbone, the conductance is about 10 times lower for pyridyls compared to thiols. A few published reports directly compare thiol anchors with pyridyls, and in general the pyridyls all display lower conductance than the corresponding thiols.¹³ In ref. 14 the benzenethiol, PhS, groups in an OPE3 wire were exchanged for Py, resulting in a 30-fold drop in conductance. In two independent studies of oligophenyls 1,4-di(pyridin-4-yl)benzene was measured to have a conductance of log(G/G₀) = −4.7,¹⁵ whereas structurally-analogous p-terphenyl dithiol has a conductance of log(G/G₀) = −3.2 (ref. 12) (also about a factor 30 difference). Therefore, our results are consistent with these previous measurements. We also studied the voltage dependence of the conductance, log(G/G₀) vs. V, presented in Fig. S4.5 (section 4 of the ESI†). In short, all compounds tested showed a moderate increase in conductance between 0 V and 1.0 V, but no major differences in log(G/G₀) vs. V behaviour were found between the para and the meta compounds. Finally, for the thiol measurements we observed a faint low-conductance group after the main plateau, which we have previously shown arises from junctions involving gold adatoms and sulfur groups from neighboring molecules.¹²

To calculate the conductance of each molecule connected to two gold electrodes, the optimal geometry and ground state Hamiltonian were obtained using the SIESTA¹⁶ implementation of density functional theory (DFT) and the room-temperature electrical conductance was calculated using the Gollum¹⁷ code (see computational methods in the ESI). Fig. 3 shows the calculated conductance of the molecules in para and meta connectivities for fluorene and fluorenone with thiol (a and c) and pyridine anchors (b and d) respectively (see relaxed structure of the molecules between leads in Fig. S5-1 and S5-2†). Since the energy difference between the molecular orbitals and the DFT-predicted Fermi energy (E_F, chosen to be zero in Fig. 3) and is usually unreliable, resulting in E_F being placed too close to the HOMO (LUMO) for thiol (pyridyl) anchors, results are shown for a range of Fermi energies in the vicinity of the middle of the HOMO–LUMO gap (see section 8 in the ESI† for further discussion). For comparison, the horizontal bands in Fig. 3 show the measured conductance values in the second column of Table 1. The widths of the horizontal bands correspond to the experimental full width at half maximum (FWHM) of the conductance peak.

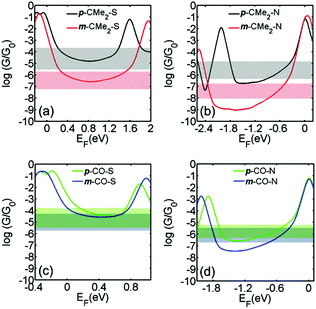Fig. 3 The calculated room-temperature conductances of (a) p-CMe₂-S and m-CMe₂-S; (b) p-CMe₂-N and m-CMe₂-N; (c) p-CO-S and m-CO-S; (d) p-CO-N and m-CO-N; connected to gold electrodes, obtained from DFT. Results are plotted against the Fermi energy E_F, where E_F = 0 corresponds to the DFT-predicted Fermi energy. For comparison, the horizontal bands show the measured conductance values in the second column of Table 1. The widths of the horizontal bands are equal to the FWHM quoted in the second column of Table 1.

Fig. 3 shows that there is qualitative agreement between calculated and measured conductance trends of the molecules, for a range of Fermi energies near the gap centre. For both thiol and pyridyl anchors, there is a large ratio (about 2 orders of magnitude) between the conductances of para vs. meta-connected fluorene molecules and a significantly smaller ratio between the conductance of the para and meta-connected fluorenones. The magnitude of the conductance with pyridyl anchors is about one order of magnitude lower than with thiol anchors. Furthermore, the conductance of the meta-connected fluorenone with thiol anchors is surprisingly high. From these results, we conclude that the bridge moiety strongly enhances the conductance of the meta-connected molecules, but does not significantly influence para-connected molecules.

Table 1 shows that there is a correlation between the DFT-predicted HOMO–LUMO gaps and the measured conductances. When switching from para to meta connectivity, the HOMO–LUMO gaps always increase. However, the increase is small for the fluorenones and significantly larger for the fluorenes. This correlates with the smaller reduction in conductance for the fluorenone core compared with fluorene, and can be attributed to conjugation between the anchor groups and the C=O in the meta-fluorenones. The gap for para-fluorenes, however, is always larger than the corresponding meta-fluorenones, yet the conductance is lower for the meta-fluorenones than the para-fluorenes. This demonstrates that HOMO–LUMO gaps are not absolute predictors of molecular conductance, and that quantum interference due to scattering from the bridge moiety plays a significant role.

To demonstrate the role of the bridge in the core of the molecule, we considered the series of tight binding models (Fig. S6.1†), which demonstrate that the main effect of the bridge moiety is to alleviate DQI from the middle of HOMO and LUMO of the meta-connected biphenyl core and increase the conductance of the resulting meta-connected fluorene and fluorenone cores.

Conclusions

We have studied the single-molecule conductance of a family of fluorene and fluorenone molecules with para or meta connectivities and thiol/pyridyl anchor groups. Our results reveal that the molecular conductances are similar for para connectivity when the binding groups are identical, whereas for meta connectivity the conductance of fluorene is much lower than that of fluorenone, which demonstrates the striking role of the bridge moiety for meta connectivity. The significant outcome is to demonstrate that when the bridge is a methylene carbon, and the anchor groups are in meta positions, DQI dominates and conductance is strongly suppressed. In complete contrast, when the bridge is a carbonyl, the anticipated DQI is almost completely absent, and the conductance of the meta-connected molecule is only three times less than the para-connected case. This is highly surprising because for meta connectivity, each thiol and pyridyl S/N anchor atoms are cross-conjugated via the carbonyl group, and no bond-alternation path directly connects the two (unlike in the para case). To understand this, we carried out DFT-based transport calculations and examined a simple tight binding model of the extended π-system. This reveals that any bridge group alleviates the DQI to a certain extent, and increasing the strength of the coupling to the bridge further suppresses DQI. This indicates that, unlike a methylene carbon, the carbonyl group provides significant coupling between the two phenyl rings.

Author contributions

HLA, EL, SJH, CJL, RJN and SS helped conceive and design the study, AA, IG, CJL, HS and SS carried out and interpreted the transport calculations, H-WJ and TK synthesized and characterized the molecules, NA, GR-B, MT-G, EL, SJH and RJN carried out and helped interpret the single molecule junction experiments and HLA, CJL, SJH and RJN directed the study. All authors contributed to the preparation of the paper, which was principally drafted by EL.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

We thank the EPSRC for support (grants EP/M016110/1, EP/M014452/1, EP/M005046/1, EP/M014169/1 and EP/M029522/1) and the EPSRC UK National Mass Spectrometry Facility at Swansea University for MALDI spectra. H. S. and S. S. acknowledge the Leverhulme Trust for Leverhulme Early Career Fellowship no. ECF-2017-186 and ECF-2018-375. H. S. also acknowledges the UKRI for Future Leaders Fellowship no. MR/S015329/1. T. K. thanks Nippon Shokubai Ltd. for funding. IMDEA Nanociencia acknowledges support from the ‘Severo Ochoa’ Programme for Centres of Excellence in R&D (MINECO, Grant SEV-2016-0686). EC H2020 FET Open project 767187 “QuIET”, the EU project BAC-TO-FUEL and by Spanish MINECO (grants MAT2014-57915-R, MAT2017-88693-R and MDM-2014-0377) and Comunidad de Madrid (grant NANOFRONTMAG-CM, S2013/MIT-2850).

Notes and references

1. (a) E. Leary, A. La Rosa, M. T. González, G. Rubio-Bollinger, N. Agraït and N. Martín, Chem. Soc. Rev., 2015, 44, 920–942; (b) H. Sadeghi, Nanotechnology, 2018, 29, 373001.
2. (a) T. Sendler, K. Luka-Guth, M. Wieser, J. Wolf, M. Helm, S. Gemming, J. Kerbusch, E. Scheer, T. Huhn and A. Erbe, Adv. Sci., 2015, 2, 1500017; (b) M. L. Perrin, E. Galán, R. Eelkema, J. M. Thijssen, F. Grozema and H. S. van der Zant, Nanoscale, 2016, 8, 8919–8923.
3. (a) E. Leary, B. Limburg, A. Alanazy, S. Sangtarash, I. Grace, K. Swada, L. J. Esdaile, M. Noori, M. T. González, G. Rubio-Bollinger, H. Sadeghi, A. Hodgson, N. Agraït, S. J. Higgins, C. J. Lambert, H. L. Anderson and R. J. Nichols, J. Am. Chem. Soc., 2018, 140, 12877–12883; (b) N. Algethami, H. Sadeghi, S. Sangtarash and C. J. Lambert, Nano Lett., 2018, 18, 4482.
4. (a) C. R. Arroyo, S. Tarkuc, R. Frisenda, J. S. Seldenthuis, C. H. Woerde, R. Eelkema, F. C. Grozema and H. S. van der Zant, Angew. Chem., 2013, 125, 3234–3237; (b) S. Sangtarash, H. Sadeghi and C. J. Lambert, Nanoscale, 2016, 8, 13199–13205; (c) S. Sangtarash, C. Huang, H. Sadeghi, G. Sorohhov, J. R. Hauser, T. Wandlowski, W. Hong, S. Decurtins, S.-X. Liu and C. J. Lambert, J. Am. Chem. Soc., 2015, 137, 11425–11431; (d) X. Liu, S. Sangtarash, D. Reber, D. Zhang, H. Sadeghi, J. Shi, Z. Y. Xiao, W. Hong, C. J. Lambert and S. X. Liu, Angew. Chem., Int. Ed., 2017, 56, 173–176; (e) H. Sadeghi, J. A. Mol, C. S. Lau, G. A. D. Briggs, J. Warner and C. J. Lambert, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 2658–2663.
5. N. M. Jenny, M. Mayor and T. R. Eaton, Eur. J. Org. Chem., 2011, 4965–4983.
6. C. M. Guédon, H. Valkenier, T. Markussen, K. S. Thygesen, J. C. Hummelen and S. J. Van Der Molen, Nat. Nanotechnol., 2012, 7, 305.
7. G. J. Ashwell, B. Urasinska, C. Wang, M. R. Bryce, I. Grace and C. J. Lambert, Chem. Commun., 2006, 4706–4708.
8. J. Alqahtani, H. Sadeghi, S. Sangtarash and C. J. Lambert, Angew. Chem., Int. Ed., 2018, 57, 15065–15069.
9. M. T. Gonzalez, E. Leary, R. García, P. Verma, M. A. Herranz, G. Rubio-Bollinger, N. Martín and N. Agraït, J. Phys. Chem. C, 2011, 115, 17973–17978.
10. M. T. González, X. Zhao, D. Z. Manrique, D. Miguel, E. Leary, M. Gulcur, A. S. Batsanov, G. Rubio-Bollinger, C. J. Lambert and M. R. Bryce, J. Phys. Chem. C, 2014, 118, 21655–21662.
11. (a) L. A. Estrada and D. C. Neckers, J. Org. Chem., 2009, 74, 8484–8487; (b) P. J. Homnick, J. S. Tinkham, R. Devaughn and P. M. Lahti, J. Phys. Chem. A, 2013, 118, 475–486.
12. E. Leary, L. A. Zotti, D. Miguel, I. R. Márquez, L. Palomino-Ruiz, J. M. Cuerva, G. Rubio-Bollinger, M. T. González and N. Agrait, J. Phys. Chem. C, 2018, 122, 3211–3218.
13. (a) W. Hong, D. Z. Manrique, P. Moreno-García, M. Gulcur, A. Mishchenko, C. J. Lambert, M. R. Bryce and T. Wandlowski, J. Am. Chem. Soc., 2012, 134, 2292–2304; (b) P. Moreno-García, M. Gulcur, D. Z. Manrique, T. Pope, W. Hong, V. Kaliginedi, C. Huang, A. S. Batsanov, M. R. Bryce, C. J. Lambert and T. Wandlowski, J. Am. Chem. Soc., 2013, 135, 12228–12240; (c) R. Frisenda, S. Tarkuç, E. Galán, M. L. Perrin, R. Eelkema, F. C. Grozema and H. S. J. van der Zant, Beilstein J. Nanotechnol., 2015, 6, 1558–1567.
14. S. Grunder, R. Huber, S. Wu, C. Schönenberger, M. Calame and M. Mayor, Eur. J. Org. Chem., 2010, 833–845.
15. M. Kamenetska, S. Y. Quek, A. Whalley, M. Steigerwald, H. Choi, S. G. Louie, C. Nuckolls, M. Hybertsen, J. Neaton and L. Venkataraman, J. Am. Chem. Soc., 2010, 132, 6817–6821.
16. J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745.
17. J. Ferrer, C. J. Lambert, V. M. García-Suárez, D. Z. Manrique, D. Visontai, L. Oroszlany, R. Rodríguez-Ferradás, I. Grace, S. W. D. Bailey, K. Gillemot, H. Sadeghi and L. A. Algharagholy, New J. Phys., 2014, 16, 093029.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9nr01235d

‡ These authors contributed equally to this work.

§ All individual traces (G–z and I–V) for the STM experiments are freely available after an embargo date of 01/10/19 at the following repository address: http://dx.doi.org/10.17638/datacat.liverpool.ac.uk/584.

---