Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Exchange coupling in a frustrated trimetric molecular magnet reversed by a 1D nano-confinement†
Oleg
Domanov
 a,
Eugen
Weschke
b,
Takeshi
Saito
a,
Eugen
Weschke
b,
Takeshi
Saito
 c,
Herwig
Peterlik
a,
Thomas
Pichler
a,
Michael
Eisterer
c,
Herwig
Peterlik
a,
Thomas
Pichler
a,
Michael
Eisterer
 d and
Hidetsugu
Shiozawa
d and
Hidetsugu
Shiozawa
 *ae
*ae
aFaculty of Physics, University of Vienna, Boltzmanngasse 5, 1090 Vienna, Austria. E-mail: hidetsugu.shiozawa@univie.ac.at; hide.shiozawa@jh-inst.cas.cz
bHelmholtz-Zentrum Berlin für Materialien und Energie GmbH, Albert-Einstein-Str. 15, 12489 Berlin, Germany
cNanomaterials Research Institute, National Institute of Advanced Industrial Science and Technology (AIST), 1-1-1 Higashi, Tsukuba 305-8565, Japan
dAtominstitut, TU Wien, Stadionallee 2, 1020 Vienna, Austria
eJ. Heyrovsky Institute of Physical Chemistry, Czech Academy of Sciences, Dolejskova 3, 182 23 Prague 8, Czech Republic
First published on 13th May 2019
Abstract
Single-molecule magnets exhibit magnetic ordering due to exchange coupling between localized spin components that makes them primary candidates as nanometric spintronic elements. Here we manipulate exchange interactions within a single-molecule magnet by nanometric structural confinement, exemplified with single-wall carbon nanotubes that encapsulate trimetric nickel(II) acetylacetonate hosting three frustrated spins. It is revealed from bulk and Ni 3d orbital magnetic susceptibility measurements that the carbon tubular confinement allows a unique one-dimensional arrangement of the trimer in which the nearest-neighbour exchange is reversed from ferromagnetic to antiferromagnetic, resulting in quenched frustration as well as the Pauli paramagnetism is enhanced. The exchange reversal and enhanced spin delocalisation demonstrate the means of mechanically and electrically manipulating molecular magnetism at the nanoscale for nano-mechatronics and spintronics.
The development of novel magnetic materials is of vital importance to advances in nanotechnology, high-density data storage applications and quantum computing. Since the field of molecular magnetism emerged in the 1980s,1 scientists have pursued the development of novel magnetic materials beyond inorganic three-dimensional (3D) solids. Single molecule and single chain magnets (SMM and SCM) are fundamentally different from traditional bulk magnets since the magnetic interaction predominantly takes place within the molecule itself in which the magnetic centers are exchange coupled via the ligands.2 The surroundings of molecular magnets become relevant at low temperature as intermolecular interactions emerge3 while at room temperature some samples degrade over time in the presence of oxygen and water.
Single-wall carbon nanotubes (SWCNT) have been intensively studied not only due to their advanced fundamental properties,4,5 but also due to their enormous potential for technological applications. One of their unprecedented abilities is to encapsulate6,7 or confine8,9 foreign substances that makes SWCNTs robust skeletons for atoms and molecules to be arranged in a one-dimensional (1D) structure while being protected from environmental factors.10 The present work focuses on a trimetric nickel(II) acetylacetonate (Ni(acac)2) molecular magnet (see Fig. 1) in which three nickel ions are superexchange coupled via the oxo ligands.11 1D arrays of Ni(acac)2 (1D-Ni(acac)2) are formed successfully inside the SWCNTs, as revealed by X-ray diffraction (XRD). Their magnetic properties are investigated using the superconducting quantum interference device (SQUID) and X-ray magnetic circular diachromism (XMCD) at various magnetic fields and temperatures. The net magnetisation of 1D-Ni(acac)2 is substantially reduced as compared with that of the bulk Ni(acac)2(3D-Ni(acac)2), which is attributed to the changes in superexchange interactions within the trimer. A detailed analysis of the magnetic susceptibility data reveals anisotropic quenching of exchange couplings among the trimetric spins. The present work demonstrates that the superexchange coupling within the molecular magnet can be controllably quenched by the uniaxial stress inside the SWCNT that paves the way towards reversible magnetic switching within nanometric scales for spintronics.
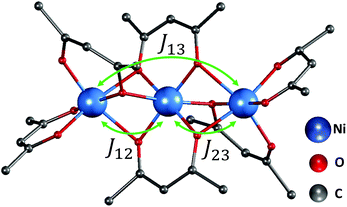 | ||
| Fig. 1 The trimer structure of nickel(II) acetylacetonate (Ni(acac)2).12 The spins of nickel ions are superexchange coupled via the oxygen ligands with exchange constant J12,23 between the nearest-neighbour spins and J13 between the terminal spins. Hydrogen atoms are not shown. | ||
In the present work, we study the magnetic properties of Ni(acac)2-filled SWCNTs with mean diameters of 1.3(±0.1)nm and 2.1(±0.1)nm, referred to as 1D-Ni(acac)2@NT1.3 and 1D-Ni(acac)2@NT2.1, respectively, in comparison to a pristine SWCNT sample with an intermediate mean diameter of 1.7 nm (NT 1.7) and Ni(acac)2 in powder form (3D-Ni(acac)2). XMCD measurements have been carried out on the Ni(acac)2-filled SWCNT with an intermediate mean diameter of 1.7(±0.1)nm (1D-Ni(acac)2@NT1.7). The encapsulation of Ni(acac)2 inside SWCNTs has been confirmed by Raman spectroscopy according to the literature10,13–19 (see the ESI, section 2† for more details).
Fig. 2 shows the X-ray diffraction (XRD) profiles of 3D-Ni(acac)2, NT1.7, 1D-Ni(acac)2@NT2.1 and 1D-Ni(acac)2@NT1.3.
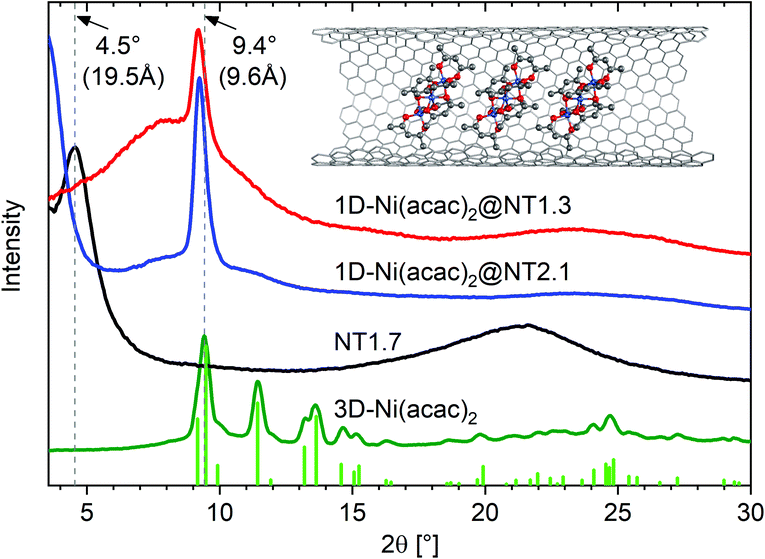 | ||
| Fig. 2 XRD profiles of 1D-Ni(acac)2@NT2.1 and 1D-Ni(acac)2@NT1.3, together with those of NT1.7 and 3D-Ni(acac)2. The vertical lines are the diffraction lines reproduced from the literature lattice parameters.12 The inset illustrates a 1D stacking geometry of 1D-Ni(acac)2 in (13, 12) carbon nanotubes with a diameter of 1.7 nm. | ||
The XRD profile for the 3D-Ni(acac)2 verifies the orthorhombic structure of the trimer that matches well with the diffraction lines simulated with the FullProf software package (wavelength: λ = 0.154 nm, crystal parameters: space group Pca21, a = 2.32 nm, b = 0.96 nm, c = 1.57 nm).12 The pristine NT1.7 exhibits a bundle peak at around 2θ = 4.5° which stems from the hexagonal arrangement of bundled SWCNTs. The complete quenching of this peak is typical of molecule-filled SWCNTs with a high filling degree20 and is due to a change in the form factor. The broad peak centered around 2θ = 22° can be assigned to carbon (002).21 After filling, the X-ray diffraction pattern is fundamentally altered as all but one peak are not observed, indicating a change from the orthorhombic structure of 3D-Ni(acac)2 to the 1D structure of Ni(acac)2 inside SWCNTs. For both 1D-Ni(acac)2@NT2.1 and 1D-Ni(acac)2@NT1.3, one prominent peak is located at a diffraction angle of 2θ = 9.2° corresponding to a periodic spacing of 9.6 Å, slightly below the first peak of the orthorhombic 3D-Ni(acac)2 at 2θ = 9.4° (9.4 Å).12 The periodic spacing of 1D-Ni(acac)2 is summarized in Table 1. dcnt − 2dvdW is the diameter available for filling molecules, where dvdW is the van der Waals distance towards the walls and dcnt is the nanotube diameter.
| d cnt | d cnt − 2dvdW | 1D spacing | Ni/C |
|---|---|---|---|
| 1.3 nm | 6.2 Å | 9.61 Å | 4.3%at |
| 2.1 nm | 14.2 Å | 9.56 Å | 1.5%at |
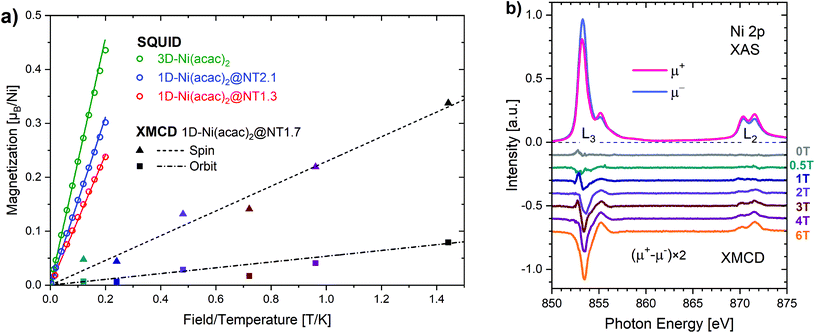
In the Ni(acac)2 trimer three nickel ions are superexchange coupled via the oxygen ligands11 (see Fig. 1). The spin only state of the nickel 3d shell has two unpaired electrons (S = 1), giving rise to a theoretical ground state magnetisation per nickel of 2.83μB. The superexchange interaction can be described by considering the exchange coupling between the neighboring ions (J = J12,23) and between the two terminal ions (J13). J can be expected to be ferromagnetic and J13 anti-ferromagnetic. The former is readily anticipated according to the Goodenough–Kanamori–Anderson rules22–26 as discussed later. In Fig. 3(a), the magnetisation data at 5 K for 3D-Ni(acac)2, 1D-Ni(acac)2@NT2.1 and 1D-Ni(acac)2@NT1.3 are plotted against a field/temperature up to 0.2 T K−1 (magnetic field up to 1 T) after subtraction of SWCNT magnetism (see the ESI, section 3† for more details). The magnetisation per nickel atom has been evaluated by taking the nickel atomic concentration derived from the XPS data into account (see ESI, section 4†).27 The magnetisation curves are linear at magnetic fields up to ±0.7 T for 3D-Ni(acac)2, ±0.8 T for 1D-Ni(acac)2@NT2.1 and ±0.9 T for 1D-Ni(acac)2@NT1.3 so that according to the Curie law we can calculate the effective magnetic moment 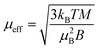 , where kB is the Boltzmann constant, μB is the Bohr magneton, T is the temperature, B is the field and M is the magnetisation.‡
, where kB is the Boltzmann constant, μB is the Bohr magneton, T is the temperature, B is the field and M is the magnetisation.‡
μ eff evaluated for 3D-Ni(acac)2 is 3.15 in units of μB, in agreement with a previously reported experimental value of 3.23,11 that is reduced to 2.68 (85% of 3.15) for 1D-Ni(acac)2@NT2.1, and further to 2.27 (72% of 3.15) for 1D-Ni(acac)2@NT1.3. The reduction is larger for 1D-Ni(acac)2 in the smaller-diameter SWCNT and is therefore attributed to the structural confinement.
The encapsulation of Ni(acac)2 in conductive SWCNTs makes them much more stable not only under ultra-high vacuum conditions but also under exposure to X-ray radiation that enables more demanding spectroscopy experiments such as X-ray magnetic circular dichroism (XMCD) that provides the element and orbital selective information on spin and orbital magnetic moments.28–31
Fig. 3(b) shows the X-ray absorption spectra over the Ni L2,3 edge, μ+ (red) and μ− (blue), for 1D-Ni(acac)2@NT1.7 (an intermediate mean tube diameter of 1.7 nm) measured at 4 K with soft X-ray synchrotron radiation with circular polarisations parallel (μ+) and anti-parallel (μ−) to the magnetic field of up to 6 T. All spectral features are characteristic of Ni2+ in the octahedral ligand geometry as demonstrated in the ESI, section 5, Fig. S9.† The XMCD spectra μ+–μ− at magnetic fields up to 6 T are plotted in the lower part of Fig. 3(b). Using the XMCD sum rules (see the ESI, section 5†) we can estimate the Ni 3d spin and orbital magnetic moments. Both increase linearly with increasing magnetic field up to 6 T as plotted together with the linear fit in Fig. 3(a), giving rise to an orbital-to-spin ratio of 0.2. Interestingly, the Ni 3d magnetisation shows no apparent saturation and reaches only 0.42μB per nickel at 6 T (∼1.44 T K−1). This points towards the presence of non 3d magnetisation that is not probed by XMCD at the Ni 3d absorption edge, possibly of delocalized nature as the oxygen orbital is non-magnetic. The corresponding orbital effective magnetic moment is μorbitaleff = 0.49 in units of μB and the spin effective magnetic moment is μspineff = 1.01. The total effective magnetic moment is μtotaleff = 1.12, much lower than those evaluated from the SQUID data (2.68 for 1D-Ni(acac)2@NT2.1 and 2.27 for 1D-Ni(acac)2@NT1.3). The orbital component is smaller by a factor of 2 than the spin component, meaning that the quenching of the orbital magnetic moment is significant enough so that we can conditionally assume a pure spin Ni 3d state in the following analysis that focuses on changes with regard to the exchange coupling energy due to the nano-confinement.
The spin Hamiltonian for the superexchange-coupled trimetric nickel spins can be given as H = −2[J12(S1S2) + J23(S2S3) + J31(S3S1)].32 In the case of Ni2+ (3d8) in the octahedral ligand geomerty, six electrons fully occupy the t2g orbital and two electrons are left unpaired in the eg orbital, giving rise to a total spin magnetic moment of S = 1 for which the following analytical formula for the magnetic susceptibility per atom in units of the Bohr magneton μB can be derived from the Hamiltonian.11,32
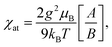 | (1) |
| A = 42e2(2x+y) + 15e2(y−x) + 15e2(x−y) + 3e2(y−3x) + 3e−2(x+y) + 3e−4y, |
| B = 7e2(2x+y) + 5e2(y−x) + 5e2(x−y) + 3e2(y−3x) + 3e−2(x+y) + 3e−4y + e−2(2x+y), |
| x = J/kBT y = J13/kBT, |
Fig. 4 shows the temperature-dependent magnetisation data measured by SQUID at 1 T for 3D-Ni(acac)2 and 1D-Ni(acac)2@NT1.3 after subtraction of the SWCNT magnetism (see ESI, section 3†). No difference is observed between the data recorded at the zero-field cooling (solid circles/triangles) and field cooling (open circles/triangles). It is noticeable that 1D-Ni(acac)2 exhibits much enhanced constant Pauli paramagnetism as compared with 3D-Ni(acac)2. Fitting the data to eqn (1) plus Pauli term Mc (see the ESI, section 6† for more details), we get Pauli paramagnetism values of Mc ∼ 0.001μB per nickel for 3D-Ni(acac)2 and 0.01μB per nickel for 1D-Ni(acac)2@NT1.3. This enhancement can be attributed to the delocalisation of the spin polarisation as a result of the interactions between 1D-Ni(acac)2 and the conduction band of the SWCNT, in line with the presence of non 3d magnetism suggested to explain the difference between the XMCD and SQUID results. The data below 5 K have been excluded from the fitting as the saturation dominates at 1 T, as seen in the field dependent data at 2 K (see the ESI, section 3, Fig. S6†). The corresponding fitting curves are inverse-plotted after subtraction of Mc in the inset in Fig. 4, alongside with the dashed black curve with zero exchange couplings, J = 0 and J13 = 0, that follows the Curie law. For 3D-Ni(acac)2, we get exchange values J = 1.49 meV and J13 = −0.89 meV, resulting in a ferromagnetic offset at high temperatures in the inverse plot. Fig. 4(b) shows a diagram of exchange coupling among the trimetric spins exhibiting spin frustration. The corresponding Weiss temperature evaluated from the Curie–Weiss fitting line (dashed green line) derived from the data in the temperature range between 150 and 300 K is TW = 14.8 K. For 1D-Ni(acac)2@NT1.3 (panel c), J turns negative and J13 is totally quenched. There is no spin frustration in this spin geometry as illustrated in Fig. 4(c). The corresponding Weiss temperature is −3.7 K.
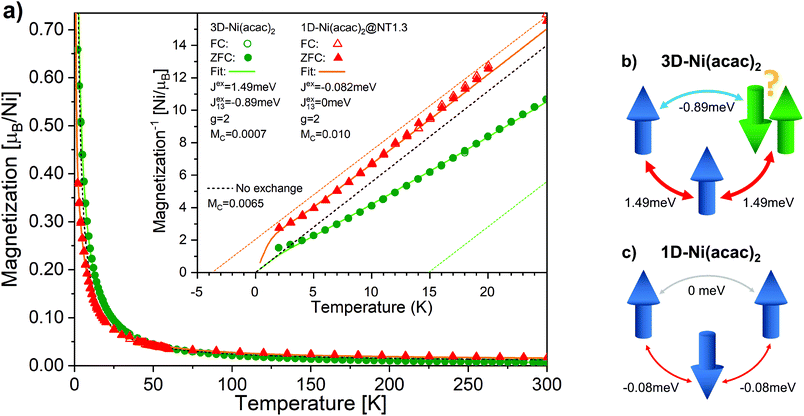 | ||
| Fig. 4 (a) The magnetisation per nickel atom versus temperature in the range between 2 K and 300 K measured under a magnetic field of 1 T for 3D-Ni(acac)2 (circles) and 1D-Ni(acac)2@NT1.3 (triangles). The solid and open circles/triangles are measured upon zero field (ZFC) and field cooling, respectively. The solid curves are the results of fitting the data with eqn (1) at temperatures above 5 K. The paramagnetic curve (dashed), eqn (1) with J = 0, J13 = 0, is also plotted. The inset shows the inverse magnetisation data and fitting curves after the subtraction of constant magnetisation offset Mc. The dashed lines are linear extrapolation of the fitting curves in the range of 150–300 K for 3D-Ni(acac)2 (green) and 1D-Ni(acac)2@NT1.3 (orange). Schematics of (b) 3D-Ni(acac)2 trimer where ferromagnetic exchange between the nearest-neighbour spins and antiferromagnetic exchange between the terminal spins lead to spin frustration and (c) 1D-Ni(acac)2 with nearest-neighbour antiferromagnetic exchange. | ||
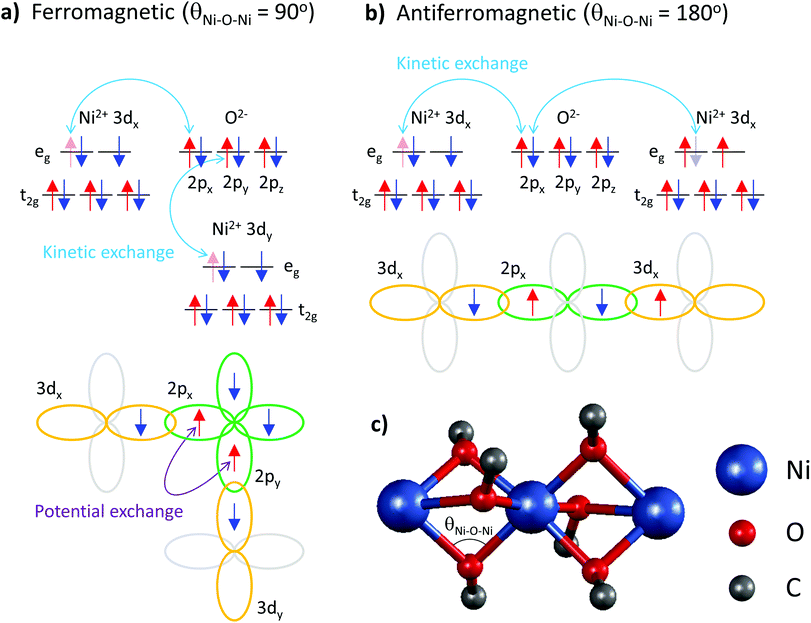
These data elucidate the following important findings. The two exchange coupling constants exhibit anisotropic quenching upon encapsulation of Ni(acac)2 in the SWCNT. The nearest-neighbour exchange J, which is positive in 3D-Ni(acac)2, turns negative in 1D-Ni(acac)2 in the small-diameter SWCNTs, while the J13 between the terminal spins, positive in 3D-Ni(acac)2, is quenched in 1D-Ni(acac)2. Both demonstrate that the superexchange coupling among the trimetric spins sees the nano-confinement forcing Ni(acac)2 into the 1D arrangement (as depicted in the inset in Fig. 2) where the trimers are being stretched and the 1D unit cell enlarged as compared with the 3D lattice, as observed in the XRD profile in Fig. 2. The ferromagnetic-to-antiferromagnetic transition of the nearest-neighbour exchange can be accompanied by the enlargement of the angle between the three oxi-ligands (M–O–M) in the stretched trimer as the superexchange coupling strongly depends on the ligand geometry according to the Goodenough–Kanamori–Anderson rule22–26,33 (see Fig. 5) Also, lattice distortions of the ligand geometry can lift the orbital degeneracy between the 3d3z2−r2 and 3dx2−y2 of the eg. This leads to an unoccupied 3d3z2−r2 or 3dx2−y2 orbital that doesn't change the sign of exchange coupling, but can reduce the exchange energy, which is in line with the reduced net magnetism.
Note that the spin frustration observed in 3D-Ni(acac)2 is absent in the 1D case, see the diagram in Fig. 4b and c. This points towards the distorted octahedral geometry leading to a 1D trimetric spin system favouring the antiferromagnetic ground state.
In conclusion, the spin-frustrated trimetic Ni(acac)2 molecular magnet has been uniquely arranged in one dimension inside SWCNTs. The effective magnetic moment per nickel is reduced from 3.14μB for 3D-Ni(acac)2 down to 2.27μB for 1D-Ni(acac)2. The superexchange interactions among the trimetric spins evaluated from the magnetic susceptibility data exhibit the anisotropic quenching due to the structural confinement. The nearest-neighbour ferromagnetic exchange J sees a stronger reduction than the anti-ferromagnetic exchange J13 between the terminal spins and it turns antiferromagnetic in the small-diameter nanotubes. A likely explanation for this ferromagnetic-to-antiferromagnetic transition is a change in the angle between the three oxo ligands (M–O–M) as it is known to be a crucial parameter within the framework of the Goodenough–Kanamori–Anderson rules.
The present work demonstrates that the nanometric structural confinement can flip the exchange coupling within the molecular magnet so as to release the spin frustration. Although a more elaborated theoretical study shall be required, the present work is an important step forward in understanding the superexchange coupling in a distorted ligand geometry, which is central for many advanced materials such as superconducting cuprates34 and their strain engineering.35 Furthermore, the enhanced Pauli paramagnetism in 1D-Ni(acac)2 suggests enhanced electron delocalisation, in line with the reduced local Ni 3d magnetism as evidenced by XMCD measurements, possibly the spin polarisation of the SWCNT's conduction state induced by the magnetic proximity effect. This might be useful as an interconnect to the molecular spins to be switched via both mechanical stress and spin current, providing the basis for nanometric switching devices for storing and manipulating quantum information.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the Austrian Science Fund (FWF), projects P30431-N36, P621333-N20 and P27769-N20, the Czech Science Foundation (GACR), project 19-15217S, and MSMT project ERC-CZ (LL1301). We thank S. Loyer, A. Stangl and P. Seebacher for technical assistance.References
- R. D. Willett, D. Gatteschi and O. Kahn, Magneto-structural correlations in exchange coupled systems, Reidel, 1985 Search PubMed.
- L. Bogani, A. Vindigni, R. Sessoli and D. Gatteschi, J. Mater. Chem., 2008, 18, 4750–4758 RSC.
- X.-N. Cheng, W.-X. Zhang, Y.-Y. Lin, Y.-Z. Zheng and X.-M. Chen, Adv. Mater., 2007, 19, 1494–1498 CrossRef CAS.
- S. Iijima, Nature, 1991, 354, 56–58 CrossRef CAS.
- S. Iijima and T. Ichihashi, Nature, 1993, 363, 603 CrossRef CAS.
- J. Sloan, A. I. Kirkland, J. L. Hutchison and M. L. H. Green, C. R. Phys., 2003, 4, 1063–1074 CrossRef CAS.
- M. d. C. Gimenez-Lopez, F. Moro, A. La Torre, C. J. Gomez-Garcia, P. D. Brown, J. van Slageren and A. N. Khlobystov, Nat. Commun., 2011, 2, 1 Search PubMed.
- S. Kyatskaya, J. Ramon Galan-Mascaros, L. Bogani, F. Hennrich, M. Kappes, W. Wernsdorfer and M. Ruben, J. Am. Chem. Soc., 2009, 131, 15143–15151 CrossRef CAS PubMed.
- M. Urdampilleta, S. Klyatskaya, J.-P. Cleuziou, M. Ruben and W. Wernsdorfer, Nat. Mater., 2011, 10, 502–506 CrossRef CAS PubMed.
- H. Shiozawa, T. Pichler, A. Gruneis, R. Pfeiffer, H. Kuzmany, Z. Liu, K. Suenaga and H. Kataura, Adv. Mater., 2008, 20, 1443–1449 CrossRef CAS.
- A. P. Ginsberg, R. L. Martin and R. C. Sherwood, Inorg. Chem., 1968, 7, 932–936 CrossRef CAS.
- G. J. Bullen, R. Mason and P. Pauling, Inorg. Chem., 1965, 4, 456–462 CrossRef CAS.
- H. Shiozawa, H. Ishii, H. Kihara, N. Sasaki, S. Nakamura, T. Yoshida, Y. Takayama, T. Miyahara, S. Suzuki, Y. Achiba, T. Kodama, M. Higashiguchi, X. Y. Chi, M. Nakatake, K. Shimada, H. Namatame, M. Taniguchi and H. Kataura, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 075406 CrossRef.
- H. Shiozawa, T. Pichler, C. Kramberger, A. Gruneis, M. Knupfer, B. Buchner, V. Zolyomi, J. Koltai, J. Kurti, D. Batchelor and H. Kataura, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 153402 CrossRef.
- H. Shiozawa, T. Pichler, C. Kramberger, M. Rummeli, D. Batchelor, Z. Liu, K. Suenaga, H. Kataura and S. R. P. Silva, Phys. Rev. Lett., 2009, 102, 046804 CrossRef CAS PubMed.
- H. Shiozawa, A. Briones-Leon, O. Domanov, G. Zechner, Y. Sato, K. Suenaga, T. Saito, M. Eisterer, E. Weschke, W. Lang, H. Peterlik and T. Pichler, Sci. Rep., 2015, 5, 15033 CrossRef CAS PubMed.
- M. V. Kharlamova, M. Sauer, T. Saito, Y. Sato, K. Suenaga, T. Pichler and H. Shiozawa, Nanoscale, 2015, 7, 1383–1391 RSC.
- M. V. Kharlamova, C. Kramberger, T. Saito, Y. Sato, K. Suenaga, T. Pichler and H. Shiozawa, Nanoscale, 2017, 9, 7998–8006 RSC.
- M. V. Kharlamova, C. Kramberger, Y. Sato, T. Saito, K. Suenaga, T. Pichler and H. Shiozawa, Carbon, 2018, 133, 283–292 CrossRef CAS.
- H. Kataura, Y. Maniwa, M. Abe, A. Fujiwara, T. Kodama, K. Kikuchi, H. Imahori, Y. Misaki, S. Suzuki and Y. Achiba, Appl. Phys. A, 2002, 74, 349–354 CrossRef CAS.
- L. Jin, C. Bower and O. Zhou, Appl. Phys. Lett., 1998, 73, 1197–1199 CrossRef CAS.
- H. A. Kramers, Physica, 1934, 1, 182–192 CrossRef CAS.
- J. Kanamori, J. Phys. Chem. Solids, 1959, 10, 87–98 CrossRef CAS.
- P. W. Anderson, Phys. Rev., 1950, 79, 350–356 CrossRef.
- J. B. Goodenough, Phys. Rev., 1955, 100, 564–573 CrossRef CAS.
- J. B. Goodenough, J. Phys. Chem. Solids, 1958, 6, 287–297 CrossRef CAS.
- A. Briones-Leon, P. Ayala, X. Liu, K. Yanagi, E. Weschke, M. Eisterer, H. Jiang, H. Kataura, T. Pichler and H. Shiozawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 195435 CrossRef.
- B. T. Thole, P. Carra, F. Sette and G. van der Laan, Phys. Rev. Lett., 1992, 68, 1943–1946 CrossRef CAS PubMed.
- P. Carra, B. T. Thole, M. Altarelli and X. Wang, Phys. Rev. Lett., 1993, 70, 694–697 CrossRef CAS PubMed.
- C. T. Chen, Y. U. Idzerda, H.-J. Lin, N. V. Smith, G. Meigs, E. Chaban, G. H. Ho, E. Pellegrin and F. Sette, Phys. Rev. Lett., 1995, 75, 152–155 CrossRef CAS PubMed.
- H. Shiozawa, T. Miyahara, K. Obu, Y. Takayama, H. Ishii, T. Matsuda, H. Sugawara, H. Sato, T. Muro and Y. Saitoh, J. Phys. Soc. Jpn., 2003, 72, 2079–2084 CrossRef CAS.
- K. Kambe, J. Phys. Soc. Jpn., 1950, 5, 48–51 CrossRef CAS.
- A. S. Moskvin, N. S. Ovanesyan and V. A. Trukhtanov, Hyperfine Interact., 1975, 1, 265–281 CrossRef CAS.
- Y. Mizuno, T. Tohyama, S. Maekawa, T. Osafune, N. Motoyama, H. Eisaki and S. Uchida, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 5326–5335 CrossRef CAS.
- A. Mukherjee, W. S. Cole, P. Woodward, M. Randeria and N. Trivedi, Phys. Rev. Lett., 2013, 110, 157201 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/C9NR00796B |
| ‡ Both the Weiss temperature and paramagnetic offset are omitted as our focus here is on the difference between the 3D-Ni(acac)2 and 1D-Ni(acac)2 cases. |
| § For simplicity g = 2 is assumed. |
| This journal is © The Royal Society of Chemistry 2019 |