Open Access Article
Open Access ArticleIon-induced assemblies of highly anisotropic nanoparticles are governed by ion–ion correlation and specific ion effects†
Tobias
Benselfelt
 *ab,
Malin
Nordenström
*ab,
Malin
Nordenström
 ab,
Mahiar Max
Hamedi
ab,
Mahiar Max
Hamedi
 ab and
Lars
Wågberg
ab and
Lars
Wågberg
 *ab
*ab
aDepartment of Fibre and Polymer Technology, Wallenberg Wood Science Center, KTH Royal Institute of Technology, Teknikringen 56-58, 10044, Stockholm, Sweden
bDepartment of Fibre and Polymer Technology, Division of Fibre Technology, KTH Royal Institute of Technology, Teknikringen 56-58, 10044, Stockholm, Sweden. E-mail: wagberg@kth.se; bense@kth.se
First published on 4th February 2019
Abstract
Ion-induced assemblies of highly anisotropic nanoparticles can be explained by a model consisting of ion–ion correlation and specific ion effects: dispersion interactions, metal–ligand complexes, and local acidic environments. Films of cellulose nanofibrils and montmorillonite clay were treated with different ions, and their subsequent equilibrium swelling in water was related to important parameters of the model in order to investigate the relative importance of the mechanisms. Ion–ion correlation was shown to be the fundamental attraction, supplemented by dispersion interaction for polarizable ions such as Ca2+ and Ba2+, or metal–ligand complexes for ions such as Cu2+, Al3+ and Fe3+. Ions that form strong complexes induce local acidic environments that also contribute to the assembly. These findings are summarized in a comprehensive semi-quantitative model and are important for the design of nanomaterials and for understanding biological systems where specific ions are involved.
Metal ions induce attractive interactions between charged polymers and colloids in water. These interactions are important for many chemical processes and products, including water treatment1 and antiperspirants or deodorants,2,3 as well as for plants and animals in the design of tissues4,5 or adhesives.6,7 Today, these supramolecular interactions are widely used to assemble organic materials such as alginate,8,9 metal–organic frameworks,10 nanocellulose,11,12 and peptides,13 or to assemble conventional inorganic materials such as clay particles14 or calcium-silicate-hydrate particles15 in cement paste. It is therefore crucial to understand the mechanisms that govern these interactions and to link the properties of colloids and ions to their ability to assemble.
The driving force behind this interaction is frequently assigned exclusively and naively to metal–ligand complexes (coordination chemistry).4,8,13,16 There are, however, several cases with an inadequate relationship between the stability of the complex and the properties of the assembled materials.11–13,16 This indicates that the assemblies originate from several separate mechanisms, which must be combined into a complete model.
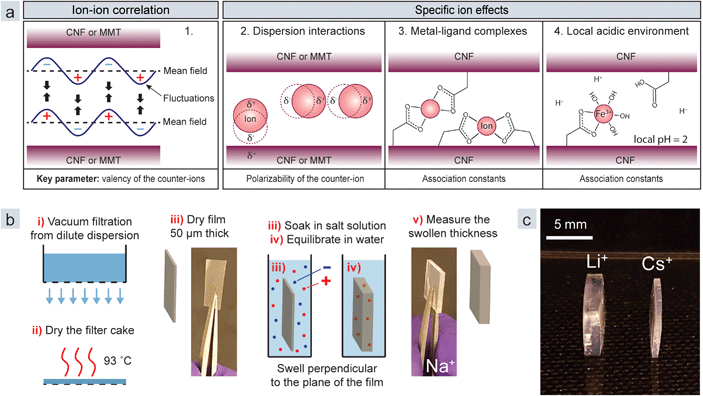
The interaction between charged colloids has traditionally been described by the DLVO theory, which posits double-layer repulsion and attractive van der Waals forces.17 The problem is, however, that in this theory ions are not allowed to interact. Moreover, the theory is based on mean field approximations, in which the average properties of the counter-ion cloud and interacting particles are used. The theories of ion–ion correlation18–20 and specific ion effects21 were developed to explain situations where the DLVO theory clearly fails. Ion–ion correlation is ubiquitous for all charged polymers or colloids, whereas the specific ion effects depend on the properties of the colloid and the ion. The model in Fig. 1a displays the four principal mechanisms in the interaction between nanoparticles in the presence of metal ions: (1) ion–ion correlation, (2) dispersion interactions, (3) metal–ligand complexes, and (4) a local acidic environment.22,23 Mechanisms 2–4 are specific ion effects.
In this paper we investigate these mechanisms by using two common anisotropic nanoparticles: cellulose nanofibrils (CNFs), and two-dimensional sheets of montmorillonite clay (MMT). CNFs are high aspect ratio cellulose nanoparticles with a high degree of crystallinity and a square cross-section of 3 nm by 3 nm. Here they are decorated with carboxyl ligands (anionic) or quaternary amines (cationic).24,25 MMT clay consists of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 phyllosilicate sheets of aluminium silicate with an exfoliated thickness of 1 nm and a diameter of less than one micron. The sheets are negatively charged due to an isomorphic substitution of Al in the octahedral layer of the crystal structure.26 The nanoparticles are strongly affected by the presence of multivalent counter-ions11,12,16,27 and we chose them because CNFs can form metal–ligand complexes,16 while there have been no such reports for MMT.
1 phyllosilicate sheets of aluminium silicate with an exfoliated thickness of 1 nm and a diameter of less than one micron. The sheets are negatively charged due to an isomorphic substitution of Al in the octahedral layer of the crystal structure.26 The nanoparticles are strongly affected by the presence of multivalent counter-ions11,12,16,27 and we chose them because CNFs can form metal–ligand complexes,16 while there have been no such reports for MMT.
To estimate the ion-induced interaction between CNFs or MMT, we measured the swelling of assemblies of CNF or MMT nanoparticles in the presence of different counter-ions and related the degree of swelling to the magnitude of the interactions between the nanoparticles. We describe the swelling at equilibrium using Flory's polyelectrolyte gel model (eqn (1), and ESI†) where the network pressure (Πnet) is the net attractive pressure between the nanoparticles, the mixing pressure (Πmix) is given by the thermodynamics of mixing the nanoparticles with water, and the ionic pressure (Πion) is the osmotic pressure at a given valency of the counter-ion (double-layer repulsion).28
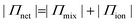 | (1a) |
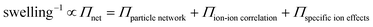 | (1b) |
The swelling of the assembly is related to the inter-particle attraction (Πnet in eqn (1)), and could be used determine the influence of the valency and polarizability of different counter-ions and the association constant of their complexes, which are the most important parameters in the ion–ion correlation and specific ion effects theories.18,19,22,29,30 We used the relationship between swelling and these parameters to estimate the relative importance of the different interaction mechanisms, and this allowed us to develop semi-quantitative models to explain these ion-induced assemblies. We also introduce the concept of an ion-induced local acidic environment as part of the model, a mechanism not yet clearly discussed in the literature. We think that this semi-quantitative model is currently the most comprehensive model explaining the interactions for all polymers or colloids, anionic or cationic, that assemble in the presence of specific counter-ions.
To measure the equilibrium swelling (eqn (2), ESI†), where d is the thickness of the film, we prepared sheets from CNFs and MMT by vacuum filtration of dilute dispersions of the respective nanoparticles (Fig. 1b). Next, we immersed the films in a solution (1 wt%) containing different ions and then allowed them to swell in Milli-Q water until equilibrium.
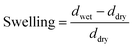 | (2) |
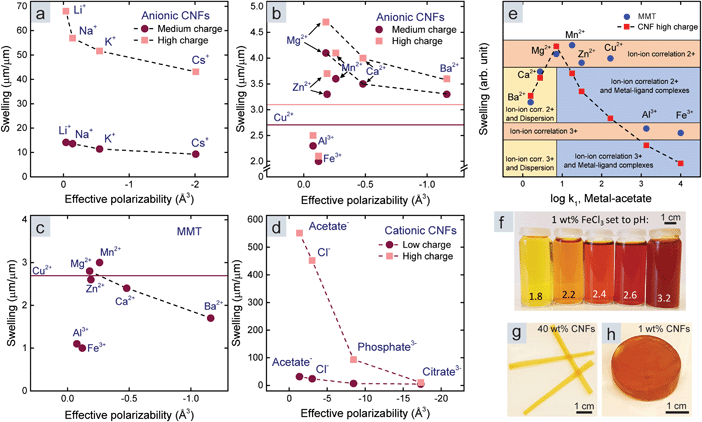
The swelling is unidirectional since the nanoparticle network collapses in one direction during filtration,9 and this means that the changed thickness of the films represents the entire swelling and can easily be measured with a thickness gauge. Fig. 1c shows swollen CNF films with Li+ and Cs+ counter-ions, demonstrating that large differences are observed for monovalent counter-ions that should behave similarly according to DLVO theory. The films swell significantly less with multivalent counter-ions (Table S1†).
We started by investigating the influence of metal–ligand complexes (mechanism 3 in Fig. 1a, and ESI†), which is the conventional explanation for the attraction between polymers or colloids in the presence of multivalent metal ions. These complexes form to minimize the energy of the ion and have an ionic and a dative covalent contribution, in which the ligand donates both electrons to the bond.31,32 Transition metals reach noble gas states by attracting ligands in order to fill their d-orbitals with shared electrons, and therefore they form strong complexes.33–35 The strength of a complex is referred to as the stability constant, which is the logarithm of the first association constant, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k1. Fig. 2a shows the stability constant between the investigated metal ions and acetate or hydroxide ions.13,31 Acetate and hydroxide were used to represent available ligands on the CNF surface and in water. The stability constant between protons and acids is the pKa value, and ions with high affinity for hydroxide ions in water, such as Fe3+, are therefore acids.
k1. Fig. 2a shows the stability constant between the investigated metal ions and acetate or hydroxide ions.13,31 Acetate and hydroxide were used to represent available ligands on the CNF surface and in water. The stability constant between protons and acids is the pKa value, and ions with high affinity for hydroxide ions in water, such as Fe3+, are therefore acids.
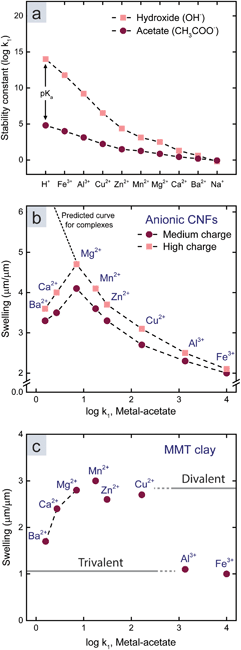 | ||
| Fig. 2 (a) Stability constants between different ions and hydroxide or acetate as models for water and the surface of CNFs.13,31 (b) Relationship between the swelling and stability constants (metal-acetate) for CNF films. (c) Relationship between the swelling and stability constants (metal-acetate) for MMT films. | ||
Fig. 2b shows that the swelling of the CNF films (Table S1†) decreases with an increasing stability constant of metal-acetate. However, the relationship does not hold for Ca2+ and Ba2+, so there has to be another explanation for the swelling in the presence of these counter-ions.
There was no significant relationship between the swelling and the stability constant of a hypothetical ligand on the surface of MMT (Fig. 2c). Instead, there were two discrete swelling levels; one for the divalent transition metals including Mg2+, and one for the trivalent ions. In accordance with previous studies,14 we postulate that ion–ion correlation is the cause of these levels.
Ion–ion correlation (mechanism 1 in Fig. 1a, and ESI†) is a large-scale analogue of London dispersion interactions in the van der Waals theory (electron–electron correlation). The spontaneous fluctuation of electrons of molecules or ions in the counter-ion cloud, for example due to thermal energy (kT), results in instantaneous dipoles. The formation of these dipoles correlate when molecules or counter-ion clouds are brought close together, leading to attractive electron–electron or ion–ion correlation interactions.18–20,36
The magnitude of the fluctuations in the counter-ion cloud is mainly governed by the valency of the counter-ion and the surface charge density of the colloid.19 A higher valency of the counter-ion results in a less crowded ion cloud, which in turn allows more fluctuations to occur without being diminished by core–core repulsion between ions.37 The medium and high charge density CNFs that we used had charge densities of 0.07 and 0.13 C m−2 respectively. This is comparable to the charge density of 0.1 C m−2 required for ion–ion correlation to overpower the double-layer repulsion for divalent ions.38
The discrete swelling levels for MMT with divalent and trivalent counter-ions (Fig. 2c) are therefore explained by the valency effect in ion–ion correlation theory. Ion–ion correlation has previously been suggested to be the main mechanism behind the absence of swelling for clays with multivalent counter-ions.14
The magnitude of the electron–electron correlation, referred to here as dispersion interactions (mechanism 2 in Fig. 1a, and ESI†), is proportional to the polarizability of molecules or atoms. Polarizable ions therefore interact with colloids or with each other mediated by van der Waals forces. This interaction reduces the double-layer repulsion or supresses the surface charge of the colloid.21,39,40 Dispersion interactions are the main component in the specific ion effect theories and are suggested to be an explanation for the Hofmeister series.40,41
The trend for Ca2+ and Ba2+ counter-ions was similar for both CNF and MMT (Fig. 2b and c), which is indicative of a ubiquitous mechanism for all colloids that is associated with the properties of these ions. Ca2+ and Ba2+ are significantly larger and their electrons are more loosely bound compared to the other ions in this work, and thus they have higher polarizability.22,42 We therefore investigated the relationship between the polarizability, representing dispersion interactions, and the swelling of the CNF and MMT films. The effective polarizabilities of these ions in water were either calculated or adapted based on the method of Ninham et al. (see eqn (S3) and (S4), Tables S4–S5, and ESI†).22
The influence of the dispersion interactions was most prominent for monovalent counter-ions, depicted in Fig. 1c, since monovalent ions do not form metal–ligand complexes and lead to weak ion–ion correlation. Fig. 3a shows a significant trend between the swelling of the CNF films and the effective polarizability in water of monovalent counter-ions. We did not observe this trend for MMT films since they dissolved completely with monovalent counter-ions. The effective polarizability of Li+ is almost zero, which best represents a non-interacting counter-ion in the DLVO theory, and this explains the large swelling of CNF films with Li+ counter-ions; however, the entangled CNF network probably prevents dissolution.
We observed a similar relationship to that of the monovalent counter-ions for Mg2+, Ca2+, and Ba2+ in the case of both CNF and MMT films (Fig. 3b and c). The transition metals and Al3+ can, like Li+, be considered non-interacting in terms of dispersion interactions due to their low effective polarizability. Indeed, we observed the different swelling in the presence of these ions (Fig. 2) to be a result of metal–ligand complexes and ion–ion correlation for CNFs, while only ion–ion correlation affected MMT due to the lack of ligands.
We also measured the swelling of cationic CNF films (Table S2†) because anions are significantly more polarizable than cations (Table S5†).22 The relationship between the swelling of cationic CNF films and the effective polarizability in Fig. 3d shows that dispersion interactions are also important for anions outside a cationic surface. Furthermore, ion–ion correlation should naturally also exist in anionic counter-ion clouds.
Fig. 3e summarizes the effect of ion–ion correlation, dispersion interactions, and metal–ligand complexes. We assembled this figure by superimposing the swelling of CNF and MMT films with respect to their respective values in the presence of Mg2+, Ca2+, and Ba2+ counter-ions (normalization), and plotted it against the stability constants of metal-acetate. Our motivation is that dispersion interactions are a ubiquitous phenomenon and do not overlap any other specific interaction mechanism. Ions interact with either dispersion interactions or metal–ligand complexes since large and polarizable ions are stable and therefore gain little energy by forming complexes, and vice versa. We then introduced coloured regions for the different mechanisms or combination of mechanisms, to indicate their importance for each counter-ion. This assignment is based on the properties of the ions and how these properties influence ion–ion correlation, dispersion interactions, and metal–ligand complexes. The coloured regions in Fig. 3e demonstrate that MMT films show discrete swelling due to ion–ion correlation (orange regions). Metal–ligand complexes further reduce the swelling of CNF films with transition metal counter-ions and lead to continuous variation throughout the blue regions. The dispersion interactions are important for both nanoparticles in the presence of Ca2+ and Ba2+ counter-ions (yellow regions).
Fig. 3e does not, however, capture the effect of the local acidic environment (mechanism 4 in Fig. 1a). To investigate this mechanism, we measured the infrared absorbance of CNF sheets treated with different counter-ions (Fig. S1†). For ions that form strong complexes, Cu2+, Al3+ and Fe3+, portions of the absorbance of the asymmetric carboxylate vibration at 1600 cm−1 moved to 1730 cm−1, which is the vibration of protonated carboxylic acids. These ions behave as acids due to their high affinity for OH− in water (Fig. 2a). Solutions of CuCl2, AlCl3, and FeCl3 (1 wt%) thus have a pH of 3.7, 3.4, and 1.9, respectively.
Fig. 3f shows that FeCl3 solutions change colour when the pH is adjusted which is due to the different ligand field split when binding water and hydroxide ions. Ligand field theory describes how the d-orbital is split into low and high energy levels upon binding ligands (ESI†).43 The energy gap, or field split, depends on the nature of the ion and the ligand and results in coloured complexes when electrons are excited between the energy levels by visible light. Iron ions can therefore be used as a pH indicator.
Fig. 3g and h show a dense CNF film and a dilute CNF gel with Fe3+ counter-ions. The colours of these materials indicate that the pH inside the film is close to 2 while it is around 3 inside the gel. This difference is explained by the effective concentration of Fe3+, which is proportional to the amount of carboxyl groups per volume, and local acidic environments therefore depend on the charge density and the volume concentration of the nanoparticle. The result of this mechanism is a lower effective charge density of the colloid and thus reduced double-layer repulsion. However, the charge density is also important for ion–ion correlation, and it is therefore difficult to specify the net effect of local environments.
We combine all these results in semi-quantitative models (Fig. 4a and b) to both explain and visualize the importance of the four mechanisms that contribute to the assembly. The colours of the bars (from Fig. 3e) represent the four mechanisms. Their relative heights represent their normalized contribution to the overall attraction. We assume that Li+ and Mg2+ only induce ion–ion correlation, since they have low effective polarizability (Fig. 3) and because Mg-acetate complexes have a relatively low stability constant (Fig. 2a). The contributions of the different mechanisms are for monovalent ions and divalent ions, except Cu2+, based only on the above assumption and the swelling data (Fig. 4a and b). The contribution of the different mechanisms for Cu2+, Al3+, and Fe3+, in the case of CNF, are chosen to be linearly related to the stability constants and the induced pH with an R2 of at least 0.9 (Fig. 4a and b insets).
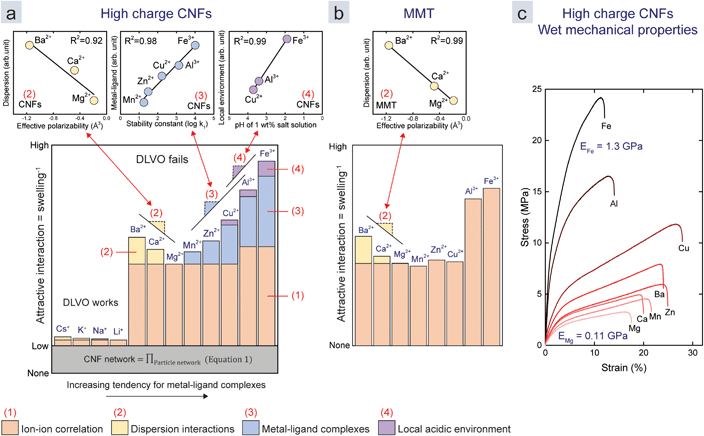 | ||
| Fig. 4 Semi-quantitative models of the attractive interaction between the nanoparticles in the films of (a) CNFs and (b) MMT normalized with respect to the Mg2–Ca2+–Ba2+ trend as in Fig. 3e. The coloured subsections of each bar represent the contribution of the mechanisms: (1) ion–ion correlation, (2) dispersion interactions, (3) metal–ligand complexes, and (4) local acidic environments as in Fig. 1. The contribution of each mechanism was derived from the trends in previous figures, or related to the investigated parameters in the case of Cu2+, Al3+, and Fe3+. The relationships between the swelling and the parameters in the model are shown in the insets above the main graphs and are referred to by colour, number, and slope symbols. (c) Stress–strain curves of high charge CNF films treated with different counter-ions. | ||
We were unable to explain the discrepancy in the effect of the valency for ion–ion correlation between MMT and CNFs (difference Cu2+ to Al3+). We speculate that this is due to the reduced effective charge density when the ions form complexes with carboxylate ligands on CNFs. Moreover, the two-dimensional shape of MMT allows for a better packing, which is beneficial due to the short range of attraction from ion–ion correlation (<5 nm).29 It is also important to mention that early work by Oosawa showed that the shape of the colloid influences the ion–ion correlation.18
The model suggests that the major part of attractive interactions for both CNFs and MMT originates from ion–ion correlation. CNFs encounter all four mechanisms, while MMT only encounters ion–ion correlation and dispersion interactions. Metal–ligand complexes lead to large differences for transition metal counter-ions if ligands are present on the surface of the nanoparticle. We propose that ion–ion correlation should be paid more attention in the future, since it is possible that metal–ligand complexes would not be strong enough to induce assemblies in a hypothetical system without ion–ion correlation.
While the MMT films with multivalent counter-ions are weak in water, the CNF films are strong enough for tensile testing in the wet state.9,11 This is probably because CNFs can entangle over large distances so that the strength in the plane is maintained. Fig. 4c shows stress–strain curves in the wet state of the films in Fig. 4a, which shows that the mechanical properties follow the same trend as that of the swelling. With a Young's modulus of 1.3 GPa, a strength of 25 MPa and elongation of 10% in the presence of Fe3+, these films are comparable to high density polyethylene (HDPE), which has a Young's modulus of 1.1 GPa and yield strength of 26 MPa at 10% elongation.44 This demonstrates that multivalent ions can be used to assemble water-resilient materials from nanoparticles that are otherwise dispersible in water.
To conclude, we showed that a model containing ion–ion correlation and specific ion effects can essentially explain the assembly of cellulose nanofibrils or montmorillonite clay in the presence of different counter-ions. This model may be able to explain the ion-induced assembly of any polymers or colloids. Ion–ion correlation is the main part of the attraction, and specific ion effects further increase the attraction depending on the specific ion and the chemistry of the particle surface. Local environments must be considered for particles with titratable surface groups in the presence of ions that affect the local pH.
This knowledge can be used to rationally design the assembly of nanoparticles in the presence of different ions. We showed that these mechanisms may be a crucial tool in the preparation of biodegradable food packages and other water-resilient materials in a renewable and circular economy.9 We also think the model is important for biological systems in general where metal ions are frequently involved.
Further research should be aimed at clarifying the influence of the dimensions and rigidity of the particle and its surface charge density. We also think it would be interesting to investigate other surface ligands such as phosphorylates or primary amines to further understand and potentially increase the stability of the assemblies.
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The funding provided by the Knut and Alice Wallenberg Foundation and the Wallenberg Wood Science Center (WWSC) are acknowledged. We thank Lilian Medina for providing the MMT clay film, and Anna Hanner and Qi Zhou for providing the cationic CNFs.References
- J. Edzwald, Water Sci. Technol., 1993, 27, 21–35 CrossRef CAS.
- Z. D. Draelos, Dermatol. Ther., 2001, 14, 220–224 CrossRef.
- A. Sone, T. Saito and A. Isogai, ACS Macro Lett., 2016, 5, 1402–1405 CrossRef CAS.
- D. A. Rees and E. J. Welsh, Angew. Chem., Int. Ed. Engl., 1977, 16, 214–224 CrossRef.
- G. E. Fantner, T. Hassenkam, J. H. Kindt, J. C. Weaver, H. Birkedal, L. Pechenik, J. A. Cutroni, G. A. G. Cidade, G. D. Stucky, D. E. Morse and P. K. Hansma, Nat. Mater., 2005, 4, 612 CrossRef CAS PubMed.
- J. J. Wilker, Angew. Chem., Int. Ed., 2010, 49, 8076–8078 CrossRef CAS PubMed.
- C. Sun, G. E. Fantner, J. Adams, P. K. Hansma and J. H. Waite, J. Exp. Biol., 2007, 210, 1481 CrossRef CAS PubMed.
- C. H. Yang, M. X. Wang, H. Haider, J. H. Yang, J.-Y. Sun, Y. M. Chen, J. Zhou and Z. Suo, ACS Appl. Mater. Interfaces, 2013, 5, 10418–10422 CrossRef CAS PubMed.
- T. Benselfelt, J. Engstrom and L. Wagberg, Green Chem., 2018, 20, 2558–2570 RSC.
- S. L. James, Chem. Soc. Rev., 2003, 32, 276–288 RSC.
- M. Shimizu, T. Saito and A. Isogai, J. Membr. Sci., 2016, 500, 1–7 CrossRef CAS.
- H. Dong, J. F. Snyder, K. S. Williams and J. W. Andzelm, Biomacromolecules, 2013, 14, 3338–3345 CrossRef CAS PubMed.
- J. C. Stendahl, M. S. Rao, M. O. Guler and S. I. Stupp, Adv. Funct. Mater., 2006, 16, 499–508 CrossRef CAS.
- R. Kjellander, S. Marcelja, R. M. Pashley and J. P. Quirk, J. Phys. Chem., 1988, 92, 6489–6492 CrossRef CAS.
- B. Jönsson, H. Wennerström, A. Nonat and B. Cabane, Langmuir, 2004, 20, 6702–6709 CrossRef PubMed.
- K. S. Williams, J. W. Andzelm, H. Dong and J. F. Snyder, Cellulose, 2014, 21, 1091–1101 CrossRef CAS.
- E. J. W. Verwey, J. T. G. Overbeek and J. T. G. Overbeek, Theory of the Stability of Lyophobic Colloids, Dover Publications, 1999 Search PubMed.
- F. Oosawa, in Polyelectrolytes, Marcel Dekker, 1971, pp. 50–126 Search PubMed.
- L. Guldbrand, B. Jönsson, H. Wennerström and P. Linse, J. Chem. Phys., 1984, 80, 2221–2228 CrossRef CAS.
- R. Kjellander and S. Marcělja, Chem. Phys. Lett., 1984, 112, 49–53 CrossRef CAS.
- M. Boström, D. R. M. Williams and B. W. Ninham, Phys. Rev. Lett., 2001, 87, 168103 CrossRef PubMed.
- B. W. Ninham and P. L. Nostro, Molecular Forces and Self Assembly: In Colloid, Nano Sciences and Biology, Cambridge University Press, 2010 Search PubMed.
- D. F. Evans and H. Wennerström, The Colloidal Domain: Where Physics, Chemistry, Biology, and Technology Meet, Wiley-Vch, 2nd edn, 1999 Search PubMed.
- T. Saito, M. Hirota, N. Tamura, S. Kimura, H. Fukuzumi, L. Heux and A. Isogai, Biomacromolecules, 2009, 10, 1992–1996 CrossRef CAS PubMed.
- A. Pei, N. Butchosa, L. A. Berglund and Q. Zhou, Soft Matter, 2013, 9, 2047–2055 RSC.
- F. Uddin, Metall. Mater. Trans. A, 2008, 39, 2804–2814 CrossRef.
- M. Segad, B. Jönsson, T. Åkesson and B. Cabane, Langmuir, 2010, 26, 5782–5790 CrossRef CAS PubMed.
- P. J. Flory, Principles of Polymer Chemistry, Cornell University Press, 1953 Search PubMed.
- B. Jönsson and H. Wennerström, J. Adhes., 2004, 80, 339–364 CrossRef.
- J. E. House, in Inorganic Chemistry, Academic Press, 2nd edn, 2013, pp. 643–664, DOI:10.1016/B978-0-12-385110-9.00019-4.
- R. D. Hancock and F. Marsicano, Inorg. Chem., 1980, 19, 2709–2714 CrossRef CAS.
- A. D. McNaught and A. D. McNaught, Compendium of chemical terminology, Blackwell Science Oxford, 1997 Search PubMed.
- R. J. P. Williams, J. Chem. Soc., 1952, 3770–3778, 10.1039/JR9520003770.
- H. Irving and R. J. P. Williams, J. Chem. Soc., 1953, 3192–3210, 10.1039/JR9530003192.
- J. E. House, in Inorganic Chemistry, Academic Press, 2nd edn, 2013, pp. 553–590, DOI:10.1016/B978-0-12-385110-9.00016-9.
- B. Joensson, H. Wennerstroem and B. Halle, J. Phys. Chem., 1980, 84, 2179–2185 CrossRef CAS.
- R. Kjellander and S. Marcelja, J. Phys. Chem., 1986, 90, 1230–1232 CrossRef CAS.
- D. Bratko, B. Jönsson and H. Wennerström, Chem. Phys. Lett., 1986, 128, 449–454 CrossRef CAS.
- W. Kunz, Curr. Opin. Colloid Interface Sci., 2010, 15, 34–39 CrossRef CAS.
- D. F. Parsons, M. Bostrom, P. L. Nostro and B. W. Ninham, Phys. Chem. Chem. Phys., 2011, 13, 12352–12367 RSC.
- F. Hofmeister, Arch. Exp. Pathol. Pharmakol., 1888, 25, 1–30 Search PubMed.
- R. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- J. E. House, in Inorganic Chemistry, Academic Press, 2nd edn, 2013, pp. 591–616, DOI:10.1016/B978-0-12-385110-9.00017-0.
- K. Sakakibara, Y. Moriki, H. Yano and Y. Tsujii, ACS Appl. Mater. Interfaces, 2017, 9, 44079–44087 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details, theoretical background regarding ion–ion correlation and specific ion effects, theoretical calculations, tables with experimental and theoretical data, a figure with FTIR data. See DOI: 10.1039/c8nr10175b |
| This journal is © The Royal Society of Chemistry 2019 |