From fiber curls to mesh waves: a platform for the fabrication of hierarchically structured nanofibers mimicking natural tissue formation

Abstract

Bioinstructive scaffolds for regenerative medicine are characterized by intrinsic properties capable of directing cell response and promoting wound healing. The design of such scaffolds requires the incorporation of well-defined physical properties that mimic the native extracellular matrix (ECM). Here, inspired by epithelial tissue morphogenesis, we present a novel approach to code nanofiber materials with controlled hierarchical wavy structures resembling the configurations of native EMC fibers through using thermally shrinking materials as substrates onto which the fibers are deposited. This approach could serve as a platform for fabricating functional scaffolds mimicking various tissues such as trachea, iris, artery wall and ciliary body. Modeling affirms that the mechanical properties of the fabricated wavy fibers could be regulated through varying their wavy patterns. The nanofibrous scaffolds coded with wavy patterns show an enhanced cellular infiltration. In addition, we further investigated whether the wavy patterns could regulate transforming growth factor-beta (TGF-β) production, a key signalling pathway involved in connective tissue development. Our results demonstrated that nanofibrous scaffolds coded with wavy patterns could induce TGF-β expression without the addition of a soluble growth factor. Our new approach could open up new avenues for fabricating bioinstructive scaffolds for regenerative medicine.

---

Introduction

Regenerative medicine has emerged as a promising strategy to repair damaged or diseased tissues. Over the years, many techniques for generating scaffolds have been exploited, such as particulate leaching, phase separation, molecular self-assembly, additive manufacturing and electrospinning. Among these methods, electrospinning shows superiority due to its ability to produce nanofibrous meshes comparable to the native extracellular matrix (ECM) in a simple and versatile manner.^1,2

Furthermore, varied patterns and structures of deposited electrospun fibers can be readily achieved by varying the collection methods, for example, randomly oriented fibers by a stationary plate, aligned fibers by a rotating mandrel or electrodes, and tubular meshes by a rotating mandrel.^3–5 Although currently electrospun scaffolds have been extensively investigated in the regenerative medicine field, little progress has been made to fabricate scaffolds resembling the wavy structural and architectural organization of ECM fibrils and/or fibers in many human tissues, such as ligaments, tendons, heart muscle, valve leaflets, cornea, iris, and intervertebral disks.^6–9 Typically, the crimped structure of native fibrous collagen has a periodicity in the range of 10 to 200 μm.⁶ Fibers with a wavy structure are capable of absorbing more deformation compared to their straight counterparts, and therefore show enhanced compliance at low strains, while holding greater strength as the load increases.^6,10 In addition, the wavy structural features may also produce instructive topographical cues and increased mechanotransduction for cell activities, such as differentiation, proliferation and ECM organization. For instance, spring-like fiber scaffolds with a structure resembling that of the wavy fibers present in the natural myocardium matrix showed superior mechanical properties compared to pristine electrospun straight fiber scaffolds and were able to support cardiomyocyte contraction.^11,12

Recently, a number of research groups have refined the process to produce wavy fibers via an ethanol treatment, utilizing a weak tangential air-flow, using mandrels with a controlled heating temperature, melt electrowriting, and including a sacrificial fiber population among other techniques.^10,13–15 Although with the above-mentioned methods it is possible to fabricate scaffolds mimicking the wavy patterns observed in native ECM to certain degrees, the major drawbacks of these methods include the limited control of the crimp patterns, relatively complicated processing steps, and the use of plasticizers potentially being toxic for cells. Moreover, these methods failed to generate multiscale and gradient wavy features, which are common in native tissues. An intriguing undulated topology, which forms as a result of tissue morphogenesis during embryonic development, is widely observed across human organs such as brain, intestine, blood vessels, and lungs. The formation of such a topology can be explained by a surface buckling principle, arising from the mechanical instabilities between epithelial tissues and their surroundings.^16,17

Inspired by epithelial tissue buckling morphogenesis, we propose a simple, versatile and efficient approach to fabricate wavy patterns in electrospun fibers through the use of thermally shrinking materials, thereby overcoming the limitations of current techniques as mentioned above. Using our bioinspired method, we readily produced fibrous scaffolds with various pattern features by manipulating processing variables, such as the orientation of deposited fibers, introduction of sacrificial fibers, and the thermally shrinking materials applied for buckling. Moreover, our technique allows the fabrication of electrospun scaffolds with gradient and multiscale, hierarchical wavy patterns, thereby mimicking the organization of multiple native tissues. To our knowledge, such a bioinspired fabrication method and resulting scaffolds have not been previously reported. Furthermore, tissue engineering (TE) applications of the scaffolds were demonstrated by enhanced cellular infiltration and higher expression of transforming growth factor-beta (TGF-β).

Results and discussion

Biomimetic fabrication of curly fibers

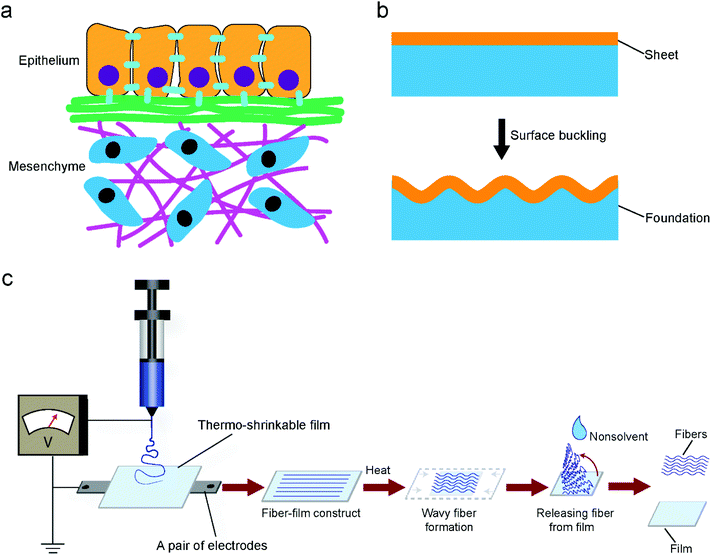
Insight into epithelial tissue morphogenesis may give rise to a biomimetic approach to generate wavy patterns. Epithelial tissue morphogenesis can be explained by a surface buckling mechanism.^16–18 Epithelial tissues are thin tissues that are initially flat in the embryo and almost always conformably adherent to mesenchyme tissues (Fig. 1a). This arrangement is similar to that of layered films and sheets in non-living systems. When exerting a uniaxial compression force on a thin film that floats on a soft elastic foundation resulting in corresponding in-plane stress, the film will form wavy or wrinkle patterns along its surface (Fig. 1b). The wrinkle patterns emerge because buckling the film leads to the deformation of the foundation. Regarding epithelial tissue buckling, the in-plane stress could arise from differential growth, either within a layer of cells or between adjacent layers. Inspired from the process of epithelial tissue buckling, we deposited electrospun fibers onto substrates of thermally shrinking thermoplastic materials to generate wavy or wrinkled patterns. Thermally shrinking polymeric materials, which tend to return to their original unstretched shape when heated above their softening point, are typically either mono- or biaxially oriented according to their manufacturing protocol.¹⁹ When the extending force is applied in one direction, monoaxial orientation occurs, whereas when the stretching force is simultaneously applied in two directions (equi) biaxial orientation is obtained. The macromolecules are frozen in this state until sufficient heat energy is applied to allow the chains to shrink back. In the present work, a monoaxial poly(lactic acid) (PLA) film was selected as a main substrate. The PLA materials had a shrinking temperature (T_s) of about 65 °C above which shrinkage occurs. To determine the materials’ shrinking properties, the PLA materials were shrunk up to 85 °C for different time periods (Fig. S1, ESI†). According to these results, optimal values for the film shrinkage were set at 75 °C for 1 min which allowed 60% shrinkage of the PLA film and enough time for manual loading into and uploading from a pre-heated oven.

Fig. 1 Biomimetic approach for fabricating wavy patterns. (a) Illustration showing the organization of epithelial tissues and their surroundings. Epithelial cell sheets attached to a basement membrane, which itself is adherent to mesenchyme tissues. (b) Illustration of layered sheets with an organization similar to that of epithelial tissues. A thin sheet adhering to the surface of a soft, elastic foundation will form wrinkle patterns out of the sheet plane when compression is applied. (c) Schematic showing a biomimetic approach for fabricating electrospun fibers with wavy patterns. In a typical process, aligned fibers are generated using a pair of electrodes. A fiber-film construct is generated by depositing fibers over a mono-axial thermo-shrinkable film, which is placed over the electrodes. Then, the fiber-film construct is heated to induce the shrinkage of the film, leading to the formation of wavy fiber patterns. The wavy fibers can be selectively detached from the thermo-shrinkable film via using a non-solvent. To fabricate various wavy patterns, the electrospinning collector can be modified from a pair of electrodes to various collectors as required, such as static metal plates, mandrels, and magnets. The thermo-shrinkable materials applied can be modified as well.

A poly(ethylene oxide terephthalate)/poly(butylene terephthalate) (PEOT/PBT) block copolymer, which has been demonstrated to be biocompatible and biodegradable, was used as a material for electrospinning.^20,21Fig. 1c shows the schematic of producing electrospun fibers with wavy patterns. In a typical process, fiber-film constructs were obtained by depositing PEOT/PBT fibers onto PLA substrates at room temperature, followed by heating at 75 °C for 1 min to allow the shrinking of the substrates. The PEOT/PBT fibers became softened and then buckled, the latter as a consequence of the substrates shrinking while the fibers adhered to them. Cooling down the fiber-film constructs to room temperature led to thermal fixation of the curled patterns generated in the PEOT/PBT fibers even when the fibers were released from the PLA substrates. This is one of the main advantages of our technique compared to previous studies where always an extra fixation agent or method was required.^6,10 Apparently, a certain applied heating temperature was crucial for permanently generating curls in the electrospun fibers. The heating temperature should be kept around or above the T_s of the substrate for the purpose of its heat-induced shrinking. In addition, the heating temperature should be capable of softening the electrospun fibers. If the fibers are not softened enough, hardly any fixation can be expected (mainly elastic recovery). Conversely, if the fibers are softened too much, there is no buckling either. Fig. S2, ESI,† shows poly(ε-caprolactone) (PCL) fibers which partially melted after shrinking the PLA film onto which they have been deposited. No curls formed because the applied heating temperature (65 °C) exceeded the melting temperature (T_m) of PCL (around 60 °C).

From single fiber curls to multiscale mesh waves

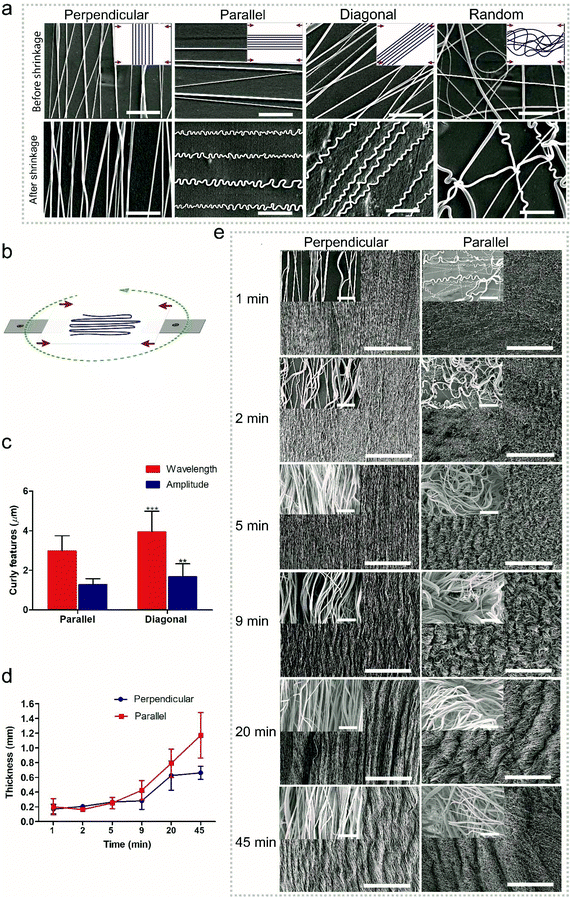
Random fibers were collected using a static ground plate, while aligned fibers were generated using a pair of parallel electrodes. Changing the angle of the PLA film during electrospinning allows the deposition of fibers relative to specific film orientations (Fig. 2b). In the case of a monoaxially oriented film, a perpendicular configuration corresponds to depositing fibers at a 90° angle with respect to the shrinkage axis; a parallel configuration corresponds to depositing fibers along the shrinkage axis; a diagonal configuration corresponds to fiber deposition at a 45° angle; a random configuration corresponds to randomly oriented fibers. As shown in Fig. 2a, after shrinking the PLA film, curled features were generated in fibers of all deposition directions at a low fiber density except for the perpendicular one. The wavelengths and amplitudes of curls for the parallel configuration showed a significant difference compared to those of diagonal configurations (Fig. 2c). However, it is difficult to assess the wavelengths and amplitudes for the random configuration since the fibers were randomly deposited and crossed each other, leading to heterogeneous curls in the fibers. With the same process, it is possible to transfer the effect of generating curl patters in fibers to the effect of generating multiscale waves in fiber meshes. The transition between the two effects depends on the density of deposited fibers, which in turn depends on the spinning time; a longer time corresponds to a thicker fiber deposition. For the given fiber chemistry and dimension in the present study, apparent multiscale waves on perpendicular samples started at 9 min deposition time with an average thickness of 0.3 ± 0.1 mm, while for the parallel samples it occurred at 5 min with the same average thickness of 0.3 ± 0.1 mm (Fig. 2d and e). Although previous methods have been proved to be capable of generating curl patterns in single fibers, they have no way of controlling the transition between generating curls on single fibers and generating multiscale waves in fiber meshes. With the present technique, the fabricated scaffolds can take on different structural configurations, which are promising as they can mimic the hierarchical organization of native tissues from the nano- to the macro-scale. The presented platform works also for fibers from other polymers. As shown in Fig. S3 and S4, ESI,† curly fibers of polyvinyl alcohol (PVA), polystyrene (PS) and polyacrylonitrile (PAN) could be generated using the oriented PLA films. Besides oriented PLA, the present technique could also be translated to other thermo-shrinkable materials. Theoretically, every thermoplastic material can be made into a stretched, oriented film, the frozen stress of which can be unlocked resulting in shrinking when reaching the stretching temperature, such as in the case of oriented PS films. Fig. S5 and S6, ESI,† show that curly features were successfully generated in PEOT/PBT and PAN fibers, respectively, using an equi-biaxially shrinkable PS film.

Fig. 2 From single fiber curls to multiscale mesh waves. (a) Comparison between fibers deposited in different directions relative to the direction of shrinkage before and after shrinking the film. Red arrows indicate the shrinking direction of the oriented PLA film. A parallel configuration corresponds to depositing fibers along the shrinkage axis; a diagonal configuration corresponds to fiber deposition at a 45° angle with respect to the shrinkage axis; a perpendicular configuration corresponds to depositing fibers at a 90° angle with respect to the shrinkage axis. (b) Schematic illustration of varying fiber orientations by changing the position of the film over the electrodes. Red arrows indicate the shrinking direction of the oriented PLA film, while the green dashed circular arrow means rotating the film to achieve different fiber orientations. (c) Histogram of wavelength and amplitude for parallel and diagonal configurations. (d) Depicting the thickness of samples with fibers deposited perpendicular or parallel to the shrinkage axis, after shrinking, according to the time of deposition. (e) Topographical evolution as the time of deposition increased and with it the mesh thickness. Samples where fibers were deposited perpendicular to the direction of shrinkage showed obvious mesh waviness rather than only curls on individual fibers after 9 min of deposition, whereas the parallel samples showed curls after 5 min. Scale bars: 20 μm (b) and 500 μm (d). **p < 0.01 and ***p < 0.001.

Tailoring a curled pattern using sacrificial fibers

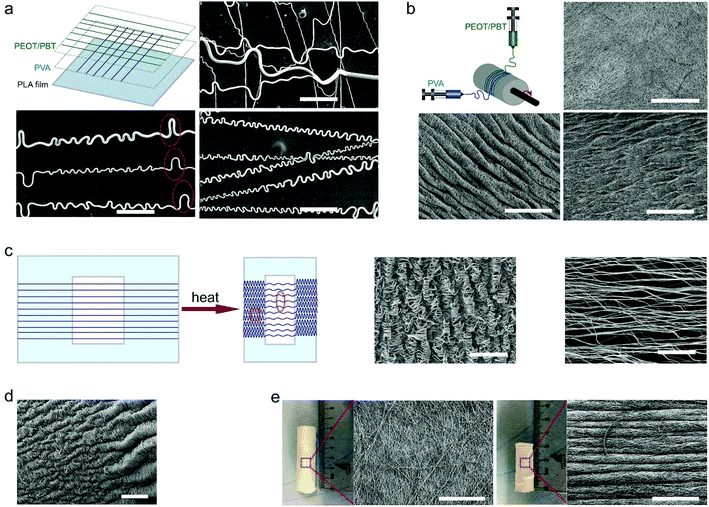
The curled pattern of fibers could also be tailored by using sacrificial fibers, such as those made from water-soluble polymers like PVA. Fig. 3a shows the schematic of fabricating a mixture of PVA and PEOT/PBT (PVA–PEOT/PBT) fibers, where first the PVA fibers were deposited on the PLA film, then PEOT/PBT fibers on top of the PVA fibers. After the removal of the sacrificial PVA fibers, PEOT/PBT fibers held a distinguishably different curled pattern having both periodical larger arches and small curls within the same fiber, which did not appear in the absence of the sacrificial polymer. However, concerning the removal of the sacrificial polymer, one could distinguish whether it was the first or second layer. As shown in Fig. S7a–c, ESI,† the final PEOT/PBT–PVA fibers, in which the PVA fibers were deposited as a second layer, had a different curly morphology after removing the PVA. The comparison of curled features between final PVA–PEOT/PBT and PEOT/PBT–PVA fibers was summarized in Fig. S7d and e, ESI.† The wavelength and amplitude for the larger arches in PVA–PEOT/PBT fibers were 47.2 ± 22.9 and 6.2 ± 1.8 μm, respectively, which is similar to the values of crimped patterns in human ligament collagen (wavelength of 45–60 μm and amplitude of 5–10 μm).¹⁴ On the other hand, the corresponding values for smaller curls in PVA–PEOT/PBT fibers were 5.2 ± 1.6 and 1.9 ± 0.5 μm, respectively. In the case of PEOT/PBT–PVA fibers, the smaller curls had an average wavelength of 3.2 ± 1.3 μm and average amplitude of 1.4 ± 0.5 μm, which were significantly different from that of PVA–PEOT/PBT fibers. Previous methods used to curl electrospun fibers could produce similar patterns to the ones achieved in the present work, but they have limited control over the range of wavelengths.^14,22,23 For example, Han et al. produced bucked electrospun fibers through manipulating the interaction between a collector surface and electrified jets that are characterized by whipping instability. The wavelength range corresponding to the buckled pattern in their study was 1.2–30.6 μm.²² Based on a complex method of calcination and reduction of copper, Chang et al. produced helical ribbons with fibers presenting a wavelength of 3.2 μm,²³ which is also in the range of the ones produced in the present work (from 3.2 ± 1.3 μm up to 47.2 ± 22.9 μm).

Fig. 3 Tailoring curled features by using additional, sacrificial electrospun fibers or tuning thermo-shrinkable materials. (a) Tailoring curled patterns along fibers by sacrificing a second layer of fibers from PVA. Illustration of fabricating PVA–PEOT/PBT fibers (top left). PVA fibers were first deposited on the surface of a PLA film, then a second layer of PEOT/PBT fibers was deposited over them; SEM images of curled PVA–PEOT/PBT fibers before (top right) and after (bottom left) sacrificing PVA fibers. The red circles indicate where PVA fibers have been before scarifying them; morphology of curled PEOT/PBT fibers without using a sacrificial layer of PVA fibers (bottom right). (b) Tailoring wavy patterns of fiber mesh through using sacrificial PVA fibers. Schematic of fabricating a blending fiber mesh of PEOT/PBT and PVA (top left); the blending fiber mesh of PEOT/PBT and PVA before (top right) and after (bottom left) shrinking; morphology of the blending wavy fiber mesh of PEOT/PBT and PVA after sacrificing PVA fibers (bottom right). (c) Fabrication of multiscale curled patterns. Schematic of fabricating multiscale curled patterns using a PLA film with an open central area (left). Square and encircled outlined areas depict different types of curled patterns obtained after shrinking; SEM images of the curled pattern in the square outlined area (middle), and in encircled outlined area (right). (d) SEM image of electrospun fibers having a gradient waviness. (e) Fabricating a buckled fiber mesh mimicking the structure of the trachea by using coiled PLA shrink films. Morphology of PEOT/PBT fibers deposited on a PLA tube before (left) and after (right) shrinking. Scale bar: 20 μm (a), 100 μm (c), and 500 μm (b, d and e).

This strategy of using a sacrificial polymer could also be translated to fiber meshes for tuning their surface and internal topographies. It has been demonstrated that topographical cues are important to cellular behaviors, including cell morphology, proliferation, migration and differentiation.^24,25Fig. 3b shows the comparison between fiber meshes before and after immersion in water. A difference in surface topographical pattern between them was visible, inclusively a smaller fraction structure after immersion due to the removal of the PVA fibers. A similar phenomenon was also observed in a previous work of Baker et al. where the authors combined electrospinning with sacrificial fibers to generate a scaffold allowing for engineered delamination.²⁶ Taken together, through the selective removal of fibers, it is possible to modulate the waviness or curliness of single fibers as well as fiber meshes.

Influence of thermally shrinkable material properties on curled features

As demonstrated in Fig. S1, ESI,† the shrinkage percentage of thermo-shrinkable materials is time dependent. Based on this concept, the curled features could be regulated via manipulating shrinkage percentages (Fig. S8, ESI†). When the shrinkage percentage increased from 10 to 40%, the number of “wrinkles” in scaffolds increased as well, and the average wavelength of the “wrinkles” decreased correspondingly. Importantly, the structure and geometry of thermo-shrinkable materials could be designed according to the specific requirements. Fig. 3c shows an electrospun mesh having multiscale buckled patterns generated using a planar oriented PLA film with an open central area. When the fiber mesh shrunk, the fibers possessed a lower ratio of shrinkage in the area where there was no film underneath compared to the area where fibers adhered to the film. Thus, multiscale buckled patterns could be generated on the fiber mesh. After shrinking, the fiber mesh had a coiled pattern on the sides, in contrast to a smoother wavy pattern in its central zone. This nice result might give rise to complex patterns by (laser) cutting or punching out complex shapes or complex arrays of simple shapes. Native tissue interfaces, such as the corresponding regions of tendons or ligaments and bone, show gradients in the structure, composition and mechanics.^27,28 In the specific case of the interface between tendons or ligaments and bone, a gradient in mechanical properties serves to mitigate stress concentrations.²⁹ Interestingly, with one corner of the oriented PLA film clamped and thus hindering from shrinking, a gradient wavy pattern could be generated (Fig. 3d). Gradients could also be approached by arrays of small circles with gradual changes in diameter. A scaffold having such a gradient waviness could be used in the field of regeneration of tissue interfaces. Fig. 3e shows electrospun fibers deposited on a coiled oriented PLA film. After shrinking, a corrugated hose-like construct having a wavelength of 104 ± 22.5 μm and mimicking the pattern of a trachea segment could be obtained. Overall, a desirable curly feature could be achieved via manipulating the properties of thermally shrinking materials, such as shrinkage percentage and geometric shapes. Regarding the geometric shapes, manufacturing thermally shrinking materials with more complex stretch patterns than only mono- or (equi)biaxially oriented films is already possible, e.g. by lab-scale (micro) thermoforming of films or blow-molding of tubes.

Mechanical properties

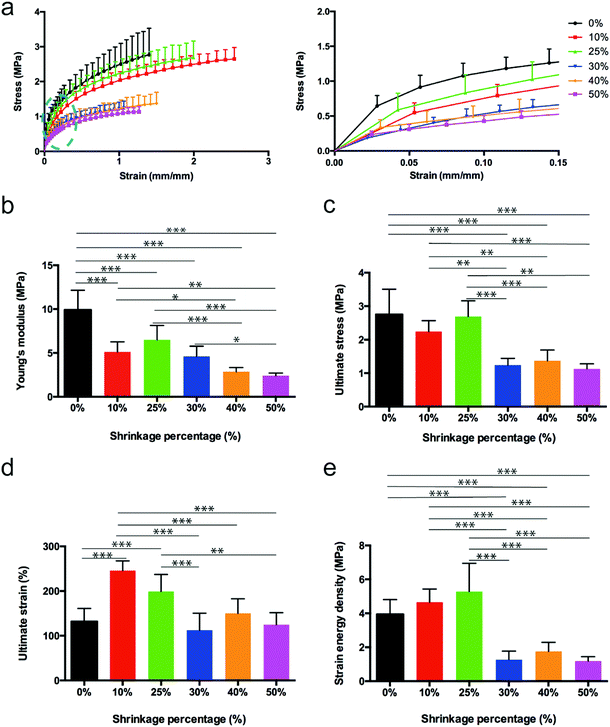
The mechanical behavior of the 3D waves was evaluated by performing uniaxial tensile tests. Scaffolds showed a limited hysteresis on the preconditioning phase. Stress–strain curves were characterized by a non-linear toe-heel region between 0 and around 1% of strain, a linear region between around 1% and 12%, and an extensive final region where the curve reached the ultimate stress always above 100%. The obtained results are listed in Table S1, ESI,† and plotted in Fig. 4a. A statistically significant decrease of the Young's modulus with the increase of the shrinkage percentage was detected (Fig. 4b). Similar trends were found for the ultimate stress and strain energy density (Fig. 4c–e). In particular, the 25% of shrinkage seemed to represent a threshold in the case of the ultimate stress and strain energy density. In order to describe the mechanical behavior of different curled fiber meshes, the experimental data obtained from the mechanical tensile tests were analyzed through a mathematical model. Hyperelastic models are commonly used to describe the behavior of skin, other soft tissues and rubber-like materials because of their extensive elastic behavior.³⁰ Here, the 3-parameter Mooney–Rivlin model was used to define a constitutive law to describe the material's stress–strain relationship as a function of the three empirically determined constants C₀₁, C₁₀ and C₂₀. Considering a uniaxial tensile test, the model can be expressed as
where σ is the applied stress, C₁₀, C₀₁ and C₂₀ are material parameter constants, and λ is the stretch ratio, defined as λ = 1 + ε. The estimation of the model parameters is provided in Table S2, Fig. S11, ESI.† The use of the Mooney–Rivlin model in the case of uniaxial tension conditions allowed fitting the experimental data obtaining three different dimensional constants. The statistical differences among the different parameters demonstrated a different mechanical behavior for different percentages of shrinkage. As our mathematical model fits the experimental data well, we may use this model as a constitutive law to predict a theoretical mechanical behaviour of curled fiber mesh for different percentages of shrinkage.

Fig. 4 Mechanical properties of wave structures. (a) Stress–strain behavior of wavy fibers fabricated from varied shrinkage percentages (left) and zoom in the encircled outlined area in the left (right). (b) Young's modulus. (c) Ultimate stress. (d) Ultimate strain. (e) Strain energy density. *p < 0.1, **p < 0.01, and ***p < 0.001.

Cell penetration

Cell penetration and growth throughout the scaffold are vitally important for tissue engineering applications.³¹ Although electrospinning scaffolds have drawn much interest in the tissue engineering field, one major limitation is that their fibers are typically densely packed, therefore hampering cellular penetration into the scaffold.^31,32 Thus, many approaches have been explored to overcome this problem, for instance sacrificial polymer electrospinning, salt particulate leaching, and electrospinning in combination with electrospraying.³¹ However, the current methods to improve cell penetration reduce scaffold stability.^26,33 Here, we hypothesized that wavy fibers enhance cell penetration into the corresponding electrospun scaffolds due to (larger) void spaces created during the buckling of fibers in the otherwise too close-meshed scaffold structure. Human mesenchymal stromal cells (hMSCs) were seeded at the same density on flat (non-wavy scaffolds) and wavy scaffolds. Scanning electron microscopy (SEM) images suggested that hMSCs on flat scaffolds dispersed on their surface while a big portion of cells on wavy meshes tended to entangle with the scaffold fibers (Fig. 5a). To further investigate their penetration and growth into/in flat and wavy scaffolds, nuclear staining was performed and cross-sections were analyzed. hMSCs on the flat scaffolds did not migrate further from superficial layers, whereas hMSCs on the wavy scaffolds migrated deeper and faster into the scaffolds (Fig. 5b). The distribution of cells in each depth section of flat and wavy scaffolds is summarized in Fig. 5c. For comparison, the depth presented in the x-axis corresponds to an average ratio of the penetration depth to the thickness of the scaffolds, since the wavy scaffolds had a higher thickness compared to the flat scaffolds, as a consequence of the buckling effect occurring during the underneath film shrinking (Fig. S9, ESI†).

Fig. 5 Cell penetration and luciferase assay. (a) Representative morphology of hMSCs grown on flat (top) and wavy (bottom) scaffolds. Red arrows indicate cells on scaffolds. Cells tend to be imbedded in fibers on wavy scaffolds compared to flat scaffolds. (b) Representative scaffold cross sections showing DAPI-labeled nuclei of cells on flat (left) and wavy (right) scaffolds at day 2 (top) and day 5 (bottom). (c) Histograms showing the distribution of cells present in each depth section of the flat (left) and wavy (right) scaffolds. For each scaffold region, the number of cells was counted and normalized to the total cell number present in the sample. The cellular penetration depth is normalized to the thickness of scaffolds. (d) Examination of the effect of wavy patterns on the TGF-β expression using luciferase assay. Quantification of DNA amount (top left); comparison of luciferase expression between flat and wavy scaffolds (top right); luciferase expression with DNA normalization (bottom). Flat, electrospun scaffolds without a wavy structure; wavy, electrospun scaffolds with a wavy structure; FBS, cell culture media contain fetal bovine serum (FBS). No FBS, cell culture media without FBS. Scale bars: 10 μm (a) and 200 μm (b). *p < 0.1, **p < 0.01, and ***p < 0.001.

By day 2, the largest number of cells stayed at the top of scaffolds and decreased in number towards the bottom of scaffolds for both wavy and flat substrates. Despite presenting the same trend, flat scaffolds presented a higher concentration of cells in the upper region (46% and 39% for 0–20% region and 20–40% region, respectively) whereas wavy scaffolds showed a better cell penetration (34% and 27% for 0–20% region and 20–40% region, respectively). After 5 days of culture, more cells migrated into the deeper regions of both scaffold types. However, more cells were present in the deeper region of the wavy scaffolds (10% for 80–100% region) compared to the flat ones (5% for 80–100% region). These results thus indicate that wavy scaffolds support a more homogenous distribution of cells throughout their thickness and a faster cell penetration than flat scaffolds.

TGF-β signaling expression

Given the resemblance of the obtained fibers with wavy patterns of connective tissues, we investigated if the wavy patterns could modulate the TGF-β pathway, a key signaling pathway involved in connective tissue development. A mink lung epithelial cell line harboring a TGF-β reporter construct (T-MLEC) was used to that end.³⁴ An increase in luciferase activity corresponds to an increase in TGF-β signaling. In the present experiments, fetal bovine serum (FBS) which contains TGF-β was used as a positive control.³⁵ As shown in Fig. 5d, no significant difference in DNA amount was observed between wavy and flat scaffolds indicating a similar cell proliferation and attachment. Cells seeded on a wavy scaffold emitted significantly more light than cells seeded on a flat scaffold at day 5, suggesting a corresponding increase in TGF-β signaling. In addition, when TGF-β signaling expression was normalized to the cell content, a significantly higher expression for wavy scaffolds was observed at day 2. Together, these results revealed that the wavy pattern showed a positive stimulus to TGF-β signaling expression.

A platform for fabricating functional scaffolds

The technique presented in this work could serve as a fabrication platform to generate functional scaffolds that could be beneficial for mimicking a variety of tissue organizations. Fig. S10, ESI,† shows a few examples of curled pattern characteristics of connective tissues that could be recreated with the fabrication technology proposed here. The organization of musculoskeletal tissues (Fig. S10a, ESI†), iris (Fig. S10c, ESI†), an artery wall (Fig. S10e, ESI†), and ciliary body (Fig. S10i, ESI†) composed of curled collagen fibers interconnected by a matrix can be mimicked by several of the curly fibers and wavy meshes that we can fabricate with our technique (Fig. S10b, d, f and j, ESI†). The trachea also displays a crimped pattern (Fig. S10g, ESI†) that could be mimicked by a wavy tubular high-fiber-density scaffold that was electrospun for 45 min on a shrink tube from a corresponding coiled film with the fibers deposited perpendicular to the shrinkage axis (Fig. S10h, ESI;† see also Fig. 3f).

Conclusions

We have demonstrated a biomimetic approach for producing nanofibers with complex wavy patterns via exploiting thermo-shrinkable substrates. Using this approach, it is facile to design wavy patterns from fiber curls to mesh waves. The wavy pattern features could be well controlled by adjusting processing variables, including the orientation of the deposited fibers, the shrinkage percentages of thermo-shrinkable substrates and the use of sacrificial fibers. This biofabrication technique can be readily extended to many other polymer fibers and thermo-shrinkable materials and opens up many possibilities for generating functional scaffolds mimicking various tissues such as trachea, iris, artery wall and ciliary body. hMSCs cultured on wavy nanofibrous scaffolds showed an enhanced cellular infiltration compared to those cultured on the non-wavy scaffolds. In addition, we also demonstrated that the fabricated wavy patterns could induce the expression of TGF-β, a common growth factor in the morphogenesis of several connective tissues, in the absence of a soluble growth factor. In future, other manufacturing techniques such as nanoimprint lithography for fabricating functional patterns and structures can be incorporated in our strategy to produce functional scaffolds with unique properties.³⁶ Besides, the fabrication of natural, thermally sensitive extracellular materials (e.g. collagen) with wavy patterns might be achieved by using solvent- instead of heat-induced unlocking of oriented substrates. We envision that wavy fibers produced by our biomimetic approach can be used as functional scaffolds, for example, for applications such as tendon, ligament and cardiac tissue regeneration. Furthermore, our new method may also inspire innovation in other application fields, such as functional textiles.

Experimental

Details of the experimental procedures are provided in the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was financially supported by the China Scholarship Council program (Grant #2011614016) and the European Research Council (Grant #637308). We thank Milena Fini and Maria Sartori for providing us musculoskeletal tissues for SEM imaging.

Notes and references

1. H. Chen, J. Huang, J. Yu, S. Liu and P. Gu, Int. J. Biol. Macromol., 2011, 48, 13–19.
2. H. Chen, X. Fan, J. Xia, P. Chen, X. Zhou, J. Huang, J. Yu and P. Gu, Int. J. Nanomed., 2011, 6, 453.
3. B. Sun, Y. Long, H. Zhang, M. Li, J. Duvail, X. Jiang and H. Yin, Prog. Polym. Sci., 2014, 39, 862–890.
4. A. Hasan, A. Memic, N. Annabi, M. Hossain, A. Paul, M. R. Dokmeci, F. Dehghani and A. Khademhosseini, Acta Biomater., 2014, 10, 11–25.
5. G. Cadafalch Gazquez, H. Chen, S. A. Veldhuis, A. Solmaz, C. Mota, B. A. Boukamp, C. A. van Blitterswijk, J. E. ten Elshof and L. Moroni, ACS Nano, 2016, 10, 5789–5799.
6. J. M. Caves, V. A. Kumar, W. Xu, N. Naik, M. G. Allen and E. L. Chaikof, Adv. Mater., 2010, 22, 2041–2044.
7. A. Hiltner, J. Cassidy and E. Baer, Annu. Rev. Mater. Sci., 1985, 15, 455–482.
8. J. Diamant, A. Keller, E. Baer, M. Litt and R. Arridge, Proc. R. Soc. London, Ser. B, 1972, 180, 293–315.
9. B. J. Rigby, N. Hirai, J. D. Spikes and H. Eyring, J. Gen. Physiol., 1959, 43, 265–283.
10. W. Liu, J. Lipner, C. H. Moran, L. Feng, X. Li, S. Thomopoulos and Y. Xia, Adv. Mater., 2015, 27, 2583–2588.
11. S. Fleischer, R. Feiner, A. Shapira, J. Ji, X. Sui, H. D. Wagner and T. Dvir, Biomaterials, 2013, 34, 8599–8606.
12. G. Zhao, X. Zhang, T. J. Lu and F. Xu, Adv. Funct. Mater., 2015, 25, 5726–5738.
13. S. E. Szczesny, T. P. Driscoll, H.-Y. Tseng, P.-C. Liu, S.-J. Heo, R. L. Mauck and P.-H. G. Chao, ACS Biomater. Sci. Eng., 2016, 3, 2869–2876.
14. D. C. Surrao, J. W. Hayami, S. D. Waldman and B. G. Amsden, Biomacromolecules, 2010, 11, 3624–3629.
15. A. Varesano, A. Montarsolo and C. Tonin, Eur. Polym. J., 2007, 43, 2792–2798.
16. C. M. Nelson, J. Biomech. Eng., 2016, 138, 021005.
17. K. Y. Volokh, Int. J. Dev. Biol., 2003, 50, 359–365.
18. M. J. Siedlik and C. M. Nelson, Cell Matrix Mech., 2014, 285.
19. P. N. Georgelos, J. E. Pelkie and D. L. Wilhoit, US Pat., US5397640A, 1995.
20. G. Beumer, C. Van Blitterswijk, D. Bakker and M. Ponec, Biomaterials, 1993, 14, 598–604.
21. G. Beumer, C. Van Blitterswijk and M. Ponec, J. Biomed. Mater. Res., 1994, 28, 545–552.
22. T. Han, D. H. Reneker and A. L. Yarin, Polymer, 2007, 48, 6064–6076.
23. G. Chang and J. Shen, Macromol. Mater. Eng., 2011, 296, 1071–1074.
24. M. Guvendiren and J. A. Burdick, Biomaterials, 2010, 31, 6511–6518.
25. S. A. Ruiz and C. S. Chen, Stem Cells, 2008, 26, 2921–2927.
26. B. M. Baker, A. O. Gee, R. B. Metter, A. S. Nathan, R. A. Marklein, J. A. Burdick and R. L. Mauck, Biomaterials, 2008, 29, 2348–2358.
27. A. Seidi, M. Ramalingam, I. Elloumi-Hannachi, S. Ostrovidov and A. Khademhosseini, Acta Biomater., 2011, 7, 1441–1451.
28. A. Di Luca, B. Ostrowska, I. Lorenzo-Moldero, A. Lepedda, W. Swieszkowski, C. Van Blitterswijk and L. Moroni, Sci. Rep., 2016, 6, 22898.
29. J. Lipner, W. Liu, Y. Liu, J. Boyle, G. Genin, Y. Xia and S. Thomopoulos, J. Mech. Behav. Biomed. Mater., 2014, 40, 59–68.
30. N. F. A. Manan, S. N. A. M. Noor, N. N. Azmi and J. Mahmud, ARPN J. Eng. Appl. Sci., 2015, 10, 6329–6335.
31. J. Rnjak-Kovacina and A. S. Weiss, Tissue Eng., Part B, 2011, 17, 365–372.
32. B. A. Blakeney, A. Tambralli, J. M. Anderson, A. Andukuri, D.-J. Lim, D. R. Dean and H.-W. Jun, Biomaterials, 2011, 32, 1583–1590.
33. A. K. Ekaputra, G. D. Prestwich, S. M. Cool and D. W. Hutmacher, Biomacromolecules, 2008, 9, 2097–2103.
34. M. Abe, J. G. Harpel, C. N. Metz, I. Nunes, D. J. Loskutoff and D. B. Rifkin, Anal. Biochem., 1994, 216, 276–284.
35. T. Oida and H. L. Weiner, J. Immunol. Methods, 2010, 362, 195–198.
36. A. Nandakumar, R. Truckenmüller, M. Ahmed, F. Damanik, D. R. Santos, N. Auffermann, J. de Boer, P. Habibovic, C. van Blitterswijk and L. Moroni, Small, 2013, 9, 3405–3409.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8nr10108f

---