Large area metal micro-/nano-groove arrays with both structural color and anisotropic wetting fabricated by one-step focused laser interference lithography†
Abstract
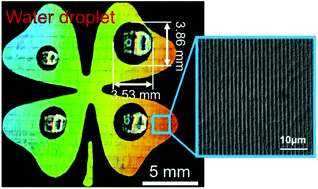
Artificial bioinspired surfaces are attracting increasing attention because of their fascinating characteristics, such as the structural color of a butterfly wing and the anisotropic wetting of a rice leaf. However, realization of the multicolor biomimetic metal surfaces with controlled anisotropy by using a simple, inexpensive and efficient method remains a challenge. Herein, we propose a focused laser interference lithography processing method, which has sufficient energy density and high processing efficiency to directly fabricate the groove structures on the metal surface. The surface is multicolor due to the diffraction grating effect of the regular groove structures, and exhibits anisotropic wetting due to its single-direction morphology. The influence of the observation angle on the diversity of colors and the anisotropic wetting under different heights and periods of grooves have been quantitatively investigated. A variety of patterns (e.g., leaf, crab, windmill, letter and so on) can be processed on various metals (e.g., stainless steel, Ti, Ni, Cu, Fe, Zn and so on) by this focused laser interference lithography because of its excellent flexibility and wide range of suitable materials. This multi-functional metal surface has broad applications in identification code, decorative beautification, anti-counterfeiting, information storage, bionic application design and so on.
- This article is part of the themed collection: Editor’s Choice: Controlling anisotropy in nanomaterials


 Please wait while we load your content...
Please wait while we load your content...