Silicon substrate effects on ionic current blockade in solid-state nanopores

Abstract

We investigated the roles of silicon substrate material compositions in ionic current blockade in solid-state nanopores. When detecting single nanoparticles using an ionic current in a Si₃N₄ nanopore supported on a doped silicon wafer, resistive pulses were found to be blunted significantly via signal retardation due to predominant contributions of large capacitance at the ultrathin membrane. Unexpectedly, in contrast, changing the substrate material to non-doped silicon led to the sharpening of the spike-like signal feature, suggesting a better temporal resolution of the cross-channel ionic current measurements by virtue of the thick intrinsic semiconductor layer that served to diminish the net chip capacitance. The present results suggest the importance of the choice of Si compositions regarding the capacitance effects to attain better spatiotemporal resolution in solid-state nanopore sensors.

---

Introduction

Solid-state nanopores have been widely used as a useful sensor platform for analyzing single particles and single molecules in liquid.^1–5 The detection principle involves measurements of an ionic current through a nanoscale hole sculpted in a thin dielectric membrane supported usually on a Si wafer.⁶ This simple mechanism allows one to detect an object passing through the conduit as it excludes ions there, thereby causing a pulse-like decrease in the current. The thus recorded resistive pulse contains valuable information concerning multiple physical parameters of single particles, including volume,^7,8 shape,^9,10 mass,¹¹ surface charges,¹² and even surface proteins.¹³

Similar to any sensor devices, a signal-to-noise ratio is a crucial issue in nanopore sensing. Usually, this has been dealt with by designing the channel size closer to the analytes of concern so as to produce more pronounced ionic current spikes by letting a larger amount of in-pore ion blockage upon translocation relative to the channel volume.⁷ Surface coating has also proven to be promising for suppressing the noise stemming from electrochemical reactions at water–dielectric interfaces¹⁴ as well as for coupling of amplifier voltage noise to device capacitance.^15–18 In addition to these strategies, the choice of substrate materials has been found to be a more basic yet effective way for improving the sensitivity of single-particle detectors.^19,20 For instance, compared to widely employed Si, low-k materials such as glass and polymers were demonstrated to offer a lower noise platform.¹⁹ However, non-Si substrates are not compatible in general with semiconductor technologies due to the rough surface that necessitates special skills to form membranes and pores.¹⁹ In contrast, we herein show that intrinsic Si can still be useful as a nanopore substrate regarding the spatiotemporal resolution of the ionic current-based single-particle analyses.

Results and discussion

Ionic current in a nanopore on doped Si

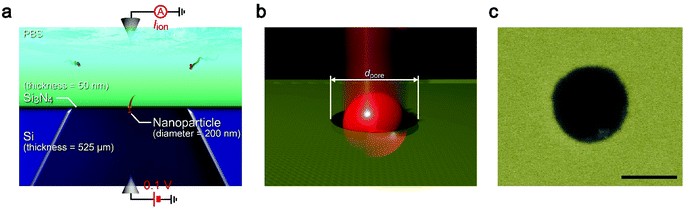
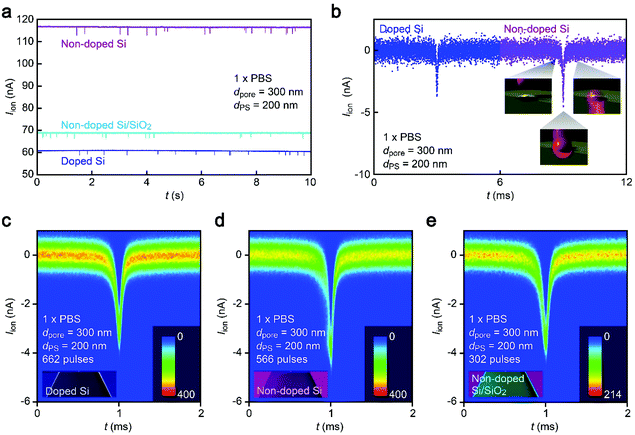
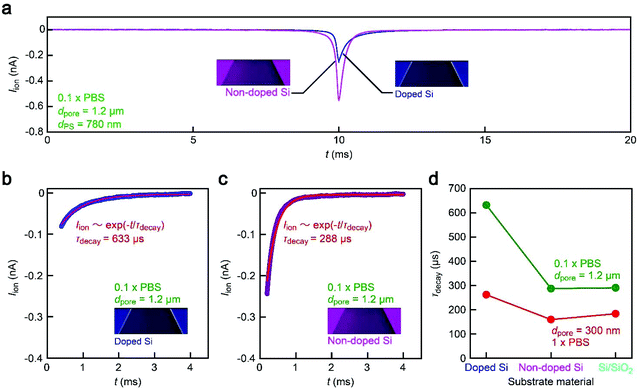
While the good insulating property of intrinsic Si posed a difficulty for exploiting electron-beam lithography to delineate nanopores, we developed a process to finely define a nanoscale channel by inserting a conductive thin film on a resist layer. By this process, we fabricated a pore of diameter d_pore in a 50 nm thick Si₃N₄ membrane suspended on doped (1–20 Ω cm) or non-doped (>1000 Ω cm) Si substrates and used it for the resistive pulse analyses of carboxylated polystyrene nanoparticles of diameter d_PS in an electrolyte solution.

The cross-membrane ionic current I_ionversus time (t) curves in 1× PBS with a nanopore of d_pore = 300 nm supported on a doped Si substrate (Fig. 1, see also Fig. S1†) showed an open pore current of 61 nA. This ionic conductance is in quantitative accordance withthe analytical expression^21,22 of the ionic resistance R_pore inside the channel, R_pore = ρ(4t_pore/πd_pore² + 1/d_pore) = 1.6 MΩ with the solution resistivity ρ = 0.4 Ω m for 1× PBS and the pore depth t_pore = 50 nm predicting I_ion = 62 nA at 0.1 V. On the other hand, resistive pulses were observed when admitting the buffer containing carboxylated polystyrene beads of d_PS = 200 nm, which are indicative of the electrophoretic translocation of the negatively charged polymeric nanoparticles through the channel (Fig. 2a).⁶ A close view of an I_ion signal revealed a rather smooth change in the current reflecting the dynamic motions of the polymer sphere in the expansive sensing zone extending by more than 500 nm from the channel due to the ultra-low thickness-to-diameter aspect ratio motif of the Si₃N₄ nanopore used (Fig. 2b and c).²³

Fig. 1 Solid-state nanopore structure. (a and b) Schematic models depicting single-nanoparticle detection in an electrolyte solution using a solid-state nanopore supported on a Si substrate. Two Ag/AgCl electrodes were utilized to apply a dc voltage of 0.1 V to a pore of diameter d_pore (b) in a thin membrane and measure the ionic current I_ion flowing through therein. (c) False-colored scanning electron micrograph of a nanopore of d_pore = 300 nm sculpted in a 50 nm thick Si₃N₄ membrane. Scale bar denotes 200 nm.

Fig. 2 Single-nanoparticle detection using a nanopore on a Si support of various compositions. (a) Temporal change in the ionic current (I_ion) through a 300 nm sized nanopore supported on a substrate made up of doped Si (blue), non-doped Si (purple), or SiO₂-coated non-doped Si (sky blue) in a dispersion solution of 200 nm sized carboxylated polystyrene nanoparticles in 1× PBS. Pulse-like signals indicate the electrophoretic translocation of the nanoparticles through the nanopore. (b) Magnified views of resistive pulses. The open pore current is offset to zero. Color coding is the same as that in (a). (c–e) Two-dimensional histograms showing a number of resistive pulses obtained with a 300 nm sized nanopore supported on a substrate of doped Si (c), non-doped Si (d), and SiO₂-coated non-doped Si (e).

Anomalous cross-pore ionic current characteristics on non-doped Si

Unexpectedly, I_ion traces of a nanopore on non-doped Si were found to be quite different. First of all, although the experimental conditions including ion concentrations and pore geometries were all set to be the same, the open pore current was higher by a factor of 2 than that in doped Si (Fig. 2a). Moreover, the ionic spike signals were also found to be slightly larger (Fig. 2b–d). This sort of difference cannot be simply ascribed to a variation in the pore diameter as larger pores should yield smaller resistive pulses in the low-thickness-to-diameter aspect ratio pore structure,²³ which is opposite to the case in Fig. 2b. In fact, the pore diameter was confirmed to differ by less than 10% under a scanning electron microscope (Fig. S1†). To shed light on this intriguing material dependence of the cross-membrane ionic current, we coated a SiO₂ layer of 50 nm thickness on the non-doped Si by chemical vapor deposition. Surprisingly, it caused only a marginal change in the resistive pulse waveforms from those found in the non-doped Si chips (Fig. 2e), whereas the open pore current became lower to a level comparable to that in the nanopore on doped Si (Fig. 2a; see also Fig. S2†). Similar effects have been observed by Lee and co-workers,¹³ wherein they attributed them to the suppression of electrochemical reactions at the Si surface. However, whether the results in Fig. 2 can also be explained by the surface effect needs further verification.

Leakage current via unintentionally formed pinholes

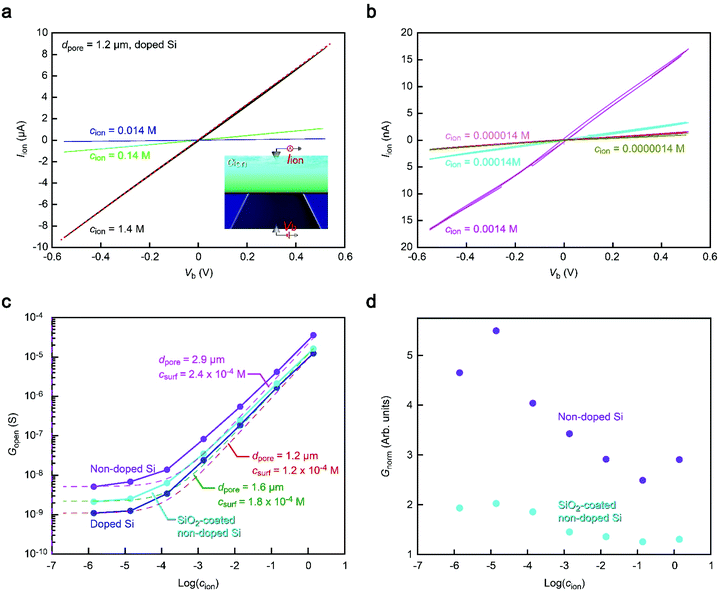
We thus explored the physical origin of the peculiar open pore conductance (Fig. 3) by measuring the I_ionversus bias voltage V_b characteristics. We investigated the salt concentration (c_ion) dependence of the open pore ionic conductance G_open. By diluting 10× PBS with ultrapure water (Merck Millipore), we prepared an electrolyte solution consisting mostly of Na⁺ and Cl⁻ ions with a vast range of c_ion from 1.4 M down to 1.4 × 10⁻⁶ M (Fig. 3a and b). The results for 1.2 μm sized Si₃N₄ pores showed a linear decrease in G_pore with decreasing salt concentration at c_ion > 10⁻³ M irrespective of the substrate materials manifesting the drift current characteristic of I_ion derived from the electric field-driven ion transport through the conduits (Fig. 3c).²⁴ In contrast, G_pore tended to level off at a certain level when further lowering c_ion. This electrolyte-independent ionic current can be attributed to predominant contributions of counterions at the pore wall surface.²⁵

Fig. 3 Substrate material dependence of the open pore ionic conductance. (a and b) I_ionversus applied voltage V_b characteristics measured in PBS buffer of various salt concentrations c_ion of high (a) and low (b) ranges. Red dashed line in (a) is a linear fit to the curve at c_ion = 1.4 M, from which we deduced the open pore conductance G_open. (c) Salt concentration dependence of G_open. The dashed line is a fit presuming contributions of the ions in bulk solution c_ion and the surface charge on the pore wall surface c_surf. Irrespective of the substrate materials, G_open scaled linearly with the ion concentration at c_ion > 10⁻³ M. On the other hand, G_open tended to level off at lower c_ion, suggesting a pronounced influence of the pore wall surface charges. (d) G_open normalized, G_norm, by that of doped Si plotted with respect to log(c_ion).

Meanwhile, it is also noticeable that the conductance remains in the order (doped Si) < (SiO₂-coated non-doped Si) < (non-doped Si) over the entire c_ion range examined (Fig. 3c), which is consistent with that shown in Fig. 2. To characterize the relative difference, we normalized G_open by that of non-doped Si. The thus obtained G_norm demonstrated that while the conductance ratio remains almost constant at c_ion > 10⁻² M, the discrepancy becomes more pronounced at lower ion concentrations until it saturates at c_ion < 10⁻⁴ M (Fig. 3d). This rather complicated behavior suggests a difference in the size of the ion-carrying channel in the Si₃N₄ membrane. For example, G_norm at the high c_ion regime indicates a larger amount of drift current suggestive of a larger space for the ions to traverse the membranes on the non-doped Si substrates. Although no conspicuous difference in d_pore was found under a scanning electron microscope together with any signs of additional channels in the membranes, it implies that some tiny pinholes were inadvertently created in the ultrathin membranes that mutually contributed to raising G_open for the cases of the non-doped substrates. As for the comparatively lower conductance in the nanopore on SiO₂-coated Si, it can be due to the filling of the pin holes by the deposited SiO₂ layer.

More quantitatively, the G_open–c_ion characteristics can be compared to the aforementioned theoretical model of G_pore = σd_pore, wherein we ignored the negligibly small resistance inside the pore compared to the access resistance in the present low thickness-to-diameter aspect-ratio pores. In the equation, the solution conductivity σ can be described as αc_net, where α is a constant and c_net is the concentration of ions relevant to the ionic current. Considering the role of the wall surface charges on G_open, c_net is further approximated to be c_net = c_ion + c_surf, where c_surf is the concentration of the surface charge-induced mobile ions. Indeed, Fig. 3c can be fitted by different d_pore values from 1.2 μm of the doped Si to 2.9 μm of the non-doped Si with similar c_surf in the range of 10⁻⁴ M. These results corroborate a variation in the net size of ion carrying pores in the membrane. We emphasize that while there seem to be additional small channels, the pore to detect nanoparticles had a size as defined in the nanofabrication processes as confirmed by electron microscopy observations that ensures no notable difference in the resistive pulse patterns among the Si substrates used.

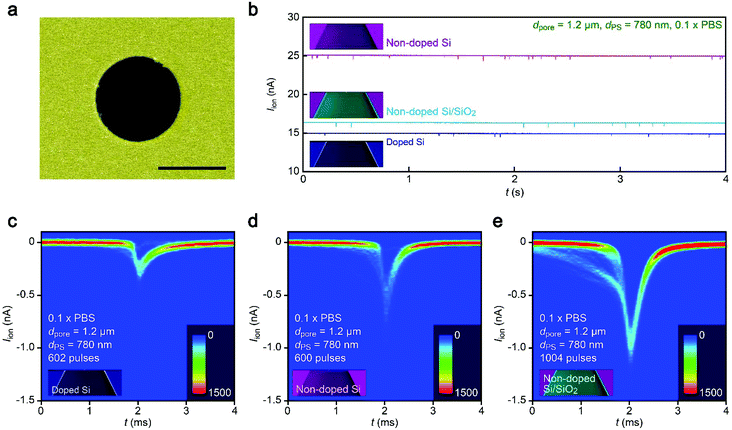
Blunted resistive pulses in a high-resistance pore

It therefore remains unclear why the resistive pulses became larger in the non-doped Si chips even when taking into account the experimental errors in the diameter of pores (Fig. S1†) as well as distributions in the size of nanoparticles (<5%). In this context, it is noticeable that the substrate effects on ionic blockades were found to be more pronounced in resistive channels as described below. The ionic current flowing through a pore of d_pore = 1.2 μm on doped Si in 0.1× PBS was found to be 15 nA at 0.1 V (Fig. 4a and b). The corresponding R_pore of 6.7 MΩ was about a factor of 4 larger than that in the 300 nm sized nanopore in 1× PBS (Fig. 2b). In this relatively high-resistance pore, the resistive pulses (obtained for 780 nm sized carboxylated polystyrene beads) showed a marked difference in their height when changing the support material from doped Si to non-doped Si (Fig. 4c–e).

Fig. 4 Resistive pulse analysis under low ionic conductance conditions. (a) False-colored scanning electron micrograph of a micropore of d_pore = 1.2 μm in a 50 nm thick Si₃N₄ membrane. Scale bar denotes 1 μm. (b) Typical ionic current curves obtained with the 1.2 μm sized pore supported on a doped Si (blue), non-doped Si (purple), and SiO₂-coated non-doped Si (skyblue). (c–e) Two-dimensional histograms showing a number of resistive pulses obtained with the 1.2 μm sized pore supported on a doped Si (c), non-doped Si (d), and SiO₂-coated non-doped Si (e). The open pore current is offset to zero.

A possible explanation for the peculiar substrate dependence of ionic current blockade is signal retardation due to the charging of capacitance in the nanopore system,¹⁸ which is described by the time constant τ = R_poreC_net, where C_net is the net capacitance of the whole chip. Indeed, the spike-like signals in the 1.2 μm sized pore can be fitted with an exponential decay function I_ion = I₀ exp(−t/τ_decay) with a longer time constant τ_decay (633 μs) for doped Si compared to the non-doped Si counterpart (288 μs) for the case of 1.2 μm sized pores (Fig. 5a–c, see also Fig. S3†). The tendency was qualitatively the same in the 300 nm sized nanopores due in part to the lower R_pore (Fig. 5d, see also Fig. S4†). This strongly suggests a prominent role of substrate-material-derived RC effects in the ionic current measurements: the resistive pulses in a pore on doped Si (non-doped Si) were significantly (less) retarded by the long (short) charging time at the capacitive components of the Si chips.

Fig. 5 Roles of substrate materials in the temporal response of the ionic current. (a) Average resistive pulses obtained with the 1.2 μm sized pore for 780 nm sized polystyrene nanoparticles in 0.1× PBS. The open pore current is offset to zero. The pulse became significantly blunt in the nanopore on doped Si than that on non-doped Si. (b and c) Ionic current decay at the resistive pulse tails for the 1.2 μm sized pore on doped (b) and non-doped Si (c). The red curves are exponential fitting that provides the decay constant τ_decay. (d) Substrate material dependence of τ_decay.

Substrate-capacitance-derived signal retardation in a nanopore

How exactly did the substrate contribute to the I_ion response to single-nanoparticle translocation then? In the description of time constant, the first term R_pore is solely determined by buffer resistivity and nanopore geometry, both of which were arranged to be the same in the experiments (except the anomalous leakage-like current in non-doped Si chips). This is in fact evident in the I_ion traces (Fig. 2a and 4b) showing a similar open pore current through the nanoscale conduit in two different substrates of doped Si and SiO₂-coated non-doped Si.

With R_pore being not so different, the distinct difference in the resistive pulse waveforms should be attributed to C_net. Usually, the nanopore structure is modeled as a parallel circuit of R_pore and the cross-membrane capacitance C_net (Fig. 6). In the present device architecture, C_net can be modeled as serial-connected capacitors of C_EDL/2, C_Si3N4, and C_Si denoting the capacitance of the electric double layers, the 50 nm thick Si₃N₄ regions, and the 525 μm thick Si support, respectively. Among the components, C_EDL is appreciably larger than the others,²⁶ and thus less important when connected in series. Whether the Si layer affects the ion blockade current therefore depends on the relative size of C_Si3N4, and C_Si. Based on the fact that the change in the composition of Si led to a pronounced effect on the resistive pulse patterns, C_Si was anticipated to be smaller or at least comparable to C_Si3N4. Indeed, from bulk physical properties, C_Si3N4 and C_nSi of non-doped Si per area are estimated to be 65 nF cm⁻² and 0.2 nF cm⁻², reflecting the two orders of magnitude difference in their thickness together with a minor influence of the relative permittivity of 11.7 and 7.3 for intrinsic Si and Si₃N₄, respectively. C_net is then deduced as C_net = C_Si3N4C_nSi/(C_Si3N4 + C_nSi) ∼ C_nSi for the intrinsic Si (Fig. 6a).

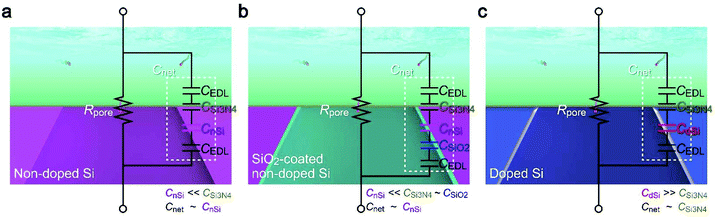Fig. 6 Capacitance of nanopore chips. (a–c) Equivalent circuits of a nanopore on non-doped Si (a), SiO₂-coated non-doped Si (b), and doped Si (c).

The discussion is the same for the case where non-doped Si is covered with 50 nm thick SiO₂ as its capacitance is only comparable to that of the Si₃N₄ layer, and hence contributes little to C_net due to the significantly smaller C_nSi connected in series (Fig. 6b). In contrast, the high conductivity of doped Si suggests a huge dielectric constant^27,28 that makes its capacitance C_dSi to be excessively larger than C_Si3N4, and hence C_net ∼ C_Si3N4. As a consequence, the net capacitance became much larger for the nanopore on doped Si, thereby rendering inadequate temporal resolution of the ionic current measurements for detecting the fast ion blockade events by the single-nanoparticle translocation (Fig. 6c). In fact, when assuming the real translocation time to be 287 μs, the pulses should be detected as 288 μs and 633 μs wide signals on non-doped and doped Si considering the RC delay with the relative difference in the specific capacitance, which is in fair agreement with the experimental results (Fig. 5). The overall findings can be used to achieve a faster temporal response of the ionic current and better signal-to-noise ratio in resistive pulse analyses using Si-based solid-state nanopores.

Signal retardation in smaller nanopores

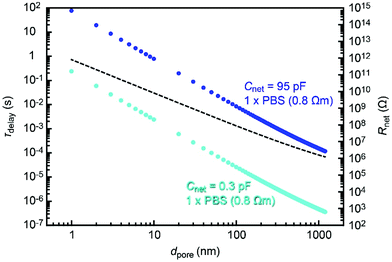
It is interesting to estimate the RC effect in smaller nanopores. For this, we calculated R_net using an access resistance model²⁹ as R_net = R_pore + R_acc, where R_pore = R_pore = 4ρL/πd_pore² and R_acc = ρ/d_pore are, respectively, the resistance inside and outside the pore of diameter d_pore and depth t_pore = 50 nm. The solution resistivity ρ in the equation was tentatively assumed to be 0.8 Ω m for 1× PBS. Then, we deduced the time constant for the cases of C_net = 95 pF and 0.3 pF corresponding to the properties of a 50 nm thick Si₃N₄ membrane on doped and non-doped 500 μm thick Si substrates, respectively. The thus obtained τ_delay − d_pore dependence (Fig. 7) suggested a significant influence of R_net on nanopores smaller than 100 nm under the conditions assumed. The detrimental influence is expected to become more significant when using a thinner membrane, which is a prerequisite for sensing ultrafine particles and molecules such as proteins³⁰ and polynucleotides.³¹ This predicts the importance to devote additional efforts to lower the capacitance by shrinking the water-touching area of thin dielectrics¹⁷ and also to decrease the net resistance by using an electrolyte solution with a higher ion concentration.

Fig. 7 Time constant in smaller nanopores. Blue and sky blue plots are τ_delay obtained for a pore of diameter d_pore in a 50 nm thick Si₃N₄ membrane supported on doped and non-doped Si, respectively, in 1× PBS. The dashed line describes the d_pore dependence of the pore resistance R_net.

Dielectric breakdown as a possible cause of pinhole generation

The variation in nanopore chip capacitance infers dielectric breakdown in a Si₃N₄ membrane as a cause of the anomalous cross-pore ionic current characteristics on non-doped Si. Yanagi et al.¹⁷ reported that electric charge imbalance between the two sides of a thin Si₃N₄ membrane would trigger a local fracture at intrinsic defects in the material in a manner akin to dielectric breakdown. The phenomenon was found to occur more easily in devices with lower capacitance due to the higher voltage induced upon injecting an electrolyte solution to a membrane.³² The resulting leakage current through the created pinholes became larger with decreasing capacitance.³² This would be a plausible explanation for the present results: the lower (higher) capacitance of the non-doped (doped) Si chips tends to trigger (hinder) dielectric breakdown yielding the larger (negligible) leakage-like ionic current through the membrane; meanwhile, SiO₂ deposition on non-doped Si contributed to slightly enlarge the net capacitance, thereby partially preventing electrical breakdown. The overall findings consistently indicate the importance of the substrate material not only for achieving a high temporal resolution of nanopore sensing but also for preventing unintentional formations of nanoholes in a membrane.

Conclusions

We systematically evaluated the influence of Si substrate materials on the performance of Si₃N₄ nanopore single-particle detectors. Although the only difference in the silicon substrate materials is the amount of impurities, and despite the fact that the substrate is located far away from the pore and so hardly imaginable to influence the cross-pore ion transport, the results demonstrated a pronounced influence on the ionic current sensitivity to single-nanoparticle translocation. Specifically, when a nanopore on a doped Si wafer was used, the relatively small capacitance at the thick silicon provided a short RC time constant with fast response of I_ion to the fast electrophoretic translocation of nanoparticles through the nanoscale conduit. In the case of doped Si, in contrast, its huge capacitance eventually raised the net capacitance of the device chip compared to that on the non-doped Si, thereby causing significant retardation of resistive pulse signals. The present results prove the usefulness of highly insulating silicon as a substrate material for attaining better performance of solid-state nanopore sensors.

Methods

Chemicals and materials

Si₃N₄-coated silicon wafers were purchased from Electronics and Materials. Carboxylated polystyrene nanoparticles were purchased from Polyscience and used without any filtering. Phosphate buffered saline (PBS) was purchased from Wako. Ultra-pure water with a resistivity of 18.2 MΩ cm was obtained using a Milli-Q Millipore system (Merck Millipore). Electron beam resist ZEP520A was purchased from Zeon.

Solid-state nanopore fabrications

Solid-state nanopores were fabricated as follows. A 525 μm thick silicon wafer with 50 nm thick Si₃N₄ layers grown on both sides via low-pressure chemical vapor deposition was diced into 30 mm × 30 mm chips using a dicer. The Si layer was either non-doped (conductivity < 1000 Ω cm) or phosphor-doped (conductivity = 1–20 Ω cm). 1 mm × 1 mm area of Si₃N₄ was removed by reactive ion etching using CF₄ gas. The exposed Si was then deep-etched in KOH solution heated to 80 degrees celsius. As a result, a 50 nm thick Si₃N₄ membrane of approximately 100 μm × 100 μm square dimension was formed at the bottom of the pyramidal-shaped trench. On the membrane, we spin-coated an electron beam resist (ZEP520A, Zeon) for electron-beam-drawing a nanopore. In the case of the non-doped Si substrate, we added a conductive spacer (ESPACER, Showa Denko) to avoid charge-up. A circle of diameter d_pore was then rendered by a standard electron-beam lithography method in a membrane. After development, the remaining resist was used as a mask to drill a nanopore by isotropically etching the surface by reactive ion etching (etchant gas = CHF₃). Then, the residual resist was dissolved in N,N-dimethylformamide followed by rinsing in ethanol and acetone. Before the measurements, we sealed the nanopore chip from both sides with two polymer blocks made of polydimethylsiloxane (PDMS). This was done by first activating the surface with oxygen plasma followed by attachment to the chip surface for eternal bonding. In the PDMS blocks, there was a microchannel to inject liquid into the nanopore.

Ionic current measurements

Resistive pulse analyses of single nanoparticles were implemented by measuring the ionic current I_ion through a nanopore of diameter d_pore sculpted in a 50 nm thick Si₃N₄ membrane under the applied dc voltage of 0.1 V using two Ag/AgCl electrodes. One side of the membrane was filled with a dilute dispersion solution of carboxylated polystyrene beads of diameter d_PS in PBS, while the other side was immersed in PBS only. The voltage created a huge electric field at the nanopore that served to electrophoretically draw the negatively charged nanobeads into the channel. As a result, I_ion tended to drop rapidly as each nanoparticle passed through the conduit due to the temporal block of the in-pore ion transport. The time-course change in the ionic current was recorded at a sampling rate of 1 MHz without any filter by using a home-built current amplifier backed by a fast digitizer (NI-5922, National Instruments) using a LabVIEW program.

Resistive pulse extraction

The moving open pore current was offset to zero by subtracting the linearly fitted base current in every 0.5 seconds of the I_ionversus t data. Resistive pulses were then obtained by searching for local minima below a threshold level followed by extraction of 0.005 seconds of data before and after each pulse apex.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

A part of this work was supported by the ImPACT Program of the Council for Science, Technology, and Innovation (Cabinet Office, Government of Japan), the “Nanotechnology Platform Project (Nanotechnology Open Facilities in Osaka University)” of the Ministry of Education, Culture, Sports, Science and Technology, Japan [No: F-12-OS-0016], and the Japan Society for the Promotion of Science (JSPS) KAKENHI Grant Number 18H01846.

Notes and references

1. J. E. Reiner, A. Balijepalli, J. W. F. Robertson, J. Campbell, J. Suehle and J. J. Kasianowicz, Chem. Rev., 2012, 112, 6431–6451.
2. C. Dekker, Nat. Nanotechnol., 2007, 2, 209–215.
3. L. Luo, S. R. German, W.-J. Lan, D. A. Holden, T. L. Mega and H. S. White, Annu. Rev. Anal. Chem., 2014, 7, 513–535.
4. S. Howorka and Z. Siwy, Chem. Soc. Rev., 2009, 38, 2360–2384.
5. D. G. Haywood, A. Saha-Shah, L. A. Baker and S. C. Jacobson, Anal. Chem., 2011, 6, 615–624.
6. W. H. Coulter, US patent, 2656508, 1953.
7. C. Y. Kong and M. Muthukumar, J. Chem. Phys., 2004, 120, 3460.
8. H. Yasaki, T. Yasui, T. Yanagida, N. Kaji, M. Kanai, K. Nagashima, T. Kawai and Y. Baba, J. Am. Chem. Soc., 2017, 139, 14137–14142.
9. E. C. Yusko, B. R. Bruhn, O. M. Eggenberger, J. Houghtaling, R. C. Rollings, N. C. Walsh, S. N. Nandivada, M. Pindrus, A. R. Hall, D. Sept, J. Li, D. S. Kalonia and M. Mayer, Nat. Nanotechnol., 2017, 12, 360–368.
10. M. Tsutsui, T. Yoshida, K. Yokota, H. Yasaki, T. Yasui, A. Arima, W. Tonomura, K. Nagashima, T. Yanagida, N. Kaji, M. Taniguchi, T. Washio, Y. Baba and T. Kawai, Sci. Rep., 2017, 7, 17371.
11. J. W. F. Robertson, C. G. Rodrigues, V. M. Stanford, K. A. Rubinson, O. V. Krasilnikov and J. J. Kasianowicz, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 8207–8211.
12. N. Arjmandi, W. Van Roy, L. Lagae and G. Borghs, Anal. Chem., 2012, 84, 8490–8496.
13. M.-H. Lee, J.-H. Lee, H.-M. Kim, Y.-R. Kim, T.-J. Jeon, Y. E. Pak and K.-B. Kim, Microfluid. Nanofluid., 2014, 16, 123–130.
14. A. Arima, A. H. Harlisa, T. Yoshida, M. Tsutsui, M. Tanaka, K. Yokota, W. Tonomura, J. Yasuda, M. Taniguchi, T. Washio, M. Okochi and T. Kawai, J. Am. Chem. Soc., 2018, 140, 16834–16841.
15. V. Tabard-Cossa, D. Trivedi, M. Wiggin, N. N. Jetha and A. Marziali, Nanotechnology, 2007, 18, 305505.
16. S. Shekar, D. J. Niedzwiecki, C.-C. Chien, P. Ong, D. A. Fleischer, J. Lin, J. K. Rosenstein, M. Drndic and K. L. Shepard, Nano Lett., 2016, 16, 4483–4489.
17. Y. Goto, I. Yanagi, K. Matsui, T. Yokoi and K.-I. Takeda, Sci. Rep., 2016, 6, 31324.
18. M. Tsutsui, K. Yokota, A. Arima, W. Tonomura, M. Taniguchi, T. Washio and T. Kawai, ACS Appl. Mater. Interfaces, 2018, 10, 34751–34757.
19. T. Jain, R. J. S. Guerrero, C. A. Aguilar and R. Karnik, Anal. Chem., 2013, 85, 3871–3878.
20. M.-H. Lee, A. Kumar, K.-B. Park, S.-Y. Cho, H.-M. Kim, M.-C. Lim, Y.-R. Kim and K.-B. Kim, Sci. Rep., 2014, 4, 7448.
21. S. W. Kowalczyk, A. Y. Grosberg, Y. Rabin and C. Dekker, Nanotechnology, 2011, 22, 315101.
22. M. Tsutsui, S. Hongo, Y. He, M. Taniguchi, N. Gemma and T. Kawai, ACS Nano, 2012, 6, 3499–3505.
23. M. Tsutsui, Y. He, K. Yokota, A. Arima, S. Hongo, M. Taniguchi, T. Washio and T. Kawai, ACS Nano, 2016, 10, 803–809.
24. W. Guan, R. Fan and M. A. Reed, Nat. Commun., 2011, 2, 506.
25. C. Lee, L. Joly, A. Siria, A.-L. Biance, R. Fulcrand and L. Bocquet, Nano Lett., 2012, 12, 4037–4044.
26. B. Skinner, M. S. Loth and B. I. Shklovskii, Phys. Rev. Lett., 2010, 104, 128302.
27. S. Dhar and A. H. Marshak, Solid-State Electron., 1985, 28, 763–766.
28. S. D. Ristic, Z. D. Prijic and S. Z. Mijalkovic, Phys. Status Solidi, 1995, 148, 575.
29. S. W. Kowalczyk, A. Y. Grosberg, Y. Rabin and C. Dekker, Nanotechnology, 2011, 22, 315101.
30. J. Wilson, L. Sloman, Z. He and A. Aksimentiev, Adv. Funct. Mater., 2016, 26, 4830–4838.
31. D. B. Wells, M. Belkin, J. Comer and A. Aksimentiev, Nano Lett., 2012, 12, 4117–4123.
32. K. Matsui, I. Yanagi and K.-I. Takeda, Sci. Rep., 2015, 5, 17819.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8nr09042d

---