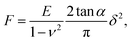Stiffness tomography of eukaryotic intracellular compartments by atomic force microscopy

Abstract

Precise localization and biophysical characterization of cellular structures is a key to the understanding of biological processes happening both inside the cell and at the cell surface. Atomic force microscopy is a powerful tool to study the cell surface – topography, elasticity, viscosity, interactions – and also the viscoelastic behavior of the underlying cytoplasm, cytoskeleton or the nucleus. Here, we demonstrate the ability of atomic force microscopy to also map and characterize organelles and microorganisms inside cells, at the nanoscale, by combining stiffness tomography with super-resolution fluorescence and electron microscopy. By using this correlative approach, we could both identify and characterize intracellular compartments. The validation of this approach was performed by monitoring the stiffening effect according to the metabolic status of the mitochondria in living cells in real-time.

---

Introduction

The mechanical properties of biological materials like cells and tissues are known to play a key role in cell differentiation,¹ cell division,² cancer,^3,4 infectious diseases⁵ and other processes.⁶ Changes in stiffness are often an early sign of these processes or diseases. Several techniques are being developed or adapted in order to probe these changes. Optical tweezers not only have a high force sensitivity, but also have a small maximum indentation and a resolution limited to the size of a bead. Micropipette aspiration is a sensitive technique for the membrane and cytoplasm but not suitable for cellular organelles. Magnetic resonance⁷ and ultrasound⁸ are non-invasive techniques but are limited by a poor resolution, above hundreds of micrometers. Deformability cytometry⁹ probes mechanics at a very high throughput (microfluidic), but only at the cellular level. Brillouin microscopy¹⁰ is an emerging, non-invasive technique, with a possible resolution below the micrometer. Since its invention in 1986 and its first biological applications in the 90s, atomic force microscopy (AFM) has emerged as one of the best tools to study the cell surface and the mechanical behavior of both cells and tissues.¹¹ By its design and uses, though AFM is a surface technique, it was still successfully manipulated to analyze the elasticity of intracellular vacuoles,¹² visualize actin filaments in cells,¹³ image mitochondria,¹⁴ and detect the nucleus.¹⁵

We demonstrated that segmenting the Force vs. tip/sample Distance (FD) curve obtained during AFM indentation experiments allows extracting stiffness values of defined 3D slices in living cells.¹⁶ This approach further permitted extension to nanotomography¹⁷ although without the identification of the internal structures. This was later tried using AFM and confocal microscopy focusing on the nucleus.¹⁸ This technique permitted the detection of stiffness differences in fixed and living macrophages,¹⁹ the study of living Arabidopsis thaliana cells²⁰ and bacteria subjected to antibiotics.²¹ Other approaches of tomography have been proposed, like using a nanoneedle²² or using the dynamic modes of an AFM.²³ Another way to gain access to the inside of a cell with the AFM is to unroof it completely,²⁴ but this alters the cell structure. A variant method has also been used to study human esophageal cells with the identification of the nucleus using confocal microscopy.¹⁸

Most of the current elasticity experiments realized using AFM on biological samples are focused on comparing the elasticity values of cells. The measurements are often made on more or less random parts of cells and all the elasticity values are collected for comparison between two or more populations. It is known that performing force curves above the nucleus or near the cell border can disperse the measured elasticity values. Here, we demonstrate that single organelles also have an influence on the measurements. Therefore, stiffness tomography contributes to a better understanding of elasticity measurements on cells.

There are still some limitations to studying the elasticity of cells. Living cells are heterogeneous, dynamic, and anisotropic. Consequently, the Hertz/Sneddon models are not thoroughly suitable to describe cells, not even fixed cells. Additionally, Poisson's ratio is assumed to be constant and set to 0.5, which remains to be demonstrated. Moreover, the Hertz/Sneddon models do not consider the viscosity of the sample, which becomes more and more important as the scanning speed of atomic force microscopes increases. Several research groups are working on different approaches for viscosity analysis^25–28 and hence, there is no doubt that new models will describe the mechanics of cells better. Limitations should also be considered when using stiffness tomography analysis. First, the intracellular compartments have to be reachable to the AFM tip without damaging the cell. Spread cells with a flat cytoplasm are privileged vs. toll cells in which the basal region remains inaccessible to the analysis. As these compartments are differently located inside the cells, the AFM tip must compress a variable amount of cytoplasm before attaining the organelle of interest and therefore it is not possible to compare the stiffness values of organelles from different cells. Instead, analyzing the functional dynamics perturbation induced upon drug exposure can be highly informative. Also, the increase of contact area during indentation with a spherical/conical tip is not considered. This could be solved by using the plateau tip as their contact surface remains constant during indentation. Moreover, the AFM tip must be able to detect the structure thanks to its size and stiffness difference from the surroundings. Resolution is limited by the convolution of the tip with the sample and sensitivity is limited by the spring constant of the cantilever. Nevertheless, the recent AFM probe developments provide the user many opportunities (smaller cantilever with a low spring constant, different tip geometries). The stiffer the organelles inside a soft cytoplasm, the better the contrast, even though soft organelles in a stiff material are theoretically detectable for small indentations.¹⁷ Lastly, the AFM scanning speed must be equal or greater than the dynamics of the observed structure. In this study, we performed stiffness tomography on actin, intracellular bacteria, Golgi apparatus and mitochondria. We found out the latter to be the most challenging, regarding its size, dynamics, and stiffness. Importantly, the identity and position of the intracellular organelle should be ascertained using photonic or electron microscopy to unambiguously correlate the change in stiffness with the presence of the intracellular component.

We propose here to exploit the heterogeneity of the mechanical properties of cells to obtain stiffness contrast at the nanoscale, allowing the detection of intracellular structures. By using a correlative approach, we can identify internal structures not only by their topography and stiffness but also by fluorescent markers and details provided by electron microscopy.²⁹ The first goal was to unambiguously identify intracellular structures, as most stiffness tomography studies were not correlated with any other type of microscopy.^19,21,30 As a proof of concept, this was first performed on fixed cells with the identification of organelles with photonic and electron microscopy. Once the identification of the intracellular structures was validated, our second goal was to follow the stiffness dynamics of these intracellular structures in living cells to carry out biomechanical studies.

Experimental

Mammalian cell culture

PtK2 cells (ATCC, CCL-56) were cultured at 37 °C under a 5% CO₂ atmosphere in Minimum Essential Media (MEM) supplemented with 10% FCS, 2 mM L-glutamine, 100 U ml⁻¹ penicillin G/streptomycin. All reactants were from Gibco, Invitrogen (Life Technologies). Cells were grown at [30–50] % confluency on 35 mm glass-bottom dishes (WillCo-dish, WillCo Wells B.V.) or on 24 mm grid labeled coverslips (Pelco) when electron microscopy was needed.

HeLa cells (ATCC, CCL-2, American Type Culture Collection) were cultured in Dulbecco's Modified Eagle's Medium (DMEM) supplemented with 2 mM L-glutamine, 10% fetal calf serum (FCS), and 100 U ml⁻¹ penicillin G/streptomycin. HeLa ManII-HRP cells³¹ were cultured in DMEM, supplemented with 1 mM sodium pyruvate, 10% FCS and 500 μg ml⁻¹ geneticin (G418).

Infection

Yersinia pseudotuberculosis IP32777 was pre-cultured overnight in Lysogeny Broth (BD, Becton Dickinson) at 37 °C under constant agitation. Before use, the bacteria were diluted to 1/50 with fresh medium. When bacteria reached their exponential growing phase (optical density 600 nm between 0.6 and 0.8), they were centrifuged and rinsed with MEM. PtK2 cells were then infected with a Multiplicity of Infection (MOI) of 10. Bacteria/host cell adhesion and synchronization were achieved by centrifugation. Cells were rinsed and gentamycin was added 30 min post infection for 30 min to get rid of extracellular bacteria. Cells were finally rinsed with PBS and fixed with 4% paraformaldehyde (Sigma-Aldrich) for 15 minutes.

Cell staining

PtK2 cells were stained for actin filaments with SiR actin (Spirochrome SC001, Switzerland) for 2 hours. LC3 labeling was performed by first permeabilizing cells with 0.2% Triton X100 in PBS for 5 minutes, and then adding a primary rabbit antibody against human LC3 (MBL, PM036, US-MA), at a 1/500 dilution at 4 °C overnight. This was followed by incubation with a secondary anti-rabbit antibody coupled with a STAR 488 (Abberior, 2-0012-006-5, Germany) at a 1/200 dilution for 1 hour. Bacteria were labeled with 10 μg ml⁻¹ DAPI for 5 minutes.

For live imaging of mitochondria, cells were incubated with 500 nM MitoTracker® (Invitrogen) for 30 minutes.

HeLa cell Golgi crosslinking was achieved as described elsewhere.³¹ Briefly, living HeLa cells stably expressing a Golgi-localized horseradish peroxidase (ManII-HRP) were incubated with 0.23 mg ml⁻¹ DAB (Sigma Fast Tablets, Sigma-Aldrich) and 0.003% H₂O₂ (Sigma-Aldrich) for 30 minutes in PBS (Invitrogen) at 0 °C in the dark. The cells were then either fixed with 4% paraformaldehyde in 0.1 M sodium cacodylate at pH 7.3 for 30 minutes or imaged directly. Golgi apparatus immunolabeling was performed on fixed HeLa cells incubated first with a primary anti-GM130 mouse antibody (BD) for 45 minutes at room temperature and then with a secondary Alexa Fluor® 488-conjugated goat anti-mouse antibody (Invitrogen) for 30 minutes at room temperature in the dark.

Live cell imaging

Experiments for fixed cells were carried out in PBS (Gibco) while living cells were imaged in MEM (Gibco) without phenol red, supplemented with 25 mM HEPES (Sigma-Aldrich) at 37 °C, using a heating sample holder on the AFM. The fluorescence light source (Lumencor SOLA) was used at the lowest intensity to prevent fluorophore bleaching and phototoxicity on cells.

Atomic force microscopy

Mitochondria and bacteria experiments were carried out either on a NanoWizard™ 3ultra AFM (JPK) coupled to a STED microscope (Stimulated emission depletion, Abberior Instruments), or a NanoWizard™ 3 (JPK) AFM coupled to an Axio Observer.Z1 (Zeiss). Cantilevers were purchased from Olympus (AC40, 0.09 N m⁻¹, 8 nm tip radius) and calibrated prior to every experiment using the Sader method³² implemented in JPK software version 6. The tip is conical at large indentation, and we measured an average half-tip angle of 13.3°. The AFM was operated by increasing the force at each pixel of the image to give a FD curve³³ in Quantitative Imaging (QI) mode. The force trigger was adjusted to have a high indentation without damaging the cell. It was set higher on fixed cells (3 nN) than on living cells (1 nN) for the same indentation range ([150–700] nm). The integrity of the cell was monitored by a live bright-field video and live approach curves (no rupture event). The tip velocity was maximized within the instrument limits (300 μm s⁻¹) and the ramp size (2 μm) was reduced with a short baseline in order to minimize the acquisition time. Also, the noise level was kept at a good level ([19–24] pN). We show here the best examples from 11 experiments.

Golgi apparatuses were imaged on a Bioscope Catalyst AFM (Bruker) in Force Volume mode with Bruker DNP probes (0.06 N m⁻¹, half tip angle 18°). Cantilever calibration (deflection sensitivity and spring constant) was performed with the manufacturer's respective software prior to imaging, by acquiring a force curve on the glass substrate for deflection sensitivity calibration, followed by a thermal tune. The trigger force was set to 10 nN (fixed) and to 14 nN (fixed, crosslinked), with 60 μm s⁻¹ tip velocity, 6 μm ramp size, and 128 × 128 pixels.

Elasticity and stiffness tomography analyses

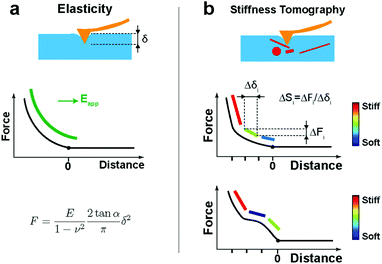
After the automatic detection of the point of contact, the approach FD curve was referred to as an indentation curve. For elasticity analysis, data were fitted by the Sneddon model to extract the elastic modulus of the sample (Fig. 1a):
where the force F is related to the indentation δ by Young's modulus E and Poisson's ratio ν of the sample, and by the half-angle of the tip α. The tip shape is neither purely spherical nor conical, but at a high indentation, the conical shape becomes more prevalent. This model was refined using the bottom effect correction³⁴ to compensate for the finite thickness of the cell. The term “apparent Young's modulus” is used because, on cells, parameters not considered in the model have an influence on the measured value (see Discussion).

Fig. 1 Benefits of elasticity or stiffness tomography analyses on cells (a) apparent Young's modulus (green) calculated by fitting all the points of the indentation curve (black) from the POC (point of contact) using Sneddon's model; (b) distortions of the FD curve occurring because of the intracellular components being detected and leading to segments with different stiffnesses (blue: soft, to red: stiff).

However, when a large indentation is performed with a fine indenter on cells, the FD curve shows non-linearities and inhomogeneities (Fig. 1b), which correspond to the differences in the stiffness of internal structures. In these cases of inhomogeneities, the classical Hertz/Sneddon models do not describe the data appropriately. However, interestingly, by restricting the data to small segments, we can obtain the stiffness contrast by calculating the slope of each segment:

ΔS_i = ΔF_i/Δδ_i,

where S_i is the stiffness, F_i is the force and δ_i is the indentation of the segment i. Stiffness tomography data can be displayed as 3D maps (XYZ) or as 2D projections (XY) for different indentation depths, as well as tomograms (stiffness slices in the XZ plane). The pixel height is calculated from the point of contact while the apparent stiffness is coded in color at the different indentation steps. This method can be performed on any commercial AFM with the suitable cantilever and parameters.

The AFM data analysis was performed with in-house developed software (pyAF, python Atomic Force).³⁵ An algorithm based on the fitting of the baseline was used to detect the point of contact on the FD curve. A linear fit was done on the baseline of the approach curve. A noise threshold was used to shift the fit along the force axis. The noise parameter can be manually adjusted by the user to optimize the detection of the point of contact. The intersection between this shifted fit and the FD curve defines the position of the point of contact. Then, we either calculated Young's modulus from the point of contact to a given indentation using Sneddon's model (with Bottom Effect Correction³⁴), or we segmented the indentation curve and computed the slope for each segment for stiffness tomography. The size of the segment must be greater than the instrumental noise but also small enough to detect stiffness differences. It is usually in the range [20–60] nm. Poisson's ratio was set to 0.5. The AFM maps could be either displayed as flat surfaces (without the topography) or as 3D objects. The different image sizes and resolutions were automatically taken into account using the software.

Electron microscopy

After atomic force microscopy and light microscopy, cells were additionally fixed with 1% glutaraldehyde in 0.1 M sodium cacodylate at pH 7.3 for 30 minutes at room temperature. Cells were next contrasted with 1% potassium ferricyanide-reduced osmium tetroxide and then 1% uranyl acetate both for 1 hour at room temperature in the dark. Cells were dehydrated in graded ethanol (VWR) solutions and finally infiltrated with epoxy resin (EMS) and cured for 24 hours at 60 °C. After the removal of the glass-bottom dish with hydrofluoric acid (Sigma-Aldrich) from polymerized resin, cells of interest were relocated thanks to the marks at the resin surface and prepared for sectioning parallel to this surface. Serial sections of 70–80 nm thickness were set down on carbon/formvar-coated slot grids and were observed with a Hitachi H7500 TEM (Milexia, France), and images were acquired with a one Mpixel digital camera from AMT (Milexia, France). See the previously published CLAFEM method for more details.²⁹

Results

Mapping stiffness of intracellular elements in fixed cells

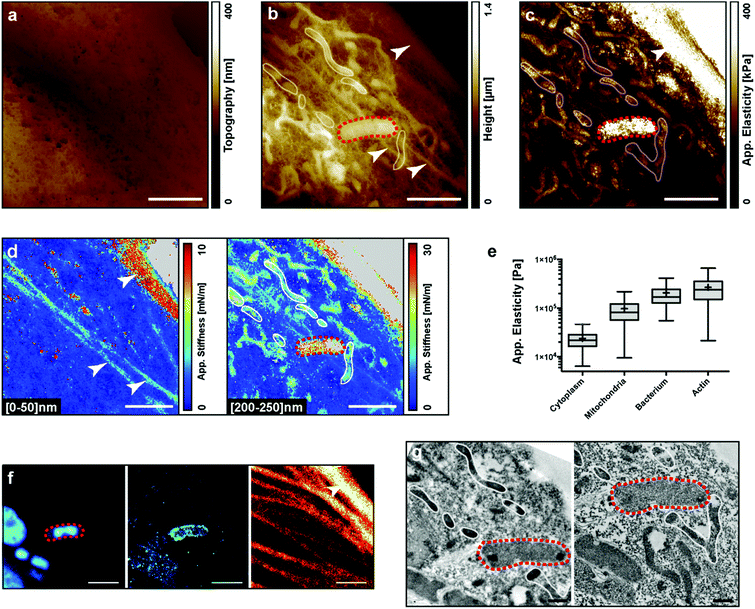
We performed AFM experiments on fixed PtK2 cells infected with the Yersinia pseudotuberculosis bacterium. Y. pseudotuberculosis is a food-borne infection in humans and can cause mesenteric lymphadenitis, granulomatous disease, and dissemination with sepsis. It can survive intracellularly by subverting the autophagy pathway.³⁶

To visualize the intracellular elements with the AFM, cells were infected, fixed, and labeled for the actin cytoskeleton, bacteria and LC3-positive autophagic vacuoles. A single cell was then subsequently imaged by bright field microscopy, fluorescence microscopy, AFM, and finally by electron microscopy (Fig. 2a, f and g, respectively). Fig. 2a shows the real topography of the cell, the so-called zero-force image. No internal compartment is visible, yet we can observe the effect of the fixation on the porosity of the membrane. Fig. 2b shows the height of the z piezo at the end of the indentation. Different stiffnesses within the sample are responsible for different maximum indentations with the same applied force. Some structures, which may correspond to a bacterium, mitochondria and the actin cytoskeleton, become visible. The bacterium (red dashed loop) was confirmed by fluorescence and electron microscopy (Fig. 2f and g). The bacterium was labelled with DAPI and LC3 indicating that the bacterium was in an autophagic vacuole (Fig. 2f left and middle). Correlation could also be obtained for the actin cytoskeleton between AFM and fluorescence observations. The internal pools of actin cables were not visible in Transmission Electron Microscopy (TEM) because the sections shown did not contain the actin bundles. Finally, mitochondria were identified by electron microscopy (Fig. 2g). After all image acquisition, we calculated the apparent elasticity map (Fig. 2c): the actin pool and the bacterium appear stiffer than the mitochondria. This was confirmed by a quantification of elasticities for the different regions of interest (Fig. 2e). Remarkably, we performed stiffness tomography on the same data at two indentation depths: [0–50] nm and [200–250] nm (Fig. 2d). At a low indentation, we could identify 3 actin bundles. At a higher indentation, these bundles faded indicating that they were on the top of the cell, while the AFM sensed several mitochondria deeper inside the cell. Even though stiffness tomography and TEM could not be performed at the exact same cell depth, we could observe a nice correlation for the mitochondria (white loops in AFM and TEM images).

Fig. 2 AFM allows distinguishing intracellular compartment stiffness features. Panels show the PtK2 fixed cell infected by Yersinia pseudotuberculosis. (a) Cell surface topography (zero force, plane-fitted). (b) Piezo height after indentation (3 nN, plane-fitted). (c) Apparent elasticity map calculated from FD curves at each pixel. (d) Stiffness tomography maps at different indentations: left: [0–50] nm, right: [200–250] nm. (e) Boxplots of the quantification of the apparent elasticity module corresponding to the different intracellular compartments. (Mean shown as+) (f) identification of compartments by coupled STED microscopy. Left: DAPI, middle: LC3, right: actin. (g) Ultrastructure obtained by correlated transmission electron microscopy (2 slices). White arrowheads: actin, dashed red loop: bacterium, white loops: mitochondria. Scale bars: white: 2 μm, black: 500 nm.

Stiffness changes of stressed organelles in living cells

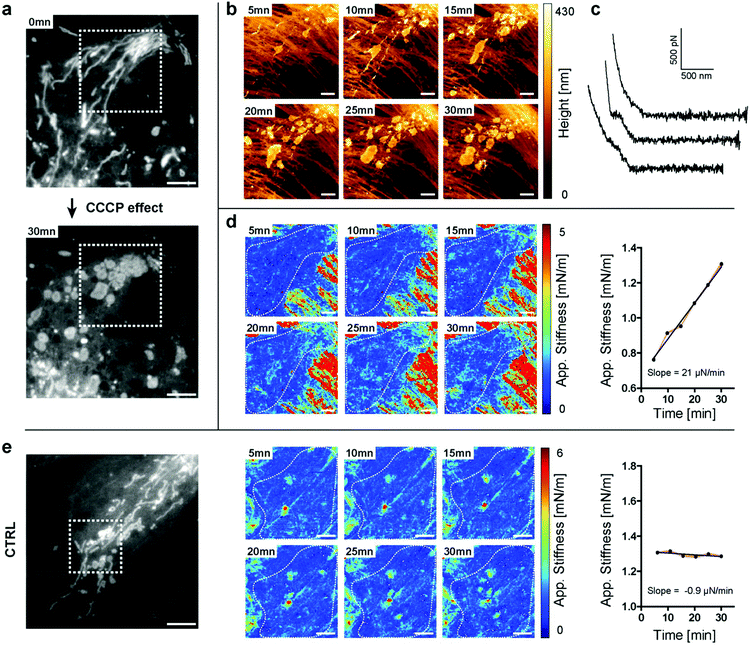
Mitochondria are responsible for providing energy sources inside the cells. They often form a dense network around the nucleus and are more sparsely distributed on the edges of the cell. They are highly dynamic and can adopt different shapes, and undergo fission and fusion.³⁷ Recently, the possibility to measure the elasticity of mitochondria in cardiomyocytes was reported.³⁰ However, the AFM data were not directly correlated with the fluorescence or electron microscopy images of the same mitochondria, hence leading to an indirect interpretation of the results. Some coupling between AFM and fluorescence was also recently achieved by using High-Speed AFM (HS-AFM) imaging, although without providing mechanical information.¹⁴

In the next experiments, we followed the stiffness changes in living cells. We first had to test whether stiffness tomography measurements were not detrimental to the organelles due to the force applied to the system. The effects of nanomechanical forces on the mitochondria by means of AFM were already reported.³⁸ The authors stressed out that the forces applied with the tip could be used to divide a mitochondrion, which we further confirmed with our observations. We performed indentation experiments on living cells at 37 °C in HEPES-buffered medium. As shown in Fig. 3b, the standard trigger force does not produce any morphological changes of the mitochondrion. We were then able to move, fuse and even fragment some mitochondria by applying a higher trigger force (Fig. 3c and videos). Choosing the appropriate force for stiffness measurements on living cells proved here to be very important. This force will depend on the cell type as well as on the geometry of the tip, as a sharper tip will have a greater local impact on the cell. For the stiffness tomography experiments shown here, the trigger force was set to 1 nN for Olympus AC40 tips, corresponding to an average indentation of 400 nm.

Fig. 3 Effect of trigger scanning force on the mitochondria (a) large scale fluorescence image of the mitochondria inside the living PtK2 cell, with the AFM scan area highlighted by a white box; (b) time-lapse fluorescence images of the mitochondria scanned with a 1 nN trigger force; (c) time-lapse fluorescence images of the mitochondria scanned with a 3 nN trigger force. Scale bar: 1 μm, white box: AFM scan area, white disks: AFM tip position, black loop: original mitochondrion shape, black arrowhead: fusion site, white arrowhead: cleavage site.

Having established the appropriate conditions that preserve mitochondrial integrity, we monitored the changes in stiffness due to physiological stress. We perturbed mitochondrial physiology using the well-characterized inhibiting drug carbonyl cyanide m-chlorophenylhydrazone (CCCP), which uncouples mitochondrial oxidative phosphorylation and mainly acts as a protonophore which decreases ATP synthetase function. We were able to follow, in real-time, the effect of the drug disrupting the elongated structure leading to mitochondrial fragmentation, using both light microscopy and AFM (Fig. 4a and b). At the beginning of the experiment, most of the mitochondria adopted a filamentous shape. After 5 minutes of drug exposure, we could already detect perturbations of the tubular network of mitochondria (Fig. 4a and b). We measured through force curve analyses (Fig. 4c) the increasing stiffness of intracellular structures (Fig. 4d) and thanks to light microscopy that we could correlate these structures with the mitochondria fragments. No such drastic changes were measured in control, non-treated cells (Fig. 4e). The approach described herein and so-called “stiffness tomography” is a robust approach that can be used to characterize living cells under stress, and conveniently correlate the measurements with other microscopy techniques to validate that changes in the stiffness of intracellular structures correspond to well-identified organelles.

Fig. 4 Mitochondrion stiffening upon CCCP treatment (a) fluorescence image of the mitochondria inside the living PtK2 cell at 0 minutes (top) and 30 minutes (bottom) of CCCP treatment (scale bar 5 μm); (b) AFM piezo height images at 1 nN; (c) sample approach FD curves from the experiment. Top: homogeneous elastic material, middle and bottom: 2 examples of discontinuities due to stiff organelle encounters (d) stiffness maps for CCCP-treated cells at the [50–100] nm indentation depth (scale bar 2 μm) (left), and the corresponding stiffness values of the mitochondrial region of interest (marked as a dashed white line on maps) as a function of time (mean ± S.E.M) (right); (e) fluorescence image of the mitochondria inside living PtK2 cells for the control (scale bar 5 μm) (left), stiffness maps for control cells at the [60–120] nm indentation depth (scale bar 2 μm) (middle), and the corresponding stiffness values of the mitochondrial region of interest (marked as a dashed white line on maps) as a function of time (mean ± S.E.M) (right).

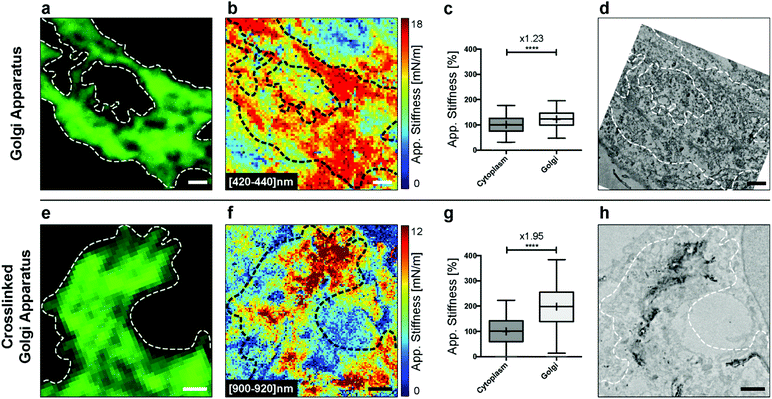
Stiffening of the Golgi apparatus in HeLa cells

We then applied the technique to another cell line (HeLa) and another type of organelle to show the broad applicability of the technique. In 1898, Camillo Golgi discovered a cellular organ later called the Golgi apparatus. It was one of the first successful staining experiments of an organelle, besides the nucleus, in eukaryotic cells. The discovery was helped by the fact that this organelle is a large structure, which is easy to spot, once correctly stained. The Golgi apparatus is usually located near the nucleus and is composed of a pile of stacked cisternae. Due to its central role in the transport and maturation of proteins and lipids, its deregulation leads to several diseases.³⁹ The Golgi apparatus has already been studied with correlative light and electron microscopy, but, to our knowledge, not with AFM.

To increase the stiffness of the Golgi apparatus and to have a contrasted staining in EM, we used stable HeLa cells expressing the ManII-HRP construct (HRP, Horseradish Peroxidase Enzyme). F. Jollivet et al. showed that it was possible to crosslink the HRP-positive Golgi apparatus using DAB (3,3′-diaminobenzidine) in the presence of a low concentration of H₂O₂ in living cells.³¹ This should lead, a priori, to stiffer cisternae.

We first explored the possibility of detecting this organelle in fixed HeLa cells without DAB crosslinking. We fixed the cells and immunolabeled the Golgi apparatus for fluorescence microscopy. Bright-field microscopy can be used to select a cell of interest (Fig. S1†). The confocal image then gives the localization of the Golgi apparatus (Fig. 5a). Analyzing the AFM indentation data above few hundreds of nanometers allowed revealing of the Golgi structures (Fig. 5b). It was possible to quantify the stiffness of the Golgi structure (inside the dashed loop) vs. the one of the surrounding cytoplasm (Fig. 5c). We noted a significant increase (× 1.23, unpaired t-test with Welch's correction) in stiffness. Finally, the ultrastructure was acquired with TEM (Fig. 5d).

Fig. 5 Golgi apparatus stiffening inside HeLa cells (a) fluorescence image of the Golgi apparatus inside the fixed HeLa cells (scale bar 1 μm), (b) stiffness map at the [420–440] nm indentation depth, (c) boxplot of apparent stiffness for the surrounding cytoplasm and the Golgi apparatus, (d) TEM ultrastructure of the Golgi, (e) fluorescence image of the crosslinked Golgi apparatus inside the fixed HeLa cell (scale bar 1 μm); (f) stiffness map at the [900–920] nm indentation depth, (g) boxplot of apparent stiffness for the surrounding cytoplasm and the crosslinked Golgi apparatus and (h) TEM ultrastructure of the crosslinked Golgi.

In the next step, we crosslinked cisternae with DAB. The Golgi apparatus was still clearly visible by fluorescence (Fig. 5e), and, as expected,³¹ we did not observe any difference with the non-treated sample (Fig. 5a). Regions corresponding to parts of the Golgi apparatus showed a clear contrast in stiffness, corresponding to the cross-linked organelle at an indentation depth around 1 μm (Fig. 5f). This was confirmed with the quantification of stiffness where we noted a greater increase (× 1.95, unpaired t-test with Welch's correction) in the Golgi region (inside the dashed loop) vs. the cytoplasm. We further explored the structures of the cross-linked Golgi using TEM, and the correlated analysis between the three microscopy techniques is shown in Fig. S2.†

To our knowledge, we report here for the first time the possibility of detecting mechanical changes affecting the Golgi apparatus at high resolution with the help of the AFM, without any specific sample preparation.

Discussion

We are confident that this work will open new opportunities to approach the inner life of cells. The applications are multifold. Cells could be systematically scanned for the detection of harder or softer features, and these could be correlated with optical or electron microscopy. Comparative experiments investigating cell response to treatment between healthy cells and damaged cells from patients are also one of the next major steps to be achieved. For example, it is known that the elasticity of cells changes in the case of cancer,^3,4 but it has not been further studied if such changes can be itemized for the single organelles in cells. Disorders affecting lipids as in diabetes or lysosomal storage diseases could also be interesting to be studied by the method described herein. It adds valuable information on the morphology and ultrastructure of the imaged organelles, which we can now directly correlate with stiffness measurements and optical imaging. The benefit offered in correlating electron microscopy with super-resolution fluorescence and AFM approaches,²⁹ using the so-called CLAFEM (correlated light atomic force electron microscopy) method, resides in obtaining ultrastructural information on the shape of internal structures of organelles, e.g. mitochondria. EM gives information on organelles not labeled with chromophores but participating in the local elasticity. Aggregates have been described in the mitochondria e.g. calcium phosphate granules in osteoblasts during mineralization.⁴⁰ Moreover, it has been shown that the importation of misfolded proteins into mitochondria played an important role in proteostasis with impacts during ageing and neurodegenerative diseases.⁴¹ Finally, a wealth of studies established the presence of aggregates inside organelles (e.g. ER and degradative pathway) with diseases linked to quality control and cell alteration. Combining the elasticity survey at the onset of the phenomenon and the identification of the organelle provides a new tool to better understand both the molecular basis operating and the associated signaling responses.

Improvements of this methodology are expected according to the technical development for each microscopy. On the AFM side, improvements in the scanning speed⁴² and the introduction of new force–distance modes^43,44 are promising. Following the mechanical dynamics of a single intracellular organelle over time using AFM could be achieved at a video frame rate. Improvements in high-resolution optical microscopy, like Stimulated-Emission-Depletion (STED) microscopy,⁴⁵ may also allow one to have access to the position of structures with nanometer resolution in living cells with higher acquisition rates, in three dimensions. Concerning electron microscopy, the development of algorithms for compensating the deformation of the sample during preparation and cutting will be of great help to better superimpose EM images with the AFM and fluorescence images.

Conclusions

In the present work, we showed the possibility to both see and feel the inner membrane compartments of a cell. We had access to the precise localization of organelles and microorganisms inside cells and to their mechanical properties. The stiffness tomography takes advantage of the contrast obtained from the stiffness maps to locate structures inside cells without specific sample preparation or staining, and additionally, it gives mechanical information at the nanoscale, which has not been accessible through other techniques to date. Optical microscopy and TEM added valuable and complementary information to the mechanical measurements. The former provides the online identity of several compartments studied whereas the latter allows ultrastructure analysis on the total height of the sample. Hence, new avenues are now opened to see and feel the same inner membrane compartments of a cell allowing another layer of analysis in the biomedicine field.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank A. Bongiovanni and J. Warein for expert technical assistance. Thanks to Y. Ciczora and S. Bovio for valuable discussions and L. Redondo-Morata for reading the manuscript. The work was funded by grants from the University Lille 1 (MP), ANR-10-EQPX-04-01, and FEDER 12001407 (FL).

Notes and references

1. A. J. Engler, S. Sen, H. L. Sweeney and D. E. Discher, Cell, 2006, 126, 677–689.
2. R. Matzke, K. Jacobson and M. Radmacher, Nat. Cell Biol., 2001, 3, 607–610.
3. L. M. Rebelo, J. S. de Sousa, J. Mendes Filho and M. Radmacher, Nanotechnology, 2013, 24, 055102.
4. M. Plodinec, M. Loparic, C. A. Monnier, E. C. Obermann, R. Zanetti-Dallenbach, P. Oertle, J. T. Hyotyla, U. Aebi, M. Bentires-Alj, R. Y. H. Lim and C. A. Schoenenberger, Nat. Nanotechnol., 2012, 7, 757–765.
5. P. Eaton, V. Zuzarte-Luis, M. M. Mota, N. C. Santos and M. Prudêncio, Nanomedicine, 2012, 8, 17–19.
6. N. V. Bukoreshtliev, K. Haase and A. E. Pelling, Cell Tissue Res., 2013, 352, 77–94.
7. A. Manduca, T. E. Oliphant, M. A. Dresner, J. L. Mahowald, S. A. Kruse, E. Amromin, J. P. Felmlee, J. F. Greenleaf and R. L. Ehman, Med. Image Anal., 2001, 5, 237–254.
8. J. Ophir, S. K. Alam, B. S. Garra, F. Kallel, E. E. Konofagou, T. Krouskop, C. R. B. Merritt, R. Righetti, R. Souchon, S. Srinivasan and T. Varghese, J. Med. Ultrason., 2002, 29, 155–171.
9. O. Otto, P. Rosendahl, A. Mietke, S. Golfier, C. Herold, D. Klaue, S. Girardo, S. Pagliara, A. Ekpenyong, A. Jacobi, M. Wobus, N. Töpfner, U. F. Keyser, J. Mansfeld, E. Fischer-Friedrich and J. Guck, Nat. Methods, 2015, 12, 199–202.
10. G. Antonacci and S. Braakman, Sci. Rep., 2016, 6 DOI:10.1038/srep37217.
11. Y. F. Dufrêne, T. Ando, R. Garcia, D. Alsteens, D. Martinez-Martin, A. Engel, C. Gerber and D. J. Müller, Nat. Nanotechnol., 2017, 12, 295–307.
12. C. Riethmüller, T. E. Schäffer, F. Kienberger, W. Stracke and H. Oberleithner, Ultramicroscopy, 2007, 107, 895–901.
13. M. Radmacher, Methods Cell Biol., 2002, 68, 67–90.
14. A. Yoshida, N. Sakai, Y. Uekusa, K. Deguchi, J. L. Gilmore, M. Kumeta, S. Ito and K. Takeyasu, Genes Cells, 2015, 20, 85–94.
15. V. Parpura, P. G. Haydon and E. Henderson, J. Cell Sci., 1993, 104(Pt 2), 427–432.
16. C. Roduit, F. G. Van Der Goot, P. De Los Rios, A. Yersin, P. Steiner, G. Dietler, S. Catsicas, F. Lafont and S. Kasas, Biophys. J., 2008, 94, 1521–1532.
17. C. Roduit, S. Sekatski, G. Dietler, S. Catsicas, F. Lafont and S. Kasas, Biophys. J., 2009, 97, 674–677.
18. A. Fuhrmann, J. R. Staunton, V. Nandakumar, N. Banyai, P. C. W. Davies and R. Ros, Phys. Biol., 2011, 8, 15007.
19. C. Roduit, G. Longo, I. Benmessaoud, A. Volterra, B. Saha, G. Dietler and S. Kasas, J. Mol. Recognit., 2012, 25, 241–246.
20. K. Radotić, C. Roduit, J. Simonović, P. Hornitschek, C. Fankhauser, D. Mutavdžić, G. Steinbach, G. Dietler and S. Kasas, Biophys. J., 2012, 103, 386–394.
21. G. Longo, L. M. Rio, A. Trampuz, G. Dietler, A. Bizzini and S. Kasas, J. Microbiol. Methods, 2013, 93, 80–84.
22. J. D. Beard, R. H. Guy and S. N. Gordeev, J. Invest. Dermatol., 2013, 133, 1565–1571.
23. R. Garcia, Nat. Nanotechnol., 2010, 5, 101–102.
24. J. Usukura, A. Yoshimura, S. Minakata, D. Youn, J. Ahn and S. J. Cho, J. Electron Microsc., 2012, 61, 321–326.
25. C. Rianna and M. Radmacher, Eur. Biophys. J., 2017, 46, 309–324.
26. F. M. Hecht, J. Rheinlaender, N. Schierbaum, W. H. Goldmann, B. Fabry and T. E. Schäffer, Soft Matter, 2015, 11, 4584–4591.
27. Y. M. Efremov, W. H. Wang, S. D. Hardy, R. L. Geahlen and A. Raman, Sci. Rep., 2017, 7 DOI:10.1038/s41598-017-01784-3.
28. A. Rigato, A. Miyagi, S. Scheuring and F. Rico, Nat. Phys., 2017, 13, 771–775.
29. S. Janel, E. Werkmeister, A. Bongiovanni, F. Lafont and N. Barois, Methods Cell Biol., 2017, 140, 165–185.
30. E. Dague, G. Genet, V. Lachaize, C. Guilbeau-Frugier, J. Fauconnier, C. Mias, B. Payré, L. Chopinet, D. Alsteens, S. Kasas, C. Severac, J. Ô. Thireau, C. Heymes, B. Honton, A. Lacampagne, A. Pathak, J. M. Sénard and C. Galés, J. Mol. Cell. Cardiol., 2014, 74, 162–172.
31. F. Jollivet, G. Raposo, A. Dimitrov, R. Sougrat, B. Goud and F. Perez, Mol. Biol. Cell, 2007, 18, 4637–4647.
32. J. E. Sader, J. A. Sanelli, B. D. Adamson, J. P. Monty, X. Wei, S. A. Crawford, J. R. Friend, I. Marusic, P. Mulvaney and E. J. Bieske, Rev. Sci. Instrum., 2012, 83 DOI:10.1063/1.4757398.
33. B. Cappella and G. Dietler, Surf. Sci. Rep., 1999, 34, 1–104.
34. R. S. Chadwick and N. Gavara, Nat. Nanotechnol., 2012, 7, 733–736.
35. M. Popoff, S. Janel, S. Bovio, V. Dupres, Y. Ciczora and F. Lafont, in Europython, Berlin, 2014.
36. L. A. Ligeon, K. Moreau, N. Barois, A. Bongiovanni, D. A. Lacorre, E. Werkmeister, V. Proux-Gillardeaux, T. Galli and F. Lafont, Autophagy, 2014, 10, 1588–1602.
37. S. A. Detmer and D. C. Chan, Nat. Rev. Mol. Cell Biol., 2007, 8, 870–879.
38. Y. R. Silberberg, A. E. Pelling, G. E. Yakubov, W. R. Crum, D. J. Hawkes and M. a. Horton, J. Mol. Recognit., 2008, 21, 30–36.
39. M. G. Bexiga and J. C. Simpson, Int. J. Mol. Sci., 2013, 14, 18670–18681.
40. S. Boonrungsiman, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 14170–14175.
41. L. Ruan, C. Zhou, E. Jin, A. Kucharavy, Y. Zhang, Z. Wen, L. Florens and R. Li, Nature, 2017, 543, 443–446.
42. M. Shibata, H. Yamashita, T. Uchihashi, H. Kandori and T. Ando, Nat. Nanotechnol., 2010, 5, 208–212.
43. D. Alsteens, D. J. Müller and Y. F. Dufrêne, Acc. Chem. Res., 2017, 50, 924–931.
44. C. Heu, A. Berquand and C. Elie-Caille, J. Struct. Biol., 2012, 178, 1–7.
45. N. T. Urban, K. I. Willig, S. W. Hell and U. V. Nägerl, Biophys. J., 2011, 101, 1277–1284.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8nr08955h

---