Controlling the dominant magnetic relaxation mechanisms for magnetic hyperthermia in bimagnetic core–shell nanoparticles†
Abstract
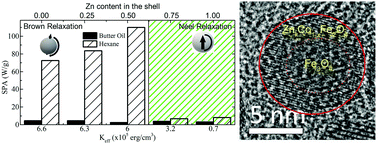
We report a simple and effective way to control the heat generation of a magnetic colloid under alternate magnetic fields by changing the shell composition of bimagnetic core–shell Fe3O4/ZnxCo1−xFe2O4 nanoparticles. The core–shell structure constitutes a magnetically-coupled biphase system, with an effective anisotropy that can be tuned by the substitution of Co2+ by Zn2+ ions in the shell. Magnetic hyperthermia experiments of nanoparticles dispersed in hexane and butter oil showed that the magnetic relaxation is dominated by Brown relaxation mechanism in samples with higher anisotropy (i.e., larger concentration of Co within the shell) yielding high specific power absorption values in low viscosity media as hexane. Increasing the Zn concentration of the shell, diminishes the magnetic anisotropy, which results in a change to a Néel relaxation that dominates the process when the nanoparticles are dispersed in a high-viscosity medium. We demonstrate that tuning the Zn contents at the shell of these exchange-coupled core/shell nanoparticles provides a way to control the magnetic anisotropy without loss of saturation magnetization. This ability is an essential prerequisite for most biomedical applications, where high viscosities and capturing mechanisms are present.
- This article is part of the themed collection: Editor’s Choice: Controlling anisotropy in nanomaterials


 Please wait while we load your content...
Please wait while we load your content...