Open Access Article
Open Access ArticlePhoton-separation to enhance the spatial resolution of pulsed STED microscopy
Giorgio
Tortarolo
 ab,
Yuansheng
Sun
ab,
Yuansheng
Sun
 c,
Kai Wen
Teng
c,
Kai Wen
Teng
 d,
Yuji
Ishitsuka
d,
Luca
Lanzanó
d,
Yuji
Ishitsuka
d,
Luca
Lanzanó
 e,
Paul R.
Selvin
d,
Beniamino
Barbieri
c,
Alberto
Diaspro
e,
Paul R.
Selvin
d,
Beniamino
Barbieri
c,
Alberto
Diaspro
 ef and
Giuseppe
Vicidomini
ef and
Giuseppe
Vicidomini
 *a
*a
aMolecular Microscopy and Spectroscopy, Istituto Italiano di Tecnologia, Via Morego 30, 16163, Genoa, Italy. E-mail: giuseppe.vicidomini@iit.it
bDepartment of Informatics, Bioengineering, Robotics and Systems Engineering, University of Genoa, Via Opera Pia 13, 16145, Genoa, Italy
cISS, Inc., 1602 Newton Drive, Champaign, IL 61822, USA
dDepartment of Physics, Biophysics and the Center for Physics of the Living Cell, University of Illinois at Urbana-Champaign, 1110 West Green Street, Urbana, IL 61801, USA
eNanoscopy and NIC@IIT, Istituto Italiano di Tecnologia, Via Morego 30, 16136, Genoa, Italy
fDepartment of Physics, University of Genoa, Via Dodecaneso 33, 16146, Genoa, Italy
First published on 9th January 2019
Abstract
Stimulated emission depletion microscopy (STED) is one of the pivotal super-resolution techniques. It overcomes the spatial resolution limit imposed by the diffraction by using an additional laser beam, the STED beam, intensity of which is directly related to the achievable resolution. Despite reaching nanometer resolution, much effort in recent years has been devoted to reducing the STED beam intensity because it may lead to photo-damaging effects. Accessing the spatial information encoded in the temporal dynamics of the detected fluorescent photons has been proved to be a powerful strategy and has contributed to the separation by lifetime tuning (SPLIT) technique. The SPLIT method uses the phasor analysis to efficiently distinguish photons emitted from the center and the periphery of the excitation spot. It thus improves the resolution without increasing the STED beam intensity. This method was proposed for architectures based on the STED beam running in continuous waves (CW-STED microscopy). Here, we extend it to pulsed STED beam implementations (pSTED microscopy). We show, through simulated and experimental data, that the pSTED-SPLIT method reduces the detection volume of the pSTED microscope without significantly decreasing the signal-to-noise ratio of the final image, thus effectively improving the resolution without increasing the STED beam intensity.
1 Introduction
Fluorescence microscopy has been established as an invaluable tool for the study of life sciences, thanks to features such as non-invasiveness, molecular specificity, and sensitivity. Furthermore, the introduction of super-resolution microscopy techniques has allowed us to overcome the spatial resolution limit imposed by diffraction,1 and thus to investigate biological phenomena with unprecedented resolution.2 Stimulated emission depletion (STED) microscopy was one of the firstly introduced super-resolution techniques;3,4 the standard point scanning STED microscope co-aligns the conventional Gaussian excitation beam with the so-called STED beam, engineered to generate a donut-shaped intensity distribution at the focus, i.e., with a “zero”-intensity point in the center. The STED beam forces all fluorophores, except those in the “zero”-intensity point at the center of the excitation spot, to de-excite to the ground state via stimulated emission, thus reducing the region from which the fluorescence signal is emitted and then recorded. Albeit theoretically the resolution of STED microscopy can reach the molecular size by increasing the intensity of the STED beam, practically it is limited by other factors, such as the noise5 and the amount of laser power that can be delivered to the sample to prevent photo-damage effects.6 For the latter reason, much effort has been made to reduce the peak power of the STED beam necessary to reach a given spatial resolution. One turnkey insight has been the comprehension of the variations in fluorescence temporal dynamics induced by the STED beam itself. The stimulated emission process opens a new fluorophore's de-excitation pathway, which rate (instantaneous probability) strongly depends on the intensity of the STED beam. Since the STED beam intensity is spatially distributed as a donut, the position of the fluorophore with respect to the center of the excitation spot is encoded in its fluorescence temporal decay (slower at the center of the excitation spot and faster at the donut crest). This understanding has been exploited to reduce the peak intensity of the STED beam needed to achieve a target resolution, enabling effective sub-diffraction resolution also under such conditions where the STED beam intensity is not sufficient to obtain a complete fluorescence depletion/quenching.7–9The first application of this principle is the so-called gated continuous-wave (CW) STED microscope.8,10 If the STED beam is implemented with a CW laser, the peak intensity reduces and the effective resolution as well. However, the further is the fluorophore from the focal point, the shorter is its (perturbed) excited state lifetime τSTED (i.e., the average time that the fluorophore spends into the excited state). Thus, by using pulsed excitation and a time-gated detection scheme – photons are collected only after a delay from the excitation events – the fluorescence at the periphery due to the incomplete depletion is removed, and the resolution improves. On the other hand, time-gating rejects also a portion of “wanted” photons from the center of the focal spot, resulting in a reduced signal-to-noise ratio (SNR) of the final image that may cancel out the resolution enhancement.5,9 For implementations based on pulsed STED (pSTED) beams, the benefits of exploring the fluorescence temporal dynamics and of the time-gated detection depend on the pulse-width of the STED beam itself.9 Early pSTED microscopes used pulse-widths below 200 ps, thus much shorter than the excited-state of typical organic fluorophores (τfl ∼ 1–10 ns). This temporal condition makes the fluorescence emitted during the action of the STED beam and the incomplete depletion negligible, and thus the time-gated detection useless.11 More recently, it has been shown that pSTED microscopy based on sub-nanosecond (∼600–1000 ps) pulsed lasers substantially reduces the photo-bleaching compared to early pSTED implementations:12 photo-bleaching is supra-linear with the STED beam intensity.13,14 In this case, since the pulse-width is comparable with the excited-state lifetime τfl and the peak intensity reduces (for a given average intensity of the pulse), the fluorescence emitted during the action of the STED beam is not negligible anymore and the benefit of time-gating is relevant. For these reasons, current pSTED microscopy implementations – including the commercial systems – rely on the sub-nanosecond fiber laser and implement a time-gated detection (gated-pSTED microscopy). However, similarly to gated-CW-STED microscopy, also for gated-pSTED microscopy the SNR of the final image is reduced.
A-posteriori approaches, such as multi-image deconvolution15 and separation of photons by lifetime tuning (SPLIT),16 can solve this problem. In particular, the SPLIT method analyses the pixel fluorescence temporal decays within the phasor framework and represents a straightforward approach to separate all the photons emitted from the long lifetime fluorophores located in the focal point (“wanted” photons), from the “unwanted” photons emitted from the short lifetime fluorophores located in the focal periphery. Here, we extend the SPLIT method to pulsed STED microscopy (pSTED-SPLIT), allowing us to recover the resolution hidden by the incomplete depletion/quenching, but without impacting the SNR.
A first method based on the phasor analysis of a pSTED image has been developed by us17 and successively improved by Wang L. et al.18 This method uses the phasor-plot representation of the pSTED image to generate a pixel segmented version of the raw data; the segmentation selects the pixels characterised by a slow fluorescence temporal dynamic, thus composed primarily of “wanted” photons, and discards the pixels identified by a fast fluorescence temporal dynamic, thus composed primarily of “unwanted” photons. In contrast, the SPLIT approach selects from each pixel only the “wanted” photons, rather than performing a simple binary pixel classification. In essence, the pSTED-SPLIT method that we propose – compared to the phasor-plot based segmentation methods – sorts photons and not pixels, thus providing more quantitative and artifact-free pSTED images. In the context of quantitative imaging, it is important to highlight that the SPLIT imaging technique preserves the linearity in the image, i.e., the pixel intensity values are linear with the fluorophore concentration.16
2 Materials and methods
2.1 Phasor-based analysis
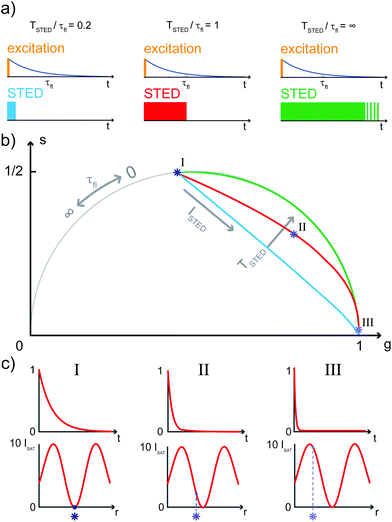
The SPLIT method is based on the analysis of the fluorescent signal dynamics through the so-called phasor analysis. The phasor analysis is a powerful tool able to describe the evolution of a signal (as a function of a variable, such as the time) as a single point in a plane with coordinates g (or cosine transform) and s (the sine transform): the phasor plot.19 In the context of SPLIT-STED imaging, the phasor approach is performed on every pixel of a time-resolved measurement (e.g., on the histogram of the photon-arrival times associated with any pixel) to discriminate molecular species with different temporal fingerprints. In particular, the phasor analysis is used to discriminate the photons emitted by the fluorophores localised in the center of the STED detection volume from the photons emitted by the fluorophores localised in the peripheral region, because these two classes of fluorophores are characterised by different excited-state lifetime, and thus fluorescence decay dynamics. In brief, it can be used to shrink the detection volume further, thus improving the effective spatial resolution of a STED microscope.We start by considering a single fluorophore and a CW-STED microscopy architecture, i.e., the STED beam runs in CW. Since the Gaussian-shaped excitation and the donut-shaped depletion intensity foci are co-aligned, if the fluorophore is in the very center of the excitation spot (r = 0), it does not interact with STED (or stimulating) photons, and thus it emits fluorescence according to its unperturbed lifetime τfl. The decay dynamics of such a fluorophore (thus, the histogram of the photon-arrival times) may be described with a single exponential exp(−t/τfl) and corresponds to a single point in the phasor space that lies on the semicircle of radius 1/2 with center (1/2,0) (Fig. 1). In contrast, if the fluorophore is located in the ring described by 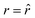 , it interacts with STED photons and it is likely to be quenched to the ground state. However, as a result of the not perfect efficiency of the stimulated emission process, it may emit fluorescence nonetheless, but following the faster single exponential decay law
, it interacts with STED photons and it is likely to be quenched to the ground state. However, as a result of the not perfect efficiency of the stimulated emission process, it may emit fluorescence nonetheless, but following the faster single exponential decay law 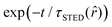 , where
, where 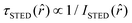 and ISTED(r) is the spatial intensity distribution of the STED beam (we suppose radial symmetry). The corresponding point in the phasor space is still lying on the same semicircle, but shifted toward higher g values; the limiting case of infinite STED intensity is the point (1,0) (Fig. 1).
and ISTED(r) is the spatial intensity distribution of the STED beam (we suppose radial symmetry). The corresponding point in the phasor space is still lying on the same semicircle, but shifted toward higher g values; the limiting case of infinite STED intensity is the point (1,0) (Fig. 1).
The key difference between pSTED and CW-STED implementations resides on the temporal dynamics of the fluorescent photons from the peripheral region of the excitation spot: the intensity temporal decay of a fluorophore illuminated by the pulsed STED beam, that can be described with a piecewise function, is faster during the STED pulse (0 ≤ t < TSTED), and slower when the STED beam is off (t ≥ TSTED):
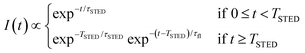 | (1) |
As a result, a fluorophore in the periphery of the excitation spot is represented in the phasor space by a point that is lying inside of the semicircle, conversely to the CW-STED implementation. In particular, this point is lying on a trajectory which again moves from the point associated with the unperturbed fluorophore (no stimulating photons) to the point (1,0), for increasing STED intensities. Notably, the shape of the trajectory in a pSTED system depends on the ratio γ = TSTED/τfl, where TSTED is the pulse-width of the STED beam, and τfl is the natural lifetime of the fluorophore. The two considered limit cases for γ are (i) very small pulse-width, γ = 0.2: the trajectory is a chord in the semicircle (Fig. 1b, light blue trajectory); infinite large pulse-width, γ ≫ 1 (equivalent to a CW-STED implementation): the trajectory is an arc of the semicircle (Fig. 1b, green trajectory).
In a real STED imaging experiment, the fluorescent signal registered by each pixel is the sum of the signals provided by all the fluorophores located within the detection region associated with the pixel. The phasor analysis isolates, from the fluorescent signal of each pixel, the component associated with the fluorophores located in the center of the excitation region, i.e., the slower components. It thus allows reducing the effective detection region and therefore improving the resolution, without increasing the STED intensity.
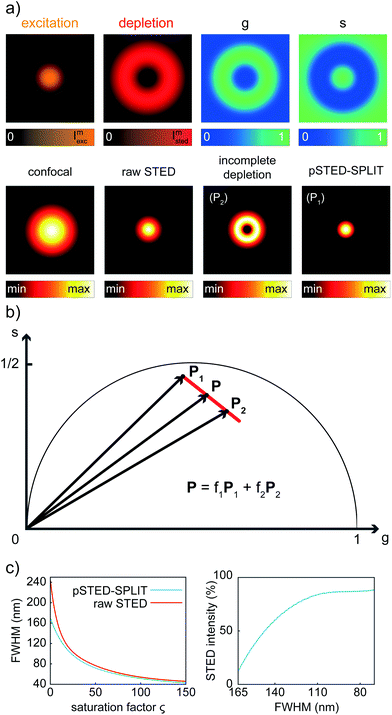
Although the dependency τSTED(r) yields to a continuous family of populations of emitters located at increasing distances from the center of the excitation spot and with increasingly faster temporal decays, for simplicity reasons it is convenient to consider only two species: the first one related to the center of the excitation spot (species 1, P1 in the phasor space) and the second one related to the periphery (species 2, P2 in the phasor space) that yields the undesired signal. Now, the problem becomes isolating the component of the signal generated from the first species. As per the rules of phasors, a combination of such two species will be represented in the phasor space as a point lying on the line P1P2. As described by the SPLIT technique,16 the contributions from these two species can be separated via a linear decomposition approach, to extract only the signal originated from fluorophores in the center of the excitation spot.
We now consider a time-resolved measurement. The total number of collected photons N in a given pixel is the sum of photons N1 and N2, emitted by molecules in the center and in the periphery of the excitation spot, respectively. As described before, the corresponding vector in the phasor space P can be described as the linear combination of the two vectors P1 = (g1,s1) and P2 = (g2,s2) describing the two pure species: P = (N1P1 + N1P2)/N = f1P1 + f2P2, where f1 and f2 are the fractional components of the detected photons. We can write this linear system in the matrix form P = Mf, where f = (f1,f2), and M = (P1,P2) is the matrix containing the temporal dynamics of the two species in the phasor domain. The solution f = M−1P allows separating photons emitted by molecules in the center of the excitation spot N1 = f1N from the undesired contributions of peripheral molecules N2 = f2N. The final image with higher resolution is obtained by iterating this process for each pixel of the raw time-resolved image.
It is important to observe that this phasor analysis is not restricted to a simple single-exponential decay, as for the CW-STED implementation, but it is valid in general for each signal evolution, thus also for the signal generated by the fluorophores in the case of pSTED microscopy.
2.2 Pulsed-STED microscope
For this study we performed measurements using an ISS Alba confocal/STED laser scanning microscopy system (http://www.iss.com/microscopy/instruments/alba.html) coupled with a Nikon Te2000 microscope.17 The excitation source is a 640 nm picosecond pulsed diode laser (Becker Hickl, BDL-SMN-640, 120 ps pulse width). A 775 nm sub-nanosecond pulsed fiber laser (OneFive, Katana 775, 600 ps pulse width) provides the STED beam. The two lasers are synchronised by either (a) using the depletion laser at the 40 MHz repetition rate (master) to trigger the excitation laser (slave); or (b) using the excitation laser at the 50 MHz repetition rate (master) to trigger the depletion laser (slave). Both lasers are also synchronised to the FastFLIM module to perform time-resolved STED measurements. The 640 nm excitation laser is mounted on the ISS 3-diode laser launcher to control its intensity, and then delivered to the Alba system via a single mode polarisation maintained fiber (QiOptics). The 775 nm STED laser intensity is controlled by the ISS intensity control unit consisting of a custom-made motorised rotating half-wave plate and a fixed Glan-Thompson polariser. We use an optical delay line (custom made) for the fine tuning (picoseconds) of the temporal delay between the STED pulses with respect to the excitation beam; the STED laser is then delivered via a single mode PMF (Thorlabs) to the STED beam conditioning module (custom made), to generate the donut-shaped profile of the depletion beam. Inside the Alba module, the excitation and the STED beams are combined using a 670 long-pass dichroic mirror (Semrock); we use a pair of galvanometric mirrors to scan both beams in the plane of the sample perpendicular to the optical axes. The objective is the highly numerical aperture Nikon Plan APO λ 60×/1.4NA oil. The scanning device is synchronised to the data acquisition unit (FastFLIM by ISS) for time-resolved Digital Frequency Domanin (DFD) measurements. We use another dichroic mirror (custom made by Chroma) to separate the descanned fluorescence signal from the excitation and STED light. We filter the emitted fluorescence by both a 720 nm short-pass NIR light blocking filter (Optical Density 8, Chroma), and a 679/41 nm band-pass emission filter (Semrock). We set the motorised confocal pinhole (from ∼20 μm to 1 mm) placed before the detector to 60 μm in diameter (∼1 Airy unit) for STED measurements. The detection unit is the single photon counting module avalanche photodiode (SPCM-ARQH-15 byExcelitas). Data acquisition is performed using the ISS VistaVision 64-bit software; phasor analysis is performed by using a custom written Matlab code, which is provided upon request.2.3 Sample preparation
Fluorescent beads: Crimson fluorescent beads of 60 nm diameter (FluoSpheres Red and Crimson), were diluted in water 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000 (v/v) for a sparse sample. We dropped the diluted solution of fluorescent beads onto a poly-L-lysine (Sigma) coated glass coverslip and waited for 5 min; then we washed the coverslip with water and dried it by blowing nitrogen onto it. Finally, we mounted it with a special medium (Mounting Medium, Invitrogen). Fixed HeLa cells: Human HeLa cells were transfected with plasmid DNA encoding GFP-ActA-Halotag20 (ActA binds to the outer mitochondrial membrane) overnight using Lipofectamine 2000 (Life Technologies) following the protocol of the manufacturer. The cells were fixed using 4% paraformaldehyde (Fisher Scientific), and permeabilised with 0.2% Triton-X 100 (Sigma). The cells were then labeled with ATTO647-GBP (GFP-Booster, Chromotek) in the presence of 3% bovine serum albumin (BSA) in PBS. After labeling, the cells were fixed using 4% paraformaldehyde for 15 minutes.
1000 (v/v) for a sparse sample. We dropped the diluted solution of fluorescent beads onto a poly-L-lysine (Sigma) coated glass coverslip and waited for 5 min; then we washed the coverslip with water and dried it by blowing nitrogen onto it. Finally, we mounted it with a special medium (Mounting Medium, Invitrogen). Fixed HeLa cells: Human HeLa cells were transfected with plasmid DNA encoding GFP-ActA-Halotag20 (ActA binds to the outer mitochondrial membrane) overnight using Lipofectamine 2000 (Life Technologies) following the protocol of the manufacturer. The cells were fixed using 4% paraformaldehyde (Fisher Scientific), and permeabilised with 0.2% Triton-X 100 (Sigma). The cells were then labeled with ATTO647-GBP (GFP-Booster, Chromotek) in the presence of 3% bovine serum albumin (BSA) in PBS. After labeling, the cells were fixed using 4% paraformaldehyde for 15 minutes.
3 Results
3.1 Synthetic data
We first applied the SPLIT method on the synthetic pSTED image of a single fluorophore. This simulation allows us also to derive the point-spread-function (PSF) of the pSTED-SPLIT system (Fig. 2a). In this context, it is important to remember that the SPLIT-STED microscope is – in general – a linear and space-invariant system;21 thus its PSF fully describes the imaging characteristics of the system: e.g., the spatial resolution is often measured as the full-width at half maximum (FWHM) of the PSF itself. Given the Gaussian- and donut-shaped focal intensity distributions of the excitation and depletion beams, respectively, and considering a STED pulse width of TSTED = 600 ps, we calculated the expected fluorescence decay for each pixel of the image (eqn (1)), i.e. the so-called temporal effective PSF (tE-PSF) of the pSTED microscope. In essence, the calculation of the tE-PSF is equivalent to simulating molecules located at different distances between the center of the excitation spot (r = 0), where the STED power is theoretically null, and rcrest, where the STED intensity is maxed.Successively, for each pixel, we computed the phasor values and we reported them in the phasor plot. The corresponding family of phasors describes a trajectory that: (i) starts (phasor corresponding to the point r = 0) in a position located inside the semicircle, since we simulated a realistic situation in which the center of the donut is not a perfect “zero”-intensity point; and (ii) does not terminate (phasor corresponding to the point rcrest, where the STED intensity is maxed) in the limiting position (1,0), due to the limited intensity of the STED beam (Fig. 2b).
We then applied the linear decomposition described above. As the P1 component (“wanted” central signal), we chose the starting point of the trajectory, the one associated with the slowest dynamics, and as P2 (“unwanted” peripheral signal) a point located at the tail of the trajectory. Results show that the method is effective in rejecting the contribution of fluorophores from the periphery of the excitation spot, thus leading to a reduction of the effective PSF (Fig. 2a). To quantitatively assess the resolution enhancement, we iterated the above-described simulation for increasing values of the saturation factor ζSTED = ISTED/Is, where Is is the STED saturation intensity, i.e., the intensity at which the rate of stimulated emission kSTED = 1/τSTED during the STED pulse equals the spontaneous rate of de-excitation kfl = 1/τfl. We conclude that the pSTED-SPLIT approach allows using notably less STED intensity to achieve a given resolution when compared to the raw STED counterpart (e.g., 50% ISTED for a target FWHM of 140 nm, Fig. 2c).
3.2 Real data
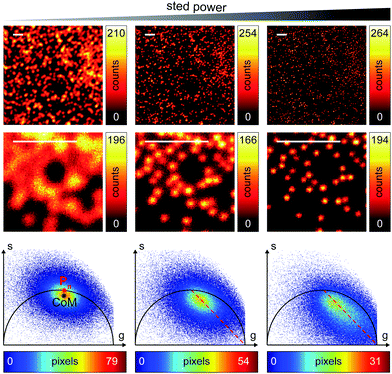
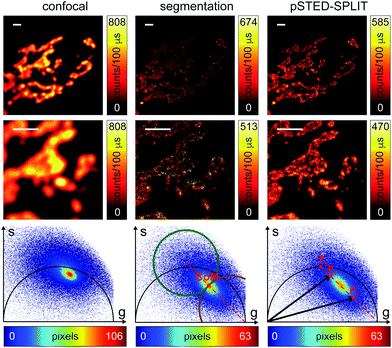
We successively validated the pSTED-SPLIT approach on real data, using a phantom sample of fluorescent beads and a biological sample.We first tested the performances of our setup by performing a series of time-resolved pSTED measurements with increasing depletion power, imaging a sample of 60 nm sized Crimson fluorescent beads (Fig. 3). The cluster of phasors, related to all pixels in the image, lies close to the semicircle when the STED beam is off (the not perfect overlapping may be a consequence of the high concentration of fluorophores on the beads, which induces a self-quenching phenomenon9). As the depletion power increases, and the spatial resolution of the resulting images improves, the cluster elongates toward the point (1,0), following the simulated expected trajectory.
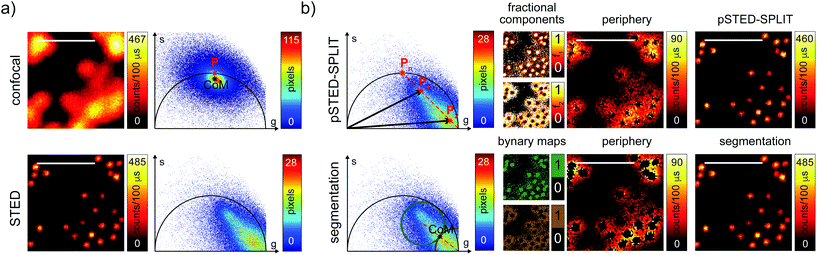
We then tested the linear decomposition approach on the same sample of 60 nm sized crimson fluorescent beads. When considering real data, a critical aspect of the pSTED-SPLIT approach is the choice of the two points P1 and P2 in the phasor plot. In this work we applied the following protocol for each measurement (Fig. 4): (i) perform a time-resolved confocal measurement (the STED beam is off) to retrieve the unperturbed fluorescence lifetime of the fluorophore; fix Pn as the corresponding phasor on the semicircle at the shortest distance from the center of mass (CoM) of the resulting cluster of phasors; (ii) simulate via a custom-made Matlab tool a molecule/fluorophore with a lifetime described by Pn; we then consider a STED impulse of duration TSTED = 600 ps, and calculate the different temporal behaviours of such molecules when interacting with increasing doses of stimulating photons: the different decays are described by a family of points in the phasor plot, or expected trajectory; (iii) perform a time-resolved pSTED measurement of the same area of step (i): the phasor analysis reveals a distribution of points in accordance with the expected trajectory; (iv) select both P1 and P2 on the simulated trajectory. A point P1 shifted towards the (1,0) with respect to Pn allows taking into consideration the non-ideal “zero” intensity condition; (v) force all the phasors P(x,y) to the line in between P1P2 and the expected trajectory; then find the fractional components f(x,y) = M−1(x,y)P(x,y). We finally obtain the pSTED-SPLIT image as N1(x,y) = f1(x,y)N(x,y) (Fig. 4b, top). Following this procedure, the pSTED-SPLIT approach succeeds in rejecting contributions from the periphery of the excitation spot and thus shrinks the size of the effective PSF when compared to the raw STED counterpart, i.e., the raw data collected during the time-resolved pSTED measurement, before applying the decomposition algorithm (FWHM of the gaussian fitting, averaged over n = 300 beads: 79 ± 28 nm and 69 ± 4 nm, for the raw STED and pSTED-SPLIT images, respectively). The reduced effective PSF of the pSTED-SPLIT method leads ultimately to better resolved images. Notably, the maximum counts of the raw and pSTED-SPLIT images are similar, which indicate that the SNR is not reduced during the process.
At this stage, it is also interesting to compare the pSTED-SPLIT approach with the phasor-based segmentation that we proposed in ref. 17. In short, we used the CoM of the cluster of points in the phasor plot to generate two circular regions of interest with the same radius and touching – externally tangent – in the cluster's CoM. The first region – centered in the point (1,0) – selects pixels with a shorter fluorescence temporal decay, and is thus composed primarily of “unwanted” photons. The second region selects pixels with a longer fluorescence temporal decay, and is thus composed primarily of “wanted” photons. By back-projecting the pixels lying in the second region we obtained a segmented pSTED image (Fig. 4b, bottom). Notably, the method proposed in ref. 18 better selects the two regions in the phasor plot (“abandoned” and “selected” areas), since it allows considering all the pixels contained in the semicircle, but the final pSTED result is still a segmented version of the raw image. Importantly, the non-linear nature of the segmentation operation (i.e. the intensity of the final images is not anymore linear with the fluorophore concentration) suggests that the measured “PSF” may not be indicative of the performance of the system. For these reasons, even if the pSTED-SPLIT method shows only a marginal improvement over the phasor-based segmentation method on fluorescent bead imaging, it performs substantially better when imaging more convoluted structures, such as the mitochondria membrane (Fig. 5). Thanks to the photon separation – rather than the pixel separation, the pSTED-SPLIT method is able to reveal the localisation of the TOM20 proteins in the membrane of the mithocondria with higher spatial resolution (with respect to confocal) and without introducing artifacts. In contrast, the phasor-based segmentation method tends to generate spotty structures, which may not adequately represent the real morphology of the mitochondria membrane. Similarly to intensity-based segmentation approaches, the phasor-based segmentation methods highlight the brighter pixels, producing good-looking results when imaging well separated point-like structures such as fluorescent beads, but tending to lose morphological information for other structures.
4 Discussion
In this study, we have extended the SPLIT technique introduced by us16 to the case of a pSTED implementation. We demonstrated with synthetic and real data that the pSTED-SPLIT method is able to enhance the spatial resolution of a time-resolved pSTED measurement with no degradation of the SNR and without introducing artifacts. The pSTED-SPLIT method rejects the photons emitted in the periphery of the excitation spot, via a simple linear decomposition algorithm in the phasor space, thus reducing the effective detection region and improving the spatial resolution, without increasing the intensity of the STED beam. A comparison with a phasor-based segmentation method is also carried out to demonstrate the higher robustness.Thanks to the continuous emerging of high photon collection efficiency (>100 Mcps) time-resolved detection architectures,17 we envisage the integration of the pSTED-SPLIT method on any commercial STED microscope. Further studies will be concentrated in the application of the SPLIT approach in the context of point-scanning reversible saturable optical linear fluorescence transition (RESOLFT) microscopy with reversible-switching fluorescent proteins (rsFP).22 Here, the rsFP's fluorescence signal induced during the RESOLFT illumination cycle (activation, de-activation, and read-out), similar to the STED microscopy, shows dynamics which change as the distance of the rsFPs from the center of the focus. Such spatial information encoded in the fluorescence dynamics can be decoded using the SPLIT approach to further enhance the resolution of the RESOFT images.
Conflicts of interest
Beniamino Barbieri is the President, and Yuansheng Sun is an employee of ISS Inc., a company commercialising microscopes.Acknowledgements
The authors would like to thank: Dr Paolo Bianchini (Istituto Italiano di Tecnologia), Dr Marco Castello (Istituto Italiano di Tecnologia), Dr Simonluca Piazza (Istituto Italiano di Tecnologia), Ulas C. Coskun (ISS) and Shih-Chu Jeff Liao (ISS) for useful discussion. We acknowledge support for the NIH and NSF to Paul R. Selvin.References
- S. W. Hell, S. J. Sahl, M. Bates, X. Zhuang, R. Heintzmann, M. J. Booth, J. Bewersdorf, G. Shtengel, H. Hess, P. Tinnefeld, A. Honigmann, S. Jakobs, I. Testa, L. Cognet, B. Lounis, H. Ewers, S. J. Davis, C. Eggeling, D. Klenerman, K. I. Willig, G. Vicidomini, M. Castello, A. Diaspro and T. Cordes, J. Phys. D: Appl. Phys., 2015, 48, 443001 CrossRef.
- S. J. Sahl, S. W. Hell and S. Jakobs, Nat. Rev. Mol. Cell Biol., 2017, 18, 685–701 CrossRef CAS PubMed.
- S. W. Hell and J. Wichmann, Opt. Lett., 1994, 19, 780–782 CrossRef CAS PubMed.
- G. Vicidomini, P. Bianchini and A. Diaspro, Nat. Methods, 2018, 15, 173–182 CrossRef CAS PubMed.
- G. Tortarolo, M. Castello, A. Diaspro, S. Koho and G. Vicidomini, Optica, 2018, 5, 32–35 CrossRef CAS.
- P. P. Laissue, R. A. Alghamdi, P. Tomancak, E. G. Reynaud and H. Shroff, Nat. Methods, 2017, 14, 657–661 CrossRef CAS PubMed.
- J. R. Moffitt, C. Osseforth and J. Michaelis, Opt. Express, 2011, 19, 4242–4254 CrossRef PubMed.
- G. Vicidomini, G. Moneron, K. Y. Han, V. Westphal, H. Ta, M. Reuss, J. Engelhardt, C. Eggeling and S. W. Hell, Nat. Methods, 2011, 8, 571–573 CrossRef CAS PubMed.
- G. Vicidomini, A. Schönle, H. Ta, K. Y. Han, G. Moneron, C. Eggeling and S. W. Hell, PLoS One, 2013, 8, e54421 CrossRef CAS PubMed.
- G. Vicidomini, I. Coto Hernàndez, M. d'Amora, F. Cella Zanacchi, P. Bianchini and A. Diaspro, Methods, 2014, 66, 124–130 CrossRef CAS PubMed.
- G. Vicidomini, G. Moneron, C. Eggeling, E. Rittweger and S. W. Hell, Opt. Express, 2012, 20, 5225–5236 CrossRef CAS PubMed.
- M. Castello, G. Tortarolo, I. C. Hernández, P. Bianchini, M. Buttafava, G. Boso, A. Tosi, A. Diaspro and G. Vicidomini, Microsc. Res. Tech., 2016, 79, 785–791 CrossRef CAS PubMed.
- M. Dyba and S. W. Hell, Appl. Opt., 2003, 42, 5123–5129 CrossRef PubMed.
- J. Oracz, V. Westphal, C. Radzewicz, S. J. Sahl and S. W. Hell, Sci. Rep., 2017, 7, 11354 CrossRef PubMed.
- M. Castello, A. Diaspro and G. Vicidomini, Appl. Phys. Lett., 2014, 105, 234106 CrossRef.
- L. Lanzanò, I. Coto Hernández, M. Castello, E. Gratton, A. Diaspro and G. Vicidomini, Nat. Commun., 2015, 6, 6701 CrossRef PubMed.
- Y. Sun, G. Tortarolo, K. W. Teng, Y. Ishitsuka, U. C. Coskun, S.-C. J. Liao, A. Diaspro, G. Vicidomini, P. R. Selvin and B. Barbieri, Multiphoton Microscopy in the Biomedical Sciences XVII, 2017 Search PubMed.
- L. Wang, B. Chen, W. Yan, Z. Yang, X. Peng, D. Lin, X. Weng, T. Ye and J. Qu, Nanoscale, 2018, 10, 16252–16260 RSC.
- M. A. Digman, V. R. Caiolfa, M. Zamai and E. Gratton, Biophys. J., 2008, 94, L14–L16 CrossRef CAS PubMed.
- E. R. Ballister, S. Ayloo, D. M. Chenoweth, M. A. Lampson and E. L. Holzbaur, Curr. Biol., 2015, 25, R407–R408 CrossRef CAS PubMed.
- L. Lau, Y. L. Lee, S. J. Sahl, T. Stearns and W. E. Moerner, Biophys. J., 2012, 102, 2926–2935 CrossRef CAS PubMed.
- T. Grotjohann, I. Testa, M. Leutenegger, H. Bock, N. Urban, F. Lavoie-Cardinal, K. Willig, C. Eggeling, S. Jakobs and S. Hell, Nature, 2011, 478, 204–208 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2019 |