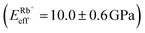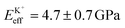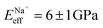Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Long-lived ionic nano-domains can modulate the stiffness of soft interfaces†
William
Trewby
 a,
Jordi
Faraudo
a,
Jordi
Faraudo
 b and
Kislon
Voïtchovsky
b and
Kislon
Voïtchovsky
 *a
*a
aUniversity of Durham, Physics Department, Durham DH1 3LE, UK. E-mail: kislon.voitchovsky@durham.ac.uk
bInstitut de Ciència de Materials de Barcelona, Bellaterra, Barcelona, Spain
First published on 25th February 2019
Abstract
Metal ions underpin countless processes at bio-interfaces, including maintaining electroneutrality, modifying mechanical properties and driving bioenergetic activity. These processes are typically described by ions behaving as independently diffusing point charges. Here we show that Na+ and K+ ions instead spontaneously form correlated nanoscale networks that evolve over seconds at the interface with an anionic bilayer in solution. Combining single-ion level atomic force microscopy and molecular dynamic simulations we investigate the configuration and dynamics of Na+, K+, and Rb+ at the lipid surface. We identify two distinct ionic states: the well-known direct electrostatic interaction with lipid headgroups and a water-mediated interaction that can drive the formation of remarkably long-lived ionic networks which evolve over many seconds. We show that this second state induces ionic network formation via correlative ion–ion interactions that generate an effective energy well of −0.4kBT/ion. These networks locally reduce the stiffness of the membrane, providing a spontaneous mechanism for tuning its mechanical properties with nanoscale precision. The ubiquity of water-mediated interactions suggest that our results have far-reaching implications for controlling the properties of soft interfaces.
Introduction
In soft and biological systems, electrostatic interactions frequently rely on alkali cations dissolved in aqueous solutions. Ions can have a profound impact on the structure, molecular organisation and dynamics of these soft systems, with key examples found in protein folding1 and lipid organisation within membranes.2 Lipids – key structural components of biological membranes – play as active a role in vivo as the proteins that were once thought to dominate function3 and as such the specific interactions of ions with lipid bilayers are of great general interest. The mobility,4,5 curvature6 and robustness7 of lipid membranes are all affected by ions in solution, which in turn has important implications for cellular-scale processes, including budding,8 endocytosis9 and protein-mediated channel regulation.3 The molecular interactions which underpin these processes are however far from trivial: the lipid headgroup chemistry,10,11 ionic composition of the solution10,12 and the precise adsorption location and hydration of the ions13 all influence the macroscopic properties of the membrane. This has occasionally resulted in conflicting pictures of the nature and strength of ions’ binding to lipid bilayers.14These intricate and diverse interactions between ions and lipids are partly driven by the latter's highly hydrated headgroups, which allows indirect complexes, mediated by water molecules, to form. Complexes such as these can significantly affect the properties of the interface itself, altering the molecular dynamics and mechanical properties on the nanoscale.15,16 Indeed, recent studies on mineral interfaces have shown that interfacial water can mediate attractive ion–ion correlations,17 and reduce the mobility of ions at the interface by orders of magnitude.15
Despite the quantity and breadth of studies probing lipid–ion interactions, there remains a significant gap in our understanding of how these molecular-level phenomena influence membranes. This is particularly true at the mesoscale, where spatial correlations can give rise to emergent properties. Part of the problem comes from our traditional view of ions at interfaces, which is shaped by continuum theories that reduce ions to point charges in a continuous, homogenous medium and considers the interface only as a structureless boundary.18 While successful at the macroscale, this view can fail markedly where molecular details are important.19–21 Indeed, it has long been known that the species-dependent hydration properties of an ion can determine its specific interactions with proteins20,21 (often referred to as Hofmeister effects) and membranes.13,22,23 Ion-specific effects such as these are the norm in biology and can often induce spatial correlations by coupling molecules together.11,23 Our general understanding of ionic effects at biointerfaces is thus hampered by the lack of a comprehensive theoretical framework to describe these nanoscale correlations and to what extent they influence the structure and mechanical properties of soft biological material. To fully capture this complexity, investigations need to be able to access molecular details of the interface while simultaneously retaining a mesoscale view of the system, over hundreds of square nanometres and up to minutes.
Here, we address this challenge using high-resolution atomic force microscopy (AFM) and all-atom molecular dynamics (MD) simulations to probe the organisation and time evolution of alkali cations at the surface of a negatively charged lipid bilayer in solution. AFM can detect and track the dynamics of singly-adsorbed ions at the electrolyte interface over long timescales,15,17 and can directly probe mechanical properties with Ångström-scale resolution.24 Molecular dynamics simulations complement this by revealing binding and conformational modes of the ions’ interactions with both water and the lipids. Thus, the combination of the techniques allows atomistic insight into the interfacial structure as well as the tracking of the ions’ evolution over many seconds.
Our lipid bilayer is composed of 1,2-dipalmitoyl-sn-glycero-3-phosphate (DPPA), an anionic lipid with a phosphate headgroup. Despite being relatively underrepresented in the lipodome, DPPA's headgroup plays a key role in signal transduction and pH sensing,25,26 and the lipid shows potential for application in liposomal drug delivery. Additionally, anionic lipids such as these are crucial for mediating protein interactions in the cytosol and signalling cell oncogenesis3 among others, and their strong electrostatic profile is likely to affect their mechanical response to ion adsorption.27
We show that the alkali cations, sodium and potassium, form correlated nano-domains at the lipid–electrolyte interface, with binding modes distinct to each ion. Rubidium, on the other hand, binds too weakly to observe these domains but still forms indirect complexes via hydration water. The domains of Na+ and K+ ions evolve remarkably slowly over many seconds, mediated by attractive interactions of order ∼−0.4kBT/ion and reduce the effective stiffness of the lipids by up to 12%. We show that this mechanical perturbation is driven by the water-mediated domains competing with directly bound ions for access to the lipid headgroups and allowing the membrane to become more flexible.
Results and discussion
Ionic structure and hydration at the bilayer interface
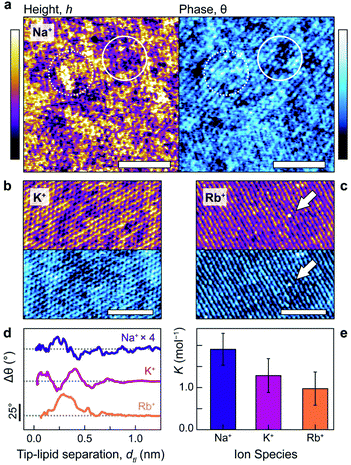
Fig. 1a–c illustrates the single-ion level resolution images that were obtained using amplitude-modulation AFM (AM-AFM)28 of the supported DPPA bilayer in aqueous solutions of NaCl, KCl or RbCl at biological concentrations (150 mM). When using gentle imaging conditions (high setpoint) and cantilever amplitudes comparable to the size of a hydrated ion (<2.0 nm), the tip probes the interfacial region where the lipid headgroups meet the electrolyte.29–32 Thus, the changes in height (purple/yellow) reflect the adsorbed ions’ modification of the lipids’ hydration landscape,33 as well the underlying hexagonal symmetry of the gel-phase membrane29 (see also the Fourier transforms in ESI Fig. S3†). The interface's appearance clearly depends characteristically on the species of ion present in the solution. In NaCl (Fig. 1a, topography), amorphous clusters of different heights form.The different heights reflect the multiplicity of sodium's binding states as it interacts with the headgroups: upper topographic levels reflect ions adsorbed in outer-sphere coordination with an intervening water molecule – an interpretation further verified in the context of the MD results below. These outer-sphere domains induce a relatively high phase difference (Fig. 1a, right, dashed circle) that indicates a more viscous interaction between the tip and bilayer.29,31 In contrast, lower levels are characterised by regions of reduced phase, reflecting a more elastic response (solid circle). In KCl (Fig. 1b), two adsorption states are still visible, but the interface's topographical features are markedly more regular: the roughness drops from RNaq = 0.037 ± 0.003 nm to RKq = 0.027 ± 0.002 nm. This reflects the fact that potassium ions adsorb more frequently in an inner-sphere configuration17,34 – that is, directly to the lipid headgroups – due to their lower charge density. Images obtained in the RbCl solution (Fig. 1c) revealed a lipid headgroup symmetry particularly marked in one direction, giving the appearance of molecular rows, with large (∼200 pm), isolated protuberances that straddle these rows (white arrow) and dominate other features. The size and location of these on the bilayer is consistent with single rubidium ions adsorbed as inner-sphere complexes,34 implying that Rb+ adsorb too rarely in this system to show significant domain formation.
We quantified the ability of Na+ and K+ to form these ionic domains by using a semi-automated algorithm based on height-thresholding to identify the locations of adsorbed ions (detail in ESI section 4.2†). The results confirm that the mean number of nearest neighbours for bound potassium, NNK+ = 2.9 ± 0.1 is substantially larger than for a random distribution of equal coverage, NNrnd = 1.3 ± 0.1. Sodium displays an even larger number of nearest neighbours, with NNNa+ = 3.2 ± 0.2, presumably due to its more varied binding state. This quantitatively confirms the cations’ predilection to form non-random networks through the hydration water-mediated interactions which dominate at this scale.17,35
The interpretation of the topography and phase images of Fig. 1a–c can be directly confirmed using phase-distance spectroscopy (Fig. 1d), in which variations in the oscillation phase, Δθ, are monitored as a function of the average separation between the AFM tip and the lipids, dtl (see ESI Fig. S6† for details). The phase is particularly sensitive to local perturbations of the interfacial hydration landscape and highlights differences in how each ion interacts with the lipids. Sodium presents a complex hydration structure with two peaks in Δθ at dtl <3 Å. However, the perturbation is relatively small (its trace in Fig. 1d is multiplied by four), likely related to the sodium ions’ non-trivial binding structure,36 which induces the heterogeneous topography of Fig. 1a. Potassium, in contrast, produces two well-defined peaks separated by 3 Å (about the diameter of a water molecule), with the second at a larger dtl than for Na+. This agrees with the more regular features observed via AM-AFM imaging (Fig. 1b), as well as the interpretation of the binding modes being mediated by water rather than by direct electrostatics.17,37 Rubidium, as the largest cation, adsorbs furthest away from bilayer interface and predominantly in single, broad configuration at dtl ∼3 Å, although with a small shoulder at ∼5.5 Å. This reflects rubidium's preference for forming inner-sphere complexes due to its relatively low charge density,38 as well as the observation of mostly single ions while imaging (Fig. 1c).
The distinctive organisation of the different cations at the interface with the bilayer has obvious consequences for their affinity to the membrane. Independent electrophoretic measurements of the ions’ the binding constants to DPPA reveal a direct Hofmeister series with KNa+ > KK+ > KRb+ (Fig. 1e). These agree with the hydration landscape measured by AFM; Na+, which has a complex, multilevel hydration structure binds most strongly and resists being displaced by the probe. The weaker attraction of K+ to the bilayer allows for a better-defined hydration structure (Fig. 1d), leading to higher imaging resolution. In RbCl, the AFM tip displaces most of the adsorbed ions, leaving water dipoles and hydronium ions to screen the DPPA surface charge17 (see ESI Fig. S4† for a detailed discussion about ion removal by the tip).
While the AFM and electrophoretic results clearly demonstrate ion-specific coordination and ordered ionic networks at the surface of the lipid membrane, the results do not permit true atomic exploration of the underlying mechanism responsible for the formation of the networks. To address this issue, we performed all-atom MD simulations using NAMD 2.9.39 The goal is to replicate as closely as possible the AFM results so as to gain atomistic insights into the interactions at play and ensure that the AFM observations are not due to tip effects, but still stand in the absence of an AFM tip. Our system consisted of 136 DPPA molecules in a free-standing, tensionless bilayer at 298 K and 1 atm pressure, and in contact with aqueous 150 mM NaCl, KCl or RbCl, hence directly mirroring our experimental set-up but without the influence of the AFM tip.
In the simulations, the interactions were modelled using the CHARMM36 force field with improved parameters for the ions.40 All technical details of the simulations are described in the ESI.† A typical snapshot is shown in Fig. 2a for KCl. The analysis of the radial correlation functions between the different (non-equivalent) oxygen atoms of the lipids, the cations and water molecules (see ESI† for details) allows us to identify binding of cations to oxygen atoms of the lipids and the sharing of water molecules in the first coordination shell of ions and lipids. We observe two distinct binding modes, illustrated in Fig. 2b and c for the case of KCl. Cations in the first binding mode (Fig. 2b, green, inner-sphere) have at least one lipid oxygen atom in the first coordination shell of the cation (with average values of 2.0, 2.5 and 2.8 lipid oxygens in the coordination shells of adsorbed Na+, K+ and Rb+ respectively). Cations are typically shared between two lipids and adsorb deep into the membrane region occupied by the headgroups, as shown in Fig. 2b. In the second mode (Fig. 2c yellow, outer-sphere), adsorbed cations retain their full hydration shell but at least one water molecule is shared between the first hydration shell of the cations and the lipid atoms. In this case, oxygen atoms from lipid headgroups are found in the second hydration shell of cations and ions are adsorbed in more external locations of the membrane (see Fig. 2c). The fraction of ions bound in this second mode decreases following the sequence Na+ > K+ > Rb+, mirroring the affinities shown in Fig. 1e, with the inverse true for the proportion of inner-sphere ions (Fig. 2d). Interestingly, previous simulations of PA− lipids with divalent cations found only inner-sphere adsorption,11 suggesting that the multiplicity of adsorption states may be unique to monovalent ions. The existence of these two different binding modes of cations in the simulations is in good agreement with the experimental results of Fig. 1. In addition, the simulations show that the multiplicity of adsorption states is partly due to the fact that the adsorbed ions retain their full hydration shell, a mechanism that cannot be detected using AFM.
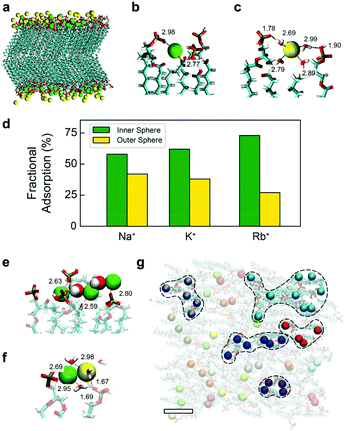 | ||
| Fig. 2 MD simulations of a DPPA bilayer in contact with water and salt (150 mM KCl) (a) snapshot of the MD simulations showing the DPPA bilayer and adsorbed cations (water molecules and non-adsorbed ions are not shown for clarity). Lipids are shown in bond representation and adsorbed cations are shown as van der Waals spheres. The colours employed for the adsorbed K+ ions indicate different coordination types with lipid oxygen atoms: green corresponds to K+ adsorbed in the first coordination shell of an oxygen atom of a lipid headgroup (inner-sphere cations) and yellow corresponds to K+ adsorbed with a bridging water molecule between an oxygen lipid and the cation (outer-sphere coordination), see the ESI† for specific details. (b) and (c) show a zoom of the snapshot showing an example of inner- and outer-sphere cation adsorption configurations, respectively (atomic distances are annotated in Å). (d) Fraction of ions adsorbed in each configuration (inner or outer) in simulations with NaCl, KCl or RbCl. (e–f) Example snapshots from (a) highlighting laterally correlated chains where cations share hydration water molecules. (g) Top view of (a) highlighting laterally correlated ions that share oxygens in their first coordination shell. The colour code here indicates ions that belong to the same connected network. Ions participating in larger-scale (>4) networks are enclosed with dashed lines. The scale bar represents 1 nm. All snapshots were made using VMD. | ||
The simulations also reveal significant lateral correlations amongst the adsorbed cations, with the first coordination peak at a cation–cation distance of 3.5 Å for Na+, 4.2 Å for K+ and 4.55 Å for Rb+, corresponding in each case to cation–oxygen–cation contacts (see ESI Fig. S14–17†). These correlations are mediated by the sharing of water molecules and/or lipid molecules in the first coordination shell of the ions (Fig. 2e).
Most outer-sphere ions share their solvation water with ions adsorbed in the inner mode, as illustrated in Fig. 2f. These correlated chains suggest that the domains observed in Fig. 1 are indeed induced by ionic networks at the surface of the membrane. By using similar colours for ions that share water or lipid oxygens with each other, Fig. 2g shows that in fact the majority of ions belong to such nano-networks, with many forming larger-scale structures of four ions or more (dashed regions). Surprisingly, the Cl− counterions in solution do not play any role in these networks. Therefore, the simulations indicate that the mechanism behind the formation of ionic networks is the sharing of lipid oxygen atoms and/or the sharing of water molecules in the first coordination shell of cations.
Dynamics of ionic domains
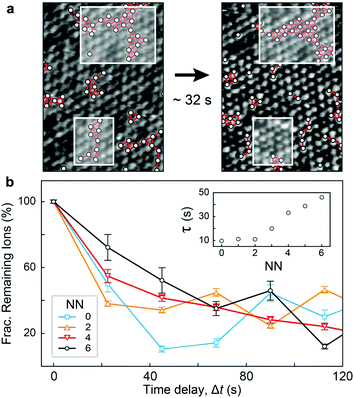
Fig. 1 and 2 highlight the complex networks formed between cations and mediated by water molecules. These ionic networks cannot be explained with traditional continuum theories and are believed to dramatically affect the charging17,41 and dynamics15 at aqueous interfaces. Here, although the MD results show ions to be essentially static at the bilayer surface once they bind, the simulations’ ∼100 ns length do not allow us to explore the evolution of the cationic networks over biologically relevant timescales (ms–s). However, the stability of the images such as those presented in Fig. 1 suggests that the ionic structures are remarkably long-lived, with dynamics that can be interrogated by AFM. Indeed, observations of ions at the mica–electrolyte interface have shown that the energetics associated with ion adsorption generated relaxation times ranging from seconds38 to minutes,42 although neither of those techniques allowed for direct identification of ionic networks, as is the case here. Fig. 3 shows the evolution of the networks observed by AFM with single-ion resolution over consecutive images. We objectively tracked the ions’ locations using the same algorithm as above, but in successive images, thus allowing time-resolved information to be obtained. The ions are highlighted in Fig. 3a by white circles, and those participating in nearest-neighbour interactions are joined by red bars. Significantly, the image demonstrates that the ionic nano-networks persist long enough to be identified with AFM, in good agreement with the electrophoretic results, which predict an attractive ion–ion correlation energy −2 < ΔEcorr < −1kBT/ion that can dominate over thermal fluctuations (ESI Fig. S2†). Fig. 3a shows some ionic domains to be stable over the order of tens of seconds, slow enough to influence many biological processes at bio-interfaces. However, there is clearly some size-dependence of the mobility of the domains (white boxes), with larger ionic networks typically more stable.To better quantify the residence time of ions within nano-networks, as well as its dependence on network size, we computed the characteristic time, τ, necessary for a given ion to desorb as a function of its number of nearest neighbours. This was achieved by tracking for each ion the degree of correlation between consecutive frames (see ESI†). As expected, the average residence timescale τ depends strongly on the number of nearest neighbours (NN, inset of Fig. 3b). Strikingly, the results show a linear relationship between τ and NN for adsorbed ions, further emphasising the fact that water-mediated ion–ion correlation dominates interactions and dynamics at this scale. The results are inconclusive for NN <2, presumably due to dynamics faster than the temporal resolution of our AFM. From the dependence of τ on NN, we estimated the free energy change associated with an adsorbed ion joining a domain on the bilayer. Assuming a decorrelation time τn ∝ exp(En/kBT),43 we obtain a change in free energy of ΔENN ∼−0.38kBT per added neighbour. This yields a total correlation energy, ΔEcorr = 6ΔENN ∼−2.27kBT/ion, slightly less than the value of ∼–6kBT calculated from our electrophoretic measurements. This difference is expected, given the fact that our algorithm only accounts for the in-plane motion of outer-sphere ions, but the agreement between these independent techniques is still remarkable.
The attractive nature of the ion–ion interaction measured here certainly agrees with the greatly reduced dynamics of Fig. 3, but a well of −0.38kBT/ion appears quite small (compared to the thermal energy), especially if it is to reduce the ions’ dynamics to such a great extent. However, we show, using a minimal model based on Eyering dynamics that in fact, small contributions per ion can lead to very large timescale shifts when entire networks are considered. We begin with the assumption that the inverse timescale of the domains’ motion, τ−1, is linked to the ions’ microscopic jump frequency, υ0 (typically in the range of 1010–1013 s−1),42 and an effective activation energy, Ea by the expression:
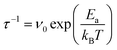 | (1) |
The activation energy depends upon the domain size, nd, mean number of nearest neighbours and ΔENN, such that Ea = nd × NN × ΔENN. Taking nd ∼25 ions, we arrive at Ea = −27.55kBT, which, for υ0 = 1011 s−1, leads to timescales of τ ∼10 s, in excellent agreement with the order of magnitude observed experimentally. While undoubtedly representing an oversimplification, this model highlights the fact that for a single ion to desorb or diffuse requires the concerted motion of many waters, ions and lipid headgroups,44 especially for high biological concentrations of 150 mM.
Thus, even a relatively small free energy well may, for larger ionic domains, result in the dramatically increased residence times found here. Previous work on the mica–electrolyte interface has demonstrated that water can mediate ion–ion correlations in similar conditions17 (albeit with different ions), and slow the relaxation times of solitary ions down to almost a second.15
There is, however, still no accepted consensus in the literature over the mobility of adsorbed ions,45 partly because water-mediated effects are usually ignored. Here, we have linked the ions’ attractive correlation energy with specific nearest-neighbour group interactions that lead to greatly retarded dynamics for large ionic domains.
Ionic perturbation of the bilayer's mechanical properties
The existence of slowly evolving, correlated ionic networks is likely to have profound implications for processes occurring at the interface, including the physical properties of the bilayer itself. For example, it is well-known that ions modulate the phase behaviour,37,46 cohesive strength7 and bending moduli27,47 of lipid membranes. These effects usually occur through liberation of bound water molecules and direct electrostatic screening that leads to a tighter lipid packing. Hence, we expect ions to alter the mechanical properties of the membrane on the same length- and timescale as that of their nano-networks. To assess this hypothesis, it is first necessary to quantify the stiffness of the bilayer with spatial and temporal resolutions comparable to that of the high-resolution AFM images. This is made possible by using bimodal AFM,24 which can image the membrane while simultaneously quantifying its effective Young's modulus, Eeff, with single-ion resolution. In bimodal AFM the cantilever is driven at its fundamental and second resonance frequencies. The first mode is used in amplitude modulation mode for imaging, exactly as in Fig. 1 & 3, while the frequency and phase of the second is controlled (i.e. in frequency modulation) in order to extract quantitative information from the ion–lipid interface (see ESI Fig. S7† and discussion for details).
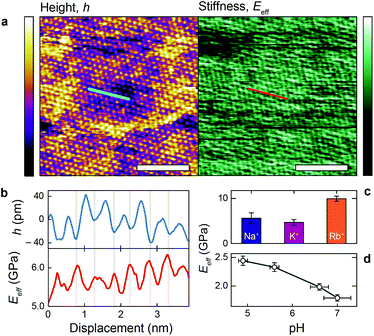
Fig. 4a shows a bimodal AFM scan acquired on the DPPA bilayer in 150 mM KCl. The topographic and stiffness maps clearly display equivalent periodicity and symmetry, emphasising the global impact of ions on the membrane biophysics. However, a line profile comparing topographic and stiffness variations reveals the two quantities to be exactly out of phase; the presence of outer-sphere adsorbed ions decreases the interfacial stiffness, here by ∼12% (Fig. 4b). This is in agreement with the phase data exhibited in Fig. 1; networks of ions adsorbed via their hydration shells make the lipid–electrolyte interface more “fluid-like” (large Δθ; light blue in Fig. 1a–c and peaks in Fig. 1d), thus reflecting the induced reduction in Eeff. From the characteristic variation in lipid hydration landscape (Fig. 1a–d), binding affinity (Fig. 1e) and adsorption mode (Fig. 2d) with each cation species, we similarly expect the Young's modulus to be ion-dependent. Specifically, rubidium, for which a larger fraction of ions directly links lipids together in inner-sphere configuration, is expected to stiffen the lipids more than sodium or potassium, which rely on indirect, water-mediated binding. Averaging of Eeff over the entirety of >10 images for each electrolyte confirms this hypothesis (Fig. 4c), with the highest stiffness given by Rb+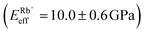 , followed by K+
, followed by K+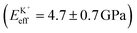 and Na+ (ENaeff = 6 ± 1 GPa). We note that the uncertainty in stiffness for sodium is much greater than that of either rubidium or potassium, likely related to sodium's less well-defined binding state (Fig. 1a and d). The overall trend of Eeffversus ionic species, as well as its order of magnitude, was confirmed with conventional ‘static’ force spectroscopy (ESI Fig. S9†), thereby ruling out possible viscoelastic effects. We note that there is a systematic offset between the static and bimodal values of Eeff, and as such the absolute values must be taken with caution, especially due to the use of a continuum indentation model to extract molecular-level stiffness variations over a 5 nm thick membrane. However, the trend shown in Fig. 4c should remain valid regardless.
and Na+ (ENaeff = 6 ± 1 GPa). We note that the uncertainty in stiffness for sodium is much greater than that of either rubidium or potassium, likely related to sodium's less well-defined binding state (Fig. 1a and d). The overall trend of Eeffversus ionic species, as well as its order of magnitude, was confirmed with conventional ‘static’ force spectroscopy (ESI Fig. S9†), thereby ruling out possible viscoelastic effects. We note that there is a systematic offset between the static and bimodal values of Eeff, and as such the absolute values must be taken with caution, especially due to the use of a continuum indentation model to extract molecular-level stiffness variations over a 5 nm thick membrane. However, the trend shown in Fig. 4c should remain valid regardless.
The present findings appear to contrast with the traditional view that dissolved salts always have a stiffening effect on biomembranes by reducing electrostatic repulsion between lipids and forming hydrogen bonds with the headgroups.7,37,48,49 Crucially however, and in contrast to many previous studies, the DPPA membrane is charged, inducing severe electrostatic repulsion at the headgroup level. Thus, the precise adsorption location of the ions will have a large impact on the membrane stiffness, an effect that is rarely taken into account. Here, we have shown that ions with greater inner-sphere populations (rubidium) indeed stiffen the membrane in a traditional manner. As the propensity of an ion to adsorb indirectly via water molecules increases however (the case for sodium and potassium), the relative rigidity of the lipids is decreased, presumably by locally disturbing inner-sphere ions and competitive adsorption. To confirm this mechanism, we quantified the effect on the membrane stiffness of altering the ratio between Na+ and hydronium ions (H3O+) in solution – that is, reducing the pH. H3O+, being composed of protonated water, cannot bind in an outer-sphere configuration, and a decrease in pH for a given NaCl concentration should allow more direct binding and hence stiffen the membrane. The experiment was conducted within a pH range where no (de)protonation of the lipid headgroups or the silicon oxide AFM tip are expected,50 hence allowing a straightforward analysis. Fig. 4d shows a clear stiffening of the membrane with decreasing pH, confirming our hypothesised mechanism. The high-resolution topography images associated with this experiment confirm that hydronium ions compete with Na+ for access to the DPPA headgroups, and that the number of adsorbed Na+ increases with pH (ESI Fig. S5†).
Overall, this validates the mechanism by which ions in solution are able to locally reduce the membrane stiffness, by forming remarkably slowly evolving nano-networks on the membrane surface mediated by water and competing with directly-adsorbed charges.
Conclusions
Our combined experimental and computational study evidences long-lived ionic nano-networks at the surface of a model lipid bilayer in solution. The formation of these water-mediated networks depends on the charge density of the ions through their binding strengths and hydration properties at the membrane. Here K+ and Na+ ions form nano-networks that evolve over tens of seconds, driven by correlation energies of the order of −0.4kBT/ion. These networks induce softening of the bilayer through local replacement of directly bound ions. Our model system is in gel-phase, unlike most biomembranes, and thus its lipids are broadly static, with small areas-per-molecule. This undoubtedly will play a role in structuring the interfacial fluid, but the networks’ origin in short-ranged hydration interactions (Fig. 2) and the elongated timescales of order of seconds (Fig. 3) imply that lipid mobility would not dramatically alter such phenomena. Indeed, similar ion-dependent effects have been observed on fluid bilayers5 and in principle, these effects could occur at any soft interface, as they rely only on water molecules mediating these common ions’ interaction with themselves and the lipids. At biological interfaces, we expect this mechanism to modulate the local viscoelastic properties on a timescale relevant for influencing processes such as molecular adsorption or the gating of mechanosensitive protein channels.Experimental
A more in-depth description of all procedures and materials used may be found in the ESI.†Small unilamellar vesicles (SUVs) and supported lipid bilayers (SLBs)
1,2-Dipalmitoyl-sn-glycero-3-phosphate (DPPA) was purchased in powder form from Avanti Polar Lipids (AL, USA) and used without further purification. For electrophoretic measurements, small unilamellar vesicles of diameter ∼100 nm were produced by rehydrating the lipids to a concentration of 1 mg ml−1 with ultrapure water buffered to pH 7.45 with 5 mM sodium phosphate dibasic. They were then bath-sonicated at 55 °C for 30 minutes, chilled to −18 °C for 30 minutes and bath-sonicated for a final 30 minutes (the so-called freeze–thaw method27) to produce a uniformly clear solution. The vesicles were then extruded through a 100 nm filter (WhatMan, Sigma Aldrich) at least 15 times, diluted with the appropriate mix of ultrapure water and electrolyte solution to a final lipid concentration of 0.1 mg ml−1 and then used immediately.The procedure for SLBs differed slightly; it used unbuffered solutions, to avoid perturbing the hydration landscape when imaging with AFM.33 Further, after the freeze–thaw procedure, the vesicles were diluted with 150 mM NaCl to a lipid concentration of 0.1 mg ml−1 and extruded in the same way as above. The solution was then pipetted onto a freshly-cleaved mica substrate, and the vesicle fusion method51–53 was used to produce at least one uniform bilayer on the surface (ESI Fig. S1†).
Electrophoresis measurements
SUV suspensions (see above) at varying concentrations of NaCl, KCl and RbCl were pipetted into a folded cuvette and their drift velocity as a function of applied potential, V, was measured using laser-Doppler interferometry with a Zetasizer ZS (Malvern Instruments, UK). This allows the calculation of the vesicles’ potential at the hydrodynamic slip plane, or ζ-potential of the lipids. Knowing ζ, the bulk ion concentration, I, and the areal lipid density, ρl, allows the calculation of the fractional adsorbed surface charge, Γ, as a function of ionic concentration. Combining Γ with an appropriate adsorption model (here Frumkin–Fowler–Guggenheim17) allows the extraction of the binding constant, K, for each ion as well as energy of correlation for the ions, Ec.Atomic force microscopy (AFM)
The images shown in Fig. 1a–c and Fig. 3a were all produced by a commercial Cypher ES AFM (Asylum Research, CA, USA) operated in amplitude-modulation mode (AM-AFM). Briefly, this entails exciting a cantilever with an attached nanometre-sharp tip near its fundamental resonance frequency so that it oscillates sinusoidally within the imaging fluid. The amplitude of oscillation is kept constant by a feedback loop, while the phase difference between the excitation signal and the cantilever is allowed to vary. This allows the interfacial topography to be tracked with Ångström-resolution, while information relating to the energy dissipated by the tip is carried in the phase signal.28The small amplitudes used here ensure that the tip interacts mostly with interfacial fluid, retaining its approximately simple harmonic motion and allowing for single-ion resolution to be achieved.29,31,32 Arrow UHF AuD cantilevers (Nanoworld, Neuchâtel, Switzerland) were used with flexural stiffnesses k1 = 1.71 N m−1 (Fig. 1 and 3), k1 = 0.956 N m−1 (Fig. 4a and c) and k1 = 6.58 N m−1 (Fig. 4d).
For the bimodal operation of Fig. 4, the cantilever was simultaneously excited at its fundamental and second resonance frequency, the latter of which is controlled via frequency modulation, which keeps the second-mode amplitude, A2, constant and its phase, θ2, locked to 90°. The first mode amplitude, A1, and second mode frequency shift, Δν2, are used to calculate Eeff with errors of <5% using the equations of Amo et al.24
Molecular dynamics simulations
Fully atomistic MD simulations were carried out using CHARMM36 force fields with TIP3P water. The bilayers had 68 DPPA molecules in each leaflet and covered an area of 64.45 Å × 64.45 Å. The simulation box contained 6463 waters, 156 cations (either Na+, K+ or Rb+) and 20 Cl− anions (equivalent to 150 mM in each case). The temperature was kept constant at 298 K and the pressure was 1 atm. For each simulation, there were ∼20 ns of equilibration followed by 100 ns of production run. All snapshots shown in Fig. 2 were produced using Visual Molecular Dynamics (VMD).54Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge funding from the Engineering and Physical Sciences Council (UK) (grants 1452230 and EP/M023915/1) and the European Council (MC-CIG grant 631186). JF acknowledges support from Spanish Ministry of Economy and Competitiveness through grant MAT2015-64442-R and through the “Severo Ochoa” Programme for Centres of Excellence in R&D (SEV-2015-0496). We thank CESGA Supercomputing Center for technical support and the use of computational resources.References
- E. Lacroix, A. R. Viguera and L. Serrano, J. Mol. Biol., 1998, 284, 173–191 CrossRef CAS PubMed.
- D. R. Slochower, Y.-H. Wang, R. W. Tourdot, R. Radhakrishnan and P. a. Janmey, Adv. Colloid Interface Sci., 2014, 208, 177–188 CrossRef CAS PubMed.
- P. A. Janmey and P. K. J. Kinnunen, Trends Cell Biol., 2006, 16, 538–546 CrossRef CAS PubMed.
- R. A. Böckmann, A. Hac, T. Heimburg and H. Grubmüller, Biophys. J., 2003, 85, 1647–1655 CrossRef.
- L. Piantanida, H. L. Bolt, N. Rozatian, S. L. Cobb and K. Voïtchovsky, Biophys. J., 2017, 113, 426–439 CrossRef CAS PubMed.
- B. Ali Doosti, W. Pezeshkian, D. S. Bruhn, J. H. Ipsen, H. Khandelia, G. D. M. Jeffries and T. Lobovkina, Langmuir, 2017, 33, 11010–11017 CrossRef CAS PubMed.
- S. Garcia-Manyes, G. Oncins and F. Sanz, Biophys. J., 2005, 89, 1812–1826 CrossRef CAS PubMed.
- W. B. Huttner and J. Zimmerberg, Curr. Opin. Cell Biol., 2001, 13, 478–484 CrossRef CAS PubMed.
- J. Dai, H. P. Ting-Beall and M. P. Sheetz, J. Gen. Physiol., 1997, 110, 1–10 CrossRef CAS PubMed.
- A. a. Gurtovenko and I. Vattulainen, J. Phys. Chem. B, 2008, 112, 1953–1962 CrossRef CAS PubMed.
- J. Faraudo and A. Travesset, Biophys. J., 2007, 92, 2806–2818 CrossRef CAS PubMed.
- Y.-C. Wen, S. Zha, X. Liu, S. Yang, P. Guo, G. Shi, H. Fang, Y. R. Shen and C. Tian, Phys. Rev. Lett., 2016, 116, 016101 CrossRef PubMed.
- A. Martín-Molina, C. Rodríguez-Beas and J. Faraudo, Biophys. J., 2012, 102, 2095–2103 CrossRef PubMed.
- A. Catte, M. Girych, M. Javanainen, C. Loison, J. Melcr, M. S. Miettinen, L. Monticelli, J. Määttä, V. S. Oganesyan, O. H. S. Ollila, J. Tynkkynen and S. Vilov, Phys. Chem. Chem. Phys., 2016, 18, 32560–32569 RSC.
- M. Ricci, W. Trewby, C. Cafolla and K. Voïtchovsky, Sci. Rep., 2017, 7, 43234 CrossRef CAS PubMed.
- J. Song, J. Franck, P. Pincus, M. W. Kim and S. Han, J. Am. Chem. Soc., 2014, 136, 2642–2649 CrossRef CAS PubMed.
- M. Ricci, P. Spijker and K. Voïtchovsky, Nat. Commun., 2014, 5, 4400 CrossRef CAS PubMed.
- J. N. Israelachvili, Intermolecular and Surface Forces, Elsevier, 3rd edn, 2011 Search PubMed.
- N. Schwierz, D. Horinek and R. R. Netz, Langmuir, 2015, 31, 215–225 CrossRef CAS PubMed.
- D. Bastos-González, L. Pérez-Fuentes, C. Drummond and J. Faraudo, Curr. Opin. Colloid Interface Sci., 2016, 23, 19–28 CrossRef.
- W. Kunz, Curr. Opin. Colloid Interface Sci., 2010, 15, 34–39 CrossRef CAS.
- H. I. Petrache, T. Zemb, L. Belloni and V. A. Parsegian, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 7982–7987 CrossRef CAS PubMed.
- A. Martín-Molina, C. Rodríguez-Beas and J. Faraudo, Phys. Rev. Lett., 2010, 104, 168103 CrossRef PubMed.
- C. A. Amo, A. P. Perrino, A. F. Payam and R. Garcia, ACS Nano, 2017, 11, 8650–8659 CrossRef CAS PubMed.
- J. J. Shin and C. J. Loewen, BMC Biol., 2011, 9, 85 CrossRef CAS PubMed.
- B. P. Young, J. J. H. Shin, R. Orij, J. T. Chao, S. C. Li, X. L. Guan, A. Khong, E. Jan, M. R. Wenk, W. A. Prinz, G. J. Smits and C. J. R. Loewen, Science, 2010, 329, 1085–1088 CrossRef CAS PubMed.
- M. M. A. E. Claessens, B. F. Van Oort, F. A. M. Leermakers, F. A. Hoekstra and M. A. C. Stuart, Biophys. J., 2004, 87, 3882–3893 CrossRef CAS PubMed.
- R. García and R. Pérez, Surf. Sci. Rep., 2002, 47, 197–301 CrossRef.
- K. Voïtchovsky, J. J. Kuna, S. A. Contera, E. Tosatti and F. Stellacci, Nat. Nanotechnol., 2010, 5, 401–405 CrossRef PubMed.
- T. Fukuma, M. Higgins and S. Jarvis, Phys. Rev. Lett., 2007, 98, 106101 CrossRef PubMed.
- K. Voïtchovsky, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 022407 CrossRef PubMed.
- E. J. Miller, W. Trewby, A. Farokh Payam, L. Piantanida, C. Cafolla and K. Voïtchovsky, J. Visualized Exp., 2016, 1–10 CAS.
- W. Trewby, D. Livesey and K. Voïtchovsky, Soft Matter, 2016, 12, 2642–2651 RSC.
- S. S. Lee, P. Fenter, K. L. Nagy and N. C. Sturchio, Langmuir, 2012, 28, 8637–8650 CrossRef CAS PubMed.
- B. Klasczyk, V. Knecht, R. Lipowsky and R. Dimova, Langmuir, 2010, 26, 18951–18958 CrossRef CAS PubMed.
- K. Kobayashi, Y. Liang, S. Murata, T. Matsuoka, S. Takahashi, N. Nishi and T. Sakka, Langmuir, 2017, 33, 3892–3899 CrossRef CAS PubMed.
- Y. A. Ermakov, K. Kamaraju, K. Sengupta and S. Sukharev, Biophys. J., 2010, 98, 1018–1027 CrossRef CAS PubMed.
- S. S. Lee, P. Fenter, K. L. Nagy and N. C. Sturchio, Nat. Commun., 2017, 8, 15826 CrossRef PubMed.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kalé and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS PubMed.
- J. Yoo and A. Aksimentiev, Phys. Chem. Chem. Phys., 2018, 20, 8432–8449 RSC.
- J. Wang and A. J. Bard, J. Phys. Chem. B, 2001, 105, 5217–5222 CrossRef CAS.
- U. Raviv, P. Laurat and J. Klein, J. Chem. Phys., 2002, 116, 5167 CrossRef CAS.
- H. Yamashita, K. Voïtchovsky, T. Uchihashi, S. A. Contera, J. F. Ryan and T. Ando, J. Struct. Biol., 2009, 167, 153–158 CrossRef CAS PubMed.
- V. A. Parsegian and T. Zemb, Curr. Opin. Colloid Interface Sci., 2011, 16, 618–624 CrossRef CAS.
- I. C. Bourg and G. Sposito, J. Colloid Interface Sci., 2011, 360, 701–715 CrossRef CAS PubMed.
- N. Shimokawa, H. Himeno, T. Hamada, M. Takagi, S. Komura and D. Andelman, J. Phys. Chem. B, 2016, 120, 6358–6367 CrossRef CAS PubMed.
- M. M. A. E. Claessens, F. A. M. Leermakers, F. A. Hoekstra and M. A. Cohen Stuart, J. Phys. Chem. B, 2007, 111, 7127–7132 CrossRef CAS PubMed.
- K. Voïtchovsky, S. Antoranz Contera, M. Kamihira, A. Watts and J. F. Ryan, Biophys. J., 2006, 90, 2075–2085 CrossRef PubMed.
- G. Pabst, A. Hodzic, J. Štrancar, S. Danner, M. Rappolt and P. Laggner, Biophys. J., 2007, 93, 2688–2696 CrossRef CAS PubMed.
- D. Marsh, CRC Handbook of Lipid Bilayers, CRC Press, 2nd edn, 2013 Search PubMed.
- M.-P. Mingeot-Leclercq, M. Deleu, R. Brasseur and Y. F. Dufrêne, Nat. Protoc., 2008, 3, 1654–1659 CrossRef PubMed.
- R. Richter, A. Mukhopadhyay and A. Brisson, Biophys. J., 2003, 85, 3035–3047 CrossRef CAS PubMed.
- I. Reviakine and A. Brisson, Langmuir, 2000, 16, 1806–1815 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8nr06339g |
| This journal is © The Royal Society of Chemistry 2019 |