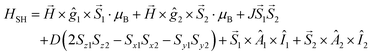Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Relationship between solid state structure and solution stability of copper(II)–hydroxypyridinecarboxylate complexes†
Nóra V.
May
 *a,
G. Tamás
Gál
a,
Zsolt
Szentendrei
a,
László
Korecz
b,
Zoltán
May
*a,
G. Tamás
Gál
a,
Zsolt
Szentendrei
a,
László
Korecz
b,
Zoltán
May
 b,
Maria Grazia
Ferlin
b,
Maria Grazia
Ferlin
 c,
Annalisa
Dean
d,
Petra
Bombicz
c,
Annalisa
Dean
d,
Petra
Bombicz
 a and
Valerio B.
Di Marco
a and
Valerio B.
Di Marco
 d
d
aResearch Laboratory of Chemical Crystallography, Research Centre for Natural Sciences Hungarian Academy of Sciences, Magyar tudósok körútja 2, H-1117 Budapest, Hungary. E-mail: may.nora@ttk.mta.hu
bInstitute of Materials and Environmental Chemistry, Research Centre for Natural Sciences Hungarian Academy of Sciences, Magyar tudósok körútja 2, H-1117 Budapest, Hungary
cDepartment of Pharmacological Sciences, University of Padova, via Marzolo 1, 35131 Padova, Italy
dDepartment of Chemical Sciences, University of Padova, via Marzolo 1, 35131 Padova, Italy
First published on 5th June 2019
Abstract
The complementary solid state/solution studies of the systematic series of bioactive ligands 3-hydroxy-1-methyl-4-pyridinecarboxylate (L1), 3-hydroxy-1,2,6-trimethyl-4-pyridinecarboxylate (L2), 4-hydroxy-1-methyl-3-pyridinecarboxylate (L3), 4-hydroxy-1,6-dimethyl-3-pyridinecarboxylate (L4), 4-hydroxy-1-(2-hydroxyethyl)-6-methyl-3-pyridinecarboxylate (L5) and 4-hydroxy-1-(2-carboxyethyl)-6-methyl-3-pyridinecarboxylate (L6) with copper(II) have been performed in order to design efficient chelating drugs for the treatment of metal overloading conditions. Single crystals of [Cu(L1)2(H2O)]·3H2O (1) (monomer) with axial water coordination, [Cu2(L2)4]·6H2O (2) and [Cu2(L3)4]·4H2O (3) (cyclic dimers), where pyridinolato and carboxylato oxygens, respectively, act as linkers between adjacent copper complexes, [Cu(L4)2]n·3H2O (4) (1D polymer) and [Cu3(L5)6]·18H2O (5) (trimer), constructed using two square-pyramidal and one elongated octahedral Cu(II) complexes have been determined by SXRD. The bidentate coordination mode of the ligands has been found preferentially with cis arrangements in 1 and 2 and trans arrangements in 3–5. The solution speciation and complex stability of aqueous solutions have been studied by pH-dependent electron paramagnetic resonance spectroscopy resulting in the detection of solely monomeric [CuL]+ and [CuL2] complexes. The stability order obtained for the [CuL]+ complexes could be correlated with the deprotonation constants of their hydroxyl group (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βLH) reflecting that the higher acidity increases the complex stability in the order L2 < L1 ≈ L6 < L4 ≈ L5 < L3. This stability order elucidates the different axial linkers in the cyclic dimers 2 and 3. DFT quantum-chemical calculations support the effect of the electron distribution on the established stability order.
βLH) reflecting that the higher acidity increases the complex stability in the order L2 < L1 ≈ L6 < L4 ≈ L5 < L3. This stability order elucidates the different axial linkers in the cyclic dimers 2 and 3. DFT quantum-chemical calculations support the effect of the electron distribution on the established stability order.
Introduction
In diverse fields of clinical practice, metal complexes of small biomolecules are frequently used as bioactive compounds, e.g. drugs, imaging agents, or chelators. Hydroxypyridinecarboxylic acid (HPC) derivatives have been proposed recently1–7 as potential chelating agents for Fe(III) and Al(III) due to their favourable properties which include low toxicity, no redox activity, complex stability and probable oral bioavailability due to their low molecular mass. The design of these compounds was based on deferiprone (1,2-dimethyl-3-hydroxypyridine-4-one) which is a worldwide used chelating drug for the treatment of iron overloading conditions. In vitro studies showed that Cu(II) is the most competitive metal ion which affects considerably the complex formation of deferiprone with Fe(III)8–14 and the same can be expected to occur for HPCs also. The investigation of the stability constants of HPCs towards Cu(II) (and other possible competing ions such as Zn(II)) is necessary as the displacement of essential metal ions by chelating drugs could affect the biological processes dependent on these metals and may cause toxicity. To this aim, complex formation studies were started with some HPCs and Cu(II).2,15The X-ray diffraction method is one of the most powerful techniques for the structural investigation of metal complexes. Though the crystallographic method can offer detailed and accurate data on the structure of these complexes, it is limited only to the solid state. In order to establish any structure–stability–activity relationships, the knowledge of the speciation, and of the most plausible chemical forms, in aqueous solution is mandatory. Electron paramagnetic resonance (EPR) spectroscopy is able to detect paramagnetic metal complexes in solution equilibrium systems. A structural comparison obtained at different phases can disclose features of the intramolecular and intermolecular interactions of the complexes, and reveal possible structural transformation which can be crucial for both their biological functions and pharmaceutical formulations. In the present paper, we introduce the synthesis of two new HPC derivatives and compare the complexation properties of some additional HPC derivatives to study the substituent effect on the complexation properties with Cu(II) in the solid state and in aqueous solution. The studied ligands are 3-hydroxy-1-methyl-4-pyridinecarboxylate, 3-hydroxy-1,2,6-trimethyl-4-pyridinecarboxylate, 4-hydroxy-1-methyl-3-pyridine-carboxylate, 4-hydroxy-1,6-dimethyl-3-pyridinecarboxylate, and the newly synthesised 4-hydroxy-1-(2-hydroxyethyl)-6-methyl-3-pyridinecarboxylate and 4-hydroxy-1-(2-carboxyethyl)-6-methyl-3-pyridinecarboxylate. These molecules are known in the literature7 as DT1, DT8126, DQ1, DQ716, DQ7167, and DQ7165, respectively. For brevity, in this paper they are indicated with the shorter abbreviations L1, L2, L3, L4, L5 and L6. Their structures in their zwitterionic forms are reported in Scheme 1 (the charges are omitted throughout the text for clarity). L1–L6, proposed as chelating agents for Fe and Al, represent the most promising HPC derivatives, as reported by Crisponi et al.7 These authors explained the different properties of compounds L1 and L2 (4-hydroxy-derivatives) with respect to L3–L6 (3-hydroxy-derivatives), and the particular properties of L5 and L6. 4-Hydroxy HPC can undergo keto–enol tautomerism, whereas it is less pronounced in 3-hydroxy HPCs; L5 and L6 represent the in vivo products of possible esterified prochelators, i.e. compounds with an enhanced ability to cross the gastro-intestinal barrier (due to their larger lipophilicity) which, once in vivo, can be deesterified to give more hydrophilic drugs which are able to be decorporated once they have bound to the toxic metal ion.7 Crystals of the bis-ligand copper HPC complexes were prepared in all cases (except for L6), and their solid-state structures were studied by single crystal X-ray diffraction (SXRD). The Cu(II) complex formation with all ligands in aqueous solution was studied using pH-dependent EPR spectroscopy at room temperature and in frozen solution (77 K). In order to interpret the effect of the electron distribution on the complexation properties of HPCs, atomic charges and bond orders were calculated by DFT quantum-chemical calculations using different basis sets. Correlations between the different parameters have been found by multivariate data analysis.
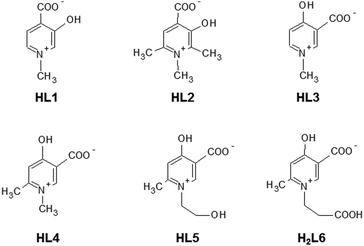 | ||
| Scheme 1 Molecular structure of the investigated ligands, shown in their zwitterionic (neutral) forms. | ||
Experimental section
Chemicals
HPCs were synthesized as described in ref. 16–18, except L5 and L6 which were synthesized according to the procedure reported in the next section. The CuCl2 stock solution was prepared from CuCl2·2H2O (Sigma-Aldrich) dissolved in doubly distilled water. The concentration was checked by ICP-OES. NaOH, HCl and buffer solutions used in pH adjustment were purchased from Sigma-Aldrich.Synthesis of compounds L5 and L6
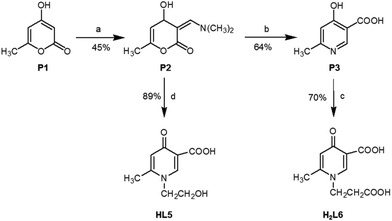
Scheme 2 describes the synthetic routes carried out to obtain final HPC derivatives L5 and L6. For this purpose, the common intermediates P2 and P3 were prepared as previously reported.3,19 Briefly, the starting material 4-hydroxy-6-methyl-2-pyrone (P1) by reacting with N,N-dimethylformamide dimethyl acetal in dioxane yielded 60% of 3-(dimethylaminomethylene)-4-hydroxy-6-methyl-2-pyrone (P2). The latter by treatment with 30% aqueous ammonia furnished P3 (64% yield). The precursor pyridinic compound P3 was reacted with acrylic acid under reflux to give the corresponding N-carboxyethyl compound H2L6 (70% yield), and the precursor pyrone compound P2 by reacting with ethanolamine at room temperature yielded the N-hydroxyethyl pyridinic compound HL5 (80% yield).Melting points were determined on a Gallenkamp MFB 595 010M/B capillary melting point apparatus, and are uncorrected. Infrared (IR) spectra were measured on a PerkinElmer 1760 FTIR spectrometer using potassium bromide pressed disks. Values are expressed in cm−1. 1H NMR spectra were recorded on Varian Gemini (200 MHz) and Bruker (300 MHz) spectrometers, using the indicated solvents. NMR data are reported as δ values (ppm) relative to tetramethylsilane as an internal standard. Elemental analyses were performed using a PerkinElmer elemental analyser model 240B; results fell in the range of calculated values ±0.4%. Mass spectra were obtained using a Mat 112 Varian Mat Bremen (70 eV) mass spectrometer and Applied Biosystems Mariner System 5220 LC/MS (nozzle potential 250.00). Starting materials as well as solvents were purchased from Sigma (Milan, Italy).
Synthesis of copper(II) complex crystals 1–5 and single crystal structure determination
Single crystals suitable for X-ray diffraction experiment of compounds [Cu(L1)2(H2O)]·3(H2O) (1), [Cu2(L2)4]·6(H2O) (2), [Cu2(L3)4]·4(H2O) (3), [Cu(L4)2]n·3(H2O) (4), and [Cu3(L5)6]·18(H2O) (5) were obtained from 10 mL water solution containing 1 mM CuCl2 and the investigated ligands in 2 mM concentration. The pH was adjusted with NaOH to 7.0. Slow evaporation of the solvent (about one or two months) resulted in green (1,2) or blue (3,4,5) crystals. Single crystals were mounted on loops and transferred to the goniometer. X-ray diffraction data were collected at 103 K (except 2 which was measured at 293 K) on a Rigaku RAXIS-RAPID II diffractometer. The diffraction measurement was performed with Mo-Kα radiation in all cases but one where a Cu-Kα source was used (crystal 3). The multi-scan absorption corrections (on crystal 2) were carried out using the CrystalClear20 software and numerical absorption corrections in the cases of 1 and 3–5 were done using NUMABS.21 Sir201422 and SHELXL23,24 under WinGX25 software were used for structure solution and refinement, respectively. The structures were solved by direct methods. The models were refined by full-matrix least squares on F2. Refinement of non-hydrogen atoms was carried out with anisotropic temperature factors. Atomic positions for water hydrogens were located in difference electron density maps, whereas all the other hydrogens were placed in geometric positions. They were included in structure factor calculations but they were not refined. The isotropic displacement parameters of the hydrogen atoms were approximated from the U(eq) value of the atom they were bonded to. The summary of data collection and refinement parameters of complexes is collected in Table S1 (ESI†). Selected bond lengths and angles were calculated using PLATON.26,27 The graphical representation was done using the Mercury28 software and the editing of CIF files was done using the PublCif29 software.pH-Potentiometric studies
Acidity constants of the newly synthesised ligands (HL5 and H2L6) were determined by pH-potentiometric titrations and UV-vis measurements (if pKa < 2) using a procedure described by Di Marco et al.30 Briefly, ligand solutions (5 × 10−4 to 2 × 10−3 m, m = mol kg−1) were titrated with 0.1 m NaOH, which was previously standardized with 0.1 m HCl. A Metrohm 715 Dosimat burette was used. The samples were in all cases thermostated at 25.0 ± 0.1 °C, and completely deoxygenated by bubbling purified nitrogen for ca. 15 min before the measurements. The bubbling gas was also passed over the solutions during the titrations. The pH-metric titrations were performed in the pH range of 2.0–11.0. The acidity constants were calculated using the PITMAP31 computer programme. UV-vis spectra were recorded at 25.0 ± 0.1 °C, in 0.5 or 1 cm quartz cuvettes, using a PerkinElmer Lambda 25 diode array spectrophotometer, for solutions containing each ligand alone at various pH values below 2. Calculations of the stability constants were performed at the wavelengths displaying the highest absorbance variation with pH.EPR measurements and evaluation of the spectra
All CW-EPR spectra were recorded using a BRUKER EleXsys E500 spectrometer (microwave frequency ∼9.7 GHz, microwave power 13 mW, modulation amplitude 5 G, modulation frequency 100 kHz). The pH-dependent isotropic EPR spectra were recorded at room temperature (25 °C) in a circulating titration system. Two series of EPR spectra were recorded in freshly prepared solutions containing 2 mM ligand and 1 mM or 2 mM CuCl2, in the pH range 2–8. At higher pH values precipitation was detected in both cases. (By adding acid to the solution the precipitate can be dissolved and the previously measured EPR spectra could be recollected.) The ionic strength I = 0.1 M was adjusted with KCl. The pH was measured using a Radiometer PHM240 pH/ion Meter equipped with a Metrohm 6.0234.100 glass electrode. A Heidolph Pump drive 5101 peristaltic pump was used for circulating the solution from the titration pot through a capillary tube into the cavity of the instrument. The titrations were carried out under a nitrogen atmosphere. For several pH values a 0.10 mL of sample was taken out of the stock solution and was measured individually in a Dewar containing liquid nitrogen (at 77 K) to obtain frozen solution EPR spectra. 0.02 mL of MeOH was added to the samples to avoid water crystallization. Temperature-dependent EPR spectra were measured using the same Bruker instrument. The measured 0.1 mL sample contained 3.8 mM ligand L6 and 1.9 mM CuCl2 at pH = 5.71. Two series of spectra were recorded: one from 150 K to 230 K in steps of 5 K, and another between 150 and 190 K in steps of 2.5 K. The temperature was adjusted with an accuracy of ±0.1 K.The room-temperature CW-EPR spectra were simulated by the “two-dimensional” method using the 2D_EPR software.32 Each component curve was described by the isotropic EPR parameters g0, ACu0 copper (ICu = 3/2) and AN0 nitrogen (IN = 1) hyperfine coupling. The relaxation parameters α, β, and γ defined the line widths through the equation σMI = α + βMI + γMI2, where MI denotes the magnetic quantum number of the paramagnetic metal ions. The concentrations of the complexes were varied by fitting their formation constants, β(MpLqHr), defined for the general equilibrium pM + qL + rH ⇌ MpLqHr as β(MpLqHr) = [MpLqHr]/[M]p[L]q[H]r, where M denotes the metal ion and L the completely deprotonated ligand.
The anisotropic EPR spectra recorded at 77 K were analysed individually with the EPR software,33 which gives the anisotropic EPR parameters gx, gy, gz (g tensor), ACux, ACuy, ACuz (copper hyperfine tensor) and ANx, ANy, ANz (nitrogen superhyperfine tensor). The orientation-dependent line width parameters were used to set up each component spectra.
Temperature-dependent EPR spectra were simulated individually by using the EPR software.33 The EPR spectra of the dimer complex were simulated by a module of the same software developed for calculating the EPR spectra of coupled spin systems (biradicals and paramagnetic dimers).58 The EPR spectrum was calculated by the complete diagonalization of the Hamiltonian of a two-spin system:
Since the naturally occurring copper contains two isotopes, 63Cu and 65Cu, the EPR spectra were calculated as the sum of the spectra of 63Cu and 65Cu weighted by their natural abundance (69.17% and 30.83%, respectively). The quality of fit was characterized by the noise-corrected regression parameter (Rj for the jth spectrum) derived from the average square deviation (SQD) between the experimental and the calculated intensities. The details of the statistical analysis were published previously.32,34 The hyperfine and superhyperfine coupling constants and the relaxation parameters were obtained in field units (Gauss = 10−4 T).
Theoretical and statistical calculations
Density functional theory (DFT) computations were performed for HPC ligands in their fully deprotonated forms (L2− for L6 and L− for all the other ligands) using the ORCA package.35–39 Calculations were carried out in vacuum and in water by using the conductor-like screening model (COSMO)40 with the dielectric constant of water. All the geometry optimizations were performed using the B3LYP41,42 hybrid functional. The two basis sets, split-valence pulse polarization (SV(P))43 and cc-pVTZ,44,45 were compared. Multivariate data analysis was performed on the matrix of solution stability, EPR spectroscopic, SXRD and DFT data in order to reveal correlations between these parameters. All statistical evaluations were accomplished using the software Statistica 13.1 (Dell Inc.)46Results
Proton dissociation processes of the ligands in solution
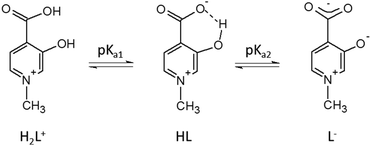
The protonation steps of the HPC ligands have been determined by pH-potentiometry, either in the present study (L5 and L6) or in previous ones (all other HPCs16–18). The constants are collected in Table 1. All ligands have two detectable deprotonation steps (Scheme 3). The first deprotonation (pKa1) is generally assigned to the aromatic –COOH proton; it happens at very low pH (pKa1 < 1) and it has therefore been obtained by UV-vis measurements. In the case of L6 this deprotonation could not be detected, and the first deprotonation is due to the aliphatic –COOH (pKa1 ≈ 3.5). The second deprotonation (denoted as pKa2 or log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β(LH), between 6 and 8) is always due to the –OH group which is in an intramolecular hydrogen bond with the deprotonated –COO− group. The inductive effect of the positively charged –NR+ groups has an impact on the pKa1 and pKa2 values being relatively low. Further effects (see also Crisponi et al.7), like the keto–enol tautomerism of the OH group (typical and well known for 2- and 4-hydroxypyridines47), and electron-donating effects of methyl substituents can modify the pKa2 values of HPCs (in keto–enol tautomerism ring aromaticity is lost and a pyridinone derivative is formed, see also Scheme S1, ESI†). As a result of all these complex effects, different electron distribution can emerge on the donor carboxylate and hydroxyl oxygens of the different HPC ligands which will determine their complex stability in solution and their coordination properties in solid state, described in this paper.
β(LH), between 6 and 8) is always due to the –OH group which is in an intramolecular hydrogen bond with the deprotonated –COO− group. The inductive effect of the positively charged –NR+ groups has an impact on the pKa1 and pKa2 values being relatively low. Further effects (see also Crisponi et al.7), like the keto–enol tautomerism of the OH group (typical and well known for 2- and 4-hydroxypyridines47), and electron-donating effects of methyl substituents can modify the pKa2 values of HPCs (in keto–enol tautomerism ring aromaticity is lost and a pyridinone derivative is formed, see also Scheme S1, ESI†). As a result of all these complex effects, different electron distribution can emerge on the donor carboxylate and hydroxyl oxygens of the different HPC ligands which will determine their complex stability in solution and their coordination properties in solid state, described in this paper.
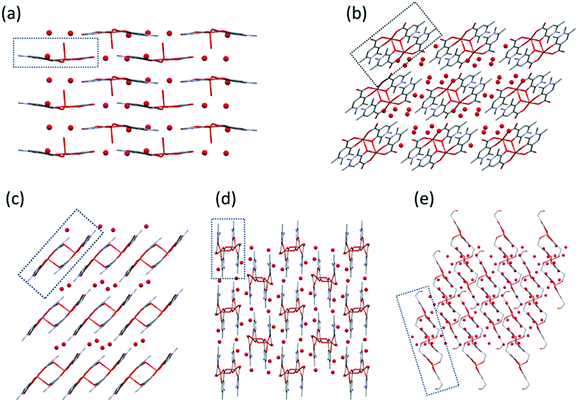
Solid state results of the bis-ligand complexes 1–5
In [Cu(L1)2(H2O)]·3(H2O) (1), Cu1 adopts a square-pyramidal environment as shown in Fig. 1, with the O2,O3 and O12,O13 chelate coordination of the two L1 ligands in cis arrangements. The coordination of the two ligands is asymmetrical, the angle between the pyridine ring N2–C16 and the equatorial coordination plane (defined by atoms O2–O3–Cu1–O12–O13) is 4.27°, as well as the Cu1–O12 and Cu1–O13 distances are 1.9258(14) Å and 1.9156(14) Å, respectively. The pyridine ring of the other ligand (N1–C2) deviates from the equatorial plane by 14.33°, and the Cu1–O2 and Cu1–O3 distances are somewhat longer, 1.9564(14) and 1.9349(13) Å, respectively. The axial position is occupied by a water molecule with a long Cu–O4 distance of 2.2340(14) Å.
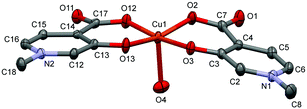 | ||
| Fig. 1 ORTEP view of [Cu(L1)2(H2O)] in crystal 1 with thermal displacement ellipsoids drawn at the 50% probability level. Hydrogen atoms and waters of crystallisation are omitted for clarity. Some selected bond lengths and angles are given in Table S2 while Fig. S1 (ESI†) shows the crystal packing arrangements. | ||
The complex [Cu2(L2)4]·12H2O (2) formed a cyclic dimer where each copper ion is coordinated by [O−carb,O−] chelate rings in cis positions in the equatorial plane, and the deprotonated hydroxyl groups form a bridge to the adjacent copper ion in the axial direction (the Cu1–O3ax distance is 2.406(2) Å), and vice versa (Fig. 2). The two Cu(L2)2 moieties are related by an inversion centre. The pyridine rings N1–C6 and N12–C16 are almost parallel to each other (the angle between the planes is 2.81°); however they form an angle with the equatorial plane which is 25.37° with the ring N1–C6 and 22.56° with N12–C16. Similar cyclic dimer structures with the bridge formation of the phenolato groups were found in the case of some mixed ligand [Cu2(Sal)2(2,2′-bpy)2] (Sal = salicylato, bpy = bipyridyl) complexes (ref. codes REPJAY,48 MAHMOY,49 DIFQAK,50 XANHUP,51 EMOJOG,52 NALLUJ53). The copper–copper distances vary from 3.168(1) Å to 3.265(4) Å in the reported structures, and the value of 3.231(1) Å obtained in crystal 2 falls in this range.
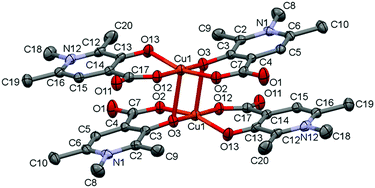 | ||
| Fig. 2 ORTEP view of [Cu2(L2)4] in crystal 2 with thermal displacement ellipsoids drawn at the 30% probability level. Hydrogen atoms and waters of crystallization are omitted for clarity. Some selected bond lengths and angles are collected in Table S2 and packing arrangements are shown in Fig. S2 (ESI†). | ||
The solid state structure of the bis-ligand copper complex of L3, similarly to L2, resulted in a cyclic dimer [Cu2(L3)4]·4H2O (3) (Fig. 3). However unlike L2, the two L3 coordinate in trans arrangements, and it is the non-coordinated carboxylate oxygen (O11), instead of the pyridinolato oxygen, which binds to the neighbouring Cu(II) centre forming a syn–anti carboxylato bridge in an equatorial–axial coordination mode. The two [Cu(L3)2] moieties are symmetrical by an inversion centre. The axial Cu1–O11 distance is 2.614(3) Å which is significantly longer than the axial bond in the complex [Cu2(L2)4].
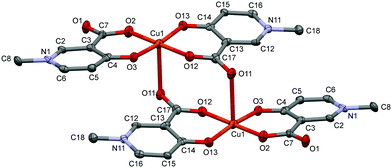 | ||
| Fig. 3 ORTEP view of [Cu2(L3)4] in crystal 3 with thermal displacement ellipsoids drawn at the 50% probability level. Hydrogen atoms and waters of crystallization are omitted for clarity. Selected bond distances and angles can be found in Table S2 and packing arrangements are shown in Fig. S3 (ESI†). | ||
The copper–copper distance is 5.266(2) Å in the cyclic dimer 3; however a much closer copper–copper distance, 3.835(1) Å, emerged between adjacent copper dimers above each other (Fig. S3, ESI†). The pyridine ring planes are almost planar to the equatorial plane (formed by the atoms O2–O3–Cu1–O12–O13); the deviation is 5.74° related to the ring N1–C6 and 8.93° related to N11–C16. There is only one copper structure reported so far with a similar carboxylato-bridged dimer in the literature which is a mixed ligand complex of [Cu2(3,5-{(NO2)Sal})(2,2′-bpy)2] ((NO2)Sal = 3,5-dinitrosalicylate, ref. code CIHQUG)54 where the copper–copper distance was found to be 4.93(1) Å. A similar zinc complex could also be found where a carboxylate oxygen instead of the phenolato oxygen is bridging two zinc centres in a syn–anti coordination mode in the coordination polymer [Zn(TCSA) (4,4′-bpy)0.5(DMF)]n (TCSA = 3,5,6-trichlorosalicylate, ref. code EBIVAO).55 It is worth mentioning that in both cases the salicylic acid is substituted with strong electron-attracting NO2 or Cl groups which significantly change the electron density on the donor oxygens.
In the crystal of L4, the bis-ligand copper moieties establish a 1D polymer chain [Cu(L4)2]n·3H2O (4) (Fig. 4). The arrangement of the ligands is trans similarly to L3. The Cu1 atom is penta-coordinated with a highly similar arrangement as in 3 but the cyclic dimer could not be formed very likely because the C9 methyl protons would be in sterically hindered by the C18 methyl protons in the case of a cyclic dimer structure. While in 3 the two copper centres have parallel arrangements, in 4 the neighbouring centres are turning outward so that the carboxylate oxygen O11 can coordinate a third copper ion axially. The angle between the two planes of the neighbouring copper centres defined by the four oxygen and copper atoms is 51.2°. The angles between the equatorial plane and the pyridine ring planes N1–C6 and N11–C16 are 19.66° and 31.60°, respectively, which are also much higher than in 4. Compared with 3 where the centres are related by an inversion centre, the monomer units are related by a 21 screw axis in 4, leading to a 1D helical structure. The same bridging mode (1D framework) was found in the Mn(II) complex of 4-hydroxynicotinic acid (ref. code SAKYOT56), where the metal centre is hexa-coordinated with a more symmetrical octahedral geometry.
In L5 a hydroxyethyl group is bound to the pyridine nitrogen, and the crystallization process with copper(II) produced crystal [Cu3(L5)6]·18H2O (5) (Fig. 5). Trimer [Cu3(L5)6] units construct the crystal with a relatively high amount of water inclusion (9 water of crystallization/asymmetric units). The three coordination centres represent two different coordination arrangements. The asymmetric unit contains half of the trimer arranged by an inversion centre at the position of Cu2. All three centres are coordinated by the [O−carb,O−] groups in trans positions in the basal plane. The outward coppers are bound by one side chain OH groups axially, generating a square-pyramidal geometry, whereas the central copper is coordinated by two side chain OH groups resulting in an elongated octahedral environment. The axial bond is significantly shorter in the square pyramid (Cu1–O24: 2.285(2) Å, see Table S2, ESI†) than in the elongated octahedron (Cu2–O14: 2.427(2) Å).
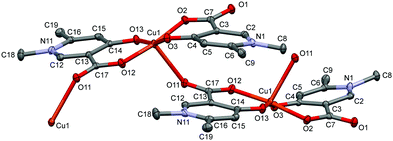 | ||
| Fig. 4 ORTEP view of the [Cu(L4)2]n·3H2O coordination polymer in crystal 4 with thermal displacement ellipsoids drawn at the 50% probability level. Hydrogen atoms and lattice water molecules are omitted for clarity. Selected bond lengths can be found in Table S2 and packing arrangements in Fig. S4 (ESI†). | ||
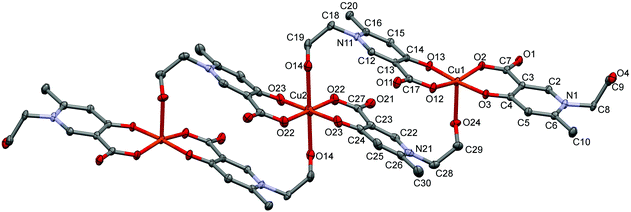 | ||
| Fig. 5 ORTEP views of [Cu3(L5)6]·18H2O in crystal 5 with thermal displacement ellipsoids drawn at the 50% probability level. Hydrogen atoms and lattice water molecules are omitted for clarity. Selected bond lengths can be found in Table S2 and packing arrangements in Fig. S5 (ESI†). | ||
In 1 the molecules are arranged in planes where the axially coordinated water molecules are directed up and down alternately. The complexes form chains by C–H⋯O hydrogen bonds between the methyl protons and the neighbouring carboxylate and water oxygens (Fig. S1, ESI†). In 2 intermolecular hydrogen bonds with water molecules and π⋯π (off-centred parallel) stacking interactions between the pyridine rings play an important role in the stabilisation of the 2D layers. The water molecules form a 5-membered ring with Ow–H⋯Ow interactions between the molecular columns (Fig. S2, ESI†). In the case of crystal 3, the two water molecules located in the asymmetric unit are mirrored by an inversion centre to form a square which connects the columns formed by the dimeric units (Fig. S3, ESI†). In 4, the 1D polymer chains and water channels are arranged in columns (Fig. 6 and Fig. S4, ESI†) while in crystal 5 the water of crystallization (18 molecules/trimer units) and the complex molecules form layers (Fig. S5, ESI†).
Complex formation in solution
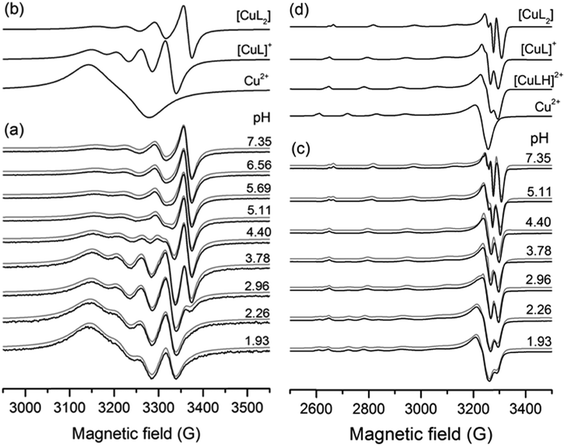
The complexation properties of HPC ligands in solution have been followed by electron paramagnetic resonance (EPR) spectroscopy. EPR is a powerful method for investigating paramagnetic copper(II) complexes. The principle of the measurement is that the degenerated energy levels of the spin states can be resolved by an external magnetic field and transitions between the levels can be detected by microwave radiation. This technique is extremely sensitive to the chemical surrounding of the unpaired electron providing unique local structural information. Due to hyperfine interactions with copper (ICu = 3/2) the EPR line splits into four lines. At room temperature, the isotropic parameters can be obtained (g0, A0), as the molecular motions average out the orientation dependent EPR parameters. This simple description and low number of fitted parameters allow us to fit all the measured pH-dependent spectra together, by varying the EPR parameters and formation constants (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β) of the components by using the simulation program “2D_EPR”.32,34 The main advantage of using this technique is that relevant structural and speciation data can be gained under ambient conditions (aqueous solution and room temperature). The EPR spectral series is collected by an in situ titration performed in a circulating system to keep the EPR measuring conditions fixed. Additional details concerning the coordination modes can be gained from the frozen solution EPR spectra obtained at 77 K. This evaluation (using the “EPR” program33) results in the anisotropic parameters (gx, gy, gz, and Ax, Ay, Az), which allow a more detailed analysis of the complex structures. In this case, the molecules are randomly oriented in the sample, but their positions are fixed during the measurement. The combination of the two methods was used previously to investigate several copper(II)–small bioligand complexes.58,59 Two series of pH-dependent EPR spectra were recorded for each Cu(II)–HPC equilibrium system, one at an equimolar metal-to-ligand ratio and another at two-fold ligand excess both in aqueous solution at room temperature and at 77 K.
β) of the components by using the simulation program “2D_EPR”.32,34 The main advantage of using this technique is that relevant structural and speciation data can be gained under ambient conditions (aqueous solution and room temperature). The EPR spectral series is collected by an in situ titration performed in a circulating system to keep the EPR measuring conditions fixed. Additional details concerning the coordination modes can be gained from the frozen solution EPR spectra obtained at 77 K. This evaluation (using the “EPR” program33) results in the anisotropic parameters (gx, gy, gz, and Ax, Ay, Az), which allow a more detailed analysis of the complex structures. In this case, the molecules are randomly oriented in the sample, but their positions are fixed during the measurement. The combination of the two methods was used previously to investigate several copper(II)–small bioligand complexes.58,59 Two series of pH-dependent EPR spectra were recorded for each Cu(II)–HPC equilibrium system, one at an equimolar metal-to-ligand ratio and another at two-fold ligand excess both in aqueous solution at room temperature and at 77 K.
The simulation of the spectra resulted in the formation constants collected in Table 2 and the isotropic and anisotropic EPR parameters of the detected species shown in Table S3 (ESI†). A series of measured and simulated EPR spectra of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 Cu(II)–L3 equilibrium system and the corresponding calculated component spectra are shown in Fig. 7. The spectra recorded in equimolar solution for the same system are shown in Fig. S7 (ESI†). In solutions containing Cu(II) and either L1, L2, L3, L4 or L5, the [CuL] and [CuL2] complexes were detected besides the Cu(II)aqua species. For all the obtained complexes, the stability values are much lower than those of deferiprone–copper(II) complexes (lg
2 Cu(II)–L3 equilibrium system and the corresponding calculated component spectra are shown in Fig. 7. The spectra recorded in equimolar solution for the same system are shown in Fig. S7 (ESI†). In solutions containing Cu(II) and either L1, L2, L3, L4 or L5, the [CuL] and [CuL2] complexes were detected besides the Cu(II)aqua species. For all the obtained complexes, the stability values are much lower than those of deferiprone–copper(II) complexes (lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β(CuL) = 10.3(9), lg
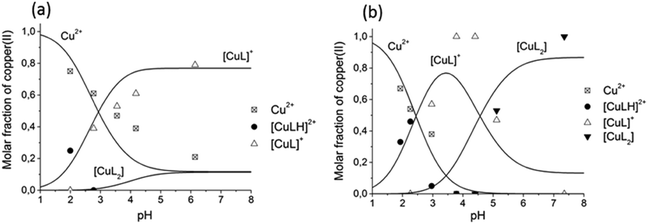
β(CuL) = 10.3(9), lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β(CuL2) = 19.2(6)).12 In the solutions containing Cu(II) and L6, the protonated complexes [CuLH] and [CuL2H] were also detected owing to the protonated carboxyethyl side chain. With this ligand, in frozen solutions, besides the mono complexes, dimer species were observed at a two-fold ligand excess, which can be assigned to [Cu2L4]. In all copper(II)–L equilibrium systems the complex [CuLH] could not be detected at room temperature, but it appeared in frozen solutions except for L2 for which this species could not be detected at low temperature either.
β(CuL2) = 19.2(6)).12 In the solutions containing Cu(II) and L6, the protonated complexes [CuLH] and [CuL2H] were also detected owing to the protonated carboxyethyl side chain. With this ligand, in frozen solutions, besides the mono complexes, dimer species were observed at a two-fold ligand excess, which can be assigned to [Cu2L4]. In all copper(II)–L equilibrium systems the complex [CuLH] could not be detected at room temperature, but it appeared in frozen solutions except for L2 for which this species could not be detected at low temperature either.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β(MpLqHr). Various derived constants are also given for comparisona
β(MpLqHr). Various derived constants are also given for comparisona
| L1 | L2 | L3 | L4 | L5 | L6 | |
|---|---|---|---|---|---|---|
a Uncertainties (SD) are shown in parentheses; for the charges of L1–L6 see Scheme 1.
b Values determined by pH-potentimetry from ref. 57: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β(CuL) = 6.63(2) β(CuL) = 6.63(2)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β(CuL2) = 12.03(2).
c Protonated complexes have also been determined with log β(CuL2) = 12.03(2).
c Protonated complexes have also been determined with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β(CuLH) = 10.07(1) and log β(CuLH) = 10.07(1) and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β(CuL2H) = 15.61(1).
d Calculated apparent stability constants at pH = 4.0 for CuL, and at pH = 6.0 for CuL2 by the equation β′ = β/αH, where αH = 1 + ∑βLHi[H]i.
e pM = −log(∑[MpHr]) at pH = 5.0, cM = 1.0 mM, cL = 1.0 mM. β(CuL2H) = 15.61(1).
d Calculated apparent stability constants at pH = 4.0 for CuL, and at pH = 6.0 for CuL2 by the equation β′ = β/αH, where αH = 1 + ∑βLHi[H]i.
e pM = −log(∑[MpHr]) at pH = 5.0, cM = 1.0 mM, cL = 1.0 mM.
|
||||||
lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β(CuL) β(CuL) |
5.87(2) | 6.63(4) | 6.34(1) | 6.47(1) | 6.32(1) | 6.13(1) |
lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β(CuL2) β(CuL2) |
10.07(4) | 10.51(5) | 11.04(1) | 11.25(1) | 10.64(1) | 11.17(1) |
lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β′(CuL)d β′(CuL)d |
3.24 | 2.57 | 4.38 | 4.17 | 4.21 | 3.63 |
lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β′(CuL2)d β′(CuL2)d |
8.63 | 6.38 | 10.48 | 10.30 | 9.92 | 10.11 |
| pM (pH = 5)e | 4.28 | 3.73 | 5.34 | 5.15 | 5.18 | 5.16 |
The comparison of the distribution curves and isotropic EPR spectra of [CuL] and [CuL2] complexes of all the measured ligands are shown in Fig. S8 and S9 (ESI†), respectively. In Fig. 8 the distribution diagram is shown for the Cu(II)–L3 system, as a typical example. The figure shows the formation of the components at two different temperatures (295 K and 77 K). We would like to note that even though the freezing of the EPR tubes in liquid nitrogen takes only a couple of seconds, we can observe that the complex equilibrium is shifted by 0.5 pH units to higher pH upon freezing. The protonated complex [CuLH] appeared, and the formation of [CuL] and [CuL2] increased at low temperature. In order to compare the stability of the Cu(II)–HPC complexes, the apparent formation constant and pM values have been calculated (see Table 2). Clearly, the 3-hydroxy-4-pyridinecarboxylate derivatives (3HPCs) show much lower stability than 4-hydroxy-3-pyridinecarboxylate derivatives (4HPCs), and there are some significant differences between 4HPCs, as well: L6 has the lowest stability, L5 and L4 are almost identical, and L3 forms the strongest Cu(II) complexes (Fig. S10, ESI†).
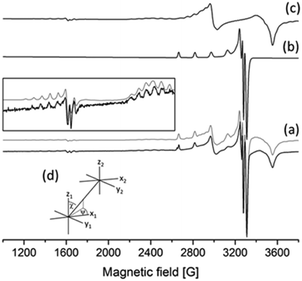
The frozen-solution EPR spectra of the complexes could be fitted by assuming the usual elongated octahedral geometry of Cu(II) complexes (Fig. 7d). For the description of the spectra of [CuL] and [CuLH] complexes, g and A tensors with axial symmetry were used; however for [CuL2] the axial symmetry was not sufficient, and a rhombic symmetry has been taken into account. EPR parameters are in good agreement with the increasing ligand field in the order of [CuLH] < [CuL] < [CuL2], since g-values decreased and A-values increased (Table S3, ESI†). The suggested coordination modes are shown in Scheme S2 (ESI†). In the case of [CuL2], a mixture of cis or trans coordination isomers can be supposed in solution, but the difference is probably below the experimental error, and EPR spectra could be satisfactorily described with one component. In the case of L6 a dimerization process has been found in frozen solution. In the presence of a ligand excess a well-resolved dimer spectrum of ferromagnetically coupled copper centres could be measured (Fig. 9) which can be assigned to [Cu2L4]. The half-field peak, measured at 1600 G, can be attributed to a double quantum transition (ΔMS = 2) of a coupled-spin system (Fig. 9a). The measured spectrum was described by the superposition of dimeric and monomeric species (Fig. 9c and 9b). The dimer spectrum was simulated by the exact solution of the Hamiltonian, using EPR software.60 This exact description resulted in effective structural parameters, based on which the Cu(II)–Cu(II) distance and the orientation of the two g-tensors relative to each other can be proposed. Identical Cu(II) centres with an almost parallel equatorial plane (all three Euler angles are zero), with polar angles of χ = 30° and ψ = 0° and dipolar coupling D = 380 G, were obtained. For the g- and A-tensor values, data obtained for the mono complexes have been used: gx = 2.057, gy = 2.066, gz = 2.331, Ax = 12.8 G, Ay = 12.0 G, Az = 150.1 G. For the exchange coupling, the estimation of J > 1500 G can be given, because under this value a doublet peak originating from this interaction should have been detected under the experimental conditions. From the dipolar coupling, the Cu(II)–Cu(II) distance of 3.82 Å can be calculated and from χ = 30° slightly shifted copper centres above each other could be suggested. The crystal structures of [Cu2(L3)4] and [Cu2(L2)4] resulted in very similar Cu(II)–Cu(II) distances (3.231(1) and 3.835(1) Å) and angles (χ ∼ 30°) suggesting that the secondary interactions detected in the solid state can also appear in frozen solution. The dimerization process has been followed by temperature-dependent EPR spectra (Fig. S11, ESI†) which indicated that the appearance of the ferromagnetically coupled dimeric species is reversible with temperature and it is detectable only below 180 K. A small amount of a similar dimer could be detected in the case of ligand L1 as well (Fig. S12, ESI†). At room temperature, in solution, line broadening or diminishing of EPR signals would have been expected in the case of dimer formation, but none of these effects were found under our measuring conditions. We can suggest that in the case of dissolution of the solid [CuL2] crystals in a 1–2 mM concentration, oligomers dissociate and only monomers are obtained.
Discussion
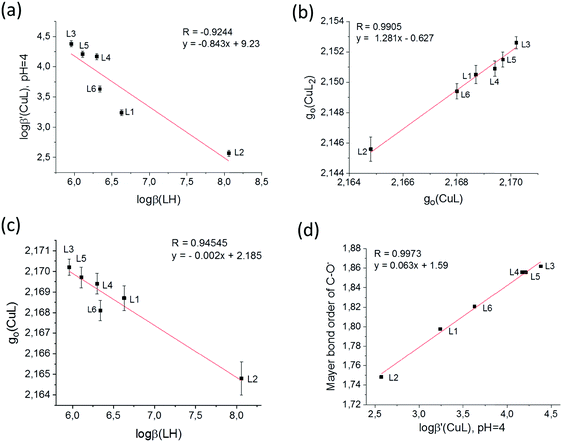
It is supposed that both the solid state coordination arrangements and the solution stability are related to the electron distribution on the donor oxygen atoms of the ligands. To compare this for the different HPCs, Mulliken charge density61 and Mayer bond order62–64 values have been calculated for the fully deprotonated ligands (L2− for L6 and L− for all the others) after geometry optimization by density functional theory (DFT). The B3LYP functional41,42 was used under three different conditions: (1) SV(P) basis set43 in gas phase, (2) SV(P) basis set using the conductor-like screening model COSMO40 of water and (3) cc-pVTZ44,45 using the same model COSMO (see Table S4, ESI†). As we had now formation constants, EPR parameters, calculated charges and bond orders together with SXRD copper–oxygen distances, all data were collected in a database and multivariate data analysis was performed using the Statistica program package46 to reveal the relations between the obtained values. By using this approach several significant (p < 0.05) correlations have been found (see Table S5, ESI†) among which four correlations are highlighted in Fig. 10. The correlation between the deprotonation constants of the hydroxyl group (pKa2 ≡ log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β(LH)) and the apparent formation constant of complex CuL (log
β(LH)) and the apparent formation constant of complex CuL (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β′(CuL) calculated at pH = 4.0) is shown in Fig. 10a. The negative slope indicates that the lower the deprotonation constants (higher acidity of the OH proton) the higher the formation constants of CuL. This is probably due to the strong intramolecular interaction between the OH proton and the adjacent carboxylate oxygen, so the deprotonation of this group necessarily precedes the binding of the copper ion. A significant correlation between the g0 values of complexes [CuL] and [CuL2] was also obtained (Fig. 5b). g0 (similarly to λmax) represents the ligand field around the Cu(II) ion, and it decreases with increasing ligand field. It is an expected correlation that the higher the ligand field in the mono-complex, the higher the ligand field in the bis-complex. Interestingly, the order of the ligands in Fig. 5a and b is very similar, and as a consequence g0(CuL) and pKa2 also show a significant correlation (Fig. 5c). The negative slope indicates that the ligand field decreases with the increasing acidity of the OH group. These results show that the complexation properties of the studied HPCs are mainly influenced by the acidic character of the OH group, whereas the nature of the carboxylate group has only little effects. This is further supported by the result of theoretical calculations. In all three calculations the Mayer bond orders of the deprotonated hydroxyl C–O− bonds were in good correlation with the apparent formation constants of the complex [CuL]. Fig. 10d shows the result of calculation (1) where R = 0.8744 was obtained. (Calculation (2) resulted in R = 0.8079 and calculation (3) in R = 0.8793.) The Mayer bond order values indicate that the C–O− bond is between a single and a double bound and the double bound character has a continuous change according to the electron donating effect of the different substituents. The different electron density is also manifested in the C–O distances measured in the crystals. These data are collected in Table S6 (ESI†) for all ligands which are in the asymmetric unit. When we compare the Cring–O3 distances of the different HPCs averaged over two (or three) structures measured in the asymmetric unit, the obtained trend is L2 (1.307(6) Å) > L1 (1.303 Å) > L4 (1.289(1) Å) > L5 (1.286(5) Å) > L3 (1.282(2) Å) which is in agreement with the increasing Mayer bond order calculated by the DFT method. Several examples for fine-tuning the physical–chemical properties of complexes by substituent effects are known, such as the redox potential for iron(II)65,66 or copper(II)67 complexes or the relaxivity and stability of Gd(III) contrast agents.68 This obtained substituent effect gives the possibility to optimize the stability of HPC chelators with copper(II). The main difference between the obtained solution and solid state structures of the bis-ligand copper(II) complexes is that in solution the same [O−carb,O−][O−carb,O−] coordinated monomer copper(II) complexes have been found for all HPCs (possibly with axial water coordination). However, in the solid state, a great structural variety has been detected owing to the fact that the axial position can be fulfilled in different ways: by a water molecule resulting in a monomer complex (1), by the ligand oxygen of a neighbouring complex forming cyclic dimer structures (2 and 3) or by the ligand side chain OH groups, in 5, resulting in this case a 5-, 6-, 5-coordinated trimer complex. When the sterical hindrance prevents cyclic dimer formation in 4, a 1D polymer evolves. Interestingly, in the cyclic dimer of ligand L2 (2) it is the pyridinolato oxygen which acts as the bridging atom; anyhow in the case of ligand L3 (3) it is the carboxylato oxygen that plays this role. The nature of the axially coordinated donor atom strongly depends on the electron distribution of the ligand oxygen donors. The solution equilibrium studies and DFT calculations revealed a systematic order in the acidic character of the OH group where the highest value was found in the case of the L3 and the lowest value in the case of the L2 (Fig. 10a) ligands. If we compare the Mulliken gross atomic charges (see Table S4, ESI†) for the deprotonated carboxyl (O1) and the hydroxyl (O3) atoms in the different ligands we can see that they are almost equal in the case of the 3HPC ligands; however O1 values are significantly more negative than O3 values in all 4HPCs. It means that the more electronegative carboxylate oxygen (O1) takes the bridging role over pyridinolate oxygen (O3) in the L3 copper complex. By examining the crystal structures of related cyclic dimers of salicylic acid, phenolato bridges can be found in the case of derivatives with electron-donating groups;48–53 however the carboxylate oxygen is found playing the bridging role when the phenyl ring contains electron-attracting groups decreasing the electron density on the hydroxyl oxygen.54,55 It is also worth mentioning that in 3HPC complexes only cis and in 4HPC complexes only trans configuration of the ligands could be detected in solid state which is probably also related to their different electron distribution. Further investigations are planned to understand the origin and nature of this cis/trans predominancy in these copper(II) complexes.
β′(CuL) calculated at pH = 4.0) is shown in Fig. 10a. The negative slope indicates that the lower the deprotonation constants (higher acidity of the OH proton) the higher the formation constants of CuL. This is probably due to the strong intramolecular interaction between the OH proton and the adjacent carboxylate oxygen, so the deprotonation of this group necessarily precedes the binding of the copper ion. A significant correlation between the g0 values of complexes [CuL] and [CuL2] was also obtained (Fig. 5b). g0 (similarly to λmax) represents the ligand field around the Cu(II) ion, and it decreases with increasing ligand field. It is an expected correlation that the higher the ligand field in the mono-complex, the higher the ligand field in the bis-complex. Interestingly, the order of the ligands in Fig. 5a and b is very similar, and as a consequence g0(CuL) and pKa2 also show a significant correlation (Fig. 5c). The negative slope indicates that the ligand field decreases with the increasing acidity of the OH group. These results show that the complexation properties of the studied HPCs are mainly influenced by the acidic character of the OH group, whereas the nature of the carboxylate group has only little effects. This is further supported by the result of theoretical calculations. In all three calculations the Mayer bond orders of the deprotonated hydroxyl C–O− bonds were in good correlation with the apparent formation constants of the complex [CuL]. Fig. 10d shows the result of calculation (1) where R = 0.8744 was obtained. (Calculation (2) resulted in R = 0.8079 and calculation (3) in R = 0.8793.) The Mayer bond order values indicate that the C–O− bond is between a single and a double bound and the double bound character has a continuous change according to the electron donating effect of the different substituents. The different electron density is also manifested in the C–O distances measured in the crystals. These data are collected in Table S6 (ESI†) for all ligands which are in the asymmetric unit. When we compare the Cring–O3 distances of the different HPCs averaged over two (or three) structures measured in the asymmetric unit, the obtained trend is L2 (1.307(6) Å) > L1 (1.303 Å) > L4 (1.289(1) Å) > L5 (1.286(5) Å) > L3 (1.282(2) Å) which is in agreement with the increasing Mayer bond order calculated by the DFT method. Several examples for fine-tuning the physical–chemical properties of complexes by substituent effects are known, such as the redox potential for iron(II)65,66 or copper(II)67 complexes or the relaxivity and stability of Gd(III) contrast agents.68 This obtained substituent effect gives the possibility to optimize the stability of HPC chelators with copper(II). The main difference between the obtained solution and solid state structures of the bis-ligand copper(II) complexes is that in solution the same [O−carb,O−][O−carb,O−] coordinated monomer copper(II) complexes have been found for all HPCs (possibly with axial water coordination). However, in the solid state, a great structural variety has been detected owing to the fact that the axial position can be fulfilled in different ways: by a water molecule resulting in a monomer complex (1), by the ligand oxygen of a neighbouring complex forming cyclic dimer structures (2 and 3) or by the ligand side chain OH groups, in 5, resulting in this case a 5-, 6-, 5-coordinated trimer complex. When the sterical hindrance prevents cyclic dimer formation in 4, a 1D polymer evolves. Interestingly, in the cyclic dimer of ligand L2 (2) it is the pyridinolato oxygen which acts as the bridging atom; anyhow in the case of ligand L3 (3) it is the carboxylato oxygen that plays this role. The nature of the axially coordinated donor atom strongly depends on the electron distribution of the ligand oxygen donors. The solution equilibrium studies and DFT calculations revealed a systematic order in the acidic character of the OH group where the highest value was found in the case of the L3 and the lowest value in the case of the L2 (Fig. 10a) ligands. If we compare the Mulliken gross atomic charges (see Table S4, ESI†) for the deprotonated carboxyl (O1) and the hydroxyl (O3) atoms in the different ligands we can see that they are almost equal in the case of the 3HPC ligands; however O1 values are significantly more negative than O3 values in all 4HPCs. It means that the more electronegative carboxylate oxygen (O1) takes the bridging role over pyridinolate oxygen (O3) in the L3 copper complex. By examining the crystal structures of related cyclic dimers of salicylic acid, phenolato bridges can be found in the case of derivatives with electron-donating groups;48–53 however the carboxylate oxygen is found playing the bridging role when the phenyl ring contains electron-attracting groups decreasing the electron density on the hydroxyl oxygen.54,55 It is also worth mentioning that in 3HPC complexes only cis and in 4HPC complexes only trans configuration of the ligands could be detected in solid state which is probably also related to their different electron distribution. Further investigations are planned to understand the origin and nature of this cis/trans predominancy in these copper(II) complexes.
Conclusions
This work provides the systematic exploration of the influence of electron distribution on the coordination properties of hydroxypyridinecarboxylate derivatives with copper(II) as potential candidates in chelating therapy of metal overloading conditions. In the solid state, the electron distribution in the ligand influences both the type of the axial coordination of the metal centre and the predominancy of cis or trans arrangement as well. While oligomerisation has been detected in the solid state and in frozen solution, solely monomer complexes have been found in room temperature solutions. A positive correlation has been found between the acidity of the hydroxyl group and the complex formation ability of the ligands with copper(II). DFT quantum-chemical calculations confirmed the effect of the electron distribution on the detected stability order. According to this, the copper(II) binding strength of the studied compounds follows the order L2 < L1 ≈ L6 < L4 ≈ L5 < L3. As a consequence, the deprotonated hydroxyl group loses the bridging role in the solid state structures of 4HPCs.The present study illustrates the potential of combined solid state/solution study of bioligand–copper(II) complexes by using single crystal X-ray diffraction together with EPR spectroscopy. The understanding of the solid state and solution structures of small bioligand copper(II) complexes paves the way to design chelators with predicted coordination modes.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Prof. Antal Rockenbauer for valuable discussions about the EPR results and Prof. Ferenc Simon for EPR measuring possibilities. This work was supported by the National Research, Development and Innovation Office-NKFIH through OTKA K115762 and K124544, by the J. Bolyai Research Scholarship of the Hungarian Academy of Sciences (N. V. M.), and by the CPDA08390X “Progetto Ateneo” of the University of Padova.References
- A. Dean, É. Sija, É. Zsigó, M. G. Ferlin, D. Marton, V. Gandin, C. Marzano, P. Pastore, D. Badocco, A. Venzoe, R. Bertatni, T. Kiss and V. Di Marco, Eur. J. Inorg. Chem., 2013, 1310–1319 CrossRef CAS.
- É. Sija, A. Dean, T. Jakusch, V. B. Di Marco, A. Venzo and T. Kiss, Monatsh. Chem., 2011, 142, 399–410 CrossRef.
- A. Dean, M. G. Ferlin, P. Brun, I. Castagliuolo, R. A. Yokel, A. Venzo, G. G. Bombi and V. B. Di Marco, Inorg. Chim. Acta, 2011, 373, 179–186 CrossRef CAS.
- V. B. Di Marco, R. A. Yokel, M. G. Ferlin, A. Tapparo and G. G. Bombi, Eur. J. Inorg. Chem., 2002, 2648–2655 CrossRef CAS.
- V. B. Di Marco, A. Tapparo and G. G. Bombi, Ann. Chim., 1999, 89, 535 CAS.
- V. B. Di Marco, A. Tapparo, A. Dolmella and G. G. Bombi, Inorg. Chim. Acta, 2004, 357, 135–142 CrossRef CAS.
- G. Crisponi, A. Dean, V. B. Di Marco, J. I. Lachowicz, V. M. Nurchi, M. Remelli and A. Tapparo, Anal. Bioanal. Chem., 2013, 405(2-3), 585–601 CrossRef CAS.
- E. T. Clarke and A. E. Martell, Inorg. Chim. Acta, 1992, 57, 191 Search PubMed.
- Y. J. Li and A. E. Martell, Inorg. Chim. Acta, 1993, 214, 103 CrossRef CAS.
- L. N. Sheppard and G. J. Kontoghiorghes, Arzneim.-Forsch./Drug Res., 1993, 43(I), 659 CAS.
- L. N. Sheppard and G. J. Kontoghiorghes, Drugs Today, 1992, 28(Suppl. A), 3 CAS.
- I. Pashadilis and G. J. Kontoghiorghes, Arzneim.-Forsch./Drug Res., 2001, 51(II), 998–1003 Search PubMed.
- G. J. Kontoghiorghes, Toxicol. Lett., 1995, 80, 1–18 CrossRef CAS PubMed.
- G. J. Kontoghiorghes, M. B. Agarwal, R. W. Grady, A. Koinagou and J. J. Marx, Lancet, 2000, 356, 428–429 CrossRef CAS.
- É. Sija, N. V. Nagy, V. Gandin, C. Marzano, T. Jakusch, A. Dean, V. B. Di Marco and T. Kiss, Polyhedron, 2014, 67, 481–489 CrossRef.
- V. B. Di Marco, A. Dean, M. G. Ferlin, R. A. Yokel, H. Li, A. Venzo and G. G. Bombi, Eur. J. Inorg. Chem., 2006, 1284–1293 CrossRef CAS.
- A. Dean, M. G. Ferlin, M. Cvijovic, P. Djurdjevic, F. Dotto, D. Badocco, P. Pastore, A. Venzo and V. B. Di Marco, Polyhedron, 2014, 67, 520–528 CrossRef CAS.
- A. Dean, M. G. Ferlin, P. Brun, I. Castagliuolo, R. A. Yokel, D. Badocco, P. Pastore, A. Venzo, G. G. Bombi and V. B. Di Marco, Dalton Trans., 2009, 1815–1824 RSC.
- H. Yamada, H. Tobiki, K. Jimpo, K. Gooda, Y. Takeuchi, S. Ueda, T. Komatsu, T. Okuda, H. Noguchi, K. Irie and T. Nakagome, J. Antibiot., 1983, 36, 532–542 CrossRef CAS.
- CrystalClear SM 1.4.0, Rigaku/MSC Inc., 2008 Search PubMed.
- T. Higashi, NUMABS, rev. 2002, Rigaku/MSC Inc., The Woodlands, TX 1998 Search PubMed.
- M. C. Burla, R. Caliandro, B. Carrozzini, G. L. Cascarano, C. Cuocci, C. Giacovazzo, M. Mallamo, A. Mazzone and G. Polidori, J. Appl. Crystallogr., 2015, 48, 306–309 CrossRef CAS.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122 CrossRef CAS.
- SHELXL-2013, University of Göttingen, Germany, 2013 Search PubMed.
- L. F. Farrugia, WinGX and ORTEP for Windows: an update, J. Appl. Crystallogr., 2012, 45, 849–854 CrossRef CAS.
- A. L. Spek, J. Appl. Crystallogr., 2003, 36, 7–13 CrossRef CAS.
- A. L. Spek, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2009, 65, 148–155 CrossRef CAS PubMed.
- F. Macrae, P. R. Edgington, P. McCabe, E. Pidcock, G. P. Shields, R. Taylor, M. Towler and J. van De Streek, J. Appl. Crystallogr., 2006, 39, 453–457 CrossRef.
- S. P. Westrip, J. Appl. Crystallogr., 2010, 43, 920–925 CrossRef CAS.
- V. B. Di Marco, A. Tapparo and G. G. Bombi, Ann. Chim., 1999, 89, 397–407 CAS.
- V. B. Di Marco, PhD thesis, University of Padova, 1998.
- A. Rockenbauer, T. Szabó-Plánka, Z. Árkosi and L. Korecz, J. Am. Chem. Soc., 2001, 123(31), 7646–7654 CrossRef CAS PubMed.
- A. Rockenbauer and L. Korecz, Appl. Magn. Reson., 1996, 10(1–3), 29–43 CrossRef CAS.
- N. V. Nagy, T. Szabó-Plánka, A. Rockenbauer, G. Peintler, I. Nagypál and L. Korecz, J. Am. Chem. Soc., 2003, 125(17), 5227–5235 CrossRef CAS PubMed.
- F. Neese, ORCA an ab initio, density functional and semi empirical program package, Version 2.6, University of Bonn, Bonn, Germany, 2008 Search PubMed.
- F. Neese, J. Chem. Phys., 2001, 115, 11080–11096 CrossRef CAS.
- F. Neese, J. Phys. Chem. A, 2001, 105, 4290–4299 CrossRef CAS.
- F. Neese, J. Chem. Phys., 2003, 118, 3939–3948 CrossRef CAS.
- F. Neese, J. Chem. Phys., 2005, 122, 034107 CrossRef PubMed.
- S. Sinnecker, A. Fajendran, A. Klamt, M. Diedenhof and F. Neese, J. Phys. Chem. A, 2006, 110, 2235 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650 CrossRef CAS.
- T. J. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- T. H. Dunning, K. A. Peterson and A. K. Wilson, J. Chem. Phys., 2001, 114, 9244–9253 CrossRef CAS.
- Dell Inc. Dell Statistica (data analysis software system), version 13, http://software.dell.com, 2016 Search PubMed.
- A. R. Katritzky and J. M. Lagowski, The principles of heterocyclic chemistry, Academic Press, New York, 1968 Search PubMed.
- N. Palanisami, G. Prabusankar and R. Murugavel, Inorg. Chem. Commun., 2006, 9, 1002–1006 CrossRef CAS.
- Y. Wang and N. Okabe, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2004, 60, m1434–m1436 CrossRef CAS.
- P. Lemoine, D. Nguyen-Huy, B. Viossat, J. M. Leger and A. Tomas, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1999, 55, 2068–2070 CrossRef.
- P. Lemoine, A. Mazurier, I. Billy, D. Nguyen-Huy and B. Viossat, Z. Kristallogr. – New Cryst. Struct., 2000, 215, 523–525 CAS.
- S.-L. Ma, S. Ren and Y. Yang, J. Inorg. Organomet. Polym. Mater., 2010, 20, 104–109 CrossRef CAS.
- J. Geng, T. Tao, K. H. Gu, G. Wang and W. Huang, Inorg. Chem. Commun., 2011, 14, 1978–1981 CrossRef.
- D.-C. Wen, S.-X. Liu and J. Ribas, Inorg. Chem. Commun., 2007, 10, 661 CrossRef CAS.
- S. Sengupta, A. Goswami, S. Ganguly, S. Bala, M. K. Bhunia and R. Mondal, CrystEngComm, 2011, 13, 6136–6149 RSC.
- D. Weng, Y. Wang, R. B. Yu, R. J. Wang, D. Wang, Q. Cai, H. D. Li and Y. W. Yao, Chem. Lett., 2004, 33(12), 1586–1587 CrossRef CAS.
- É. Sija, A. Dean, T. Jakusch, V. B. Di Marco, A. Venzo and T. Kiss, Monatsh. Chem., 2011, 142, 399–410 CrossRef.
- F. Bacher, O. Dömötör, A. Chugunova, N. V. Nagy, L. Filipović, S. Radulović, É. A. Enyedy and V. B. Arion, Dalton Trans., 2015, 44, 9071–9090 RSC.
- N. V. Nagy, S. Van Doorslaer, T. Szabó-Plánka, S. Van Rompaey, A. Hamza, F. Fülöp, G. K. Tóth and A. Rockenbauer, Inorg. Chem., 2012, 51, 1386–1399 CrossRef CAS PubMed.
- F. Bacher, É. A. Enyedy, N. V. Nagy, A. Rockenbauer, G. M. Bognár, R. Trondl, M. S. Novak, E. Klapproth, T. Kiss and V. B. Arion, Inorg. Chem., 2013, 52, 8895–8908 CrossRef CAS PubMed.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833 CrossRef CAS.
- I. Mayer, Int. J. Quantum Chem., 1984, 26, 151–154 CrossRef CAS.
- I. Mayer, Chem. Phys. Lett., 1983, 97, 270–274 CrossRef CAS.
- I. Mayer, Int. J. Quantum Chem., 1986, 29, 73–84 CrossRef CAS.
- D. C. Ashley and E. Jakubikova, Inorg. Chem., 2018, 57(16), 9907–9917 CrossRef CAS PubMed.
- C. A. Joseph, M. S. Lee, A. V. Iretskii, G. Wu and P. C. Ford, Inorg. Chem., 2006, 45(5), 2075–2082 CrossRef CAS PubMed.
- P. M. Bush, J. P. Whitehead, C. C. Pink, E. C. Gramm, J. L. Eglin, S. P. Watton and L. E. Pence, Inorg. Chem., 2001, 40, 1871–1877 CrossRef CAS PubMed.
- V. C. Pierre, M. Botta, A. Aime and K. N. Raymond, Inorg. Chem., 2006, 45(20), 8355–8364 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Crystal data and structure refinement of crystals 1–5; selected data of bond lengths and angles and figures about packing arrangements and crystal voids, comparison of concentration distribution curves; experimental and calculated EPR spectra; results of DFT calculations and statistical analysis. CCDC 1865730–1865734. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9nj01469a |
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2019 |