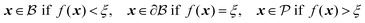Small-angle X-ray scattering of nanoporous materials
Received
24th May 2019
, Accepted 16th August 2019
First published on 16th August 2019
Abstract
Small-angle X-ray Scattering (SAXS) is a non-invasive reciprocal space characterization technique that provides statistically representative microstructural information about a material. This focus article examines SAXS as a tool to probe the microstructure of nanoporous materials. We seek to educate the reader on scattering instrumentation and requisite scattering theory pertinent to nanoporous materials, and describe analytical models used to fit SAXS data, to elucidate the microstructure of these nanoporous materials including their morphological features such as the pore size distribution, pore curvature, and specific surface area. Finally, we fit and compare the aforementioned models to real scattering data of nanoporous gold synthesized in our laboratory. The models yield realistic material parameters for the nanoporous gold morphology, in agreement with electron micrograph images. In addition, we have investigated the scattering patterns and characteristic electron micrographs of nanoporous copper and nanoporous antimony also synthesized in our laboratory. The models discussed in this paper do not yield realistic material parameters for specific nanoporous copper and nanoporous antimony morphologies, however. This could be the subject of follow-up work.
1 Introduction
While the properties of dense macroscopic materials are governed by bulk atoms, many material properties become governed by surface atoms and related phenomena when structural size is on the order of nanometers. In this regime, surface atoms constitute a much larger fraction of the material than bulk atoms. One such high surface-to-volume ratio class of materials corresponds to nanoporous (NP) materials, including NP metals,1–24 NP metal oxides,25–28 metal–organic frameworks (MOFs),26,29–35 zeolites,29,30,36–39 covalent organic frameworks (COFs),40–42 carbonaceous materials such as carbide-derived carbon (CDC),43–47 and porous polymer networks (PPNs),48,49 all characterized by open channels or pores classified according to the IUPAC's ranking in micropores (less than 2 nm), mesopores (between 2–50 nm), and macropores (larger than 50 nm). These NP materials have been widely investigated for various applications including gas storage (e.g. H2 storage and CO2 capture),30,35,44,45,50 biotechnology,51 radiation resistance,52 plasmonics,16,53–57 (photo)catalysis,17,18,35,38,55,58–66 sensing,67,68 actuation,8,68–71 and energy storage and conversion.6,9,11,12,19,21,43,47,60,72–75 In all of these applications, the characteristic size, specific interfacial area, and curvature are critical and necessitate proper quantification. (i) Starting with the characteristic size, usually the average pore size is manually measured from scanning and transmission electron micrographs (SEM and TEM).5,76 However, SEM and TEM data only capture a small fraction of the billions of pores within the often voluminous NP materials. Structure sizes deduced from SEM and TEM micrographs, therefore, are not statistically representative of the whole specimen. In an effort to improve upon this limitation, McCue et al. recently developed an automated computational method to calculate average ligament and pore sizes, specific to NP metals, reducing the need for by-hand measurement.77 While useful, this method still relies on incomplete data from electron micrographs.5,76 (ii) Next, in terms of specific surface area, even though porosimetry techniques such as nitrogen adsorption (BET) are commonly used to determine the specific surface area of NP materials,11,13,14 these techniques usually require a large amount of porous materials to yield reliable values. In several cases, it is not straightforward to produce a large amount of NP materials for porosimetry studies. In an effort to overcome this limitation, Detsi et al. derived an analytical expression for a direct computation of the specific surface area of NP materials.78 Though useful,79–84 this analytical model is only valid in specific situations where the size of ligaments and pores in NP metals are comparable.78 An effective approach to characteristic size and specific surface areas of NP materials is needed, and SAXS can provide this information. (iii) Finally, in terms of curvature, the surface curvature of a structure (which is associated with the surface free energy) provides a driving force for morphological evolution via the Gibbs–Thomson effect.85,86 In order to study the curvature of a nanoscale structure, we currently rely heavily on computer models,85,87 and other intensive techniques, including X-ray tomography (which cannot resolve nanoscale features). In this article, we expand on a SAXS method capable of providing this information.
SAXS is a reciprocal space technique utilized by researchers in various fields, spanning polymer science,88 biology,89 metallurgy,90–92 and astronomy.93 The technique was pioneered by André Guinier, who measured crystallite size in age-hardened Al–Cu alloys using the scattering instrument he built for his dissertation, the ‘Guinier Camera’.90,94,95 Guinier, along with colleague Gérard Fournet, wrote a 1955 book on the topic, Small-Angle Scattering of X-rays. The book serves as an excellent general reference for scattering data interpretation, and the reader is encouraged to consult it for theory beyond the scope of this paper.90 Guinier's book develops scattering intensity functions for a wide variety of particle shapes (sphere, cylinder, etc.), but the NP materials we are interested in do not fit neatly into these categories; therefore, general models are appropriate. The aims of this focus paper are to: (i) provide those who are interested in this field with useful background information on SAXS techniques and its benefits and limitations; (ii) elucidate the theoretical foundations of SAXS, expand in depth for models related to NP metals, in particular NP gold (NP-Au), and offer insight on the morphology and topology of NP materials using simulated structures; (iii) provide a description of other models used to fit scattering data for a broad range of NP materials and demonstrate its applicability for the determination of characteristic size, and specific surface area.
2 Scattering instrumentation
While X-ray diffraction (XRD) measures coherent scattering of atomic planes at wide scattering angles, SAXS can measure much larger feature sizes, on the order of 1–100 nm, in transmission or reflection mode. This reflection mode is commonly referred to as grazing incidence small-angle X-ray scattering (GISAXS), however the present article will focus on measurement in transmission mode (SAXS). If the instrument has a long enough sample-to-detector distance, it is capable of probing micron-sized dimensions in what is named Ultra Small-Angle X-ray Scattering (USAXS). Fig. 1 displays a simplified diagram of a typical SAXS instrument in transmission geometry. In the lab-scale SAXS setup shown in Fig. 1a, polychromatic and unfocused X-rays, whose characteristic wavelength is determined by the elemental nature of the source, are generated at point (b). Various monochromation and beam collimation instruments are used after the beam exits the source, encompassed in point (c) in our diagram. After exiting point (c), the X-rays bombard the sample at point (d), and one of three things can happen: they can be scattered, transmitted, or absorbed by the material. When scattered, the interaction between the material's electrons and the incoming X-ray produces a secondary, so-called scattered, wave.96 Such an X-ray-electron interaction is typically assumed to be elastic, where the incoming wave's energy and momentum are conserved after the scattering event.90
 |
| | Fig. 1 SAXS instrumentation (a) and geometry (b–e). X-rays are generated at point (b) and are monochromated and collimated at point (c). The beam bombards the material at point (d), where the X-rays do one of three things: scatter with the electrons in the material, transmit through the material, or absorb into the material. The transmitted beam and secondary scattered waves travel down an evacuated tube of length R, and are detected at point (e). In addition, the geometry of the scattering theory described in the theory section is displayed above (d). Both the SEM of the sample (d) and the detector pattern (e) are from NP-Au. | |
Both the scattered and transmitted X-rays travel the sample-to-detector distance R as illustrated in Fig. 1, and finally interact with the detector at point (e). We display the commonly used 2D area detector, however this can be replaced by a 1D line or 0D point detector. By increasing R, the range of accessible scattering angles becomes smaller, resulting in larger real-space dimensions due to the inverse proportionality between real and reciprocal space. Thus, transmission SAXS is limited by the instrumental geometry: to probe length scales pertinent to NP materials, which can have characteristic dimensions of hundreds of nanometers, a large instrument is required. For example, to probe real-space dimensions of ∼350 nm with a Cu source (λ = 1.5406 Å), s needs to be roughly 5 m. Due to this length requirement, performing SAXS with an elemental X-ray source in a lab setting is typically carried out under vacuum to minimize incoherent background scattering by air. Synchrotron radiation mitigates the incoherent scattering issue by making use of high energy and high flux X-rays, and thus SAXS can be performed in air. The reader is referred to sources provided in references90,97 for further detailed instrumental information.
3 Scattering theory
3.1 Scattering by a discrete charge distribution
When X-rays impinge on an atom within a particle, the atom's electrons are forced to vibrate with the radiation's electric field and become emission sources for electromagnetic scattered waves.98 In principle, the X-ray's magnetic field also interacts with the spin and orbital magnetic moments of the electrons, however the quantity of such scattered waves is negligible in comparison to those originating from the electric field.98 For a single atom, this outgoing radiation is emitted in all directions (in the case of an unpolarized X-ray source, spherically).98 Its amplitude depends on the atom's electronic structure (i.e. the number of electrons it contains and their spatial arrangement) and the source X-ray's amplitude. The electric field of a scattered wave at a distance R from emitted atomic position Pj (Fig. 1) can be described by eqn (1):90| | 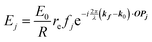 | (1) |
Here, E0 is the electric field amplitude of the incoming wave, re is the classical electron radius, fj is the atomic form factor (derived in the Appendix), kf is the unit wave vector after scattering, k0 is the unit wave vector before scattering, λ is the X-ray's wavelength, and OPj is a vector from an arbitrary origin O and point Pj. Conservation of energy requires the amplitude to be inversely proportional to the distance from the source, R, as the electric field spreads equally around spherical shells of area 4πR2 with increasing distance from the emission source. The inclusion of the classical electron radius, re = e2/4πε0mec2, where e is the elementary charge, ε0 is the permittivity of free space, and me and c are the mass of the electron and speed of light, respectively, ensures proper electric field units. Its inclusion here can be derived from Maxwell's equations.96,98 The scattering vector q is defined by the difference between the incoming and outgoing wavevectors as 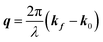 and has magnitude
and has magnitude 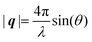 . Further in this article, the magnitude |q| will simply be referred to as q.
. Further in this article, the magnitude |q| will simply be referred to as q.
Noting the principle of superposition of waves, we can determine the electric field of all irradiated atoms at a distance R (sample-to-detector distance in Fig. 1) from the source by summing over all atoms within the irradiated volume (eqn (2)). The intensity of the field at the detector positioned at distance R is deduced from its amplitude multiplied by the complex conjugate, |E|2 (eqn (3)):90
| | 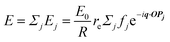 | (2) |
| | | I(q) = I0Σk,jfk*fjeiq·(OPk−OPj) | (3) |
In
eqn (3),
I0 =
E0*
E0re2R−2 absorbs the incident intensity |
E0|
2, the classical electron radius, and the sample-to-detector distance. Note that this definition holds true for the rest of this article. When the waves in
eqn (2) are in phase, (
i.e. when there is a repetitive structural size in the irradiated material like atomic planes or, in NP materials, the characteristic pore–pore spacing) they give rise to peaks in intensity at specific values of
q (
eqn (3)). In this way, the intensity at the detector as a function of the scattering vector
q is a Fourier series that relies on the positions of atoms in the sample and their atomic form factors. While these general expressions for a discrete charge distribution are useful in understanding X-ray-electron interactions, we can consider the continuous case for practical matters. In the next section, we will derive a general scattering equation for a continuous charge distribution and apply it later to NP materials.
3.2 Scattering by continuous charge distribution and notion of correlation function
In this section, we discuss scattering from the perspective of a continuous electron density function, ρ(x), which we can mathematically construct considering the geometry of the material structure. This method rose to prominence from the work of Debye, Anderson, Brumberger, and Bueche, and will be further referred to as the Debye model.99,100 Consider a solid with density of electrons ρ(x) in a given volume V:where ρ0 is the average electron density and η(x) represents the fluctuations around ρ0. In the discrete description above, eqn (3) includes values for the positions of individual atoms and their atomic form factor fj. In the continuous description, we replace the form factors fj with ρ(x) (eqn (4)), and the scattered intensity may be written as:| | 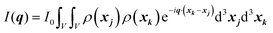 | (5) |
where ρ(xj) and ρ(xk) are the electron densities at points xj and xk, respectively. The intensity can be rewritten as a function of the electron density fluctuations η(x) in the material (see Appendix):| | 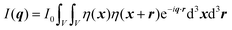 | (6) |
In eqn (6), we have substituted r = xk − xj, the distance between scatterers, and removed the subscript on xj. Debye defines the correlation function γ(r) as:99| | 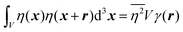 | (7) |
The mean square fluctuation, 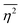 , is defined in the Appendix. In an isotropic system, γ(r) depends only on the magnitude |r| = r, and corresponds to the probability of two endpoints of a rod with length r being within the same type of matter. For example, it is the probability of being in the solid phase of a NP material after moving a radius r away from any random point in the NP material's solid phase.101 Thus, the correlation function will tend to 1 (having been normalized by
, is defined in the Appendix. In an isotropic system, γ(r) depends only on the magnitude |r| = r, and corresponds to the probability of two endpoints of a rod with length r being within the same type of matter. For example, it is the probability of being in the solid phase of a NP material after moving a radius r away from any random point in the NP material's solid phase.101 Thus, the correlation function will tend to 1 (having been normalized by 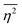 and V) for r → 0 (short distances correlate very well), and 0 for r → ∞ (long distances do not correlate). After some manipulation and assuming isotropy (using the average value of e−iq·r = sin(qr)/(qr), replacing the vectors q and r with their magnitudes), the intensity integral can be written as:100
and V) for r → 0 (short distances correlate very well), and 0 for r → ∞ (long distances do not correlate). After some manipulation and assuming isotropy (using the average value of e−iq·r = sin(qr)/(qr), replacing the vectors q and r with their magnitudes), the intensity integral can be written as:100| | 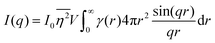 | (8) |
Several system parameters may be extracted from the correlation function, whose functional form is developed from arguments based on some knowledge of the system. Debye et al. used a ‘square wave’ (for details, see ref. 100) model of electron density to construct the correlation function (γD(r), eqn (9)), and with it derived the surface-area-to-volume ratio (S/V, eqn (10)) in an inhomogeneous and porous medium with void fraction ϕ:100| | 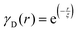 | (9) |
| | 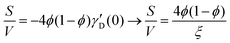 | (10) |
In eqn (9) and (10), ξ is the mean width of the Debye correlation function and is called the correlation length, a characteristic length scale which describes how fast electron density fluctuation correlations decay spatially. γD′(0) represents the derivative of the correlation function at r = 0. Thus, with knowledge of the functional form of the correlation function and the void fraction ϕ,100 the surface-area-to-volume ratio can be obtained. Note that the surface-area-to-volume ratio is a function of the derivative of γD(r) when r → 0, as this region describes correlations at smaller length scales (interfaces).
The specific surface area may also be calculated from the region over which the intensity decays as q−4 (note, this power law is not always −4, as will be discussed in Section 3.4) without any prior knowledge of γ(r) by analyzing scattering data in absolute units, or by normalizing with the Porod invariant (see Appendix). The latter method has been described in numerous articles including Dotzler et al. who used it to calculate the specific surface area of nanoporous gold (NP-Au) during dealloying in nitric acid.90,101,102 The result was independently discovered by Guinier and Debye's contemporary, Porod, and is thus named the Porod regime.90,100 For clarity, this method has been detailed in the Appendix.
After performing the Fourier transform of γD(r), the resultant intensity function is:
| | 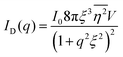 | (11) |
This function does not contain a Bragg-like peak (
Fig. 3a), and thus does not map onto the structure of NP materials which have some characteristic length scale not captured by
ID.
3.3 Models for nanoporous materials with a strong scattering peak
In the late 1980s and early 1990s, there were many different approaches to determine the origin of a peak in the scattering data of bicontinuous microemulsions (oil and water mixtures).103–113 Depending on the temperature and composition of the mixture, the oil and water arrange into different microstructural phases. One such phase is bicontinuous, implying that if one were to start moving within the water phase, they could traverse the entire water network without crossing into the oil phase. While they look disordered and random, bicontinuous materials have a characteristic and quasi-repetitive length scale which gives rise to a Bragg-like scattering peak in the small-angle scattering regime.103–113 Many NP material classes exhibit such a bicontinuous structure,85,114–118 opening up an opportunity to study these systems with X-ray scattering. One such class is NP metals, typically synthesized by an (electro)chemical etching process known as dealloying, in which the sacrificial component of an alloy is selectively removed to form a bicontinuous network of struts (ligaments) and channels (pores), both with characteristic diameter in the nanoscale range.87,119–127 Advances in tomography techniques have enabled 3D reconstruction of several NP metals; these findings indicate that the ligament and pore structures are inverse of one another and are morphologically and topologically equivalent, and thus exhibit the so-called bicontinuous structure.128–130 Computation of NP metal structures with Kinetic Monte Carlo, molecular dynamics, and phase field methods yield similar results.85,123,125–127,131–135 These bicontinuous networks (both NP metals and microemulsions), have been modeled as spinodally decomposed structures.85,105,113,119,136–138 In this section we focus on this type of microstructure and how SAXS can aid in determining this microstructure.
3.3.1 Cahn spinodal decomposition.
The spinodal decomposition model stems from the work of J. W. Cahn and J. E. Hilliard, who developed a model for the free energy function for a non-uniform system in the late 1950s.139 In several subsequent articles, Cahn describes spinodal decomposition of isotropic systems in terms of local concentration, c(q,r;t), and its gradients (see Appendix).120,140–142 In essence, the spinodal concentration c(q,r;t) is found by implementing the Cahn–Hilliard free energy expansion into Fick's diffusion equations and solving them in terms of Fourier components, leading to a superposition of waves:| | | c − c0 = ΣqeR(q)t(A(q)cos(q·r) + B(q)sin(q·r)) | (12) |
Where R(q) is the amplification factor (defined in Cahn),120 and q is the wavevector of the Fourier components with magnitude q. By assuming the only important Fourier component is q0, that which maximizes R(q), Σq can be replaced by Σq0 in eqn (12). In this case, c becomes a superposition of waves that all have the same magnitude wavevector, but with random orientation, amplitude, and phase.120 Cahn computed several binarized 2D level cuts of this so-called stochastic standing wave in one of the first computer simulations of material structure,120 predicting the bicontinuous two-phase structure of characteristic size denoted by the wavelength of the maximizing wavevector q0, i.e.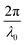 .
.
3.3.2 Leveled-wave model.
Recently, Soyarslan et al. provided evidence for the applicability of Cahn's model to NP metals by mapping it to their mechanical behavior and specific surface area.122 We use their notation for clarity. Cahn's stochastic standing wave equation (eqn (12)) is restructured into cosine waves with random orientation and phase:| | 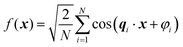 | (13) |
where N is the total number of waves used, qi are the random directions distributed on a sphere with radius q0 (i.e. the wavevectors have equivalent magnitude), and φi are random phases. Once N waves are generated (104 waves are used, as mentioned in Soyarslan et al., to ensure isotropy in the simulated structure),122 points in real space are assigned as part of the bulk or void by thresholding f(x) with a value ξ (not to be confused with the correlation length):
where 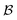 is the bulk (the metal),
is the bulk (the metal), 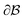 is the interface, and
is the interface, and 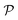 is the pore.122 The threshold value is a function of the bulk fraction
is the pore.122 The threshold value is a function of the bulk fraction 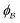 ,
, 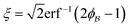 . This thresholding process produces a leveled-wave, which can be computed to provide structural visualization for a scattering dataset. As a demonstration of this concept for one wavelength, we used Mathematica143 to compute one such structure, which is displayed in Fig. 2. Here we used fitted values (discussed later in Section 4) for ligament–ligament distance to determine q0.
. This thresholding process produces a leveled-wave, which can be computed to provide structural visualization for a scattering dataset. As a demonstration of this concept for one wavelength, we used Mathematica143 to compute one such structure, which is displayed in Fig. 2. Here we used fitted values (discussed later in Section 4) for ligament–ligament distance to determine q0.
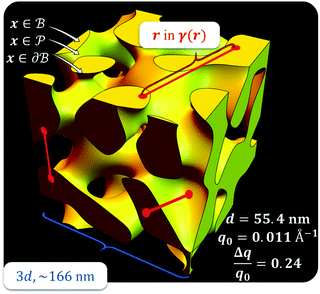 |
| | Fig. 2 Example of a 3D structure generated by the leveled-waved model found in Berk111,112 and Soyarslan et al.122 using one wavelength, q0 determined by fitting the dataset in Section 4. | |
3.3.3 Berk model.
In two mathematically rigorous articles on the subject, N. F. Berk used the leveled-wave scheme discussed above to investigate the scattering properties of a three-phase system (such as oil/interface/water), which can be reduced to a two-phase system (such as ligament/pore in NP metals).111,112 The correlation function for f(x) is the first spherical Bessel function:122| | 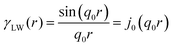 | (14) |
The Fourier transform of eqn (14) predicts a very sharp peak at q0, as the function used only one magnitude of q (i.e. q0), unlike the SAXS data shown in Fig. 3. Berk added Gaussian dispersion around q0 and solved for the scattering intensity analytically:111,112| | 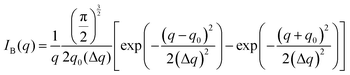 | (15) |
for which the probability density for the wavevector q is a Gaussian distribution centered around q0 with variance (Δq)2.112 This function has been reduced from its original form (eqn (11) in Berk), where here we are assuming equal pore and bulk volume percentages 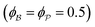 . Since this intensity function is derived based on a correlation function expansion that does not converge quickly as r → 0, the asymptotic curve at higher values of q (in the Porod regime) cannot be well matched with any finite number of expansion terms.111Eqn (15) has been plotted in Fig. 3c, which shows how this function changes when the both distribution (Δq) and the characteristic spacing (q0) are varied. We can clearly see that this intensity distribution does not match the high-q tail of the NP-Au scattering spectrum in Fig. 5.
. Since this intensity function is derived based on a correlation function expansion that does not converge quickly as r → 0, the asymptotic curve at higher values of q (in the Porod regime) cannot be well matched with any finite number of expansion terms.111Eqn (15) has been plotted in Fig. 3c, which shows how this function changes when the both distribution (Δq) and the characteristic spacing (q0) are varied. We can clearly see that this intensity distribution does not match the high-q tail of the NP-Au scattering spectrum in Fig. 5.
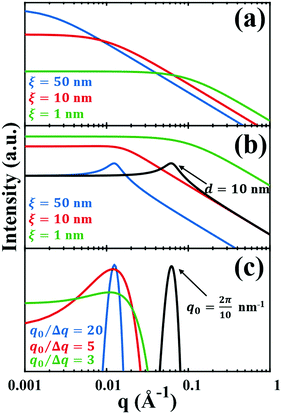 |
| | Fig. 3 Comparison of the (a) Debye, (b) Teubner–Strey, and (c) Berk models and variation in their key parameters. In the Debye model, altering the correlation length shifts the curve, but it maintains its shape. In the TS (b) and Berk (c) models, the curves center around a value of q corresponding to the characteristic size (i.e.d or q0). Here, the colored lines represent a constant characteristic size and we vary the correlation length (in b), or the ratio q0/Δq (in c), to alter the distribution around that q-value. In the black curves, we have changed the characteristic size while maintaining the distribution in the blue curve. | |
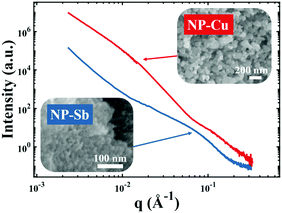 |
| | Fig. 4 Nanoporous materials which do not give rise to a strong, Bragg-like scattering peak. Scattering patterns of NP-Cu (red curve) and NP-Sb (blue curve) and corresponding scanning electron micrographs. | |
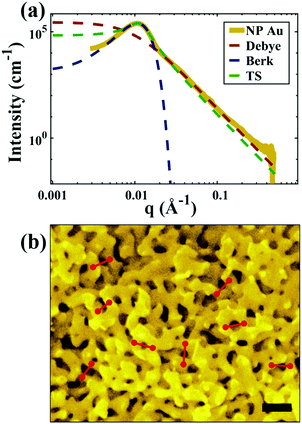 |
| | Fig. 5 (a) SEM and (b) SAXS data from a ∼5 μm-thick film of NP-Au dealloyed by free corrosion in concentrated HNO3 for 30 minutes (scale bar is 100 nm). The peak in the scattering data comes from the characteristic ligament–ligament spacing (red lines on the SEM), and we model the data with the I(q) functions discussed in Section 3.3. | |
3.3.4 Teubner–Strey (TS) model.
In another attempt to determine the origin of the scattering peak in microemulsions, Teubner and Strey developed a free energy expansion in terms of an order parameter, ψ, and its gradients, ∇ψ:113
| f(ψ,∇ψ,∇2ψ,…) = a0 + a1ψ + a2ψ2 + a3ψ3 +… + c1(∇ψ)2 + c2(∇2ψ)2 +… |
where f is the local free energy per molecule. The order parameter ψ in the case of microemulsions is the water-oil ratio, and all coefficients except for a2 > 0, c1 < 0, and c2 > 0 were taken to be zero. Choosing these coefficient values was a system-based decision: a0 and a1 are zero by symmetry, terms higher than a2 were ignored as the fluctuations are small, c1 was chosen to be negative as there is negative microscopic surface tension in microemulsions and considering this, c2 must be positive to provide phase stability.113 This methodology is known as Landau–Ginzberg phenomenological theory, and we refer the reader to Chapter 3 of Kardar's Statistical Physics of Fields, which connects it to scattering.144 Upon Fourier transformation of the fluctuations of ψ, one can extract a correlation function and a scattering intensity relationship with two length scales, d and ξ:| | 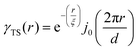 | (16) |
| | 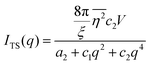 | (17) |
where fit parameters a2 and c1,2 are functions of d and ξ. Here, d is a characteristic domain size (periodicity) which captures local order and the peak in the intensity distribution; ξ is the correlation length which, as mentioned previously, describes how fast electron density fluctuation correlations decay spatially. We have plotted eqn (17) in Fig. 3b to demonstrate how the intensity changes with parameters d (represented by the black curve) and ξ (represented by the colored curve). As shown in Fig. 3, The Teubner–Strey correlation function combines those of Debye, e(−r/ξ), and Berk, j0(q0r), so that ITS captures both the peak and a characteristic q−4 Porod regime. This model has been used extensively in the microemulsion literature due to its satisfactory evaluation of characteristic size and ease of model fitting.103,106,145,146 However, it misses an important intermediate regime after the peak and before the Porod regime, which is present in some bicontinuous microemulsions and is a consequence of another length scale in the scattered volume. The following model adds a third length scale, δ, to capture this intermediate regime, which appears in the data as a shoulder and corresponds to interfacial roughness, or the correlations in the wrinkles at the surface.
3.3.5 Choi and Chen modified leveled-wave model.
The Debye, Berk, and Teubner–Strey models do not adequately describe the entire scattering intensity curve of NP-Au, as will be discussed further in Section 4. To deal with this discrepancy, Choi and Chen introduced a third length scale that modifies the Berk model – an interfacial length δ.145 Their model replaces the single wavevector magnitude, q0, for qi in eqn (13), with a distribution of magnitudes, f(q), called a spectral density function. This distribution can take on any form as long as it is normalizable, i.e.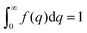 , however the choice should have some relevance to the scattering data.111 Choi and Chen have used an inverse 8th-order polynomial with three length scales (a, b, and c) for f(q):145
, however the choice should have some relevance to the scattering data.111 Choi and Chen have used an inverse 8th-order polynomial with three length scales (a, b, and c) for f(q):145| | 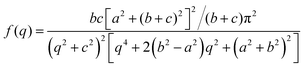 | (18) |
where 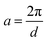 ,
, 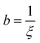 , and
, and 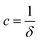 . It was shown by Teubner that the Gaussian curvature 〈K〉 and the square mean curvature 〈H2〉 are functions of the 2nd and 4th moments of f(q), 〈q2〉 and 〈q4〉, respectively.104 This high degree polynomial was chosen in order to capture the 4th moment, whereas in the other cases (Debye, Berk, and TS models), only odd moments exist, or the 4th moment diverges.145 Curvature analysis in this model is therefore more robust than in the aforementioned models. One can obtain these parameters by fitting a form of f(q) to an experimental correlation function γE(r) using the steps outlined in the Appendix.
. It was shown by Teubner that the Gaussian curvature 〈K〉 and the square mean curvature 〈H2〉 are functions of the 2nd and 4th moments of f(q), 〈q2〉 and 〈q4〉, respectively.104 This high degree polynomial was chosen in order to capture the 4th moment, whereas in the other cases (Debye, Berk, and TS models), only odd moments exist, or the 4th moment diverges.145 Curvature analysis in this model is therefore more robust than in the aforementioned models. One can obtain these parameters by fitting a form of f(q) to an experimental correlation function γE(r) using the steps outlined in the Appendix.
We will study the pattern of NP-Au in more details in Section 4, during which the Choi and Chen model will be used, and we will provide an example of interfacial shape distribution (ISD) analysis to share its usefulness as a tool for quantitative analysis of ISD evolution and evaluation of self-similarity in coarsening. For the remainder of Section 3 (namely Section 3.4 below), we will discuss scattering from porous materials that do not give rise to a Bragg-like peak.
3.4 Models for nanoporous materials without a strong scattering peak
While NP materials with a well-defined and quasi-repetitive characteristic length over a long range give rise to a strong, Bragg-like scattering peak as mentioned in the previous sections, other NP materials do not. Instead of a peak, they exhibit distinct features in their scattering spectra. In particular, ‘shoulders,’ or plateaus, in the data indicate an important length scale that can be characterized by combining both the high-q Porod-like power-law decay discussed in Section 3.2 and low-q analysis put forward by Guinier.90 Guinier approximated the scattering at very low angles to decay exponentially in what is sometimes referred to as Guinier's law:90| | 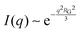 | (19) |
introducing the concept of the radius of gyration (RG) in scattering. In the context of scattering, the radius of gyration of an object (of arbitrary shape) is the root-mean-squared distance from its electronic center of mass. This quantity can be obtained from the slope of a linear fit of ln(I(q)) vs. q2 in the so-called Guinier regime (RG × q < 1.3, for spherical objects90). The relationship between the radius of gyration and some real physical length depends on the shape of the object in question. For a spherical particle, for example, 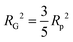 , where Rp is the radius of the particle.96 Feigin and Svergun have tabulated several of these relationships for simple shapes,147 and this relatively simple analysis is performed frequently in X-ray and neutron scattering data.45,148–154 In a seminal paper on carbide-derived carbon, Gogotsi et al. fit scattering data to show that there is a very narrow distribution of pores which can be controlled well by synthesis temperature.45 They used an analysis put forward by Kyutt et al. which determines pore size by a series of RG fits of the SAXS data.155–157
, where Rp is the radius of the particle.96 Feigin and Svergun have tabulated several of these relationships for simple shapes,147 and this relatively simple analysis is performed frequently in X-ray and neutron scattering data.45,148–154 In a seminal paper on carbide-derived carbon, Gogotsi et al. fit scattering data to show that there is a very narrow distribution of pores which can be controlled well by synthesis temperature.45 They used an analysis put forward by Kyutt et al. which determines pore size by a series of RG fits of the SAXS data.155–157
R
G was derived for particles of various shapes which are separated from each other in some solution,90 however many NP materials consist of grains comprised of nanoscopic subunits, often with a distribution of sizes, which are not widely separated. Such a material will scatter across those multiple length scales, producing overlapping spectra which can be difficult to interpret. For example, one may find a Guinier shoulder between two power-law decay regimes. Fitting this type of curve has been the subject of numerous models, as one would be hard-pressed to fit with any of those previously mentioned. Beaucage addressed the issue in a unified exponential/power-law model which, by way of local fitting in important regions (i.e. around the Guinier shoulder), one may determine physical parameters on these different length scales.151 Hammouda developed on the unified Beaucage model by adding continuity equations on some of the fitted parameters to eliminate discontinuities in the fits.150 Spalla et al. developed a model for two distinct power-law regimes which offers a way to extract physical parameters (specific surface area, pore radius, porosity) if the exact chemical composition of the sample is known. Using the Hammouda and Spalla models, Panduro et al.158 have studied the SAXS patterns of CeO3 particles of average radius 2.3 μm, which contain two distributions of pores (micro- and nanoscale). Using USAXS, they resolve the different pore sizes as separate entities with their own physical parameters (e.g. average size).
There are also cases where the Porod power-law decay deviates from q−4 as discussed in Section 3.2. This deviation of α in I(q) ∼ q−α is controlled by the scatterer's fractal dimension, a notable concept in the scattering literature96,154,158–163 which is beyond the scope of this focus article. Martin and Hurd discuss the subject at length in an article on the subject.164 Briefly, the high-q decay rate, α, can be thought of as describing a particle's surface by its smoothness. For example, if α = 4, the surface is smooth, and when α = 3, the surface is rough.150 We also note that if α < 3, the scatterer is a mass fractal, and if 3 < α < 4, it is a surface fractal.150,164 Both the unified Beaucage model and Hammouda's extension can capture the deviation, and was part of the analysis in Panduro et al.158
Fig. 4 shows two different NP metal scatterers synthesized in our laboratory, namely nanoporous antimony (NP-Sb) and nanoporous copper (NP-Cu), which do not give rise to strong, Bragg-like scattering. The NP-Sb and NP-Cu were made by selective removal of sacrificial Mn from Mn-rich Sb–Mn and Cu–Mn alloys, respectively (details of the synthesis are beyond the scope of this article). We have attempted to use the various models mentioned in this section to fit these data, but by comparing to the SEM micrographs shown in the insets, we note that the models yield unrealistic parameters for characteristic size. Development of new models to fit these data are beyond the scope of this focus article, but will be the subject of a follow-up work.
4 Case study for NP-Au
The most common and practical way to tune the structural size of a NP metal is by thermal treatment, which has been the subject of numerous studies using various techniques, including X-ray tomography,129,165 Laue diffraction,129 electron microscopy,76,166–170 positron annihilation spectroscopy,168 and thermal conductivity measurements.171 Kinetic Monte Carlo (KMC) simulations indicate that diffusion-controlled Rayleigh instabilities cause coarsening, where a reduction in topological genus drives growth of the framework.129,132 An X-ray tomography study by Chen-Wiegart et al. indicated that the scaled surface curvature and surface orientation evolves during coarsening, indicating it is non-self-similar. The self-similarity classification requires that the topology and morphology do not evolve temporally when scaled under a time-dependent quantity like surface area.129 More recent work by Lilleodden and co-workers have revealed that the coarsening process is nearly self-similar;172,173 however, the full picture of the coarsening process remains open for debate.174
In this section, we fit the models discussed in Section 3.3 to real scattering data of a ∼5 μm-thick film of NP-Au made by free corrosion of a Au35Ag65 leaf (custom order, Norris Blattgoldfabrik) in 15 M HNO3 for 30 minutes (gold curve in Fig. 5). These scattering data were acquired at the University of Pennsylvania's Dual Source and Environmental X-ray Scattering (DEXS) facility. The DEXS facility is home to a scattering instrument, equipped to probe length scales from 1 Å to 570 nm by utilizing variable sample-to-detector distances (up to 6.4 m), and both copper and molybdenum X-ray sources. The data in Fig. 5 combines two collections at different sample-to-detector distances to encompass a larger q range, and intensity was calibrated to absolute units (cm−1) with a glassy carbon standard.175
For all models shown in Fig. 5a, we have chosen equivalent bulk and pore fractions (ϕ = ϕ = 0.5), the isometric case, to compare with the Choi and Chen model. The values for volumetric and mass specific surface, SV and Sm, respectively, will decrease if the bulk fraction is changed, but not by orders of magnitude. Fit parameters and specific surface area calculations have been summarized in Table 1. The ligament-ligament spacing, d, fitted by the Berk and Teubner–Strey models are nearly the same, ∼55 nm. This characteristic distance in real space was evaluated by taking manual measurements of the SEM image in Fig. 5b, where 30 measurements of ‘obvious’ adjacent ligament centers (red lines in Fig. 5b are examples) yield a spacing of ∼62 nm. To convert between SV and Sm, the effective density of NP-Au was chosen to be 0.65 × 19.3 g cm−3, which takes into account its porosity when the 65 at% sacrificial Ag content has been removed during free corrosion.
Table 1 Fitted parameters for all four models used to evaluate the SAXS data
| Model |
Fitted parameters |
Predicted values |
| Δq/q0 |
d (nm) |
S
v (m2 cm−3) |
S
m (m2 g−1) |
| Berk |
0.24 |
55.3 |
66.1 |
3.4 |
| Model |
Fitted parameters |
Predicted values |
|
ξ (nm) |
d (nm) |
S
v (m2 cm−3) |
S
m (m2 g−1) |
| Debye |
10.3 |
— |
149.3 |
7.7 |
| Teubner–Strey |
31.9 |
55.5 |
48.3 |
2.5 |
Of the models fitted in Fig. 5a, the Teubner–Strey model is clearly the most descriptive of the real scattering data. However, it fails to capture the intermediate shoulder in the curve after the peak and through its transition into the high-q Porod scattering regime (I(q) ∼ q−4). This shoulder corresponds to another characteristic length scale in the system – we model this third length scale with the Choi and Chen model parameter δ (surface roughness parameter), generate structures that look qualitatively similar to NP-Au, and evaluate the mean and Gaussian curvatures of these structures (Fig. 6). The fitted δ value was on the order of 3 nm. One can immediately distinguish the structure in Fig. 6a (Choi and Chen spectral distribution, eqn (18)) from the structure in Fig. 2, which uses a single magnitude of q, by a few distinct features. Namely, there are ‘capped’ regions, and ‘necked’ regions in this simulated structure. Fig. 6b and c show that the curvature of much of the structure is nearly zero, however, the necked and capped regions have non-zero curvature. These regions are integral to the coarsening behavior, as they represent the parts of the structure involved in the Rayleigh instabilities that reduce the material's topological genus.127,165,172,174
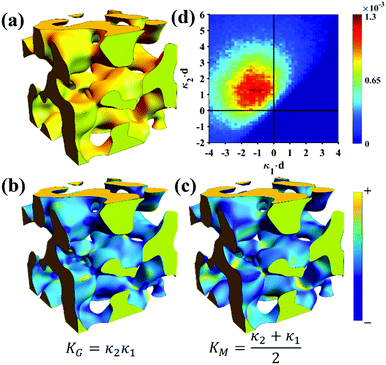 |
| | Fig. 6 Structure generation and ISD analysis using the Choi and Chen model fits to real experimental data from Fig. 3. (a) 3D structure generated from fitted Choi and Chen model, (b and c) Gaussian and mean curvature maps of (a), using the convention that convex regions have negative mean curvature. (d) Interfacial shape distribution of the generated structure. | |
5 Conclusion
In this focus article, we have introduced SAXS as an important tool to characterize the structure of NP materials. To bring unfamiliar and interested investigators up to speed, we discuss the geometry of a scattering experiment and develop SAXS theory from fundamentals. We explore a variety of models to fit our data, starting from the Debye model, and adding multiple length scales in the Berk, Teubner–Strey, and Choi & Chen models to capture the significant features of the scattering intensity of NP materials with a strong scattering peak. We successfully apply these models to the scattering pattern of NP-Au in a case study, and put SAXS forward as a method to investigate the morphological characteristics of NP materials by linking structural similarities to bicontinuous microemulsions. In addition, we have discussed the scattering patterns of nanoporous materials without strong scattering peak. It is found that the models investigated in this work do not yield realistic material parameters for specific nanoporous copper and nanoporous antimony morphologies, however. A follow-up work will investigate appropriate models for these morphologies.
Conflicts of interest
There are no conflicts to declare.
A. Appendix
A.1 Atomic form factor fj
In Section 3, we described the atomic form factor as the scattering ability of the jth atom. The atomic form factor takes into consideration the probability distribution of electrons in an atom, which can be described by the square of its wavefunction, |ψ(r)|2 = ρa(r). Its mathematical form is similar to that of the continuous electron distribution discussed in Section 3.2 (i.e., a Fourier transform):| | 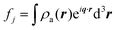 | (20) |
Thus, it is a function of the scattered angle, the radiation's wavelength, and the distribution of electrons in the atom. All atomic form factors decrease from the atomic number Z at q = 0 to 0 at high q.176,177 NIST178 and the International Tables for Crystallography179 have useful tables and calculators for the form factors.
A.2 Detailed derivation of scattering from a continuous charge distribution
The following derivation stems from two seminal papers of Debye and co-workers,99,100 and can also be found in Chapter 2 of Small-Angle Scattering of X-rays.90 As defined in Section 3.2,Which can be rewritten as follows:
The average value of the fluctuation is zero, meaning that:
| | 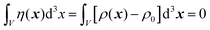 | (23) |
In Section 3.2 we have left out the steps between eqn (5) and (6), so we have included them here for convenience. Substituting eqn (4) into equation eqn (5) yields:
| | 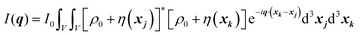 | (24) |
We can break up this integral into four parts, including the principal and cross terms. We can ignore three of the terms,90 and we are left with only one term will remain as given in eqn (25):
| | 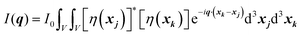 | (25) |
We substitute r = xk − xj, and consider the x integral:
| | 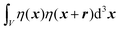 | (26) |
If |r| = 0, this integral goes to:
| | 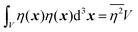 | (27) |
defining the mean squared fluctuations of electronic density,
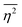
where
V represents the irradiated volume. This factor is used to normalize the correlation function
γ(
r) to 1.
A.3 Inverting intensity, Porod invariant, and specific surface
While we cannot obtain the spatial distribution of electrons from scattering data directly, we can extract the correlation function using the inverse Fourier transform:| | 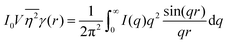 | (28) |
As stated in Section 3.2, the correlation function tends to 1 as r → 0, and 0 as r → ∞. We can use this fact to obtain the Porod invariant, Q*, where we set r = 0 in the Fourier inversion equation:| | 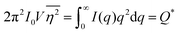 | (29) |
The Porod invariant is named as such because it varies only with the mean squared fluctuations of electron density within the scattered volume, and not their spatial arrangement (i.e. their structure).101 In a two-phase system with electron densities ρ1 and ρ2, we can use the fact that the mean squared fluctuations 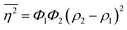 to associate Q* with physical properties of the scattered volume:101
to associate Q* with physical properties of the scattered volume:101
| | | Q* = Φ1Φ2(ρ2 − ρ1)2VI02π2 | (30) |
In the case of NP-Au scattering in vacuum, the contrast Δρ = ρ2 − ρ1 is simply equivalent to the electron density of Au (ρ1 = 0), Φ1 is the void fraction, and Φ2 = (1 − Φ1). When absolute intensity calibration is not possible, Q* can be used to normalize the data in order to extract specific surface area:96,102
| | 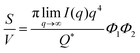 | (31) |
In this way, we can determine the specific surface area without using absolute calibration by plotting the normalized 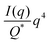 vs. q and finding the constant value it tends to. It is important to note, however, that in a scattering experiment we do not have data for q → ∞, thus absolute intensity will give a more accurate representation of the specific surface. If the intensity data is in absolute units, the invariant calculation is not needed, and the specific surface is:
vs. q and finding the constant value it tends to. It is important to note, however, that in a scattering experiment we do not have data for q → ∞, thus absolute intensity will give a more accurate representation of the specific surface. If the intensity data is in absolute units, the invariant calculation is not needed, and the specific surface is:
| | 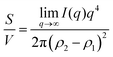 | (32) |
A.4 Fitting Choi & Chen model
An experimental correlation function γE(r) (found by extrapolating and Fourier transforming the I(q), we used SASview to accomplish this)180 can be fitted to the spectral density function f(q) in eqn (18) by the following analytical relationship for an isometric (ϕB = ϕP = 0.5) two-phase system as shown in Berk, and Choi et al.:111,145| | 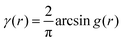 | (33) |
where 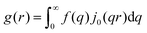 . Choi and Chen explicitly solve for g(r) in their first article on the subject.146
. Choi and Chen explicitly solve for g(r) in their first article on the subject.146
Acknowledgements
The authors are thankful to Penn Engineering for the financial support through the PI startup and to the Vagelos Institute for Energy Science and Technology (VIEST) for the support through the 2019 VIEST Graduate Fellowship support. The authors acknowledge use of the Dual Source and Environmental X-ray Scattering facility operated by the Laboratory for Research on the Structure of Matter at the University of Pennsylvania (NSF MRSEC 17-20530). The equipment purchase was made possible by an NSF MRI grant (17-25969), an ARO DURIP grant (W911NF-17-1-0282), and the University of Pennsylvania. This work was carried out in part at the Singh Center for Nanotechnology, part of the National Nanotechnology Coordinated Infrastructure Program, which is supported by the NSF grant NNCI-1542153. This work benefited from the use of the SasView application, originally developed under NSF award DMR-0520547. SasView contains code developed with funding from the European Union's Horizon 2020 research and innovation program under the SINE2020 project, grant agreement no. 654000. The authors also thank A. Pröschel and K. Mysore for their help in simulating structures of various sizes, and Z. Wang and J. Fu for the SEM images of NP-Sb and NP-Cu.
References
- J. Fu, E. Detsi and J. T. M. De Hosson, Surf. Coat. Technol., 2018, 347, 320–336 CrossRef CAS.
- Z. Deng and E. Detsi, Nanoscale, 2017, 9, 11858–11863 RSC.
- E. Detsi, P. Onck and J. T. M. De Hosson, ACS Nano, 2013, 7, 4299–4306 CrossRef CAS.
- E. Detsi, M. S. Sellès, P. R. Onck and J. T. M. De Hosson, Scr. Mater., 2013, 69, 195–198 CrossRef CAS.
- K. Ma, J. S. Corsi, J. Fu and E. Detsi, ACS Appl. Nano Mater., 2018, 1, 541–546 CrossRef CAS.
- J. B. Cook, T. C. Lin, E. Detsi, J. N. Weker and S. H. Tolbert, Nano Lett., 2017, 17, 870–877 CrossRef CAS.
- E. Detsi, S. H. Tolbert, S. Punzhin and J. T. M. De Hosson, J. Mater. Sci., 2015, 51, 615–634 CrossRef.
- S. Punzhin, E. Detsi, A. Kuzmin and J. T. M. De Hosson, J. Mater. Sci., 2014, 49, 5598–5605 CrossRef CAS.
- J. Fu, Z. Deng, T. Lee, J. S. Corsi, Z. Wang, D. Zhang and E. Detsi, ACS Appl. Energy Mater., 2018, 1, 3198–3205 CrossRef CAS.
- E. Detsi, S. Punzhin, J. Rao, P. R. Onck and J. T. M. De Hosson, ACS Nano, 2012, 6, 3734–3744 CrossRef CAS.
- E. Detsi, X. Petrissans, Y. Yan, J. B. Cook, Z. Deng, Y. L. Liang, B. Dunn and S. H. Tolbert, Phys. Rev. Mater., 2018, 2, 1–10 Search PubMed.
- J. B. Cook, H. S. Kim, T. C. Lin, S. Robbennolt, E. Detsi, B. S. Dunn and S. H. Tolbert, ACS Appl. Mater. Interfaces, 2017, 9, 19063–19073 CrossRef CAS.
- E. Detsi, J. B. Cook, B. K. Lesel, C. L. Turner, Y. L. Liang, S. Robbennolt and S. H. Tolbert, Energy Environ. Sci., 2016, 9, 540–549 RSC.
- E. Detsi, Z. Vuković, S. Punzhin, P. M. Bronsveld, P. R. Onck and J. T. M. D. Hosson, CrystEngComm, 2012, 14, 5402–5406 RSC.
- H. Yaghoobnejad Asl, J. Fu, H. Kumar, S. S. Welborn, V. B. Shenoy and E. Detsi, Chem. Mater., 2018, 30, 1815–1824 CrossRef CAS.
- E. Detsi, M. Salverda, P. R. Onck and J. T. M. De Hosson, J. Appl. Phys., 2014, 115, 044308 CrossRef.
- A. Pröschel, J. Chacko, R. Whitaker, M. A. U. Chen and E. Detsi, J. Electrochem. Soc., 2019, 166, H146–H150 CrossRef.
- E. Detsi, J. B. Cook, B. K. Lesel, C. L. Turner, Y. L. Liang, S. Robbennolt and S. H. Tolbert, Energy Environ. Sci., 2016, 9, 540–549 RSC.
- M. Li, Z. Wang, J. Fu, K. Ma and E. Detsi, Scr. Mater., 2019, 164, 52–56 CrossRef CAS.
-
K. Ma, Z. Wang, J. Fu, J. S. Corsi, S. S. Welborn, J. T. M. De Hosson and E. Detsi.
- H. Yaghoobnejad Asl, J. Fu, H. Kumar, S. S. Welborn, V. B. Shenoy and E. Detsi, Chem. Mater., 2018, 30, 1815–1824 CrossRef CAS.
- J. B. Cook, E. Detsi, Y. Liu, Y. L. Liang, H. S. Kim, X. Petrissans, B. Dunn and S. H. Tolbert, ACS Appl. Mater. Interfaces, 2017, 9, 293–303 CrossRef CAS.
- E. Detsi, S. Punzhin, P. R. Onck and J. T. M. De Hosson, J. Mater. Chem., 2012, 22, 4588–4591 RSC.
- J. B. Cook, E. Detsi, Y. Liu, Y. L. Liang, H. S. Kim, X. Petrissans, B. Dunn and S. H. Tolbert, ACS Appl. Mater. Interfaces, 2017, 9, 293–303 CrossRef CAS.
- J. Dendooven, K. Devloo-Casier, M. Ide, K. Grandfield, M. Kurttepeli, K. F. Ludwig, S. Bals, P. Van Der Voort and C. Detavernier, Nanoscale, 2014, 6, 14991–14998 RSC.
- R. R. Salunkhe, Y. V. Kaneti and Y. Yamauchi, ACS Nano, 2017, 11, 5293–5308 CrossRef CAS.
- T. Li, S. Karwal, B. Aoun, H. Zhao, Y. Ren, C. P. Canlas, J. W. Elam and R. E. Winans, Chem. Mater., 2016, 28, 7082–7087 CrossRef CAS.
- A. C. Alba-Rubio, B. J. O’Neill, F. Shi, C. Akatay, C. Canlas, T. Li, R. Winans, J. W. Elam, E. A. Stach, P. M. Voyles and J. A. Dumesic, ACS Catal., 2014, 4, 1554–1557 CrossRef CAS.
- Z. Liu, N. Fujita, K. Miyasaka, L. Han, S. M. Stevens, M. Suga, S. Asahina, B. Slater, C. Xiao, Y. Sakamoto, M. W. Anderson, R. Ryoo and O. Terasaki, J. Electron Microsc., 2013, 62, 109–146 CAS.
- R. E. Morris and P. S. Wheatley, Angew. Chem., Int. Ed., 2008, 47, 4966–4981 CrossRef CAS PubMed.
- E. Stavitski, M. Goesten, J. Juan-Alcañiz, A. Martinez-Joaristi, P. Serra-Crespo, A. V. Petukhov, J. Gascon and F. Kapteijn, Angew. Chem., Int. Ed., 2011, 50, 9624–9628 CrossRef CAS PubMed.
- C. S. Tsao, M. S. Yu, T. Y. Chung, H. C. Wu, C. Y. Wang, K. Sen Chang and H. L. Chen, J. Am. Chem. Soc., 2007, 129, 15997–16004 CrossRef CAS.
- S. J. Yang, T. Kim, J. H. Im, Y. S. Kim, K. Lee, H. Jung and C. R. Park, Chem. Mater., 2012, 24, 464–470 CrossRef CAS.
- C. Chen, J. Kim and W.-S. Ahn, Korean J. Chem. Eng., 2014, 31, 1919–1934 CrossRef CAS.
- S. T. Meek, J. A. Greathouse and M. D. Allendorf, Adv. Mater., 2011, 23, 249–267 CrossRef CAS.
- T. M. Davis, T. O. Drews, H. Ramanan, C. He, J. Dong, H. Schnablegger, M. A. Katsoulakis, E. Kokkoli, A. V. Mccormick, R. L. Penn and M. Tsapatsis, Nat. Mater., 2006, 5, 400–408 CrossRef CAS.
- L. R. A. Follens, A. Aerts, M. Haouas, T. P. Caremans, B. Loppinet, B. Goderis, J. Vermant, F. Taulelle, J. A. Martens and C. E. A. Kirschhock, Phys. Chem. Chem. Phys., 2008, 10, 5574–5583 RSC.
- A. Aerts, L. R. A. Follens, M. Haouas, T. P. Caremans, M. A. Delsuc, B. Loppinet, J. Vermant, B. Goderis, F. Taulelle, J. A. Martens and C. E. A. Kirschhock, Chem. Mater., 2007, 19, 3448–3454 CrossRef CAS.
- P.-P. E. A. de Moor, T. P. M. Beelen, R. A. van Santen, K. Tsuji and M. E. Davis, Chem. Mater., 1999, 11, 36–43 CrossRef CAS.
- B. J. Smith, L. R. Parent, A. C. Overholts, P. A. Beaucage, R. P. Bisbey, A. D. Chavez, N. Hwang, C. Park, A. M. Evans, N. C. Gianneschi and W. R. Dichtel, ACS Cent. Sci., 2017, 3, 58–65 CrossRef CAS.
- D. Beaudoin, T. Maris and J. D. Wuest, Nat. Chem., 2013, 5, 830–834 CrossRef CAS.
- T. Ma, E. A. Kapustin, S. X. Yin, L. Liang, Z. Zhou, J. Niu, L. H. Li, Y. Wang, J. Su, J. Li, X. Wang, W. D. Wang, W. Wang, J. Sun and O. M. Yaghi, Science, 2018, 361, 48–52 CrossRef CAS.
- V. Presser, J. McDonough, S. H. Yeon and Y. Gogotsi, Energy Environ. Sci., 2011, 4, 3059–3066 RSC.
- M. Oschatz, E. Kockrick, M. Rose, L. Borchardt, N. Klein, I. Senkovska, T. Freudenberg, Y. Korenblit, G. Yushin and S. Kaskel, Carbon N. Y., 2010, 48, 3987–3992 CrossRef CAS.
- Y. Gogotsi, A. Nikitin, H. Ye, W. Zhou, J. E. Fischer, B. Yi, H. C. Foley and M. W. Barsoum, Nat. Mater., 2003, 2, 591–594 CrossRef CAS PubMed.
- Y. Korenblit, M. Rose, E. Kockrick, L. Borchardt, A. Kvit, S. Kaskel and G. Yushin, ACS Nano, 2010, 4, 1337–1344 CrossRef CAS PubMed.
- J. Chmiola, P. L. T. Celine Largeot, P. Simon and Y. Gogotsi, Science, 2010, 328, 480–483 CrossRef CAS PubMed.
- W. Lu, D. Yuan, D. Zhao, C. I. Schilling, O. Plietzsch, T. Muller, S. Bräse, J. Guenther, J. Blümel, R. Krishna, Z. Li and H. C. Zhou, Chem. Mater., 2010, 22, 5964–5972 CrossRef CAS.
- P. Kuhn, A. Forget, D. Su, A. Thomas and M. Antonietti, J. Am. Chem. Soc., 2008, 130, 13333–13337 CrossRef CAS.
- Q. Zhang, E. Uchaker, S. L. Candelaria and G. Cao, Chem. Soc. Rev., 2013, 42, 3127–3171 RSC.
- S. A. Ansari and Q. Husain, Biotechnol. Adv., 2012, 30, 512–523 CrossRef CAS PubMed.
- E. M. Bringa, J. D. Monk, A. Caro, A. Misra, L. Zepeda-Ruiz, M. Duchaineau, F. Abraham, M. Nastasi, S. T. Picraux, Y. Q. Wang and D. Farkas, Nano Lett., 2012, 12, 3351–3355 CrossRef CAS.
- X. Lang, L. Qian, P. Guan, J. Zi and M. Chen, Appl. Phys. Lett., 2011, 98, 093701 CrossRef.
- F. Yu, S. Ahl, A. M. Caminade, J. P. Majoral, W. Knoll and J. Erlebacher, Anal. Chem., 2006, 78, 7346–7350 CrossRef CAS.
- S. Linic, P. Christopher and D. B. Ingram, Nat. Mater., 2011, 10, 911–921 CrossRef CAS.
- H. A. Chen, J. L. Long, Y. H. Lin, C. J. Weng and H. N. Lin, J. Appl. Phys., 2011, 110, 54302 CrossRef.
- J. Biener, G. W. Nyce, A. M. Hodge, M. M. Biener, A. V. Hamza and S. A. Maier, Adv. Mater., 2008, 20, 1211–1217 CrossRef CAS.
- A. Wittstock, J. Biener and M. Bäumer, Phys. Chem. Chem. Phys., 2010, 12, 12919–12930 RSC.
- V. Zielasek, B. Jürgens, C. Schulz, J. Biener, M. M. Biener, A. V. Hamza and M. Bäumer, Angew. Chem., Int. Ed., 2006, 45, 8241–8244 CrossRef CAS.
-
H.-J. Qiu, H.-T. Xu, L. Liu and Y. Wang, Nanoscale, 2015, 7, 386–400 Search PubMed.
- N. Cheng, L. Ren, X. Xu, Y. Du and S. X. Dou, Adv. Energy Mater., 2018, 8, 1801257 CrossRef.
- T. Fujita, P. Guan, K. McKenna, X. Lang, A. Hirata, L. Zhang, T. Tokunaga, S. Arai, Y. Yamamoto, N. Tanaka, Y. Ishikawa, N. Asao, Y. Yamamoto, J. Erlebacher and M. Chen, Nat. Mater., 2012, 11, 775 CrossRef CAS.
- Y. Ding, M. Chen and J. Erlebacher, J. Am. Chem. Soc., 2004, 126, 6876–6877 CrossRef CAS PubMed.
- C. Xu, Y. Liu, J. Wang, H. Geng and H. Qiu, J. Power Sources, 2012, 199, 124–131 CrossRef CAS.
- C. Xu, X. Xu, J. Su and Y. Ding, J. Catal., 2007, 252, 243–248 CrossRef CAS.
- T. Fujita, T. Tokunaga, L. Zhang, D. Li, L. Chen, S. Arai, Y. Yamamoto, A. Hirata, N. Tanaka, Y. Ding and M. Chen, Nano Lett., 2014, 14, 1172–1177 CrossRef CAS.
- Z. Liu and P. C. Searson, J. Phys. Chem. B, 2006, 110, 4318–4322 CrossRef CAS.
- E. Detsi, Z. G. Chen, W. P. Vellinga, P. R. Onck and J. T. M. De Hosson, J. Nanosci. Nanotechnol., 2012, 12, 4951–4955 CrossRef CAS.
- H. J. Jin and J. Weissmüller, Adv. Eng. Mater., 2010, 12, 714–723 CrossRef CAS.
- J. Biener, A. Wittstock, L. A. Zepeda-Ruiz, M. M. Biener, V. Zielasek, D. Kramer, R. N. Viswanath, J. Weissmüller, M. Bäumer and A. V. Hamza, Nat. Mater., 2009, 8, 47–51 CrossRef CAS.
- E. Detsi, P. R. Onck and J. T. M. De Hosson, Appl. Phys. Lett., 2013, 103, 193101 CrossRef.
- O. Ruiz, M. Cochrane, M. Li, Y. Yan, K. Ma, J. Fu, Z. Wang, S. H. Tolbert, V. B. Shenoy and E. Detsi, Adv. Energy Mater., 2018, 8, 1801781 CrossRef.
- S. L. Candelaria, Y. Shao, W. Zhou, X. Li, J. Xiao, J. G. Zhang, Y. Wang, J. Liu, J. Li and G. Cao, Nano Energy, 2012, 1, 195–220 CrossRef CAS.
- A. González, E. Goikolea, J. A. Barrena and R. Mysyk, Renewable Sustainable Energy Rev., 2016, 58, 1189–1206 CrossRef.
- S. Liu, J. Feng, X. Bian, Y. Qian, J. Liu and H. Xu, Nano Energy, 2015, 13, 651–657 CrossRef CAS.
- E. Detsi, M. Van De Schootbrugge, S. Punzhin, P. R. Onck and J. T. M. De Hosson, Scr. Mater., 2011, 64, 319–322 CrossRef CAS.
- I. McCue, J. Stuckner, M. Murayama and M. J. Demkowicz, Sci. Rep., 2018, 8, 6761 CrossRef.
- E. Detsi, E. De Jong, A. Zinchenko, Z. Vuković, I. Vuković, S. Punzhin, K. Loos, G. Ten Brinke, H. A. De Raedt, P. R. Onck and J. T. M. De Hosson, Acta Mater., 2011, 59, 7488–7497 CrossRef CAS.
- J. W. Kim, T. Wada, S. G. Kim and H. Kato, Scr. Mater., 2016, 122, 68–71 CrossRef CAS.
- M. K. Khristosov, L. Bloch, M. Burghammer, Y. Kauffmann, A. Katsman and B. Pokroy, Nat. Commun., 2015, 6, 8841 CrossRef CAS.
- T. Kou, D. Li, C. Zhang, Z. Zhang and H. Yang, J. Mol. Catal. A: Chem., 2014, 382, 55–63 CrossRef CAS.
- Y. H. Tan, J. a. Davis, K. Fujikawa, N. V. Ganesh, A. V. Demchenko and K. J. Stine, J. Mater. Chem., 2012, 22, 6733–6745 RSC.
- H. J. Qiu, L. Peng, X. Li, H. T. Xu and Y. Wang, Corros. Sci., 2015, 92, 16–31 CrossRef CAS.
- M. Mokhtari, C. Le Bourlot, J. Adrien, A. Bonnin, T. Wada, J. Duchet-Rumeau, H. Kato and E. Maire, Mater. Charact., 2018, 144, 166–172 CrossRef CAS.
- J. Erlebacher and I. McCue, Acta Mater., 2012, 60, 6164–6174 CrossRef CAS.
- R. D. MacPherson and D. J. Srolovitz, Nature, 2007, 446, 1053–1055 CrossRef CAS.
- J. Erlebacher, M. J. Aziz, A. Karma, N. Dimitrov and K. Sieradzki, Nature, 2001, 410, 450–453 CrossRef CAS.
- B. Chu and B. S. Hsiao, Chem. Rev., 2001, 101, 1727–1761 CrossRef CAS.
- I. S. Dmitri and H. J. K. Michel, Rep. Prog. Phys., 2003, 66, 1735 CrossRef.
-
A. Guinier and G. Fournet, Small angle scattering of x-rays, John Wiley & Sons, Inc., New York, 1st edn, 1955 Search PubMed.
- A. J. Guinier, Proc. Phys. Soc., 1945, 57, 310–324 CrossRef CAS.
- W. Liu, W. L. Johnson, S. Schneider, U. Geyer and P. Thiyagarajan, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 11755–11759 CrossRef CAS.
- D. P. Rolf, Nature, 1983, 302, 46–48 CrossRef.
- A. Guinier, Nature, 1938, 142, 569–570 CrossRef CAS.
- A. Guinier, Ann. Phys., 1939, 11, 161–237 Search PubMed.
-
O. Glatter and O. Kratky, Small Angle X-ray Scattering, London, 1982 Search PubMed.
- B. R. Pauw, J. Phys.: Condens. Matter, 2013, 25, 383201 CrossRef.
-
J. Als-Nielsen and D. McMorrow, Elements of modern X-ray physics, John Wiley & Sons Ltd., West Sussex, 2nd edn, 2011 Search PubMed.
- P. Debye and A. M. Bueche, J. Appl. Phys., 1949, 20, 518–525 CrossRef CAS.
- P. Debye, H. R. Anderson and H. Brumberger, J. Appl. Phys., 1957, 28, 679–683 CrossRef CAS.
-
O. Spalla, Chapter 3, Neutrons, X-rays and Light: Scattering Methods Applied to Soft Condensed Matter, North-Holland, 1st edn, 2002 Search PubMed.
- C. J. Dotzler, B. Ingham, B. N. Illy, K. Wallwork, M. P. Ryan and M. F. Toney, Adv. Funct. Mater., 2011, 21, 3938–3946 CrossRef CAS.
- S. H. Chen, S. L. Chang and R. Strey, J. Appl. Crystallogr., 1991, 24, 721–731 CrossRef CAS.
- M. Teubner, Europhys. Lett., 1991, 14, 403–408 CrossRef CAS.
- S. H. Chen, S. L. Chang, R. Strey, J. Samseth and K. Mortensen, J. Phys. Chem., 1991, 95, 7427–7432 CrossRef CAS.
- M. Peltomäki, G. Gompper and D. M. Kroll, J. Chem. Phys., 2012, 136, 134708 CrossRef.
- K. V. Schubert, R. Strey, S. R. Kline and E. W. Kaler, J. Chem. Phys., 1994, 101, 5343–5355 CrossRef CAS.
- T. Sottmann, R. Strey and S.-H. Chen, J. Chem. Phys., 2002, 106, 6483–6491 CrossRef.
- L. E. Scriven, Nature, 1976, 263, 123–125 CrossRef CAS.
-
S. H. Chen, S. L. Chang and R. Strey, in Trends in Colloid and Interface Science IV, ed. M. Zulauf, P. Lindner and P. Terech, Steinkopff, Darmstadt, 2007, pp. 30–35 Search PubMed.
- N. F. Berk, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 44, 5069–5079 CrossRef CAS.
- N. F. Berk, Phys. Rev. Lett., 1987, 58, 2718–2721 CrossRef CAS.
- M. Teubner and R. Strey, J. Chem. Phys., 1987, 87, 3195–3200 CrossRef CAS.
- S. Ichilmann, K. Rücker, M. Haase, D. Enke, M. Steinhart and L. Xue, Nanoscale, 2015, 7, 9185–9193 RSC.
- E. S. Hatakeyama, B. R. Wiesenauer, C. J. Gabriel, R. D. Noble and D. L. Gin, Chem. Mater., 2010, 22, 4525–4527 CrossRef CAS.
- Y. Ito, H. J. Qiu, T. Fujita, Y. Tanabe, K. Tanigaki and M. Chen, Adv. Mater., 2014, 26, 4145–4150 CrossRef CAS.
- B. Krause, H. J. P. Sijbesma, P. Münüklü, N. F. A. Van Der Vegt and M. Wessling, Macromolecules, 2001, 34, 8792–8801 CrossRef CAS.
- S. Kim, M. Yoo, N. Kang, B. Moon, B. J. Kim, S. H. Choi, J. U. Kim and J. Bang, ACS Appl. Mater. Interfaces, 2013, 5, 5659–5666 CrossRef CAS.
-
J. Erlebacher, R. C. Newman and K. Sieradzki, Nanoporous Gold: From an Ancient Technology to a High-Tech Material, The Royal Society of Chemistry, 2012, pp. 11–29 Search PubMed.
- J. W. Cahn, J. Chem. Phys., 1965, 42, 93–99 CrossRef CAS.
- M. Graf, B. N. D. Ngô, J. Weissmüller and J. Markmann, Phys. Rev. Mater., 2017, 1, 76003 CrossRef.
- C. Soyarslan, S. Bargmann, M. Pradas and J. Weissmüller, Acta Mater., 2018, 149, 326–340 CrossRef CAS.
- I. McCue, E. Benn, B. Gaskey and J. Erlebacher, Annu. Rev. Mater. Res., 2016, 46, 263–286 CrossRef CAS.
- Y. Ding, Y. J. Kim and J. Erlebacher, Adv. Mater., 2004, 16, 1897–1900 CrossRef CAS.
- I. McCue, A. Karma and J. Erlebacher, MRS Bull., 2018, 43, 27–34 CrossRef CAS.
- J. Erlebacher, J. Electrochem. Soc., 2004, 151, C614 CrossRef CAS.
- J. Erlebacher and K. Sieradzki, Scr. Mater., 2003, 49, 991–996 CrossRef CAS.
- T. Fujita, L. H. Qian, K. Inoke, J. Erlebacher and M. W. Chen, Appl. Phys. Lett., 2008, 92, 251902 CrossRef.
- Y. C. K. Chen-Wiegart, S. Wang, Y. S. Chu, W. Liu, I. McNulty, P. W. Voorhees and D. C. Dunand, Acta Mater., 2012, 60, 4972–4981 CrossRef CAS.
- Y. C. K. Chen-Wiegart, T. Wada, N. Butakov, X. Xiao, F. De Carlo, H. Kato, J. Wang, D. C. Dunand and E. Maire, J. Mater. Res., 2013, 28, 2444–2452 CrossRef CAS.
- K. Kolluri and M. J. Demkowicz, Acta Mater., 2011, 59, 7645–7653 CrossRef CAS.
- J. Erlebacher, Phys. Rev. Lett., 2011, 106, 225504 CrossRef CAS.
- I. McCue, B. Gaskey, P. A. Geslin, A. Karma and J. Erlebacher, Acta Mater., 2016, 115, 10–23 CrossRef CAS.
- P. A. Geslin, I. McCue, B. Gaskey, J. Erlebacher and A. Karma, Nat. Commun., 2015, 6, 1–19 Search PubMed.
- I. McCue, J. Snyder, X. Li, Q. Chen, K. Sieradzki and J. Erlebacher, Phys. Rev. Lett., 2012, 108, 225503 CrossRef CAS PubMed.
- H. Jinnai, Y. Nishikawa, S. Chen, S. Koizumi and T. Hashimoto, Phys. Rev. E, 2000, 61, 6673–6780 Search PubMed.
- S. H. Chen, D. D. Lee, K. Kimishima, H. Jinnai and T. Hashimoto, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54, 6526–6531 CrossRef.
- H. Jinnai, T. Koga, Y. Nishikawa, T. Hashimoto and S. T. Hyde, Phys. Rev. Lett., 1997, 78, 2248–2251 CrossRef CAS.
- J. W. Cahn and J. E. Hilliard, J. Chem. Phys., 1958, 28, 258–267 CrossRef CAS.
- J. W. Cahn, Acta Metall., 1962, 10, 179–183 CrossRef CAS.
- J. W. Cahn, Acta Metall., 1961, 9, 795–801 CrossRef CAS.
- J. W. Cahn, Acta Metall., 1966, 14, 1685–1692 CrossRef CAS.
-
I. Wolfram, Research, Mathematica, Wolfram Research, Inc., Version 11., 2018.
-
M. Kardar, Statistical Physics of Fields, Cambridge University Press, 2012 Search PubMed.
- S. M. Choi, S. H. Chen, T. Sottmann and R. Strey, Phys. A, 2002, 304, 85–92 CrossRef CAS.
- S.-H. Chen and S.-M. Choi, J. Appl. Crystallogr., 1997, 30, 755–760 CrossRef CAS.
-
L. A. Feigin and D. I. Svergun, Structure Analysis by Small-Angle X-Ray and Neutron Scattering, 1987 Search PubMed.
- R. E. Winans and P. Thiyagarajan, Energy Fuels, 1988, 2, 356–358 CrossRef CAS.
- F. Gao, C. C. Ho and C. C. Co, Macromolecules, 2006, 39, 9467–9472 CrossRef CAS.
- B. Hammouda, J. Appl. Crystallogr., 2010, 43, 716–719 CrossRef CAS.
- G. Beaucage, J. Appl. Crystallogr., 1995, 28, 717–728 CrossRef CAS.
- D. Eliezer, P. A. Jennings, P. E. Wright, S. Doniach, K. O. Hodgson and H. Tsuruta, Science, 1995, 270, 487 CrossRef CAS.
- T. J. Prosa, B. J. Bauer, E. J. Amis, D. A. Tomalia and R. Scherrenberg, J. Polym. Sci., Part B: Polym. Phys., 1997, 35, 2913–2924 CrossRef CAS.
- K. Sinkó, V. Torma and A. Kovács, J. Non-Cryst. Solids, 2008, 354, 5466–5474 CrossRef.
- E. Smorgonskaya, R. Kyutt, A. Danishevskii, C. Jardin, R. Meaudre, O. Marty, S. Gordeev and A. Grechinskaya, J. Non-Cryst. Solids, 2002, 299–302, 810–814 CrossRef CAS.
- É. A. Smorgonskaya, R. N. Kyutt, V. B. Shuman, A. M. Danishevskii, S. K. Gordeev and A. V. Grechinskaya, Phys. Solid State, 2002, 44, 2001–2008 CrossRef.
- R. N. Kyutt, É. A. Smorgonskaya, A. M. Danishevskii, S. K. Gordeev and A. V. Grechinskaya, Phys. Solid State, 1999, 41, 1359–1363 CrossRef CAS.
- E. A. Chavez Panduro, T. Beuvier, M. Fernández Martínez, L. Hassani, B. Calvignac, F. Boury and A. Gibaud, J. Appl. Crystallogr., 2012, 45, 881–889 CrossRef CAS.
- G. Beaucage, J. Appl. Crystallogr., 1996, 29, 134–146 CrossRef CAS.
- R. Diduszko, A. Swiatkowski and B. J. Trznadel, Carbon N. Y., 2000, 38, 1153–1162 CrossRef CAS.
- K. Kaneko, M. Sato, T. Suzuki, Y. Fujiwara, K. Nishikawa and M. Jaroniec, J. Chem. Soc., Faraday Trans., 1991, 87, 179–184 RSC.
- M. H. Reich, S. P. Russo, I. K. Snook and H. K. Wagenfeld, J. Colloid Interface Sci., 1990, 135, 353–362 CrossRef CAS.
- J. Teixeira, J. Appl. Crystallogr., 1988, 21, 781–785 CrossRef.
- J. E. Martin and A. J. Hurd, J. Appl. Crystallogr., 1987, 20, 61–78 CrossRef CAS.
- Y. C. K. Chen, Y. S. Chu, J. Yi, I. McNulty, Q. Shen, P. W. Voorhees and D. C. Dunand, Appl. Phys. Lett., 2010, 96, 043122 CrossRef.
- A. A. El-Zoka, J. Y. Howe, R. C. Newman and D. D. Perovic, Acta Mater., 2019, 162, 67–77 CrossRef CAS.
- M. Hakamada and M. Mabuchi, J. Mater. Res., 2009, 24, 301–304 CrossRef CAS.
- R. N. Viswanath, V. A. Chirayath, R. Rajaraman, G. Amarendra and C. S. Sundar, Appl. Phys. Lett., 2013, 102, 253101 CrossRef.
- S. Kuwano-Nakatani, K. Uchisawa, D. Umetsu, Y. Kase, Y. Kowata, K. Chiba, T. Fujita, M. Chen, T. Tokunaga, S. Arai, Y. Yamamoto and N. Tanaka, Mater. Trans., 2015, 56, 468–472 CrossRef CAS.
- M. Hakamada and M. Mabuchi, Mater. Lett., 2008, 62, 483–486 CrossRef CAS.
- J. Wang, R. Xia, J. Zhu, Y. Ding, X. Zhang and Y. Chen, J. Mater. Sci., 2012, 47, 5013–5018 CrossRef CAS.
- M. Ziehmer, K. Hu, K. Wang and E. T. Lilleodden, Acta Mater., 2016, 120, 24–31 CrossRef CAS.
- K. Hu, M. Ziehmer, K. Wang and E. T. Lilleodden, Philos. Mag., 2016, 96, 3322–3335 CrossRef CAS.
- E. T. Lilleodden and P. W. Voorhees, MRS Bull., 2018, 43, 20–26 CrossRef CAS.
- C. A. Dreiss, K. S. Jack and A. P. Parker, J. Appl. Crystallogr., 2006, 39, 32–38 CrossRef CAS.
-
D. S. Sivia, Elementary Scattering Theory for X-ray and Neutron Users, Oxford University Press, 2011 Search PubMed.
-
S. R. Stock and B. D. Cullity, Elements of X-ray diffraction, 3rd edn, 2001 Search PubMed.
-
C. T. Chantler, K. Olsen, R. A. Dragoset, J. Chang, A. R. Kishore, S. A. Kotochigova and D. S. Zucker, Detailed Tabulation of Atomic Form Factors, Photoelectric Absorption and Scattering Cross Section, and Mass Attenuation Coefficients for Z = 1–92 from E = 1–10 eV to E = 0.4–1.0 MeV, NIST, NIST Stand., 2005.
- P. Brown, A. Fox, E. Maslen, M. A. O’Keefe and B. T. M. Willis, Int. Tables Crystallogr., 2004, C, 554–595 Search PubMed.
- SasView, https://www.sasview.org/.
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  ab and
Eric
Detsi
ab and
Eric
Detsi
 *ab
*ab
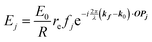
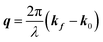 and has magnitude
and has magnitude 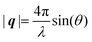 . Further in this article, the magnitude |q| will simply be referred to as q.
. Further in this article, the magnitude |q| will simply be referred to as q.
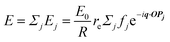
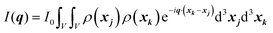
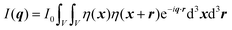
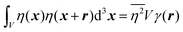
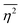 , is defined in the Appendix. In an isotropic system, γ(r) depends only on the magnitude |r| = r, and corresponds to the probability of two endpoints of a rod with length r being within the same type of matter. For example, it is the probability of being in the solid phase of a NP material after moving a radius r away from any random point in the NP material's solid phase.101 Thus, the correlation function will tend to 1 (having been normalized by
, is defined in the Appendix. In an isotropic system, γ(r) depends only on the magnitude |r| = r, and corresponds to the probability of two endpoints of a rod with length r being within the same type of matter. For example, it is the probability of being in the solid phase of a NP material after moving a radius r away from any random point in the NP material's solid phase.101 Thus, the correlation function will tend to 1 (having been normalized by 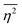 and V) for r → 0 (short distances correlate very well), and 0 for r → ∞ (long distances do not correlate). After some manipulation and assuming isotropy (using the average value of e−iq·r = sin(qr)/(qr), replacing the vectors q and r with their magnitudes), the intensity integral can be written as:100
and V) for r → 0 (short distances correlate very well), and 0 for r → ∞ (long distances do not correlate). After some manipulation and assuming isotropy (using the average value of e−iq·r = sin(qr)/(qr), replacing the vectors q and r with their magnitudes), the intensity integral can be written as:100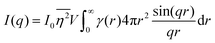
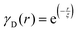
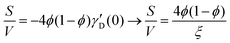
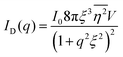
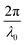 .
.
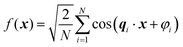
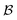 is the bulk (the metal),
is the bulk (the metal), 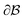 is the interface, and
is the interface, and 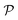 is the pore.122 The threshold value is a function of the bulk fraction
is the pore.122 The threshold value is a function of the bulk fraction 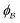 ,
, 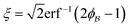 . This thresholding process produces a leveled-wave, which can be computed to provide structural visualization for a scattering dataset. As a demonstration of this concept for one wavelength, we used Mathematica143 to compute one such structure, which is displayed in Fig. 2. Here we used fitted values (discussed later in Section 4) for ligament–ligament distance to determine q0.
. This thresholding process produces a leveled-wave, which can be computed to provide structural visualization for a scattering dataset. As a demonstration of this concept for one wavelength, we used Mathematica143 to compute one such structure, which is displayed in Fig. 2. Here we used fitted values (discussed later in Section 4) for ligament–ligament distance to determine q0.
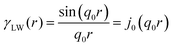
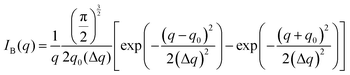
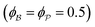 . Since this intensity function is derived based on a correlation function expansion that does not converge quickly as r → 0, the asymptotic curve at higher values of q (in the Porod regime) cannot be well matched with any finite number of expansion terms.111Eqn (15) has been plotted in Fig. 3c, which shows how this function changes when the both distribution (Δq) and the characteristic spacing (q0) are varied. We can clearly see that this intensity distribution does not match the high-q tail of the NP-Au scattering spectrum in Fig. 5.
. Since this intensity function is derived based on a correlation function expansion that does not converge quickly as r → 0, the asymptotic curve at higher values of q (in the Porod regime) cannot be well matched with any finite number of expansion terms.111Eqn (15) has been plotted in Fig. 3c, which shows how this function changes when the both distribution (Δq) and the characteristic spacing (q0) are varied. We can clearly see that this intensity distribution does not match the high-q tail of the NP-Au scattering spectrum in Fig. 5.
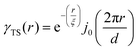
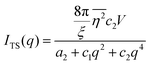
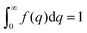 , however the choice should have some relevance to the scattering data.111 Choi and Chen have used an inverse 8th-order polynomial with three length scales (a, b, and c) for f(q):145
, however the choice should have some relevance to the scattering data.111 Choi and Chen have used an inverse 8th-order polynomial with three length scales (a, b, and c) for f(q):145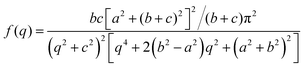
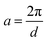 ,
, 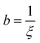 , and
, and 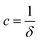 . It was shown by Teubner that the Gaussian curvature 〈K〉 and the square mean curvature 〈H2〉 are functions of the 2nd and 4th moments of f(q), 〈q2〉 and 〈q4〉, respectively.104 This high degree polynomial was chosen in order to capture the 4th moment, whereas in the other cases (Debye, Berk, and TS models), only odd moments exist, or the 4th moment diverges.145 Curvature analysis in this model is therefore more robust than in the aforementioned models. One can obtain these parameters by fitting a form of f(q) to an experimental correlation function γE(r) using the steps outlined in the Appendix.
. It was shown by Teubner that the Gaussian curvature 〈K〉 and the square mean curvature 〈H2〉 are functions of the 2nd and 4th moments of f(q), 〈q2〉 and 〈q4〉, respectively.104 This high degree polynomial was chosen in order to capture the 4th moment, whereas in the other cases (Debye, Berk, and TS models), only odd moments exist, or the 4th moment diverges.145 Curvature analysis in this model is therefore more robust than in the aforementioned models. One can obtain these parameters by fitting a form of f(q) to an experimental correlation function γE(r) using the steps outlined in the Appendix.
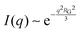
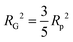 , where Rp is the radius of the particle.96 Feigin and Svergun have tabulated several of these relationships for simple shapes,147 and this relatively simple analysis is performed frequently in X-ray and neutron scattering data.45,148–154 In a seminal paper on carbide-derived carbon, Gogotsi et al. fit scattering data to show that there is a very narrow distribution of pores which can be controlled well by synthesis temperature.45 They used an analysis put forward by Kyutt et al. which determines pore size by a series of RG fits of the SAXS data.155–157
, where Rp is the radius of the particle.96 Feigin and Svergun have tabulated several of these relationships for simple shapes,147 and this relatively simple analysis is performed frequently in X-ray and neutron scattering data.45,148–154 In a seminal paper on carbide-derived carbon, Gogotsi et al. fit scattering data to show that there is a very narrow distribution of pores which can be controlled well by synthesis temperature.45 They used an analysis put forward by Kyutt et al. which determines pore size by a series of RG fits of the SAXS data.155–157

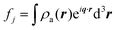
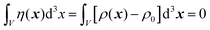
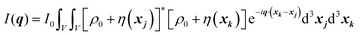
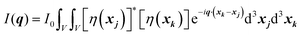
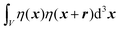
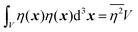
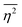 where V represents the irradiated volume. This factor is used to normalize the correlation function γ(r) to 1.
where V represents the irradiated volume. This factor is used to normalize the correlation function γ(r) to 1.
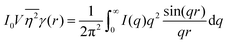
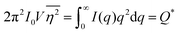
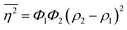 to associate Q* with physical properties of the scattered volume:101
to associate Q* with physical properties of the scattered volume:101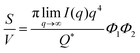
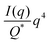 vs. q and finding the constant value it tends to. It is important to note, however, that in a scattering experiment we do not have data for q → ∞, thus absolute intensity will give a more accurate representation of the specific surface. If the intensity data is in absolute units, the invariant calculation is not needed, and the specific surface is:
vs. q and finding the constant value it tends to. It is important to note, however, that in a scattering experiment we do not have data for q → ∞, thus absolute intensity will give a more accurate representation of the specific surface. If the intensity data is in absolute units, the invariant calculation is not needed, and the specific surface is: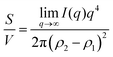
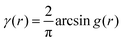
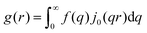 . Choi and Chen explicitly solve for g(r) in their first article on the subject.146
. Choi and Chen explicitly solve for g(r) in their first article on the subject.146