Converting plasmonic light scattering to confined light absorption and creating plexcitons by coupling a gold nano-pyramid array onto a silica–gold film†
Peng
Zheng‡
 a,
Sujan
Kasani‡
a,
Sujan
Kasani‡
 b and
Nianqiang
Wu
b and
Nianqiang
Wu
 *acd
*acd
aDepartment of Mechanical and Aerospace Engineering, West Virginia University, Morgantown, West Virginia 26506-6106, USA. E-mail: nick.wu@mail.wvu.edu; Tel: +1-304-293-3326
bLane Department of Computer Science and Electrical Engineering, West Virginia University, Morgantown, West Virginia 26506, USA
cC. Eugene Bennett Department of Chemistry, West Virginia University, Morgantown, WV 26506-6045, USA
dDepartment of Pharmaceutical Science, West Virginia University, Morgantown, WV 26506-9530, USA
First published on 29th November 2018
Abstract
This report presents a facile microfabrication-compatible approach to fabricate a large area of plasmonic nano-pyramid array-based antennas and demonstrates effective light management by tailoring the architecture. First, a long-range ordered gold nano-pyramid array is fabricated, which exhibits strong light scattering. The maximum electric field enhancement (|E|/|E0|) of 271 is achieved at the corner but decays rapidly away from the pyramid bottom. After the gold nanopyramid array is coupled to a gold film, strong light scattering is converted into strong light absorption due to the excitation of a spectrally tunable plasmonic gap mode, where an intense electric field enhancement of 233 and a strong magnetic field enhancement (|H|/|H0|) of 25 are simultaneously excited for a 10 nm silica gap. The electric field decays much slower away from the pyramid bottom while the magnetic field keeps almost constant. In addition, both experiments and finite-difference time-domain (FDTD) simulations have confirmed that strong plasmon–exciton coupling between the plasmonic gap mode and the J-aggregates can take place when quantum emitters such as J-aggregates are embedded in the gap, creating plexcitons. This can overcome the problems of high energy loss and weak nonlinearity, which are typically associated with surface plasmon polaritons (SPPs) supported on plasmonic metallic nanostructures. The coherent plasmon–exciton coupling (plexciton) generated by the film-coupled nano-pyramid nanostructure is expected to find promising applications in light-emitting devices, photodetectors, photovoltaics and photoelectrochemical cells.
Conceptual insightsStrong light scattering of a gold nanopyramid array has been demonstrated to be converted into strong light absorption by coupling it to an underlying gold film because of the excitation of the spectrally tunable plasmonic cavity mode. The film-coupled gold nanopyramid array exhibits unique features as compared to the gold nanopyramid array alone. First, not only an intense electric field but also a strong magnetic field is supported. Second, the electric field is confined within the gap of the coupled nanostructure while it occurs at the corners for the gold nanopyramid array alone. Third, the magnetic field is almost constant in the gap and the electric field undergoes only a small decay across the gap. In stark contrast, the electric field from the corner mode for the gold nanopyramid array alone decays exponentially away from the corner. These unique features endow the film-coupled gold nanopyramid array with significant advantages over the gold nanopyramid array alone, which has implications in state-of-the-art optoelectronic devices. Our study confirms that strong coupling can be achieved between the plasmonic cavity mode and the quantum emitters embedded at the gap, which can overcome the problems of high energy loss and weak nonlinearity typically associated with surface plasmon polaritons. |
Plasmonic nanostructures are promising antennas because they have strong ability to harvest light due to their large absorption cross-sections; and the incident light can be managed to transmit, scatter or absorb by controlling the chemical composition, size, shape and coupling of the nanostructures. Therefore, plasmonic antennas find extensive applications in photosynthesis, photovoltaics, photo-detection, optical biosensing, therapeutics and super-resolution microscopy.1–4 Plasmonic antennas fall into two categories, that is, free-standing nanoparticles and chip-based nanostructures. Large-area ordered nanostructure array patterns on chips are of particular interest. However, it remains a significant challenge to fabricate chip-based plasmonic antennas to realize light management in a controlled manner (light reflection versus absorption versus transmission, resonance band position and spatial distribution). It is difficult to achieve nanoscale resolution for conventional photolithography techniques due to the diffraction limit of light. Although focused-ion-beam (FIB) and electron-beam lithography (EBL) can reach nanoscale resolution, they suffer from low throughput, impeding massive production. In contrast, nanosphere lithography (NSL) is a simple, inexpensive, and high-throughput method for manufacturing periodic nanostructure arrays. In our previous work,5 we have developed a method to create a large-area, well-ordered and close-packed polystyrene sphere monolayer template, which enables the fabrication of large-area ordered nanostructure array patterns such as nanotriangle arrays and nanohole arrays with NSL. By taking advantage of this, herein we fabricate a large-area ordered nano-pyramid array pattern. The reason for selecting pyramids and not spheres is that pyramids exhibit much larger electromagnetic (EM) field enhancement at the corners and edges as compared to round-shaped nanoparticles. Our results demonstrate that the resulting nano-pyramid array pattern shows large electric field enhancement (|E|/|E0| up to 271) and strong light reflection/scattering. That is, light scattering is dominant in the total extinction spectra while light absorption is small for the array of Au nano-pyramids (179 nm in base edge length and 200 nm in height for individual pyramids). To further improve the EM enhancement near the pyramids, the ideal way is to reduce the in-plane gap between adjacent pyramids to less than 10 nm in order to enable in-plane (X–Y direction) plasmonic field coupling, which is difficult to achieve due to the fabrication limit. To convert the light scattering to confined light absorption, an effective way is to reduce the size of an individual pyramid down to 15 nm. But this will reduce the total area/volume of the chip for harvesting incident light.
On the other hand, our research interest is triggered by coupling nanoparticles to a metal film to form a metal–insulator–metal (MIM) sandwich structure. It has been reported that MIM structures are characteristic of the out-of-plane plasmonic field coupling (plasmonic gap mode) between the top-surface metal nanoparticles and the underneath metal film, which can be modulated by the thickness of the sandwiched space layer.6–11 The plasmonic gap mode is able to have the harvested light be absorbed in the space layer between the metal nanoparticle layer and the underneath metal film, and to create “hot spots” in the out-of-plane direction (Z direction). By taking advantage of the MIM structure, the nano-pyramid array is herein coupled to a silica–gold double-layer to form a metal–insulator–metal (MIM) sandwich structure in order to expand the space of enhanced electric and magnetic fields and to convert the light scattering to light absorption.
Furthermore, efficient tuning of the light–matter interactions is essential for a variety of applications. However, it is difficult to control the light–matter interactions. For example, there exists a fundamental mismatch between the diffraction-limited spatial confinement of visible-light and the size of quantum emitters (QEs).12 The diffraction limit, however, can be broken by surface plasmon polaritons (SPPs), which are light-coupled propagating electromagnetic (EM) waves of coherent electron oscillations on metallic surfaces.13 SPPs come with two prominent features.14,15 First, they are bosons, leading to strong transportability of the EM energy. Second, they have the most harmonic behavior known in nature. Unfortunately, the plasmonic cavity, which supports SPPs, lacks essential functionalities in modern optoelectronic devices due to very weak nonlinear response and a high metal loss.16,17 Coincidently, QEs are highly nonlinear in nature despite a low transportability.18 They are extensively exploited to realize optical gain in lasers and other optoelectronic devices.19–23 The integrated SPPs–QEs system can thus well balance and compensate the nonlinearity and transportability of the two counterparts except that a strong damping from the metal loss persists.
One promising approach to overcome the metal loss is to make conditions for the interaction of the SPPs–QEs system to take place in the strong-coupling regime.24–32 Realizing strong coupling demands an intense interaction between the transition dipole μ of QEs and the plasmonic cavity: 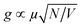 , where V is the effective mode volume of the plasmonic cavity in which the EM energy is confined and N is the number of QEs in V.12,17,33 The diffraction-unlimited nature of SPPs allows light to be confined in a significantly smaller plasmonic cavity than the photonic counterpart until the emergence of charge transfer plasmons due to quantum tunneling or nonlocal effects at a gap below 1 nm.34–37 Such extraordinarily small plasmonic cavities have been demonstrated on nanoparticle-on-mirror geometry, bowtie antennas, patch antennas, etc.24,38,39 Minimizing the effective mode volume, however, is also at the expense of reducing the number of QEs participating in light–matter interactions, which compromises the coupling strength. Moreover, it is also a technical challenge to fabricate ultra-small plasmonic cavities. Therefore, from a practical point of view, modern optoelectronic devices working in the strong-coupling regime require a delicate balance between fabrication and performance.
, where V is the effective mode volume of the plasmonic cavity in which the EM energy is confined and N is the number of QEs in V.12,17,33 The diffraction-unlimited nature of SPPs allows light to be confined in a significantly smaller plasmonic cavity than the photonic counterpart until the emergence of charge transfer plasmons due to quantum tunneling or nonlocal effects at a gap below 1 nm.34–37 Such extraordinarily small plasmonic cavities have been demonstrated on nanoparticle-on-mirror geometry, bowtie antennas, patch antennas, etc.24,38,39 Minimizing the effective mode volume, however, is also at the expense of reducing the number of QEs participating in light–matter interactions, which compromises the coupling strength. Moreover, it is also a technical challenge to fabricate ultra-small plasmonic cavities. Therefore, from a practical point of view, modern optoelectronic devices working in the strong-coupling regime require a delicate balance between fabrication and performance.
In this work, the Au nanopyramid array–silica–Au film structure is predicted to enable SPP–QE systems to enter into the strong plasmon–exciton coupling regime. First, the plasmonic gap mode of such a MIM sandwich structure is tunable both spectrally and in terms of the effective mode volume. Second, if QEs are incorporated into the spacer layer, they exactly fall into the effective mode volume, which ensures that the largest coupling strength possible is achieved. Third, it can be fabricated massively on a large area by the well-established and cost-effective NSL technique.40 The spacer layer can be easily replaced with any other QEs of interest to realize different functionalities. Fourth, the long-range order of the nano-array structure ensures the robustness and reproducibility of fabrication. In addition, the two-dimensional nanostructure makes it practically easy to be integrated into optoelectronic devices. Therefore, in this study, the ability of the Au nanopyramid array–silica/QE–Au film structure to manipulate light–matter interactions is studied both experimentally and with finite-difference time-domain (FDTD) simulation when achieving strong coupling between the plasmonic gap mode and the QEs.
Results and discussion
Structure of the plasmonic antenna
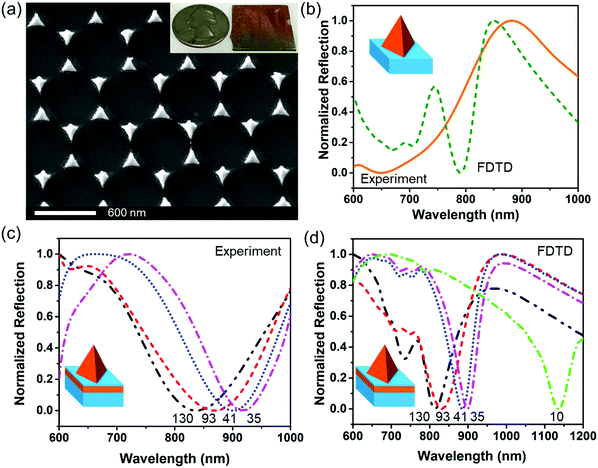
Fig. S1 (ESI†) and Fig. 1 show the procedure for fabrication of the Au nanopyramid array pattern directly on a glass substrate, and the Au nanopyramid array–silica–Au film structure, respectively. The fabricated Au nanopyramid arrays with and without an underlying Au film looked similar to each other from the top-view SEM images as shown in Fig. 2(a) and Fig. S2 (ESI†). The Au nanopyramids were 179 nm in base edge length and 200 nm high (Fig. S3, ESI†). The silica space layer was controlled to be from 35 nm to 130 nm. The overall lateral size of the as-fabricated chips was typically comparable to that of a coin, as shown in the inset of Fig. 2(a). This confirmed the strong capability of nanosphere lithography for long-range ordered nano-array nanofabrication. In contrast, it would take several days for e-beam lithography to produce such a large area of nanostructured patterns.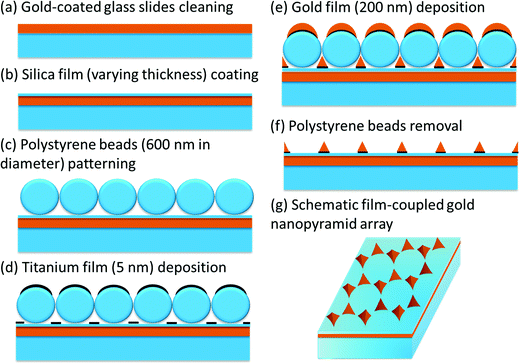 | ||
| Fig. 1 Protocol of nanosphere lithography fabrication for the film-coupled gold nanopyramid array. Polystyrene beads with a diameter of 600 nm were used. 200 nm of gold was deposited. | ||
Strong light reflection by the Au nanopyramid array alone
The fabricated Au nanopyramid array on the glass substrate displayed an intense reflection peak centered at 865 nm corresponding to the plasmonic corner mode, the orange solid curve as shown in Fig. 2(b), which was consistent with the reflection peak at 850 nm calculated by FDTD, as shown by the olive dashed curve. The minor reflection peak at around 750 nm in the calculated reflection spectrum was ascribed to the edge mode, which was not clearly seen in the experimental data due to the rounded edge. The reflection peak contributed to strong light scattering of individual nanopyramids under excitation of the localized surface-plasmon resonance (LSPR) mode at the corner while light absorption by individual nanopyramids was small, as shown in Fig. S4 (ESI†). It was not surprising because the size/volume of the nanopyramids was quite large. For the LSPR-associated total extinction spectra of the nanoparticles, both light absorption and scattering contribute to the total extinction.6 When the particle size is relatively small (typically less than 15 nm), light absorption is dominant. When the particle size increases, light scattering becomes dominant. In addition, the major reflection peak corresponding to the plasmonic corner mode redshifts with a decrease in the pyramid height, as shown in Fig. S5 (ESI†). The FDTD simulation results show that the localized electric field enhancement took place primarily on the four corners, where surface polarization charges accumulate at the corners as shown in Fig. S6 (ESI†). As a result, the plasmonic corner mode exhibits intense electric field enhancement. The calculated maximum electric field enhancement (|E|/|E0|) at the corners was estimated to be 271, as shown in Fig. S7 (ESI†).Strong light absorption in the film-coupled gold nanopyramid array
Although the top-view SEM images looked the same for the Au nanopyramid arrays with and without an underlying Au film, their optical properties were significantly different, as shown in Fig. 2. After the Au nanopyramid array was coupled to a gold film with a silica film as the spacer layer, the strong reflection peak disappeared completely. Instead, the film-coupled Au nanopyramid array exhibited strong light absorption, which was featured as an intense dip in the reflection spectra, as shown in Fig. 2(c). When the thickness of the silica spacer layer was reduced from 130 nm to 35 nm, the reflection dip underwent a redshift from 834 nm to 918 nm. This trend was also confirmed by FDTD simulation, as shown in Fig. 2(d).The observed intense reflection dip was ascribed to the plasmonic gap modes, which were induced in the spacer layer between the Au nanopyramid array and the underlying Au film. Since a transmission line type of resonance can be sustained at the gap,41 the incident light can be guided into the gap region and adjust itself to satisfy the boundary conditions. The impedance mismatch at the gap edge causes most of the incident light to be trapped inside the gap, and thus contributes to the strong absorption. This was confirmed by calculation of surface polarization charge distributions for a film-coupled Au nanopyramid array with a 10 nm thick silica spacer layer (Fig. 3). This plasmonic antenna exhibited two dips at 1135 nm and 790 nm in the reflection spectrum, as shown in the green dash-dotted curve in Fig. 2(d). The primary plasmonic gap mode at 1135 nm showed a stronger reflection dip than the one at 790 nm, which can be interpreted by the fact that the positive and negative surface polarization charges were well separated from each other, as shown in the middle column in Fig. 3. The higher-order plasmonic gap mode at 790 nm displayed a less intense reflection dip because its net dipole momentum was partially cancelled. By varying the thickness of the spacer layer, the plasmonic gap modes can be spectrally tuned (Fig. 2(c and d)). Herein, the study was focused on the primary plasmonic gap mode, which will be called the plasmonic gap mode in the following sections.
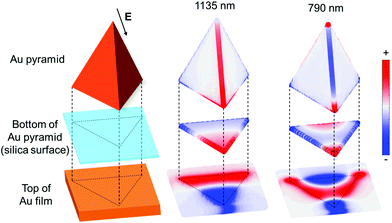 | ||
| Fig. 3 FDTD-simulated surface polarization charge distributions at the reflection dip wavelengths of 1135 nm and 790 nm for a silica thickness of 10 nm (the green curve in Fig. 2(d)). Left: Scheme of different parts of the structure; middle: the primary plasmonic gap mode at 1135 nm; right: the higher-order plasmonic gap mode at 790 nm. The back arrow indicates the incident polarization direction. | ||
It is noted that the plasmonic gap modes generated in the film-coupled nanopyramid structure in this work are different from that of the film-coupled nanosphere reported previously.42–45 For the film-coupled nanosphere structure, the plasmonic gap modes result from hybridization of plasmonic resonances, which lead to the symmetric and the anti-symmetric resonances. The symmetric resonance is featured by a horizontal electric dipole in the nanosphere and an induced electric dipole in the film, which cancel each other. The anti-symmetric resonance is characterized by a vertical electric dipole in the nanosphere and an induced electric dipole in the film, which add up and produce an even larger vertical electric dipole. Therefore, the anti-symmetric resonance is responsible for coupling to the free space with a doughnut-like far-field emission profile. The spectral tunability of the film-coupled nanosphere structure is limited by the gap size because of the electric dipole nature. In contrast, for the film-coupled nanopyramid structure, the plasmonic gap modes are generated due to the Fabry–Perot-like resonance after the incident light gets trapped inside the gap through multiple reflections at the gap edges. Simultaneous to the formation of plasmonic gap modes, opposite charges are induced on the opposite sides of the gap, as shown in Fig. 3, generating fictitious current density. This forms a large horizontal magnetic dipole that is absent in the film-coupled nanosphere structure. In short, the plasmonic gap mode in the film-coupled nanopyramid structure is coupled to the free space primarily through the magnetic dipole with a vertical far-field emission profile. Owing to the magnetic dipole nature, large spectral tunability can be achieved by tuning either the dimension of the pyramidal bottom plane or the gap size, which provide more flexibility than the film-coupled nanosphere structure.
Electromagnetic field enhancement by plasmonic gap mode
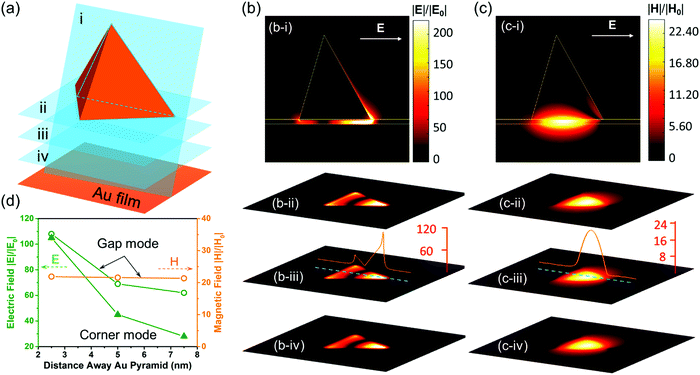
A prominent feature of the plasmonic gap mode was that the charges with opposite signs were induced on the opposite sides of the gap. These charges resulted in an intense EM field localized inside the gap (Fig. 4). Since the surface polarization charges are accumulated at the corner for individual Au pyramids on the glass substrate, the maximum electric field enhancement (|E|/|E0|) of 271 was achieved at the corner (Fig. S7, ESI†). Likewise, the maximum electric field enhancement of 233 was achieved at the gap for the film-coupled Au nanopyramid array with a 10 nm thick silica spacer layer (Fig. 4(b)). It is worth noting that the film-coupled Au nanopyramid array had a few unique features as compared to the Au nanopyramid array on the glass. First, not only the electric field but also an intense magnetic field (an enhancement factor |H|/|H0| of 25) was supported in the gap (Fig. 4(c)), whereas the magnetic field enhancement was negligible for the Au nanopyramid array on the glass. Second, the electric field was confined within the gap for the film-coupled Au pyramid array while a radial electrical field appeared at the corners for the Au nanopyramid array alone. Third, the magnetic field was kept almost constant in the gap for the film-coupled Au pyramid array and the electric field underwent only a small decay with an increase in the distance away from the pyramid bottom along the cross-section (Fig. 4(b and c)). In stark contrast, the electric field from the corner mode of the Au pyramid array alone decayed exponentially away with an increase in the distance away from the pyramid bottom (Fig. S7(b), ESI†). Thanks to these unique features, the localized EM energy oscillated back and forth between the electric and magnetic counterparts inside the gap; and it only got damped either because of metal loss or by coupling to the free space. The gap which confines the spatially oscillating EM energy thus defines a spectrally tunable plasmonic cavity mode with an effective mode volume that is approximately the physical size of the gap. This feature provides an excellent configuration to enable the maximum interaction between SPPs and the spacer layer in the gap.Compared to previous work on metal–insulator–metal structures,46,47 the film-coupled Au nanopyramid array reported in this work can be easily fabricated over a large area using cost-effective nanosphere lithography, as shown in Fig. 1 and 2(a). The plasmonic gap mode supported is thus highly tunable and controllable, as shown in Fig. 2(c and d). Compared to cubic and spherical planes, the reduced degree of symmetry for the triangular pyramidal bottom plane partially lifts the degeneracy and allows higher-order plasmonic gap modes to be easily resolved, as shown in Fig. 2(d) and 3. The three-dimensional pyramidal geometry also makes the film-coupled Au nanopyramid array more sensitive to the incident radiation and more efficiently confine incident light as EM energy at the gap, as shown in Fig. 4. This paves the way for the plasmonic gap mode to strongly interact with quantum emitters embedded at the gap.
Strong coupling between a quantum emitter and plasmon
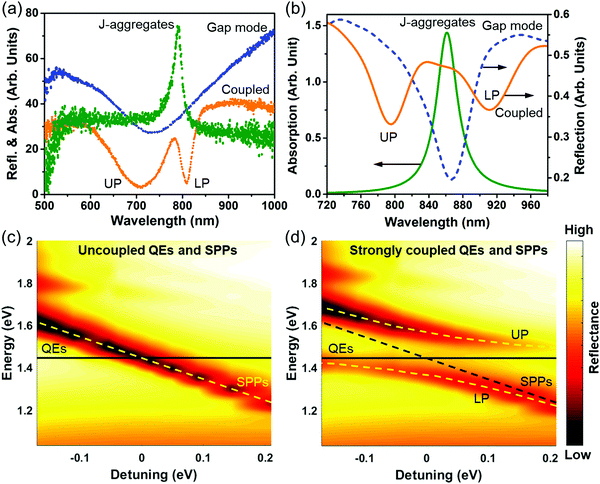
As mentioned above, surface plasmon polaritons (SPPs) supported on plasmonic metallic nanostructures suffer from high energy loss and weak nonlinearity. One promising approach to overcome the metal loss is to make the interaction of SPPs with QEs take place in the strong-coupling regime.24–32 The coupling strength g is characterized by Rabi frequency ΩR (ΩR = 2g), which quantifies the rate of energy exchange between the plasmonic cavity and QEs.33 In the strong-coupling regime, the coupling strength is strong enough to compensate for the damping rate κ of the plasmonic cavity and the spontaneous decay rate τ0 of QEs, i.e., g > κ,τ0. The extraordinary coupling strength facilitates an extremely rapid, coherent and reversible energy exchange between the plasmonic cavity and QEs, leading to two newly formed hybridized states called upper and lower plexcitons, which are half-light, half-matter, and are split by Rabi frequency.12,17,33,48 Given the dependence of the hybridized plexciton states on the coupling strength, the strongly coupled SPPs–QEs system has strong implications in state-of-the-art optoelectronic devices such as ultrafast switching, all-optical control, etc.49–51 In comparison, in the weak-coupling regime where the damping rate of the plasmonic cavity outcompetes the spontaneous decay rate of QEs and the coupling strength, i.e. κ > τ0,g, the interaction is incoherent and irreversible.12,17,33 The energy extracted from QEs is unidirectionally transferred to the cavity with the spontaneous decay rate enhanced by the cavity-dependent Purcell factor.The film-coupled Au nanopyramid array structure provides an excellent platform for achieving strong coupling between the QEs and the plasmonic cavity mode, as schematically shown in Fig. S8 (ESI†). For example, J-aggregates are typical QEs. In this work, J-aggregates are taken as the spacer layer to test the possibility of strong coupling by a combination of experimental measurements and FDTD simulations, as shown in Fig. 5. The experimentally measured reflection spectrum for the plasmonic gap mode and the absorption spectrum for J-aggregates are shown in Fig. 5(a). To sandwich J-aggregates in the gap, they were first mixed with polyvinyl alcohol (PVA) and then spin-coated on the Au film followed by fabrication of Au nanopyramid arrays (see Methods for detailed experimental procedures). The plasmonic gap mode was found to split into two new modes separated by 218 meV, which was the Rabi frequency. One new mode was blueshifted from the plasmonic gap mode and the other redshifted from the absorption peak of J-aggregates. To verify whether coherent coupling can be achieved between the plasmonic gap mode and the exciton of J-aggregates, FDTD simulations were conducted. In FDTD simulations, the permittivity of J-aggregates is assumed to follow the Lorentz Model, which is given by28
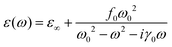 | (1) |
The calculated absorption spectrum of J-aggregates is derived from the imaginary part of the complex permittivity given by eqn (1) and is shown in Fig. 5(b). In the meantime, the reflection spectra for the corresponding plasmonic gap modes were calculated using FDTD simulations by modelling the spacer layer as an insulator with a fixed refractive index of 1.25, roughly the mean value of the real part of the permittivity of J-aggregates.
Without coupling, the calculated dispersion of the plasmonic gap modes was found to be independent of the absorption line of J-aggregates, as shown in Fig. 5(c), where the detuning is defined as the energy difference between the plasmonic gap mode and the absorption peak of the J-aggregates. With a layer of 16 nm J-aggregates sandwiched into the spacer, the plasmonic gap mode and J-aggregates were spectrally mixed. Instead of being independent of each other, their spectral mixture led to the Rabi splitting of the plasmonic gap mode and generated two new hybridized plexciton modes at 795 nm and 912 nm, respectively, as shown in Fig. 5(d). The mode splitting, however, does not necessarily guarantee that the strong-coupling regime is reached. As documented previously, the plasmonic coupling and a Fano resonance could also cause similar features.52,53 A positive confirmation of strong coupling requires that the coupling strength far exceeds any other damping rates.
For the case with a layer of 16 nm J-aggregates sandwiched between the Au film and the gold nanopyramid array pattern, the Rabi frequency was calculated as ΩR = 200 meV, comparable with the experimentally measured Rabi frequency. The coupling strength was found as 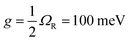 . The damping rate of SPPs was obtained by fitting the reflection dip with a Lorentzian function, which was given as κ = 56 meV. The fact that g > κ,γ0 confirms that strong coupling was indeed achieved in this nanostructure. The two new hybridized modes are actually two newly formed plexciton states corresponding to the upper plexciton (UP) and lower plexciton (LP), which are half-light, half matter. These entangled states are characteristic of strong coupling where SPPs and J-aggregates lose their own identities. The confined energy is rapidly and coherently exchanged between SPPs and J-aggregates at a rate of the Rabi frequency. By varying the thickness of the J-aggregate layer, the anti-crossing behavior of the two plexciton states is observed, as shown in Fig. 5(d), which would not occur in the weak-coupling regime.17
. The damping rate of SPPs was obtained by fitting the reflection dip with a Lorentzian function, which was given as κ = 56 meV. The fact that g > κ,γ0 confirms that strong coupling was indeed achieved in this nanostructure. The two new hybridized modes are actually two newly formed plexciton states corresponding to the upper plexciton (UP) and lower plexciton (LP), which are half-light, half matter. These entangled states are characteristic of strong coupling where SPPs and J-aggregates lose their own identities. The confined energy is rapidly and coherently exchanged between SPPs and J-aggregates at a rate of the Rabi frequency. By varying the thickness of the J-aggregate layer, the anti-crossing behavior of the two plexciton states is observed, as shown in Fig. 5(d), which would not occur in the weak-coupling regime.17
The anti-crossing region is of great fundamental significance. It has been predicted to give rise to numerous intriguing optical effects such as photon blockade, emission of correlated photons, nonclassical or squeezed state generation, super-radiant phase transitions and ultra-efficient light emission.17,54 Furthermore, the problems of high energy loss in metallic nanostructures can be effectively circumvented since the rates of any other damping channels are outcompeted by the overwhelmingly strong coupling rate in the strong-coupling region. The demonstration of reaching the strong-coupling regime by sandwiching a layer of excitonic material in the film-coupled gold nanopyramid array has strong implications in designing state-of-the-art optoelectronic devices with new functionalities by fully utilizing the nonlinearity of QEs and the transportability of SPPs.
Conclusions
In summary, a long-range ordered gold nanopyramid array pattern was fabricated on a glass substrate by nanosphere lithography. The gold nanopyramid array exhibited strong light scattering, displaying an intense reflection peak. The maximum electric field enhancement (|E|/|E0|) was estimated to be 271 at the corners, which decayed exponentially away from the pyramid bottom. After the gold nanopyramid array was coupled to a gold film, a plasmonic gap mode was generated in the silica spacer layer, which led to strong light absorption confined in the space layer. In the case of a 10 nm thick space layer, the maximum electric field enhancement (|E|/|E0|) and the magnetic field enhancement (|H|/|H0|) were estimated to be 233 and 25, respectively, which occurred at the gap edge. The magnetic field remained almost constant and the electric field decayed much slower with an increase in the distance away from the pyramid bottom. Because of the induced charges on opposite sides of the gap, the confined EM energy was found to oscillate back and forth between the spatially separated electric and magnetic counterparts, which caused the effective mode volume to be approximately the actual volume of the gap region. Filling the gap with J-aggregates, strong coupling between the plasmonic gap mode and J-aggregates occurred, creating two plexciton states. The demonstration of strong plasmon–exciton coupling on this two-dimensional metallic nanostructure not only effectively circumvents the unavoidable high loss on metals, but also makes it possible to fully utilize the nonlinearity of QEs and the high transportability of SPPs. It is worth noting that the coherent plasmon–exciton coupling (plexciton) is the most efficient way to transfer energy between plasmons and excitons, which will find promising applications in devices based on light–matter interactions.Methods
Chemicals and materials
Gold-coated glass slides were purchased from Fisher Scientific Inc. Polystyrene microspheres with a diameter of 600 nm were purchased from Thermo Scientific (Waltham, MA). XR1541 e-beam resist was purchased from Dow Corning. Acetone, methanol, and sulphuric acid (H2SO4) and hydrogen peroxide were purchased from Alfa Aesar (Haverhill, MA). Deionized (D.I.) water was produced by the Milli-Q Integral 3/5/10/15 system (18.2 MΩ cm, Millipore Corp., U.S.A.).Nanosphere lithography fabrication
Fig. S1 (ESI†) shows the procedure for fabrication of the Au nanopyramid array pattern on a glass substrate by NSL. Fig. 1 reveals the procedure for fabrication of the Au nanopyramid array–silica–Au film structure. Specifically, a thin layer with varying thicknesses of silica was first coated on a commercially available Au-coated glass slide by spin coating a layer of silica precursor (XR-1541) at varying speeds and then conducting heat treatment at 400 °C for 1 hour. Subsequently, a monolayer of polystyrene beads with a diameter of 600 nm was patterned on the silica surface by dip-coating. After natural drying in air, a layer of 5 nm Ti film was deposited, followed by depositing a 200 nm thick Au film. After the polystyrene beads were removed by ultrasonication, the film-coupled Au nanopyramid array was obtained. The entire fabrication process, which could be scaled up for mass production, was done in just one day in the cleanroom.Fabrication of the Au film–J-aggregates–Au nanopyramid structure
5 mg ml−1 of J-aggregates in water were mixed with 25 mg ml−1 of poly vinyl alcohol (PVA) in water, and then stirred for 3 h. The mixture was spin-coated on cleaned 1 cm × 1 cm gold-coated glass chips at 4000 rpm for 60 s to form a J-aggregate polymer thin film. A 5 nm thick silica layer was then deposited on the top of the J-aggregate polymer thin film for two reasons. The silica layer acted as a protective layer to prevent the J-aggregates from being damaged when depositing the gold pyramids; and it also helped to enable a hydrophilic surface for dip-coating whereas the J-aggregate polymer thin film was hydrophobic in nature. Later a monolayer of 500 nm sized polystyrene beads was dip-coated on the surface of silica. After drying in air, 5 nm thick Ti and 200 nm thick Au films were deposited successively on the monolayer. Finally, the chips were ultra-sonicated in methanol to remove the polystyrene beads, leaving the Au nanopyramid array on the top surface.Instrumentation
An e-beam evaporator (Kurt J. Lesker) was used to deposit gold. A spin coater (Laurel Technologies 600 spinner) was used to coat the silica precursor to make the silica films with different thickness. A scanning electron microscope (JEOL-JSM-7600F) was used to characterize the fabricated film-coupled gold nanopyramid array. Reflection spectra were acquired by an Ocean Optics USB 4000 spectrometer and DT-MINI-2-GS.Finite-difference time-domain (FDTD) simulations
FDTD simulations were implemented throughout the paper to study the film-coupled gold nanopyramid array using commercially available software Lumerical FDTD Solutions. A mesh size of 2 nm was imposed in the simulation region. The permittivity of gold was from Johnson & Christy.55 The refractive index of silica was set as 1.52. A plane wave was used as the input light source. Back reflection spectra, electromagnetic field enhancement, and surface polarization charges were calculated. Perfectly Matched Layer (PML) boundary conditions were imposed on all these simulations.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
Use of WVU Shared Research Facilities was acknowledged. This work was supported by the NIH (R15NS087515). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.References
- D. G. Nocera, The Artificial Leaf, Acc. Chem. Res., 2012, 45(5), 767–776 CrossRef CAS PubMed.
- A. I. Hochbaum and P. D. Yang, Semiconductor Nanowires for Energy Conversion, Chem. Rev., 2010, 110(1), 527–546 CrossRef CAS PubMed.
- J. N. Anker, W. P. Hall, O. Lyandres, N. C. Shah, J. Zhao and R. P. Van Duyne, Biosensing with plasmonic nanosensors, Nat. Mater., 2008, 7(6), 442–453 CrossRef CAS.
- T. Grotjohann, I. Testa, M. Leutenegger, H. Bock, N. T. Urban, F. Lavoie-Cardinal, K. I. Willig, C. Eggeling, S. Jakobs and S. W. Hell, Diffraction-unlimited all-optical imaging and writing with a photochromic GFP, Nature, 2011, 478(7368), 204–208 CrossRef CAS.
- H. Q. Li and N. Q. Wu, A large-area nanoscale gold hemisphere pattern as a nanoelectrode array, Nanotechnology, 2008, 19(27), 275301 CrossRef PubMed.
- J. Cesario, R. Quidant, G. Badenes and S. Enoch, Electromagnetic coupling between a metal nanoparticle grating and a metallic surface, Opt. Lett., 2005, 30(24), 3404–3406 CrossRef.
- Q. Y. Lin, Z. Y. Li, K. A. Brown, M. N. O'Brien, M. B. Ross, Y. Z. S. Butun, S. Butun, P. C. Chen, G. C. Schatz, V. P. Dravid, K. Aydin and C. A. Mirkin, Strong Coupling between Plasmonic Gap Modes and Photonic Lattice Modes in DNA-Assembled Gold Nanocube Arrays, Nano Lett., 2015, 15(7), 4699–4703 CrossRef CAS PubMed.
- A. Moreau, C. Ciraci, J. J. Mock, R. T. Hill, Q. Wang, B. J. Wiley, A. Chilkoti and D. R. Smith, Controlled-reflectance surfaces with film-coupled colloidal nanoantennas, Nature, 2012, 492(7427), 86 CrossRef CAS PubMed.
- F. Ding, J. Dai, Y. T. Chen, J. F. Zhu, Y. Jin and S. I. Bozhevolnyi, Broadband near-infrared metamaterial absorbers utilizing highly lossy metals, Sci. Rep., 2016, 6, 39445 CrossRef CAS PubMed.
- T. Maurer, P. M. Adam and G. Leveque, Coupling between plasmonic films and nanostructures: from basics to applications, Nanophotonics, 2015, 4(3), 361–382 Search PubMed.
- F. Ding, Y. Q. Yang, R. A. Deshpande and S. I. Bozhevolnyi, A review of gap-surface plasmon metasurfaces: fundamentals and applications, Nanophotonics, 2018, 7(6), 1129–1156 CAS.
- J. T. Hugall, A. Singh and N. F. van Hulst, Plasmonic Cavity Coupling, ACS Photonics, 2018, 5(1), 43–53 CrossRef CAS.
- S. A. Maier, Plasmonics: Fundamentals and Applications, Springer, US, 2010 Search PubMed.
- M. I. Stockman, Spasers explained, Nat. Photonics, 2008, 2(6), 327–329 CrossRef CAS.
- R. Kolesov, B. Grotz, G. Balasubramanian, R. J. Stohr, A. A. L. Nicolet, P. R. Hemmer, F. Jelezko and J. Wrachtrup, Wave-particle duality of single surface plasmon polaritons, Nat. Phys., 2009, 5(7), 470–474 Search PubMed.
- K. F. MacDonald, Z. L. Samson, M. I. Stockman and N. I. Zheludev, Ultrafast active plasmonics, Nat. Photonics, 2009, 3(1), 55–58 CrossRef CAS.
- P. Vasa and C. Lienau, Strong Light–Matter Interaction in Quantum Emitter/Metal Hybrid Nanostructures, ACS Photonics, 2018, 5(1), 2–23 CrossRef CAS.
- A. Maser, B. Gmeiner, T. Utikal, S. Gotzinger and V. Sandoghdar, Few-photon coherent nonlinear optics with a single molecule, Nat. Photonics, 2016, 10(7), 450–453 CrossRef CAS.
- M. Pfeiffer, P. Atkinson, A. Rastelli, O. G. Schmidt, H. Giessen, M. Lippitz and K. Lindfors, Coupling a single solid-state quantum emitter to an array of resonant plasmonic antennas, Sci. Rep., 2018, 8, 3415 CrossRef PubMed.
- V. I. Klimov, A. A. Mikhailovsky, S. Xu, A. Malko, J. A. Hollingsworth, C. A. Leatherdale, H. J. Eisler and M. G. Bawendi, Optical gain and stimulated emission in nanocrystal quantum dots, Science, 2000, 290(5490), 314–317 CrossRef CAS.
- P. Zhang, I. Protsenko, V. Sandoghdar and X. W. Chen, A Single-Emitter Gain Medium for Bright Coherent Radiation from a Plasmonic Nanoresonator, ACS Photonics, 2017, 4(11), 2738–2744 CrossRef CAS.
- Y. Zhou, Z. Wang, A. Rasmita, S. Kim, A. Berhane, Z. Bodrog, G. Adamo, A. Gali, I. Aharonovich and W. Gao, Room temperature solid-state quantum emitters in the telecom range, Sci. Adv., 2018, 4(3), eaar3580 CrossRef.
- S. Lichtmannecker, M. Florian, T. Reichert, M. Blauth, M. Bichler, F. Jahnke, J. J. Finley, C. Gies and M. Kaniber, A few-emitter solid-state multi-exciton laser, Sci. Rep., 2017, 7, 7420 CrossRef CAS PubMed.
- R. Chikkaraddy, B. de Nijs, F. Benz, S. J. Barrow, O. A. Scherman, E. Rosta, A. Demetriadou, P. Fox, O. Hess and J. J. Baumberg, Single-molecule strong coupling at room temperature in plasmonic nanocavities, Nature, 2016, 535(7610), 127–130 CrossRef CAS.
- H. Gross, J. M. Hamm, T. Tufarelli, O. Hess and B. Hecht, Near-field strong coupling of single quantum dots, Sci. Adv., 2018, 4(3), eaar4906 CrossRef PubMed.
- K. Chevrier, J. M. Benoit, C. Symonds, J. Paparone, J. Laverdant and J. Bellessa, Organic Exciton in Strong Coupling with Long-Range Surface Plasmons and Waveguided Modes, ACS Photonics, 2018, 5(1), 80–84 CrossRef CAS.
- E. Eizner, O. Avayu, R. Ditcovski and T. Ellenbogen, Aluminum Nanoantenna Complexes for Strong Coupling between Excitons and Localized Surface Plasmons, Nano Lett., 2015, 15(9), 6215–6221 CrossRef CAS.
- G. Zengin, G. Johansson, P. Johansson, T. J. Antosiewicz, M. Kall and T. Shegai, Approaching the strong coupling limit in single plasmonic nanorods interacting with J-aggregates, Sci. Rep., 2013, 3, 3074 CrossRef.
- P. Torma and W. L. Barnes, Strong coupling between surface plasmon polaritons and emitters: a review, Rep. Prog. Phys., 2015, 78(1), 013901 CrossRef CAS.
- H. Wang, H. Y. Wang, A. Bozzola, A. Toma, S. Panaro, W. Raja, A. Alabastri, L. Wang, Q. D. Chen, H. L. Xu, F. De Angelis, H. B. Sun and R. P. Zaccaria, Dynamics of Strong Coupling between J-Aggregates and Surface Plasmon Polaritons in Subwavelength Hole Arrays, Adv. Funct. Mater., 2016, 26(34), 6198–6205 CrossRef CAS.
- G. Zengin, M. Wersall, S. Nilsson, T. J. Antosiewicz, M. Kall and T. Shegai, Realizing Strong Light–Matter Interactions between Single-Nanoparticle Plasmons and Molecular Excitons at Ambient Conditions, Phys. Rev. Lett., 2015, 114(15), 157401 CrossRef PubMed.
- R. M. Liu, Z. K. Zhou, Y. C. Yu, T. W. Zhang, H. Wang, G. H. Liu, Y. M. Wei, H. J. Chen and X. H. Wang, Strong Light–Matter Interactions in Single Open Plasmonic Nanocavities at the Quantum Optics Limit, Phys. Rev. Lett., 2017, 118(23), 237401 CrossRef PubMed.
- D. G. Baranov, M. Wersall, J. Cuadra, T. J. Antosiewicz and T. Shegai, Novel Nanostructures and Materials for Strong Light Matter Interactions, ACS Photonics, 2018, 5(1), 24–42 CrossRef CAS.
- N. A. Mortensen, S. Raza, M. Wubs, T. Sondergaard and S. I. Bozhevolnyi, A generalized non-local optical response theory for plasmonic nanostructures, Nat. Commun., 2014, 5, 3809 CrossRef CAS.
- R. Esteban, A. G. Borisov, P. Nordlander and J. Aizpurua, Bridging quantum and classical plasmonics with a quantum-corrected model, Nat. Commun., 2012, 3, 825 CrossRef PubMed.
- R. Jurga, S. D'Agostino, F. Della Sala and C. Ciraci, Plasmonic Nonlocal Response Effects on Dipole Decay Dynamics in the Weak- and Strong-Coupling Regimes, J. Phys. Chem. C, 2017, 121(40), 22361–22368 CrossRef CAS.
- W. Q. Zhu, R. Esteban, A. G. Borisov, J. J. Baumberg, P. Nordlander, H. J. Lezec, J. Aizpurua and K. B. Crozier, Quantum mechanical effects in plasmonic structures with subnanometre gaps, Nat. Commun., 2016, 7, 11495 CrossRef CAS.
- K. Santhosh, O. Bitton, L. Chuntonov and G. Haran, Vacuum Rabi splitting in a plasmonic cavity at the single quantum emitter limit, Nat. Commun., 2016, 7, 11823 CrossRef PubMed.
- T. B. Hoang, G. M. Akselrod and M. H. Mikkelsen, Ultrafast Room-Temperature Single Photon Emission from Quantum Dots Coupled to Plasmonic Nanocavities, Nano Lett., 2016, 16(1), 270–275 CrossRef CAS PubMed.
- C. L. Haynes and R. P. Van Duyne, Nanosphere lithography: A versatile nanofabrication tool for studies of size-dependent nanoparticle optics, J. Phys. Chem. B, 2001, 105(24), 5599–5611 CrossRef CAS.
- A. Zangwill, Modern Electrodynamics, Cambridge University Press, 2013 Search PubMed.
- F. Le, N. Z. Lwin, J. M. Steele, M. Käll, N. J. Halas and P. Nordlander, Plasmons in the Metallic Nanoparticle−Film System as a Tunable Impurity Problem, Nano Lett., 2005, 5(10), 2009–2013 CrossRef CAS PubMed.
- J. J. Mock, R. T. Hill, A. Degiron, S. Zauscher, A. Chilkoti and D. R. Smith, Distance-Dependent Plasmon Resonant Coupling between a Gold Nanoparticle and Gold Film, Nano Lett., 2008, 8(8), 2245–2252 CrossRef CAS PubMed.
- A. Rose, T. B. Hoang, F. McGuire, J. J. Mock, C. Ciracì, D. R. Smith and M. H. Mikkelsen, Control of Radiative Processes Using Tunable Plasmonic Nanopatch Antennas, Nano Lett., 2014, 14(8), 4797–4802 CrossRef CAS PubMed.
- G. Lévêque and O. J. F. Martin, Optical interactions in a plasmonic particle coupled to a metallic film, Opt. Express, 2006, 14(21), 9971–9981 CrossRef.
- J. Mertens, M.-E. Kleemann, R. Chikkaraddy, P. Narang and J. J. Baumberg, How Light Is Emitted by Plasmonic Metals, Nano Lett., 2017, 17(4), 2568–2574 CrossRef CAS PubMed.
- K. Q. Le, Q. M. Ngo and T. K. Nguyen, Nanostructured Metal–Insulator–Metal Metamaterials for Refractive Index Biosensing Applications: Design, Fabrication, and Characterization, IEEE J. Sel. Top. Quantum Electron., 2017, 23(2), 388–393 Search PubMed.
- J. Sun, H. Hu, D. Zheng, D. Zhang, Q. Deng, S. Zhang and H. Xu, Light-Emitting Plexciton: Exploiting Plasmon–Exciton Interaction in the Intermediate Coupling Regime, ACS Nano, 2018, 12(10), 10393–10402 CrossRef CAS PubMed.
- P. Vasa, R. Pomraenke, G. Cirmi, E. De Re, W. Wang, S. Schwieger, D. Leipold, E. Runge, G. Cerullo and C. Lienau, Ultrafast Manipulation of Strong Coupling in Metal-Molecular Aggregate Hybrid Nanostructures, ACS Nano, 2010, 4(12), 7559–7565 CrossRef CAS PubMed.
- Z. Chai, X. Hu, F. Wang, X. Niu, J. Xie and Q. Gong, Ultrafast All-Optical Switching, Adv. Opt. Mater., 2017, 5(7), 1600665 CrossRef.
- P. M. Walker, L. Tinkler, D. V. Skryabin, A. Yulin, B. Royall, I. Farrer, D. A. Ritchie, M. S. Skolnick and D. N. Krizhanovskii, Ultra-low-power hybrid light–matter solitons, Nat. Commun., 2015, 6, 8317 CrossRef CAS PubMed.
- E. Prodan, C. Radloff, N. J. Halas and P. Nordlander, A hybridization model for the plasmon response of complex nanostructures, Science, 2003, 302(5644), 419–422 CrossRef CAS PubMed.
- M. F. Limonov, M. V. Rybin, A. N. Poddubny and Y. S. Kivshar, Fano resonances in photonics, Nat. Photonics, 2017, 11(9), 543–554 CrossRef CAS.
- K. M. Birnbaum, A. Boca, R. Miller, A. D. Boozer, T. E. Northup and H. J. Kimble, Photon blockade in an optical cavity with one trapped atom, Nature, 2005, 436(7047), 87–90 CrossRef CAS PubMed.
- P. B. Johnson and R. W. Christy, Optical Constants of the Noble Metals, Phys. Rev. B: Solid State, 1972, 6(12), 4370–4379 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Fig. S1–S8. See DOI: 10.1039/c8nh00286j |
| ‡ The first co-authors contributed to this work equally. |
| This journal is © The Royal Society of Chemistry 2019 |