Open Access Article
Open Access ArticleNegative Poisson's ratio in 2D life-boat structured crystals†
Ruhao
Fang
 ad,
Xiangyuan
Cui
*bc,
Catherine
Stampfl
a,
Simon P.
Ringer
bc and
Rongkun
Zheng
ad,
Xiangyuan
Cui
*bc,
Catherine
Stampfl
a,
Simon P.
Ringer
bc and
Rongkun
Zheng
 *acd
*acd
aSchool of Physics, The University of Sydney, New South Wales 2006, Australia. E-mail: rongkun.zheng@sydney.edu.au
bSchool of Aerospace, Mechanical and Mechatronic Enigineering, The University of Sydney, Sydney, New South Wales 2006, Australia. E-mail: carl.cui@sydney.edu.au
cAustralian Centre for Microscopy and Microanalysis, The University of Sydney, Sydney, New South Wales 2006, Australia
dNano Institute, The University of Sydney, Sydney, New South Wales 2006, Australia
First published on 12th December 2018
Abstract
Two-dimensional auxetic materials with negative Poisson's ratio expand in response to a tensile strain in cross-section. Such counter-intuitive behaviours have been mainly ascribed to concave structures with ideal rigid ball-stick models. Here, based on first-principles calculations, we systematically analyze the mechanical behaviours of three life-boat structured two-dimensional (2D) materials and report two new auxetic materials: δ-arsenic and δ-graphane. The calculated Poisson's ratio values are correlated with Young's modulus, cohesive energy, and valence shell electron pair repulsion of isostructures. Combining with previous research, we provide a self-consistent explanation of the origin of the 2D in-plane negative Poisson's ratio and an algorithmic route to discover new auxetic materials by comparing the energy restored in bond rotation and stretch.
Introduction
The Poisson's ratio (PR) of a material is defined as νji = −εj/εi, where εi is an applied strain in the active (i-axis) direction and εj is the corresponding strain in the transverse (j-axis) direction. It reflects the response in the transverse direction to a uniaxial strain in the longitudinal direction. For normal solids, Poisson's ratio usually falls in the range 0–0.5,1 which behaves as a geometrically inverse feedback to external strain. However, counter-intuitively, there exist a group of materials with negative Poisson's ratio (NPR), namely auxetic materials, exhibiting expansion in the transverse direction when a tensile strain is applied in the longitudinal direction.2 Materials with NPR are of great interest in biomedicine,3 fasteners,4 tougher composites,5 tissue engineering applications6 for their enhanced toughness7 and shear resistance.8 R. Lakes firstly correlated these phenomena to the unique mechanical structure of the auxetic materials.9 Since ordinary crystals commonly have the convex structure (bonds in which are located at the edge of the unit cell), the perpendicular cross section of the unit cell tends to decrease under a tensile strain, compelling the atoms to shrink in the transverse direction. On the contrary, concave structure (the bonds in which are located inside or on the surface of the unit cell) tends to behave in a positive feedback to strain, exhibiting an NPR.10 For three-dimensional (3D) auxetic materials, such as α-cristobalite,11 the A7 structure,12 the cubic metals,13 and the honeycomb,14 the more concave the structure is, the higher the NPR will be.15 In such an ideal treatment, crystal structures were assumed to be made of rigid sticks linked by flexible hinges (i.e. ball-stick model), neglecting the chemical effects arising from distinct electronic configurations at different bond angles.Since the discovery of graphene in 2004, two-dimensional (2D) materials have been under intensive research for diverse applications due to their larger elastic strain duration than their bulk counterparts16 In particular, α-phosphorene was the first auxetic 2D material discovered in 2014, with an NPR of −0.027 in the zigzag direction.17 Its peculiar geometry in the unit cell is formed by three P–P bonds and a lone pair, each with two sp3 orbital electrons from neighbouring phosphorus atoms.18 Crystals with such bonding framework may result in four tetragonal systems (α-, β-, γ-, and δ-phase) and more monoclinic allotropes (such as ε-phase), as found in phosphorene,18,19 and arsenic.20 Similarly, graphane, a hydrocarbon with the C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H ratio = 1
H ratio = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, may also form in these structures (see ref. 21 and references therein)21 since the electrons around carbon atoms have similar distribution: three pairs of C–C sp3 bonding electrons and one pair of C–H sp3 bonding electrons taking the place of the lone pair in phosphorene or arsenic. Subsequently, many 2D materials with puckered structure, such as SnSe,22 penta-graphene23 and W2C,24 were reported to have NPR. Recently, δ-phosphorene, one of the 2D tetragonal-system phosphorene allotropes with the so-called life-boat structure, has been reported with a significantly low NPR ∼ −0.267.25 Moreover, 1T-phased 2D transition metal dichalcogenides (TMDCs) have been systematically investigated and some possess positive PR (PPR) while others have NPR.26 The variation of PR values was attributed to the distinct p–d orbital electronic interactions between the chalcogen p orbitals and the transition-metal d orbitals. This highlights the fundamental role of chemical bonding in affecting the PR values for iso-structural materials.
1, may also form in these structures (see ref. 21 and references therein)21 since the electrons around carbon atoms have similar distribution: three pairs of C–C sp3 bonding electrons and one pair of C–H sp3 bonding electrons taking the place of the lone pair in phosphorene or arsenic. Subsequently, many 2D materials with puckered structure, such as SnSe,22 penta-graphene23 and W2C,24 were reported to have NPR. Recently, δ-phosphorene, one of the 2D tetragonal-system phosphorene allotropes with the so-called life-boat structure, has been reported with a significantly low NPR ∼ −0.267.25 Moreover, 1T-phased 2D transition metal dichalcogenides (TMDCs) have been systematically investigated and some possess positive PR (PPR) while others have NPR.26 The variation of PR values was attributed to the distinct p–d orbital electronic interactions between the chalcogen p orbitals and the transition-metal d orbitals. This highlights the fundamental role of chemical bonding in affecting the PR values for iso-structural materials.
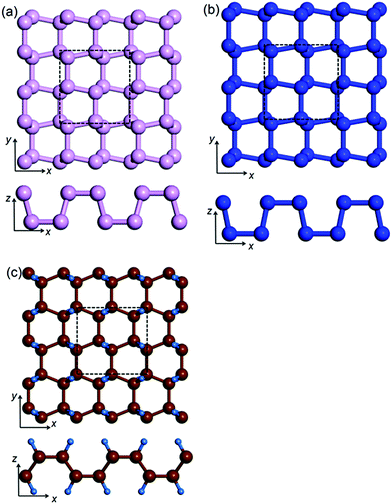
Although different elements with isostructures are expected to have different PR values, we notice that the underlying mechanism of NPR from a chemical sp3 bonding perspective is unclear. According to Lakes' theory, any material with concave life-boat structure (see Fig. 1) should have an NPR. In a practical process, tensile strain enlarges the length of the bonds, and the valence shell electron pair repulsion (VSEPR) tends to limit the bonds rotational freedom. As such, the NPR values of iso-structural systems consisting of different elements should be related to their corresponding elemental electronic configurations. To study the intrinsic logic behind PR values of iso-structural systems, we select the life-boat structure (one of the 2D structure with reported lowest PR) and calculate the PR values for δ-arsenic,20 δ-phosphorene and δ-graphane21 (a mechanically stable hydrocarbon with the same structure as δ-phosphorene) and correlate NPR values with their chemical structures. Moreover, combining with previous auxetic material research, we analyse and summarize the correlation between the NPR and electronic configurations and provide an operating route to find new 2D auxetic materials.
Methods
DFT computational details
The first-principles calculations were based on the density functional theory (DFT) as implemented in the Vienna ab initio simulation package (VASP) and were used to determine the atomic structure and electronic properties of atomic-layer δ-phosphorene, δ-arsenic and δ-graphane under certain strains. We employed the generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof (PBE)27 with van der Waals (VdW) corrections in exchange and correlation functions.28 Convergence testing was performed for cut-off energies from 100 eV to 1000 eV and k-point meshes from 4 × 4 × 4 to 24 × 24 × 24. In a balance of time consumption and accuracy, a cut-off energy of 400 eV for phosphorene and graphene and 800 eV for arsenic were adopted to ensure total energy convergence. A sampling of the reciprocal space Brillouin zone was set as a grid of 8 × 8 × 8 k-points. To simulate 2D crystals, a unit cell with periodic boundary conditions was used, in which a vacuum space of at least 20 Å was applied to minimize the interaction from z-direction neighbours.The uniaxial strain is defined as
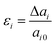 | (1) |
The stress is defined as
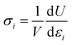 | (2) |
Results and discussion
Crystal structure
The unit cell of monolayer δ-phosphorene (δ-arsenic and δ-graphane) consisting of 8 phosphorus (arsenic and carbon-hydrogen) atoms, forming two atomic layers, are shown in Fig. 1. The lattice constants are shown in Table 1. The lattice constants in our calculations are systematically smaller than previously reported values (in the bracket in Table 1) due to the inclusion of VdW correction in our work. We found that VdW interaction among neighbouring, but not chemically bonded, atoms leads to non-negligible changes in the lattice constants even in these monolayer 2D materials. The life-boat shape of these structures along the x-direction and the zigzag shapes in the y-direction results in anisotropic mechanical responses in different directions, including anisotropic Poisson's ratios. We also tested solid nitrogen and antimony in this structure and confirmed these structures were mechanically unstable.| a Values for δ-graphane are for carbon and C–C bonds. | |||
|---|---|---|---|
| Crystal | δ-Phosphorene | δ-Arsenic | δ-Graphane |
| Lattice constant a (Å) | 5.50 (5.56 (ref. 18)) | 5.86 (5.91 (ref. 20)) | 3.76 (3.83 (ref. 21)) |
| Lattice constant b (Å) | 5.40 (5.42 (ref. 18)) | 5.90 (5.93 (ref. 20)) | 3.69 (3.83 (ref. 21)) |
| Cohesive energy Ec (eV per atom) | 3.67 (3.23 (ref. 18)) | 2.80 (3.06 (ref. 20)) | 3.29a |
| Atom radius (pm) | 195 | 205 | 170a |
| Bond length (Å) | 2.27 | 2.51 | 1.09a |
Poisson's ratios and mechanical properties
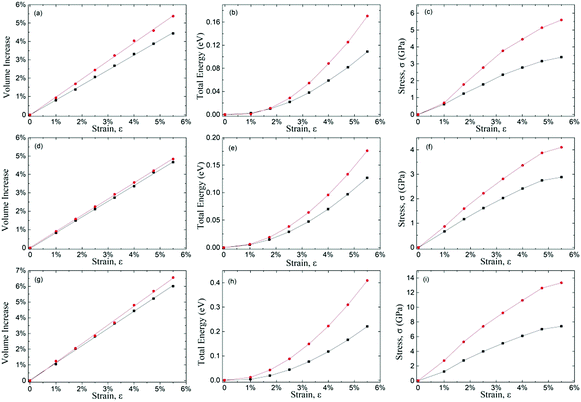
Table 2 shows the calculated Poisson's ratio (νxy and νyx) and mechanical properties for δ-phosphorene, δ-arsenic and δ-graphane subjected to an up-to 5.5% tensile strain in either x- or y-direction. The negative PRs are found in both directions for all these life-boat structured crystals. This indicates that the occurrence of NPR can be expected based on a purely geometric consideration. However, the PR values vary from −0.072 to −0.148 in the x-direction and −0.090 to −0.265 in the y-direction for these similar puckered structures of different elements. Evidently, the NPR value is strongly affected by the chemical structure.| Property | δ-Phosphorene | δ-Arsenic | δ-Graphane |
|---|---|---|---|
| Poisson's ratio νxy | −0.148 | −0.072 | −0.080 |
| Poisson's ratio νyx | −0.265 | −0.090 | −0.160 |
| Young's modulus Ex (GPa) | 83.1 | 67.1 | 200 |
| Young's modulus Ey (GPa) | 145.2 | 97.3 | 340 |
Table 3 shows the comparison of NPR values of recently predicted 2D materials, where δ-graphane ranks 6th.
| System | Method | Poisson's ratio νxy | Poisson's ratio νyx |
|---|---|---|---|
| a Values in brackets are the calculation results in ref. 25. | |||
| α-Phosphorene (BP) | PBE17 | 0.046 | −0.027 |
| δ-Phosphorene | PBE + D2 (ref. 25) | −0.148 (−0.158)a | −0.265 (−0.267)a |
| δ-Arsenic | PBE + D2 | −0.072 | −0.090 |
| δ-Graphane | PBE + D2 | −0.080 | −0.160 |
| Penta-graphene | PBE23 | −0.068 | — |
| SnSe | PBE22 | — | −0.17 |
| 1T-MoS2 | PBE26 | −0.07 | −0.07 |
| 1T-WSe2 | PBE26 | −0.2 | −0.2 |
| 1T-TcTe2 | PBE26 | −0.38 | −0.38 |
| W2C | PBE24 | −0.33 | −0.36 |
Mechanical behaviour under tensile strain
To understand the strain behaviours of the auxetic materials, we systematically calculated the volume, total energy and stress as a function of tensile strain (up to 5.5%) of δ-phosphorene, δ-graphane and δ-arsenic (shown in Fig. 2(a–i)). During the calculation for volume–strain curves, the volume (V) of the 2D unit cell is defined as the product of the two in-plane lattice constants and the effective layer thickness.29 For positive Poisson's ratio (PPR) materials, enlarged longitudinal (the direction of applied strain) lattice constant reduces the other two in the transverse and vertical directions. The volume of NPR materials with the life-boat structure increases linearly-like upon tensile strain, but faster than PPR materials since both in-plane lattice constants increase upon longitudinal tensile strain. The ratio of the increment of volume to the strain is approximately 1 for all the three 2D materials studied here, while the ratio for traditional cubic mononitrides is less than 0.6.30 The parabolic trend of total energy–strain curves is similar to those of non-auxetic behaviour materials, which indicates that for both PPR and NPR materials, the external work done upon elastic strain is transformed into strain energy due to deformation.The anisotropic mechanical responses in different directions are evident in the calculated strain–stress curves, where the stress increases monotonously, but slows down as the tensile strain rises, which implies the PR is a strain-dependent property. These facts above indicate that the NPR phenomenon is more counter-intuitive in macroscopic geometrical behaviour than in mechanical behaviours.
Bond rigidity
The different PR values of TMDCs was ascribed to the t2g-bonding orbitals with different d-orbital electrons,26 yet neither phosphorene nor graphane has d-orbital electrons. Here we put forward a more general explanation. For a given auxetic structure, the length of rigid bonds in an ideal ball-stick model is unchanged and the sticks can rotate freely around the “knot” (ball) under applied strain. However, if the length of the bonds is changeable, the “sticks” tend to extend to bear the strain in order to reduce the extent of change in the transverse lattice constant. To quantify the rigidity of the chemical bonds among these three systems, we compare the cohesive energies of these three systems. From δ-arsenic, δ-graphane to δ-phosphorene, the increasing high cohesive energy values reflect that it is more difficult to elongate the chemical bond (Table 1). For those structures with greater stiffness, they tend to rearrange the geometrical structure so as to extend the transverse lattice constant in responding the longitudinal tensile strain, which means smaller PR; hence νphosphorene < νgraphane < νarsenic.For a given structure, the stiffness partially reflects the rigidity of the bond. Thus, we also calculated the effective Young's modulus for each system based on the stress–strain curves (shown in Table 2). δ-Phosphorene and δ-arsenic have the greatest similarity as they are both isostructures with similar charge distribution. The phosphorus-based life-boat structure has a greater Young's modulus (83.1 GPa in the x-direction and 145.2 GPa in the y-direction) than the arsenic-based one (67.1 GPa in the x-direction and 97.3 GPa in the y-direction), which implies δ-phosphorene has stronger bonds than δ-arsenic. Also, δ-phosphorene has smaller values of PR than δ-arsenic, which is consistent with our previous discussion.
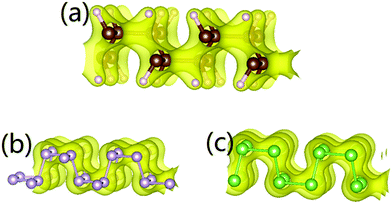
Though δ-graphane has the highest Young's modulus (200 GPa in the x-direction and 340 GPa in the y-direction), it is δ-phosphorene that shows the most obvious auxetic behaviour, with the lowest PR, −0.265 in the y-direction and −0.148 in the x-direction (in agreement with the previous work25). This indicates that the stiffness is a collective macroscopic property, which reflects how difficulty we change the length of the whole material rather than just a specific chemical bond. This paradox is also observed in 1T-TMDCs.26 The variation of NPR values for isostructures is believed to be determined by their distinct elemental electronic configurations. To fully explain this phenomenon, we calculate the electron charge distribution (shown in Fig. 3) of the three systems, which reveals a deeper understanding.
sp3 VSEPR
Ideal geometrical analysis of auxetic materials assumed that bonds can freely rotate around connected atoms. However, the valence shell electron pair repulsion (VSEPR)31 among neighbouring bonding or lone paired electrons constrain the rotation. In a life-boat structure, there are four sp3 orbitals around each P (As, C) atom, three of which are occupied by pairs of bonding electrons from neighbouring P (As, C) atoms, and the last one is occupied by 2 lone paired electrons (δ-phosphorene and δ-arsenic) or 2 bonding electrons from the C–H bond (δ-graphane). Fig. 3 shows the charge distribution of these three systems, from which the lone pairs in δ-phosphorene and δ-arsenic are closer to P or As atoms compared to the C–H orbital electrons in δ-graphane to the C atoms. When a tensile strain is applied, P–P and As–As bonds are easier to rotate towards the paired electrons as the paired electrons can move further away from the P or As atoms. On the other hand, C–H bonds show greater VSEPR to C–C bonds than that among lone pair to P–P or As–As bond. Smaller VSEPR allows P–P bonds in δ-phosphorene to rotate more freely than C–C bonds in δ-graphane. As a result, νphosphorene is greater than νgraphane, and νgraphane is closer in value to νarsenic than νphosphorene.Deformation mechanism
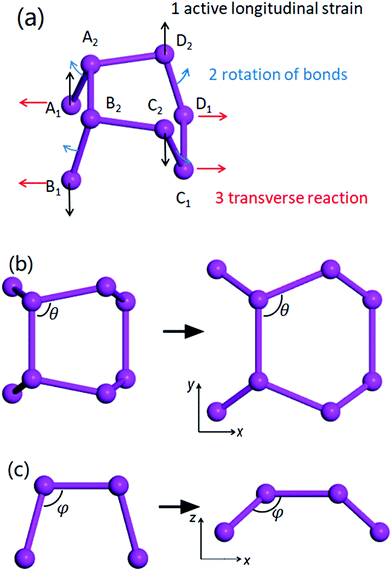
To systematically understand the microscopic auxetic behaviour of the life-boat structured materials, we plot a diagram of the deformation mechanism in a unit cell under longitudinal tensile strain in the y-direction (Fig. 4). The ball-stick model in the figure is used to represent either the carbon framework in δ-graphane or the unit cell of δ-phosphorene or δ-arsenic. There are 3 different motions including 2 translational motions for both the x- and y-directions (marked red and black, respectively) and 1 rotational motion (marked in blue) during the rearrangement of the 8 atoms (or 8 pairs of CH for δ-graphane) in the unit cell. When a tensile strain is applied, the outer four atoms (A1, B1, C2 and D2) in the y-direction move outwards correspondingly (as shown by black arrows). The two bonds D1D2 and A2D2 constrain the movement of atom D2 and pull the D1 and A2 (so as to A1 B1 and C2 due to the symmetry as shown in Fig. 4). The bonds A2B2 and C1D1 are slightly stretched and store the energy from the work done by tensile strain and the bonds A1A2, B1B2, C1C2 and D1D2 are forced to rotate (as shown by blue arrows). However, the repulsion from the paired electrons in the last sp3 orbital (either in the C–H bond or a suspended orbital) around all 8 atoms limits the rotation. Under this mechanism, the energy stored in the stretched A2B2 and C1D1 bonds should balance that in the compressional deformation of electron density by bond rotation. As a result, the rotations reduce the effective thickness and push the inner 4 atoms (A2, B2, C1 and D1) outwards as well (as shown by the red arrows). The collection of these processes manifests the enlarged transverse lattice constant.Pattern to find new auxetic material
Combining our analysis and previous NPR research, we can now summarize the origin of the NPR phenomenon for 2D materials at the atomic level. Here we define a (x-direction) and b (y-direction) as the two in-plane lattice constants of a 2D material unit cell, and c as the reduced effective thickness in the z-direction. For a 2D material, the effective thickness is much less than a and b, and the decrease of c is predominantly caused by the flatting of the chemical bonds connecting interlayer atoms under a tensile strain. As a result, the effective volume enlarges with increasing applied tensile strain. Indeed, the thickness of both α-phosphorene and penta-graphene obviously decrease under tensile strains.17,23 Hypothetically, if we apply an unrealistically large strain in either the x- or y-directions, but keep the neighbouring atom is bonded at in a reasonable distance (same value as the strain-free bond distance), the atoms tend to arrange in a single atomic plane. Thus, to perform NPR, the 2D structure must be arranged in at least 2 atomic layers.Another important feature of 2D auxetic materials is that the atoms are connected by the chemical bonds inside the unit cell or on the surface instead of on the edge, which is often described as a puckered, buckled or corrugated structure. The tetragonal or hexagonal systems under strain remain in similar shapes, but the bond angles change. SnSe, α-phosphorene and life-boat structures have only 4 atoms at the vertices of the tetragonal unit cell, while bonds of TMDCs lie on the lateral surface of the hexagonal unit cell. The non-zero thickness and the lack of constraint on the edge are two prerequisites for an NPR in terms of the geometrical structure.
The work done by strain can be restored both in stretched chemical bonds and distorted charge distribution caused by VSEPR. The whole system tends to distort to an away-from-equilibrium-state with lower total energy. For a given geometrical structure, rigid bonds tend to force other bonds to rotate, while soft bonds tend to be stretched. Either PPR or NPR is determined by whether the enlargement or rotation of the chemical bonds plays a dominant role in energy restoration. Both rigidity and ease of rotation are important in the auxetic phenomenon. This can be explained by the gradient of the total energy in a spherical coordinate system referred by bonds:
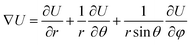 | (3) |
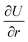 , rotation in a plane for
, rotation in a plane for 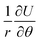 or thinning for
or thinning for 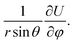 The ratio of
The ratio of 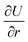 to
to 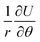 in δ-phosphorene, δ-arsenic and δ-graphene under strain in the armchair direction are approximately 5
in δ-phosphorene, δ-arsenic and δ-graphene under strain in the armchair direction are approximately 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2.2
1, 2.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 1.2
1, and 1.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, respectively (more details see ESI†).
1, respectively (more details see ESI†).
For those NPR structures having similar charge distribution, such as life-boat phosphorene and arsenic systems, larger cohesive energy and Young's modulus imply stronger bonding. The stronger bonds force other bonds to rotate under a tensile strain, thus larger Young's modulus shows lower PR value. However, in some cases, the stronger VSEPR from neighboured bonds or lone pairs weakens this effect, often along with different charge distribution and density of states. For life-boat graphane, the VSEPR between the C–H bond and the C–C bond constrains the rotation of freedom and the PR of δ-graphane is greater than δ-phosphorene though the C–C bond is stronger than the P–P bond. Similarly, weak t2g–p coupling in d0, d5 and d6 TMDCs causes strong repulsion among the M–X bonds, reducing the NPR and some even become PPR.26 The mechanical formation or deformation pattern for bonds is fundamentally determined by the elemental electronic configuration, in which to achieve NPR behaviour, the bonds have to be both rigid and free for rotation.
This conclusion is not contradictory to Lakes' theory. The geometrical structure decides the mechanical reaction upon a tensile strain and depends on the electronic configuration of the elements selected, which also decides the bonding information. Fig. 5 simplifies the critical factors in the origin of NPR, which provides a route to predict 2D NPR material. In practice, starting with a discovered NPR material, first one needs to find several isostructures with different elements, then to investigate the charge density and charge distribution to compare the VSEPR. If the new structure has a similar VSEPR, the structure with greater rigidity will lead to a lower NPR. If there exists a new factor affecting the rotational freedom, then the final criterion is the comparison between the energy restored in bonds stretch and rotation under tensile strain. If the bonds tend to flatten then it should have NPR. To verify such an idea we have calculated the PR values of another allotrope of phosphorene – ε-phosphorene,19 which has a similar side view and bond information to that of δ-phosphorene. Indeed, ε-phosphorene is found to have an isotropic NPR with the value of −0.09. The increased PR value compared to that of δ-phosphorene is due to the limitation of the rotational freedom caused by VSEPR (derived via charge distribution). For a new material with a particular structure, our proposed pattern can be utilized to estimate the likelihood of whether it has an NPR value. Yet, it remains our future endeavour to use this method to design a group of materials with controllable NPR values.
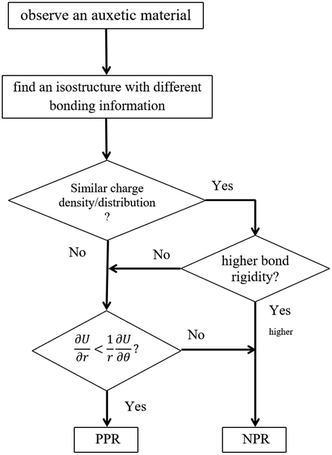 | ||
| Fig. 5 The flow chart to predict new 2D NPR materials. The squares symbols are processes while the rhombus symbols are decisions. | ||
The auxetic behaviour we discuss here is in the elastic region, with the original definition of NPR as νji = −εj/εi. There is another PR defined by the formula νji = −∂εj/∂εi often used under large strains.32–34 We also notice that the PR νzy = −εz/εy (z means the vertical direction and the y means the armchair direction) in the α-arsenic has been found to be negative.35 However, the positive in-plane PR reflects the increasing trend of NPR as the As–As bond is softer than the P–P bond in α-phosphorene, which is in agreement with our conclusion. The original in-plane (νxy or νyx) NPR describes the intrinsic positive feedback in mechanical respond under strain.
Conclusion
Among the materials, we have selected and those mentioned in references, δ-phosphorene has shown the highest PR value due to the unique concave structure and moderate VSEPR and bond rigidity. Based on our calculation of these isostructures and analysis of mechanical deformation, we have concluded that the NPR only reflects a positive feedback in the geometry parameter rather than in energy storage. The origin of the auxetic phenomenon can be explained as that the energy is more easily stored in the extension in the transverse direction rather than compress when a tensile strain is applied in the longitudinal direction. The auxetic behaviours are determined by not only the concave geometry structure but also the high bond rigidity and flexibility for bond rotation. The latter two factors are strongly correlated with the chemical properties of elements within the system, such as cohesive energy, VSEPR, charge distribution etc. By summarising the logical connections the NPR, we have provided an algorithmic method to discover new possible candidate 2D material through analysing the chemical structures of the isostructures of the known auxetic material.Conflicts of interest
The authors declare no competing financial or non-financial interests.Acknowledgements
The authors would like to thank Zijun Zhao, Jason Cheng, Hansheng Chen, and Ping Wu for the useful discussion. This research was undertaken with the assistance of resources from the National Computational Infrastructure (NCI), which is supported by the Australian Government. This work was partially supported by the Australian Research Council (DP150100018). Ruhao Fang designed the project, performed the calculations and wrote the manuscript. X. Cui and R. Zheng contributed to technical support, analysing and writing the manuscript. C. Stampfl and S. P. Ringer contributed to analysing and revising the manuscript.Notes and references
- R. Lakes, Adv. Mater., 1993, 5, 293–296 CrossRef CAS.
- W. Shi, W. Yang, Z.-m. Li, B.-h. Xie and M.-b. Yang, Polym. Bull., 2003, 6, 48–57 Search PubMed.
- F. Scarpa, IEEE Signal Process Mag., 2008, 25, 126–128 Search PubMed.
- J. Choi and R. Lakes, Cell. Polym., 1991, 10, 205–212 CAS.
- Y. Sun and N. Pugno, Materials, 2013, 6, 699–712 CrossRef CAS PubMed.
- Y. J. Park and J. K. Kim, Adv. Mater. Sci. Eng., 2013, 2013, 853289 Search PubMed.
- J. Choi and R. Lakes, Int. J. Fract., 1996, 80, 73–83 CrossRef.
- J. Choi and R. Lakes, J. Mater. Sci., 1992, 27, 5375–5381 CrossRef CAS.
- R. Lakes, Science, 1987, 235, 1038–1040 CrossRef CAS PubMed.
- G. N. Greaves, A. Greer, R. Lakes and T. Rouxel, Nat. Mater., 2011, 10, 823 CrossRef CAS PubMed.
- A. Yeganeh-Haeri, D. J. Weidner and J. B. Parise, Science, 1992, 257, 650–652 CrossRef CAS PubMed.
- D. Gunton and G. Saunders, J. Mater. Sci., 1972, 7, 1061–1068 CrossRef CAS.
- F. Milstein and K. Huang, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 19, 2030 CrossRef CAS.
- L. J. Gibson, Proc. R. Soc. London, Ser. A, 1982, 382, 43–59 CrossRef CAS.
- G. W. Milton, J. Mech. Phys. Solids, 1992, 40, 1105–1137 CrossRef.
- N. Mounet, M. Gibertini, P. Schwaller, D. Campi, A. Merkys, A. Marrazzo, T. Sohier, I. E. Castelli, A. Cepellotti and G. Pizzi, Nat. Nanotechnol., 2018, 13, 246 CrossRef CAS PubMed.
- J.-W. Jiang and H. S. Park, Nat. Commun., 2014, 5, 4727 CrossRef CAS PubMed.
- J. Guan, Z. Zhu and D. Tománek, Phys. Rev. Lett., 2014, 113, 046804 CrossRef PubMed.
- M. Wu, H. Fu, L. Zhou, K. Yao and X. C. Zeng, Nano Lett., 2015, 15, 3557–3562 CrossRef CAS PubMed.
- S. Mardanya, V. K. Thakur, S. Bhowmick and A. Agarwal, Phys. Rev. B, 2016, 94, 035423 CrossRef.
- C. He, C. Zhang, L. Sun, N. Jiao, K. Zhang and J. Zhong, Phys. Status Solidi RRL, 2012, 6, 427–429 CrossRef CAS.
- L.-C. Zhang, G. Qin, W.-Z. Fang, H.-J. Cui, Q.-R. Zheng, Q.-B. Yan and G. Su, Sci. Rep., 2016, 6, 19830 CrossRef CAS.
- Z. Shunhong, Z. Jian, W. Qian, C. Xiaoshuang, K. Yoshiyuki and J. Puru, RENSIT, 2015, 7, 192–207 Search PubMed.
- D. Wu, S. Wang, S. Zhang, J. Yuan, B. Yang and H. Chen, Phys. Chem. Chem. Phys., 2018, 20, 18924–18930 RSC.
- H. Wang, X. Li, P. Li and J. Yang, Nanoscale, 2017, 9, 850–855 RSC.
- L. Yu, Q. Yan and A. Ruzsinszky, Nat. Commun., 2017, 8, 15224 CrossRef CAS PubMed.
- K. Burke, J. Perdew and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 Search PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- L. Yu, A. Ruzsinszky and J. P. Perdew, Nano Lett., 2016, 16, 2444–2449 CrossRef CAS PubMed.
- B. Fulcher, X. Cui, B. Delley and C. Stampfl, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 184106 CrossRef.
- R. Gillespie, Coord. Chem. Rev., 2008, 252, 1315–1327 CrossRef CAS.
- D. T. Ho, S.-D. Park, S.-Y. Kwon, K. Park and S. Y. Kim, Nat. Commun., 2014, 5, 3255 CrossRef.
- J.-W. Jiang, T. Chang, X. Guo and H. S. Park, Nano Lett., 2016, 16, 5286–5290 CrossRef CAS PubMed.
- R. Qin, J. Zheng and W. Zhu, Nanoscale, 2017, 9, 128–133 RSC.
- J. Han, J. Xie, Z. Zhang, D. Yang, M. Si and D. Xue, Appl. Phys. Express, 2015, 8, 041801 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8na00352a |
| This journal is © The Royal Society of Chemistry 2019 |