Open Access Article
Open Access ArticleDirect TEM observation of the “acanthite α-Ag2S–argentite β-Ag2S” phase transition in a silver sulfide nanoparticle†
S. I.
Sadovnikov
 *a and
E. Yu.
Gerasimov
*a and
E. Yu.
Gerasimov
 b
b
aInstitute of Solid State Chemistry, Ural Branch of the Russian Academy of Sciences, Ekaterinburg 620990, Russia. E-mail: sadovnkov@ihim.uran.ru
bBoreskov Institute of Catalysis, Siberian Branch of the Russian Academy of Sciences, Ak. Lavrentieva 5, 630090 Novosibirsk, Russia. E-mail: gerasimov@catalysis.ru
First published on 12th February 2019
Abstract
For the first time, the α-Ag2S (acanthite)–β-Ag2S (argentite) phase transition in a single silver sulfide nanoparticle has been observed in situ using a high-resolution transmission electron microscopy method in real time. Colloid solutions of Ag2S nanoparticles and nanostructured powders of silver sulfide have been synthesized by one-stage chemical bath deposition from an aqueous solution of silver nitrate, sodium sulfide and sodium citrate. Ag2S nanoparticles were heated to different temperatures directly in an electronic microscope by regulating the energy of the electron beam. This allowed observation of the transition of acanthite into argentite and the reversible transition of argentite into acanthite in real time, and this phase transition to be filmed. Temperature dependence of the lattice constant aarg of argentite β-Ag2S in the temperature range 448–723 K is established by in situ high-temperature X-ray diffraction. The orientation relationships between the monoclinic acanthite α-Ag2S and the body-centered cubic argentite β-Ag2S are determined. It is shown that the possible distances between silver atoms in cubic argentite, in contrast to those in acanthite, are too small for the positions of the metal sublattice to be occupied by Ag atoms with a probability equal to 1.
Introduction
According to ref. 1 and 2, TEM has an extraordinary capability to probe and manipulate complex nanomaterials both in real space and in reciprocal space. Indeed, TEM studies of various nanomaterials have developed greatly in the last decade.3–7 For example, anisotropic nanocrystals (nanorods and nanowires)8,9 and branched and core–shell nanocrystals10,11 have been investigated. The effects induced by an electron beam on nanocrystals are very varied. Such effects include phase transformation,5,12–14 thermally activated cation exchange,4,15,16 chemical transformations in inorganic nanocrystal films,7 morphological changes of nanocrystals,5,17,18 atom diffusion, surface changes, etc. A lot of TEM studies of nanocrystals are carried out by the scientific groups of Prof. L. Manna3–5,7,8 and Prof. K. Terabe.12,13Nanostructured sulfides are the most promising group of nanostructured materials for various applications.19 Among nanostructured semiconductor sulfides, nanostructured silver sulfide Ag2S has attracted special attention.
Silver sulfide Ag2S, which is a semiconductor below ∼450 K and a superionic conductor at T > 452 K, is one of the most important sulfides.20 Application of nanostructured silver sulfide holds much promise in microelectronics, where Ag2S/Ag heteronanostructures and nanocomposites are used in nonvolatile memory devices and resistive switches.21–23 Their action is based on the phase transition of acanthite α-Ag2S into argentite β-Ag2S.12–14,23–28
According to the phase diagram of the Ag–S system,29 silver sulfide Ag2S has three polymorphic modifications. The low-temperature semiconductor phase α-Ag2S (acanthite) with a monoclinic crystal structure exists at temperatures below ∼450 K. β-Ag2S (argentite) phase has a body-centered cubic (bcc) lattice, exists in the temperature range 452–859 K, and possesses superionic conductivity. High-temperature face centered cubic (fcc) γ-Ag2S phase is stable from ∼860 K up to melting temperature.
The crystal structure of coarse-crystalline and nanocrystalline silver sulfide powders, synthesized by chemical bath deposition from aqueous solutions of silver nitrate, sodium sulfide and sodium citrate, has been refined recently.30,31 According to ref. 30, synthesized coarse-crystalline Ag2S powder with an average particle size of about 500 nm has a monoclinic (space group no. 14 – P21/c (P121/c1)) α-Ag2S acanthite-type structure and is stoichiometric. Two Ag1 and Ag2 silver atoms occupy the crystallographic positions 4(e). All details of the refinement of the synthesized artificial coarse-crystalline Ag2S phase with a monoclinic (space group P21/c) acanthite-type crystal structure are given in the ESI (http://dx.doi.org/10.1016/j.spmi.2015.03.024) of the article.30
Nanocrystalline silver sulfide powders with an average particle size of 40–50 nm have the same monoclinic (space group P21/c) acanthite-type structure but the occupancy of crystallographic positions 4(e) of the metal sublattice by Ag atoms is equal to 0.96–0.97.31 (see also Table S1 in the ESI†). This means that silver sulfide nanoparticles with a size of less than ∼50 nm are nonstoichiometric, have the composition ∼Ag1.93S and contain vacant sites in the metal sublattice.31
The unit cell of β-Ag2S argentite has a cubic (space group no. 229 – Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (I4/m
m (I4/m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 2/m) (Oh9)) structure. Two S atoms occupy crystallographic positions 2(a) and form a bcc sublattice. According to ref. 32 and 33, four silver atoms are statistically distributed in 54 positions 6(b) and 48(j) (see also ESI, Table S2†).
2/m) (Oh9)) structure. Two S atoms occupy crystallographic positions 2(a) and form a bcc sublattice. According to ref. 32 and 33, four silver atoms are statistically distributed in 54 positions 6(b) and 48(j) (see also ESI, Table S2†).
When monoclinic α-Ag2S acanthite is heated above the transition temperature Ttrans ≈ 452 K under equilibrium conditions, a polymorphous phase transformation takes place, giving rise to cubic β-Ag2S argentite, and upon cooling of β-Ag2S argentite to below ∼450 K, monoclinic α-Ag2S acanthite is formed.33–41
X-ray diffraction (XRD) and electron microscopy are the two main methods for determining the structure of solids. However, XRD studies a sufficiently large volume of matter and gives results averaged over a large ensemble of particles. Unlike XRD, high-resolution transmission electron microscopy (HRTEM) is a local method and allows one to study the structure of separate nanoparticles. HRTEM is especially useful for studying changes in the structure of a nanoparticle during phase transition.
In the present study, the direct in situ observation of the α-Ag2S (acanthite)–β-Ag2S (argentite) phase transition in nanostructured silver sulfide is carried out for the first time using high-resolution transmission electron microscopy.
Experimental
Colloid solutions of Ag2S nanoparticles and nanocrystalline Ag2S powders were synthesized by chemical deposition from aqueous solutions of AgNO3, Na2S and Na3C6H5O7 with concentrations of 50.0, 25.5 and 12.5 mmol L−1, respectively (see ESI†). The synthesis technique has been described previously.19,31In situ high-temperature XRD (HT-XRD) experiments were performed with CuKα1 radiation using an X’Pert PRO MPD (Panalytical) diffractometer equipped with a Anton Paar HTK-1200 Oven furnace. In addition, an in situ high-temperature XRD study was carried out on a STADI-P (STOE) diffractometer using Debye–Scherrer geometry. The diffractometer was equipped with a quartz capillary furnace STOE. The diffraction measurements were carried out with the use of a linear position-sensitive detector, with continuous rotation of the capillary with silver sulfide powder at a temperature from 295 to 773 K with a step of ∼25–30 K (see the experimental details of the HT-XRD measurements in the ESI†). The determination of the crystal lattice parameters and final refinement of the structure of the synthesized silver sulfide powders were carried out with the use of the X’Pert HighScore Plus software package.42
The average particle size D in the synthesized silver sulfide powder was estimated by XRD methods from the diffraction reflection broadening β(2θ) using the dependence of reduced reflection broadening β*(2θ) = [β(2θ)cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ]/λ on the scattering vector s = (2
θ]/λ on the scattering vector s = (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)/λ.43 (see also ESI†).
θ)/λ.43 (see also ESI†).
The phase transition α-Ag2S (acanthite)–β-Ag2S (argentite) in colloid silver sulfide nanoparticles was directly observed by an in situ HRTEM method. The HRTEM images were recorded on a JEOL JEM-2010 transmission electron microscope with 0.14 nm (1.4 Å) lattice resolution (see ESI†). In all the experiments, the standard TEM operating voltage was 200 kV, the beam current was ∼104 μA, the magnification was 600×, and for TEM mode the aperture number and spot size number were set as 3. For direct TEM observation of the phase transformation, heating of an Ag2S nanoparticle with a size of ∼50 nm was carried out for 10–15 s using an electron beam with a size of about 30–40 nm. Standard TEM observations without heating were performed at the beam current density 60 pA cm−2. During heating, the current density was controlled from 120 to 140 pA cm−2. Experimental measurements at a current density of more than 140 pA cm−2 led to radiation damage to the nanoparticle. Previously a similar in situ HRTEM study using electron beam irradiation to heat a Cu nanoparticle was carried out by Chulin Chen et al.44
The heating temperature of the nanoparticles was estimated indirectly by a variation in the interplanar distances and, accordingly, the lattice constant, which was compared with the temperature dependences of the lattice constants determined by the XRD method.
The transmission electron microscope settings for observing nanoparticles in TEM (HRTEM) mode and in diffraction mode are different. The transition to the diffraction mode led to a change in the experimental conditions and microscope settings; therefore, the observed electron diffraction pattern did not correspond to the HRTEM image observed at a given time. For this reason, when observing a change in the crystal lattice in real time, only Fast Fourier Transform (FFT) was used to obtain the electron diffraction pattern.
The elemental chemical composition of Ag2S nanoparticles was studied on the same microscope with the use of a Phoenix (EDAX) Energy Dispersive Spectrometer with a Si(Li) detector with an energy resolution of 130 eV. Colloid solutions of Ag2S nanoparticles were placed on a copper grid for examination. Ag2S nanoparticles were heated directly in an electronic microscope by regulating the energy of the electron beam.
Results and discussion
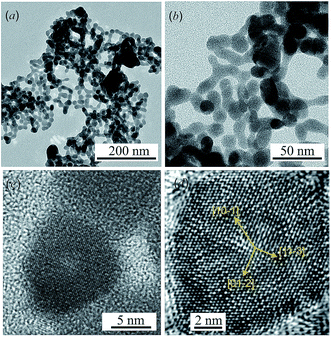
TEM images of colloidal solutions of Ag2S nanoparticles with different magnifications are shown in Fig. 1a and b. The average size of the Ag2S nanoparticles is 15–25 nm, and the smallest and largest sizes are 8–10 and 40–50 nm, respectively. TEM and HRTEM images of an Ag2S nanoparticle with a size of ∼10 nm are shown in Fig. 1c and d.The rows of atoms observed on the HRTEM image (Fig. 1d) form a regular grid with interplanar distances of ∼0.417, ∼0.338, ∼0.284 and ∼0.209 nm, characteristic of monoclinic α-Ag2S acanthite. Indeed, the distance ∼0.417 nm corresponds to the interplanar distance between the [10−1] atomic planes of acanthite, the distance ∼0.338 nm is equal to the distance between the [01−2] planes, the distances ∼0.284 and ∼0.209 nm are equal to the distance between the [11−3] planes in the first case and the distance between the [20−2] atomic planes in the second case. All these interplanar distances are observed in the [121] plane of monoclinic α-Ag2S acanthite.
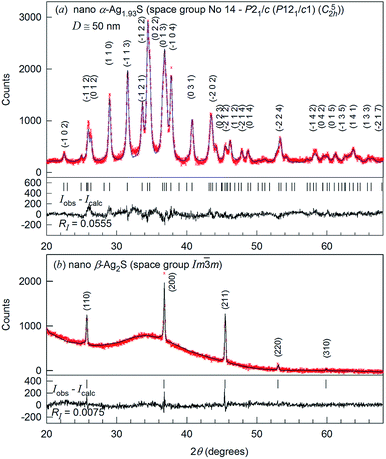
The XRD patterns of nanocrystalline silver sulfide Ag2S powder recorded in situ at a temperature of 298 and 463 K are shown in Fig. 2.
Comparison of the XRD pattern (Fig. 2a) of the synthesized nanopowder with data31 reveals that the observed set of diffraction reflections corresponds to one-phase nonstoichiometric silver sulfide with a monoclinic (space group no. 14 – P21/c) acanthite-type structure. According to XRD data, the average particle size of the nanopowder is equal to ∼50 nm. The quantitative refinement of the structure showed that the degrees of occupation of the crystallographic positions 4(e) by silver atoms Ag1 and Ag2 in the monoclinic unit cell are smaller than 1, namely 0.97 and 0.96, respectively (see ESI, Table S1†). This agrees with the data.31 Thus, silver sulfide nanopowder with a size of less than ∼50 nm has the composition ∼Ag1.93S and is nonstoichiometric.
The refinement of the silver sulfide nanopowder XRD pattern collected at 463 K (Fig. 2b) showed that silver sulfide contains one phase with a cubic (space group no. 229 – Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (I4/m
m (I4/m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 2/m) (Oh9)) structure of β-Ag2S argentite type.33 According to the present study, the atomic coordinates and occupation degrees within the errors of measurements are the same as in ref. 33: four silver atoms are distributed in 54 positions 6(b) and 48(j) of the considered structure with occupation degrees of 0.0978(7) and 0.0711(0), respectively (see ESI, Table S2†).
2/m) (Oh9)) structure of β-Ag2S argentite type.33 According to the present study, the atomic coordinates and occupation degrees within the errors of measurements are the same as in ref. 33: four silver atoms are distributed in 54 positions 6(b) and 48(j) of the considered structure with occupation degrees of 0.0978(7) and 0.0711(0), respectively (see ESI, Table S2†).
The effect of temperature on the evolution of the XRD patterns of nanostructured silver sulfide is shown in Fig. S1–S3 (ESI†). Dependence of the lattice constant aarg(T), constructed on the generalized data of high-temperature in situ XRD measurements in the present study and the literature,38,39 is non-linear and curves weakly upward (see ESI, Fig. S4†), and is described by a polynomial in the interval 448–723 K
| aarg(T) = a0 + a1T + a2T2, | (1) |
Overall, in situ XRD study of silver sulfide revealed only acanthite at T ≤ 433 K and only argentite at T > 453 K. No other phases were found. Taking this into account along with the data,33–37,45 when monoclinic acanthite α-Ag2S is heated to a temperature of ∼449–451 K, a polymorphic phase transition occurs with the formation of bcc β-Ag2S argentite.
A scheme of the displacements of the S atoms from the crystallographic positions of the bcc argentite sublattice, and also the monoclinically distorted sublattice of S atoms that was constructed by taking into account the sulfur atom coordinates in the monoclinic (space group P21/c) α-Ag2S phase (see ESI, Table S1†), is shown in Fig. S5 (ESI†). As a result of the displacements of the S atoms from the 2(a) positions of the bcc argentite lattice, monoclinic translation vectors a, b, and c appear. The directions of these vectors can be represented as a combination of basic translational vectors of the bcc argentite lattice: a‖[11−1]bcc/2, b‖[1−10]bcc and c‖[001]bcc. However, in absolute values, monoclinic vectors |a|, |b| and |c| are slightly more than √3·(abcc/2), √2·abcc and 2abcc. To explain this, we consider interatomic distances in β-Ag2S argentite.
Interatomic (interstitial) distances for different coordination spheres (CS) of the crystal structure of cubic (space group Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) β-Ag2S argentite (Table 1) were calculated taking into account the found lattice constant as well as the coordinates of silver and sulfur atoms in argentite (see ESI, Table S2†). Since the occupation degree of the sites of the metal sublattice of argentite by silver atoms is very small, it is more correct to talk about the distances between the sites at which Ag atoms can be located.
m) β-Ag2S argentite (Table 1) were calculated taking into account the found lattice constant as well as the coordinates of silver and sulfur atoms in argentite (see ESI, Table S2†). Since the occupation degree of the sites of the metal sublattice of argentite by silver atoms is very small, it is more correct to talk about the distances between the sites at which Ag atoms can be located.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) argentite β-Ag2S at a temperature of 453 K
m) argentite β-Ag2S at a temperature of 453 K
| Pair of atoms (sites) | CS number | Distance d (nm) | Pair of atoms (sites) | CS number | Distance d (nm) |
|---|---|---|---|---|---|
| a CS is coordination sphere. | |||||
| Ag1 – S | 1 | 0.24307 | Ag2 – Ag2 | 5 | 0.15013 |
| 6(b) – 2(a) | 48(j) – 48(j) | 6 | 0.16466 | ||
| Ag2 – S | 1 | 0.25691 | 7 | 0.17674 | |
| 48(j) – 2(a) | 2 | 0.26015 | 8 | 0.18543 | |
| Ag1 – Ag1 | 1 | 0.24307 | 9 | 0.19607 | |
| 6(b) – 6(b) | 2 | 0.34376 | 10 | 0.22352 | |
| Ag1 – Ag2 | 1 | 0.09271 | 11 | 0.22732 | |
| 6(b) – 48(j) | 2 | 0.16630 | 12 | 0.24279 | |
| 3 | 0.21670 | 13 | 0.25044 | ||
| 4 | 0.29451 | 14 | 0.25996 | ||
| 5 | 0.29734 | 15 | 0.26951 | ||
| 6 | 0.32561 | 16 | 0.28343 | ||
| Ag2 – Ag2 | 1 | 0.05611 | 17 | 0.28570 | |
| 48(j) – 48(j) | 2 | 0.08530 | 18 | 0.29491 | |
| 3 | 0.09893 | 19 | 0.29756 | ||
| 4 | 0.13112 | 20 | 0.30020 | ||
The use of the parameters of the crystal lattices of monoclinic acanthite and cubic argentite, determined from the temperature dependences of the crystal lattice constants of monoclinic acanthite and cubic argentite,38,41 allows estimation of the interatomic distances in these phases at temperatures close to the temperature of the “acanthite – argentite” transformation, Ttrans. In the crystal lattice of monoclinic acanthite α-Ag2S at a temperature of 433 K, the smallest distances between S and Ag1 atoms are in the range of 0.2516 to 0.3066 nm, and the smallest distances between S and Ag2 atoms are in the range of 0.2562 to 0.2950 nm. The distance between Ag1 and Ag1 atoms in α-Ag2S acanthite at 433 K is 0.3353 nm, and the smallest distances between Ag1 and Ag2 atoms are in the range of 0.3087 to 0.3205 nm. The radius of the Ag+ ion is ∼0.126 nm.46 It is clear that the atoms (ions) of silver in monoclinic acanthite are located at sufficiently large distances from each other and therefore occupy their crystallographic positions with a probability equal to 1.
In cubic argentite β-Ag2S, the possible distances between sulfur and silver atoms and between silver atoms at a temperature of 453 K, close to 433 K, are much smaller (see Table 1). According to the temperature dependence of the lattice constant (1), constructed on the generalized data of high-temperature in situ XRD measurements in the present study and the literature,38,41 the argentite lattice constant at 453 K is equal to 0.4861 nm. In the crystal lattice of cubic argentite β-Ag2S at a temperature of 453 K, the possible smallest distance between Ag1 and Ag1 atoms is 0.2431 nm, those between Ag1 and Ag2 atoms are in the interval from 0.0927 to 0.3256 nm, and the distances between Ag2 and Ag2 atoms are from 0.0561 to 0.3002 nm (Table 1). The sites of the silver sublattice, especially sites 48(j), are so close to each other that the arrangement of the Ag+ ion in one of them makes it impossible to fill the nearest neighboring site with another silver ion, since the diameter of the Ag+ ion is larger than the distance between these sites. Indeed, the interatomic distances in cubic argentite are such that, in the presence of a silver ion in site 6(b), another Ag+ ion can occupy one of sites 48(j) located only in the 4th or 5th coordination sphere at a distance of 0.2945 or 0.2973 nm from site 6(b). Similarly, if the Ag+ ion occupies one of the sites 48(j), then the other Ag+ ion can be located at the site 48(j) located at a distance of at least 0.252 nm from the first site, that is, not closer than in the 14th coordination sphere.
Thus, in cubic β-Ag2S argentite, the possible distances between silver atoms are very small, and this does not allow the Ag atoms to occupy positions 6(b) and 48(j) with a probability equal to 1. For this reason, the occupation degrees of the 6(b) and 48(j) positions by Ag atoms (put another way, the probabilities of finding Ag atoms in the 6(b) and 48(j) sites) are very small, less than 0.1 (see ESI, Table S2†). Physically, this means that 4 silver atoms in the cubic argentite lattice are in constant motion over 54 possible crystallographic positions. It is this constant motion of Ag atoms that provides the crystal lattice stability of cubic argentite and its superionic conductivity.
Due to the monoclinic distortion of the lattice, the atoms (ions) of silver in acanthite are at sufficiently large (larger than in argentite) distances from each other and therefore occupy their crystallographic positions 4(e) with a probability close to 1.
Let us consider the results of TEM observations of the transformation of monoclinic acanthite to cubic argentite due to the heating of a silver sulfide nanoparticle by an electron beam.
The synthesized monoclinic α-Ag2S nanopowder was heated directly in a JEOL-JSM LA 6390 microscope by the electron beam. Heating silver sulfide nanoparticles up to different temperatures was carried out by regulating the energy of the electron beam. This allowed observation of the transition of acanthite into argentite and the reversible transition of argentite into acanthite in real time (see Movie-S1, available online in the ESI†). This is the main achievement of our study.
A HRTEM image of an Ag2S nanoparticle heated by an electron beam to a temperature of ∼448–449 K, close to the temperature of the “acanthite–argentite” phase transformation, is shown in Fig. 3a. Fig. 3b and c shows a magnified HRTEM image of the area highlighted by a square in Fig. 3a, and the electron diffraction pattern of the same area obtained by Fast Fourier Transform (FFT) of the magnified HRTEM image. The magnified HRTEM image (Fig. 3b) shows atomic rows directed from the upper left to the lower right corner of the image. The successive alternation of three darker atomic rows separated by a lighter row is visible in the central part of Fig. 3b. The observed HRTEM image (Fig. 3b) corresponds to the formation of a transition state between the structures of acanthite and argentite. This is confirmed by the electron diffraction pattern (Fig. 3c) obtained by FFT. The streaky reflections observed in the electron diffraction pattern (Fig. 3c) correspond to the reflections of the distorted crystal lattices of monoclinic acanthite and cubic argentite, between which transformation occurs.
Similar streaky reflections were observed during the phase transition from a monoclinic to a body-centered cubic (bcc) structure of Ag2Te nanowires.47
A HRTEM image of an Ag2S nanoparticle heated by an electron beam to a temperature of about 450–451 K is shown in Fig. 4.
Near the edge of the nanoparticle, wavelike Moire fringes are clearly visible. The appearance of the Moire fringes indicates the strained structure of the lattice, i.e. the presence of microdistortions in the lattice. The Moire fringes are caused by the formation of a state that is transitional between the equilibrium structures of acanthite and argentite. Fig. 4b shows a magnified HRTEM image of the area with Moire stripes highlighted by a white square in Fig. 4a. Fig. 4c shows the electron diffraction pattern obtained by FFT of the HRTEM image of the nanoparticle area highlighted by a yellow square in Fig. 4a. The observed distance of ∼0.308 nm corresponds to the distance between the [110] planes of monoclinic acanthite. In addition, in this region, judging by FFT (Fig. 4c), a local ordering of atoms is also observed, leading to the formation of a superperiodic lattice in the [111] direction of the monoclinic structure. The distance, ∼0.486 nm, of this locally ordered lattice is equal to twice the [111] interplanar distance of monoclinic acanthite, i.e., 2 × d111 ≈ 2 × 0.245 nm. Apparently, the emergence of superperiodicity indicates the beginning of the formation of cubic argentite, the distance between the [100] atomic planes of which is ∼0.486 nm, while the argentite lattice constant aarg is ∼0.486 nm. In accordance with the found temperature dependence aarg(T) (1), argentite has a lattice constant aarg ≈ 0.486 nm at a temperature of 451–452 K.
When the Ag2S nanoparticle is heated from room temperature to ∼450 K, the monoclinic structure remains unchanged but the lattice constants increase. Heating up to 455–460 K is accompanied by the lattice transformation of monoclinic acanthite α-Ag2S into the cubic structure of argentite β-Ag2S. Further heating leads to an increase in the lattice constant of the cubic argentite. As the energy of the electron beam decreases, the argentite lattice constant decreases, and at a temperature of ∼455 K a transition occurs from the cubic structure of the argentite to the monoclinic structure of the acanthite (see Movie-S1 in the ESI†).
TEM images of silver sulfide nanoparticles at room temperature and at maximal heating are presented in Fig. 5 and 6.
Fig. 5a presents the HRTEM image of a silver sulfide nanoparticle before radiation heating. Fig. 5b presents a part of the HRTEM image at larger magnification. HRTEM allowed the selected areas of electron diffraction to be directly seen. However, such direct electron-microscopic observation of diffraction did not give a clear picture of diffraction reflections, and changed the electron beam size. Therefore, to obtain an electron diffraction pattern, Fast Fourier Transform (FFT) of the original HRTEM image was used. Fig. 5c is an electron diffraction pattern obtained by FFT of the HRTEM image area in the white square.
The comparison of the interplanar distances of 0.778, 0.697, 0.518, and 0.338 nm found in the electron diffraction pattern (Fig. 5c) with data31 showed that the observed diffraction spots can have the crystallographic indices (001), (010), (011), and (012) of monoclinic (space group P21/c) acanthite. The analysis showed that these reflections are observed along the [100] zone axis of monoclinic (space group P21/c) acanthite α-Ag2S. The observed angles of 41.7°, 19.5°, and 29.1° between the (010) and (011), (011) and (012), and (012) and (001) spots of monoclinic α-Ag2S acanthite (see ESI, Fig. S6†) coincide, within measurement error, with the calculated theoretical values of 41.77°, 18.99° and 29.24° of these angles. The method for calculating the angles between electron diffraction spots of low-symmetry structures is described in the literature.19,48,49 Thus, the electron diffraction pattern (Fig. 5c) confirms the monoclinic structure of the Ag2S nanoparticle at room temperature.
A HRTEM image of the silver sulfide nanoparticle heated by an electron beam to a temperature higher than the transition temperature Ttrans is shown in Fig. 6. According to literature data [ref. 34, 36 and 38], the “acanthite–argentite” transition temperature is ∼449–452 K. It is clear that the Ag2S nanoparticle with a cubic structure (see Fig. 6b and c) is heated to temperatures higher than 452 K.
Fig. 6c represents a magnified part of the HRTEM image, which is highlighted by a white rectangle in Fig. 6b. The electron diffraction pattern obtained by FFT of the HRTEM image area in the white rectangle is shown in Fig. 6d. The comparison of the interplanar distances of ∼0.344, ∼0.244, and ∼0.199 nm found in the electron diffraction pattern (Fig. 6d) with data33 showed that the observed diffraction spots have the crystallographic indices (110), (002), and (112) of cubic (space group Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) argentite. Listed reflections are observed along the [1−10] zone axis of cubic argentite β-Ag2S. Detailed crystallographic information on β-Ag2S argentite is presented as “Crystal structure data” in the CIF-file (Crystallographic Information File, https://summary.ccdc.cam.ac.uk/structure-summary?ccdc=1062400), attached to the article.33 The lattice constant aarg of argentite β-Ag2S heated by an electron beam to a temperature above the transition temperature Ttrans is ∼0.4871 ± 0.0003 nm. Taking into account the accuracy of TEM and XRD measurements, a comparison of the observed interplanar distances (see Fig. 6) and lattice constant of argentite with the temperature dependence aarg(T) (see eqn (1)) shows that the observed lattice constant aarg = 0.4871 ± 0.0003 nm corresponds to heating of argentite up to ∼530 ± 20 K.
m) argentite. Listed reflections are observed along the [1−10] zone axis of cubic argentite β-Ag2S. Detailed crystallographic information on β-Ag2S argentite is presented as “Crystal structure data” in the CIF-file (Crystallographic Information File, https://summary.ccdc.cam.ac.uk/structure-summary?ccdc=1062400), attached to the article.33 The lattice constant aarg of argentite β-Ag2S heated by an electron beam to a temperature above the transition temperature Ttrans is ∼0.4871 ± 0.0003 nm. Taking into account the accuracy of TEM and XRD measurements, a comparison of the observed interplanar distances (see Fig. 6) and lattice constant of argentite with the temperature dependence aarg(T) (see eqn (1)) shows that the observed lattice constant aarg = 0.4871 ± 0.0003 nm corresponds to heating of argentite up to ∼530 ± 20 K.
The Ag/S atomic ratio for silver sulfide nanoparticles was determined by an EDS method. According to the EDS results, the amounts of Ag and S for the nanoparticle before heating are equal to ∼86.7 ± 0.4 and ∼13.3 ± 0.1 wt%, respectively, and for the silver sulfide nanoparticle after electron beam heating with a current density of 120 pA cm−2 they are ∼86.9 ± 0.4 and ∼13.1 ± 0.1 wt% (see ESI, Fig. S7†). It is seen that the Ag/S atomic ratios for the silver sulfide nanoparticle before and after electron beam heating within the errors of measurements are almost the same and correspond to a sulfide ∼Ag1.94–1.98S. Experimental measurements have also shown that a change of the composition (the content of Ag and S) of the nanoparticles and radiation damage of the nanoparticles are observed at a current density of 140 pA cm−2 and higher.
As noted, the monoclinic (space group P21/c) structure of acanthite α-Ag2S is the result of small displacements of sulfur atoms from the positions of the body-centered cubic (space group Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) lattice of argentite β-Ag2S. As a result of the “acanthite–argentite” transition, the [010]P21/c‖[020]P21/c and [001]P21/c atomic planes of acanthite are transformed into argentite [1−10]Im
m) lattice of argentite β-Ag2S. As a result of the “acanthite–argentite” transition, the [010]P21/c‖[020]P21/c and [001]P21/c atomic planes of acanthite are transformed into argentite [1−10]Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and [221]Im
m and [221]Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m atomic planes. Between these planes of acanthite and argentite, the following orientation relationships are satisfied: [010]P21/c‖[1−10]Im
m atomic planes. Between these planes of acanthite and argentite, the following orientation relationships are satisfied: [010]P21/c‖[1−10]Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, [020]P21/c‖[1−10]Im
m, [020]P21/c‖[1−10]Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, and [001]P21/c‖[221]Im
m, and [001]P21/c‖[221]Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, that correspond to the axis orientation [100]P21/c‖[110]Im
m, that correspond to the axis orientation [100]P21/c‖[110]Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m.
m.
The perfect atomic plane 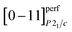 of acanthite, in which atomic displacements from positions of the argentite lattice are not taken into account, is parallel to the [−3 1 3/2]Im
of acanthite, in which atomic displacements from positions of the argentite lattice are not taken into account, is parallel to the [−3 1 3/2]Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m plane. The real (taking into account atomic displacements) [0−11]P21/c atomic acanthite plane passes through Ag1 atoms with coordinates (0.0715 0.0151 0.3094) and (0.0715 0.4849 0.8094) (see ESI, Table S1†) and similar atoms in neighboring unit cells; the distance between the [0−11]P21/c planes of acanthite is equal to ∼0.517 nm. [0−11]P21/c and [−3 1 3/2]Im
m plane. The real (taking into account atomic displacements) [0−11]P21/c atomic acanthite plane passes through Ag1 atoms with coordinates (0.0715 0.0151 0.3094) and (0.0715 0.4849 0.8094) (see ESI, Table S1†) and similar atoms in neighboring unit cells; the distance between the [0−11]P21/c planes of acanthite is equal to ∼0.517 nm. [0−11]P21/c and [−3 1 3/2]Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m atomic planes, as a result of atomic displacements, turn out to be not parallel, but directed relative to each other at a small angle of ∼1.86°. The [011]P21/c atomic plane of acanthite passing through Ag2 atoms with coordinates (0.7264 0.3240 0.4375) and (0.2736 0.6760 0.5625) and the same atoms in neighboring unit cells is parallel to the [1 −3 3/2]Im
m atomic planes, as a result of atomic displacements, turn out to be not parallel, but directed relative to each other at a small angle of ∼1.86°. The [011]P21/c atomic plane of acanthite passing through Ag2 atoms with coordinates (0.7264 0.3240 0.4375) and (0.2736 0.6760 0.5625) and the same atoms in neighboring unit cells is parallel to the [1 −3 3/2]Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m plane of argentite.
m plane of argentite.
The [001]P21/c atomic plane of acanthite passes through Ag2 atoms with the coordinate z = 0.0625 (ESI, Table S1†) in the neighboring unit cells and is therefore parallel to the [221]Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m plane of argentite. The distance between the [001]P21/c planes is ∼0.775 nm.
m plane of argentite. The distance between the [001]P21/c planes is ∼0.775 nm.
Conclusion
For the first time, the α-Ag2S (acanthite)–β-Ag2S (argentite) phase transition in nanostructured silver sulfide has been observed in situ using a high-resolution transmission electron microscopy method in real time. Ag2S nanoparticles were heated directly in an electron microscope by regulating the energy of the electron beam.The transformation of argentite to acanthite is accompanied by a monoclinic distortion of the nonmetallic bcc argentite sublattice, due to which the distances between the silver atoms (ions) increase compared with the interatomic distances in argentite, and the occupancy probability of crystallographic positions by Ag atoms reaches 1.
Despite the presence of displacements, some atomic planes of acanthite remain parallel to the planes of argentite: [010]P21/c‖[1−10]Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, [020]P21/c‖[1−10]Im
m, [020]P21/c‖[1−10]Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, and [001]P21/c‖[221]Im
m, and [001]P21/c‖[221]Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m.
m.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is financially supported by the Russian Science Foundation (Grant 14-23-00025) through the Institute of Solid State Chemistry of the Ural Division of the RAS. Authors are grateful to Dr A. P. Tutunnik and A. V. Chukin for the help with high-temperature XRD measurement.Notes and references
- Y. Gong, J. Lin, X. Wang, G. Shi, S. Lei, Z. Lin, X. Zou, G. Ye, R. Vajtai, B. I. Yakobson, H. Terrones, M. Terrones, B. K. Tay, J. Lou, S. T. Pantelides, Z. Liu, W. Zhou and P. M. Ajayan, Nat. Mater., 2014, 13, 1135–1142 CrossRef CAS PubMed.
- L. Chen, C. Wang, X. Wu, J. Zhang and J. Chu, Small, 2017, 13, 1604259 CrossRef PubMed.
- M. V. Kovalenko, L. Manna, A. Cabot, Z. Hens, D. V. Talapin, C. R. Kagan, V. I. Klimov, A. L. Rogach, P. Reiss, D. J. Milliron, P. Guyot-Sionnnest, G. Konstantatos, W. J. Parak, T. Hyeon, B. A. Korgel, C. B. Murray and W. Heiss, ACS Nano, 2015, 9, 1012–10157 CrossRef CAS PubMed.
- A. Casu, A. Genovese, L. Manna, P. Longo, J. Buha, G. A. Botton, S. Lazar, M. U. Kahaly, U. Schwingenschloegl, M. Prato, H. Li, S. Ghosh, F. Palazon, F. de Donato, S. L. Mozo, E. Zuddas and A. Falqui, ACS Nano, 2016, 10, 2406–2414 CrossRef CAS PubMed.
- Z. Dang, J. Shamsi, F. Palazon, M. Imran, Q. A. Akkerman, S. Park, G. Bertoni, M. Prato, R. Brescia and L. Manna, ACS Nano, 2017, 11, 2124–2132 CrossRef CAS PubMed.
- Y. Liu, M. Liu, D. Yin, L. Qiao, Z. Fu and M. T. Swihart, ACS Nano, 2018, 12, 7803–7811 CrossRef CAS PubMed.
- F. Palazon, M. Prato and L. Manna, J. Am. Chem. Soc., 2017, 139, 13250–13259 CrossRef CAS PubMed.
- M. Imran, F. DiStasio, Z. Dang, C. Canale, A. H. Khan, J. Shamsi, R. Brescia, M. Prato and L. Manna, Chem. Mater., 2016, 28, 6450–6454 CrossRef CAS PubMed.
- G. Z. Shen, Y. Bando, D. Golberg and C. W. Zhou, J. Phys. Chem. C, 2008, 112, 12299–12303 CrossRef CAS.
- X. Huang, M.-G. Willinger, H. Fan, Z. Xie, L. Wang, A. Klein-Hoffmann, F. Girgsdies, C.-S. Lee and X.-M. Meng, Nanoscale, 2014, 6, 8787–8795 RSC.
- W. J. Zhang, G. J. Chen, J. Wang, B.-C. Ye and X. H. Zhong, Inorg. Chem., 2009, 48, 9723–9731 CrossRef CAS PubMed.
- K. Terabe, T. Hasegawa, T. Nakayama and M. Aono, Nature, 2005, 433, 47–50 CrossRef CAS PubMed.
- C. H. Liang, K. Terabe, T. Hasegawa and M. Aono, Nanotechnology, 2007, 18, 485202 CrossRef.
- Z. Xu, Y. Bando, W. Wang, X. Bai and D. Golberg, ACS Nano, 2010, 4, 2515–2522 CrossRef CAS PubMed.
- J. B. Rivest and P. K. Jain, Chem. Soc. Rev., 2013, 42, 89–96 RSC.
- L. de Trizio and L. Manna, Chem. Rev., 2016, 116, 10852–10887 CrossRef CAS PubMed.
- W. P. Lim, Z. Zhang, H. Y. Low and W. S. Chin, Angew. Chem., Int. Ed., 2004, 43, 5685–5689 CrossRef CAS PubMed.
- F. Zhu, L. Men, Y. Guo, Q. Zhu, U. Bhattacharjee, P. M. Goodwin, J. W. Petrich, E. A. Smith and J. Vela, ACS Nano, 2015, 9, 2948–2959 CrossRef CAS PubMed.
- S. I. Sadovnikov, A. I. Gusev and A. A. Rempel, Semiconductor Nanostructures of Lead, Cadmium and Silver Sulfides, Fizmatlit, Moscow, 2018, p. 432 Search PubMed.
- S. I. Sadovnikov and A. I. Gusev, J. Mater. Chem. A, 2017, 5, 17676–17704 RSC.
- J. Yang and J. Y. Ying, Angew. Chem., Int. Ed., 2011, 50, 4637–4643 CrossRef CAS PubMed.
- G. X. Zhu and Z. Xu, J. Am. Chem. Soc., 2011, 133, 148–157 CrossRef CAS PubMed.
- D. Wang, C. Hao, W. Zheng, Q. Peng, T. Wang, Z. Liao, D. Yu and Y. Li, Adv. Mater., 2008, 20, 2628–2632 CrossRef CAS.
- D. Wang, L. Liu, Y. Kim, Z. Huang, D. Pantel, D. Hesse and M. Alexe, Appl. Phys. Lett., 2011, 98, 243109 CrossRef.
- A. Gubicza, M. Csontos, A. Halbritter and G. Mihály, Nanoscale, 2015, 7, 4394–4399 RSC.
- A. Gubicza, M. Csontos, A. Halbritter and G. Mihály, Nanoscale, 2015, 7, 11248–11254 RSC.
- S. I. Sadovnikov and A. I. Gusev, J. Nanopart. Res., 2016, 18, 277 CrossRef.
- A. I. Gusev and S. I. Sadovnikov, Mater. Lett., 2017, 188, 351–354 CrossRef CAS.
- R. S. Sharma and Y. A. Chang, Bull. Alloy Phase Diagrams, 1986, 7, 263–269 CrossRef CAS.
- S. I. Sadovnikov, A. I. Gusev and A. A. Rempel, Superlattices Microstruct., 2015, 83, 35–47 CrossRef CAS.
- S. I. Sadovnikov, A. I. Gusev and A. A. Rempel, Phys. Chem. Chem. Phys., 2015, 17, 12466–12471 RSC.
- T. Blanton, S. Misture, N. Dontula and S. Zdzieszynski, Powder Diffr., 2011, 26, 110–118 Search PubMed.
- S. I. Sadovnikov, A. I. Gusev and A. A. Rempel, Phys. Chem. Chem. Phys., 2015, 17, 20495–20501 RSC.
- C. M. Perrott and N. H. Fletcher, J. Chem. Phys., 1969, 50, 2344–2350 CrossRef CAS.
- W. T. Thompson and S. N. Flengas, Can. J. Chem., 1971, 49, 1550–1563 CrossRef CAS.
- F. Grønvold and E. F. Westrum, J. Chem. Thermodyn., 1986, 18, 381–401 CrossRef.
- S. I. Sadovnikov, A. V. Chukin, A. A. Rempel and A. I. Gusev, Phys. Solid State, 2016, 58, 30–36 CrossRef CAS.
- S. I. Sadovnikov, A. I. Gusev, A. V. Chukin and A. A. Rempel, Phys. Chem. Chem. Phys., 2016, 18, 4617–4626 RSC.
- S. I. Sadovnikov and A. I. Gusev, J. Therm. Anal. Calorim., 2018, 131, 1155–1164 CrossRef CAS.
- A. I. Gusev and S. I. Sadovnikov, Thermochim. Acta, 2018, 660, 1–10 CrossRef CAS.
- S. I. Sadovnikov and E. G. Vovkotrub, J. Alloys Compd., 2018, 766, 140–148 CrossRef CAS.
- X’Pert HighScore Plus. version 2.2e (2.2.5), PANalytical B. V., Almedo, The Netherlands, 2009 Search PubMed.
- A. I. Gusev and A. A. Rempel, Nanocrystalline Materials, Cambridge Intern. Science Publ., Cambridge, 2004, p. 351 Search PubMed.
- C. L. Chen, Z. Hu, Y. Li, L. Liu, H. Mori and Z. Wang, Sci. Rep., 2016, 6, 19545 CrossRef CAS PubMed.
- S. I. Sadovnikov, A. A. Rempel and A. I. Gusev, Russ. Chem. Rev., 2018, 87, 303–327 CrossRef CAS.
- A. F. Etris, in Kirk-Othmer Encyclopedia of Chemical Technology, Wiley, New York, 2001, vol.4, pp. 781–803 Search PubMed.
- J. In, Y. Yoo, J.-G. Kim, K. Seo, H. Kim, H. Ihee, S. H. Oh and B. Kim, Nano Lett., 2010, 10, 4501–4504 CrossRef CAS PubMed.
- S. I. Sadovnikov and A. I. Gusev, Biointerface Res. Appl. Chem., 2016, 6, 1797–1804 CAS.
- S. I. Sadovnikov, A. A. Rempel and A. I. Gusev, Nanostructured Lead, Cadmium and Silver Sulfides: Structure, Nonstoichiometry and Properties, Springer Intern. Publ. AG, Cham-Heidelberg-New York-Dordrecht-London, 2018, p. 331 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details of synthesis and evidence of silver sulfide nanoparticles, crystal structure of acanthite and argentite phases of silver sulfide, and movie of the phase transformation of acanthite into argentite in real time. See DOI: 10.1039/c8na00347e |
| This journal is © The Royal Society of Chemistry 2019 |