Starting a subnanoscale tank tread: dynamic fluxionality of boron-based B₁₀Ca alloy cluster

Abstract

Alloying an elongated B₁₀ cluster with Ca is shown to give rise to a dynamically fluxional B₁₀Ca cluster, the latter behaving like a tank tread at the subnanoscale. Computer global search identifies the B₁₀Ca C₂ (¹A) global-minimum structure, which is chiral in nature and retains the quasi-planar moiety of bare B₁₀ cluster with Ca capped at one side, forming a half-sandwich. The rotation barrier of B₁₀Ca cluster is reduced with respect to B₁₀ by one order of magnitude, down to 1 kcal mol⁻¹ at the PBE0/6-311+G* level, which demonstrates structural fluxionality at 600 K and beyond via molecular dynamics simulations. Structurewise, the Ca alloying in B₁₀Ca cluster generates rhombic defect holes, preactivating the species and making it flexible against deformation. Chemical bonding analyses indicate that the B₁₀Ca cluster is a charge-transfer [B₁₀]²⁻[Ca]²⁺ complex, being doubly π/σ aromatic with the 6π and 10σ electron-counting. Such a pattern offers ideal π/σ delocalization and facilitates fluxionality. In contrast, bare B₁₀ cluster has conflicting aromaticity with 6π and 8σ electrons, which is nonfluxional with a barrier of 12 kcal mol⁻¹. Double π/σ aromaticity versus conflicting aromaticity is a key mechanism that distinguishes between fluxional B₁₀Ca and nonfluxional B₁₀ clusters, offering a compelling example that the concept of aromaticity (and double aromaticity) can be exploited to design dynamically fluxional nanosystems.

---

1. Introduction

Molecular rotors are interesting nanoscale or subnanoscale systems,^1–18 in which the constituent fragments move collectively and concertedly against each other, akin to nanomachines. Such nanosystems are rare in chemistry and were primarily discovered during the past decade. Boron appears to be a magic element for nanorotors. Several types of boron-based nanorotors have been developed. Firstly, a Wankel motor B₁₉⁻ cluster was described by Merino and coworkers¹ with a negligible in-plane rotation barrier (less than 0.1 kcal mol⁻¹), immediately following an experimental study of the gas-phase B₁₉⁻ cluster with concentric dual π aromaticity via photoelectron spectroscopy (PES) in 2010.¹⁹ Similar molecular dynamics was discussed earlier in mixed B–C clusters (C₂B₈, C₃B₉³⁺, and C₅B₁₁⁺),² although those species are highly energetic on their potential energy surfaces and thus not viable. Molecular Wankel motors have since been expanded to other systems,^3–9 such as the B₁₃⁺ cluster. Second, Zhai and coworkers¹⁰ discovered in 2015 the so-called subnanoscale tank treads, which feature elongated rather than circular geometries with a peripheral ring gliding freely around an elongated inner core. Typical examples are the B₁₁⁻ and B₁₁ clusters, which have a rotation barrier of 0.35 and 0.60 kcal mol⁻¹, respectively. An isoelectronic B₁₀C model cluster¹² was designed subsequently for mechanistic insights into subnanoscale tank treads. Third, a binary Mg₂B₈ cluster was shown to function like a nanocompass¹⁴ and a coaxial triple-layered Be₆B₁₁⁻ cluster was characterized in 2017 with dual dynamic modes: revolution (orbiting) of the peripheral B₁₁ ring versus rotation (twisting) of the prismatic Be₆ core.¹⁵ Intriguingly, the Be₆B₁₁⁻ cluster mimics the dynamic Earth-Moon system at the subnanoscale and yet miniaturizes the latter in size by 18 orders of magnitude.

The ultimate mechanisms of boron-based nanorotors should lie in the electron-deficiency of boron, which leads to highly unusual geometries of boron clusters,^19–36 featuring planar or quasi-planar (2D) structures up to 40 atoms for anions.³⁰ Among other notable boron clusters are a bowl-like B₃₆ borophene²⁹ and cage-like B₄₀⁻/B₄₀ borospherenes.^30,37 In terms of chemical bonding, boron clusters are governed by π/σ aromaticity, antiaromaticity, double aromaticity, and conflicting aromaticity,³⁵ which underlie their 2D geometries (as well as their unique structural dynamics). Note that the delocalized π/σ electrons in boron clusters are clouded over a 2D plane,^19,25–36 rather than on a single ring such as in benzene.

It is of fundamental importance to “tune” the rotation barrier of molecular rotors, which not only provides key insights into mechanisms for structural dynamics, but also facilitates control of the movements: halting or starting. Merino and coworkers⁷ showed that one C substitution stops the B₁₉⁻ Wankel motor, resulting in a nonfluxional B₁₈C cluster with a barrier of 27.6 kcal mol⁻¹. On the other hand, Popov et al.¹⁷ reported that complexation of B₁₂ with a metal atom can reduce the rotation barrier of half-sandwich RhB₁₂⁻ and CoB₁₂⁻ clusters from 19.5 kcal mol⁻¹ down to 8.7–8.9 kcal mol⁻¹. Likewise, Liu et al.¹⁸ designed a metal doped IrB₁₂⁻ Wankel motor with a barrier of 5.0 kcal mol⁻¹. Nevertheless, these barriers are still quite substantial. It is highly desirable to further reduce the barrier, for example, down to 1 kcal mol⁻¹ or less.

We shall meet the above challenge using the B₁₀Ca and B₁₀ clusters. The clusters are chosen for a couple of reasons. First, the bare B₁₀ cluster is known to be nonfluxional, with a triangularly close-packed 2D structure. Second, its elongated shape intuitively makes it rather challenging to control or reduce the dynamic barrier. Lastly, as will be shown below, the B₁₀ cluster is an unusual bonding system with 6π/8σ conflicting aromaticity. Thus, the present work offers a case to tune/control dynamic fluxionality using the concepts of aromaticity, double aromaticity, and antiaromaticity. The strategy has not been exploited in the literature, to our knowledge.

In this contribution, we report on the structural, bonding, and dynamic properties of a binary B₁₀Ca cluster using quantum chemical calculations and chemical bonding analyses. The alloy cluster assumes a half-sandwich structure, in which an elongated B₁₀ moiety largely inherits that of bare B₁₀ cluster (with subtle variations) and the Ca atom is capped on the B₁₀ moiety. This alloy cluster is used to tune the dynamics of bare B₁₀ cluster, starting structural fluxionality of the B₁₀Ca cluster as a subnanoscale tank tread. The rotation barrier is effectively reduced by one order of magnitude and down to 1 kcal mol⁻¹ for B₁₀Ca cluster at the PBE0 level, in contrast to 12.32 kcal mol⁻¹ for the B₁₀ cluster. The relevant mechanisms are fully elucidated via chemical bonding analyses, which should guide further designs of fluxional dynamic nanosystems.

2. Methods

Global-minimum (GM) search for the B₁₀Ca cluster was conducted using the unbiased Coalescence Kick (CK) algorithm^38,39 at the B3LYP/3-21G level. About 3000 stationary points were probed on the potential energy surface. Low-lying isomers were then fully reoptimized and their relative energies evaluated at the PBE0/6-311+G* level.^40,41 Vibrational frequencies were calculated at the same level to ensure that the reported structures are true minima unless stated otherwise. To benchmark the energetics, single-point CCSD(T) calculations^42–44 were carried out for the top two lowest-energy structures, that is, at the CCSD(T)/6-311+G*//PBE0/6-311+G* level, which also serve to validate the PBE0 method for the present system. The QST2 and intrinsic reaction coordinate (IRC) calculations were performed at the PBE0/6-311+G* level to locate and confirm transition state (TS) structures associated with in-plane rotation.

Natural bond orbital (NBO)⁴⁵ calculations were carried out at the PBE0/6-311G* level to obtain Wiberg bond indices (WBIs) and natural atomic charges. Chemical bonding was understood via CMO analyses and AdNDP.⁴⁶ The latter was done at the PBE0/6-31G level owing to the fact that such analysis is not sensitive to the level of theory or basis sets used. Born–Oppenheimer molecular dynamics (BOMD) simulations were accomplished at the PBE/DZVP level using the CP2K package.⁴⁷ All electronic structure calculations were performed using Gaussian 09.⁴⁸ AdNDP analyses were conducted using the AdNDP program.⁴⁶ The visualization of AdNDP results was realized using Molekel 5.4.0.8.⁴⁹

3. Results

3.1. Global-minimum and transition-state structures of the B₁₀Ca cluster

The GM structure of B₁₀Ca (C₂, ¹A) cluster at the PBE0/6-311+G* level is shown in Fig. 1, along with that of bare B₁₀ (C_2h, ¹A_g) cluster. Alternative top 30 low-lying structures of B₁₀Ca cluster, as identified from computer CK search and reoptimized at the PBE0/6-311+G* level, are presented in Fig. S1 (ESI†). The nearest isomeric structure is 0.83 eV higher in energy at PBE0 and 0.85 eV at single-point CCSD(T), suggesting that the B₁₀Ca GM structure is well defined on its potential energy surface. The B₁₀Ca (C₂, ¹A) cluster (Fig. 1b) is chiral in nature. It contains a bowl-like convex B₁₀ fragment onto which the Ca atom caps, forming a half-sandwich complex. It is 4.48 Å in length and 3.35 Å in width (with a length-to-width ratio of 1.34), which has an elongated overall shape and yet it is more circular than bare B₁₀ cluster.⁵⁰ The peripheral B₈ ring is not perfectly planar, and inner B9 and B10 atoms are popped out from the ring by about 0.8 Å.⁵¹ Note that the B₁₀ fragment of B₁₀Ca (C₂, ¹A) largely inherits the bare B₁₀ cluster in geometry (Fig. 1a), except that the latter has C_2h symmetry with sort of a rugged surface (atom B9 being slightly out-of-plane toward inside and B10 toward the opposite side), which is likely due to mismatch in size between the B₂ core and peripheral B₈ ring.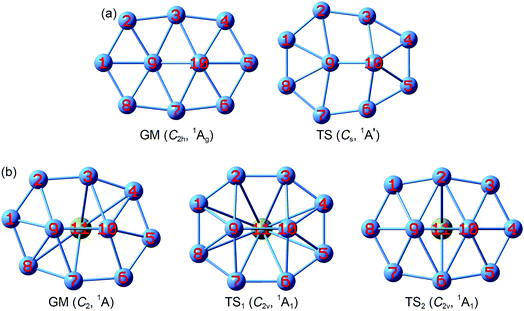

Fig. 1 Optimized structures of (a) B₁₀ (C_2h, ¹A_g) global minimum (GM) and (b) B₁₀Ca (C₂, ¹A) GM at the PBE0/6-311+G* level. Also shown are their transition-state (TS) structures associated with in-plane rotation: B₁₀ TS (C_s, ¹A′), B₁₀Ca TS₁ (C_2v, ¹A₁), and B₁₀Ca TS₂ (C_2v, ¹A₁). Two TS structures are found for B₁₀Ca, which effectively correspond to clockwise and anticlockwise rotations of the peripheral B₈ ring around the B₂ core, respectively. See Fig. S2 (ESI†) for their bond distances.

The B₁₀Ca GM cluster has a soft rotation mode (188.0 cm⁻¹). Following the mode one reaches, via QST2 and IRC calculations, two TS₁/TS₂ structures (Fig. 1b) with an imaginary frequency of 102.5i and 207.4i cm⁻¹, respectively, were observed. Both TS₁ and TS₂ have C_2v symmetry and the former is practically circular.⁵⁰ The IRC data confirm that the two TS structures are truly associated with the GM, corresponding to a clockwise/anticlockwise rotation of the peripheral B₈ ring around the B₂ core. Their rotation barriers are 0.95 and 1.25 kcal mol⁻¹ at PBE0, respectively. In contrast, the TS structure of bare B₁₀ cluster (Fig. 1a) has C_s symmetry. The energy barrier amounts to 12.32 kcal mol⁻¹ at PBE0, one order of magnitude greater than those of B₁₀Ca cluster. Notable structural changes occur between GM and TS of the B₁₀ cluster: expansion at one end, shrinkage at the other, and atom B10 being substantially popped out.⁵¹ The changes hinder the interconversion between GM and TS. The anticipated barrier lies in the distinct coordination environments: two hexacoordinate B centers in GM versus one heptacoordinate B and one pentacoordinate B in TS.

Structural parameters of B₁₀Ca and B₁₀ GM/TS clusters at PBE0 are presented in Fig. S2 (ESI†). All five structures have similar perimeters for the outer B₈ ring: 12.5–12.8 Å. However, bond distances in the inner B₂ core are slightly expanded from 1.63–1.66 Å in B₁₀ to 1.70–1.72 Å in B₁₀Ca. Radial B–B links are 1.79 Å in average for B₁₀Ca GM, which are elongated relative to B₁₀ GM (1.70 Å in average). Thus, upon Ca alloying, interior B–B links undergo discernible expansion, leading to bowl-like B₁₀Ca clusters (GM, TS₁, and TS₂). Note that such changes do not necessarily imply that interior B–B links in B₁₀Ca have lower bond orders (vide infra).

3.2. Wiberg bond indices and natural atomic charges

The NBO analyses provide quantitative data for WBIs (Fig. 2) and natural atomic charges (Fig. S3, ESI†). WBIs are highly non-uniform among peripheral and interior B–B links, between GM and TS structures, and between B₁₀Ca and B₁₀ clusters. We mention a couple of general observations. First, WBIs on the periphery are greater than 1.0, whereas those for interior links are below 1.0. The observation implies that the periphery is bound by two-center two-electron (2c–2e) skeleton σ bonds along with delocalized π/σ bonds. In contrast, interior B–B links are entirely held together by delocalized π/σ clouds. Second, there appears to be enhanced peripheral bonding in B₁₀Ca GM (WBIs in total: 10.1) as compared to B₁₀ GM (WBIs in total: 9.6). Third, WBIs of B–Ca links in B₁₀Ca GM are minor: 0.07/0.10/0.15 for the B9–Ca/B3–Ca/B4–Ca links, suggesting negligible covalent bonding between Ca and B atoms.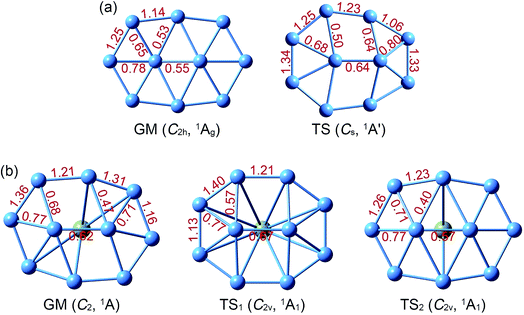

Fig. 2 Calculated Wiberg bond indices (WBIs) from natural bond orbital (NBO) analysis at the PBE0/6-311G* level. (a) B₁₀ GM and TS. (b) B₁₀Ca GM, TS₁, and TS₂.

Natural atomic charges in the B₁₀Ca GM cluster (Fig. S3b, ESI†) are consistent with a charge transfer complex: [B₁₀]²⁻[Ca]²⁺. Specifically, Ca atom has a positive charge of +1.52 |e|, with the peripheral B₈ ring collectively carrying a negative charge of −1.44 |e| and the inner B₂ dimer being roughly neutral. Note that atoms B4 and B8 each has −0.31 |e|, which are the most negative due to their closeness to the Ca center. The B₁₀ GM (Fig. S3a, ESI†) shows intramolecular charge redistribution, so that the central B9B3B10B7 diamond carries negative charges (−0.22/−0.17 |e| per atom) and the four B2/B4/B6/B8 corners are positive (+0.20 |e| per atom). Going from B₁₀ GM to B₁₀Ca GM, the major change in charges also lies in the above four corners, where the B4/B8 centers each gains −0.51 |e| from Ca and B2/B6 each gets −0.35 |e|. Overall, the distribution of negative charges is more uniform in B₁₀Ca GM relative to B₁₀ GM.⁵²

4. Discussion

4.1. Chemical bonding in the B₁₀Ca cluster

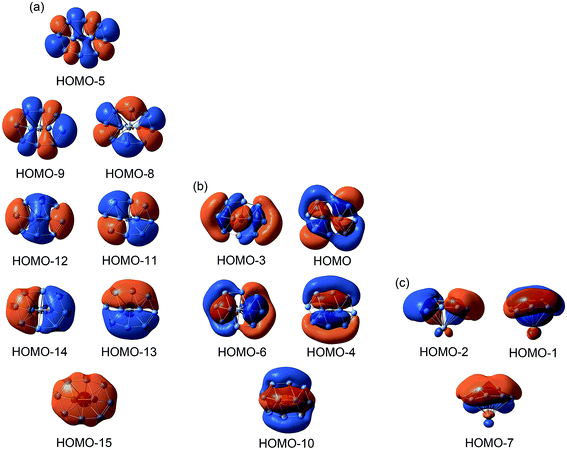
The nature of bonding ultimately governs the dynamic fluxionality of a molecular system. Therefore, we start our discussion with chemical bonding in B₁₀Ca cluster. Considering the electron configurations of B 2s²2p¹ and Ca 4s², the B₁₀Ca cluster has 32 valence electrons. The occupied CMOs are all based on the B₁₀ fragment (Fig. 3), consistent with a [B₁₀]²⁻[Ca]²⁺ charge-transfer complex; see above. The CMOs can be straightforwardly sorted into three categories. Subset (a) is primarily clouded on the periphery with major contributions from B 2s atomic orbitals (AOs). These CMOs have 0 to 4 nodal planes from bottom up (with three quasi-degenerate pairs in the middle), which follow the orbital building principles and readily recombine as eight 2c–2e Lewis B–B σ single bonds on the periphery.⁵³

Fig. 3 Pictures of occupied canonical molecular orbitals (CMOs) of B₁₀Ca GM cluster, calculated at the PBE0/6-311+G* level. The CMOs are sorted to three subsets: (a) peripheral two-center two-electron (2c–2e) Lewis B–B σ single bonds; (b) global, delocalized 10σ framework; and (c) global, delocalized 6π framework.

For the π framework in subset (c), three CMOs have 0 and 1 (quasi-degenerate) nodal planes, where the intrinsic nodal plane associated with p_z AOs is not counted, as routine. The three CMOs are analogous to the prototypical π sextet in benzene, thus endowing the B₁₀Ca cluster with π aromaticity according to the (4n + 2) Hückel rule. The Ca atom only contributes less than 7% in these π CMOs. For the delocalized σ framework (subset (b)), the five CMOs again follow the orbital building principles with 0 up to 2 nodal planes (including two quasi-degenerate pairs). This CMO pattern makes it imperative to claim σ aromaticity for the B₁₀Ca cluster. Indeed, the 10σ electron-counting conforms to the (4n + 2) Hückel rule. In summary, the CMO analysis indicates that the B₁₀Ca cluster possesses π/σ double aromaticity with 6π and 10σ electrons, respectively. In this model, there are no 2c–2e Lewis B–B π/σ bonds inside the peripheral B₈ ring, which explains why all those B–B links have low WBI values (less than 1.0; Fig. 2b).

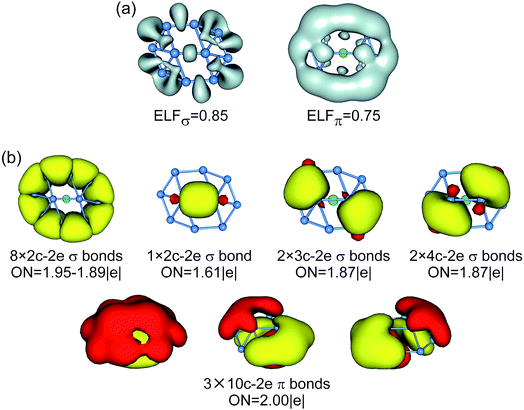
The bonding picture is borne out from electron localization functions (ELFs)⁵⁴ and AdNDP analysis (Fig. 4). The ELF_π and ELF_σ data are consistent with localized Lewis bonds on the periphery, as well as delocalized π/σ frameworks. The AdNDP scheme of B₁₀Ca cluster (Fig. 4b) reproduces peripheral 2c–2e σ bonds⁵³ and global π bonds. For the delocalized σ framework, we chose to partition it as one 2c–2e σ bond on the inner B₂ dimer and four 3c–2e/4c–2e σ bonds around the four corners, as hinted by the ELF_σ data. It should be stressed that this “island” σ scheme is only an approximation. In particular, the 2c–2e σ bond has an occupation number (ON) of 1.61 |e| only. Nonetheless, the scheme is useful in elucidating the structural dynamics (vide infra).

Fig. 4 (a) Electron localization functions, ELF_σ and ELF_π, of B₁₀Ca GM cluster. (b) Chemical bonding pattern of B₁₀Ca GM cluster on the basis of adaptive natural density partitioning (AdNDP) analysis, wherein the global 10σ framework is approximated to “island” σ bonds. Occupation numbers (ONs) are indicated.

The CMOs, ELFs, and AdNDP schemes of TS₁/TS₂ structures of the B₁₀Ca cluster are shown in Fig. 5 and S4–S6 (ESI†). The basic bonding information is similar to that described above, except for a slight spatial shift of the π/σ clouds, which is associated with geometric changes between GM and TS₁/TS₂ structures. For example, the AdNDP scheme for the 10σ framework in TS₁ (Fig. 5b) is similar to that in the GM (Fig. 4b). However, upon clockwise rotation of TS₁ relative to GM, two diamond 4c–2e σ bonds in the GM shrink spatially and become 3c–2e ones. This effectively generates a flow of σ clouds within the islands, whose direction is anticlockwise. For a following step (not shown), certain 3c–2e σ bonds may expand to 4c–2e ones. Therefore, during dynamic rotation of the B₁₀Ca cluster, delocalized σ clouds flow (and shrink/expand) continuously like a liquid and counter the direction of geometric rotation, which are maintained approximately on the four corner islands and underlie the low rotation barrier. The delocalized π clouds behave similarly.

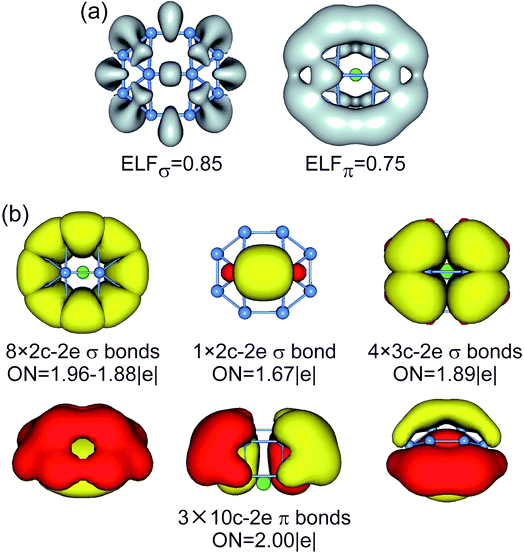Fig. 5 (a) ELF_σ and ELF_π of B₁₀Ca TS₁ cluster. (b) AdNDP bonding pattern of B₁₀Ca TS₁ cluster, wherein the global 10σ framework is approximated to island σ bonds. ONs are indicated.

For comparison, the CMOs, ELFs, and AdNDP patterns of GM/TS structures of bare B₁₀ cluster are shown in Fig. 6 and S7–S9 (ESI†). The B₁₀ GM cluster (Fig. S7b, ESI†) differs from B₁₀Ca GM (Fig. 3b) by one CMO less in the delocalized σ framework, which becomes the lowest unoccupied molecular orbital (LUMO) in the former species. Based on the above understanding of B₁₀Ca, bare B₁₀ cluster should be classified as σ antiaromatic, which has a delocalized 8σ system and follows the 4n Hückel rule.^55,56 Indeed, the B₁₀ cluster is more elongated than B₁₀Ca, a typical consequence of σ antiaromaticity; see Section 3.1.⁵⁰ Overall, the B₁₀ cluster has conflicting aromaticity with 6π and 8σ electrons.

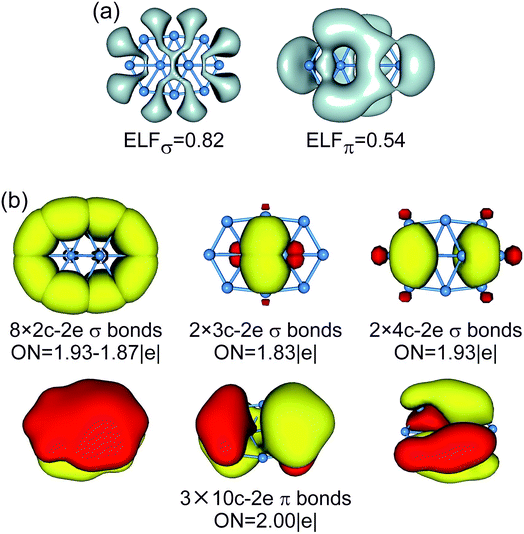Fig. 6 (a) ELF_σ and ELF_π of B₁₀ GM cluster. (b) AdNDP bonding pattern of B₁₀ GM cluster, wherein the global 8σ framework is approximated to island σ bonds. ONs are indicated.

It is interesting to quantitatively follow the orbital contributions of the inner B₂ core in B₁₀Ca GM and B₁₀ GM clusters. The B₂ core in B₁₀Ca contributes 3.32, 1.84, and 0.87 |e| to subsets (a)–(c), respectively (Fig. 3), compared to 3.89, 1.02, and 1.52 |e| in B₁₀ (Fig. S7, ESI†). In other words, the B₂ core has similar total contributions to σ CMOs: 5.16 |e| in B₁₀Ca versus 4.91 |e| in B₁₀. However, its contributions to π CMOs differ for the species: 0.87 |e| in B₁₀Ca versus 1.52 |e| in B₁₀. The latter observation suggests that the π clouds are probably more delocalized on the plane in B₁₀ GM, which is a con for the dynamic fluxionality of bare B₁₀ cluster, in particular considering that it has a rugged shape. In contrast, the π clouds in B₁₀Ca GM appear to lean to the periphery, which benefits a low dynamic barrier, as supported by the comparative ELF_π patterns (Fig. 4aversusFig. 6a). The above data also indicate that the B₂ core has collectively 5.84 |e| in B₁₀Ca GM versus 6.43 |e| in B₁₀ GM. Indeed, NBO data on natural atomic charges show that the B₂ core is practically neutral in B₁₀Ca and negatively charged in B₁₀ (by −0.22 |e| per atom; Fig. S3, ESI†).

4.2. Starting a subnanoscale tank tread: distinct structural dynamics of B₁₀Ca and B₁₀ clusters

Two key structural features of the present B₁₀Ca and B₁₀ systems make it rather challenging to tune/control their rotation barriers. First, the clusters assume elongated (rather than circular) geometries akin to tank treads, which are generally less fluxional than molecular Wankel motors. Second, bare B₁₀ cluster is composed entirely of close-packed B₃ triangles without “defect” holes, which is intuitively anticipated to be rigid against deformation. Nonetheless, the energetics data in Section 3.1 clearly show that Ca alloying in the B₁₀Ca GM cluster effectively diminishes its rotation barrier down to 0.95 and 1.25 kcal mol⁻¹ at the PBE0 level, with respect to TS₁ and TS₂, respectively. This is a remarkable achievement considering that bare B₁₀ cluster is nonfluxional with a barrier of 12.32 kcal mol⁻¹. To our knowledge, this is the first example of barrier reduction of a molecular rotor by one order of magnitude and down to ∼1 kcal mol⁻¹,^17,18 a highly desirable level for dynamic fluxionality.

With the GM and TS₁/TS₂ structures of the B₁₀Ca cluster being identified (Fig. 1b), the dynamic structural evolution is relatively simple as illustrated in Fig. 7, assuming that the peripheral ring rotates clockwise. Starting with GM₁ and let the B9–B2 link rotate by about 18.9°, one reaches TS₁₋₂ that corresponds to TS₁ in Fig. 1b. From GM₁ to TS₁₋₂, rhombic B2B3B10B9 and B7B9B10B6 holes turn to squares. Going down the barrier, the B9–B2 link rotates by another 17.5° and the system returns to GM₂. Due to the chiral nature of B₁₀Ca cluster with C₂ symmetry, GM₁ and GM₂ are a pair of enantiomers and thus isoenergetic. However, the system does not recover its initial orientation. Further rotating the B9–B2 link slightly by 7.1° and making the B10–B2 and B9–B6 links, one reaches TS₂₋₃. The latter differs from TS₁₋₂ with a higher barrier and it corresponds to TS₂ in Fig. 1b. From TS₂₋₃ to GM₃, the B9–B2 link rotates another 7.1° and breaks, generating two new rhombic holes: B1B2B10B9 and B6B9B10B5. This completes a fully cycle, in which the cluster returns to its initial structure as well as orientation. During this process, the peripheral ring moves by one B–B link (or about 51°).

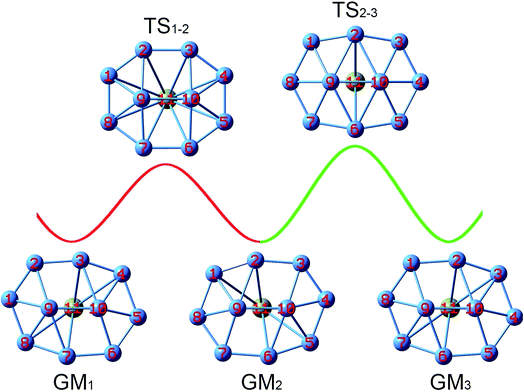Fig. 7 Structural evolution of the B₁₀Ca GM cluster during dynamic rotation, assuming that the peripheral B₈ ring moves clockwise around the B₂ core. Two energy barriers, TS₁₋₂ and TS₂₋₃, are to be overcome for the cluster in order to fully recover its initial structure and orientation. These barriers correspond to the TS₁ and TS₂ structures (Fig. 1b), respectively.

Despite being nonfluxional with a substantial barrier, the structural evolution of bare B₁₀ cluster can be followed on the basis of GM and TS structures identified. The process is simpler (Fig. 8). Upon rotation of the B9–B2 link clockwise by 12.0°, the B9–B3 link breaks and two rhombic B9B2B3B10 and B7B9B10B6 holes emerge, which leads to TS₁₋₂ that corresponds to TS in Fig. 1a. Further rotate the B9–B2 link by 38.1° and the system recovers GM₂. Overall, the peripheral atoms move by one B–B link (or about 50°) from GM₁ to GM₂.

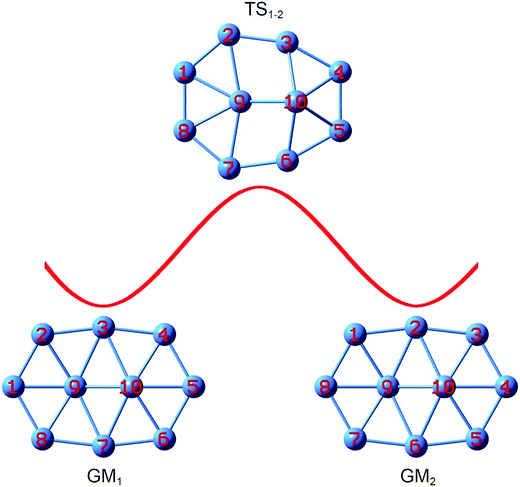Fig. 8 Structural evolution of the B₁₀ GM cluster during dynamic rotation, assuming that the peripheral B₈ ring moves clockwise around the B₂ core. Energy barrier TS₁₋₂ is associated with the TS structure (Fig. 1a).

To demonstrate the dynamic fluxionality of B₁₀Ca cluster, we performed BOMD simulations at selected temperatures of 300, 600, and 900 K. A typical simulation at 900 K is presented in the form of a short movie (see the ESI†), which was carried out for 50 ps using the CP2K package at the PBE0/DZVP level. Initial conditions were chosen to correspond to the microcanonical ensemble (NVE). The extracted movie roughly covers a time span of 2.5 ps. It is obvious that at 900 K the B₁₀Ca cluster behaves vividly like a subnanoscale tank tread, with the peripheral B₈ ring gliding freely as a flexible chain around the B₂ core. In particular, the peripheral B₈ ring appears to be rather robust during rotation, which rotates but does not break. Similar motion is observed at 600 K except that it is slower, whereas preliminary data at 300 K do not reveal dynamic fluxionality.

As for mechanisms that distinguish between the dynamic properties of B₁₀Ca and B₁₀ clusters, the most important one is their bonding, as detailed in Section 4.1. Note that in prior studies people have attempted to unravel the connection between aromaticity (or electron delocalization) and fluxionality, in which the magnetic response is discussed.⁵⁷ The present data offer key insights using the CMOs and AdNDP analyses. While both B₁₀Ca and B₁₀ are 6π aromatic, they differ in the σ framework: B₁₀ is σ antiaromatic^55,56 with 8σ electrons and B₁₀Ca has σ aromaticity (10σ electrons). Double π/σ aromaticity in B₁₀Ca cluster makes it sort of circular with a smooth bowl-shaped surface, facilitating π/σ delocalization and structural fluxionality. In contrast, the B₁₀ cluster has a rugged surface⁵¹ and deteriorated π/σ delocalization.

In terms of geometry, the C₂ symmetry of B₁₀Ca GM cluster (Fig. 1b) has two rhombic defect holes, while B₁₀ GM cluster features triangular close-packing. Such defects are known to be critical for the dynamic fluxionality of subnanoscale tank treads (and nanorotors in general).¹⁰ Thus, alloying with Ca induces structural flexibility for B₁₀Ca cluster, which serves as “preactivation” of the system and effectively reduces the dynamic barrier. As for the B₁₀ cluster, 8σ antiaromaticity leads to an elongated GM as well as substantial geometric changes between GM and TS (Fig. 1a): expansion at the left side versus shrinkage at the right. In fact, while delocalized σ clouds in the GM are balanced for left versus right (Fig. 6b), they become highly uneven in the TS so that the left side only has one 5c–2e σ bond and the right has three 3c–2e/4c–2e bonds (Fig. S9b, ESI†). Such a change is induced entirely by a rotation of the peripheral ring, which is an intriguing consequence of σ antiaromaticity and clearly underlies its large barrier. Lastly, we comment on a consequence of the two inequivalent TS structures of B₁₀Ca cluster (Fig. 1b). All molecular rotors to date move randomly (clockwise or anticlockwise). However, the occurrence of two inequivalent TS structures for B₁₀Ca hints that the system can at least be initiated with one direction preferred to another, which simplifies further control or manipulation of the dynamics.

4.3. Change in WBIs as a semi-quantitative indicator of dynamic fluxionality

To shed further light on the distinct dynamics of B₁₀Ca and B₁₀ clusters, we make use of the WBI data from NBO analyses. Intuitively, the barrier of a molecular rotor is connected to the WBI change between the GM and TS structures, which is denoted here as ΔWBI. In the present systems, the radial links govern in-plane rotation and determine the barrier. Thus, we follow all radial B–B links. As an example, ΔWBI values of the B₁₀Ca cluster with respect to TS₂ are plotted in Fig. 9, which are compared to those of bare B₁₀ cluster. Here the B–B links are labeled numerically based on GM₃ and TS₂₋₃ (anticlockwise rotation; Fig. 7). Link B9–B8 at the far left is labeled “1”, counting clockwise up to “10”. These include B9–B2 and B10–B6 as “3” and “8”, respectively. By definition, a positive ΔWBI is associated with bond elongation, and vice versa.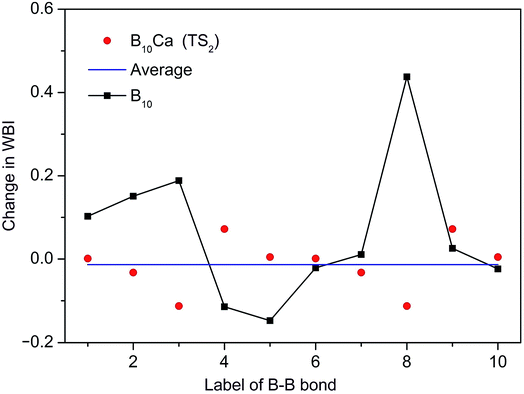

Fig. 9 Change in WBIs (that is, ΔWBIs) for the radial B–B links in the B₁₀Ca cluster from GM to TS₂ during dynamic rotation. The WBI data are obtained explicitly from GM₃ to TS₂₋₃ in Fig. 7 (anticlockwise rotation). The B–B links are labelled numerically, starting from the far-left link (B9–B8) as “1” and counting clockwise up to “10” (links B9–B2 and B10–B6 included). Positive ΔWBI indicates elongation and negative compression. Red dots are ΔWBIs of the B₁₀Ca cluster and a horizontal blue line is their average. Comparative data of the B₁₀ cluster are shown with filled squares.

The B₁₀Ca cluster shows a smooth ΔWBI curve with relatively minor and uniform values for all radial B–B links, consistent with a low barrier. In contrast, large ΔWBIs and in particular spikes are present for the B₁₀ cluster, whose B–B links are labeled again with the far-left one (B9–B1) being “1” and counted clockwise up to “10”. Specifically, link “8” (B10–B7; Fig. 1a) has the largest ΔWBI, which has to elongate substantially and eventually break in order for the cluster to reach the TS structure, thus defining the barrier height of B₁₀ cluster. For comparison, links B9–B3 and B10–B7 in B₁₀Ca GM₁ (Fig. 7) are “preactivated” upon alloying with Ca atom, and they are no longer the bottleneck for fluxionality, which effectively diminish the barrier (for TS₁). Moreover, there is no need to break any B–B links from GM₃ to TS₂₋₃ (anticlockwise; Fig. 7), but to shrink links B9–B2 and B10–B6, which have the largest negative ΔWBIs, in line with a low barrier for TS₂. The comparative ΔWBI data of B₁₀Ca and B₁₀ clusters distinguish between the two species, demonstrating a semi-quantitative measure for dynamic fluxionality.

5. Conclusions

We have demonstrated, via alloying with Ca atom, a means to tune the structural dynamics of a subnanoscale tank tread B₁₀Ca cluster. The strategy efficiently reduces the rotation barrier by one order of magnitude, from 12 kcal mol⁻¹ in B₁₀ down to around 1 kcal mol⁻¹ in B₁₀Ca. The B₁₀Ca global-minimum cluster is half-sandwich in shape, which is dynamically fluxional at 600 K and beyond, whereas bare B₁₀ cluster is nonfluxional. In terms of structures, Ca alloying generates two rhombic defect holes in B₁₀Ca cluster, which preactivates the system for fluxionality. Chemical bonding analyses show that the B₁₀Ca cluster is a charge-transfer complex and can be formulated as [B₁₀]²⁻[Ca]²⁺, featuring double (6π and 10σ) aromaticity. The bonding pattern leads to a more circular geometry and ideal π/σ delocalization, facilitating dynamic fluxionality. In contrast, the B₁₀ cluster has conflicting aromaticity (6π versus 8σ), as well as a more elongated and rugged shape. Thus, our work demonstrates that π/σ aromaticity can be utilized as a key concept to design dynamically fluxional nanosystems. To semi-quantitatively describe dynamic fluxionality, the change in Wiberg bond indices between global-minimum and transition-state structures serves as a useful indicator, which clearly distinguishes between a fluxional B₁₀Ca cluster and a nonfluxional B₁₀ cluster.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (21873058, 21573138), the Natural Science Foundation of Xinzhou Teachers University (201711), and the Sanjin Scholar Distinguished Professors Program.

References

1. J. O. C. Jiménez-Halla, R. Islas, T. Heine and G. Merino, Angew. Chem., Int. Ed., 2010, 49, 5668.
2. S. Erhardt, G. Frenking, Z. F. Chen and P. v. R. Schleyer, Angew. Chem., Int. Ed., 2005, 44, 1078.
3. G. Martínez-Guajardo, A. P. Sergeeva, A. I. Boldyrev, T. Heine, J. M. Ugalde and G. Merino, Chem. Commun., 2011, 47, 6242.
4. J. Zhang, A. P. Sergeeva, M. Sparta and A. N. Alexandrova, Angew. Chem., Int. Ed., 2012, 51, 8512.
5. G. Merino and T. Heine, Angew. Chem., Int. Ed., 2012, 51, 10226.
6. D. Moreno, S. Pan, L. L. Zeonjuk, R. Islas, E. Osorio, G. Martínez-Guajardo, P. K. Chattaraj, T. Heine and G. Merino, Chem. Commun., 2014, 50, 8140.
7. F. Cervantes-Navarro, G. Martínez-Guajardo, E. Osorio, D. Moreno, W. Tiznado, R. Islas, K. J. Donald and G. Merino, Chem. Commun., 2014, 50, 10680.
8. S. Jalife, L. Liu, S. Pan, J. L. Cabellos, E. Osorio, C. Lu, T. Heine, K. J. Donald and G. Merino, Nanoscale, 2016, 8, 17639.
9. M. R. Fagiani, X. W. Song, P. Petkov, S. Debnath, S. Gewinner, W. Schöllkopf, T. Heine, A. Fielicke and K. R. Asmis, Angew. Chem., Int. Ed., 2017, 56, 501.
10. Y. J. Wang, X. Y. Zhao, Q. Chen, H. J. Zhai and S. D. Li, Nanoscale, 2015, 7, 16054.
11. Y. J. Wang, X. R. You, Q. Chen, L. Y. Feng, K. Wang, T. Ou, X. Y. Zhao, H. J. Zhai and S. D. Li, Phys. Chem. Chem. Phys., 2016, 18, 15774.
12. Y. J. Wang, J. C. Guo and H. J. Zhai, Nanoscale, 2017, 9, 9310.
13. Y. G. Yang, D. M. Jia, Y. J. Wang, H. J. Zhai, Y. Man and S. D. Li, Nanoscale, 2017, 9, 1443.
14. Y. J. Wang, L. Y. Feng, J. C. Guo and H. J. Zhai, Chem.–Asian J., 2017, 12, 2899.
15. J. C. Guo, L. Y. Feng, Y. J. Wang, S. Jalife, A. Vásquez-Espinal, J. L. Cabellos, S. Pan, G. Merino and H. J. Zhai, Angew. Chem., Int. Ed., 2017, 56, 10174.
16. L. Y. Feng, J. C. Guo, P. F. Li and H. J. Zhai, Phys. Chem. Chem. Phys., 2018, 20, 22719.
17. I. A. Popov, W. L. Li, Z. A. Piazza, A. I. Boldyrev and L. S. Wang, J. Phys. Chem. A, 2014, 118, 8098.
18. L. Liu, D. Moreno, E. Osorio, A. C. Castro, S. Pan, P. K. Chattaraj, T. Heine and G. Merino, RSC Adv., 2016, 6, 27177.
19. W. Huang, A. P. Sergeeva, H. J. Zhai, B. B. Averkiev, L. S. Wang and A. I. Boldyrev, Nat. Chem., 2010, 2, 202.
20. E. Oger, N. R. M. Crawford, R. Kelting, P. Weis, M. M. Kappes and R. Ahlrichs, Angew. Chem., Int. Ed., 2007, 46, 8503.
21. L. Hanley, J. L. Whitten and S. L. Anderson, J. Phys. Chem., 1988, 92, 5803.
22. J. E. Fowler and J. M. Ugalde, J. Phys. Chem. A, 2000, 104, 397.
23. J. Aihara, J. Phys. Chem. A, 2001, 105, 5486.
24. J. Aihara, H. Kanno and T. Ishida, J. Am. Chem. Soc., 2005, 127, 13324.
25. H. J. Zhai, A. N. Alexandrova, K. A. Birch, A. I. Boldyrev and L. S. Wang, Angew. Chem., Int. Ed., 2003, 42, 6004.
26. H. J. Zhai, B. Kiran, J. Li and L. S. Wang, Nat. Mater., 2003, 2, 827.
27. B. Kiran, S. Bulusu, H. J. Zhai, S. Yoo, X. C. Zeng and L. S. Wang, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 961.
28. A. P. Sergeeva, D. Y. Zubarev, H. J. Zhai, A. I. Boldyrev and L. S. Wang, J. Am. Chem. Soc., 2008, 130, 7244.
29. Z. A. Piazza, H. S. Hu, W. L. Li, Y. F. Zhao, J. Li and L. S. Wang, Nat. Commun., 2014, 5, 3113.
30. H. J. Zhai, Y. F. Zhao, W. L. Li, Q. Chen, H. Bai, H. S. Hu, Z. A. Piazza, W. J. Tian, H. G. Lu, Y. B. Wu, Y. W. Mu, G. F. Wei, Z. P. Liu, J. Li, S. D. Li and L. S. Wang, Nat. Chem., 2014, 6, 727.
31. W. L. Li, Q. Chen, W. J. Tian, H. Bai, Y. F. Zhao, H. S. Hu, J. Li, H. J. Zhai, S. D. Li and L. S. Wang, J. Am. Chem. Soc., 2014, 136, 12257.
32. Q. Chen, W. L. Li, Y. F. Zhao, S. Y. Zhang, H. S. Hu, H. Bai, H. R. Li, W. J. Tian, H. G. Lu, H. J. Zhai, S. D. Li, J. Li and L. S. Wang, ACS Nano, 2015, 9, 754.
33. Y. J. Wang, Y. F. Zhao, W. L. Li, T. Jian, Q. Chen, X. R. You, T. Ou, X. Y. Zhao, H. J. Zhai, S. D. Li, J. Li and L. S. Wang, J. Chem. Phys., 2016, 144, 064307.
34. Q. Chen, W. J. Tian, L. Y. Feng, H. G. Lu, Y. W. Mu, H. J. Zhai, S. D. Li and L. S. Wang, Nanoscale, 2017, 9, 4550.
35. A. N. Alexandrova, A. I. Boldyrev, H. J. Zhai and L. S. Wang, Coord. Chem. Rev., 2006, 250, 2811.
36. A. P. Sergeeva, I. A. Popov, Z. A. Piazza, W. L. Li, C. Romanescu, L. S. Wang and A. I. Boldyrev, Acc. Chem. Res., 2014, 47, 1349.
37. Borospherene B₄₀ cluster is shown to behave dynamically like a nanobubble at high temperatures. See: G. Martínez-Guajardo, J. L. Cabellos, A. Díaz-Celaya, S. Pan, R. Islas, P. K. Chattaraj, T. Heine and G. Merino, Sci. Rep., 2015, 5, 11287.
38. M. Saunders, J. Comput. Chem., 2004, 25, 621.
39. P. P. Bera, K. W. Sattelmeyer, M. Saunders, H. F. Schaefer III and P. v. R. Schleyer, J. Phys. Chem. A, 2006, 110, 4287.
40. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650.
41. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158.
42. J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Chem. Phys., 1987, 87, 5968.
43. G. E. Scuseria, C. L. Janssen and H. F. Schaefer III, J. Chem. Phys., 1988, 89, 7382.
44. G. E. Scuseria and H. F. Schaefer III, J. Chem. Phys., 1989, 90, 3700.
45. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899.
46. D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207.
47. J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103.
48. M. J. Frisch, et al., Gaussian 09, revision D.01, Gaussian Inc., Wallingford, Connecticut, 2009.
49. U. Varetto, Molekel 5.4.0.8, Swiss National Supercomputing Center, Manno, Switzerland, 2009.
50. The B₁₀ GM cluster has a length of 4.76 Å and width of 3.13 Å (with length-to-width ratio of 1.52). Those of the B₁₀ TS, B₁₀Ca TS₁, and B₁₀Ca TS₂ species are 4.13/3.54, 4.01/3.38, and 4.50/3.28 Å, with ratios of 1.17, 1.19, and 1.37, respectively. Thus, there is a marked ratio change from B₁₀ GM to B₁₀ TS. Also, B₁₀Ca TS₁ is particularly circular.
51. Of all five key structures in Fig. 1, the peripheral B₈ ring is perfectly planar only in B₁₀ GM. For other species, the out-of-plane distortions of central B atoms are estimated roughly. In B₁₀ GM cluster, atom B9 is slightly out-of-plane toward inside (by 0.3 Å) and B10 toward the opposite side. For the B₁₀ TS, B₁₀Ca TS₁, and B₁₀Ca TS₂ species, atoms B9/B10 are popped out by 0.3/1.0, 0.9/0.9, and 0.8/0.8 Å, respectively.
52. There appears to be a general trend that a B center with a higher coordination and stronger bonds gets some net negative charges from surrounding B atoms. In this way, the hexacoordinate B9/B10 centers and tetracoordinate B3/B7 atoms in B₁₀ GM carry negative charges (Fig. S3a; ESI†). For B₁₀ TS, the B10 center remains strongly coordinated by five B atoms, whereas the B9 center is only loosely bound despite its heptacoordination nature. The latter leads to less negative charge.
53. Strictly speaking, the assignment of eight peripheral Lewis σ bonds is an approximation. The bottom five of these CMOs have nonnegligible contributions from central B9/B10 atoms (Fig. 3a). Quantitatively, the B9/B10 core accounts for 20.7% of these eight σ CMOs, which explains why their occupation numbers (ONs; Fig. 4b) in the AdNDP scheme deviate from an ideal value of 2.00 |e|.
54. B. Silvi and A. Savin, Nature, 1994, 371, 683.
55. A previous work⁵⁶ assigned the delocalized σ framework of B₁₀ GM cluster as one 2c–2e σ bond in B₂ core (although specifically called for caution) and three global σ bonds. The latter were proposed to render σ aromaticity for B₁₀ cluster, due to the 6σ electron-counting. Our present analysis suggests that all these 8σ electrons should be treated collectively (Fig. S7b, ESI†) and B₁₀ cluster is σ antiaromatic rather than σ aromatic. Indeed, the ELF_σ data and our AdNDP scheme (island version; Fig. 6) do not support the idea of a 2c–2e σ bond within the B₂ core.
56. D. Y. Zubarev and A. I. Boldyrev, J. Comput. Chem., 2007, 28, 251.
57. R. Islas, T. Heine and G. Merino, Acc. Chem. Res., 2012, 45, 215.

---

Footnotes

† Electronic supplementary information (ESI) available: A short movie extracted from the BOMD simulation at 900 K for B₁₀Ca cluster; Cartesian coordinates for GM structures of B₁₀Ca and B₁₀ at the PBE0/6-311+G* level (Table S1); alternative optimized structures of B₁₀Ca at PBE0 (Fig. S1); optimized GM and TS structures of B₁₀ and B₁₀Ca at PBE0 with bond distances indicated (Fig. S2); natural atomic charges for GM and TS structures of B₁₀ and B₁₀Ca (Fig. S3); CMOs of two B₁₀Ca TS structures (Fig. S4 and S5); ELFs and AdNDP data of B₁₀Ca TS₂ structure (Fig. S6); CMOs of B₁₀ GM and TS structures (Fig. S7 and S8); and ELFs and AdNDP data of B₁₀ TS structure (Fig. S9). See DOI: 10.1039/c8na00256h

‡ These authors contributed equally to this work.

---