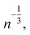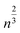Open Access Article
Open Access ArticleStructure–property relationships on thiolate-protected gold nanoclusters†
Michael J.
Cowan
and
Giannis
Mpourmpakis
 *
*
Department of Chemical and Petroleum Engineering, University of Pittsburgh, Pittsburgh, PA 15261, USA. E-mail: gmpourmp@pitt.edu
First published on 23rd November 2018
Abstract
Since their discovery, thiolate-protected gold nanoclusters (Aun(SR)m) have garnered a lot of interest due to their fascinating properties and “magic-number” stability. However, models describing the thermodynamic stability and electronic properties of these nanostructures as a function of their size are missing in the literature. Herein, we employ first principles calculations to rationalize the stability of fifteen experimentally determined gold nanoclusters in conjunction with a recently developed thermodynamic stability theory on small Au nanoclusters (≤102 Au atoms). Our results demonstrate that the thermodynamic stability theory can capture the stability of large, atomically precise nanoclusters, Au279(SR)84, Au246(SR)80, and Au146(SR)57, suggesting its applicability over larger cluster size regimes than its original development. Importantly, we develop structure–property relationships on Au nanoclusters, connecting their ionization potential and electron affinity to the number of gold atoms within the nanocluster. Altogether, a computational scheme is described that can aid experimental efforts towards a property-specific, targeted synthesis of gold nanoclusters.
Introduction
In 1994, Brust et al. introduced a synthetic method to create a new class of gold nanoparticles protected by thiolate ligands.1 Since then, these nanoparticles have attracted tremendous research interest due to their intriguing properties ranging from structural, to optical, to electrochemical,2–6 giving rise to vast potential for applications in the fields of catalysis, chemical sensing, and biomedicine.7 A class of these nanoparticles are known as thiolate-protected gold nanoclusters (Au NCs). With sizes ranging from a dozen to a couple of hundred gold atoms (i.e. <2 nm, giving rise to the term nanocluster8), these thermally stable, atomically precise Au NCs represent an exciting and rapidly growing field.9Since the early synthesis of Au NCs, a major topic of research focus has been determining the origin of the high stability with certain molecular formulas (Aun(SR)m), i.e. what gives rise to “magic numbers” in their synthesis (specific n and m). One of the first steps towards answering this question with respect to the structure of the NCs was the divide-and-protect theory proposed by Häkkinen et al.10 Confirmed in the next couple years,11,12 the theory stated that instead of just thiol ligands surrounding a metallic core, there is a more sophisticated makeup of a smaller metallic core protected by a shell of thiol-gold staple motifs. As a result, the Aun(SR)m NCs, where n and m are the number of gold atoms and ligands, respectively, could be viewed as Aun−xRS(AuSR)x, where x indicates the motif type.13 This was the foundation of the staple motifs found in all stable Au NCs known today.
Although the divide-and-protect theory describes the overall structural characteristics of Au NCs, it does not explain the origin of the magic size NC stability. By diving deeper into electronic reasons that could give rise to NC stability, the superatom theory was developed.14 As the name suggests, the theory treats a Au NC as one large superatom – rationalizing its electronic stability by assuming that the valence electrons occupy a set of orbitals made up by the entire Au NC. Thus, Au NCs are stable when their valence electrons make up a closed-shell electronic system. Other models stemming from the superatom theory have been developed as well,15,16 but none have been able to explain the stability of all Au NCs.13 The aforementioned models have significantly advanced our understanding of Au NCs, but there is still a need for models able to rationalize the stability of a wider array of NCs. In 2017, Taylor et al. introduced the thermodynamic stability theory17 which connects core–shell structural characteristics with the thermodynamics of formation of Au NCs. The theory revealed an energy balance between the binding strength of a Au NC shell to its core (BE) and the cohesive energy of its metallic core (CE). The results showed an excellent parity of these energies for numerous experimentally synthesized Au NCs with different sizes and structures, laying the foundation for the theory's applicability as a general stability model. Since its conception, others have utilized the theory to test the stability of Au NC isomers.18,19 However, more work is still needed to expand the model's reach, namely the analysis of Au NCs in different size regimes. In addition, using this theory in concert with other developed structure–property relationships on Au NCs could potentially generate a very effective predictive tool bridging the structure with the stability and properties of Au NCs. Herein, we apply first principles calculations to examine fifteen experimentally determined Au NC structures,5,20–32 first using the thermodynamic stability theory. Next, we introduce models to predict the ionization potential (IP) and electron affinity (EA) of Au NCs. Both models are based on the number of gold atoms within a nanocluster (NC size), a property that can be identified experimentally.7 Most importantly, we demonstrate how models describing thermodynamic stability, IP, EA, and stoichiometry can be used together to guide researchers towards property-driven design of Au NCs.
Computational methods
DFT calculations were performed using the Perdew–Burke–Ernzerhof (PBE)33 exchange-correlation functional along with the double-ζ valence polarized basis set (DZVP) and Goedecker, Teter, and Hutter (GTH)34 pseudopotentials as implemented in the CP2K35 package. All structures were fully relaxed until the max forces were below 0.002 eV Å−1 while the total energies were converged to 10−7 Ha. Core CE and shell-to-core BE were calculated based on previously reported methods.17 Vertical ionization potentials (EIP) and electron affinities (EEA) were calculated according to the following expressions:| EIP = ENC+1 − ENC0 | (1) |
| EEA = ENC−1 − ENC0 | (2) |
Results and discussion
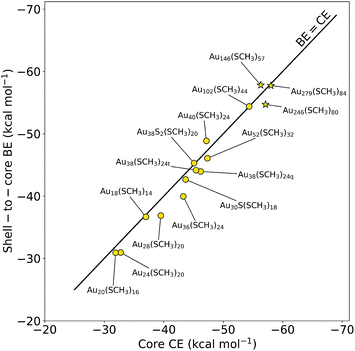
We fully optimized fifteen experimentally determined Au NCs5,20–32 (see ESI Fig. S1†) with the number of gold atoms ranging from 18–279. Based on the methodology reported by Taylor et al.,17 each structure was then split into its respective core and shell regions and the core CE and shell-to-core BE were calculated. Fig. 1 depicts the energy balance between the core CE and shell-to-core BE for the Au NCs studied. Notably, Au38S2(SCH3)20, Au40(SCH3)24, Au52(SCH3)32, Au146(SCH3)57, Au246(SCH3)80, and Au279(SCH3)84 have never been analyzed with this theory. Interestingly, the three largest structures (denoted with stars in Fig. 1), Au146(SCH3)79, Au246(SCH3)80, and Au279(SCH3)84, are in excellent agreement with the theory, falling very close to the parity line. The results of these larger Au NCs support the model's capability as a tool for capturing the stability of Au NCs approaching a few hundred gold atoms. It should be noted that the thermodynamic stability theory had been applied up to a Au102(SCH3)44 NC and this is the first time we demonstrate that the theory is extendable to a significantly larger NC, Au279(SCH3)84. Along with these large NCs, Au38S2(SR)20, Au40(SR)24 and Au52(SR)32 were analyzed with this theory for the first time to further explore different core packing structures and size regions of Au NCs. The three structures were found to display a fine CE-to-BE energy balance. Though the remaining structures had been previously computationally investigated using the thermodynamic stability theory,17 our work herein has been performed using a different exchange-correlation functional, namely the Perdew–Burke–Ernzerhof (PBE).33 As a result, utilizing different computational methods provides further evidence towards the legitimacy of the thermodynamic stability theory, which is agnostic to the functional choice, but is solely based on thermodynamic foundations.The work herein uses methylthiols in place of full ligands. Prior studies have shown that the full-to-methyl ligand change may affect the core CE and shell-to-core BE when there is a reconstruction of the Au NC during relaxation (i.e. deviation from the crystal structure).17 Thus, it is important to note that there was no reconstruction during optimization for any of the Au NCs presented in Fig. 1. Additionally, recent work has demonstrated that the thermodynamic stability theory also captures stability when using full ligands,36 illustrating its effectiveness across different ligand types.
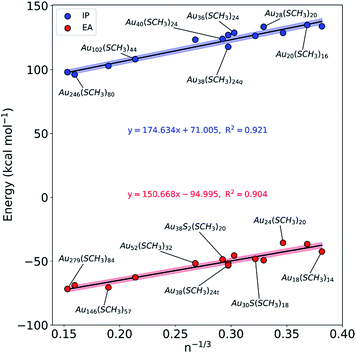
Understanding the electronic properties of Au NCs is of great importance for their use in catalysis and chemical sensing.7,9 Moreover, unraveling simple relationships based on experimentally measurable properties (e.g. number of Au atoms on the NC) could allow for the development of practical models that researchers could employ to screen the electronic properties of NCs as a function of their size. In consideration of this, the ionization potential (IP) and electron affinity (EA) of the fifteen Au NCs were calculated. As shown in Fig. 2, it was found that there is a size effect for both IP and EA that is dominated by the number of gold atoms within a NC. As the Au NC size increases (i.e. number of gold atoms increases), the IP decreases (becomes less endothermic). The EA follows the same trend, only that since the values are negative, as the NC size increases the EA becomes more exothermic. In other words, the larger NCs, like Au279(SCH3)84, require the least amount of energy to remove an electron and exhibit the highest affinity to receive an electron. Previous work has indicated that certain ligands, especially the ones with electron withdrawing character, can impact the EA and IP of Au NCs.37,38 For this reason, we note that slight deviations from the models could potentially exist for Au NCs stabilized with electron withdrawing ligands (e.g. para-mercaptobenzoic acid), but the general trends (i.e. size effect) provided by the models will still remain valid. The results presented in Fig. 2 trend with the general size dependence of HOMO–LUMO gaps previously reported for Au NCs.39 Additionally, we note that the IP and EA models are indiscriminate of the core packing structure, as the cores of the Au NCs studied herein include FCC-, HCP- and BCC-like packing.
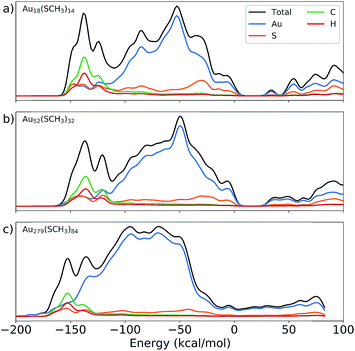
To further understand the structural trends of IP and EA, the projected and total density of states (PDOS and TDOS, respectively) for three nanoclusters – including both the smallest and largest Au NCs studied herein – are plotted in Fig. 3. It is known that as the size of Au NCs increases, there exists a region in which the Au NCs transition from molecular- to metallic-like character.40 Looking at the plots in Fig. 3, one can observe clear HOMO–LUMO gaps, a molecular characteristic, present for both Au18(SCH3)14 and Au52(SCH3)32. However, the largest nanocluster, Au279(SCH3)84, does not display a gap indicating that the system is metallic. In fact, Au279(SR)84 was determined to be metallic experimentally and exhibits surface plasmon resonance.41 Furthermore, the TDOS of the Au NCs suggests the emergence of discrete states as the size of the nanocluster decreases. The resulting size-dependent NC electronic properties are what lead to the structure–property relationships shown in Fig. 2. Additionally, the energy states near the Fermi level are vastly dominated by gold, further supporting the use of n as a descriptor for IP and EA.
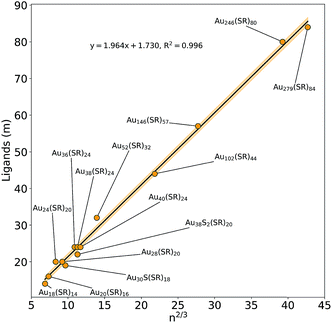
First introduced by Dass et al.,42Fig. 4 shows the results of a nano-scaling law applied to the Au NCs studied in this work. Similar to Fig. 2, the number of gold atoms is an important factor, in this case to describe the number of ligands present on each Au NC. Notably, even the largest Au146(SR)57, Au246(SR)80, and Au279(SR)84 NCs are found to follow the model providing strong evidence that virtually all magic-sized Au NCs scale with this simple structural relationship. Although the stoichiometric model cannot entirely predict new Au NC structures, it still plays a significant role in the NC prediction process, identifying the number of ligands needed to stabilize a specific number of Au atoms. In fact, along with the IP and EA models developed in this work, as well as the thermodynamic stability theory,17 one can start building a framework enabling a property-specific design of new Au NCs. Starting with a targeted application that requires a gold nanocluster with a specific ionization potential, the IP model portrayed in Fig. 2 can be used in concert with the stoichiometric model (Fig. 4) to determine the appropriate Au NC composition needed. Previous work has revealed that the type of thiol ligand (i.e. the “R” group in Aun(SR)m) plays a central role in the stoichiometry of the stable nanocluster synthesized.13,43,44 Therefore, an experimentalist could utilize these ligand effects to control the number of gold atoms desired within the NC and thus, the resulting electronic properties. Additionally, the thermodynamic stability theory can aid in screening the stability of potential NC candidates in a (NC size) focused effort due to the aforementioned stoichiometric relationship (Fig. 4). Overall, this approach, which utilizes computationally discovered structure–property (electronic and stability) relationships, could guide experimentation towards a property-targeted synthesis of Au NCs.
Conclusions
Using electronic structure calculations in conjunction with the recently developed thermodynamic stability theory,17 we investigated the electronic properties and stability of 15 experimentally synthesized Au NCs of different sizes. We reveal that the thermodynamic stability theory can be applied to larger Au NC sizes than the ones on which it was developed. Specifically, we demonstrate that Au146(SCH3)57, Au246(SCH3)80, and Au279(SCH3)84 were found to follow the energy balance stability criterion. These results reveal the theory's ability to capture stability over much larger Au NC size regimes. In addition, we revealed strong correlations between the number of gold atoms in a Au NC and both its IP and EA (electronic properties). These relationships were further rationalized based on the structure-dependent density of states profiles of the Au NCs. It was also verified that the number of gold atoms for each Au NC correlated with their number of ligands even for the larger Au NCs. Utilizing all these thermodynamic and structure–property models can aid in a property-specific design of new gold nanoclusters.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the National Science Foundation (NSF, CBET-CAREER program) under Grant No. 1652694. The authors would like to acknowledge computational support from the Center for Research Computing at the University of Pittsburgh and the Extreme Science and Engineering Discovery Environment, which is supported by the NSF (ACI-1548562).References
- M. Brust, M. Walker, D. Bethell, D. J. Schiffrin and R. Whyman, J. Chem. Soc., Chem. Commun., 1994, 801–802 RSC.
- S. Knoppe, H. Hakkinen, T. Verbiest and K. Clays, J. Phys. Chem. C, 2018, 122, 4019–4028 CrossRef CAS.
- R. Ho-Wu, K. Sun and T. Goodson, J. Phys. Chem. C, 2018, 122, 2315–2329 CrossRef CAS.
- N. V. Karimova and C. M. Aikens, J. Phys. Chem. C, 2018, 122, 11051–11065 CrossRef CAS.
- C. Zeng, Y. Chen, C. Liu, K. Nobusada, N. L. Rosi and R. Jin, Sci. Adv., 2015, 1, e1500425 CrossRef PubMed.
- K. N. Swanick, M. Hesari, M. S. Workentin and Z. Ding, J. Am. Chem. Soc., 2012, 134, 15205–15208 CrossRef CAS PubMed.
- R. Jin, C. Zeng, M. Zhou and Y. Chen, Chem. Rev., 2016, 116, 10346–10413 CrossRef CAS PubMed.
- H. Qian, M. Zhu, Z. Wu and R. Jin, Acc. Chem. Res., 2012, 45, 1470–1479 CrossRef CAS PubMed.
- I. Chakraborty and T. Pradeep, Chem. Rev., 2017, 117, 8208–8271 CrossRef CAS PubMed.
- H. Häkkinen, M. Walter and H. Grönbeck, J. Phys. Chem. B, 2006, 110, 9927–9931 CrossRef PubMed.
- P. D. Jadzinsky, G. Calero, C. J. Ackerson, D. A. Bushnell and R. D. Kornberg, Science, 2007, 318, 430 CrossRef CAS PubMed.
- M. W. Heaven, A. Dass, P. S. White, K. M. Holt and R. W. Murray, J. Am. Chem. Soc., 2008, 130, 3754–3755 CrossRef CAS PubMed.
- Z. Y. Ma, P. Wang, L. Xiong and Y. Pei, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7, e1315 Search PubMed.
- M. Walter, J. Akola, O. Lopez-Acevedo, P. D. Jadzinsky, G. Calero, C. J. Ackerson, R. L. Whetten, H. Gronbeck and H. Hakkinen, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 9157–9162 CrossRef CAS PubMed.
- L. Cheng, Y. Yuan, X. Zhang and J. Yang, Angew. Chem., Int. Ed., 2013, 52, 9035–9039 CrossRef CAS.
- D. M. P. Mingos, Dalton Trans., 2015, 44, 6680–6695 RSC.
- M. G. Taylor and G. Mpourmpakis, Nat. Commun., 2017, 8, 15988 CrossRef CAS.
- W. W. Xu, X. C. Zeng and Y. Gao, Nanoscale, 2018, 10, 9476–9483 RSC.
- P. Wang, X. X. Sun, X. Liu, L. Xiong, Z. Y. Ma, Y. Wang and Y. Pei, Nanoscale, 2018, 10, 10357–10364 RSC.
- Y. Li, G. Galli and F. Gygi, ACS Nano, 2008, 2, 1896–1902 CrossRef CAS PubMed.
- H. Qian, W. T. Eckenhoff, Y. Zhu, T. Pintauer and R. Jin, J. Am. Chem. Soc., 2010, 132, 8280–8281 CrossRef CAS PubMed.
- C. Zeng, H. Qian, T. Li, G. Li, L. Rosi Nathaniel, B. Yoon, N. Barnett Robert, L. Whetten Robert, U. Landman and R. Jin, Angew. Chem., Int. Ed., 2012, 51, 13114–13118 CrossRef CAS.
- C. Zeng, T. Li, A. Das, N. L. Rosi and R. Jin, J. Am. Chem. Soc., 2013, 135, 10011–10013 CrossRef CAS.
- D. Crasto, S. Malola, G. Brosofsky, A. Dass and H. Häkkinen, J. Am. Chem. Soc., 2014, 136, 5000–5005 CrossRef CAS.
- A. Das, T. Li, G. Li, K. Nobusada, C. Zeng, N. L. Rosi and R. Jin, Nanoscale, 2014, 6, 6458–6462 RSC.
- C. Zeng, C. Liu, Y. Chen, N. L. Rosi and R. Jin, J. Am. Chem. Soc., 2014, 136, 11922–11925 CrossRef CAS PubMed.
- A. Das, C. Liu, H. Y. Byun, K. Nobusada, S. Zhao, N. Rosi and R. Jin, Angew. Chem., Int. Ed., 2015, 54, 3140–3144 CrossRef CAS.
- S. Tian, Y.-Z. Li, M.-B. Li, J. Yuan, J. Yang, Z. Wu and R. Jin, Nat. Commun., 2015, 6, 8667 CrossRef CAS.
- N. A. Sakthivel, S. Theivendran, V. Ganeshraj, A. G. Oliver and A. Dass, J. Am. Chem. Soc., 2017, 139, 15450–15459 CrossRef CAS PubMed.
- S. Vergara, D. A. Lukes, M. W. Martynowycz, U. Santiago, G. Plascencia-Villa, S. C. Weiss, M. J. de la Cruz, D. M. Black, M. M. Alvarez, X. López-Lozano, C. O. Barnes, G. Lin, H.-C. Weissker, R. L. Whetten, T. Gonen, M. J. Yacaman and G. Calero, J. Phys. Chem. Lett., 2017, 8, 5523–5530 CrossRef CAS PubMed.
- C. Liu, T. Li, G. Li, K. Nobusada, C. Zeng, G. Pang, N. L. Rosi and R. Jin, Angew. Chem., Int. Ed., 2015, 54, 9826–9829 CrossRef CAS PubMed.
- C. Zeng, Y. Chen, K. Kirschbaum, K. J. Lambright and R. Jin, Science, 2016, 354, 1580 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS.
- J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 4, 15–25 Search PubMed.
- M. G. Taylor and G. Mpourmpakis, J. Phys. Chem. Lett., 2018, 9, 6773–6778 CrossRef CAS.
- R. Guo and R. W. Murray, J. Am. Chem. Soc., 2005, 127, 12140–12143 CrossRef CAS.
- A. Tlahuice-Flores, R. L. Whetten and M. Jose-Yacaman, J. Phys. Chem. C, 2013, 117, 20867–20875 CrossRef CAS.
- W. W. Xu and Y. Gao, J. Phys. Chem. C, 2015, 119, 14224–14229 CrossRef CAS.
- Y. Negishi, T. Nakazaki, S. Malola, S. Takano, Y. Niihori, W. Kurashige, S. Yamazoe, T. Tsukuda and H. Häkkinen, J. Am. Chem. Soc., 2015, 137, 1206–1212 CrossRef CAS.
- S. Malola, L. Lehtovaara, J. Enkovaara and H. Häkkinen, ACS Nano, 2013, 7, 10263–10270 CrossRef CAS.
- A. Dass, Nanoscale, 2012, 4, 2260–2263 RSC.
- Y. Chen, C. Zeng, D. R. Kauffman and R. Jin, Nano Lett., 2015, 15, 3603–3609 CrossRef CAS.
- Y. Chen, C. Zeng, C. Liu, K. Kirschbaum, C. Gayathri, R. R. Gil, N. L. Rosi and R. Jin, J. Am. Chem. Soc., 2015, 137, 10076–10079 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8na00246k |
| This journal is © The Royal Society of Chemistry 2019 |