Open Access Article
Open Access ArticleEffective chemical potential for non-equilibrium systems and its application to molecular beam epitaxy of Bi2Se3†
Na
Wang
 abc,
Damien
West
c,
Wenhui
Duan
abc,
Damien
West
c,
Wenhui
Duan
 a and
S. B.
Zhang
*cd
a and
S. B.
Zhang
*cd
aDepartment of Physics, Tsinghua University, Beijing 100084, China
bDepartment of Physical Chemistry, University of Science and Technology Beijing, Beijing 100083, China
cDepartment of Physics, Applied Physics & Astronomy, Rensselaer Polytechnic Institute, Troy, NY 12180, USA. E-mail: zhangs9@rpi.edu
dBeijing Computational Science Research Center, Beijing 100193, China
First published on 10th October 2018
Abstract
First-principles studies often rely on the assumption of equilibrium, which can be a poor approximation, e.g., for growth. Here, an effective chemical potential (![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) ) method for non-equilibrium systems is developed. A salient feature of the theory is that it maintains the equilibrium limits as the correct limit. In application to molecular beam epitaxy, rate equations are solved for the concentrations of small clusters, which serve as feedstock for growth. We find that
) method for non-equilibrium systems is developed. A salient feature of the theory is that it maintains the equilibrium limits as the correct limit. In application to molecular beam epitaxy, rate equations are solved for the concentrations of small clusters, which serve as feedstock for growth. We find that ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) is determined by the most probable, rather than by the lowest-energy, cluster. In the case of Bi2Se3,
is determined by the most probable, rather than by the lowest-energy, cluster. In the case of Bi2Se3, ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) is found to be highly supersaturated, leading to a high nucleus concentration in agreement with experiment.
is found to be highly supersaturated, leading to a high nucleus concentration in agreement with experiment.
The concept of chemical potential is one of the most fundamental quantities associated with thermodynamic equilibrium. It generalizes the effect of the environment on the energetics of a single type of particle. Through the use of atomic chemical potentials, we can compare the energies of systems consisting of different numbers of atoms. In defect physics, this plays a central role in the calculation of the formation energies of defects and allows for a statistical determination of defect concentrations which determine the electronic properties of semiconductors. Further, surface reconstruction and even the shape of nanocrystals are intimately tied with the availability of different chemical species, with the surface energy generally depending on the atomic chemical potentials of the various species. While kinetic Monte Carlo (kMC) or molecular dynamics (MD) can be used to investigate system evolution, when comparing the energies of systems containing different numbers of particles, calculation within the grand canonical ensemble requires knowledge of the chemical potentials of the atomic species. The most ubiquitous approximation used to determine the range of chemical potentials is that of so-called near equilibrium growth (NEG),1,3 in which the stoichiometric sum of the atomic chemical potentials is assumed to be equal to that of the bulk crystal. This assumption, however, is an outstanding issue in the theoretical community as growth itself is a highly non-equilibrium process.
The chemical potential, μ, is a thermodynamic quantity, defined by 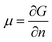 , where G is the Gibbs free energy and n is the number of the nth species.4 For equilibrium or near-equilibrium growth (NEG), there is a well-defined relationship between the μ′s of the species in the system.4 Consider, for example, a AmBn binary, we have
, where G is the Gibbs free energy and n is the number of the nth species.4 For equilibrium or near-equilibrium growth (NEG), there is a well-defined relationship between the μ′s of the species in the system.4 Consider, for example, a AmBn binary, we have
| mμA + nμB = μAmBn. | (1) |
As a result of eqn (1), only one μ is an independent variable, i.e., one can use μB for this purpose and μA will be given by μA = (μAmBn − nμB)/m. Should μ for a species i exceeds its upper bound μi0, defined as the chemical potential of the corresponding elemental solid or gas, this species will precipitate,1,5 thereby preventing any further increase of μ. In other words,
| μi ≤ μi0 (i = A, B). | (2) |
Using the μ′s, the state of the system, whether it is a defect, a surface, or a crystal structure (denoted here as X) is determined by its formation energy with respect to bulk,
| ΔHf[X] = Etot[X] − Etot[bulk] − ∑niμi, | (3) |
This NEG theory has been applied to numerous materials behaviors with ample successes, ranging from surface reconstruction5,6 and defect physics,1,7 to nanostructures.8,9 For systems in which a subsystem of concern can be isolated from the rest due, for example, to high reaction barriers, one can also use the NEG theory, provided that one can establish an approximate equilibrium within the subsystem.10–12 However, when such a division is not obvious and the system is far away from equilibrium, the NEG theory can run into problems. For instance, recent interest in the physics of topological insulators (TIs) has spurred considerable activity to grow high-quality TIs such as Bi2Se3 with controlled properties.13–18 Molecular beam epitaxy (MBE) is widely accepted as an effective method to grow high-quality films.15–18 However, the defect density is still far from being satisfactory, due in part to the small size of the islands. Strictly speaking, MBE is not an equilibrium process;19 its outcome may rely heavily on the dynamics of the source atoms/molecules. On the other hand, MBE is relatively simple for its slow growth rate and the simplicity of the sources. This raises the question: can one incorporate kinetics into the chemical potential-based approach for non-equilibrium process?
Note that considerable theoretical efforts have been made in the past to study growth. Analytical rate equation approach, based on empirical kinetic parameters, has been employed to study island formation and growth.20–26 Statistical approaches such as kinetic Monte-Carlo simulation and molecular dynamics have been used to study film growth.27–32 Molecular dynamics based on first-principles calculations could provide a vast amount of information, however, it is generally limited to smaller systems and shorter times due to the high computational cost. kMC offers a great advantage for efficiency and capability by simulating the time evolution of the system via statistically evaluating the probability of selected events. kMC relies on knowing the rate and mechanism of all the relevant transitions from a given initial state, with loss of reality. Moreover, it appears that these non-equilibrium approaches do not use the concept of chemical potential, which had served as a basis for NEG, except perhaps for the thermodynamic theory of nucleation.2 Recently, a renewed interest in the chemical potential has emerged, as it can help choosing lowest-energy paths for growth,33 without knowing relevant transitions in advance during a significant time scale.
In this paper, we derive a generic effective chemical potential (![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) ) theory, which is suited for non-equilibrium physics. Taking the MBE growth of Bi2Se3 as an example, the use of
) theory, which is suited for non-equilibrium physics. Taking the MBE growth of Bi2Se3 as an example, the use of ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) allows us to simplify the overall complex process. We divide the non-equilibrium growth (nonEG) into three stages: pre-nucleation, nucleation, and island growth. For pre-nucleation, we determine
allows us to simplify the overall complex process. We divide the non-equilibrium growth (nonEG) into three stages: pre-nucleation, nucleation, and island growth. For pre-nucleation, we determine ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) by explicitly solving rate equations. First-principles calculation shows that
by explicitly solving rate equations. First-principles calculation shows that ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) is solely determined by the most probable, rather than by the lowest-energy, cluster(s) on the surface. For nucleation, it is found that the nucleation barrier vanishes when the critical size of the clusters is only a few molecule large due to the highly supersaturated nature of
is solely determined by the most probable, rather than by the lowest-energy, cluster(s) on the surface. For nucleation, it is found that the nucleation barrier vanishes when the critical size of the clusters is only a few molecule large due to the highly supersaturated nature of ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) . This results in a high concentration of nuclei – a conclusion that contradicts the NEG model, but is in qualitative agreement with experiment.
. This results in a high concentration of nuclei – a conclusion that contradicts the NEG model, but is in qualitative agreement with experiment.
One can define chemical potentials for an individual cluster α, irrespective of equilibrium,4,34
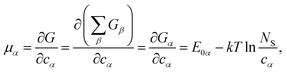 | (4) |
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) that enters eqn (3) is given by
that enters eqn (3) is given by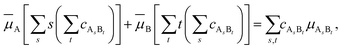 | (5) |
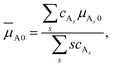 | (6) |
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) A. The same is true for species B. Therefore,
A. The same is true for species B. Therefore,![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) i ≤ i ≤ ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) i0 (i = A, B). i0 (i = A, B). | (7) |
It is necessary to point out that eqn (5) and (7) are analogous to eqn (1) and (2), respectively.
To calculate ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) , we solve the following rate equations,2
, we solve the following rate equations,2
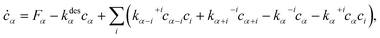 | (8) |
kdesα = ν![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−φdesα/kT), exp(−φdesα/kT), | (9) |
k−iα = ν![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−φ−iα/kT), exp(−φ−iα/kT), | (10) |
| k+iα = 2π(Dα + Di), | (11) |
Dα/i = a2ν![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−φdiffα/i/kT), exp(−φdiffα/i/kT), | (12) |
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e002.gif) 0 in eqn (8).
0 in eqn (8).
Note that in the limit when all the barriers in eqn (8)–(12) can be ignored, the system is dominated by its lowest-energy form, namely, the concentrations for all clusters, as well as for all finite-sized islands diminish, leaving only the AmBn bulk. In this case, eqn (5) and (7) become eqn (1) and (2) respectively, i.e., the system approaches its NEG limit. Also note that chemical potential is not an easily measurable quantity. People may, instead, use the off-stoichiometry of the system, which can be directly measured, as an indirect indicator of μi. This is true not only for the NEG model36 but also for the nonEG model here.
First-principles calculations were performed using the VASP code37 to determine the relevant cluster size, structure, and energy barrier. The projector augmented wave (PAW) method38 and the local density approximation (LDA) to the exchange–correlation functional39 were used. Plane waves with a kinetic energy cutoff of 210 eV were used as the basis set. Integration of the Brillouin zone was done with sufficient k-point sampling40 such that the numerical error is less than 0.01 eV. All atoms were fully relaxed until forces on the atoms were less than 0.01 eV Å−1. The improved tangent finding method,41 within the framework of the nudged elastic band (NEB) method, was used to determine the energy barriers. Experimental growth temperature of 500 K (ref. 15–17) was assumed in the rate calculations.
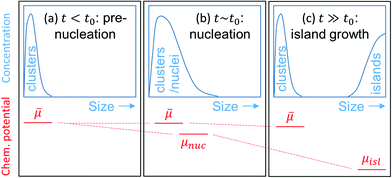
Denoting t0 as the time when nucleation takes place, the aforementioned 3 growth stages can be restated as follows: stage 1: t ≤ t0 (pre-nucleation), stage 2: t ∼ t0 (nucleation), stage 3: t ≫ t0 (island growth). Fig. 1 illustrates schematically the evolution of the size of the clusters, and those of the nuclei and islands, and the corresponding μ′s.
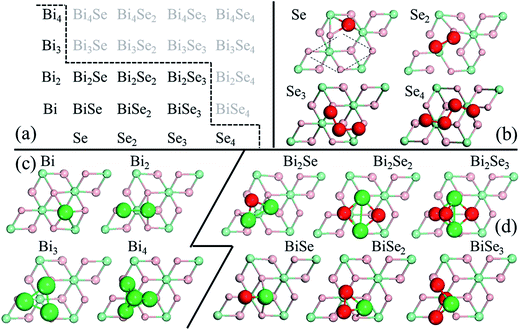
In stage 1, there are only clusters, no nuclei, on the surface of Bi2Se3, whose thickness in the calculation is taken as five atomic layers, or called one quintuple layer (QL). Because the binding between QLs is van der Waals (vdW),13–15 adding QLs to the thickness of the substrate is unlikely to affect our results. An in-plane supercell of 6 × 6 is used to conduct the cluster-adsorption calculation to avoid interactions among periodic images. Fig. 2 depicts the clusters we considered in our ab initio calculations. They are organized according to the chart in Fig. 2(a), where dashed line denotes the cutoff size of the clusters considered in this study (see details in Fig. S2, ESI†). Our calculations show that stable clusters on the surface are the same as those in vacuum. This can be expected as Bi tends to form 3 bonds, whereas Se tends to form 2 bonds, in line with the octet rule.42Fig. 3 shows the calculated diffusion barrier (φdiffα), desorption barrier (φdesα), and dissociation barrier (φ−iα) for the clusters: φdiffα is generally small, often a couple tenth of an eV, except for atomic Se and BiSe2. φdesα is higher, especially for smaller clusters. φ−iα is also generally higher and depends sensitively on the reaction pathway. Both φdesα and φ−iα exhibit a large variation over a couple eV.
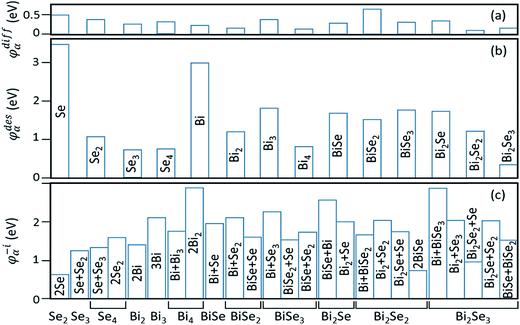 | ||
| Fig. 3 Calculated barriers for (a) diffusion (φdiffα), (b) desorption (φdesα), and (c) dissociation (φ−iα) of the clusters in Fig. 2. Cluster names for both (a) and (b) are given in (b). For cluster dissociation in (c), a cluster labeled in the horizontal axis can have multi-reaction pathways, which are labeled inside or by the vertical bars. | ||
Fig. 4(a and b) show cα and the corresponding μα, which reveal that the highest concentrations of clusters are that of atomic Se and BiSe2, respectively. At first glance, it may appear counterintuitive that some clusters with lower μα, e.g., Bi2Se2 and Bi2Se3, also have low cα. This is because of the low-desorption barrier of Bi2Se3 in Fig. 3, which depletes not only Bi2Se3 but also Bi2Se2 (via an association with atomic Se, see Fig. S1†). In MBE, the Se partial pressure is much higher than that of Bi. As a result, the population of Se is determined almost entirely by pure Se clusters viaeqn (7),
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) Se = Se = ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) Se0 = μSe(atom). Se0 = μSe(atom). | (13) |
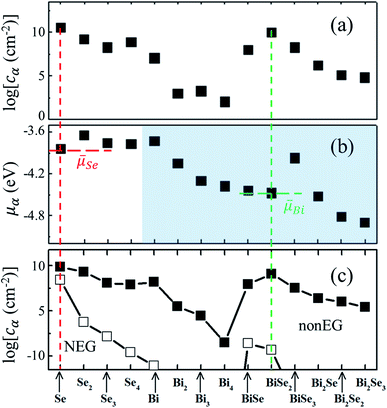 | ||
Fig. 4 (a) Logarithmic concentration of small clusters in stage 1. (b) The corresponding chemical potentials by eqn (4) and ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) 's by eqn (13) and (14), respectively. (c) Logarithmic concentration of small clusters in stage 3. Solid squares are based on the nonEG model with cisland = 109 cm−2, whereas open squares are the prediction by the NEG model. 's by eqn (13) and (14), respectively. (c) Logarithmic concentration of small clusters in stage 3. Solid squares are based on the nonEG model with cisland = 109 cm−2, whereas open squares are the prediction by the NEG model. | ||
And for Bi, one has
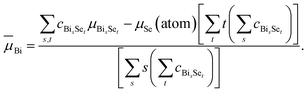 | (14) |
These ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) values,
values, ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) Bi = −4.44 eV and
Bi = −4.44 eV and ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) Se = −3.82 eV, are given in Fig. 4(b) as horizontal dashed lines. Our study reveals that it is the most-probable, not the lowest-energy, clusters that determine
Se = −3.82 eV, are given in Fig. 4(b) as horizontal dashed lines. Our study reveals that it is the most-probable, not the lowest-energy, clusters that determine ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) . This conclusion is in line with the basic principles of statistical physics, irrespective of the computational details, whereby it reinforces the notion that using cα as the weighting factor for
. This conclusion is in line with the basic principles of statistical physics, irrespective of the computational details, whereby it reinforces the notion that using cα as the weighting factor for ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) in eqn (5) is physically correct. It has been experimentally realized that the observed clusters were not the lowest energy ones in silicon cluster anions under non-equilibrium conditions.
in eqn (5) is physically correct. It has been experimentally realized that the observed clusters were not the lowest energy ones in silicon cluster anions under non-equilibrium conditions.
Note that there is a large (3.08 eV) difference between the current model (2![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) Bi + 3
Bi + 3![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) Se = −20.34 eV) and the NEG model (2μBi + 3μSe = −23.42 eV). The fact that the former is significantly higher than the latter gives rise to supersaturation during the growth. In other words, eqn (7) sets a new set of boundaries for chemical potentials as the prime reason that account for the differences between nonEG and NEG. Importantly, this finding allows one to reexamine defects in Bi2Se3, as it suggests that native defects may be more easily formed than predicted by NEG theory,44 highlighting experimental challenges in growing high-quality epitaxial films.45
Se = −20.34 eV) and the NEG model (2μBi + 3μSe = −23.42 eV). The fact that the former is significantly higher than the latter gives rise to supersaturation during the growth. In other words, eqn (7) sets a new set of boundaries for chemical potentials as the prime reason that account for the differences between nonEG and NEG. Importantly, this finding allows one to reexamine defects in Bi2Se3, as it suggests that native defects may be more easily formed than predicted by NEG theory,44 highlighting experimental challenges in growing high-quality epitaxial films.45
Before finishing up the discussion of stage 1, we would like to point out that our consideration of the availability of clusters is important, but only a first, step in improving upon NEG theory. Within the framework of the current development, higher order effects (such as the kinetics associated with the incorporation of available species into the growth front) can also be incorporated, which however will be deferred to future work. For stages 2 and 3, i.e., nucleation and island growth, due to continued deposition, we do not expect the concentrations of the small clusters to change considerably (as will be shown later).
In stage 2, owing to the formation of nuclei, bifurcation of μ will take place – one for the nuclei (μnuc) and one for the small clusters (![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) ), as depicted in Fig. 1(b). Bifurcation reflects the fact that once nuclei are formed, it is energetically favorable for them to grow further by consuming available smaller clusters on the surface, rather than consuming themselves. This should be contrasted to NEG where bifurcation of μ is strictly forbidden. Once
), as depicted in Fig. 1(b). Bifurcation reflects the fact that once nuclei are formed, it is energetically favorable for them to grow further by consuming available smaller clusters on the surface, rather than consuming themselves. This should be contrasted to NEG where bifurcation of μ is strictly forbidden. Once ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) for clusters are determined, one may approach the nucleation problem in different ways. For example, to study the temperature T dependence of nucleus density, one could apply eqn (4)–(12) to potential nuclei [which should be among the larger clusters in Fig. 2 and beyond (=embryo nuclei)] to determine μnuc and cα,nuc, respectively. The non-negligible association barriers [see, e.g., Fig. S1(a)† for clusters] suggest that increasing T could help increasing the nucleus size and hence decreasing its density. However, the window for the increase can be limited, as although dissociation barriers are usually higher than association barriers [e.g., by comparing Fig. S1(a)† with Fig. 3(c)], the difference may not be that dramatic. As a result, further increasing T could also lead to the dissociation of already-formed nuclei, thereby increasing the nucleus density. Although rather qualitative, the conclusion here is already in line with experiments.16,43
for clusters are determined, one may approach the nucleation problem in different ways. For example, to study the temperature T dependence of nucleus density, one could apply eqn (4)–(12) to potential nuclei [which should be among the larger clusters in Fig. 2 and beyond (=embryo nuclei)] to determine μnuc and cα,nuc, respectively. The non-negligible association barriers [see, e.g., Fig. S1(a)† for clusters] suggest that increasing T could help increasing the nucleus size and hence decreasing its density. However, the window for the increase can be limited, as although dissociation barriers are usually higher than association barriers [e.g., by comparing Fig. S1(a)† with Fig. 3(c)], the difference may not be that dramatic. As a result, further increasing T could also lead to the dissociation of already-formed nuclei, thereby increasing the nucleus density. Although rather qualitative, the conclusion here is already in line with experiments.16,43
If, however, our interest is only on the critical size of the nuclei, not on its T dependence, explicitly invoking kinetic theory here can be an overkill. Instead, we only need calculate the nucleation barrier, which is defined as the maximum of the Gibbs free-energy,2
ΔG = ΔEtot − (nSe![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) Se − nBi Se − nBi![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) Bi). Bi). | (15) |
After reaching the critical size, adding additional atoms/clusters to the nuclei is energetically favored. Using ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) in stage 1, we obtain Fig. 5, showing that ΔG is remarkably small and even negative for (Bi2Se3)n clusters with n > 3. Usually, ΔG for cluster of these sizes is significantly positive due to its high surface energy. Due to high
in stage 1, we obtain Fig. 5, showing that ΔG is remarkably small and even negative for (Bi2Se3)n clusters with n > 3. Usually, ΔG for cluster of these sizes is significantly positive due to its high surface energy. Due to high ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) and the relatively low energy of the vdW surface, however, this is no longer the case here. Fig. S3† shows that except for n = 1 and 3, the desorption barriers are reasonably large so the nuclei in Fig. 5 do grow into islands. Consequently, the island concentration is expected to be high. In other words, the small nuclei size is consistent with measured high island concentration, cisl ∼ 109 to 1010 cm−2.16,17
and the relatively low energy of the vdW surface, however, this is no longer the case here. Fig. S3† shows that except for n = 1 and 3, the desorption barriers are reasonably large so the nuclei in Fig. 5 do grow into islands. Consequently, the island concentration is expected to be high. In other words, the small nuclei size is consistent with measured high island concentration, cisl ∼ 109 to 1010 cm−2.16,17
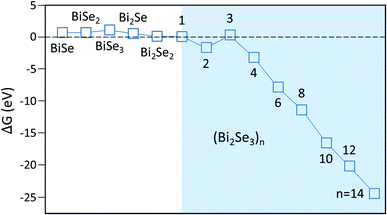 | ||
| Fig. 5 Free-energy barrier ΔG for nucleation on various clusters. Shaded area is where only stoichiometric molecular clusters (Bi2Se3)n are considered in the calculation. | ||
In stage 3, the basic physics should be the same as in stage 2. Due to the presence of the islands, however, one should recalculate cα and ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) by adding a term −k+iislcislci to eqn (8), where cisl is the concentration of the islands and k+iisl = 2π(Di). Fig. 4(c) shows the results for a typical cisl = 109 cm−2. More results on the cisl-dependence can be found in Fig. S4, ESI.† As it turns out, neither cα nor
by adding a term −k+iislcislci to eqn (8), where cisl is the concentration of the islands and k+iisl = 2π(Di). Fig. 4(c) shows the results for a typical cisl = 109 cm−2. More results on the cisl-dependence can be found in Fig. S4, ESI.† As it turns out, neither cα nor ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) is changed significantly. As a comparison, Fig. 4(c) also shows cα under the NEG condition. They are many orders of magnitude smaller.
is changed significantly. As a comparison, Fig. 4(c) also shows cα under the NEG condition. They are many orders of magnitude smaller.
In summary, an effective chemical potential approach for non-equilibrium growth is developed. We find that ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) for an atomic species is determined primarily by the most probable cluster in which the atom resides during growth. Because “most probable” is a balance between energetics and kinetics, our findings thus set a new criterion for most relevant events during growth. Application to MBE growth of Bi2Se3 suggests that
for an atomic species is determined primarily by the most probable cluster in which the atom resides during growth. Because “most probable” is a balance between energetics and kinetics, our findings thus set a new criterion for most relevant events during growth. Application to MBE growth of Bi2Se3 suggests that ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) is highly supersaturated, resulting in an exceedingly small critical size of nuclei. While a high concentration of islands is in agreement with experiment, our results also reveal that to grow better-quality films requires finding ways to stabilize the most probable clusters, thereby lowering
is highly supersaturated, resulting in an exceedingly small critical size of nuclei. While a high concentration of islands is in agreement with experiment, our results also reveal that to grow better-quality films requires finding ways to stabilize the most probable clusters, thereby lowering ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) . Our formulation is general. It may be used to study structure, surface morphology, and shape of a nanoparticle, as well as defect and impurity, in non-equilibrium-grown solids. While kinetic theory has been around for a long time, most first-principles studies today are still based on the NEG model. Our chemical potential-based development here offers a natural vehicle to transform such bulk studies into the more experimentally relevant non-equilibrium regime.
. Our formulation is general. It may be used to study structure, surface morphology, and shape of a nanoparticle, as well as defect and impurity, in non-equilibrium-grown solids. While kinetic theory has been around for a long time, most first-principles studies today are still based on the NEG model. Our chemical potential-based development here offers a natural vehicle to transform such bulk studies into the more experimentally relevant non-equilibrium regime.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank X. Liu and J. Wang for stimulating discussions. Chemical potential theory was supported by the US Department of Energy (DOE) under Grant No. DESC0002623. Bi2Se3 growth study was supported by NSF Award No. EFMA-1542798. Work in China was supported by the Ministry of Science and Technology of China (Grant No. 2011CB921901 and 2011CB606405), and the National Natural Science Foundation of China (Grant No. 11334006). Supercomputer time was provided by NERSC under the Grant No. DE-AC02-05CH11231 and the Center for Computational Innovations (CCI) at RPI.References
- S. B. Zhang and J. E. Northrup, Phys. Rev. Lett., 1991, 67, 2339 CrossRef CAS PubMed.
- I. V. Markov, Crystal Growth for Beginners: Fundamentals of Nucleation, Crystal Growth and Epitaxy, World Scientific, New Jersey, 2nd edn, 2003 Search PubMed.
- C. G. Van de Walle and J. Neugebauer, J. Appl. Phys., 2004, 95, 3851 CrossRef CAS.
- P. Attard, in Thermodynamics and Statistical Mechanics, Academic Press, London, 2002, p. 1 Search PubMed.
- G.-X. Qian, R. M. Martin and D. J. Chadi, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 7649 CrossRef CAS.
- C. G. Van de Walle and J. Neugebauer, Phys. Rev. Lett., 2002, 88, 066103 CrossRef PubMed.
- C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti and C. G. Van de Walle, Rev. Mod. Phys., 2014, 86, 253 CrossRef.
- N. Moll, A. Kley, E. Pehlke and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 8844 CrossRef CAS.
- N. Wang, Y. Sun, Y. Zhang, D. West, W. Duan and S. Zhang, Phys. Rev. B, 2016, 93, 115306 CrossRef.
- S. B. Zhang and S.-H. Wei, Phys. Rev. Lett., 2001, 86, 1789 CrossRef CAS PubMed.
- Y. Yan, S. B. Zhang and S. T. Pantelides, Phys. Rev. Lett., 2001, 86, 5723 CrossRef CAS PubMed.
- Z. Zheng, Y.-Y. Sun, W. Xie, J. Zhao and S. Zhang, J. Phys. Chem. C, 2016, 120, 27085 CrossRef CAS.
- W. Lu, Y. Ding, Y. Chen, Z. L. Wang and J. Fang, J. Am. Chem. Soc., 2005, 127, 10112 CrossRef CAS PubMed.
- D. Kong, W. Dang, J. J. Cha, H. Li, S. Meister, H. Peng, Z. Liu and Y. Cui, Nano Lett., 2010, 10, 2245 CrossRef CAS PubMed.
- X. Chen, X.-C. Ma, K. He, J.-F. Jia and Q.-K. Xue, Adv. Mater., 2011, 23, 1162 CrossRef CAS PubMed.
- L. He, X. Kou and K. L. Wang, Phys. Status Solidi RRL, 2013, 7, 50 CrossRef CAS.
- M.-H. Xie, X. Guo, Z.-J. Xu and W.-K. Ho, Chin. Phys. B, 2013, 22, 068101 CrossRef.
- J. Dai, D. West, X. Wang, Y. Wang, D. Kwok, S. W. Cheong, S. B. Zhang and W. Wu, Phys. Rev. Lett., 2016, 117, 106401 CrossRef PubMed.
- M. A. Herman and H. Sitter, Molecular Beam Epitaxy: Fundamentals and Current Status, Springer Berlin Heidelberg, Berlin, Heidelberg, 1989 Search PubMed.
- G. Zinsmeister, Thin Solid Films, 1968, 2, 497 CrossRef.
- J. A. Venables, G. D. T. Spiller and M. Hanbucken, Rep. Prog. Phys., 1984, 47, 399 CrossRef.
- J. A. Venables, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 36, 4153 CrossRef CAS.
- J. A. Nieminen and K. Kaski, Phys. Rev. A, 1989, 40, 2096 CrossRef.
- M. C. Bartelt and J. W. Evans, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 12675 CrossRef.
- G. S. Bales and D. C. Chrzan, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 6057 CrossRef CAS.
- J. G. Amar and F. Family, Phys. Rev. Lett., 1995, 74, 2066 CrossRef CAS PubMed.
- F. Family and P. Meakin, Phys. Rev. Lett., 1988, 61, 428 CrossRef CAS PubMed.
- R. Hrach and M. Sobotka, Int. J. Electron., 1990, 69, 49 CrossRef CAS.
- K. Reuter and M. Scheffler, Phys. Rev. Lett., 2003, 90, 046103 CrossRef PubMed.
- K. Reuter, D. Frenkel and M. Scheffler, Phys. Rev. Lett., 2004, 93, 116105 CrossRef PubMed.
- T. J. Woehl, C. Park, J. E. Evans, I. Arslan, W. D. Ristenpart and N. D. Browning, Nano Lett., 2014, 14, 373 CrossRef CAS PubMed.
- J. Zeng, P. Cui and Z. Zhang, Phys. Rev. Lett., 2017, 118, 046101 CrossRef PubMed.
- V. I. Artyukhov, Y. Liu and B. I. Yakobson, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 15136 CrossRef CAS PubMed.
- R. Ouyang, J.-X. Liu and W.-X. Li, J. Am. Chem. Soc., 2013, 135, 1760 CrossRef CAS PubMed.
- P. Atkins and J. D. Paula, Physical Chemistry, Oxford University Press, Great Britain, 8th edn, 2006 Search PubMed.
- A. Samanta, W. E and S. B. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 195107 CrossRef.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188 CrossRef.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978 CrossRef CAS.
- L. Pauling, The Nature of the Chemical Bond and the Structure of Molecules and Crystals: An Introduction to Modern Structural Chemistry, Cornell University Press, 1960 Search PubMed.
- C.-Z. Chang, K. E. He, L.-L. Wang, X.-C. Ma, M.-H. Liu, Z.-C. Zhang, X. I. Chen, Y.-Y. Wang and Q.-K. Xue, SPIN, 2011, 01, 21 CrossRef CAS.
- D. West, Y. Y. Sun, H. Wang, J. Bang and S. B. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86(12), 121201 CrossRef.
- J. Dai, D. West, X. Wang, Y. Wang, D. Kwok, S.-W. Cheong, S. B. Zhang and W. Wu, Phys. Rev. Lett., 2016, 117(10), 106401 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8na00136g |
| This journal is © The Royal Society of Chemistry 2019 |