Open Access Article
Open Access ArticleBrittle fracture to recoverable plasticity: polytypism-dependent nanomechanics in todorokite-like nanobelts
Md Ruhul
Amin Shikder
a,
Mahjabin
Maksud
a,
Gokul
Vasudevamurthy
b,
Bryan W.
Byles
c,
David A.
Cullen
d,
Karren L.
More
e,
Ekaterina
Pomerantseva
c and
Arunkumar
Subramanian
 *a
*a
aDepartment of Mechanical and Industrial Engineering, University of Illinois at Chicago, Chicago, IL 60607, USA. E-mail: sarun@uic.edu
bGeneral Atomics Corporation, San Diego, CA, USA
cDepartment of Materials Science and Engineering, Drexel University, Philadelphia, Pennsylvania 19104, USA
dMaterials Science and Technology Division, Oak Ridge National Laboratory, Oak Ridge, TN 37831, USA
eCenter for Nanophase Materials Sciences, Oak Ridge National Laboratory, Oak Ridge, TN 37831, USA
First published on 14th September 2018
Abstract
Atomic force microscopy (AFM) based nanomechanics experiments involving polytypic todorokite-like manganese dioxide nanobelts reveal varied nanomechanical performance regimes such as brittle fracture, near-brittle fracture, and plastic recovery within the same material system. These nanobelts are synthesized through a layer-to-tunnel material transformation pathway and contain one-dimensional tunnels, which run along their longitudinal axis and are enveloped by m × 3 MnO6 octahedral units along their walls. Depending on the extent of material transformation towards a tunneled microstructure, the nanobelts exhibit stacking disorders or polytypism where the value for m ranges from 3 to up to ∼20 within different cross-sectional regions of the same nanobelt. The observation of multiple nanomechanical performance regimes within a single material system is attributed to a combination of two factors: (a) the extent of stacking disorder or polytypism within the nanobelts, and (b) the loading (or strain) rate of the AFM nanomechanics experiment. Controllable engineering of recoverable plasticity is a particularly beneficial attribute for advancing the mechanical stability of these ceramic materials, which hold promise for insertion in multiple next-generation technological applications that range from electrical energy storage solutions to catalysis.
Introduction
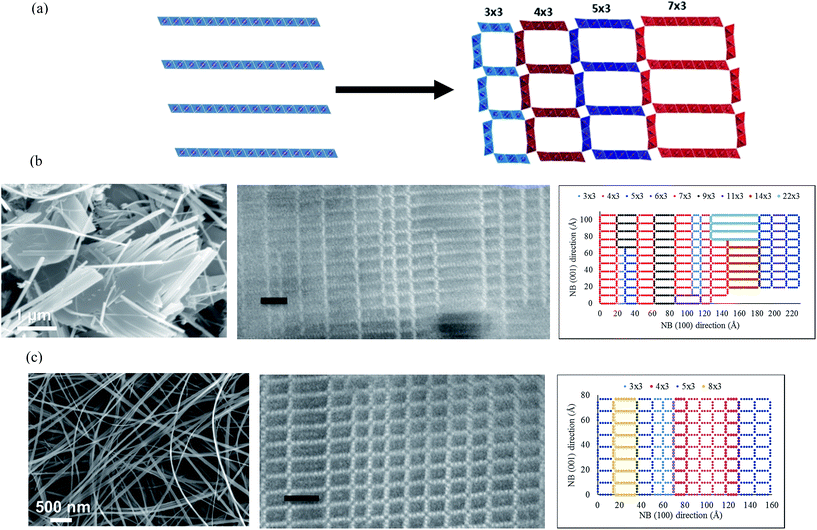
Tunnel-structured, one-dimensional manganese oxides have been advanced as potential solutions to meet the next-generation material needs in applications such as rechargeable battery cathodes,1 catalysts,2 molecular sieves,3 supercapacitors,4 and water desalination.5 In the case of rechargeable battery cathodes, different polymorphs of this material system present microporous tunnels with tunable size and geometry, which facilitate the reversible insertion and extraction of charge carrying ions such as Li+ or Na+ during electrochemical cycling.6–8 Apart from favorable charge-storage performance, materials sourced from manganese are also anticipated to offer other advantages in terms of cost, safety, and abundance in availability. From a battery material perspective, measuring and optimizing the mechanical properties of these tunnel manganese oxides is critical towards engineering them with an ability to withstand ionic-intercalation induced volume, microstructural, and/or phase changes without electrode fracture, disintegration, and dissolution into the electrolyte.9–11In their bulk form and at room temperature, ceramic materials exhibit brittle behavior.12 This is because dislocation slip activity within ceramic crystals is suppressed by their strong inter-atomic bonds and hence, stress release occurs primarily through crack propagation mechanisms. Past reports on the mechanics of ceramic nanomaterials such as nanowires synthesized from zinc oxide (ZnO),13 gallium arsenide (GaAs),14,15 and silicon carbide (SiC)16,17 have, on the other hand, shown both brittle and ductile behavior. The reports evidencing ductility have pointed to high surface-to-volume ratios and the resultant large open surfaces in nanostructured materials, which can abundantly nucleate dislocations.14,16,17 Furthermore, the reduced defect density within nanoscopic crystals enables them to withstand higher stresses, which may rise above the critical resolved shear stress, and thereby make the surface nucleated dislocations glissile. As a result, SiC nanowires have been shown to exhibit dislocation-mediated plasticity accompanied by a crystalline-to-amorphous phase transition. For instance, ref. 16 reports on a four-step sequence involving dislocation activity, amorphization, superplastic amorphous flow, and plastic fracture, which results in localized super-plastic elongation of above 200% during the tensile stretching of 3C-SiC nanowires (NWs). In addition, dislocation mediated plasticity and its subsequent recovery upon release of the mechanical load has been found to occur in GaAs NWs.14
There has been no comparable evidence of ductility within one-dimensional manganese oxides, even though engineering these crystals with ductility and/or recoverable plasticity properties will be particularly beneficial for their cycling performance in rechargeable battery applications. In this paper, we present results from atomic force microscopy based three-point bending tests that indicate recoverable plasticity in one-dimensional, todorokite-like nanobelts (T-NBs).6,18 These T-NB cross-sections exhibit stacking disorder-induced polytypism within a microstructural matrix of magnesium-stabilized, one-dimensional channels or grains. The lateral dimensions of these grains vary in terms of the number of MnO6 octahedral units encompassing their walls. Specifically, these heterogeneously-sized grains contain m × 3 MnO6 octahedral units along their walls, where m ≥ 3 and the largest value for m within a given nanobelt cross-section depends on its width. This NB width is, in turn, controlled by the extent to which the layer-to-tunnel transformation has occurred during the hydrothermal synthesis process.
Our nanomechanics experiments reveal that it is possible to not only initiate/sustain plastic deformation but, also recover it upon release of loading in the case of NBs with larger widths when they are subjected to bending loads at slow rates. On the other hand, NBs with smaller widths or higher loading rates exhibit brittle or near-brittle behavior. While plastic recovery has previously been observed to occur predominantly in metallic, FCC crystals19,20 (with the exception of one previous report involving GaAs nanowires14), these results represent the first demonstration of such behavior in ceramic, manganese oxide nanomaterials. This is particularly important since it points to avenues for alleviating mechanical fracture in tunnel manganese oxide nanowire battery cathodes through a suitable combination of material engineering and strain-rate control strategies.
Material system and nanomechanical testing
Todorokite-like manganese oxide NBs were synthesized from Mg-buserite, a layered manganese oxide (Fig. 1).6 Mg-buserite is composed of layers of MnO6 octahedra and contains hydrated Mg2+ ions between the layers. The hydration shell of the Mg2+ results in a double layer of water in the interlayer space and an interlayer spacing of ∼9.6 Å. The layers are oriented in the a–b plane, and this material has a platelet morphology. Under hydrothermal conditions, transformation to todorokite-like nanobelts first involves the migration of MnO6 octahedra from the layer to interlayer positions, forming the tunnel walls present in todorokite manganese oxide. This atomic rearrangement happens primarily in the [001] direction to form structural tunnels around the stabilizing hydrated Mg2+ ions. Since the interlayer spacing of 9.6 Å is maintained in this process, the tunnels are constructed predominantly of 3 octahedra in the [001] direction.The synthesis process for these NBs involves the following procedure, which has previously been reported in ref. 6. The process started with the synthesis of the layered manganese oxide precursor with birnessite crystal structure. First, 50 mL of 0.5 M NaOH (Acros Organics) and 1 M H2O2 (Fisher Scientific, 30 wt%) solution was mixed into 25 mL of 0.3 M Mn(NO3)2 (Alfa Aesar) solution, leading to the formation of a precipitate. The precipitate (Na-birnessite) was aged for 1 hour, and then filtered and washed with a copious amount of deionized water. Na+ ions were exchanged with Mg2+ ions in the interlayer region by placing wet Na-birnessite powder into 1 L of 1 M MgCl2 (Sigma Aldrich) solution. To complete the ion exchange process, the manganese oxide powder was filtered and placed in a fresh 1 L solution of 1 M MgCl2 after 24 hours. The process was repeated again after 24 hours for three exchanges of the MgCl2 solution, for a total interaction between the precipitate and solution of 72 hours. The product (Mg-buserite) was then filtered, washed with deionized water and dried at 70 °C in air for 8 hours. Todorokite nanobelts were obtained by dispersing 100 mg of this Mg-buserite powder in 17 mL of 1 M MgCl2 solution. This mixture was then placed in 23 mL Teflon-lined stainless steel autoclaves (Parr Instruments) and hydrothermally treated for 96 hours at 220 °C. Such hydrothermal treatment conditions result in the formation of todorokite-MnO2 with predominantly one-dimensional morphology.6 This study has explicitly shown that the particles are nanobelts and not nanowires as it was believed before, and the width of the nanobelts varies. Prior to material characterization, the product obtained after hydrothermal treatment was filtered, washed with deionized water, and dried at 100 °C in air for 8 hours.
In this paper, we will employ an “m × n” terminology to indicate the dimensions or geometry of an individual tunnel, where m and n represent the number of octahedra in the [100] and [001] directions, respectively. While the value of n is fixed by the interlayer spacing at 3, the value of m or the tunnel width parameter (i.e., the tunnel dimension in the [100] direction) evolves with the hydrothermal synthesis process in terms of both, its size and homogeneity. As the synthesis process proceeds with increasing inter-linking of layers, it is accompanied by the simultaneous splitting of 2D-platelets into progressively smaller width NBs (approaching its terminal 1D geometry and 3 × 3 tunnel size) over time.
It is important to note that we find this layer-to-tunnel transformation process to be partway complete and exhibits non-uniformity among the NBs observed in our powder sample. As a result, the tunnel width parameter (m) within a given nanobelt assumes a range of values greater than 3. The maximum value for m decreases with reducing nanobelt width, indicating that the platelet-to-nanobelt transformation mechanism involves progressively growing cross-linking of neighboring layers. Furthermore, the homogeneity of tunnel widths (i.e., the range of values assumed by m) within the cross-section of a given nanobelt is also correlated to its width, and is found to improve with reducing widths or increasing inter-layer cross-linking. This is evident from Fig. 1(b and c), where the left-most image in each of these panels show a scanning electron micrograph (SEM) of agglomerated T-NBs, which were drawn at different stages of the layer-to-tunnel transformation process. The wider NBs of panel ‘b’ were in the earlier stages of this transformation as compared to the narrower NBs of panel ‘c’. In addition, Fig. 1(b and c) show the cross-sectional scanning transmission electron micrograph (STEM, middle panel) and its respective tunnel-matrix cartoons (right panel) for representative nanobelts drawn from these samples. The STEM image of panel ‘b’ shows a cross-sectional segment inside a 196 nm wide nanobelt, which is in the earlier stages of its layer-to-tunnel transformation process. In this nanobelt section, n varies over a large range from 3 to 22 and the contiguous tunnels for each value of m form a separate grain with a characteristic unit cell. This small nanobelt cross-sectional region contains 16 such grains, each of which have physical widths varying between 0.96 nm to 5.52 nm. Furthermore, there is also non-uniformity in tunnel widths within some of the individual tunnel columns. On the other hand, representative cross-sectional regions of nanobelts with widths on the order of 50 nm or less (Fig. 1(c)), which are in the later stages of their layer-to-tunnel transformation pathway, indicate a much smaller variation in tunnel width parameter m. In the case of cross-sectional regions imaged in these panels, the tunnel width parameter, m, varies between 3 and 8. We also find that these smaller width nanobelts have larger grain sizes and uniform tunnel widths along any given column. Thus, each nanobelt has multiple grains within its cross-section even though the size, columnar uniformity, and areal density of such individual grains varies with its physical width.
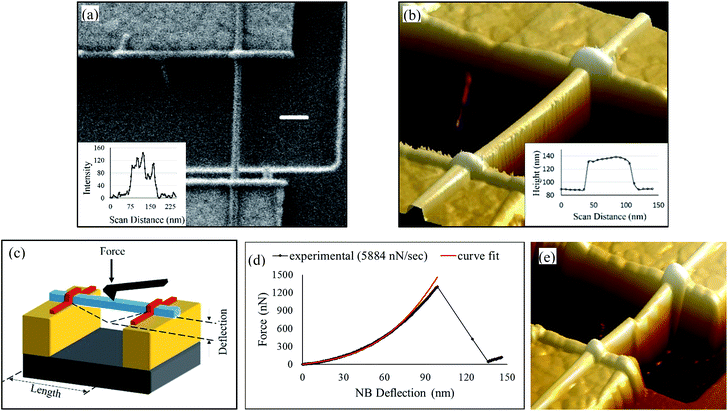
In order to investigate the mechanical properties of multi-crystalline T-NBs, individual NBs are integrated into doubly-clamped nanobeams by assembling them on top of spatially separated mechanical anchors using dielectrophoresis (DEP) (Fig. 2). The samples are comprised of silicon chips with an array of such individual nanodevices. Further details on this technique can be found in our past reports, where this approach has been employed to assemble and characterize the physical properties of other one-dimensional nanomaterials.21–24 As shown in Fig. 2(a and b), each device consists of a pair of 150 nm thick gold nanoelectrodes, which are separated by a design gap of either 600 nm or 1 μm in different designs. When the nanobelt is assembled on top of this gold nanoelectrode pair, its distal ends are secured to the underlying electrode using van der Waals forces. Further clamping of the nanobelt from the top-side is achieved through electron beam induced deposition (EBID) of Platinum metal inside a focused ion beam scanning electron microscope (FIB-SEM) system. This insures slippage-free probing of the nanobelts in a doubly-clamped configuration.
Results and discussion
Fig. 2(a) shows the SEM image of an assembled nanobelt. Inset to this panel, which was taken from the inter-electrode suspended region of the nanobelt using an image processing algorithm in MATLAB, shows the pixel intensity plot of this micrograph as a function of scan distance along a representative row of pixels (from left-to-right). This algorithm is also used to extract the rising and falling edges of the NB intensity plots, and the width of the NB is then estimated as the average value of the separation between these edges at each row along the NB length within its suspended region. An atomic force micrograph (AFM) of this NB is shown in Fig. 2(b). The thickness of the NB is estimated from its AFM height plot, which is averaged over the length of the NB that remains on top of its metal contacts and is shown in the inset. For the NB shown in Fig. 2, the width and thickness are estimated as 56 nm and 42 nm, respectively.The DEP assembled and EBID clamped T-NB is then subjected to AFM-based three-point bending tests, as shown in Fig. 2(c).13,23–26 This process involves the following steps: (a) positioning of the AFM tip in nanoscopic proximity to but, directly above the NB mid-length using a tapping mode-scan taken prior to the bending test, (b) movement of the sample stage z-piezo to bring the NB sample in contact with AFM tip, thereby inducing out-of-plane deflections in both, the tip and the NB, and (c) the recording of the tip deflection vs. stage movement (i.e., its z-piezo) plot during this process. If the spring constant of the AFM tip is pre-calibrated (using the Sader's method13), the tip deflection vs. z-piezo plot can be converted to the NB force (FNB) vs. deflection (δNB) plot, as shown in Fig. 2(d). This data processing procedure has been explained in detail in our past reports and can be found elsewhere.23,24 From this plot, it can be observed that the T-NB undergoes fracture. This is also further confirmed with an AFM scan obtained from the device after the three-point test (panel ‘e’).
In order to determine if the T-NB exhibits purely brittle fracture or if it experiences mechanical yielding prior to the fracture event, an analytical model, which describes its elastic behavior, is compared with the experimentally observed data. Due to its 1-D geometry, the T-NB experiences a combination of bending and tensile stretching when it is subjected to a transverse load. This results in a non-linear FNBvs. δNB curve (as seen in panel ‘d’) and can be modeled using the following equation:26
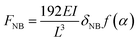 | (1) |
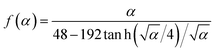 | (2) |
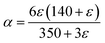 , and
, and 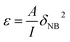 .
.
It is important to note that both, A and I depend on the microstructural porosity of the NB. This porosity is, in turn, determined by the distribution of tunnel sizes and the extent of their heterogeneity within the cross-section of any given NB. As discussed previously, the NB samples are comprised of m × 3 tunnels, where m assumes values ranging between 3 and 8 in smaller width T-NBs, and assumes much larger values (up to ∼20) with greater heterogeneity in the case of larger width T-NBs. In the analytical models, a homogenous distribution of 5 × 3 tunnels is assumed in the NBs, and these tunnel unit-cells are approximated as open-cornered, hollow rectangles with dimensions as shown in Fig. 3(a). The moment of inertia of the T-NB is then calculated as the summation of the contributions from each individual 5 × 3 tunnel within the NB cross-section (using the parallel axis theorem).
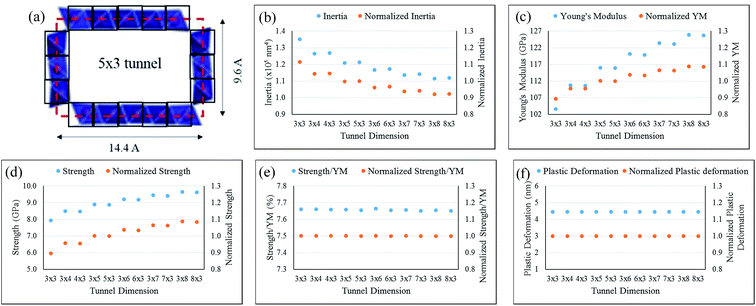 | ||
| Fig. 3 (a) An illustration of the unit-cell geometric approximation, which is employed in area and moment of inertia calculations, using a 5 × 3 tunnel geometry as an example. The black square boxes indicate the regions employed within these calculations and the red dashed rectangle indicates the tunnel dimensions used. (b–f) Dependence of the estimates for T-NB moment of inertia, Young's Modulus, strength, strength-to-YM ratio, and plastic deformation, respectively as a function of the tunnel dimension assumption. In each of these plots, the primary (i.e., left-side) y-axis shows the variation in absolute value of the parameter under consideration. The secondary (i.e., right-side) y-axis represents the variation in normalized value of the parameter under consideration with respect to its value corresponding to the 5 × 3 tunnel dimension. The data presented here, involves the T-NB shown in Fig. 2(b). | ||
Once the T-NB moment of inertia is determined using the method described above, the experimental data is fitted to the analytical model presented in eqn (1) [using a MATLAB code] and the YM of the T-NB is extracted. The experimental data and its curve fit is shown in Fig. 2(d), and the YM of this T-NB was calculated as 115.8 GPa. At large deformations prior to fracture, the NB exhibits a very small plastic deformation of up to 4 nm. We define the critical load (Fy), associated with the yield point, as the load at which the plastic deformation reaches 2 nm (in order to distinctly locate the yield point above the measurement noise). The yield strength of the NB can then be computed as:23,24
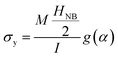 | (3) |
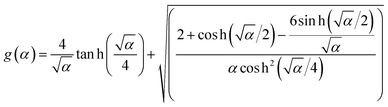 .
.
In addition, HNB denotes the NB thickness and M represents the maximum value of the bending moment 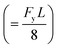 .
.
From the above equation, the yield strength, or simply the strength, of this T-NB was calculated to be 8.9 GPa. The strength-to-YM ratio of this NB, which is indicative of the defect density in the NB, was computed as 7.65%. Furthermore, the plastic deformation component (4 nm) of this T-NB device is an order of magnitude smaller than its elastic deformation component (94 nm), and the NB exhibits near-brittle behavior. In past reports involving nanomechanics of metallic19,27,28 and ceramic nanomaterials,14,16,17 mechanisms such as dislocation-mediated activity and grain boundary sliding have been identified as the underlying causes for plasticity. In the case of NBs tested in this effort, dislocation-mediated activity causing this ultra-small yielding regime is highly unlikely due to their polytypic nature and very small grain sizes. However, the possibility of mechanisms such as grain-boundary sliding or increased inter-linking of isolated larger width tunnel grains (for example, the 8 × 3 tunnels of the STEM cross-section in Fig. 1) under strain, which will be discussed later, contributing to the ultra-small yielding regime cannot be ruled out. Furthermore, beyond this small plastic regime, the NB undergoes fracture and thus, behaves predominantly like bulk-scale ceramics.
There are two important assumptions involving tunnel sizes and orientations, which have been used in these analytical models: (a) the NB is assumed to be comprised of tunnels with an average dimension of 5 × 3, and (b) the mechanical load is assumed to act perpendicular to the width of the tunnels (i.e., perpendicular to the m axis). In order to understand the validity of these assumptions, the sensitivity of extracted geometric/material properties on the values chosen for tunnel size as well as tunnel orientation (with respect to the mechanical load) within the analytical models has been calculated and shown in Fig. 3(b–f). Fig. 3(b) shows that the calculated value for NB moment of inertia can vary over a range of +11.5% (for a 3 × 3 tunnel assumption) to −8.0% (for a 3 × 8 tunnel assumption) as compared to the values calculated for the nominal 5 × 3 tunnel-size assumption used in our analytical models. For a NB with given cross-sectional dimensions, this observation of progressively decreasing moment of inertia values with an increase in its constituent tunnel size is explained by the larger cross-sectional porosity in large-sized tunnels. Similarly, as shown in Fig. 3(c and d), the extracted values of the YM vary from −10.6% (for a 3 × 3 tunnel assumption) to +8.7% (for a 3 × 8 tunnel assumption) and those of the calculated strength vary from −10.5% (for a 3 × 3 tunnel assumption) to +8.7% (for a 3 × 8 tunnel assumption), as compared to the nominal 5 × 3 tunnel-size assumption. On the other hand, the strength-to-YM ratio remains within 0.2% and the plastic deformation remains unchanged for the tunnel dimensions shown in Fig. 3(e and f), as compared to the nominal 5 × 3 tunnel-size. Thus, we find that the estimates for T-NB YM and strength are moderately dependent on the assumption used for the tunnel size. On the other hand, the calculated values for the YM-to-strength ratio and the estimates for plastic deformation/elastic regimes within the NB loading curves are not sensitive to the tunnel-size assumption that is employed in the analytical models. Hence, we have predominantly employed the YM-to-strength ratio and the elastic/plastic regime estimates to discuss the mechanics of these polytypic T-NBs in this work. Another aspect that emerges from the data presented in Fig. 3 is the weak dependence of these mechanical properties on the assumed orientation of the tunnels (i.e., m × 3 or 3 × m) with respect to the applied load. In addition, all of the T-NB devices chosen in this effort for mechanical property characterization have a larger width as compared to their height and this, insures that we are applying the mechanical load perpendicular to the tunnel width (i.e., the m axis).
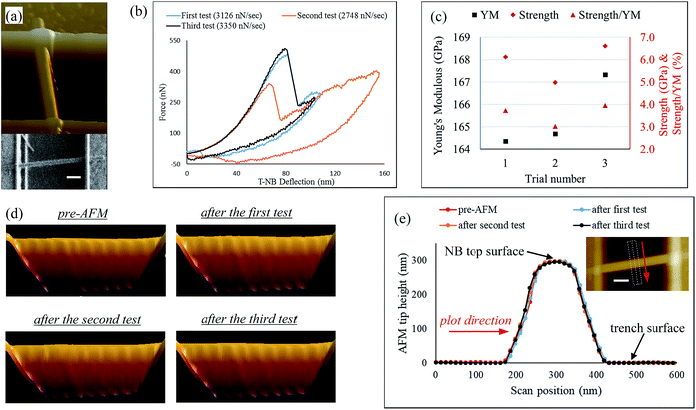
Fig. 4 shows the mechanical characterization of a T-NB that exhibited plastic recovery and did not experience fracture (i.e., different from the behavior demonstrated in Fig. 2). The NB force vs. deflection plots from three successive loading experiments are shown in panel ‘b’ of this figure. In these experiments, which were performed at time intervals on the order of ∼3 to 5 minutes (due to the need to acquire an AFM scan and image the NB at the end of each trial), the NB exhibits elastic behavior prior to the onset of a load drop during the loading curve. Post-occurrence of this load drop, the NB undergoes further straining at increasing loads and does not exhibit signs of complete fracture. While plastic deformation has been associated with dislocation mediated plasticity in the case of GaAs-based ceramic single-crystals,14 we hypothesize that the plastic deformation in these polytypic nanoceramics (with small grain sizes) occurs through a strain-induced, dynamic re-crystallization process. Specifically, the AFM tip induces shear distortions within the top and bottom walls of the larger width m × 3 tunnels. When these shear stresses exceed a characteristic threshold, Mn–O bonds break within edge-sharing MnO6 octahedral units on the horizontally oriented (i.e., top and bottom) tunnel walls.29 This breakage of Mn–O bonds is attributed to the load drop observed in Fig. 4(b).
Next, these broken bonds are replaced by new ones formed between the Mn and O atoms in vertically contiguous tunnel walls (thereby, interlinking them). This results in increased interlinking of the NB tunnels, which in turn results in smaller tunnel widths. This argument is supported by the computational results presented in ref. 29, which describes the shear-distortion induced layer-to-tunnel transitions that occur during the hydrothermal synthesis of tunnel manganese dioxide polymorphs (such as α-MnO2, β-MnO2, and γ-MnO2) from a 2D, layered δ-MnO2 phase. Using a stochastic surface walking (SSW) sampling pathway method, this report calculated very low energetic barriers for the layer-to-tunnel transition (at 0.2 to 0.3 eV per MnO2 formula unit) and identified energetically favored synthesis pathways for different tunnel-structured polymorphs.
In addition, this report also presented potential transformation schematics for the formation of todorokite-type, 3 × 3 tunnels through this shear distortion-induced layer-to-tunnel inter-linking process. The transformation of larger width tunnels to progressively smaller ones through increased inter-linking is also experimentally observed during the progression of the hydrothermal synthesis of these NBs, as previously shown in Fig. 1. The association of the observed load-drop with strain-induced dynamic recrystallization as opposed to grain boundary diffusion/sliding, is due to the specificity of this load-drop as well as plastic recovery behavior to only larger width T-NBs (as will be discussed further using the results of Fig. 5). These larger width NBs contain a higher distribution of larger-width tunnels and thereby, lend themselves to increased inter-linking between vertically contiguous tunnel walls.
It is important to note that the todorokite NBs are polytypic and this inter-layer cross-linking/dynamic recrystallization mechanism is favored to occur only within grains that contain larger width tunnels. On the other hand, the remaining smaller-width grains in the NB are expected to undergo elastic accommodation at flow stresses that progressively increase with re-loading as seen in Fig. 4(b). Thus, beyond the occurrence of the sharp load drop, the larger-width and smaller-width tunnel regions of the NB simultaneously experience plastic and elastic straining, respectively. During the unloading process, we hypothesize that the recovery of elastic strain in these smaller-width tunnels releases internal stresses, which are opposite in direction to the applied loading stress and support the reversal of the inter-linking process in the larger-width NB tunnels. As a result, the plastic deformation is reversed when the external loading is removed. This reversal of plastic deformation upon unloading is confirmed with the data presented in Fig. 4(d and e). Fig. 4(d) shows the NB profile prior to the first AFM test and its evolution after each subsequent bending trial. Furthermore, the height of the NB top-surface at the mid-length of its suspended region is shown before AFM-based nanomechanical testing and after each loading-unloading experiment in Fig. 4(e). The height of the NB top-surface (peak position) with respect to the trench surface is extracted to be 296 nm, 298 nm, 297 nm, and 295 nm from the pre-AFM, post-first test, post-second test, and post-third test data, respectively. This near-invariance in suspended height at the mid-length of a 955 nm long NB, after multiple loading–unloading experiments in which it is subjected to a maximum deformation of up to 155 nm, confirms that the NB undergoes plastic recovery.
The mechanism hypothesized above for the reversibility of plastic deformation using energy stored in elastically strained regions of the nanomaterial is supported by the discussion in ref. 14 and 19. The recovery of dislocation-mediated plastic deformation in bending experiments involving single-crystalline GaAs NWs was previously attributed to a similar release of opposing internal stresses, which were associated with the recovery of simultaneously strained, elastic regions in the same NW.14 Dislocation backflow during unloading, which is aided by inhomogenous, high residual internal stresses, are also reported as the prime mechanism of plastic recovery in 50-to-65 nm grain-sized, polycrystalline Al and Au thin films.19 While reversal in plastic deformation through the release of elastic stresses is hypothesized in our effort as well, it is unlikely that the much smaller grains observed in the current experiments can accommodate dislocation sources and hence, we attribute the plastic deformation in T-NBs to strain-induced inter-linking between larger-width tunnel walls. While arguments have been advanced here in support of the proposed hypothesis through the use of AFM force spectroscopy and surface topography data, real-time nanomechanics investigation using TEM techniques will provide complementary information on the evolution in tunnel microstructure and represents a future direction for this effort.
The magnitude of forces employed in the loading experiments of the NB in Fig. 4 [up to 483 nN] are smaller than those used for the NB in Fig. 2 [up to 1300 nN] predominantly due to differences in beam inertia (26 nm thick beam in Fig. 4vs. a 42 nm thick beam in Fig. 2). Specifically, the moment of inertia varies by a factor of more than 3 between the two NB devices (121![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 187 nm4 for the NB of Fig. 2vs. 35
187 nm4 for the NB of Fig. 2vs. 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130 nm4 for the device of Fig. 4). In addition, the negative force regime in the unloading curves of the NB in Fig. 4 arises from the tip-NB adhesion due to van der Waals' interactions and the associated extension of the AFM tip during the sample disengagement process.
130 nm4 for the device of Fig. 4). In addition, the negative force regime in the unloading curves of the NB in Fig. 4 arises from the tip-NB adhesion due to van der Waals' interactions and the associated extension of the AFM tip during the sample disengagement process.
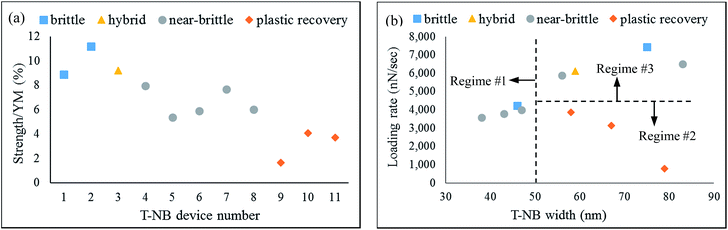
The possible variations in nanomechanical behavior (i.e., brittle vs. recoverable plasticity) emerge from the nature of polytypism in a given T-NB and from the loading (or, strain) rate that it is subjected to. This is evident in the data gathered from 11 different T-NB devices as a part of this effort. Fig. 5(a) plots the strength-to-YM ratio observed in these devices, and the data-set in this panel is grouped in terms of the different types of nanomechanical behavior observed during the three-point bending tests: (i) purely brittle fracture, (ii) hybrid performance, which involved plastic recovery after a steep load drop (to near-zero load) in the first loading cycle followed by brittle fracture in the second loading curve, (iii) near-brittle fracture with a very small plastic deformation component on the order of a few nm (of the type discussed in Fig. 2), land (iv) recoverable plasticity. Here, the strength value refers to the yield strength for all samples, except for brittle NBs where it refers to the ultimate (i.e., fracture) strength.
The strength-to-YM ratio metric is directly related to the defect density within one-dimensional nanomaterials.30–32 In the T-NB samples, crystal defects arise predominantly from stacking disorder induced polytypism. Thus, a lower strength-to-YM ratio (i.e., substantively below 10% (ref. 30–32)) is indicative of a higher degree of polytypism in the material, which implies that the NB under consideration is in the comparatively earlier stages of its tunnel-to-layered structure transition in the hydrothermal synthesis process. As discussed in Fig. 1(b), these NBs will have larger physical widths and will be comprised of the following tunnel features: (a) a higher distribution of larger-width tunnels, (b) smaller grain sizes, and (c) non-uniformity in tunnel widths within individual columns due to a higher degree of stacking disorders.
As seen in Fig. 5(a), the strength-to-YM ratio was observed to decrease in the following order: brittle and hybrid NBs > near-brittle NBs > NBs exhibiting recoverable plasticity. Thus, we hypothesize that the NBs with lower strength-to-YM ratios (≤4%) will have larger widths and a polytypic microstructure, which is closer to the representation in Fig. 1(b) and susceptible to undergo recoverable plasticity. This argument is supported by the results summarized in Fig. 5(b), which illustrates the dependence of the observed nanomechanical behavior on the average loading (i.e., strain) rate and the NB width. In this plot, the average loading rate is defined as the maximum force prior to yielding (or fracture, as the case maybe) divided by the loading duration. Regime #2 of this plot shows that each of the three NWs that exhibited plastic recovery had a geometric width value that was in the higher end of the tested samples. Thus, these NBs contain larger width tunnels with a higher degree of stacking-disorder induced polytypism, which are susceptible to undergo dynamic re-crystallization mediated plasticity (through shear distortion-induced interlinking between neighboring tunnel layers).
It is important to note that not all of the NBs with larger widths exhibited plastic recovery. In fact, the larger width NBs are categorized into two regimes in Fig. 5(b) depending on the average rate at which the load (i.e., strain) is applied during the bending tests. When the average loading rate was below 4000 nN s−1, the NBs underwent repetitive plastic recovery during multiple loading trials (as discussed above). On the other hand, when the average loading rate exceeded ∼5800 nN s−1 in these larger width NBs, three of the four devices within this regime (labeled #3 in Fig. 5(b)) exhibited brittle or near-brittle fracture. The fourth NB within this regime experienced plastic recovery subsequent to a steep load drop during the first loading curve and then, fractured during its elastic regime during the second loading curve. We conclude that at increased loading (or, strain) rates above a characteristic threshold, the NBs experience brittle fracture at high strength-to-YM ratios even though they contain a higher degree of stacking disorder-induced polytypism. This is because the shear distortion of the tunnel walls occurs at a rate that is too high to permit the re-formation of Mn–O bonds between the neighboring tunnel layers. Thus, the dynamic recrystallization process is suppressed within these devices and the broken Mn–O bonds within the horizontal tunnel walls initiate/propagate cracks towards catastrophic failure.
On the other hand, the smaller width NBs (i.e., <50 nm widths) were observed to exhibit brittle or near-brittle fracture at higher strength-to-YM ratios as compared to that of plastic recovery samples (regime #1 in Fig. 5). As discussed previously in Fig. 1, these smaller width NBs are in the later stages of their layer-to-tunnel transformation and will be comprised of the following tunnel features: (a) smaller individual tunnel sizes (i.e., m is less than ∼8), (b) larger grain sizes, and (c) constant tunnel widths along individual columns. This combination of smaller tunnel sizes and reduced stacking disorders suppresses the tendency to undergo re-crystallization mediated plasticity in these samples. Hence, they undergo either brittle or near-brittle fracture through crack initiation/propagation through the tunnel columns.
The results presented in this work have important implications for the technological applications of polytypic tunnel manganese oxides, especially in the area of battery cathodes. During the discharging process of a battery, lithium (or other inorganic) ions are intercalated into the cathodic crystals such as the T-NBs discussed here. The insertion of lithium into the host lattice results in mechanical strain, and at high lithium loading conditions causes mechanical degradation/fracture of the electrodes. Among the different degradation mechanisms that impact the performance life of a battery electrode, this mechanical disintegration and its subsequent dissolution into the electrolyte is a key failure mode that has attracted significant attention in recent years. The identification of a new regime involving recoverable plasticity within these cathodic electrode candidates is particularly significant since it presents new avenues to avoid mechanical degradation induced failure modes in these material systems.
Conclusions
In summary, we have characterized the mechanical performance of polytypic, todorokite-like nanobelts, which have been prepared through a hydrothermal synthesis process. The extent of progression in the tunnel-to-layer transformation process, which underlies this hydrothermal synthesis procedure, was observed to be non-uniform within different NBs sourced from a given powder sample and hence, resulted in a non-homogenous distribution of polytypism within the synthesized T-NBs. As a result, the extent of tunnel size in-homogenity and its size distribution was larger within NBs that presented larger physical widths and were in the comparatively earlier stages of the layer-to-tunnel transformation process. AFM-based three point bending tests of these T-NBs revealed that devices with a higher in-homogenity in tunnel sizes exhibited recoverable plasticity when subjected to loading rates below a characteristic threshold. Other T-NB samples, which were either subjected to high loading rates or were in the comparatively later stages of this layer-to-tunnel transformation pathway, exhibited brittle fracture. These results provide new insights and pathways for engineering mechanical stability in tunnel manganese oxide materials when used as electrode materials in electrochemical energy storage systems.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partly supported by the National Science Foundation under Grant No. CBET-1655496 and Grant No. CBET-1604483. Use of the Center for Nanoscale Materials, an Office of Science user facility, was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Contract No. DE-AC02-06CH11357. Aberration-corrected STEM imaging was conducted at Oak Ridge National Laboratory's Center for Nanophase Materials Sciences, which is a U.S. DOE Office of Science User Facility.References
- B. W. Byles, N. K. R. Palapati, A. Subramanian and E. Pomerantseva, APL Mater., 2016, 4, 046108 CrossRef.
- H. Cao and S. L. Suib, J. Am. Chem. Soc., 1994, 116, 5334–5342 CrossRef CAS.
- Y. F. Shen, R. P. Zerger, R. N. DeGuzman, S. l. Suib, L. McCurdy, D. I. Potter and C. L. O'Young, Science, 1993, 260, 511–515 CrossRef CAS PubMed.
- V. Aravindan, M. V. Reddy, S. Madhavi, G. V. S. Rao and B. V. R. Chowdari, Nanosci. Nanotechnol. Lett., 2012, 4, 724–728 CrossRef CAS.
- B. W. Byles, D. A. Cullen, K. L. More and E. Pomerantseva, Nano Energy, 2018, 44, 476–488 CrossRef CAS.
- B. W. Byles, P. West, D. A. Cullen, K. L. More and E. Pomerantseva, RSC Adv., 2015, 5, 106265 RSC.
- J. Huang, A. S. Poyraz, S.-Y. Lee, L. Wu, Y. Zhu, A. C. Marschilok, K. J. Takeuchi and E. S. Takeuchi, ACS Appl. Mater. Interfaces, 2017, 9, 4333–4342 CrossRef CAS PubMed.
- B. W. Byles, M. Clites, D. A. Cullen, K. L. More and E. Pomerantseva, Ionics, 2018 DOI:10.1007/s11581-018-2715-z.
- K. Zhang, X. Han, Z. Hu, X. Zhang, Z. Tao and J. Chen, Chem. Soc. Rev., 2015, 44, 699–728 RSC.
- C. M. Julien and A. Mauger, Nanomaterials, 2017, 44, 396 CrossRef PubMed.
- M. M. Thackerey, Prog. Solid State Chem., 1997, 25, 1–71 CrossRef.
- D. J. Green, An Introduction to the Mechanical Properties of Ceramics, Cambridge University Press, Cambridge 1998 Search PubMed.
- B. Wen, J. E. Sader and J. J. Boland, Phys. Rev. Lett., 2008, 101, 175502 CrossRef PubMed.
- P. Bao, Y. Wang, X. Cui, Q. Gao, H.-W. Yen, H. Liu, W. K. Yeoh, X. Liao, S. Du, H. H. Tan, C. Jagadish, J. Zou, S. P. Ringer and R. Zheng, Appl. Phys. Lett., 2014, 104, 021904 CrossRef.
- Y. Wang, H. J. Joyce, Q. Gao, X. Liao, H. H. Tan, J. Zou, S. P. Ringer, Z. Shan and C. Jagadish, Nano Lett., 2011, 11, 1546–1549 CrossRef CAS PubMed.
- Y. Zhang, X. Han, K. Zheng, Z. Zhang, X. Zhang, J. Fu, Y. Ji, Y. Hao, X. Guo and Z. L. Wang, Adv. Funct. Mater., 2007, 17, 3435–3440 CrossRef CAS.
- X. D. Han, Y. F. Zhang, K. Zheng, X. N. Zhang, Z. Zhang, Y. J. Hao, X. Y. Guo, J. Yuan and Z. L. Wang, Nano Lett., 2007, 7, 452–457 CrossRef CAS PubMed.
- X. Hu, D. A. Kitchaev, L. Wu, B. Zhang, Q. Meng, A. S. Poyraz, A. C. Marschilok, E. S. Takeuchi, K. J. Takeuchi, G. Ceder and Y. Zhu, J. Am. Chem. Soc., 2018, 140, 6961–6968 CrossRef CAS PubMed.
- J. Rajagopalan, J. H. Han and M. T. A. Saif, Science, 2007, 315, 1831–1834 CrossRef CAS PubMed.
- X. Li, Y. Wei, W. Yang and H. Gao, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 16108–16113 CrossRef CAS PubMed.
- N. K. R. Palapati, E. Pomerantseva and A. Subramanian, Nanoscale, 2015, 7, 3109–3116 RSC.
- A. Subramanian, N. S. Hudak, J. Y. Huang, Y. Zhan, J. Lou and J. P. Sullivan, Nanotechnology, 2014, 25, 265402 CrossRef CAS PubMed.
- M. Maksud, N. K. R. Palapati, B. W. Byles, E. Pomerantseva, Y. Liu and A. Subramanian, Nanoscale, 2015, 7, 17642–17648 RSC.
- M. Maksud, J. Yoo, C. T. Harris, N. K. R. Palapati and A. Subramanian, APL Mater., 2015, 3, 116101 CrossRef.
- L. T. Ngo, D. Almécija, J. E. Sader, B. Daly, N. Petkov, J. D. Holmes, D. Erts and J. J. Boland, Nano Lett., 2006, 6, 2964–2968 CrossRef CAS PubMed.
- A. Heidelberg, L. T. Ngo, B. Wu, M. A. Phillips, S. Sharma, T. I. Kamins, J. E. Sader and J. J. Boland, Nano Lett., 2006, 6, 1101–1106 CrossRef CAS PubMed.
- Y. Liu and Y. Wei, Extreme Mech. Lett., 2016, 9, 158–164 CrossRef.
- Y. J. Wei, A. F. Bower and H. J. Gao, J. Mech. Phys. Solids, 2008, 56, 1460–1483 CrossRef CAS.
- Y.-F. Li, S.-C. Zhu and Z.-P. Liu, J. Am. Chem. Soc., 2016, 138, 5371–5379 CrossRef CAS PubMed.
- D. K. Felbeck and A. G. Atkins, Strength and fracture of engineering solids, Prentice-Hall, Englewood Cliffs, NJ, 1984 Search PubMed.
- A. Kelly and N. H. Macmillan, Strong Solids, Oxford University Press, New York, 1986 Search PubMed.
- G. Stan, S. Krylyuk, A. V. Davydov and R. F. Cook, J. Mater. Res., 2011, 27, 562–570 CrossRef.
| This journal is © The Royal Society of Chemistry 2019 |