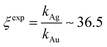Open Access Article
Open Access ArticleRelating the rate of growth of metal nanoparticles to cluster size distribution in electroless deposition†
M.
Iatalese
a,
M. L.
Coluccio
b,
V.
Onesto
 b,
F.
Amato
b,
E.
Di Fabrizio
b,
F.
Amato
b,
E.
Di Fabrizio
 c and
F.
Gentile
c and
F.
Gentile
 *d
*d
aAkka Technologies, Via Giacomo Leopardi 6, 40122 Bologna, Italy
bDepartment of Experimental and Clinical Medicine, University Magna Graecia, 88100 Catanzaro, Italy
cPhysical Science & Engineering Division, King Abdullah University of Science and Technology, Thuwal, 23955-6900, Saudi Arabia
dDepartment of Electrical Engineering and Information Technology, University Federico II, 80125 Naples, Italy. E-mail: francesco.gentile2@unina.it
First published on 17th August 2018
Abstract
Electroless deposition on patterned silicon substrates enables the formation of metal nanomaterials with tight control over their size and shape. In the technique, metal ions are transported by diffusion from a solution to the active sites of an autocatalytic substrate where they are reduced as metals upon contact. Here, using diffusion limited aggregation models and numerical simulations, we derived relationships that correlate the cluster size distribution to the total mass of deposited particles. We found that the ratio ξ between the rates of growth of two different metals 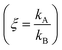 depends on the ratio γ between the rates of growth of clusters formed by those metals
depends on the ratio γ between the rates of growth of clusters formed by those metals 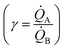 through the linearity law ξ = 14(γ − 1). We then validated the model using experiments. Different from other methods, the model derives k using as input the geometry of metal nanoparticle clusters, decoded by SEM or AFM images of samples, and a known reference.
through the linearity law ξ = 14(γ − 1). We then validated the model using experiments. Different from other methods, the model derives k using as input the geometry of metal nanoparticle clusters, decoded by SEM or AFM images of samples, and a known reference.
1 Introduction
Electroless deposition is a chemical method of plating in which a metal is deposited on a surface without the support of external fields or driving voltages.1–5 In the technique, absorption of metal ions at the surface is activated by catalytic and reducing agents added in the solution with the ions. If the substrate is made up of silicon, the substrate itself performs simultaneously as a reducing and catalytic agent and the process of deposition is greatly facilitated. Since silicon serves as a basis of the majority of micro- and nano-fabrication processes and techniques and can be easily integrated with other materials,6–9 electroless deposition on silicon displays potential to be used for the synthesis of metal nanoparticles, metal nanomaterials or other nanostructures.The method enables the fabrication of nanostructures by incrementally depositing smaller building blocks on a flat substrate. Pre-patterning of the substrate by optical or electron beam lithography allows site selective formation of metal nanoparticles with tight control over the final aspects of the nanoparticles.5 On the active sites of the silicon surface exposed to growth, metal ions aggregate into clusters where the geometrical characteristics of the aggregate will depend on a fine-tuning of size and shape of preexisting patterns on the substrate, and the parameters of electroless growth including temperature, pH, and concentration of metal ions in solution.5
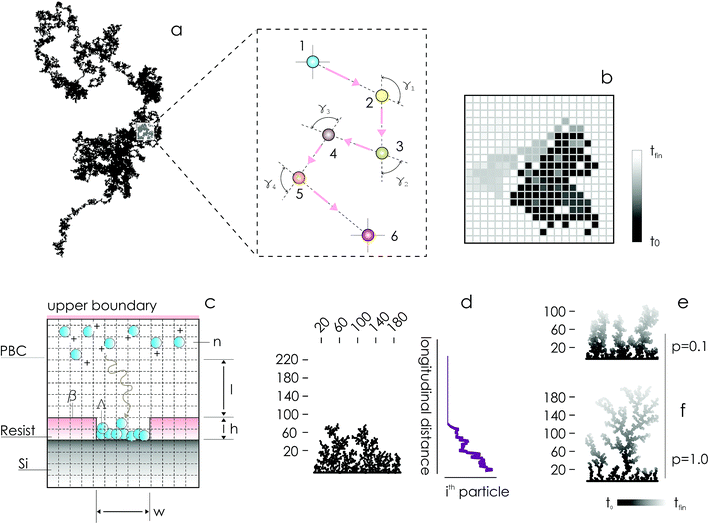
In the absence of stirring or other convective flows, ions are transported towards the active sites of the substrate by pure diffusion. Since the mechanisms of diffusion are very well understood,10,11 electroless deposition can be simulated using discrete models of transport in cellular spaces. In the models, cells of a grid can take definite 0 or 1 states – 1 indicates the presence of a particle (ion). A particle will move with time in a continuous time probabilistic Brownian motion (Fig. 1a), which is discretized in the space as a random walk (Fig. 1b). Particles aggregate upon contact. Displacement of a great many particles in a lattice (Fig. 1c) enables the formation of numerical aggregates with a dendritic appearance that is typical of fractals (Fig. 1d). Simulation of particle growth using iterative arrays is called Diffusion Limited Aggregation (DLA).12–17 In previously reported analyses, we have used DLA models to examine the effects of pattern size4,5 and pattern distance18 on the characteristics of metal nanoparticles in electroless growth. Here, we revise DLA models of particle growth to consider the effects of the sticking probability of an ion to the aggregate – p.
On changing p between 0 and 1, one can modulate the packing fraction and superficial aspect of the aggregates. Low values of p generate aggregates with high atomic packing densities (Fig. 1e), in contrast to low-density aggregates obtained from high values of p (Fig. 1f). p regulates the adhesion of ions to the substrate. If p is low (p → 0) the probability of adhesion of a particle to the aggregate is low, meaning that a particle may not immediately stick to the aggregate upon contact. Under these conditions, a particle may penetrate more deeply in the structure without being captured by the external shells of the aggregate. Higher penetration depths imply, in turn, higher final densities of the numerical clusters of particles. Notice though that, even if for small p the surface density of the aggregates is high, the growth of the aggregate is slow compared to systems with larger sticking probabilities, as demonstrated in the following sections of the paper. If p = 0, no adhesion can occur on the surface.
Using data from the simulations, we developed models that correlate the cluster size distributions and the mean cluster size with p. Since p is related, in turn, to the kinetics of metal deposition, these models enable extraction of the rate of growth of nanoparticles from topographical maps of samples, obtained by SEM, AFM or other similar techniques of imaging. We tested the performance of the model analyzing the growth of gold and silver aggregates in patterned silicon substrates. The model predicted a difference of growth rate between the two metals of a factor of 10. The growth kinetics of metal nanoparticles measured by UV spectrophotometric techniques matched the predictions of the models with a good level of accuracy.
Coupled to experimental SEM or AFM data, this scheme can be used to derive the growth rate kinetics of metals plated on a substrate by electroless methods.
2 Results
2.1 Generating numerical DLA aggregates
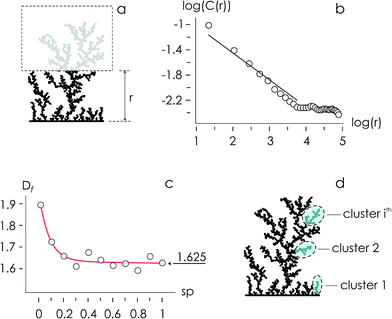
Using the numerical scheme described in the methods and in Fig. 1, we generated numerical aggregates of metal particles on patterned silicon substrates. Particles in the aggregate form non-continuous dendritic structures with details over multiple scales that are typical of fractals. For each imposed value of sticking probability p, we extracted the local density at different distances from the substrate r. Information on the density of the aggregate at a local scale was used to derive the density–density correlation function c(r).The density–density correlation function c(r), also called pair correlation function, is a distribution routinely used in statistical mechanics to describe how density varies as a function of distance from a reference point. In the present configuration, we used as a reference point the lines of nucleation sites of the aggregate, i.e. the base of the aggregate. c(r) is a measure of the probability of finding a particle at a distance r from the reference. It describes the internal structure of an aggregate as a function of continuous, smoothly varying spatial coordinates – for this it can be used to link the microscopic to the macroscopic characteristics of a system: c(r) delivers the information content of an aggregate as a function of the scale of the aggregate.
In a log–log plot, c(r) is a line with a slope α (Fig. 2). Since the fractal dimension Df of an aggregate is an index that quantifies the change in detail to a change of scale, Df may be derived from α as Df = 2 − α (Methods). The fractal dimension varies with the sticking probability and rapidly undergoes transition from an initial value Df ∼ 1.9 for p = 0 to Df ∼ 1.625 for p = 1. Notice that for sufficiently high values of p, p > 0.2, the best fit of Df attains the steady state value Df ∼ 1.625, similar to the theoretical limit 5/3 ∼ 1.667.14 The purpose of calculating the fractal dimension is deriving the cluster size distribution of an aggregate. Clusters are defined as naturally separated trees – a collection of particles connected to the same nucleation site through nearest neighbours forming the deposit16,17 (Fig. 2d). From ref. 16, the average cluster size 〈S〉 of an aggregate with fractal dimension Df and mass N is
| 〈S〉 ∼ NDf/(Df−1) | (1) |
| Q = N/〈S〉 | (2) |
The cluster-size distribution I(S,N), i.e. the number of clusters in an N-aggregate as a function of cluster size S, is:19
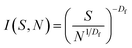 | (3) |
The probability of finding an S-site tree on a nucleation site is limited by N.
2.2 Structure of aggregates and cluster size distribution
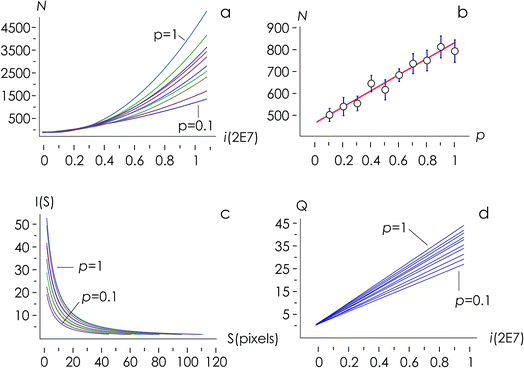
The structure of occupied sites was characterized applying relationships (1) to (3). The mean cluster size was estimated by arithmetic average after calculating the largest branch and fixing the smallest cluster containing 10 particles. Fig. 3a reports the mass N of the aggregates as a function of the time of deposition (i.e. the number of iterations) for different values of the sticking probability p. For a fixed p, the size of the aggregate increases with a quadratic function of time, which is easily explained considering that the larger the number of pixels in an aggregate, the larger the number of docking sites to which diffusing ions in solution can possibly bind. For a fixed time, the size of the aggregate increases linearly with the sticking probability p. Thus, approximately i = 6 M iterations from the beginning of the simulations, the number of particles in the aggregate is N ∼ 500 for p = 0.1, rises to N ∼ 650 for p = 0.6 and reaches N ∼ 800 for p = 1 (Fig. 3b). Remarkably, the linear form of the N(p) characteristic indicates that the kinetics of metal deposition k is proportional to the sticking probability p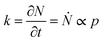 | (4) |
2.3 Connecting the rate of metal growth to the kinetics of cluster deposition
Fig. 3d, reproduced in a separate Fig. 4a for the sake of clarity, reunites in one unique diagram (i) the time evolution of the number of clusters in an aggregate![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) and (ii) the sticking probability p. The sticking probability is proportional to the kinetics of metal deposition p → k through relationship (4).
and (ii) the sticking probability p. The sticking probability is proportional to the kinetics of metal deposition p → k through relationship (4).
![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) is a measure of the number of separate particles that are deposited on a substrate over time. This assertion is substantiated by the following argument. A cluster is a structure, in the aggregate, with some internal correlation. An operational definition of a cluster is that it is a structure clearly distinguishable as a subsystem – a self-contained system within the larger system. For this, it is the analogue of an isolated particle in a real process of chemical deposition. Therefore,
is a measure of the number of separate particles that are deposited on a substrate over time. This assertion is substantiated by the following argument. A cluster is a structure, in the aggregate, with some internal correlation. An operational definition of a cluster is that it is a structure clearly distinguishable as a subsystem – a self-contained system within the larger system. For this, it is the analogue of an isolated particle in a real process of chemical deposition. Therefore, 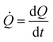 can be considered a good estimate of the number of separate particles that are deposited on a substrate in the unit time.
can be considered a good estimate of the number of separate particles that are deposited on a substrate in the unit time.
k is a key parameter in materials science and nanotechnology and is relevant for the rational design of processes or structures that imply the deposition, growth and self-assembly of metal nano-materials. On the other hand, ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) is experimentally observable and can be readily determined through conventional imaging techniques, including SEM and AFM. It may therefore be convenient to express p as a function of
is experimentally observable and can be readily determined through conventional imaging techniques, including SEM and AFM. It may therefore be convenient to express p as a function of ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) .
.
Since numerical simulations and Fig. 4a reflect metal deposition less quantitatively than qualitatively – calibration standards may be required for matching the predictions of the model with experimental data (see comments in the Discussion) – in the following we will use ratios between variables rather than the absolute values of variables to describe particle growth.
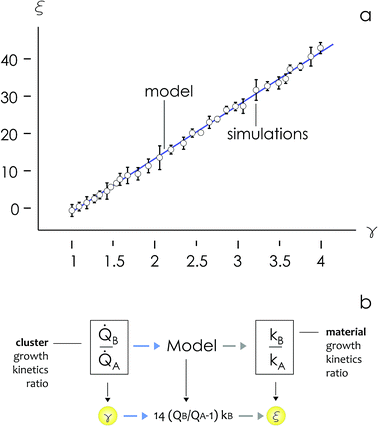
We then define the non-dimensional parameters ξ = p2/p1, γ = ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) (p2)/
(p2)/![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) (p1), the subscript i = 1, 2 indicates two different states or materials with p2 > p1. Then, we derive from the diagram in Fig. 4aξ as a function of γ: ξ(γ). The best fit of data and graphical representation of ξ(γ) (Fig. 4b) indicate that ξ varies linearly with γ as
(p1), the subscript i = 1, 2 indicates two different states or materials with p2 > p1. Then, we derive from the diagram in Fig. 4aξ as a function of γ: ξ(γ). The best fit of data and graphical representation of ξ(γ) (Fig. 4b) indicate that ξ varies linearly with γ as
| ξ = 14.34γ − 13.7 | (5) |
In separate ESI 1,† we provide a full statistical report of the linear regression, including values for the parameter table, r2, adjusted r2, estimated variance and ANOVA table. We used at least 25 simulations for each p to fit data and evaluate the model.
Eqn (5) puts in relation the growth kinetics of different materials expressed in different forms. ξ is the ratio between the kinetics of growth of two materials, γ is the ratio between the rates of growth of clusters emerging from the deposited volume of those materials. The proportion between ξ and γ is ∼14. Say that we have two different metals A and B, the kinetics of deposition of A is known, being kA. Then kB can be readily derived using an approximate form of eqn (5):
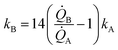 | (6) |
![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) may be determined through direct optical inspection of samples.
may be determined through direct optical inspection of samples.
2.4 Predicting the relative rates of growth of silver and gold
We used experimental data to benchmark the model. Using electroless deposition techniques described in the methods, we deposited clusters of (i) silver and (ii) gold nanoparticles on patterned silicon substrates. Patterns on the silicon surface are hexagonal arrays of disks penetrating into the positive resist S1813 with a size d, spacing δ and thickness h: d = 10 μm, δ = 30 μm and h ∼ 1 μm.On comparing the experiments with the predictions of the model, we propose that the aspect ratio of the patterns exposed to growth is the same in the experiments and in the numerical DLA scheme. In this configuration, the patterns are short systems, with d > h and aspect ratio lower than one 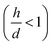 . Since the model is a comparative method of analysis, it does not necessitate a one-to-one correspondence between the geometry of the real physical prototype and the model. More sophisticated evolutions of the model that will be developed over time will enable direct simulation of real systems and the determination of absolute values of growth. As regarding spacing between patterns, δ, we have used in the experiments spacing between patterns three times larger than the pattern size, which guarantees non-interference between patterns18 and justifies the use of a single-well numerical scheme and an isolated system to simulate particle formation.
. Since the model is a comparative method of analysis, it does not necessitate a one-to-one correspondence between the geometry of the real physical prototype and the model. More sophisticated evolutions of the model that will be developed over time will enable direct simulation of real systems and the determination of absolute values of growth. As regarding spacing between patterns, δ, we have used in the experiments spacing between patterns three times larger than the pattern size, which guarantees non-interference between patterns18 and justifies the use of a single-well numerical scheme and an isolated system to simulate particle formation.
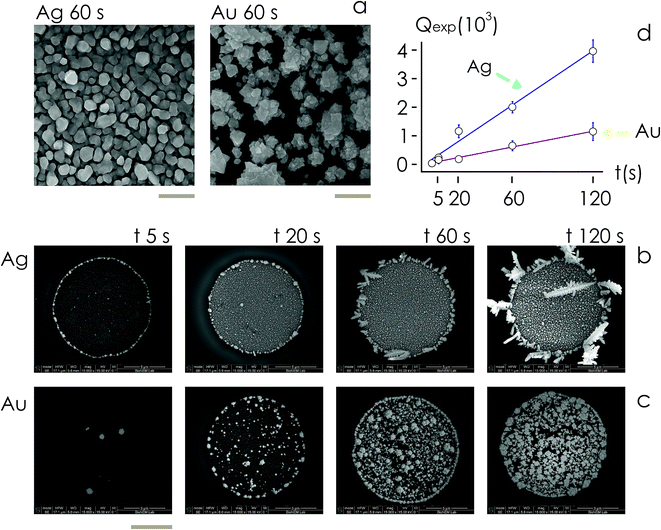
Then, we examined the structure of metal clusters at different times t from immersion in the electroless solution, t = 5, 20, 60, 120 s, using scanning electron microscopy (SEM) and atomic force microscopy (AFM) imaging techniques. We fabricated at least 5 different samples per time of deposition, and acquired more than 25 SEM images and 2 AFM images for the samples. We used SEM images for determining the rate of growth of the nanoparticles, and AFM imaging to extract the topographical details of the clusters.
For fixed values of time, we observe that the number and density of isolated particles on the silicon surface are greater for silver compared to gold deposition (Fig. 5a). This trend is maintained for all considered time frames of growth (Fig. 5b). Using standard image analysis algorithms, we extracted the number Q of isolated particles formed during silver and gold deposition over time (Fig. 5c). Q varies linearly with time (r2 = 0.989 for gold, r2 = 0.984 for silver; the statistical significance of the linear regression is reported in separate ESI 2†), in agreement with the theoretical model and the simulations. We elaborated information contained in Fig. 5c to derive how rapidly the number of clusters in an image changes with time: at any time deposition of silver is more rapid than that observed for gold. Numerical analysis of data yields the values 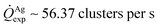 for silver and
for silver and 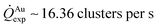 for gold, and a ratio between the two γAg/Au ∼ 3.45. This value of γ will be used in the model to determine k.
for gold, and a ratio between the two γAg/Au ∼ 3.45. This value of γ will be used in the model to determine k.
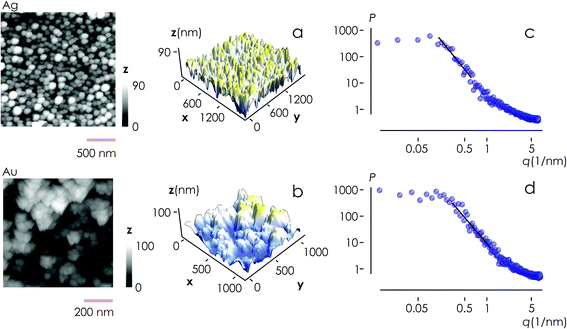
From AFM imaging (Fig. 6a) one can observe that the number of particles deposited during electroless growth of silver is larger than the number of gold nanoparticles deposited in the same time (60 s), in accordance with the results of the model and SEM inspection of samples. Few clusters of gold nanoparticles are particularly large, this is deceptive and may suggest that the cluster growth rate of gold is larger than silver – that it is not as proved by image analysis algorithms applied to AFM images that yield an estimate of QAg ∼ 106 clusters in a square pattern of 2 μm for silver, and QAu ∼ 29 clusters for gold, with a ratio 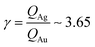 . While AFM imaging may be as accurate as SEM in deriving the topographical characteristics of a sample surface, we use here SEM results to benchmark the model because SEM imaging of samples is faster compared to AFM. SEM images are more in number, have larger formats, include more particles, are more informative and statistically significant than AFM images. While AFM can achieve ultra-high resolution and can examine sample topography at the sub nanometer level, it is not high-throughput.
. While AFM imaging may be as accurate as SEM in deriving the topographical characteristics of a sample surface, we use here SEM results to benchmark the model because SEM imaging of samples is faster compared to AFM. SEM images are more in number, have larger formats, include more particles, are more informative and statistically significant than AFM images. While AFM can achieve ultra-high resolution and can examine sample topography at the sub nanometer level, it is not high-throughput.
Post-processing of AFM topographic data enabled us to derive the power spectrum density function for both silver and gold (Fig. 6b). From this, we derived the values of fractal dimensions for the clusters of Ag (Df = 2.7) and Au (Df = 2.65). Notice that, remarkably, the experimental values of fractal dimension derived in the space are about one dimension higher than the corresponding numerical values derived in the plane, D3df ∼ D2df + 1.
Using the ratio between cluster growth dynamics (γ) determined from experiments in the model of eqn (6), we estimate that the ratio between the rates of growth of silver (kAg) and gold (kAu) is about ξ(γ) = ξmodel ∼ 34.
2.5 Model validation
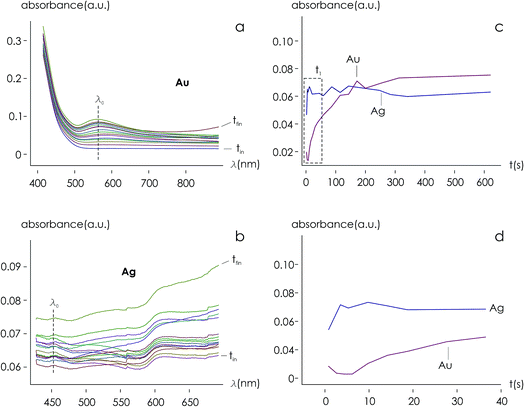
Using data from electroless deposited silver and gold nanoparticle clusters, we found that the ratio between the kinetics of growth of these two metals is ξ ∼ 34. We then verified the output of the model using independent UV spectrophotometric measurements (Methods). We produced nanoporous silicon particles (NP-Si-NPs) using electrochemical porosification of bulk silicon20,21 followed by ultrasonic disintegration of silicon into nanoparticles.22 We then suspended NP-Si-NPs into two separate aqueous solutions with (i) hydrofluoric acid (HF) and silver nitrate (AgNO3) and (ii) HF and gold chloride (AuCl3) (Methods). Immersion of NP-Si-NPs in solution triggered immediate reaction of deposition of gold and silver within the porous silicon matrix of the particles. We used UV/Vis spectrophotometry to analyze the resulting electroless reaction of deposition. We determined the dynamics of Au and Ag nanoparticle formation as the onset of the variation of absorbance of the solutions measured at λ1 = 560 nm for gold (Fig. 7a) and λ2 = 460 nm for silver (Fig. 7b). Rate constants of growth were determined as the reciprocal of the time constant τ resulting from the best fit of data with a first-order system model (Fig. 7c and d) – the time constant is defined as the time necessary for the system to reach 90% of its final value. From the fit, we determined kAg ∼ 0.02 ± 0.0034 (s−1) (τ ∼ 3.4 ± 0.57 s) and kAu ∼ 0.00054 ± 0.00007 (s−1) (τ ∼ 120 ± 14 s), with an experimentally derived value of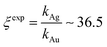 . Data are reported as mean ± standard deviation. Analysis was carried out over a set of 10 measurements, another example of which is reported in separate ESI 3.† The measured ratio of growth kinetics ξexp matches the predictions of the model ξmodel with a good level of significance and ∼93% accuracy.
. Data are reported as mean ± standard deviation. Analysis was carried out over a set of 10 measurements, another example of which is reported in separate ESI 3.† The measured ratio of growth kinetics ξexp matches the predictions of the model ξmodel with a good level of significance and ∼93% accuracy.
3 Discussion
The rate of growth k in electroless deposition is an index that quantifies how rapidly a metal is deposited on a surface. If ν is a certain measure of the bulk metal being deposited, then k is the change of ν to a change of time, k = dν/dt. ν can be the mass, volume, or thickness (extensive properties of a system), or concentration or density (intensive properties of a system), thus k is usually given in terms of the magnitude of ν per s. In all cases, measuring k implies estimating the magnitude or intensity of some physical quantity as a function of time. Consolidated methods for the determination of k are cyclic (CV) or linear sweep (LSV) voltammetry, or methods concerning the use of a quartz crystal microbalance (QCM). The first CV or LSV methods measure the shift of peak potentials ΔEp that develop under conditions where an external voltage of increasing intensity is cyclically (CV) or linearly (LSV) applied to the system.23–25 Then, ΔEp is correlated with k. The second QCM method measures a mass variation in the unit time by measuring the change in frequency of a quartz crystal resonator.26–28 While they are accurate in determining the rate constants of reactions involving reduction of metals, these methods (a) require the acquisition, installation and set-up of electrochemical workstations and electrodes in sometimes complicated configurations (CV and LSV methods) – or of QCM systems – that are not always available in nanotechnology or materials science laboratories; (b) may be conducted under conditions that deviate to a significant extent from the real conditions of metal deposition; (c) raise the problem of the integration of different components or parts: using hydrofluoric acid in a QCM or connecting a patterned silicon substrate in a three-electrode configuration in CV is not obvious; (d) necessitate repeated measures in wide time or frequency intervals for data fitting and the identification of the parameters (i.e. k) from those fits (definition of a calibration standard); (e) realize blind estimates of a physical quantity (i.e. potential, current, or mass) of a system that do not necessarily account for the geometrical variables of that system, i.e. size, shape, distribution, topographical or topological properties of metal nanoparticle clusters that are being formed over time.The last point implies that, while in nanotechnology the geometrical characteristics of metal nanomaterials are relevant for their functions,29–33 traditional methods for the determination of k ignore the geometrical form of the material assembling into nanostructures.
Here, we used mathematical modelling and numerical simulations to correlate the topological properties (![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) ) of a system grown by electroless deposition with the variation of its volume (Ṅ → p) to determine k. Different from other existing methods, our approach centers on geometry. The geometry of target structures, in turn, can be easily reconstructed using SEM, AFM, or other techniques of imaging that can be easily found in a nanotechnology laboratory and that are, on the other hand, routinely used to examine the aspects of the structures and the efficiency of a method of fabrication. Thus, incidentally, much of the SEM, AFM, TEM material produced during ordinary inspection of samples and reports can be redirected as the input of the model – generating high volumes of data (big data) that can contribute to reducing noise, reducing uncertainty, and increasing the accuracy of the estimate of k. Moreover
) of a system grown by electroless deposition with the variation of its volume (Ṅ → p) to determine k. Different from other existing methods, our approach centers on geometry. The geometry of target structures, in turn, can be easily reconstructed using SEM, AFM, or other techniques of imaging that can be easily found in a nanotechnology laboratory and that are, on the other hand, routinely used to examine the aspects of the structures and the efficiency of a method of fabrication. Thus, incidentally, much of the SEM, AFM, TEM material produced during ordinary inspection of samples and reports can be redirected as the input of the model – generating high volumes of data (big data) that can contribute to reducing noise, reducing uncertainty, and increasing the accuracy of the estimate of k. Moreover
(i) Our model uses as input the ratio between cluster multiplication velocity of two species, 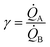 . In the more general case,
. In the more general case, ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) A and
A and ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) B should be determined as the variation of Q over time, which in turn implies determining the number of clusters Q at different times through multiple measurements. Nevertheless, assuming linearity, γ can be more simply determined as the ratio between one of the possible couples QA(ta) and QB(ta),
B should be determined as the variation of Q over time, which in turn implies determining the number of clusters Q at different times through multiple measurements. Nevertheless, assuming linearity, γ can be more simply determined as the ratio between one of the possible couples QA(ta) and QB(ta), 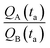 , measured at any time ta comprised between zero and the final time of growth, 0 < ta < tfin. This reduces the search for k to the estimate of the number of clusters (i.e. isolated metal nanoparticles) in two different SEM or AFM images, and the division between the two – that dramatically reduces the number of measurements and the time necessary to find k compared to other experimental techniques of analysis. In determining the number of clusters Q from SEM or AFM imaging of samples, it is preferable that the nanoparticles do not overlap (or overlap partially) on the substrate to assure accuracy. Images may be analyzed using algorithms developed over time,5,34,35 which deconvolute information using maximum likelihood methods and Fourier transform decomposition/reconstruction of images. Image analysis is accurate under sparse and sub-confluent conditions. When particles on the substrate overgrow, non-dense assumption breaks down and the number of clusters/particles in the field of view can be under-estimated. To avoid miscalculations, one should limit the analysis to the early time of particle deposition, or in any case to the linear regime of particle growth, which is the case of Fig. 5d and results presented in this work. When Q(t) deviates from linearity, results of the analysis can be inaccurate.
, measured at any time ta comprised between zero and the final time of growth, 0 < ta < tfin. This reduces the search for k to the estimate of the number of clusters (i.e. isolated metal nanoparticles) in two different SEM or AFM images, and the division between the two – that dramatically reduces the number of measurements and the time necessary to find k compared to other experimental techniques of analysis. In determining the number of clusters Q from SEM or AFM imaging of samples, it is preferable that the nanoparticles do not overlap (or overlap partially) on the substrate to assure accuracy. Images may be analyzed using algorithms developed over time,5,34,35 which deconvolute information using maximum likelihood methods and Fourier transform decomposition/reconstruction of images. Image analysis is accurate under sparse and sub-confluent conditions. When particles on the substrate overgrow, non-dense assumption breaks down and the number of clusters/particles in the field of view can be under-estimated. To avoid miscalculations, one should limit the analysis to the early time of particle deposition, or in any case to the linear regime of particle growth, which is the case of Fig. 5d and results presented in this work. When Q(t) deviates from linearity, results of the analysis can be inaccurate.
(ii) Our model derives k using direct optical, SEM or AFM inspection of samples. The method does not require sample treatment, preparation or modification, it is not destructive, does not hamper and has no adverse loading effects in the process of growth. The measure of k is carried on the real physical prototype and not on a simplified version of it. The size and shape of the patterns on the silicon exposed to growth are preserved and their effects are correctly incorporated in k, which must not be therefore further adjusted.
(iii) Our model is general in nature. It simulates the assembly of ions or atoms into supramolecular structures and can be used to estimate the ratio between the rates of growth of several materials, including non-metallic materials, provided that the process of deposition is limited by diffusion and the process of chemical reaction at the interface is fast compared to diffusion. Under similar assumptions, a material can be examined using DLA. As a rule of thumb, if a material exhibits a dendritic structure, with some level of order and recursive patterns in the structure – like crystals – it can be analyzed using this model.
In its current form, the model makes the following assumptions and has the following limitations:
(1) In electroless deposition, motion of metal ions in a solution is much slower than the chemical reaction of reduction of those ions into metal on a patterned silicon substrate (DLA assumption).
(2) The diffusion lengths of different metals is the same – assuming that the thermodynamics conditions of growth are held constant, using the Stokes–Einstein relationship10 this is equivalent to state that the sizes of different metals is the same.
(3) The differences between different species are lumped in the sole chemical reaction of deposition, i.e. in p.
(4) It is a comparative method of analysis. This depends on the fact that, in this current form, the model shows a very high sensitivity to the geometry of the system. Since it may be impractical and computationally intractable to reproduce the entire physical system and simulate a real electroless process of growth, we use ratios between variables rather than the absolute values of variables to describe particle growth. In doing so, we can examine exclusively and focus on the parameter of interest, i.e. k, with the remaining conditions held constant. The effects of an inaccurate representation of the systems would cancel each other out when we compare two different metals. This in turn reduces uncertainty and increases the precision of the model. The cost of an augmented precision is the use of the model as a comparative rather than absolute method of analysis.
More sophisticated formulations of the model that will be developed over time may potentially relax the above constraints and be used for a more complete and precise description of metal growth for applications in materials science.
4 Conclusions
We used DLA simulations to develop models that correlate the ratio (γ) between the rates of particle growth of different metals with the ratio (ξ) between the rates of deposition of those metals in the bulk form. The best fit of numerical simulations yields a linear relationship between γ and ξ that reads ξ = 14(γ − 1). Particle growth kinetics is more than a factor of 10 lower than material growth kinetics. We validated the model using electroless deposition of gold and silver nanoparticles on patterned silicon substrates. Different from other existing methods, including CV, LSV or QCM, the method enables determination of the rates of growth (k) from the geometry of clusters of metal nanoparticles and a known reference. SEM or AFM micrographs, routinely taken in a laboratory during sample inspection and analysis, can be used as a source for the model, and the yield and estimation of k even without dedicated equipment.5 Materials and methods
5.1 Simulating metal nanoparticle growth
We used a diffusion limited aggregation (DLA) model to simulate metal nanoparticle growth. In DLA, randomly displaced particles stick together to form the intended structures.4,5,12,14–16 The model assumes that the main mechanism of metal ion transportation in a solution is Brownian diffusion. This assumption implies that the metal reduction and deposition on the silicon surface is instantaneous, which is true when diffusion times are much larger than the time associated with surface chemical reaction on the silicon surface.4,5,18 The assumption also implies that convective flows are vanishingly small everywhere in the domain. Brownian motion is a continuous-time probabilistic process, it can be discretized in a grid where each position of the grid can take 0 or 1 values, 0 (1) indicating the absence (presence) of a particle or ion in that position (Fig. 1a and b).Brownian motion is a mechanism of ion transportation implemented at the atomic level – it describes the process of particle deposition using a discrete sequence of events in time, and guarantees maximum accuracy in reproducing the structure of an aggregate. Fick's laws of diffusion are derived from Brownian motion and molecular diffusion: they represent a generalization of Brownian motion at the continuum limit. Thus, direct numerical simulation using DLA is more appropriate for micro- and nano-scale systems, for which the continuity assumption breaks down, while continuous Fick diffusion is more efficient when one considers macro-scale systems.
In what follows, the word particle is used interchangeably with ion, they both indicate the smallest building blocks that assemble together to form the final aggregates. Ions drift in the domain (grid) due to pure diffusion. Therefore, displacement of ions in the grid obeys a random uniform distribution; at each time of the process particles move from a position of the grid to one of its nearest neighbors, each of those positions being equally probable. We call Δx the size of the cells (pixels) of the grid. It is the size of the smallest features in the grid and corresponds to the resolution of the system. Since the motion of a particle in a grid takes discrete steps, in a macroscopic interpretation Δx is also the mean path length of the particles, i.e. the average distance traveled by a particle between successive collisions. Cases in which the mean path length is different from the resolution of the systems are discussed below. During motion, particles have a fixed velocity v. The mean time interval between collisions is thus 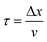 . The nature of Δx, v and τ is determined by the energy of the system and its temperature.10 Consider the scheme in Fig. 1c.
. The nature of Δx, v and τ is determined by the energy of the system and its temperature.10 Consider the scheme in Fig. 1c.
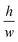 determines the aspect ratio of the well. If the aspect ratio is lower than one, then we have a short geometry. In contrast, tall geometries have aspect ratios greater than one. Short geometry reproduces more accurately the real physical prototype and the experimental set up, where the dimension of lithographed patterns (10 μm) is larger than the thickness of the resist (∼1 μm). Here, we chose w and h as w = 100 pixels, h = 50 pixels, such that
determines the aspect ratio of the well. If the aspect ratio is lower than one, then we have a short geometry. In contrast, tall geometries have aspect ratios greater than one. Short geometry reproduces more accurately the real physical prototype and the experimental set up, where the dimension of lithographed patterns (10 μm) is larger than the thickness of the resist (∼1 μm). Here, we chose w and h as w = 100 pixels, h = 50 pixels, such that 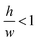 . Dimensions of the entire domain are 400 pixels (length) and 500 pixels (height).
. Dimensions of the entire domain are 400 pixels (length) and 500 pixels (height).
| 〈r2〉 = 〈x2〉 + 〈y2〉 = 4Dt | (7) |
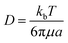 | (8) |
| D = δx2/2τ | (9) |
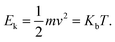 | (10) |
Combining these equations, one obtains:
| δx = 2D/v = f(T) | (11) |
5.2 Deriving the fractal dimension of numerical aggregates
Fractals are irregular, broken geometries for which conventional Euclidean metrics cannot provide a complete description.30 Fractal dimension quantifies the complexity of a fractal as a change of detail to a change of scale. A possible method to calculate the fractal dimension of numerical aggregates is to make use of a density–density correlation function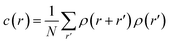 | (12) |
5.3 Electroless deposition of metals on a substrate
In electroless deposition, metal ions in solution are transported and deposited as metals on a substrate. We consider here the case in which the substrate is silicon. Metal reduction on a silicon surface is regulated by the general law:| Men+ + Red = Me0 + Ox | (13) |
| Si + 2H2O → SiO2 + 4H+ + 4e− | (14) |
| Ag+ + e− → Ag0 | (15) |
| Si + 2H2O → SiO2 + 4H+ + 4e− | (16) |
| Au3+ + 3e− → Au0 | (17) |
5.4 Synthesis of metal nanoparticle clusters by electroless deposition
The fabrication of aggregates of metal nanoparticles occurred in two steps: (i) the realization of micropatterns by optical lithography and (ii) the electroless deposition of silver nanoparticles within the patterns. De-ionized (D.I.) water (Milli-Q Direct 3, Millipore) was used for all experiments. Silver nitrate (AgNO3), gold chloride (AuCl3) and hydrofluoric acid (HF) were purchased from Sigma. All chemicals, unless mentioned otherwise, were of analytical grade and were used as received. P-type (100) silicon wafers were used as substrates. Substrates were accurately cleaned with acetone and ethanol to remove possible contaminants and then etched with a 20% in weight HF solution (hydrofluoric acid 50% RPE ACS-ISO, Carlo Erba Reagents) to eliminate the superficial native oxide and create the dangling bonds necessary for metal reduction. Using optical lithography (i) we obtained ordered arrays of holes in the positive resist S1813, with a diameter d = 10 μm and a depth h ∼ 1 μm. We then exposed patterned silicon surfaces to solutions of gold chloride and hydrofluoric acid for depositing gold nanoparticles, and silver nitrate and hydrofluoric acid for depositing silver nanoparticles, for 5, 20, 60 and 120 s. In both cases, the concentration ψ of metal salts in solution was chosen to be ψ(AgNO3) = ψ(AuCl3) = 5 mM, the concentration of hydrofluoric acid was set as ψ(HF) = 150 mM, and the temperature of the system was maintained constant as T = 20 °C throughout the whole duration of the experiments. Resulting nanostructures were imaged using scanning electron microscopy (SEM) and atomic force microscopy (AFM).5.5 SEM sample characterization
SEM images of metal nanoparticle clusters were captured using a Dual Beam (SEM-FIB) – FEI Nova 600 NanoLab system. During the acquisitions beam energies of 5 and 15 keV, and corresponding electron currents of 0.98 pA and 0.14 nA, were used. In some cases the mode 2 configuration was set, through which images could be magnified over 2.5 × 106 times to achieve ultrahigh resolution.5.6 AFM sample characterization
Atomic force microscopy (integrated Raman AFM system, Alpha 300 RA, Witec) was used for sample characterization. All the measurements were performed in a dry environment in intermittent contact mode over a sampling area of 1 × 1 μm2. Room temperature was held fixed for all the acquisitions. Ultra-sharp Si probes with a nominal tip radius less than 5 nm were used for achieving high resolution. Multiple measurements were done in different scan directions to avoid artefacts. At least four images in height mode (trace and retrace) were recorded for each sample. The images had a resolution of 512 × 512 points and were acquired at a scanning rate of 1 Hz. Images were processed using either flattening or plane fit according to the relief characteristics, with the minimal polynomial order needed. The characteristic average surface roughness Sa was thus deconvolved for each substrate. Fast Fourier Transform (FFT) algorithms were used for data processing and fractal extraction of the characteristic dimension of the sample surface.5.7 Deriving the fractal dimension of metal nanoparticles
AFM profiles of metal nanoparticle clusters were processed using the algorithms developed and described in ref. 34. We derived the characteristic power density function for gold and silver nanoparticle clusters at 60 s after immersion in the electroless solution. In a log–log plot, the power spectrum density appears as a line with a slope β. The slope β is related to the Hurst parameters as β = 2(H + 1). The fractal dimension Df of the surface can be equivalently derived as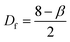 or Df = 3 − H. The fractal dimension Df of a surface ranges from 2 (Euclidean dimension of a flat surface) to 3 (representing an extremely rough surface).
or Df = 3 − H. The fractal dimension Df of a surface ranges from 2 (Euclidean dimension of a flat surface) to 3 (representing an extremely rough surface).
5.8 UV spectrophotometric measurement of metal nanoparticle growth kinetics
We used indirect measurements to determine the growth dynamics of Ag and Au nanoparticles. We put in an aqueous solution nanoporous silicon submicrometric particles with (i) silver (AgNO3) and (ii) gold (AuCl3) salts. The resulting electroless reactions were examined using UV/Vis spectrophotometry.39–42 Metal ions in solution react with the silicon sub-micrometric particles forming metal nanoparticles in the porous matrix. We prepared two samples of HF (0.15 M) plus either (i) AgNO3 1 mM or (ii) AuCl3 1 mM in one ml of DI water. Addition of silicon particles in the solutions caused the start of the electroless reaction of reduction. We added nearly ∼1017 silicon sub-micrometric particles in each milliliter sample. Then, we used a LAMBDA 25 UV/Vis spectrophotometer to determine the growth dynamics of Au and Ag nanoparticles as the variation of absorbance of solutions at different times. Absorbance was measured at wavelengths λ1 = 560 nm for gold and λ2 = 460 nm for silver, which are the values of wavelength for which spectral intensities are maximum in the considered ranges of frequencies. Rate constants of metal nanoparticle growth were determined as the slope of the absorbance versus time diagrams at the initial time of metal deposition. Nanoporous silicon sub-micrometric particles were fabricated through electrochemical porosofication of silicon as described in ref. 22.Conflicts of interest
There are no conflicts to declare.References
- A. R. Tao, S. Habas and P. Yang, Small, 2008, 4, 310–325 CrossRef CAS.
- S. R. Schofield, P. Studer, C. F. Hirjibehedin, N. J. Curson, G. Aeppli and D. R. Bowler, Nat. Commun., 2013, 4, 1649 CrossRef CAS PubMed.
- T. Qiu and P. Chu, Mater. Sci. Eng., R, 2008, 61, 59–77 CrossRef.
- F. Gentile, M. Coluccio, A. Toma, E. Rondanina, M. Leoncini, F. De Angelis, G. Das, C. Dorigoni, P. Candeloro and E. Di Fabrizio, Microelectron. Eng., 2012, 98, 359–362 CrossRef CAS.
- M. L. Coluccio, F. Gentile, M. Francardi, G. Perozziello, N. Malara, P. Candeloro and E. Di Fabrizio, Sensors, 2014, 14, 6056–6083 CrossRef PubMed.
- H. Han, Z. Huang and W. Lee, Nano Today, 2014, 9, 271–304 CrossRef CAS.
- F. Gentile, M. L. Coluccio, R. P. Zaccaria, M. Francardi, G. Cojoc, G. Perozziello, R. Raimondo, P. Candeloroa and E. D. Fabrizio, Nanoscale, 2014, 6, 8208–8225 RSC.
- D. Fine, A. Grattoni, R. Goodall, S. S. Bansal, C. Chiappini, S. Hosali, A. L. van de Ven, S. Srinivasan, X. Liu, B. Godin, L. Brousseau III, I. K. Yazdi, J. F. Moure, E. Tasciotti, H.-J. Wu, Y. Hu, S. Klemm and M. Ferrari, Adv. Healthcare Mater., 2013, 2, 625 CrossRef.
- Y.-W. Fan, F.-Z. Cui, S.-P. Hou, Q.-Y. Xu, L.-N. Chen and I.-S. Lee, J. Neurosci. Methods, 2002, 120, 17–23 CrossRef CAS PubMed.
- M. Saltzmann, Drug Delivery, Oxford University Press, Oxford, 2001 Search PubMed.
- A. Einstein, Ann. Phys., 1905, 17, 549–560 CrossRef CAS.
- Z. Zhang and M. Lagally, Science, 1997, 276, 377–383 CrossRef CAS PubMed.
- D. C. Wyld, J. Zizka and D. Nagamalai, Advances in Computer Science, Engineering and Applications, New Delhi, India, 2012 Search PubMed.
- T. Witten and L. Sander, Phys. Rev. Lett., 1981, 47, 1400–1403 CrossRef CAS.
- T. Witten and L. Sander, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 27, 5686–5697 CrossRef.
- Z. Racz and T. Vicsek, Phys. Rev. Lett., 1983, 51, 2382–2385 CrossRef CAS.
- P. Meakin, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30, 4207–4214 CrossRef.
- F. Gentile, M. L. Coluccio, P. Candeloro, M. Barberio, G. Perozziello, M. Francardi and E. Di Fabrizio, J. Vac. Sci. Technol., B: Nanotechnol. Microelectron.: Mater., Process., Meas., Phenom., 2014, 32, 031804 Search PubMed.
- R. Pastor-Satorras and J. Wagensberg, Physica A, 1996, 224, 463–479 CrossRef CAS.
- G. Marinaro, R. La Rocca, A. Toma, M. Barberio, L. Cancedda, E. Di Fabrizio, P. Decuzzi and F. Gentile, Integr. Biol., 2015, 7, 184–197 RSC.
- H. Foll, M. Christophersen, J. Carstensen and G. Hasse, Mater. Sci. Eng., 2002, 39, 93–141 CrossRef.
- F. De Angelis, A. Pujia, C. Falcone, E. Iaccino, C. Palmieri, C. Liberale, F. Mecarini, P. Candeloro, L. Luberto, A. de Laurentiis, G. Das, G. Scala and E. Di Fabrizio, Nanoscale, 2010, 2, 2230–2236 RSC.
- B. Zheng, L. P. Wong, L. Y. L. Wu and Z. Chen, Int. J. Electrochem., 2016, 2016, 1–11 CrossRef.
- T. Yang and Y. Han, Cryst. Growth Des., 2016, 16, 2850–2859 CrossRef CAS.
- J. G. Velasco, Electroanalysis, 1997, 9, 880–882 CrossRef.
- S. Zhang, H. Bai, J. Pi, P. Yang and J. Cai, Anal. Chem., 2015, 87, 4797–4805 CrossRef CAS PubMed.
- M. E. J. Newman, SIAM Rev., 2003, 45, 167–256 CrossRef.
- I. Mannelli, M. Minunni, S. Tombelli and M. Mascini, Biosens. Bioelectron., 2003, 18, 129–140 CrossRef CAS PubMed.
- S. Glotzer, Nature, 2012, 481, 450–452 CrossRef CAS PubMed.
- F. Gentile, E. Battista, A. Accardo, M. Coluccio, M. Asande, G. Perozziello, G. Das, C. Liberale, F. De Angelis, P. Candeloro, P. Decuzzi and E. Di Fabrizio, Microelectron. Eng., 2011, 88, 2537–2540 CrossRef CAS.
- P. Decuzzi, R. Pasqualini, W. Arap and M. Ferrari, Pharm. Res., 2009, 26, 235–243 CrossRef CAS PubMed.
- A. Carpinteri and N. Pugno, Nat. Mater., 2005, 4, 421–423 CrossRef CAS PubMed.
- V. Amendola, O. M. Bakr and F. Stellacci, Plasmonics, 2010, 5, 85–97 CrossRef CAS.
- F. Gentile, L. Tirinato, E. Battista, F. Causa, C. Liberale, E. Di Fabrizio and P. Decuzzi, Biomaterials, 2010, 31, 7205–7212 CrossRef CAS PubMed.
- F. Gentile, R. Medda, L. Cheng, E. Battista, P. Scopelliti, P. Milani, E. Cavalcanti-Adam and P. Decuzzi, Sci. Rep., 2013, 3, 1461 CrossRef PubMed.
- F. Gentile, M. Monteferrante, L. Chiodo, A. Toma, M. L. Coluccio, G. Ciccotti and E. Di Fabrizio, Molecular Physics, 2014, 112, 1375–1388 CrossRef CAS.
- D. Goia and E. Matijevic, New J. Chem., 1998, 22, 1203–1215 RSC.
- S. Yae, N. Nasu, K. Matsumoto, T. Hagihara, N. Fukumuro and H. Matsuda, Electrochim. Acta, 2007, 53, 35–41 CrossRef CAS.
- S. A. Wadhwani, U. U. Shedbalkar, R. Singh, P. Vashisth, V. Pruthi and B. A. Chopad, Indian J. Microbiol., 2016, 56, 439–444 CrossRef CAS PubMed.
- M. Luty-Blocho, K. Pacławski, W. Jaworski, B. Streszewski and K. Fitzner, Prog. Colloid Polym. Sci., 2011, 138, 39–44 CAS.
- K. Esumi, T. Hosoya, A. Suzuki and K. Torigoe, J. Colloid Interface Sci., 2000, 226, 346–352 CrossRef CAS.
- S. A. AL-Thabaiti, F. M. Al-Nowaiser, A. Y. Obaid, A. O. Al-Youbi and Z. Khan, Colloids Surf., B, 2008, 67, 230–237 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8na00040a |
| This journal is © The Royal Society of Chemistry 2019 |