Hypothesis: entatic versus ecstatic states in metalloproteins

Abstract

Over half a century ago the hypothesis was put forth that redox-active metal ions and multidentate protein ligands may combine to form a local state of entasis: an irregular symmetry intermediate between those dictated by coordination chemistry for the two redox states involved. Such an energetically poised domain would be at the basis of high activity (notably electron-transfer rates) in biological systems. Today the concept of the entatic state has become textbook material. Based on EPR spectroscopic data it is proposed here that poised, entatic states may only be of marginal existence; rather the occurrence of relatively wide distributions of coordination geometries (or: ecstatic states) afford a stochastic tuning of structure towards low-energy unimolecular transition states.

---

Wilfred R. Hagen

Fred Hagen received his PhD in Biochemistry from the University of Amsterdam in 1982. After a post-doc in the Biophysics Research Division of the University of Michigan he returned to the Netherlands in 1984 to the Biochemistry Department of Wageningen University where he built a research group on complex metalloenzymes. In 1995 he became full professor of Physical Chemistry in Nijmegen and in 1998 also of Bioinorganic Chemistry in Wageningen. In 2000 he moved to Delft as professor of Enzymology. In 2017 he became emeritus and since then he can be found full time in the lab building novel EPR spectrometers and applying them to problems in bioinorganic chemistry.

---

Null hypothesis: entatic states in proteins, in particular in electron-transfer metalloproteins

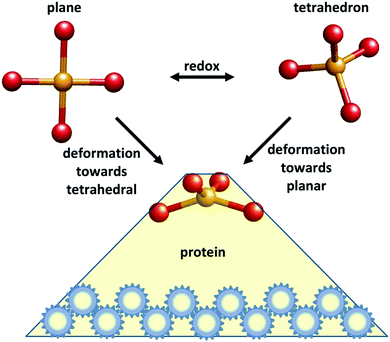
In 1968 F. A. Cotton communicated a seminal paper by B. L. Vallee and R. J. P. Williams to the Proceedings of the National Academy of Sciences of the USA entitled “Metalloenzymes: the entatic nature of their active sites”.¹ The authors proposed that “Enzymatic catalysis… would be facilitated by a state of entasis: the existence in the enzyme of an area with energy, closer to that of a unimolecular transition state than to that of a conventional, stable molecule, thereby constituting an energetically poised domain” (their italicization). The key motive that inspired them to the formulation of this hypothesis was a number of perceived peculiarities in the optical and EPR spectroscopic properties of metalloproteins when compared to synthetic metal complexes, pointing to unusual environments in the former. Fig. 1 gives a schematic representation of what became over time the most well-known instance of an entatic state.

Fig. 1 A schematic representation of a typical case of entasis in a metalloprotein. Depending on its redox state a transition ion has preference for a particular coordination geometry in small model complexes. In this example the metal ion is in a tetrahedron when reduced and in a planar structure when oxidized. Binding of the complex to a macromolecular structure (in this case a protein) creates a strained, or entatic state with a geometry that is intermediate between tetrahedral and planar. The extra energy input required to create this local strain in both redox states is mandatorily more than compensated for by (a distribution of) conformational changes in the rest of the protein here symbolized by the action of a set of cogs. Note the impossibility, under this description, for a coordination complex to be in an entatic state in the absence of a macromolecular ligand.

Clearly the most conspicuous case was the biological “blue copper” centers with their extremely high absorption in the visible spectrum combined with their unprecedentedly small parallel hyperfine splitting from the copper nucleus in the EPR spectrum. A second case brought forward, that of the non-heme iron proteins with their g values without parallel amongst synthetic mononuclear octahedral iron complexes, was later de facto falsified when the structure and exchange coupling of iron–sulfur clusters was established.² The third case in point, the observation of shoulders in the optical spectra of Co(II)-substituted Zn enzymes, which were not observed in simple high-spin Co(II) compounds of regular symmetry, was perhaps the least convincing argument. Indeed, it has never been repeated in the ensuing discussion on entatic states up to this date. Taken together, of the three spectroscopic cases that incited the formulation of the entatic-state hypothesis, only the blue-copper case has stood the test of time.

The original hypothesis speaks of ‘enzyme’, and not of electron-transfer proteins. In the mind of the authors the entatic-state concept was applicable to all active centers including catalytic metal sites, catalytic radical sites, and catalytic sites formed by amino-acids without or with additional non-metal prosthetic groups or cofactors [1]. It is informative to briefly consider the development over time of the application of the entatic-state concept to these different classes of proteins. Vallee and Williams note that “Metalloenzymes would seem exceptionally well suited for the examination of the physicochemical basis of enzymatic properties, for the physical and chemical characteristics of certain metals constitute intrinsic probes of their protein environments.” On the contrary, they decide that, by 1968, with the class of nonmetallo-enzymes “it has not been feasible to examine the possibility that enzymes might be poised for catalytic action in the absence of substrate, i.e., are in an entatic state”.¹ From a view to the literature on entatic states it transpires that the validity of these two statements has not been affected over the last five decades.

Although Williams returns to the possibility of entasis in radical enzymes in a 1976 discussion at a Solvay Conference³ and later in a 1995 review, where he designates the active center of Escherichia coli ribonucleotide reductase as “a very unusual entatic tyrosine radical”,⁴ I know of no studies on enzymes with radical active sites in which the concept of the entatic state has been explored experimentally or computationally. Note that entasis has been a framework to describe the chemistry of radical-forming Co(II)balamin systems but only for the metal site and only for the situation before the homogeneous Co–C bond splitting.⁵ Likewise, entasis in the active site of Fusarium spp. galactose oxidase was ascribed solely to the Cu(II) site and not to the Cu-coordinating tyrosine radical.⁶

The situation is similar for enzymes with active sites made of amino-acid side chains only. Vallee's and Williams above cited original assertion that looking for an entatic state in a protein without a metal had not been feasible, returned in a statement by Williams at a 1971 Cold Spring Harbour Symposium on Quantitative Biology as “It is not clear whether or not similar discussion is suitable in the case of enzymes which do not contain metals”.⁷ However, at the 1976 Solvay meeting Williams proposed that “a peculiar interaction” between a glutamate and a tryptophane in lysozyme, and also “a peptide bond that is distorted into a form close to the transitions state of the trypsin reaction” in trypsin inhibitor, are manifestations of entatic states.³ Subsequenly, in his 1995 review he draws the specific example of an entatic state in a serine protease in the absence of substrate in which the serine –OH group is activated by a set of hydrogen bonds afforded by the overall protein structure.⁴ And this is where the thread appears to be running out. Once more, no studies have appeared on non-metal enzymes in which the concept of the entatic state has been explored experimentally or computationally. Equally, the original invitation to apply the concept to catalytic sites formed by amino-acids with additional non-metal prosthetic groups or cofactors appears to have never been picked up.

And so we are bound to stick to the metalloproteins as putative test systems. However, here a clear-cut distinction has been made from the onset between metalloenzymes and electron-transferring metalloproteins. For the latter the entatic-state discussion is, and indeed always has been, cast in terms of a structural and/or electronic configuration that is somewhere intermediate between respective coordination chemical dictates for the two redox states involved. In other words, the two structures have been ‘deformed’, each in a different way, by strain imposition of the coordinating protein, in order to minimize reorganization energy associated with the redox event. To apply this concept to a description of the workings of a metalloenzyme active site in not trivial. Whether or not the catalysis is a redox reaction, there is always the substrate looming around the corner. Vallee and Williams originally tried to resolve this problem by explicitly excluding the substrate from participation: “The ideas here suggested rest upon the properties of the enzyme itself and are not intended to bear upon the role of substrate; hence, they make no contribution to the manner in which the substrate will subsequently affect its complex with the enzyme or lower the activation energy further”.¹ The implication here is that the combination of metal ion and apo-enzyme results in an active site that is entatically prepared (that is, of unusual geometry) to react with the substrate, however, how this state can be experimentally identified as entatic without the involvement of the substrate remains somewhat of a logical trap. A few years later Williams re-visits the problem by reviewing literature data on the structure of active sites in metalloproteins in the context of entasis. This is the approach he takes: “In each case the ‘curious’ nature of the coordination site (if it exists) will be proved or suggested before a discussion is undertaken as to whether or not this could have catalytic significance”.⁸ The outcome of this test is not encouraging: although the review is entitled “Catalysis by metalloenzymes: the entatic state”, the word entatic does not re-appear anywhere else in the paper.

Nevertheless in the ensuing years a discussion develops in the literature around the question whether the active site of carboxypeptidase A (CPA) is entatic or not. Vallee's group kicks off by interpreting its finding that substitution of the active-site Zn(II) with Co(II) leads to higher activity, as a proof that the protein imposes an entatic state on the metal before substrate activation.⁹ Gray's group replies in the negative based on its finding of regular coordination geometries in active M(II)CPA and they conclude that “very ordinary metal-ion ground states are not easily reconciled with the entatic state concept.¹⁰ In a subsequent paper they add that “The observed variation of coordination number from four to six while full peptidase activity is retained is not easily reconciled with the entatic state hypothesis”.¹¹ Some years later Libscomb's group publishes corrections to the previously reported metal coordinations but in a bottom-line statement they find it ‘unlikely that the differences in peptidase and esterase activities can be explained in terms of the entatic state hypothesis”.¹² With this another thread has run out, although the entatic Co(II) returns in recent times in its low-spin form as part of the adenosylcobalamin cofactor. The latter is present in the enzyme methylmalonyl-coenzyme A mutase in Propionibacterium shermanii for which Evans’ group determined the crystal structure in the presence of substrate analog desulfo-coenzymeA. When they found an ‘unusually long’ bond of ca. 2.5 Å between the axial histidine nitrogen and the cobalt they concluded that “the protein holds the His side chain too far from the corrin, putting the cobalt into a strained or ‘entatic’ state”.¹³ Note that in his early work Williams has repeatedly questioned the validity of protein crystallography for the identification of entatic states because “Studying single crystals… will give data on the structure of greatest stability in the lattice under consideration”,⁸ and also because of the static nature of the data and of a lack of resolution (of the fine details associated with the formation of an entatic state).⁷ There is also the problem of separating the influence of the binding of substrate (or substrate analog) on protein conformation from the entatic state formation by the protein. Indeed, when Evans’ group later determined the structure of the free enzyme¹⁴ and the natural substrate bound enzyme¹⁵ they concluded that substrate binding induces a large conformational change, and the entatic state went offstage. When the joint groups of Oppermann and Yue later determined the structure of the human enzyme they found that substrate binding induces structural rearrangement in the cofactor as well as in the protein.¹⁶ Once more we find no reason to call for entatic states in enzymes.

And so it transpires that in our quest for test systems of the entatic-state hypothesis we appear to be limited to a subclass of the metalloproteins, namely, the non-enzymatic electron-transfer proteins. However, before we address this theme we are incited to make a brief detour into the realm of non-protein coordination compounds. Very recently the entatic cobalamin resurfaced but now as a free cofactor in the absence of protein. The joint groups of Watter and Kräutler reported the biosynthesis of the cobalt-free B₁₂ corrin and concluded from its X-ray structure that “the corrin ligand coordinates cobalt ions in de-symmetrized ‘entatic’ states”.⁵ This assignment actually presents a head-on collision with the original entatic-state hypothesis which mandatorily required the presence of a protein (or a similarly large structure with a flattened energy landscape). The entatic cobalamin is actually a present-day mark of an increasing trend that developed over the last two decades in which ever more non-protein, free coordination compounds were stickered as entatic-state complexes.

Bootstrapping free coordination compounds into entatic states

The entatic-state hypothesis was originally formulated by Vallee and Williams¹ to apply to proteins (enzymes or electron-transfer proteins), and Williams, in all his subsequent work, never explicitly extended applicability to include non-biological model compounds. This does not exclude the possibility that model systems might be entatic, but if we want to include them then we have the obligation to re-formulate the hypothesis and to be clear about what entasis might mean in relatively small molecules. To the best of my knowledge such an explication has yet to be made. Imposition of a local entatic state (a local increase in energy) can be energetically compensated in a macromolecular ligand by virtue of its wide conformational landscape. As this property is restricted in smaller molecules the realm of their putative entatic states is also restricted possibly to the extent of being insignificant. Fig. 2 reproduces two versions of a simple energy scheme for the reaction of an entatic-state complex. At first sight the two representations appear to be essentially identical, however, their interpretations in the accompanying texts are very different.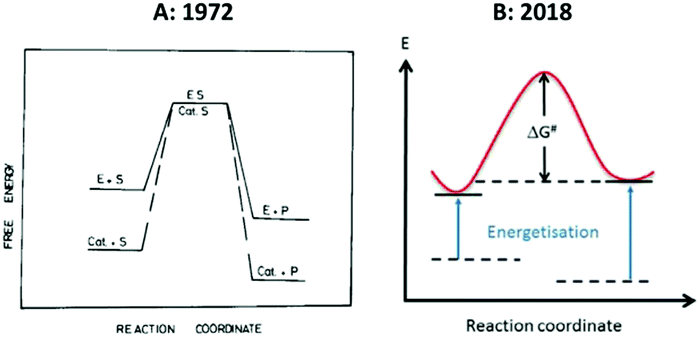

Fig. 2 Simple energy schemes for the reaction of an entatic system. (A) 1971-representation by Williams;⁸ (B) 2018-representation by the group of Herres-Pawlis.¹⁷ See the text for the very different interpretation of these apparently similar figures. Reprinted from ref. 8 and 17 with permission from Elsevier.

The left-hand panel of Fig. 2 is a drawing by Williams that he published twice, originally in Inorganica Chimica Acta Reviews,⁸ and later in his contribution to the 1971 Cold Spring Harbour Symposium⁷ with a different figure legend, in which he seeks to convey the basic idea of an entatic state by juxtaposing it to a figure describing classical lowering of transition-state energy in enzymology. The crucial point is that, in comparing an enzyme with a small molecule homogeneous catalyst, “the raised energy of E resides in a part of an enzyme and is due to its unimolecular activation through the internal energy of the large protein which support it” (my italizations). In other words: “This strain is considered to be due to the conformational demands which gave stability to other parts of the protein, the whole being at a minimum free energy”.⁷ In yet other (my) words: no protein, no significant entatic state. The right-hand panel is from a 2018 paper in Coordination Chemistry Reviews by the group of Herres-Pawlis entitled “Renaissance of the entatic state principle”.¹⁷ The figure is clearly inspired by the early work, but where Williams remarks that “No special significance is attached to the coincidental placing of the transition states”, in 2018 this becomes: “The reactant and product energies as well as the degree of energization are arbitrarily chosen. Now we have a problem: the raising of energies may be ‘arbitrary’, but where do they come from in the absence of a macromolecule with a wide conformational distribution? Just raising them as a deus ex machina for a free coordination compound would be like lifting oneself from a swamp by pulling one's own hair (or in a different part of the world: pulling oneself up by one's bootstraps). Under this ‘definition’ any 3d ion coordinated by anything else than six H₂O ligands would be entatic to some extent. But without quantification of the extent would this not sentence the whole concept of entatis to meaninglessness?

The review builds on a series of earlier reviews by Comba around 2000, also in Coordination Chemistry Reviews, in which the idea of entatic states in simple coordination compounds is conceived.^18–20 In his 2000 review “Coordination compounds in the entatic state” Comba proclaims that “entasis is not confined to metalloproteins; reactions induced by metal-free enzymes or by small coordination compounds may also involve strained, that is entatic states”.¹⁹ In his 2003 review “Fit and misfit in metal ligand interactions” Comba gives a detailed view on entasis²⁰ which is too long to be reproduced here, but which nowhere addresses the question where the energy comes from to create entatic states. This notion of entatic coordination compounds is perhaps retraceable to an earlier paper in which Comba et al. formulate the concept of ‘preorganization’ of macrocyclic ligands.²¹ Originally, Artz and Cram had defined ‘the principle of preorganization’ as “the most highly host and guest are organized for binding and for low solvation prior to their complexation, the more stable will be their complexes”.²² In this context host is a macrocyclic ligand and guest is a metal ion. Comba et al. subsequently venture that “in contrast to the original definition of ligand preorganization, we analyze the extent of preorganization as a continuum involving partially and fully preorganized systems”.²¹ The claimed contrast is not obvious: in the original definition the words “the most highly organized” and “the most stable” equally well define a continuum of preorganization. Be that as it may, the point of key relevance here is that ‘preorganization’ and ‘entasis’ are orthogonal concepts. Quantified preorganization of a ligand may hold information on the subsequent stability, or the lack thereof, of a metal–ligand complex, and it may have some predictive value for the complex as a homogeneous catalyst. But to equate ‘preorganization’ to ‘entatis’ would reduce the meaning of the latter to that of a synonym.

Entatic states ascribed to coordination complexes

Possibly by inspiration from Comba's work, the literature of the ensuing years holds an increasing number of studies in which entasis is ascribed to coordination complexes. [FeFe]hydrogenase have an unusual active site consisting of a [4Fe–4S] cubane Cys-thiol-bridged to a low valent di-iron cluster with CN and CO ligands and a bridging aza-dithiolate ligand.²³ Darensbourg's group synthesizes model compounds that should mimic this active site. In structural dinuclear Fe^IFe^I models^24,25 and Fe^IFe^II models^26,27 they found a rotation of one of the irons and its external ligands. Interestingly, this ‘rotated’ or ‘twisted’ conformation is also found in the crystal structure of the hydrogenase enzyme, from which one would conclude that apparently no entasis is involved since the protein does not change the geometry of the cofactor. Contrarily, the authors posit that the active site in hydrogenase is entatic and from there conclude that the ‘rotated’ model compounds are entatic. And they add that: “Desirable properties as are elusive in thermodynamically stable model compound, the structures of which are dictated solely by first coordination sphere requirements of metal and ligand, require structural forms of higher energy, similar to intermediates or transition states along reaction paths or molecular rearrangement profiles. This is a statement of the entatic-state principle as expressed by Vallee and Williams in 1968”.²⁴ I would rather venture that this is a statement that has no bearing on the entatic-state hypothesis.

Numerous reports have appeared over the last two decades on presumed entatic states in copper coordination compounds.¹⁷ It is beyond our scope to give a comprehensive evaluation of these studies, but we look at a few salient examples of particular relevance to our present discourse. Rorabacher's group claims to have identified “A definitive example of a geometric entatic state effect” when they find that in the combination of Cu(II)/Cu(I) with a particular macrocyclic ligand providing NNSSS ligation the geometries of the two redox states are nearly identical and the electron self-exchange rate is very high and on a par with electron-transferring blue copper proteins.²⁸ Let's try to re-phrase their argument: the entatic-state hypothesis states that proteins may impose a deformed geometry on a metal site so as to bring it closer to the geometry of a unimolecular transition state thereby affording an increase in activity, that is in reaction rate. Therefore, if we find/make a coordination complex with an unusual geometry that is similar in the initial and the final state of a catalytic reaction while the reaction rate is unusually high, then we have identified an entatic-state complex. Why, however, do we need to invoke the concept of a local strain compensated by the conformational redistribution of a macromolecular ligand (i.e. entasis) when we simply optimize a coordination geometry, by synthetic design, in order to optimize a reaction rate? Interestingly, the paper cites earlier work by the group of Stanbury who also made Cu(II)/(I) complexes with similar geometries for the two redox state, but who found very low electron self-exchange rates.^29,30 Should we now conclude that we have identified a definitive example of a geometric anti entatic state effect? The interpretation of Stanbury's group goes into a different direction: “Thus it is clear that the entatic hypothesis is not entirely correct in its implication that the fastest electron-transfer reactions should occur for systems having the least structural change”.²⁹ Two notions are mixed up in this conclusion: for one, electron-transfer rates of coordination complexes are not only determined by structural change but also by several other factors such as solvation. Secondly, and more fundamentally, properties of free coordination compounds simply have no bearing on the testing of the entatic-state hypothesis because they were never included in the hypothesis in the first place.

Entatic electron-transfer proteins and the problem of testability

Let us now focus on the class of proteins that has become the main protagonist in half a century of discussion on entasis and whose members are generally believed to be good candidates to develop entatic states: the electron-transfer metalloproteins. Right from the onset¹ the blue-copper proteins took center stage with their unusual color and magnetism, but several other classes are lined up. In some, e.g., the Fe(III)/Fe(II) containing cytochromes and iron–sulfur proteins entatis may be expected to materialize mainly as a suppression of change in coordination bond lengths, but the Cu(II)/Cu(I) case is clearly one to which the cartoon of Fig. 1 would apply. X-ray structures of blue copper proteins were not known at the time of the formulation of the entatic state hypothesis, so when the structure of poplar plastocyanin became available with ever increasing resolution in the period 1977–1994,^31–36 showing a remarkable invariance of the copper coordination with redox state (Fig. 3) this finding was taken as solid support for the hypothesis by the crystallographers (“Plastocyanin provides a good example of ‘entasis’”)³¹ and by Williams^4,37–39 and the concept found its way into the textbooks of bioinorganic chemistry (e.g., ref. 40–44) although its treatment was in general admittedly somewhat of an anecdotal aside rather than a systematic framework, and indeed some textbook writers decided to ignore the subject altogether.^45,46 Note, however, that the reduced protein was never independently crystallized; structures were determined on reduced crystals of the oxidized plastocyanin.³⁴ Also, the oxidation state of the metal in the oxidized protein was never checked after X-ray data collection, although later EXAFS studies clearly showed reduction of the Cu(II) in the synchrotron beam^47,48 (see also ref. 49).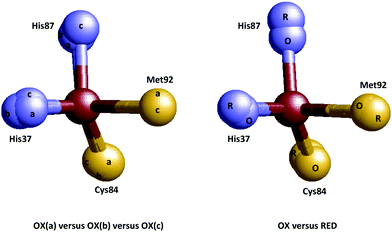

Fig. 3 Coordination invariance in the Cu(II/I) site of poplar plastocyanin. Left: Overlay of the metal sites in three independently determined structures of the oxidized protein (a = 1PNC.pdb, b = 1PND.pdb, c = 1PCL.pdb).^35,36 Right: overlay of the metal sites in oxidized and reduced protein (O = 1PNC.pdb, R = 4PCY.pdb).³⁴

Additional support for entasis was in the finding that the copper ligands in the apoprotein (i.e. no copper) were in similar positions as in the holoprotein.^32,33 In the words of the crystallographers: “In particular, the positions of the copper-binding residues in the apo- and holoproteins differ by only 0.1–0.3 Å. This indicates that the irregular geometry of the “type 1” copper site is imposed upon the metal atom by the polypeptide moiety”.³³ How hard is this conclusion? Let's make a simple overlay of the first coordination sphere of the copper site in the oxidized and the apo-plastocyanin (Fig. 4A).

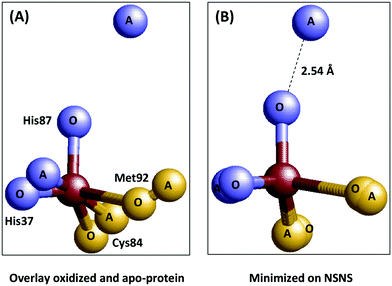Fig. 4 Plastocyanin is only partially pre-arranged to impose geometry on the copper. Left: Overlay of the metal sites in oxidized (1PNC.pdb) and apo-(2PCY.pdb) plastocyanin.^33,36 Right: Same overlay but now minimized with respect to the sum of the mutual distances between the ligand atoms in the two structures.

Even for isomorphous crystals we can of course not expect a perfect match, but the overlay is close especially for the His37 nitrogen, the Cys84 sulfur, and the Met92 sulfur, but not so much for the His87 nitrogen. When we minimize the geometric distances between the ligand atom positions in the two structures for all four ligand atoms (panel B) we find that, in contrast to what the crystallographers claim, one of the ligand atoms in the apoprotein is not within 0.1–0.3 Å from its position in the holoprotein; it is a long 2.5 Å away. In other words the protein may be said to be pre-arranged to accommodate the copper ion with three of its ligands, but a fourth one is not pre-arranged at all. A similar conclusion was reached by Vila and coworkers on basis of NMR⁵⁰ and molecular dynamics simulations.⁵¹ Is this a serious blow to the idea that plastocyanin is entatic? Possibly not, as Williams has always been quite adamant about entatis being the combined result of the action of the protein on the metal and concomitantly of the action of the metal onto the proteins (in particular see ref. 4). And here, apparently, binding of the copper ion induces a move of the His87 nitrogen over a considerable distance. What emerges, however, is a problem of a different order: what criteria can we agree upon to decide whether a system is entatic or not, and how are we going to test systems against these criteria?

In the original proposal of Vallee and Williams we should look for unusual physico-chemical properties such as strong blue color, or small hyperfine interaction, as an indication of ‘unusual’ geometry. But is unusual always equivalent to low, deformed, irregular? And how do we quantify irregularity? Is the amount of correspondence between the geometries in the two (redox) states of the essence? And are we going to measure these with crystallography where we run the risk of fixation on a non-natural frozen-out conformation? Or should we look at NMR structures with their intrinsic uncertainties for paramagnetic systems? Should we look at how well the protein is pre-arranged to accommodate the irregular structure? Or should the accommodation be induced by the metal? And how do we define the structure to be accommodated as a free coordination complex? Should the latter one be (meta)stable or rather instable? Should we consider the electron transfer rate (or the electron self-exchange rate)? And what should that number be compared to? To the same protein with its metal site in a different, less irregular, site, possibly created by mutation, or by a change in the medium? Or should we compare to the activity of a different protein with a similar but less deformed site? Should we be on the lookout for strain, and should that be strain at the metal site, or also strain in the rest of the protein? And how do we experimentally identify strain? Or should we determine strain computationally as the difference between the actual geometry of the metal site in the protein and the calculated optimal vacuum geometry of the isolated site as done by Ryde's group who found only a minor difference and concluded that there is no entasis in blue copper proteins.^52–54 Alternatively, should we compute strain as “the difference between the energy of the ensemble averaged QM/MM active site structure in the gas-phase and the energy of the corresponding optimized active-site gas phase structure” as recently done by Hurd et al. who thus found ‘significant’ strain on the coordination center in both redox states and concluded the numbers to be consistent with the concept of an entatic state.⁵⁵ Or should we follow the spectroscopic approach of Solomon's group and focus on calculating the electronic coupling matrix element in the rate equation?⁵⁶

In summary, after 50 years we have not been able to agree on what entasis is, on what criteria should be tested to its identification or refutation, and on how this testing in the laboratory or in the computer should be carried out. Developing clear and unequivocal definitions of these matters could perhaps initiate a true renaissance of the entatic state. Let's try to make a start.

Distributed states in metalloproteins

In their initial launching of the hypothesis Vallee and Williams described the entatic state of a metal site as a single unique geometry.¹ No suggestion was made that the state might be, in any way, distributed, let alone that this distribution might be differential with respect to beginning and end (redox) states. Things started to turn a few years down the line when Williams discussed ‘organized systems’: “The central chemical factor to be kept in mind is that the metal/ligand bonding is held in a particular geometry which is open to modification by small energy increments and that this is also true of the protein to which it is bound. In other words there may well be a series of structures closely related in energy for many individual proteins”.⁸ A year later he extends this concept of static distribution to a time-dependent one when discussing spin-state equilibria in hemoproteins: “There is a ready flow of energy to and from the more stable and the entatic region of the protein”.⁷ Perhaps the most specific allusion to distributed entatic states can be found in the transcript of a discussion at the 1976 Solvay conference: “Electron transfer reactions at an atom are aided by vibrations that equilibrate the interatomic distances that differ for the two oxidation states. Thus a low-energy, high amplitude vibration is desirable. The vibration could have the further function that it provided a time-dependent fluctuation of the redox potential”.³ Later the comments become more sporadic and less specific: “This strain will fluctuate at each electron transfer step”,⁵⁷ and ultimately they disappear from the discourse.^4,37

The theme of distributed (entatic or otherwise) states does not appear to have been picked up to any significant degree by the bioinorganic chemical community at large with the exception of the theoretical chemists. Early QM/MM calculations by Ryde and collaborators indicated the Cu–S-methionine bond in oxidized and reduced plastocyanin to be changed by the protein by no more than <5 kJ mol⁻¹, and this led them to conclude that “Our results show that the proteins have exploited the floppiness of the Cu–S_Met bond; they have selected a ligand that has a very flat potential surface and they have ensured that it does not cost much energy to change this bond in the protein either”. Their bottom line is “The blue copper site is in a floppy state, rather than in an entatic state”,⁵² (see also ref. 53 and 54), where we can read ‘floppy’ as ‘distributed in time’ (but not necessarily entatically distributed). In a more recent QM/MM study on plastocyanin Hurd et al. calculate much higher strain energies of 12.8–14.5 kcal mol⁻¹ for the complete metal site which they then conclude to be consistent with the concept of an entatic state.⁵⁵ Perhaps more consequential, however, is their finding that “There is considerable variation in the computed instantaneous energy difference between the oxidized and the reduced forms of the protein arising from the thermal fluctuations in the structure at room temperature. This necessitates some averaging over conformation in determining the reorganization energy, and means that the view of the protein constraining the active site in a structure that is optimal for electron transfer does not provide the complete picture of the electron transfer process”.⁵⁵ Once more we see the emergence of a distribution in time, this time of an entatic nature. But here we get stuck with the fact that ‘some averaging’ appears to be a bridge too far: “This illustrates the challenge of modeling the electron transfer in these systems with a QM/MM framework. Treating a very large region of the protein surrounding the active site at the QM level is desirable for a reliable estimate of the reorganization energy. However, these calculations are very computationally demanding and are not practical for the study of many conformations or the use in molecular dynamics simulations”.⁵⁵ And so the distributed state seems to fall into the same trap as the entatic state: an untestable concept has minimal value in experimental science. Let us, therefore, try to formulate the concept a little bit more clearly, and then go and look for possible, and practical tests for its existence.

Ecstatic states in metalloproteins

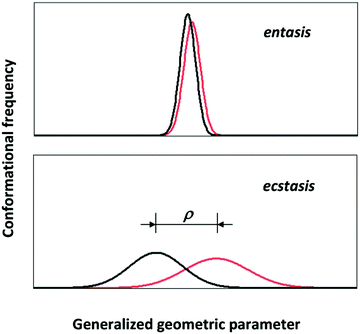
Consider the following simple model of a distributed metal site: the 3D coordinates of each first-coordination sphere atom are distributed with respect to the metal ion which is fixed in space. In order to create a human-comprehensible picture we make the further, non-fundamental simplification to assume that only a single atom is subject to a significant distribution and only so in a single dimension. The approach is not completely unrealistic; it would be an approximate description of the ‘entatic’ state of ferromyoglobin which is mainly determined by the length of the bond between the axial histidine nitrogen and the ferrous ion.⁸ With some reductive imagination we could even take the presumed entatic state of the copper site in plastcyanin as being dominated by the bond length between the methionine sulfur and the copper ion.⁵² This dumbing-down of the distribution will allow us its envisioning in a plot of density of states versus a single molecular geometric parameter, that is a single bond length. For the sake of the argument let us further assume that the distribution happens to be normal, that is one fully defined by its mean and standard deviation. Then the geometric distributions of the initial and the final state (e.g., high-spin and low-spin Fe(II) in myglobin; Cu(I) and Cu(II) in plastocyanin) will look like the plots in Fig. 5.

Fig. 5 One-dimensional conformational distribution of an entatic versus ecstatic site in a metalloprotein. The initial (black) and final (red) states of an entatic system have a small standard deviation and small difference in mean values; the corresponding states in an ecstatic system have large standard deviations and a large difference, ρ, in mean values.

In line with the indications from theoretical chemists cited above, the import of Fig. 5 is that it may not be meaningful to consider the rigorous, strained, unique geometry of an entatic state without also taking into consideration the distributed nature of that geometry. Let's call the latter the ‘ecstatic’ (from the Greek “ekstatikos”, ἐκστατικóς, meaning unstable, inclined to depart from) character of the state, which is obviously related in a linear manner to the standard deviation of the distribution. The entatic character, on the other hand, is rather inversely related to the distribution width. It is also inversely related to the difference, ρ, in mean value for the initial and the final state. So in pseudo-mathematics, when σ_i and σ_f are the standard deviations of the distributions for the initial and final state and ρ is the difference between their mean:

entasis ∝ ρ⁻¹σ_i⁻¹σ_j⁻¹

ecstasis ∝ σ_iσ_j

and so the two characteristics are each other's inverse

ecstasis × entasis ∝ ρ⁻¹

In other words, a metal site that is not particularly entatic can compensate by being ecstatic, that is having available many conformations to the extent that there is always significant overlap between the geometries of the initial and the final state, and the reorganization energy of the transition is small.

A key advantage of this rudimentary description is that it points us to an experimental way, not to verify, but to falsify the occurrence of entasis: identifying wide distributions that eliminate the need for an entatic state. But how do we measure distributions and how do we determine their breadth? Pdb files of protein structure contain information about displacement of atoms from their mean positions in the form of the temperature factor (or: displacement factor) and – if available – in the ANISOU records as the elements of the mean square displacement tensor. For example, the temperature factors of the ligand atoms in apo-plastocyanin (2PCY.pdb) are, on average, 2.6 times greater than the corresponding factors for oxidized plastocyanin (1PCL.pdb), which once more attests to the notion that the apoprotein is not really very much pre-arranged at all to strain the metal ion. Mutual comparison between different proteins, with the aim to discover trends in distribution widths rather than absolute values, is unfortunately less straightforward because the temperature factor is the result of structure refinement procedures, which are model dependent. Temperature factors also encompass differences between molecules in the unit cell. More fundamentally, crystallization is likely to force a protein into a distribution with mean and width whose values differ significantly from those in random aqueous solution. The alternative structure-determination method of high-resolution NMR produces bundles of slightly different structures (also known as ‘uncertainty ensembles’) based on uncertainties in distance constraints from which a root-mean-square-displacement parameter can be deduced. The latter, unfortunately, is a global parameter, and also depends strongly on the quality of the experimental data. Its value (typically 1–3 Å) is usually much greater than what we would expect for a local bond variation. More sophisticated approaches to deal with conformational distributions, with emphasis on paramagnetic proteins, are under development^58,59 and may eventually provide practical tools to address our present theme.

EPR spectra of frozen solutions of metalloproteins have long been known to exhibit ‘inhomogeneous broadening’ of the resonance line reflecting a normal distribution in g values about a mean. The phenomenon is generally known under the name of “g-strain”,^2,60 and it has been proposed to be directly related to a geometric distribution of the metal site in turn connected to a – frozen in – conformational distribution of the surrounding protein.⁶¹ Let us, therefore, explore to what extent a study of g-strain can provide us with criteria, qualitative or quantitative, to probe the balance between ecstasis and entasis in metalloproteins.

g-strain as a measure for ecstasis

Fig. 6A shows EPR data from plastocyanin taken at two microwave frequencies that differ by an order of magnitude, namely 34.4. GHz (Q-band) and 3.29 GHz (S-band). The S-band spectrum is dominated by hyperfine interaction from the copper nucleus (I = 3/2). Super-hyperfine splitting from the N_δ's of the two histidine ligands is not resolved. This is consistent with a reported isotropic splitting of 22 MHz (ca. 8 gauss) for both histidines from ENDOR spectroscopy⁶³ where the linewidth (fwhh) in the S-band spectrum is ca. 20–30 gauss. The copper parallel hyperfine splitting, A_‖, is ca. 60 gauss. In Q-band this splitting is unresolved since the linewidth in the parallel direction is here ca. 90 gauss. Taken together this means that in the parallel direction broadening of the resonance line should be completely determined by g-strain at both frequencies. That this is indeed the case can be seen from the normalized plot in Fig. 6 in which the first hyperfine line in S-band and the parallel line in Q-band have been plotted on a g-value scale. The two lines overlap and, furthermore, they are approximately Gaussian. This implies that they can be taken to represent a normal distribution in g-values corresponding to a distribution in conformations at the copper site. The mean g_z value is 2.247. Going out one or two standard deviations affords shifts in the g_z values of ca. 0.008 and 0.015, respectively. Sinnecker and Neese have attempted to reproduce the experimental g values of plastocyanin in QM/MM calculations.⁶⁴ They used three levels of approximation which they called ‘gas’, ‘continuum’, and ‘protein’, which stands for neglecting the protein surrounding, including it as an unstructured, polarizable continuum, or treated by including the net charges of all MM atoms in the single point calculations. For g_z the difference between ‘continuum’ and ‘protein’ corresponded to a shift of 0.006–0.007; the difference between ‘gas’ and ‘protein’ made a shift of 0.011–0.012. Although the experimental g-strain distribution may not leave room for a change of the distorted tetrahedral coordination into something completely different, it does indicate that a significant fraction of the molecules differ from the mean by an amount that would correspond to replacing the surrounding protein structure by a ‘continuum’, or even by ignoring the protein altogether. It seems only fair to conclude that the copper site in plastocyanin has significant ecstatic character, which, by definition, goes at the expense of its entatic character.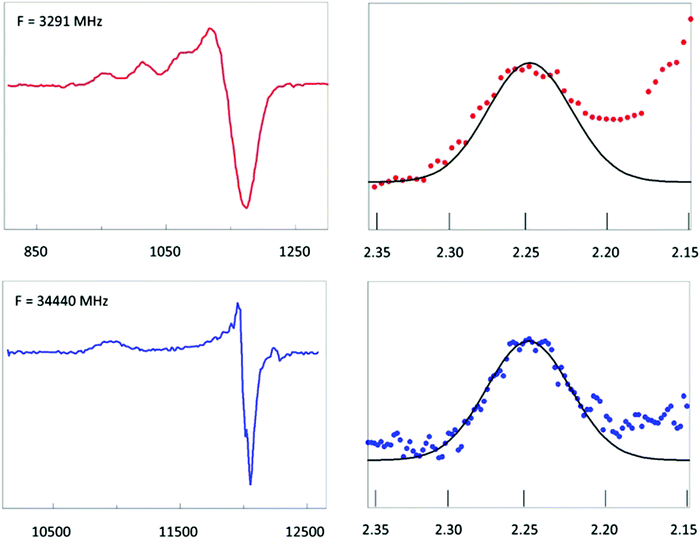

Fig. 6 EPR of spinach plastocyanin at two microwave frequencies. Red traces are S-band spectra at 3291 MHz; blue traces are Q-band spectra at 34 440 MHz. The first hyperfine peak in S-band has been shifted over the hyperfine splitting, 1.5 A_z to be centralized at g_z and then plotted on the same g-value scale as the complete g_z peak of the Q-band spectrum. Their shape identity shows that inhomogeneous broadening is fully determined by a Gaussian g-strain distribution. Its extent suggests the metal site to be in an ecstatic state. Data taken from ref. 62.

How is the ecstatic-entatic balance influenced by the magnitude of the macromolecular ligand? We expect larger proteins to have increased capacity to compensate the extra energy required for local entatic strain by accommodation of backbone structure distribution. We should look for EPR data of simple S = 1/2 systems dominated by g strain. Low-spin heme proteins are a case in point as they typically have constant linewidths (in g-value units) over a wide frequency range.⁶¹ In Table 1 some literature data are collected for azido and hydroxo derivatives of heme proteins of different size.

Table 1 EPR linewidth^a,b of g_z-peak from low-spin hemoproteins

Protein	Subunit (kDa)	(6th ligand on heme)
		Azide^a	Hydroxy^a
a Full width at half height in g-value units. b All data taken from ref. 65. c Ref. 66. d Ref. 67.
Horse microperoxidase-11	1.77	—	0.329^d
Horse cytochrome c	12.4	0.132	—
Horse hemoglobin	16.1	0.113	0.065
Sperm whale myoglobin	17.2	0.109	0.069
Bovine cytochrome aa3 (COX-1)	58.4	0.067^c	0.037

---

There is a clear trend for the linewidth to decrease with increasing protein size. Comparison of the hemoglobin versus myoglobin data indicates that the mass of the subunit, rather than the mass of the multimeric protein, determines the extent of g strain. The EPR data corroborate our expectation that ecstatic character decreases and entatic character increases with increasing size of the macromolecular ligand. In yet other words, metal sites in small electron transfer proteins appear to be less entatic, and more ecstatic than metal sites in larger enzymes. Possibly an extreme case of ecstasis may be found in the copper amyloid beta peptide complex (truncated to 16 residues) for which it has been proposed that electron transfer occurs via a rare (circa 0.1%) conformation of both the oxidized and the reduced state.^68,69

New hypothesis: entatic–ecstatic product states in metalloproteins

Time for a change. Blue copper proteins have always been the paradigm of the entatic state, however, plastocyanin is not very entatic at all. The apoprotein is not set to strain the metal, and the metal site itself is rather more distributed, or ecstatic, or, in Ryde's words⁵² in a floppy state, than strained. And half a century of tossing the idea of entasis around does not seem to have given bioinorganic chemistry its longed for unifying concept. It certainly hasn’t provided an easily measurable and testable criterion for the existence of states strained to higher biological activity. In the meantime evidence has been building up that the distributed nature of the active site, which was an early concept in Willams’ discourse, but which he later abandoned for unknown reasons, may actually be a fundamental and all-important intrinsic property of entasis if only as its inverse manifestation. And while theoretical chemists and protein NMR spectroscopists are anticipating a necessary quantum leap in availability of CPU time to deal with distributions in a realistic manner, a few basic observations in metalloprotein EPR spectroscopy may have given the first intimation that this inverse entasis may actually be straightforwardly detectable in experiments. So now would seem to be the right time indeed to formulate new working hypotheses on entasis. Here is one:

To boost the biocatalytic activity of a metal center (and perhaps even of any activity center) nature builds it into a protein to, in addition to the creation of binding specificity, harmonize geometric and electronic properties of its initial and final catalytic states. This can be achieved either by creating broad, low amplitude distributions of site conformation (ecstatic states), characterized by flexibility, with sufficient overlap for the two states, or, inversely, by creating sharp, high amplitude distributions (entatic states), characterized by strain, with near coincidence of mean values. In practice any implementation will be somewhere in between, that is it will encompass a combination of geometric/electronic distribution and strain. In other words, ecstasis and entasis are inseparable sites of the same coin. In all cases the protein is a mandatory scaffold since any energy increase inherent in the creation of the local entatic–ecstatic state is compensated for in a global re-distribution of backbone conformations. This vibrational re-distribution potential is greater in proteins of greater mass. In the absence of a protein the potential is null.

And for those who prefer a practical rule of thumb (but still a working hypothesis):

(i) Model compounds in the absence of a protein ligand are presumably neither entatic nor ecstatic to any significant extent; (ii) electron-transferring proteins are only mildly entatic, but they are quite floppy/ecstatic. This is a favorable property for fast electron transfer; (iii) larger enzymes can have sites of notable entatic character, and they are less floppy/ecstatic. This is a favorable property for catalysis.

It is my hope and expectation that it will take less than the next half century to subject this working hypothesis to quantitative experimental and computational scrutiny.

Conflicts of interest

There are no conflicts of interest to declare.

References

1. B. L. Vallee and R. J. P. Williams, Proc. Natl. Acad. Sci. U. S. A., 1968, 59, 498–505.
2. J. Fritz, R. Anderson, J. Fee, G. Palmer, R. H. Sands, J. C. M. Tsibris, I. C. Gunsalus, W. H. Orme-Johnson and H. Beinert, Biochim. Biophys. Acta, 1971, 253, 110–133.
3. R. Lefever and A. Goldberg (ed.), Molecular movement and chemical reactivity as conditioned by membranes, enzymes and other. XVth Solvay Conference on Chemistry, Brussels, Nov 22-26, 1976. Advances in Chemical Physics Vol. XXXIX. John Wiley & Sons, New York, 1978. General discussion pp 338-340.
4. R. J. P. Williams, Eur. J. Biochem., 1995, 234, 363–381.
5. C. Kienigner, E. Deery, A. D. Lawrence, M. Podewitz, K. Wurst, E. Nemeto-Smith, F. J. Widner, J. A. Baker, S. Jockusch, C. R. Kreutz, K. R. Liedl, K. Gruber, M. J. Warren and B. Kräutler, Angew. Chem., 2019 DOI:10.1002/ange.201904713.
6. R. M. Wachter and B. P. Branchaud, Biochim. Biophys. Acta, 1998, 1384, 43–54.
7. R. J. P. Williams, The entatic state. Cold Spring Harbour Symposia in Quantitative Biology 1972, 36, 53-62.
8. R. J. P. Williams, Inorg. Chim. Acta, Rev., 1971, 5, 137–155.
9. W. D. Behnke and B. L. Vallee, Proc. Natl. Acad. Sci. U. S. A., 1972, 69, 2442–2445.
10. R. C. Rosenberg, C. A. Root, R.-H. Wang, M. Cerdonio and H. B. Gray, Proc. Natl. Acad. Sci. U. S. A., 1973, 70, 161–163.
11. R. C. Rosenberg, C. A. Root and H. B. Gray, J. Am. Chem. Soc., 1975, 97, 21–26.
12. K. D. Hardman and W. N. Lipscomb, J. Am. Chem. Soc., 1984, 106, 463–464.
13. F. Mancia, N. H. Keep, A. Nakagawa, P. F. Leadlay, S. McSweeney, B. Rasmussen, P. Bösecke, O. Diat and P. R. Evans, Structure, 1996, 4, 339–350.
14. F. Mancia and P. R. Evans, Structure, 1998, 6, 711–720.
15. F. Mancia, G. A. Smith and P. R. Evans, Biochemistry, 1999, 38, 7999–8005.
16. D. S. Froese, G. Kochan, J. R. C. Muniz, X. Wu, C. Gileadi, E. Ugochukwu, E. Krysztofinska, R. A. Gravel, U. Oppermann and W. W. Yue, J. Biol. Chem., 2010, 285, 38204–38213.
17. J. Stanek, A. Hoffmann and S. Herres-Pawlis, Coord. Chem. Rev., 2018, 365, 103–121.
18. P. Comba, Coord. Chem. Rev., 1999, 182, 343–371.
19. P. Comba, Coord. Chem. Rev., 2000, 200–202, 217–245.
20. P. Comba and W. Schliek, Coord. Chem. Rev., 2003, 238–239, 21–29.
21. P. Comba, A. Fath, A. Kühner and B. Nuber, J. Chem. Soc., Dalton Trans., 1997, 1889–1898.
22. S. P. Artz and D. J. Cram, J. Am. Chem. Soc., 1984, 106, 2160–2171.
23. A. Silakov, B. Wenk, E. Reijerse and W. Lubitz, Phys. Chem. Chem. Phys., 2009, 11, 6592–6599.
24. M. Y. Darensbourg, E. J. Lyon, X. Zhao and I. P. Georgakaki, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 3683–3688.
25. I. P. Georgakaki, L. M. Thomson, E. J. Lyon, M. B. Hall and M. Y. Darensboug, Coord. Chem. Rev., 2003, 238–239, 255–266.
26. T. Liu and M. Y. Darensbourg, J. Am. Chem. Soc., 2007, 129, 7008–7009.
27. C. M. Thomas, M. Y. Darensbourg and M. B. Hall, J. Inorg. Biochem., 2007, 101, 1752–1757.
28. G. Chaka, J. L. Sonnenberg, H. B. Schlegel, M. J. Heeg, G. Jaeger, T. J. Nelson, L. A. Ochrymowycz and D. B. Rorabacher, J. Am. Chem. Soc., 2007, 129, 5217–5227.
29. B. Xie, T. Elder, L. J. Wilson and D. M. Stanbury, Inorg. Chem., 1999, 38, 12–19.
30. B. Xie, L. J. Wilson and D. M. Stanbury, Inorg. Chem., 2001, 40, 3606–3614.
31. P. M. Colman, H. C. Freeman, J. M. Guss, M. Murata, V. A. Norris, J. A. M. Ramshaw and M. P. Ventakappa, Nature, 1978, 272, 319–324.
32. J. M. Guss and H. C. Freeman, J. Mol. Biol., 1983, 169, 521–563.
33. T. P. J. Garrett, D. J. Clingeleffer, J. M. Guss, S. J. Rogers and H. C. Freeman, J. Biol. Chem., 1984, 259, 2822–2825.
34. J. M. Guss, P. R. Harrowell, M. Murata, V. A. Norris and H. C. Freeman, J. Mol. Biol., 1986, 192, 361–387.
35. J. M. Guss, H. D. Bartunik and H. C. Freeman, Acta Crystallogr., Sect. B: Struct. Sci., 1992, B48, 790–811.
36. B. A. Fields, H. H. Bartsch, H. D. Bartunik, F. Cordes, J. M. Guss and H. C. Freeman, Acta Crystallogr., Sect. D: Biol. Crystallogr., 1994, D50, 709–730.
37. R. J. P. Williams, Chem. Commun., 2003, 1109–1113.
38. H. A. O. Hill and P. J. Sadler, J. Biol. Inorg. Chem., 2016, 21, 5–12.
39. H. A. O. Hill and A. J. Thomson, Biogr. Mem. Fellows R. Soc., 2016, 62, 541–570.
40. R. J. P. Williams and J. J. R. Fraústo da Silva, The natural selection of the chemical elements, Oxford University Press, Oxford, UK, 1997.
41. J. J. R. Fraústo da Silva and R. J. P. Williams, The biological chemistry of the elements; the inorganic chemistry of life, Oxford University Press, Oxford, UK, 2nd edn, 2001.
42. W. Kaim, B. Schwederski and A. Klein, Bioinorganic chemistry: inorganic elements in the chemistry of life, Wiley, Chichester, UK, 2nd edn, 2013.
43. S. J. Lippard and J. M. Berg, Principles of bioinorganic chemistry, University Science Books, Mill Valley, CA, 1994.
44. R. R. Crichton, Biological inorganic chemistry; a new introduction to molecular structure and function, Academic Press, Elsevier, London, UK, 3rd edn, 2018.
45. R. M. Roat-Malone, Bioinorganic Chemistry; A short course, John Wiley & Sons, Hoboken, NJ, 2nd edn, 2007.
46. D. Rehder, Bioinorganic chemistry, Oxford University Press, Oxford, UK, 2014.
47. J. E. Penner-Hahn, M. Murata, K. O. Hodgson and H. C. Freeman, Inorg. Chem., 1989, 28, 1826–1832.
48. L. M. Murphy, B. R. Dobson, M. Neu, C. A. Ramsdale, R. W. Strange and S. S. Hasnain, J. Synchrotron Radiat., 1995, 2, 64–69.
49. H. Taberman, Crystals, 2018, 8, 8040157.
50. M.-E. Zaballa, L. A. Abriata, A. Donaire and A. J. Vila, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 9254–9259.
51. L. A. Abriata, A. J. Vila and M. Dal Peraro, J. Biol. Inorg. Chem., 2014, 19, 565–575.
52. J. O. A. De Kerpel and U. Ryde, Proteins: Struct., Funct., Genet., 1999, 36, 157–174.
53. U. Ryde, M. H. M. Olsson, B. O. Roos, J. O. A. De Kerpel and K. Pierloot, J. Biol. Inorg. Chem., 2000, 5, 565–574.
54. U. Ryde, M. H. M. Olsson, B. O. Roos and A. C. Borin, Theor. Chem. Acc., 2001, 105, 452–462.
55. C. A. Hurd, N. A. Besley and D. Robinson, J. Comput. Chem., 2017, 38, 1432–1437.
56. E. I. Solomon, R. G. Hadt and B. E. R. Snyder, Isr. J. Chem., 2016, 56, 649–659.
57. R. J. P. Williams, FEBS Lett., 1987, 226, 1–7.
58. W. Andrałojć and E. Ravera, in New developments in NMR No 16: Paramagnetism in experimental biomolecular NMR, ed. C. Luchinat, G. Parigi and E. Ravera, Roy Soc Chem, 2018, ch. 4.
59. L. Gili, W. Andrałojć, A. Dalaloyan, G. Parigi, E. Ravera, D. Goldfarb and C. Luchinat, Phys. Chem. Chem. Phys., 2018, 20, 27429–27438.
60. W. R. Hagen, H. O. Hearshen, R. H. Sands and W. R. Dunham, J. Magn. Reson., 1985, 61, 220–232.
61. W. R. Hagen, in Applications in biology and biochemistry. ed. Hoff A. J., Elsevier, Amsterdam, The Netherlands, 1989.
62. W. R. Hagen, Electron paramagnetic resonance of metalloproteins with emphasis on components of the respiratory chain, PhD thesis, University of Amsterdam, 1982.
63. M. M. Werst, C. E. Davoust and B. Hoffman, J. Am. Chem. Soc., 1991, 113, 1533–1538.
64. S. Sinnecker and F. Neese, J. Comput. Chem., 2006, 27, 1463–1475.
65. W. R. Hagen, J. Magn. Reson., 1981, 44, 447–469.
66. R. Wever, J. H. Van Drooge, A. O. Muijsers, E. P. Bakker and B. F. Van Gelder, Eur. J. Biochem., 1977, 73, 149–154.
67. H. M. Marques and C. B. Perry, J. Inorg. Biochem., 1999, 75, 281–291.
68. V. Balland, C. Hureau and J. M. Savéant, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 17133–17138.
69. C. Cheignon, M. Jones, E. Atrián-Blasco, I. Kieffer, P. Faller, F. Collin and C. Hureau, Chem. Sci., 2017, 8, 5107–5118.

---