DOI:
10.1039/C8MT00286J
(Paper)
Metallomics, 2019,
11, 1049-1059
Dynamic homeostasis modeling of Zn isotope ratios in the human body†
Received
8th October 2018
, Accepted 20th February 2019
First published on 5th March 2019
Abstract
Recent research performed on volunteers and patients suggested that diet, health, and basal metabolic rates (BMR) are factors controlling the bodily Zn isotope compositions (isotopic homeostasis). However, our poor understanding of the variability of Zn distribution among the different organs and fluids of the human body, and the ensuing isotope fractionation, limits the use of this isotopic system as a typical diagnostic tool for cancers and for past hominin diet reconstructions. Using box model calculations, we investigated the dynamics of Zn isotope variability in blood and other body tissues as well as the consistency of the hypothesis of heavy Zn isotope accumulation through time in the human body. We compare the results of the model with data obtained from control feeding experiments and from archeological samples. Model simulations indicate that the absence of an aging drift in non-circumpolar populations cannot be explained by their lower BMR. We argue that the drift observed in the blood of a circumpolar population results from a differential diet between young and older individuals in this population. When applied to the δ66Zn measured in blood, bones, or teeth, the present box model also offers insight into the isotope composition of the human diet, and therefore into its nature. Applying the model to isotopic observations on the remains of past hominins is a promising tool for diet reconstruction.
Significance to metallomics
The present box model is the first of its kind to assess the evolution of Zn isotope ratios in the human body. It determines the response of the different Zn body reservoirs to a change of diet or metabolism and highlights the complex response of reservoirs with short Zn residence times (e.g. red blood cells) to such a perturbation. The model can also be adapted for other elements such as Ca, Mg or Cu whose isotope ratios are also investigated as new paleodietary or cancer diagnostic tools.
|
The study of Zn isotope composition in body tissues is rapidly expanding and its fate is connected to the recent development of TIMS and MC-ICPMS techniques.1,2 Initial efforts by Stenberg et al. (2002) to document these Zn isotope signatures focused on mammal organs with further primary research focusing on humans by Helal et al. (2002), Stenberg et al. (2005), and Ohno et al. (2005).3–6 However, it was not until 2011 that studies of human blood, bones and teeth7–15 were conducted with large sample sizes. So far, these studies have constituted the bulk of the Zn isotope data available for human tissues. Despite their limited number, they already highlight the great potential of Zn isotope variations to detect breast cancers based on blood values and to reconstruct past hominin diets using dental enamel data.10,11 Nevertheless, Zn homeostasis and its bearing on the mechanisms of Zn isotope fractionation in the human body remain poorly investigated. This considerably limits the comprehension and interpretation of the variability of Zn isotope ratios in human tissues and their application to the fossil remains of past hominins.
Zinc isotope fractionation in the human body: state of the art
Zinc has five stable isotopes: 64Zn (48.27%), 66Zn (27.90%), 68Zn (18.80%), 67Zn (4.10%), and 70Zn (0.63%). It has a single oxidation state (2+) and 99% of the zinc is intracellular. It has multiple ligands with more than 300 associated enzymes.12 Zn isotope fractionation is controlled by the coordination of Zn with the different ligands in the body tissues. This fractionation has already been estimated through ab initio calculations,13,14 but those calculations did not explore fractionation by the ligands present in food products and bodily tissues. It has been hypothesized that, due to preferential precipitation of light Zn isotopes with phytates in the intestinal tract,20,21 plant-eaters exhibit higher δ66Zn in their body tissues than meat-eaters. Preferential absorption of heavy Zn isotopes during intestinal absorption was observed in three controlled feeding experiments on mice and sheep.18,22,23 If kinetics does not allow us to quantitatively predict the extent of Zn isotope fractionation, equilibrium fractionation factors nevertheless provide strong constraints on the nature of interacting Zn compounds, both dissolved and structural, throughout the body and on the direction of isotopic changes. For instance, when Zn is bound to the phosphate groups of phytates, those groups preferentially bond with heavy isotopes.19 Since it seems that Zn heavy isotopes are preferentially absorbed, it looks like Zn light isotopes preferentially precipitate with the phytates. In the intestinal tract, isotopic fractionation is therefore rather due to kinetic than to equilibrium mechanisms.
An important question is whether abundances of Zn isotopes change through life in the body and its organs. It has been suggested that 66Zn is preferentially absorbed and retained in the body relative to 64Zn throughout the lifetime of sheep.22 These predictions are supported by the observation that the isotopic composition of sheep feces, which accounts for most of the daily Zn excretion, is enriched in light Zn isotopes relative to diet.22,23 Similarly, a positive correlation was found between the age of Yakut individuals, who live in a circumpolar region, and whole blood δ66Zn.14 Such a trend, however, was not observed in whole blood samples from a Belgian population,10 which we confirmed with new red blood cell (RBC) data on a French population sample (Fig. 1 and Table S1 in the ESI†). We also observed that the blood δ66Zn values of the Yakut are higher than their European and Japanese counterparts.14 This was attributed to the higher basal metabolic rate of the Yakut population due to cold stress adaptation. However, in light of the recent evidence suggesting a relationship between bodily δ66Zn values and diet,11,12,20,21,24 we cannot exclude that the Zn isotope peculiarity of the Yakut blood is also explained by specific dietary habits. Yakuts are indeed incorporating more and more market food into their daily meals, which homogenize their diet with the other populations studied so far.25,26 The youngest generations are particularly likely to adopt the new dietary habits.
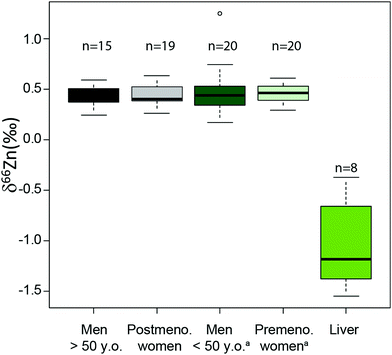 |
| | Fig. 1 Zn isotope variations of RBC per sex in a French population and in liver samples reported as δ66Zn = [(66Zn/64Zn)sample/(66Zn/64Zn)standard − 1] with the standard being the Lyon Zn isotope standard JMC 3-0749 L. The boxes represent the 25th–75th percentiles (with the median as a bold vertical line), while the whiskers show the 10th–90th percentiles. RBC and liver isotope data are all from the present study except for the δ66Zn values, labelled with the superscript (a), on young individuals, which are from Albarède et al. (2011).15 | |
The motivation of the present work is to assess the causes of Zn isotope variability in the human body using a box (compartment or reservoir) model of Zn isotope homeostasis. Over the past few decades, multiple kinetic models have been developed from nutritional studies using Zn isotope supplementation. These studies established the Zn fluxes among pools in the human body and, along with δ66Zn data on mammalian organs, enabled dynamic numerical models of Zn isotope variability in each bodily reservoir to be developed. The present work returns to these models using an improved dynamic description of the fluxes and natural isotopic variability. We will discuss the influence of diet on Zn isotope ratios of blood, bones, and teeth by comparing the results of this model with actual isotope ratios measured in human and animal tissues. Due to the growing interest in Zn isotopes in archeological sciences9,16,20 for dietary reconstruction, we will present and discuss the relationship between the isotope ratios of food products and those of body mineral tissues (bones and teeth).
Methods
1. A model design for Zn homeostasis
Literature kinetic models were dedicated to the evaluation of Zn mass in each organ and body fluid, particularly those exchanging rapidly with the plasma, and to their turnover times.27–33 Most of the Zn is passively held in muscles and bones. In blood, it is located in red blood cells, where it is bound to carbonic anhydrase34 and superoxide dismutase. The brain, muscles, and bones have characteristically slow Zn turnover times27,29 and it is very difficult to quantify the exchange of Zn between these reservoirs and the plasma. Wastney et al.29 have quantitatively estimated the Zn turnover time in muscles. We used these authors’ estimates for Zn fluxes in the human body. We excluded the brain from our model on the grounds that it represents a minor fraction of the total bodily Zn (1.5%)35,36 and that the Zn turnover time in the brain is poorly known. We therefore included the ten following reservoirs (Fig. 2): the bolus (D), the plasma of the portal vein upstream from the liver (PV), the plasma (P), erythrocytes (R = RBC), the liver itself (L), muscles (M), bones (B), kidneys (K), the bladder (U = urine), and the skin (S). The diet function k (forcing term) can be any arbitrary non-negative function of time. The exchange among reservoirs was treated as first-order kinetic coefficients or, equivalently, as probabilities of exit per unit of time. Excretion cannot be negative and was therefore also treated as a probability of irreversible loss (from the bolus to the kidney, from the skin to desquamation, and from the kidney to urine). All fluxes are listed in Table 1 and discussed in the ESI.†
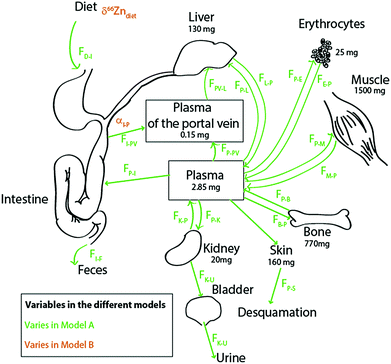 |
| | Fig. 2 Schematic diagram of the Zn isotope cycle in the human body with parameters chosen for models A (in green) and B (in orange). The bone fluxes (in blue) vary in both models, as described in the text. All values and boxes were used for the box model calculations. For the values of the fluxes, see Table 1. | |
Table 1 List of the parameters and their symbols used in the text, figures and calculations (standard model) for a man of 70 kg, their values, and bibliographic references. Isotopic compositions of the boxes are the expected values at the steady state. All isotopic initial values are fixed at 0‰
| Reservoirs |
|
Zinc content in organ & tissue |
|
|
|
δ66Zn(‰) |
Ref. |
M (mg) |
Ref.a |
|
Mass estimated for a Zn total content of the body of 2600 mg. The Zn distribution among different Zn pools was borrowed from King et al. (2000).35
The fluxes are normalized to those provided by Wastney et al. (1986)29 with correction for an absorption of 4 instead of 5.6 mg d−1.
|
| Bolus (intestinal tract) (D) |
NA |
|
10 |
29 and 30
|
| Bones (B) |
0.77 |
7
|
770 |
35
|
|
|
| Kidney (K) |
NA |
|
20 |
36
|
| Liver (L) |
−1.05 |
This study |
130 |
36
|
| Muscle (M) |
0.03 |
Pers. comm. |
1500 |
36
|
| Plasma (P) |
0.17 |
15
|
2.85 |
34
|
| Portal vein plasma (PV) |
NA |
|
0.15 |
40
|
| Erythrocyte (R) |
0.42 |
3, 4, 6, 10, 12, 15, this study |
25 |
34
|
| Skin (S) |
NA |
|
160 |
|
| Bladder (U) |
NA |
|
NA |
|
| Diet |
−1.00 to 1.00 |
See text |
0.1 |
|
| Urine (bladder) |
Similar to plasma |
Pers. Com. |
NA |
NA |
| Fluxesb |
|
Fractionation coefficient |
|
| Symbol |
Value (mg d−1) |
Ref. |
Symbol |
Value |
Ref. |
|
F
D–I
|
10.00 |
17 and 34
|
α
D–I
|
1.000000 |
Deduced |
|
F
I–F
|
9.00 |
17 and 34
|
α
I–F
|
1.000000 |
Deduced |
|
F
I–PV
|
4.00a |
17 and 34
|
α
I–PV
|
1.000180 |
See text |
|
F
P–I
|
3.45 |
Deduced |
α
P–I
|
1.000000 |
See text |
|
F
P–B
|
0.09 |
29
|
α
P–B
|
1.000295 |
7 and 15
|
|
F
B–P
|
0.09 |
29
|
α
B–P
|
0.999705 |
7 and 15
|
|
F
P–R
|
4.05 |
29
|
α
P–E
|
1.000120 |
15, this study |
|
F
R–P
|
4.05 |
29
|
α
E–P
|
0.999880 |
15, this study |
|
F
M–P
|
2.53 |
29
|
α
P–M
|
0.999930 |
Pers. comm |
|
F
P–M
|
2.53 |
29
|
α
M–P
|
1.000070 |
Pers. comm |
|
F
PV–L
|
114.25 |
29 and 39
|
α
L–P
|
1.001230 |
15, this study |
|
F
P–PV
|
117.25 |
Deduced |
α
PV–P
|
1.000000 |
15, this study |
|
F
PV–P
|
1.00 |
32
|
α
P–V
|
1.000000 |
Deduced |
|
F
L–P
|
156.00 |
28
|
α
PV–L
|
1.000000 |
Deduced |
|
F
P–L
|
38.75 |
29 and 39
|
α
P–L
|
0.999693 |
15, this study |
|
F
K–U
|
0.30 |
27 and 29
|
α
K–U
|
1.000000 |
Pers. comm |
|
F
K–P
|
2.0 |
41 and 42
|
α
K–P
|
1.000000 |
Pers. comm |
|
F
P–K
|
2.30 |
41 and 42
|
α
P–K
|
1.000000 |
Pers. comm |
|
F
P–S
|
0.25 |
34
|
α
P–S
|
1.000000 |
Deduced |
Fig. 2 presents the Zn circulation throughout the human body and fluxes among all reservoirs.17,27,31,34,37 The body of a 70 kg man contains about 2.6 g of zinc, mainly distributed between bones and muscles.17 Around 4 mg (FI–P) is absorbed each day.17 Zinc is partially absorbed by the intestine enterocytes (FI→P) (about 30% of the diet Zn is absorbed17,34,37,38). This partial absorption balances urinary excretion (FP→U) through the kidneys (FP→K and FK→P), desquamation (FP→S),11 and intestinal secretion (FP→I). Zinc is directly transported from the enterocytes to the liver through the portal vein (FPV–L) and returned to the plasma (FL→P), which reallocates the metal to the other organs and fluids of the body.17 Fluxes from the hepatic artery to the liver (FP–L) represent 25% of the Zn input into the liver. After erythrocyte destruction by macrophages, Zn is released in the plasma (FR→P) and transferred to the bone marrow where new RBCs are formed (FP→R). The daily intake of zinc is small compared to the total amount of zinc present in the body (∼0.5‰). Fluxes between muscles, bones and plasma are extremely slow29 (FP→B and FB→P; FM→P and FP→M).
We determined the Zn isotope fractionation coefficients from literature data on humans (Table 1). The calculations used are described in the Supplementary Information 2 (ESI†). We assumed no isotopic fractionation upon output whenever a reservoir had only one exit channel (e.g., bolus to feces or portal vein to liver). We estimated Zn isotope fractionation during intestinal absorption following Balter et al. (2010). The αP–B value, possibly overestimated, was calibrated from modern plasma δ66Zn values and archeological bone δ66Zn values. The method might be somewhat biased since the teeth in this archeological population have higher δ66Zn values than their modern counterparts.8 However, the estimate of this αP–B is consistent with the value estimated for mice (Table S2, ESI†). In addition, an enrichment of heavy Zn isotopes during the incorporation of this element in bioapatite is expected because of its high content of phosphates. In contrast, diffusion during Zn renal excretion and reabsorption does not seem to bring about detectable kinetic isotope fractionation, presumably because Zn is bound to a transporter in the process (see ESI†).
The fluxes, masses, and isotope fractionation coefficients used for the model are described in Table 1. We first built the reference model (model 0). We then proceeded to evaluate the effect of the basal metabolic rate (BMR) through model A (Fig. 2). As dietary needs are more important for individuals characterized by high BMR, we assumed a stronger Zn intake. The fluxes (FD–I + FI–F, Fig. 2) used in model A are expressed in mg of Zn ingested per day. The fluxes between the different reservoirs were considered to be proportionally impacted. In model B (Fig. 2), we tested the influence of diet. We evaluated the isotope composition of each reservoir through time as a function of the Zn isotope composition of diet (δ66Zndiet) and of isotopic fractionation during intestinal absorption (αI–P). Ranges of variations are presented in Table 2. The δ66Zn values of dental enamel were estimated from those of δ66Zn values in bones after a correction of 0.2‰ which corresponds to the average difference between the two tissues reported by studies on mammals and humans.8,20
Table 2 List of values used for calculations
|
|
Standard model |
Influence of the BMR |
Influence of the diet |
| Model A |
Model B |
|
The fluxes correspond to the daily intake of Zn through the food and not the flux actually absorbed by the digestive tract.
|
| Parameters |
|
α
I–P
|
1.00018 |
1.00018 |
0.9999–1.0010 |
| Body mass (kg) |
70 |
70 |
70 |
| δ66Zndiet (‰) |
0 |
0 |
−1.0 to +1.0 |
|
F
D–I
(mg d−1) |
10 |
5–20 |
10 |
2. Mathematical formalism
The evolution of the number of milligram mi of a particular species in the i-th amongst r interacting reservoirs is described by the following equation modified from Albarède (1996)43 to account for global inputs and outputs:| | 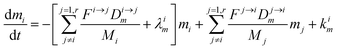 | (1) |
where Mi is the mass of the i-th reservoir, Fi→j is the increment of material lost by box i to reservoir j per unit time (flux), Di→jm is the partition coefficient of species m between this increment and reservoir j, and λim is the probability of irreversible loss (excretion) from the i-th reservoir to the surrounding per unit of time (e.g., towards urine and feces), and kim is the input flux (from the diet to the reservoir i through the bolus).
Eqn (1) can be reformulated in the matrix form:
| | 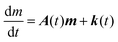 | (2) |
where the bold-face characters collect the different variables in each reservoir and
A(
t) is a square matrix. The inverse of the eigenvalues of the matrix
A are all negative and their modulus define the dynamics of the system.
From this point onward, we will label 64Zn as m and 66Zn as n. Because of the mass conservation for each reservoir, we have:
| | 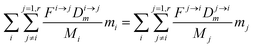 | (3) |
which reflects, using
eqn (2) together with
eqn (1), the total budget of
m in the body:
| | 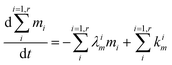 | (4) |
Using
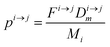
,
(1) simplifies as:
| | 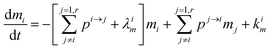 | (5) |
Fig. 3 illustrates the formalism with two reservoirs, 1 and 2, with input into reservoir 1 and irreversible output from reservoir 2.
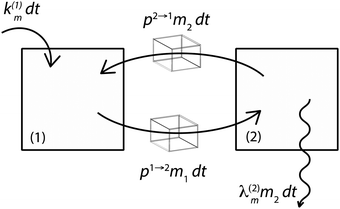 |
| | Fig. 3 Illustration of the model for a two-reservoir system. λim is the probability of irreversible loss (excretion) from the i-th reservoir to the surrounding per unit of time, kim is the input flux, pi→j is the probability of Zn loss from the i-th reservoir to the j-th reservoir. | |
If pi→j, λim, and kim are constants, the system described by (5) can be explicitly solved by matrix algebra. The residence time of species m in the i-th reservoir is the inverse of the corresponding diagonal term 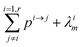 .
.
In order to describe the dynamics of the denominator species n, and of ratios n/m, we can now add a fractionation coefficient 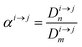 acting upon extraction of the material from reservoir i into reservoir j, so that eqn (1) becomes:
acting upon extraction of the material from reservoir i into reservoir j, so that eqn (1) becomes:
| | 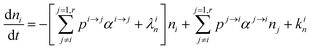 | (6) |
The variation of the ratio
Ri =
n/
m =
66Zn/
64Zn is simply:
| | 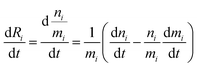 | (7) |
and therefore
| | 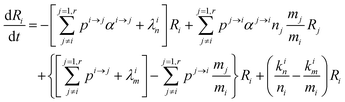 | (8) |
This equation can be rewritten:
| | 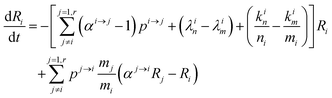 | (9) |
Changing
Ri into
Rstd(1 +
δi) with
Rstd being the ratio
m/
n in a reference material (here Lyon JMC for
66Zn/
64Zn), we get
| | 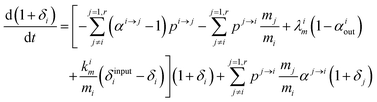 | (10) |
with
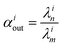
, measuring relative
n/
m fractionation upon excretion from reservoir
i. This non-linear differential system has been integrated using the
ode15s stiff solver of Matlab to ensure the robustness of the solutions. Radioactive tracers can be easily accommodated by adding a radioactive decay ‘channel’ to the
λ constants. The source code can be obtained on demand from the authors or at https://github.com/lpouillo/boxmodel.
Results and discussion
Zinc dynamic homeostasis in the human body (model 0)
For the sake of illustration, an example of system evolution is provided in Fig. 4, in which the p's, k, λ, and α values are kept constant, and the initial δ66Zn value of the bolus is arbitrarily shifted by 1‰ relative to the steady state values. As in most cooperative systems, it is observed that the Zn pools and isotope compositions of each reservoir adjust to one another in the order defined by the eigenvalues of the system (Table 3 and Fig. 4), and not by the residence times. Although the ‘slow’ reservoirs (bones, muscles) drive the system in the long run (Tables 3 and 4), the rate of readjustment of the ‘fast’ reservoirs (plasma, plasma of the portal vein, liver, etc.) has a more complex relationship with residence times. This is shown in the loadings of each reservoir (Table 4). The evolution of the δ66Zn values in the ‘fast’ reservoirs such as the RBC is highly dependent on the initial δ66Zn value of the muscles and, to a lesser extent, that of the liver (Fig. 5). As a consequence, an initial δ66Znmuscle value drastically different from the steady state value of the system slows down the rate of adjustment of the fast reservoir: in Fig. 5A, the RBC reaches the steady state in about three months when the δ66Znmuscle is initially at the steady state, and takes 8 years for an initial value shift of 0.4‰. The initial values of the diet and the bones play a minor role in the evolution of the δ66Zn values in the fast reservoirs (Fig. 5C).
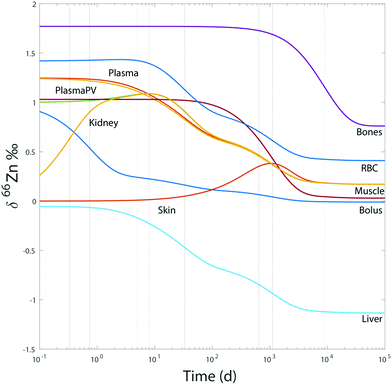 |
| | Fig. 4 Model 0: evolution of δ66Zn in the different reservoirs for a bolus initially shifted by 1‰ and random initial values for the other reservoirs with respect to steady state values. The dotted lines correspond to the different relaxation times deduced from the eigenvalues (Table 3). | |
Table 3 Eigenvalues and relaxation times of Zn dynamics in the human body
| Eigenvalues (d−1) |
Relaxation times (d) |
| −1.13 × 10−4 |
8.83 × 103 |
| −9.09 × 10−4 |
1.11 × 103 |
| −1.56 × 10−3 |
6.40 × 102 |
| −3.01 × 10−2 |
3.32 × 101 |
| −0.125 |
8.03 |
| −0.200 |
5.01 |
| −1.35 |
0.739 |
| −3.03 |
0.333 |
| −59.52 |
1.68 × 10−2 |
| −680 |
1.47 × 10−3 |
Table 4 Residence time of Zn in the different reservoirs, and the associated tissue or content renewal time
| Reservoirs |
Zinc residence times in the different reservoirs estimated from model 0 (in days) |
Tissue or content renewal |
| Bolus (intestinal tract) |
18 hours |
A few hours |
| Plasma |
0.41 hours |
0.4 hours |
| Plasma (portal vein) |
2 minutes |
0.4 hours |
| Bones |
24 years |
10–20 years |
| Muscles |
1.6 year |
? |
| Liver |
20 hours |
120 to 400 days44 |
| Kidney |
9 days |
0.4 hours (content), several days for renal cell regeneration43 |
| RBC |
6 days |
120 days |
| Skin |
1.75 year |
45 days43 |
| Bladder |
8 hours |
A few hours |
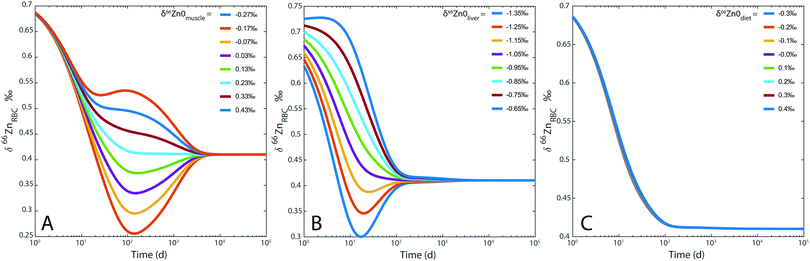 |
| | Fig. 5 Model 0: evolution of δ66Zn in the erythrocytes (RBC) for (A) different δ66Zn initial values of the muscle reservoir; (B) different δ66Zn initial values of the liver reservoir; (C) different δ66Zn initial values of the bolus reservoir. | |
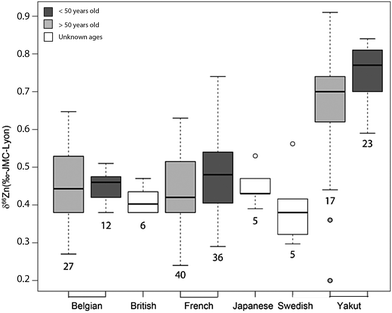 |
| | Fig. 6 Whisker plot of δ66Zn in the blood of various populations. The numbers below the boxes correspond to the sample size. The upper and lower limits of the boxes represent the 25th–75th percentiles (with the median as a bold horizontal line) and the whiskers show the 10th–90th percentiles. Data correspond to whole blood or erythrocyte values of populations from various geographical areas: Belgian individuals (whole blood);10–12 Swedish individuals3 (whole blood); Japanese individuals4 (RBC), French individuals <50 years old15 (RBC); Yakut individuals (whole blood),14 and French individuals >50 years old (RBC) (this study, Supplementary Information 1, ESI†). | |
The reservoirs based on the residence times (Table 4) can be subdivided into ‘slow’ (bones, muscles, and skin), which require between 1.5 and 24 years to adjust, ‘fast’ (erythrocytes, kidneys, and liver), which react on a day-to-week time scale, and ‘ultrafast’ reservoirs (plasma), which react in less than a few hours. For the slow reservoirs, the order of the eigenvalues calculated from the model reflects the order of residence times (Table 4): the bones, skin, and muscles induce values corresponding to a relaxation time of ∼103 days, whereas all the other reservoirs exchange very quickly between each other. Bones and muscles are therefore not involved in the short Zn metabolism. The residence time in bones controls the overall relaxation time of the system. This time is equal to about 24 years, i.e., the order of magnitude of a lifetime. On the year scale or less, the homeostatic steady state of the human body seems to be in a pseudo-steady state, with bones and muscles being practically left out of exchange processes. Interestingly, these two slow reservoirs are the main reservoirs of Zn in the body: in the case of Zn dietary distress, they help buffer any Zn deficiency in the more active reservoirs (plasma, RBC, liver) and protect the homeostasis of the system (Fig. 5A). This conclusion is consistent with Wastney et al.'s (1986) experiments, which demonstrated that the muscle Zn turnover significantly increased (along with the intestinal secretions and urinary excretion) when the dietary intake of Zn is increased by a factor of ten, but was unable to measure the impact on the FB–P flux, which is too slow.29
An important question is whether fluxes correspond to exchanges through cell membranes or to cell renewal. Intense flux exchanges have been reported between the plasma and the liver, without a clear determination of the ligands involved in Zn transport.34 For rat livers, an experiment demonstrated that the Zn uptake reaches a plateau after 10–15 hours.34 This time frame is consistent with the findings of our model. The fluxes through the membrane of the red blood cells are also very intense. They also fit with the residence time of the element identified by our model.30,34,45 The plasma depuration by the kidney is shorter than the residence time of the Zn in this reservoir, which can be explained by (1) the element selective discrimination performed by the kidney during urinary excretion or (2) the renewal time of the renal cells, which takes at least several days.46 The time required for renewal of the skin is clearly shorter than the residence time of this organ estimated by the model, and is related to the fact that during keratinocyte mitosis, some cells migrate outwards to the epiderma, whereas others remain in the basal lamina until the next mitosis. This time of 45 days therefore is only relevant for half of the cells.47
Model 0 steady-state
As expected, the steady state isotope ratios that resulted from the simulation of model 0 are consistent with the average values reported in the literature (Table 5).
Table 5 Steady state δ66Zn values from model 0 for different organs and tissues and reported values in the literature, this study, and personal communication7,15
| Organ or tissue |
Steady state δ66Zn values of model 0 (‰) |
Average δ66Zn value reported in the literature (‰) |
| Liver |
−1.135 |
−1.05 |
| Bone |
0.757 |
0.77 |
| Erythrocyte |
0.407 |
0.42 |
| Plasma |
0.167 |
0.18 |
| Kidney |
0.167 |
NA |
| Muscle |
0.027 |
0.03 |
The small differences observed between steady-state and observed values are mainly due to the fact that both isotope fractionation and fluxes associated with the intestinal absorption (αI–P, FI–P) are not fully compensated for by intestinal Zn excretion (αI–P = 1, FI–P = FP–I + FK–U + FP–S). As a result, the steady-state δ66Zn value of the dietary bolus contained in the intestinal tract is δ66Zn = −0.015‰, i.e., slightly lower than the reference δ66Zndiet value of the diet (0‰). The difference of δ66Zn between the diet and feces (Δδ66Zndiet–feces) of −0.015‰ falls between the values observed for sheep (Δδ66Zndiet–feces = −0.1‰)22 and mice (Δδ66Zndiet–feces = +0.09).23
Zn isotope status and age (model A)
Here, we address the effect of the diet vs. the effect of metabolic rates. Age does not seem to be a major factor. Contrary to the Yakut whole-blood samples,14 no δ66Zn drift with age is observed in the plasma of French and Belgian individuals19 (Fig. 1, 5 and Supplementary Information 1, ESI†). To explain the isotopically heavy Cu of Yakut blood, we previously suggested that it was an effect of their basal metabolic rate22 which, relative to Europeans, is boosted by the cold stress. The turnover of elements and their isotopes is faster in circumpolar populations than in inhabitants of temperate zones, a fact which has been used to quantify the basal metabolic rate using double-labeled water.48 The same interpretation seems to hold for Zn isotopes, but with a depletion in the light isotopes. The average BMR difference between circumpolar and non-circumpolar populations reported in the literature is about 17% for men and 6% for women.49 Therefore, one can imagine that the enrichment of heavy Zn and light Cu isotopes in the body through the lifespan is faster for circumpolar populations than for populations from tropical or temperate latitudes. It may explain why the isotopic drift is detectable in Yakut populations but not in Belgian or French ones. However, it should also trigger an isotope difference between male and female Yakuts, which has not been evidenced.
In order to test the assumption that δ66Zn is modulated by the rate of Zn turnover, we turned to the box model “Model A” (Table 2). This model explores the influence of dietary Zn flux on the δ66Zn of various organs and tissues. As dietary needs are more important for circumpolar populations, we postulated that the Zn demand would increase proportionally. For model A, the FI–P flux from the intestinal tract to the plasma is varied from 2 to 8 mg d−1. All input and output fluxes are varied proportionally. The initial delta values for model A were set 0.3‰ higher for the RBC and 0.3‰ lower for the bones. These values were selected with reference to the average difference observed between trophic levels.20,24 The model therefore gives the response time of the body to a change of diet as a function of its metabolic rate.
Dietary Zn input slightly impacts the RBC and bone isotope composition by delaying the steady state, which is reached after several months to decades depending on the initial reservoir delta values (Fig. 7). Steady-state values are similar for each simulation regardless of the BMR values. The steady state is simply reached at a slightly earlier time for individuals with high BMR. The effect of BMR remains below the detection limit by Zn isotope analyses: for a variation of 20% of metabolism, the difference between the δ66Znbones values of low and high metabolism would be about 0.01‰. Even after 25 years, such a shift is much lower than the analytical error of Zn isotope measurements (Fig. 7). A change of diet will take several decades to be isotopically recorded in blood and bones. Therefore, a drift of δ66Zn with age is not expected in adult blood, regardless of the latitude of residence. Changes of the diet δ66Zn, however, cause changes in the RBC δ66Zn within 100 days (Fig. 7A). When the initial δ66Znmuscle value is shifted from the steady state one, most of the drift of δ66ZnRBC values happens during the first 100 days and the last 0.1‰ slowly evolves over the following years (about 0.03‰ year−1 from medium to high metabolic rates, Fig. 5A). In this case, the steady state will be reached after several decades (Fig. 7C).
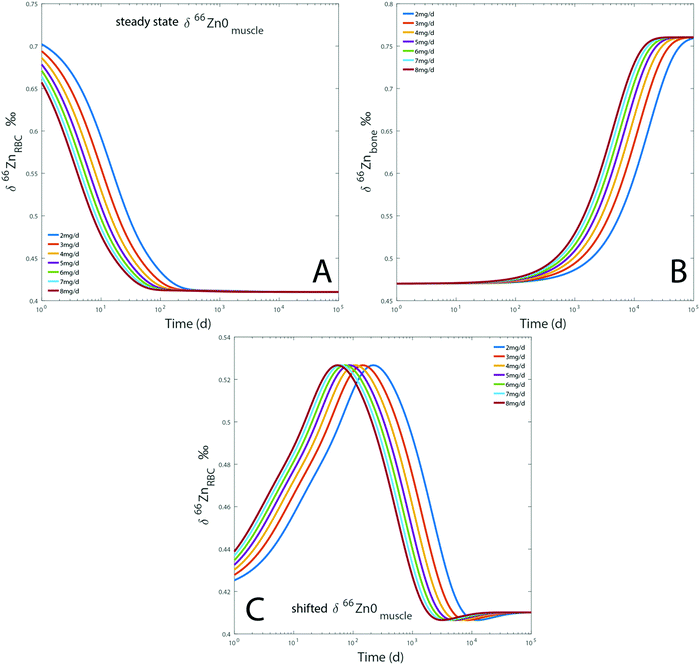 |
| | Fig. 7 Results of model A: evolution over time of the computed δ66Zn of erythrocytes (A) and bones (B), for a diet with a constant isotope composition. Each line represents a given proportion of Zn absorbed each day. The evolution of the δ66Zn of erythrocytes with a shifted δ66Zn0muscle value but a steady state δ66Zn0RBC was also tested (C). Details are available in the ESI.† | |
Zn isotope compositions as a diet tracer (model B)
Model B explores the impact of two dietary parameters: the fractionation coefficient during intestinal absorption (αI–P or αI–PV) and the Zn isotope composition of diet (δ66Zndiet, Fig. 2). Isotope fractionation is impacted (1) by the different types of reactions happening during intestinal absorption and their kinetics, (2) the pH of the intestinal tract, (3) the electronic environment of the Zn contained in different food products, and (4) the intestinal absorption rate, which describes the ratio between the Zn flux crossing the intestinal border and the proportion of Zn re-entering the intestinal tract (absorption = FI–P/FD–I). The higher the absorption is, the closer the αI–P value is to 1. The absorption will strongly depend on the plant/meat ratio in the diet with the additional complexity that Zn ingested with plants is poorly bioavailable.50,51 For the present box model, the absorption rate was arbitrarily set at 40%. The associated αI–P (model 0, αI–P = 1.00018) might correspond in reality to a different absorption rate. We estimated that a variation of the absorption of 10% for a constant αI–P would impact the different reservoir values by about 0.03‰ (ESI,† Fig. S2). The other factors influencing the fractionation coefficient mentioned above cannot be assessed by the present model, but theoretically through ab initio calculations and in the lab by controlled feeding experiments.
For a given value of αI–P, the range of isotopic variation in blood reflects the range of the diet. The fractionation coefficient αI–P also plays an important role in the final δ66ZnRBC, δ66Znbone, and δ66Znenamel values as a variation of 1‰ causes 1‰ isotope fractionation, since the reservoirs are at the steady state (Fig. 7). The two main parameters influencing the steady-state isotope compositions of the different reservoirs are therefore the isotope fractionation during intestinal absorption (αI–P) and the isotope composition of the diet (δ66Zndiet, Fig. 7).
Knowing the isotope composition of the diet and that of body organs and tissues measured in mice and sheep,18,22,23 we can compare the coefficients of isotope fractionation during intestinal absorption deduced from the δ66Zn values of plasma and diet 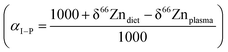 to that determined from our model based on the δ66Zndiet, δ66ZnRBC, and δ66Znbone values. We also estimated this coefficient from the bone and enamel values of modern grazers and browsers from Kenya and those of local plants (Fig. 6B and C). We report these coefficients in Table 6. For wild herbivores, the deduced ranges confirm the preferential absorption of heavy zinc isotopes during intestinal absorption. The range deduced for mice and minipigs also corresponds to the range calculated from plasma and diet data.18 However, there is a discrepancy between the ranges predicted from blood and bone values for the mice and sheep studied by Balter et al. (2010, 2013).22,23 Sheep may not be a good reference since they have no bile excretion. This could explain the different δ66ZnRBC steady-state values that our model does not account for. Additional discussion on the control feeding experiment results can be found in the Supplementary Information 3 (ESI†).
to that determined from our model based on the δ66Zndiet, δ66ZnRBC, and δ66Znbone values. We also estimated this coefficient from the bone and enamel values of modern grazers and browsers from Kenya and those of local plants (Fig. 6B and C). We report these coefficients in Table 6. For wild herbivores, the deduced ranges confirm the preferential absorption of heavy zinc isotopes during intestinal absorption. The range deduced for mice and minipigs also corresponds to the range calculated from plasma and diet data.18 However, there is a discrepancy between the ranges predicted from blood and bone values for the mice and sheep studied by Balter et al. (2010, 2013).22,23 Sheep may not be a good reference since they have no bile excretion. This could explain the different δ66ZnRBC steady-state values that our model does not account for. Additional discussion on the control feeding experiment results can be found in the Supplementary Information 3 (ESI†).
Table 6 Isotope fractionation coefficient for intestinal absorption (αI–P or αI–PV) deduced from model B compared with literature data
|
|
Calculated αI–P |
α
I–P deduced from δ66Znerythrocyte values |
α
I–P deduced from δ66Znbone values |
α
I–P deduced from δ66Znenamel values |
Range overlap |
| Experimental studies on animals |
| Sheep22 |
1.001–1.003 |
0.9995–0.9997 |
0.9997–1.0001 |
|
None |
| Mice23 |
NA |
1.0000–1.0003 |
0.9996–0.99995 |
|
None |
| Mice18 |
0.9997–1.002 |
0.99985–1.00025 |
0.9996–1.0000 |
|
0.99985–1.0000 |
| Minipig52 |
0.9999341–1.00015 |
0.9997–1.0001 |
|
|
0.99993–1.0001 |
|
|
| Studies on foodwebs |
| Grazers20 |
|
|
1.0000–1.0008 |
1.0035–1.0012 |
1.0035–1.0008 |
| Browsers20 |
|
|
0.9998–1.0005 |
1.0001–1.0007 |
1.0001–1.0005 |
In previous studies20,21,24 from our group, we hypothesized that fractionation during intestinal absorption only occurred during plant consumption because of the precipitation of complexes between Zn and phytates in the intestinal tract. The predicted αI–P values are generally higher for grazers than for other animals (Table 6, Fig. 8B and C), which fits with this hypothesis. In contrast, the αI–P values deduced from control feeding experiments tend to be lower than 1. However, the composition of the diet was not documented. Mice reingest their feces (cecotrophes), which might impact the αI–P because of an increased absorption rate, while sheep and human metabolism is quite different.
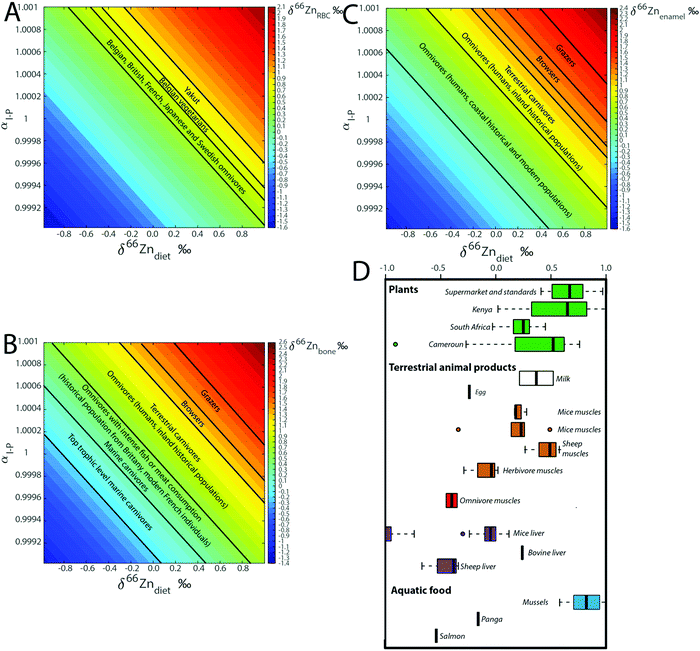 |
| | Fig. 8 Computed steady-state δ66Zn values in (A) RBC, (B) bones and (C) teeth as a function of the isotope fractionation coefficient during intestinal absorption (αI–P) and the Zn isotope composition of the diet (δ66Zndiet). The δ66Zn ranges observed for diverse populations and animals are reported, as well as (D) δ66Zn values of food taken from the literature.3,9,26–28,32,33,51 | |
There is no δ66Zn data on carnivores and we can only propose a working model. Muscles of sheep and mice δ66Zn are definitely higher than their diet.18,22,23 A carnivore diet is expected to be associated with a quantitative absorption of zinc. The αI–P of a carnivore diet should therefore be equal to 1, which suggests that, on average, Zn from the different carnivore organs should be isotopically light (since the herbivore muscles are usually enriched in Zn light isotopes). δ66Zn data on blood and bones of carnivores paired with data on prey's muscles are missing. The absorption effect cannot therefore be rigorously tested using the currently available data. Yet, given the range of values observed for different food categories, it may be an important factor of Zn isotope variability in organs and fluids (Fig. 8D). Additional discussion on the implications of the model for the interpretation of human blood Zn isotope signatures is available in the Supplementary Information 3 (ESI†).
Conclusion
We successfully modeled Zn elemental and isotopic homeostasis through a robust 10-box dynamic model of the human body taking the diet and the excretion channels into account. We obtained residence time for each reservoir and the characteristic times of chemical and isotopic readjustment to changes in diet. This study confirms the stability of the Zn isotope compositions of the blood throughout the human life for a stable diet. A drift of isotope ratios due to aging is unlikely. We showed that the Zn isotope composition of human blood is strongly related to diet and possibly anthropogenic contamination.
We also demonstrated the potential of the present box model to identify the composition of the diet of mammals from the Zn isotope ratios of the different body tissues, which opens perspectives for paleodietary reconstructions. We show that the isotope fractionation during absorption and the original isotope composition of the diet are the two main factors controlling the Zn isotope values of the body. We compared the values predicted from our model of the isotope fractionation during intestinal absorption to isotope ratios of animal tissues and associated food products. The results of this comparison fit with the hypothesis of a preferential absorption of heavy isotopes with plant-based diets for wild animals, but not for animals of control feeding experiments, which may be suspected to introduce a bias.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
We are grateful to Douglas Baxter for providing data on individuals from his study on Zn isotope composition in blood (Stenberg et al., 2005). Many thanks to Jeroen Sonke and Franck Vanhaecke for very helpful discussions. We also thank Francis Camoin from the Etablissement Français du Sang in Lyon for providing the blood samples, and Michelle Gigou and Christian Bréchot from the Hepatobiliary Center (U785 INSERM) of the Paul Brousse Hospital for providing the liver samples. Axelle Zacaï and Jean-Michel Brazier are thanked for their help during sample preparation. Funding for reagents and isotope analyses was supported by the Bullukian Foundation and the Mérieux Foundation. We also thank the Max Planck Society for salary support. Finally, we would like to express our gratitude to Geraldine Fahy and Carin Molenaar for the English editing of the different drafts. Open Access funding provided by the Max Planck Society.
References
- I. Rodushkin, E. Engström and D. C. Baxter, Anal. Bioanal. Chem., 2005, 1–13 Search PubMed.
- F. Albarède, P. Telouk, J. Blichert-Toft, M. Boyet, A. Agranier and B. Nelson, Geochim. Cosmochim. Acta, 2004, 68, 2725–2744 CrossRef.
- A. Stenberg, D. Malinovsky, B. Öhlander, H. Andrén, W. Forsling, L. M. Engström, A. Wahlin, E. Engström, I. Rodushkin and D. C. Baxter, J. Trace Elem. Med. Biol., 2005, 19, 55–60 CrossRef CAS.
- T. Ohno, A. Shinohara, M. Chiba and T. Hirata, Anal. Sci., 2005, 21, 425–428 CrossRef CAS PubMed.
- A. Stenberg, D. Malinovsky, I. Rodushkin, H. Andrén, C. Pontér, B. Öhlander and D. C. Baxter, J. Anal. At. Spectrom., 2002, 18, 23–28 RSC.
- A. Helal, N. Zahran and A. Rashad, Int. J. Mass Spectrom., 2002, 213, 217–224 CrossRef CAS.
- K. Jaouen, V. Balter, E. Herrscher, A. Lamboux, P. Telouk and F. Albarède, Am. J. Phys. Anthropol., 2012, 148, 334–340 CrossRef PubMed.
- K. Jaouen, E. Herrscher and V. Balter, Am. J. Phys. Anthropol., 2017, 162, 491–500 CrossRef PubMed.
- K. Jaouen, R. Colleter, A. Pietrzak, M.-L. Pons, B. Clavel, N. Telmon, É. Crubézy, J.-J. Hublin and M. P. Richards, Sci. Rep., 2018, 8, 5077 CrossRef PubMed.
- L. Van Heghe, O. Deltombe, J. Delanghe, H. Depypere and F. Vanhaecke, J. Anal. At. Spectrom., 2014, 29, 478–482 RSC.
- L. Van Heghe, E. Engström, I. Rodushkin, C. Cloquet and F. Vanhaecke, J. Anal. At. Spectrom., 2012, 27, 1327 RSC.
- M. Costas-Rodríguez, L. Van Heghe and F. Vanhaecke, Metallomics, 2014, 6, 139–146 RSC.
- F. Larner, L. N. Woodley, S. Shousha, A. Moyes, E. Humphreys-Williams, S. Strekopytov, A. N. Halliday, M. Rehkämper and R. C. Coombes, Metallomics, 2015, 7, 112–117 RSC.
- K. Jaouen, M. Gibert, A. Lamboux, P. Telouk, F. Fourel, F. Albarède, A. N. Alekseev, E. Crubézy and V. Balter, Metallomics, 2013, 5, 1016–1024 RSC.
- F. Albarède, P. Telouk, A. Lamboux, K. Jaouen and V. Balter, Metallomics, 2011, 3, 926–933 RSC.
- K. Jaouen, Quat. Sci. Rev., 2018, 197, 307–318 CrossRef.
- B. L. Vallee and K. H. Falchuk, Physiol. Rev., 1993, 73, 79–118 CrossRef CAS PubMed.
- F. Moynier, T. Fujii, A. S. Shaw and M. Le Borgne, Metallomics, 2013, 5, 693–699 RSC.
- T. Fujii and F. Albarède, PLoS One, 2012, 7, e30726 CrossRef CAS PubMed.
- K. Jaouen, M. Beasley, M. Schoeninger, J.-J. Hublin and M. P. Richards, Sci. Rep., 2016, 6, 26281 CrossRef CAS PubMed.
- K. Jaouen, M.-L. Pons and V. Balter, Earth Planet. Sci. Lett., 2013, 374, 164–172 CrossRef CAS.
- V. Balter, A. Zazzo, A. P. Moloney, F. Moynier, O. Schmidt, F. J. Monahan and F. Albarède, Rapid Commun. Mass Spectrom., 2010, 24, 605–612 CrossRef CAS PubMed.
- V. Balter, A. Lamboux, A. Zazzo, P. Télouk, Y. Leverrier, J. Marvel, A. P. Moloney, F. J. Monahan, O. Schmidt and F. Albarède, Metallomics, 2013, 5, 1470–1482 RSC.
- K. Jaouen, P. Szpak and M. P. Richards, PLoS One, 2016, 11, e0152299 CrossRef PubMed.
- W. R. Leonard, S. B. Levy, L. A. Tarskaia, T. M. Klimova, V. I. Fedorova, M. E. Baltakhinova, V. G. Krivoshapkin and J. J. Snodgrass, Am. J. Hum. Biol., 2014, 26, 437–445 CrossRef CAS PubMed.
- D. M. Vinokurova, A. A. Vinokurova and I. Z. Borisova, Journal of Siberian Federal University. Humanities & Social Sciences, 2018, 11, 670–678 Search PubMed.
- D. M. Foster, R. L. Aamodt, R. I. Henkin and M. Berman, Am. J. Physiol.: Regul., Integr. Comp. Physiol., 1979, 237, R340–R349 CrossRef CAS PubMed.
- D. M. Foster, M. E. Wastney and R. I. Henkin, Math. Biosci., 1984, 72, 359–372 CrossRef CAS.
- M. E. Wastney, R. L. Aamodt, W. F. Rumble and R. I. Henkin, Am. J. Physiol.: Regul., Integr. Comp. Physiol., 1986, 251, R398–R408 CrossRef CAS PubMed.
- M. E. Wastney, I. G. Gokmen, R. L. Aamodt, W. F. Rumble, G. E. Gordon and R. I. Henkin, Am. J. Physiol.: Regul., Integr. Comp. Physiol., 1991, 260, R134–R141 CrossRef CAS PubMed.
- K. C. Scott and J. R. Turnlund, Am. J. Physiol.: Endocrinol. Metab., 1994, 267, E165–E173 CrossRef CAS PubMed.
- N. M. Lowe, D. M. Shames, L. R. Woodhouse, J. S. Matel, R. Roehl, M. P. Saccomani, G. Toffolo, C. Cobelli and J. C. King, Am. J. Clin. Nutr., 1997, 65, 1810–1819 CrossRef CAS PubMed.
- J. C. King, D. M. Shames, N. M. Lowe, L. R. Woodhouse, B. Sutherland, S. A. Abrams, J. R. Turnlund and M. J. Jackson, Am. J. Clin. Nutr., 2001, 74, 116–124 CrossRef CAS.
- R. J. Cousins, Physiol. Rev., 1985, 65, 238–309 CrossRef CAS PubMed.
- J. C. King, D. M. Shames and L. R. Woodhouse, J. Nutr., 2000, 130, 1360S–1366S CrossRef CAS PubMed.
-
C. F. Mills, Zinc in Human Biology, Springer Science & Business Media, 2013 Search PubMed.
- J. R. Turnlund, J. C. King, W. R. Keyes, B. Gong and M. C. Michel, Am. J. Clin. Nutr., 1984, 40, 1071–1077 CrossRef CAS.
- B. Lönnerdal, J. Nutr., 2000, 130, 1378S–1383S CrossRef.
- V. Vilgrain, M. Zappa, A. Sibert and M.-P. Vullierme, Hépato Gastro et Oncologie Digestive, 2007, 14, 191–203 Search PubMed.
-
P. Lozeron, Circulation hépatique, 2017, https://webcache.googleusercontent.com/search?q=cache:aKsFe74jsxcJ:https://l3bichat2017-2018.weebly.com/uploads/9/1/0/9/91095670/circulation_he%25CC%2581patique_2017_2023.pdf+&cd=1&hl=fr&ct=clnk&gl=fr.
- A. A. Yunice, R. W. King, S. Kraikitpanitch, C. C. Haygood and R. D. Lindeman, Am. J. Physiol.
Renal. Physiol., 1978, 235, F40–F45 CrossRef CAS.
- V. A. Yuzbasiyan-Gurkan, G. J. Brewer, A. J. Vander, M. J. Guenther and A. S. Prasad, Am. J. Hematol., 1989, 31, 87–90 CrossRef CAS.
-
F. Albarède, Introduction to geochemical modeling, Cambridge University Press, 1996 Search PubMed.
- E. Universalis, FOIE, http://www.universalis.fr/encyclopedie/foie/, accessed August 21, 2018.
- T. J. B. Simons, J. Membr. Biol., 1991, 123, 73–82 CrossRef CAS PubMed.
- Y. Rinkevich, D. T. Montoro, H. Contreras-Trujillo, O. Harari-Steinberg, A. M. Newman, J. M. Tsai, X. Lim, R. Van-Amerongen, A. Bowman, M. Januszyk, O. Pleniceanu, R. Nusse, M. T. Longaker, I. L. Weissman and B. Dekel, Cell Rep., 2014, 7, 1270–1283 CrossRef CAS PubMed.
- Le renouvellement de la peau, http://polgm.free.fr/travail/TPE/partie1.html, accessed August 23, 2018.
- D. A. Schoeller, J. Nutr., 1988, 118, 1278–1289 CrossRef CAS PubMed.
- J. J. Snodgrass, W. R. Leonard, L. A. Tarskaia, V. P. Alekseev and V. G. Krivoshapkin, Am. J. Hum. Biol., 2005, 17, 155–172 CrossRef PubMed.
- S. Samman and M. Foster, FASEB J., 2014, 28, 1043.1 Search PubMed.
- M. Foster, A. Chu, P. Petocz and S. Samman, J. Sci. Food Agric., 2013, 93, 2362–2371 CrossRef CAS.
- B. Mahan, F. Moynier, A. L. Jørgensen, M. Habekost and J. Siebert, Metallomics, 2018, 10, 1264–1281 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8mt00286j |
| ‡ These authors contributed equally to this work. |
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab,
Laurent
Pouilloux‡
c,
Vincent
Balter
*ab,
Laurent
Pouilloux‡
c,
Vincent
Balter
 d,
Marie-Laure
Pons
d,
Marie-Laure
Pons
 e,
Jean-Jacques
Hublin
e,
Jean-Jacques
Hublin
 a and
Francis
Albarède
a and
Francis
Albarède
 d
d


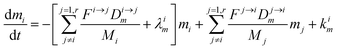
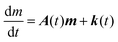
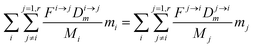
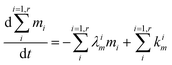
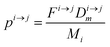 , (1) simplifies as:
, (1) simplifies as: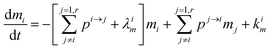
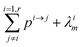 .
.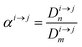 acting upon extraction of the material from reservoir i into reservoir j, so that eqn (1) becomes:
acting upon extraction of the material from reservoir i into reservoir j, so that eqn (1) becomes: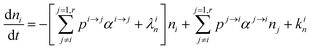
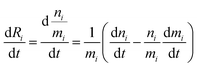
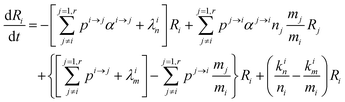
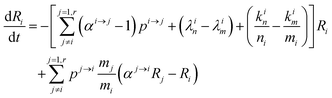
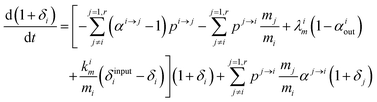
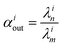 , measuring relative n/m fractionation upon excretion from reservoir i. This non-linear differential system has been integrated using the ode15s stiff solver of Matlab to ensure the robustness of the solutions. Radioactive tracers can be easily accommodated by adding a radioactive decay ‘channel’ to the λ constants. The source code can be obtained on demand from the authors or at https://github.com/lpouillo/boxmodel.
, measuring relative n/m fractionation upon excretion from reservoir i. This non-linear differential system has been integrated using the ode15s stiff solver of Matlab to ensure the robustness of the solutions. Radioactive tracers can be easily accommodated by adding a radioactive decay ‘channel’ to the λ constants. The source code can be obtained on demand from the authors or at https://github.com/lpouillo/boxmodel.



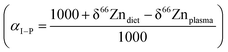 to that determined from our model based on the δ66Zndiet, δ66ZnRBC, and δ66Znbone values. We also estimated this coefficient from the bone and enamel values of modern grazers and browsers from Kenya and those of local plants (Fig. 6B and C). We report these coefficients in Table 6. For wild herbivores, the deduced ranges confirm the preferential absorption of heavy zinc isotopes during intestinal absorption. The range deduced for mice and minipigs also corresponds to the range calculated from plasma and diet data.18 However, there is a discrepancy between the ranges predicted from blood and bone values for the mice and sheep studied by Balter et al. (2010, 2013).22,23 Sheep may not be a good reference since they have no bile excretion. This could explain the different δ66ZnRBC steady-state values that our model does not account for. Additional discussion on the control feeding experiment results can be found in the Supplementary Information 3 (ESI†).
to that determined from our model based on the δ66Zndiet, δ66ZnRBC, and δ66Znbone values. We also estimated this coefficient from the bone and enamel values of modern grazers and browsers from Kenya and those of local plants (Fig. 6B and C). We report these coefficients in Table 6. For wild herbivores, the deduced ranges confirm the preferential absorption of heavy zinc isotopes during intestinal absorption. The range deduced for mice and minipigs also corresponds to the range calculated from plasma and diet data.18 However, there is a discrepancy between the ranges predicted from blood and bone values for the mice and sheep studied by Balter et al. (2010, 2013).22,23 Sheep may not be a good reference since they have no bile excretion. This could explain the different δ66ZnRBC steady-state values that our model does not account for. Additional discussion on the control feeding experiment results can be found in the Supplementary Information 3 (ESI†).


