Recent advances in manipulation of micro- and nano-objects with magnetic fields at small scales
Abstract
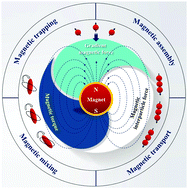
Manipulation of micro- and nano-objects has been widely studied in the past two decades due to its potential applications in various fields. In this review, we focus primarily on magnetic field-based manipulation techniques, which have shown to be extremely promising for the motion control of such objects at small scales. We start from the fundamental analysis of the magnetic forces and the torques acting on objects subjected to magnetic fields, and then summarize the most recent contributions in magnetic manipulation employed in four typical applications: micro-mixing, trapping, colloidal assembly, and object transport. Moreover, how magnetic fields can be applied to object manipulation and the physical principles underlying these manipulation processes are highlighted.
- This article is part of the themed collection: Recent Review Articles


 Please wait while we load your content...
Please wait while we load your content...