Digging for topological property in disordered alloys: the emergence of Weyl semimetal phase and sequential band inversions in PbSe–SnSe alloys
Abstract
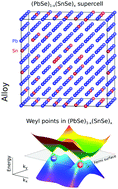
The search for topological systems has recently broadened to include random substitutional alloys, which lack the specific crystalline symmetries that protect topological phases, raising the question of whether topological properties can be preserved, or are modified by disorder. To address this question, we avoid methods that assumed at the outset high (averaged) symmetry, using instead a fully-atomistic, topological description of an alloy. Application to the (PbSe)1−x(SnSe)x alloy reveals that topology survives in an interesting fashion: (a) spatial randomness removes the valley degeneracy (splitting ≥150 meV), leading to a sequential inversion of the split valley components over a range of compositions; (b) the absence of inversion lifts spin degenerates, leading to a Weyl semimetal phase without the need of an external magnetic field, an unexpected result, given that the alloy constituent compounds are inversion-symmetric. (a) and (b) underpin the topological physics at low symmetry and complete the missing understanding of possible topological phases within the normal-topological insulator transition.


 Please wait while we load your content...
Please wait while we load your content...