4D printing reconfigurable, deployable and mechanically tunable metamaterials†
Abstract
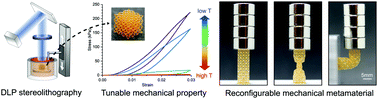
The exotic properties of mechanical metamaterials emerge from the topology of micro-structural elements. Once manufactured, however, the metamaterials have fixed properties without the ability to adapt and adjust. Here, we present geometrically reconfigurable, functionally deployable, and mechanically tunable lightweight metamaterials created through four-dimensional (4D) printing. Using digital micro 3D printing with a shape memory polymer, dramatic and reversible changes in the stiffness, geometry, and functions of the metamaterials are achieved.
- This article is part of the themed collections: Winners of the 2019 Horizons Outstanding Paper awards and A selection of 2019 articles


 Please wait while we load your content...
Please wait while we load your content...