Ultra-programmable buckling-driven soft cellular mechanisms

Abstract

Buckling, which was once considered the epitome of design failure, has been harnessed during the last few years to develop mechanical metamaterials with advanced functionalities. Soft robotics in general and soft actuators in particular could greatly benefit from such designer materials. Unlocking the great potential of buckling-driven materials is, however, contingent on resolving the main limitation of the designs presented to date, namely the limited range of their programmability. Here, we present multi-material buckling-driven metamaterials with high levels of programmability. We combined rational design approaches based on predictive computational models with advanced multi-material additive manufacturing techniques to 3D print cellular materials with arbitrary distributions of flexible and stiff materials in the central and corner parts of their unit cells. Using the geometry and spatial distribution of material properties as the main design parameters, we developed soft mechanical metamaterials behaving as mechanisms whose actuation force and actuation amplitude could be adjusted both independently and concomitantly within wide ranges. Our designs also resulted in the emergence of a new lowest instability mode, i.e. double-side buckling, in addition to the already known modes of side-buckling and symmetric compaction. Finally, we proposed a general approach to pre-dispose our soft mechanical metamaterials such that they can reliably actuate their higher instability modes without any need for additional boundary conditions or fixtures. To demonstrate this approach, we created a cellular mechanism with a rotational buckling pattern that clones the functionality of mechanical machines. The potential of the presented designs in robotics is then demonstrated by applying them as a force switch, kinematic controllers, and a pick and place end-effector.

---

New concepts

Owing to their soft touch, soft robots can safely and effectively interact with humans and other delicate objects. Soft programmable mechanisms are required to power this new generation of robots. Flexible mechanical metamaterials working on the basis of mechanical instability offer unprecedented functionalities programmed into their architectured fabric that make them potentially very promising as soft mechanisms. The tunability of the mechanical metamaterials proposed so far have been, however, very limited. Here, we present some new designs of ultra-programmable mechanical metamaterials where not only the actuation force and amplitude but also the actuation mode could be selected and tuned within a very wide range. Moreover, we demonstrate some examples of how these soft actuators could be used in robotics.

Mechanical metamaterials^1–4 enable the development of advanced materials with novel functionalities that originate from their unusual mechanical properties. The unusual mechanical properties often include either negative properties or extreme properties. Examples of negative properties are negative Poisson's ratio,^5–7 negative thermal expansion coefficient,^8–10 negative compressibility,¹¹ and negative stiffness.^12,13 Extremely high stiffness to mass ratio^14–16 and extremely high (low) resistance against deformation in specific directions^17,18 are examples of the extreme properties. Such otherwise “impossible” material properties allow for new approaches to material design. Soft mechanical metamaterials^19–22 have been of particular interest in this regard, as the combination of large recoverable (asymmetric) deformations, nonlinearity, and instability provides a fertile ground for development of novel properties and functionalities for application in, among other areas, soft robotics.

Within the context of soft robotics, the usually undesired concept of instability could be harnessed to create programmable mechanisms. Soft cellular mechanisms with certain levels of programmability such as the possibility to adjust the onset of instability or to switch between simple instability modes (e.g., side buckling vs. symmetric compaction) have been demonstrated before.^19,23,24 The level of programmability has, however, been limited so far. In particular, critical strains are usually geometry-dependent, meaning that it is impractical to drastically change the critical behavior once a specific type of geometry is chosen.^21,23,25 More importantly, the buckling patterns (i.e. the instability modes) have been limited to a few^19,23,24 without a clear strategy for reliable activation of the higher modes of instability that could support a much richer set of actuation modes. Furthermore, most designs presented to have been limited to 2D.^6,23,24 This level of adjustability is far below what would be required to make buckling-driven soft cellular mechanisms versatile enough to be used in soft robotics. The main challenge lies in achieving complex activation modes in 3D with a highly adjustable onset of instability. Even more difficult to achieve is a complex actuation pattern in 3D, as it would require activation of complex instability (i.e. buckling) modes. Soft mechanical metamaterials exhibit very complex activation patterns in their higher modes of instability. However, reliable activation of those modes is not easily achievable with simple forces and without imposing additional constraints that limit the applicability of the soft matter.

Although simple actuation modes (e.g. bending) have been already shown to be very useful in soft robotics,^26–30 in the case of buckling-driven soft cellular materials, truly versatile applications can be best achieved through designs that satisfy three major requirements. First, it should be possible to adjust the actuation force and actuation amplitude within wide ranges. Second, the designs should allow for both independent and concomitant adjustment of the actuation force and actuation amplitude. Finally, the actuation modes should cover a large number of possible modes including not only simple actuation modes but also a rich set of more complex actuation patterns. These requirements are ordered according to their difficulty. For example, it is much more challenging to design buckling-driven soft mechanisms that exhibit novel modes of buckling as compared to adjusting the actuation force/amplitude of an already existing buckling mode (e.g. symmetric compaction and side buckling). Here, we present a class of 3D mechanical metamaterials with geometrical and multi-material designs that enable them to satisfy all the above-mentioned requirements.

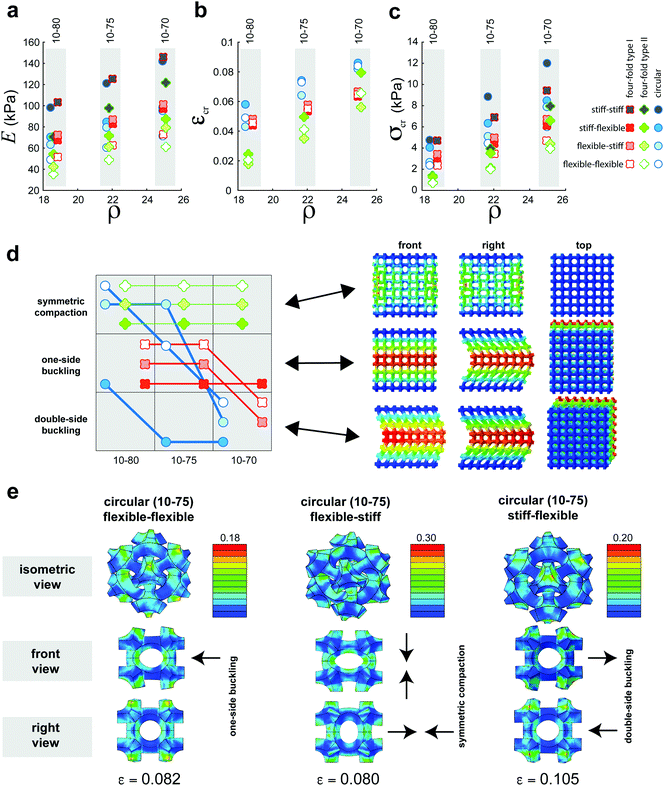
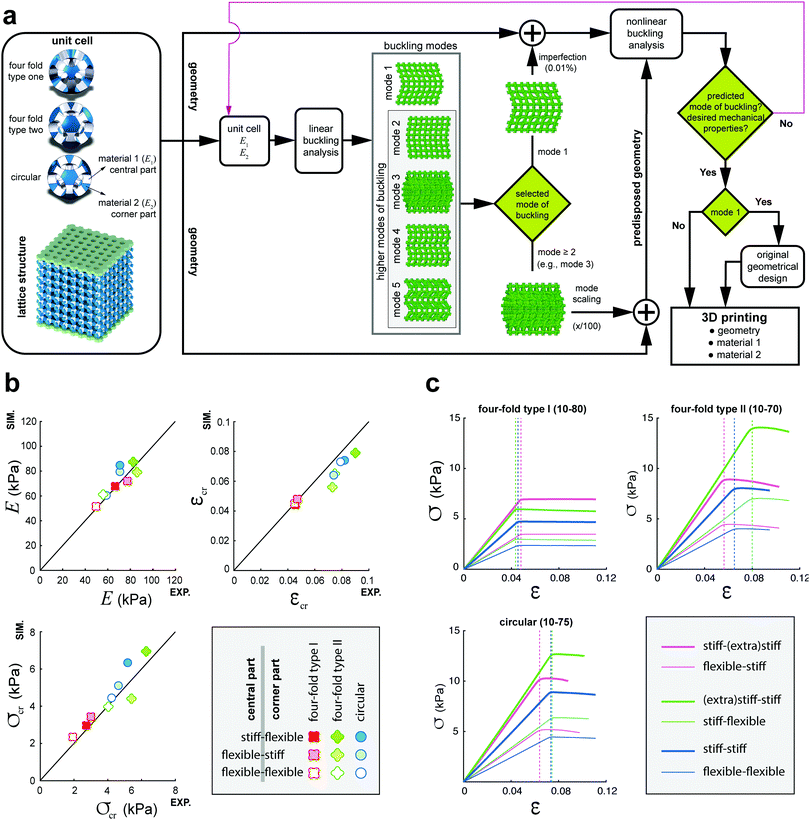
We designed 3D cellular arrays made by repeating single unit cells (Fig. 1a and Fig. S1, ESI†) in all spatial directions. The unit cells have been formed based on projections of 2D void shapes onto the six external tangential planes from the three major mid-planes of a hollow sphere. The symmetric voids were then formed by cutting-loft through the internal and external void shapes forming a porous ball with 6 holes (Fig. S1, ESI†). The projected 2D voids on the surfaces of the corresponding cube were respectively scaled up by 7.0, 7.5 and 8.0 times to create the representative unit cells with four-fold type II, circular, and four-fold type I void shapes. The selected projection ratios assured that the dimensions of the generated ligaments were similar and that the integrity of the unit cells was preserved. Because of the voids, twelve compliant connections were formed within each representative unit cell (Fig. 1a). We divided the unit cells into two parts, namely the corner and central parts, each of which has a different set of mechanical properties (flexible or stiff). The ratio of the mechanical properties of both parts were varied between values ≪1 and values ≫1. Nine different types of cellular mechanical metamaterials with three different types of unit cells and with three different ratios of the mechanical properties of the corner parts to the central parts were 3D printed using a multi-material additive manufacturing technique. The buckling and post-buckling behaviors of all nine types of cellular structures were also studied using computational models. The computational models were extended to include a wider study of how unit cell types and spatial distributions of the flexible and stiff materials influence the actuation force and actuation amplitude. Since the cellular materials work on the basis of buckling, the strain, ε_cr, and stress, σ_cr, at the onset of instability respectively regulate the actuation force and actuation amplitude, which is why we discuss our results in terms of those variables.

Fig. 1 (a) A schematic drawing illustrating the different steps followed in the current study to analyze and program the buckling behavior of our soft cellular mechanisms. The representative unit cells of the cellular structures are presented on the left side of this subfigure. The translational unit cells, which could be repeated in different directions to create the cellular structure, are somewhat different (see Fig. S1, ESI†). The labels 10–70 to 10–80 specify the ratio of the projected shapes to the faces of the reference cube, meaning that the projected geometries were scaled up to 7, 7.5, or 8 times of the 2D shapes on the mid-planes. (b) Comparison between the experimental and computational values of the Young's moduli, critical strains, and critical stresses for a selection of the designs considered here. (c) The critical strain can be adjusted independently from the total stiffness and critical stress by scaling the stiffness values of the central and corner parts.

Regarding the first requirement, we found that varying the void geometry and spatial distribution of the material properties are effective tools for adjusting the stiffness of the actuators, E, the actuation force (critical stress, σ_cr), and the actuation amplitude (critical strain, ε_cr) (Fig. 1 and 2). For the designs considered here, the stiffness, actuation amplitude, and critical stress respectively changed by 4 (35–146 kPa), 5 (0.018–0.086), and 16 (0.73–12.02 kPa) folds. Computational predictions were generally in good agreement with experimental data (Fig. 1b), meaning that the behavior of the proposed mechanisms could be predicted in advance. Computational models were therefore used for the rational design of buckling-driven mechanisms, as demonstrated below.

Independent as well as coupled adjustment of the actuation force and actuation amplitude (second design requirement) is usually very challenging to achieve, when the only design variable is the void geometry. Multi-material additive manufacturing offers the additional freedom to arbitrarily distribute the stiff and flexible materials in space.^31–34 When applied in conjunction with geometrical designs, multi-material designs form a firm basis for achieving the second design requirement. For example, the actuation force of the metamaterials with four-fold type I geometry substantially changed between stiff–flexible, flexible–stiff, and flexible–flexible designs while the actuation amplitude, remained practically the same (Fig. 1b and c). This particular design therefore results in cellular materials whose behavior is highly geometry-dependent, as different material properties only change the magnitude of the forces but not the principal features of the mechanism movement. On the other hand, simultaneous adjustment of the actuation force and actuation amplitude were possible using circular and four-fold type II geometries and by varying the spatial distribution of the flexible and stiff materials (Fig. 1b and c). More interestingly, the actuation force (i.e. critical stress) can be adjusted independent from the actuation amplitude (i.e. critical strain). This can be achieved by varying the stiffnesses of the central and corner parts while keeping their ratio constant. Fig. 1c demonstrates that the critical stress related to each design can be adjusted (here it is doubled for each design) by simply scaling the stiffness values of the central and corner parts. Taken together, these design parameters allow for designing a wide range of buckling-driven mechanisms. For example, combining large amplitude with small force is critical for applications where delicate objects such as soft tissues need to be manipulated. For such sensitive applications, the buckling could not only be used as the main actuation mechanism but may also serve as a safety switch preventing the actuation force to exceed the levels considered safe for the patient.

Designing novel as well as complex actuation modes was the most challenging design requirement and required unprecedented approaches that took full advantage of the form-freedom and material distribution-freedom offered by multi-material additive manufacturing techniques. The mere point of combining flexible and stiff materials in the central and corner regions resulted in the emergence of a new instability (buckling) mode, namely double-side buckling (Fig. 2 and Fig. S5, ESI†). The cellular materials studied to date^19,23,24 usually exhibit one of the two instability modes of side buckling or symmetric compaction. One of the reasons has been that most such metamaterials have been studied in 2D where double-side buckling is not possible. However, even a handful of 3D designs^19,35,36 did not report double-side buckling. Our computational models clearly showed that not only geometrical design parameters such as the type of unit cell and porosity but also the distribution of the material properties influence the type of instability mode (Fig. 2d). This is because both types of design parameters could substantially change the distribution of strains in each of the 12 complaint links making up the unit cells (Fig. 2e).

Fig. 2 The effects of the spatial distribution of material properties and geometrical design including void shape and relative density, ρ, on the actuation behavior of the multi-material metamaterials studied here: (a) total stiffness, (b) critical strain, and (c) critical stress. (d) A map of how different design parameters influence the first instability (actuation) mode of the metamaterials. The first instability modes include symmetric compaction, single-side buckling, and double-side buckling. (e) The strain distribution in the middle unit cells for the cellular structures with circular voids and with different combinations of material properties in the central and corner parts of the unit cells. The arrows indicate the direction of the deformations pertaining to the first buckling mode.

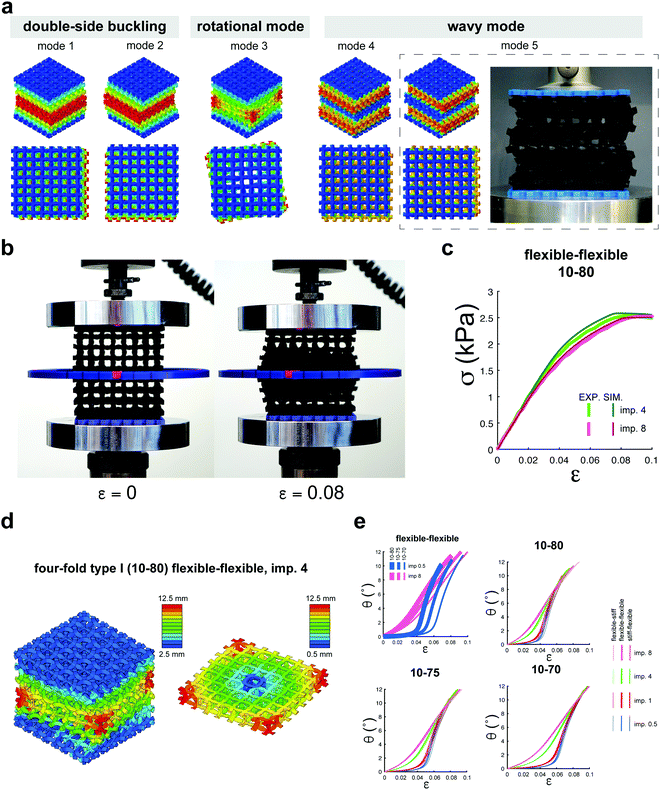
When trying to meet the third design requirement, even more important than the emergence of a new type of instability mode is actuating one of the higher modes of metamaterial instability (higher modes of buckling). The instability modes are determined in the linear theory of stability as the solutions to an eigenvalue problem in which the eigenvalues correspond to the linear values of the critical loading while the eigenvectors define the instability modes. The eigenvalues are numbered in an increasing order. The “higher modes of instability” therefore refer to the eigenvectors corresponding to the higher values of the instability load. Since the loading required to activate the first mode of instability is achieved first, the first mode of instability is the only one that can be reliably activated in most designs. Our extensive computational study showed that multi-material metamaterials possess a very rich physics and very complex higher instability modes. The problem, however, is that it is usually not possible to reliably actuate any of those modes, because the lower modes are activated before reaching the threshold required for activating the higher modes. Adding boundary conditions and designing fixtures that apply the actuation force in specific ways may enable activation of some of the higher instability modes.^37,38 However, that calls for a complex design process and mode-specific apparatus that will limit the practical application of such buckling-driven actuators. Here, we propose a simple and generally applicable technique for activating the higher modes of instability without any need for additional boundary conditions or fixtures. In this approach (Fig. 1a), we pre-dispose the mechanical metamaterials such that the first mode they activate is the desired mode of instability (Fig. 1a). We started off by computationally predicting the shape of the higher instability modes (predicted based on a linear bulking analysis). The desired actuation mode was then selected from the computationally predicted modes of instability. We then introduced the computed mode shape into the geometry of our mechanical metamaterial as imperfections with different amplitudes (i.e. imperfection severity). This allowed for reliable actuation of the desired mode without any need for additional boundary conditions or clamping devices. Fig. 3a illustrates the first five modes of instability (the buckling modes one to five) for the cellular structure four-fold type I. The fifth mode of instability was introduced to the initial geometry of the cellular material to realize a wavy mode of buckling (Fig. 3a).

Fig. 3 We actuated higher modes of instability by introducing imperfections that pre-disposed the cellular structure so that it would buckle under the desired mode. (a and b) To demonstrate this general approach, we fabricated wavy and rotating metamaterials that were based on cellular structures with the four-fold type I void geometry. In this case, imperfections (scale = 4) from the third and fifth modes of buckling were introduced to a cellular structure with 10–80 projection ratio and flexible–flexible distribution of materials to make it buckle without any need for boundary conditions or fixtures. (c) Comparison between experimental and computational values of axial stress vs. axial strain for two specimens with imperfection scales of 4 and 8. (d) The third instability mode as predicted by our computational models. (e) The effects of the geometrical design and imperfection magnitude on the characteristic curve of the actuator (i.e. rotational angle vs. axial strain) as well as the effects of the imperfection magnitude and spatial distribution of the stiff and flexible materials on the characteristic curves calculated for three different relative densities.

To demonstrate this general approach, we chose a rotational mode of actuation. Creating rotational actuation is generally challenging as highlighted by others.³⁵ However, rotational actuation is crucial for the concept of machine matter, as it bring us one step closer to the usual mode of mechanical machines, i.e. rotation.³⁵ We introduced the predicted mode shape as imperfections with different amplitudes to the original shape and studied how the imperfection amplitude as well as other design parameters affected the mechanical behavior and characteristic curves (rotational angle vs. axial strain) of the designed metamaterials. The measured stress–strain curves of the additively manufactured specimens (Fig. 3b) closely matched those predicted computationally (Fig. 3c). The specimens clearly showed a rotational behavior (Video V1, ESI,†Fig. 3b and d) with characteristic curves that were strongly dependent on the amplitude of the introduced imperfections and the projection ratio (Fig. 3e). Not only the scale but also the general trend of the characteristic curve changed with the imperfection amplitude (Fig. 3e). Smaller imperfections led to a two-stage actuation with limited rotations for the smaller values of axial strain followed by a second stage where the rotational angle sharply increased with the axial strain (Fig. 3e). Larger imperfections, however, made the rotation angles increase faster even for small axial strains and blurred the boundary between both stages (Fig. 3e). The effects of material distribution on the characteristic curve were small in comparison (Fig. 3e). The material properties of the central and corner parts, however, significantly influenced the actuation force (axial stress), meaning that the characteristic curves could be adjusted independently from the actuation forces. The near-perfect decoupling of the actuation force from the actuation kinematics presents a valuable tool for designing buckling-driven mechanisms for a multitude of applications.

To demonstrate the potential of the proposed designs for application in soft robotics, we performed three experiments in which our soft mechanisms were used as a force switch, as kinematic (position/velocity) controllers, and as a pick and place grasping mechanism (Fig. 4). As previously mentioned, the buckling mechanism could function as a force switch, allowing us to keep the force below a certain threshold over a large range of displacements. This type of force switch could be very useful, for example, in medical instruments and robotic surgery where a soft touch of the instrument significantly reduces the invasiveness of the treatment and (soft) tissues need to be protected against high values of gripping forces. In the case of our experiment, the buckling mechanism prevented the load applied to the egg to go beyond 40 N over a range of >15 mm (Video V2, ESI† and Fig. 4a). Such a large range of displacement will translate into a very comfortable tolerance for controlling the movements of robotic arms. In a second experiment, we used the rotational actuation modes (Fig. 3) of the specimens with different levels of imperfections to control the movement patterns of two table tennis balls (Video V3, ESI† and Fig. 4b). The different levels of imperfection introduced to both cellular structures caused very distinct movement patterns (Fig. 4b). Moreover, higher imperfection amplitudes linearized the behavior of the rotational mechanism, while instability patterns dominated the kinematics of the soft cellular mechanisms with smaller imperfection amplitudes. Finally, the same rotational mode of instability was used to design a pick and place ratchet and pawl assisted grasping mechanism, where the rotating mechanism locked into the object with the initial push enabling it to be moved to a new position at which point a second push released the object (Video V4, ESI† and Fig. 4c).

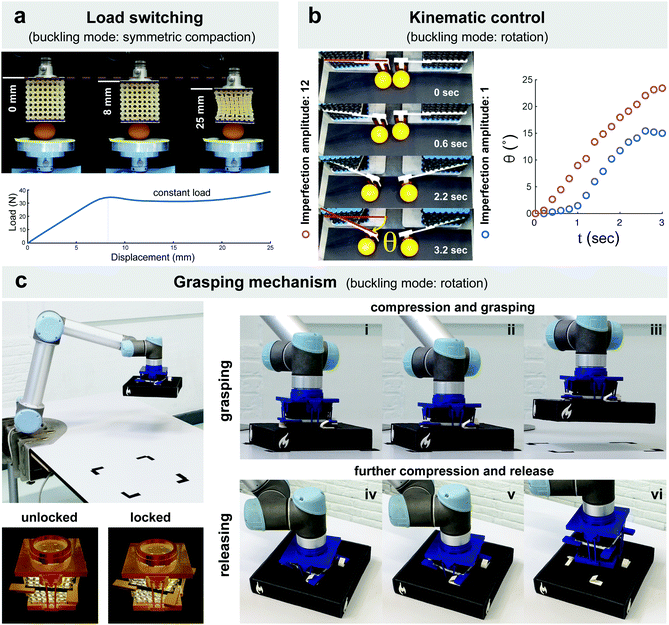Fig. 4 Some potential applications of the proposed soft mechanical metamaterials in robotics. (a) A force switch. The buckling of a sample cellular structure (four-fold type II (ϕ, r, d, n) = (0.45, 0.8, −1, 4), projection ratio: 10–70) allows for keeping the force applied to a raw egg almost constant and below 40 N for a large range (>15 mm) of displacements. (b) Kinematic (i.e. position/velocity) controllers. Two cellular structures (four-fold type I (ϕ, r, d, n) = (0.45, 0.7, +1, 4), projection ratio: 10–70) were pre-disposed to actuate their third instability mode (Fig. 3) using two imperfection amplitudes of 12 and 1. The different imperfection amplitudes caused distinct movement patterns and different absolute values of the position angle for two table tennis balls moved by both actuators. (c) A pick and place ratchet and pawl assisted grasping mechanism as the end effector of a robotic arm. The axial compression of the grasping mechanism is used to actuate the grasp and release mechanism. The rotational actuation mode of a cellular specimen (four-fold type I (ϕ, r, d, n) = (0.45, 0.7, +1, 4), projection ratio: 10–70, imperfection amplitude: 12) constrained between two clamps was used to lock the end effector into the object with the first push (i–iii). The clamps were linked to each other through four ratchet and pawl mechanisms. The object could then be moved to the desired location at which point a second push releases it (iv–vi).

It is important to note that all these different types of behavior are exhibited by the same type of material, meaning that one single design and manufacturing platform could be used to integrate a force-limiting switch into the mechanism, to control the speed of actuation, and to grasp objects. Even though none of these applications are unique in their own right, this combination of various functionalities is very interesting for real world applications at later stages. For example, these materials may be useful for the design of medical devices and prostheses that require a soft touch, a light weight, and the possibility to include flexible electronics (e.g., sensors). In such applications, the soft nature of these metamaterials provides the soft touch and maximizes patient safety while the cellular structure ensures that the weight of the device is minimized while lending itself to the incorporation of other functional devices (e.g., flexible electronics).

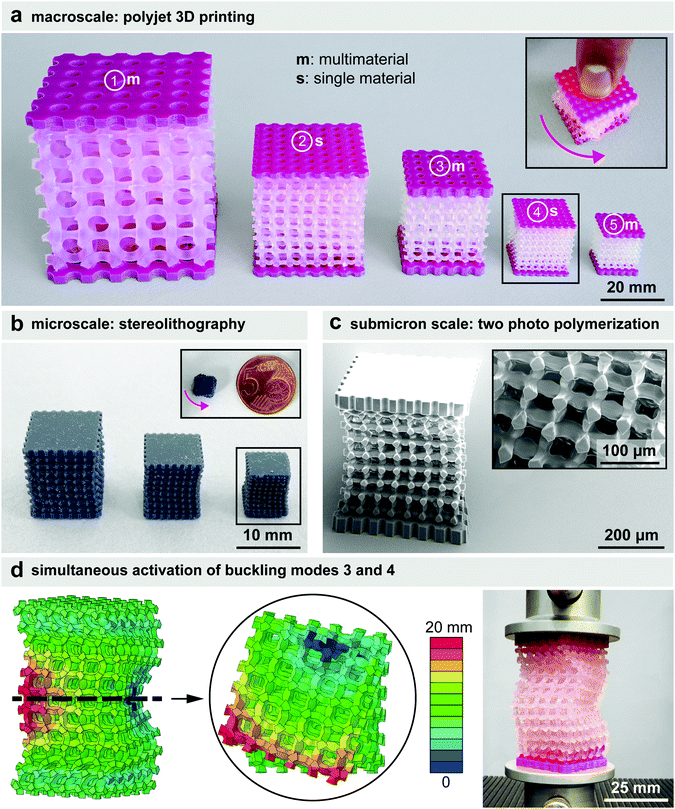
There are, however, several challenges that need to be overcome before such applications are realized. We considered two of such challenges including the miniaturization of the cellular structures and the possibility to create more complex deformations by combining multiple modes of buckling. Regarding the first aspect, we used three different 3D printing techniques to miniaturize our designs at the macro-, micro-, and submicron-scales (Fig. 5a–c). The macroscale specimens were made using the same multi-material 3D printing technique through which all our previous specimens were fabricated and included both geometrically perfect designs and designs that incorporated imperfections aimed at pre-disposing the cellular structures such that they activated their higher modes of buckling (Fig. 5a). Specimens with up to >5 times smaller dimensions could be realized through this approach (Fig. 5a). At the microscale, we used stereolithography to decrease the size of the specimens even further with dimensions that were up to >13 times smaller than the original dimensions of our specimens (Fig. 5b). The same rotational behavior resulting from the pre-disposition of the lattice structures could also be observed for these much smaller specimens (Fig. 5b). Finally, we used the two-photon polymerization technique to fabricate specimens that were >180 times smaller than our original specimens (Fig. 5c). The scanning electron microscopy images of these specimens clearly show that such specimens can be fabricated with submicron geometrical features (Fig. 5c). The main limitation regarding the stereolithography and two-photon polymerization techniques is that they are generally considered to be single-material 3D printing techniques. However, similar techniques have been recently developed that enable the fabrication of multi-material miniaturized mechanisms.^39,40 The possibility to miniaturize these buckling-driven soft mechanisms may also open up an avenue towards the design of programmable photonic⁴¹ and phononic⁴² devices.

Fig. 5 Miniaturization of our buckling-driven soft mechanical metamaterials (a–c) and the design of a more complex mechanism whose deformation pattern combines multiple buckling modes (d). (a) Application of the Polyjet-based 3D printing for macroscale fabrication of multi-material and single-material specimens with and without the pre-dispositions aimed at the activation of the higher buckling modes (e.g., rotational mode). All specimens were designed using unit cells with circular voids (i.e., (ϕ, r, d, n) = (0.45, 0, —, —), projection ratio = 10–75). To design the specimens that were pre-disposed to activate their higher modes of buckling (i.e., mode 4), the deformation pattern associated with that buckling mode was introduced as a geometrical imperfection (amplitude = 8) to the geometry of the specimens. The inset depicts the rotational behavior of a pre-disposed specimen. (b) Application of stereolithography for microscale fabrication of specimens that were geometrically similar to the pre-disposed specimens presented in subfigure a. A microscope slide was used to compress one of the specimens and confirm that it exhibits a rotational movement under compression. (c) The scanning electron microscopy images of a pre-disposed structure (i.e., four-fold type I, (ϕ, r, d, n) = (0.45, 0.7, +1, 4), projection ratio: 10–80, imperfection amplitude = 8 from the mode 3 of buckling) fabricated at the submicron scale using the two-photon polymerization technique. (d) Simultaneous activation of multiple buckling modes (i.e., modes 3 and 4) to combine rotation with a wavy-shaped deformation pattern. The imperfection introduced into the geometry of this specimen was the sum of the imperfections resulting from the scaling of both buckling modes (imperfection amplitudes of 8 and 4 for the buckling modes 3 and 4, respectively). The geometry of the specimen was based on the four-fold type I unit cells ((ϕ, r, d, n) = (0.45, 0.7, +1, 4), projection ratio: 10–70, scale = 50%).

Regarding the second aspect (i.e., simultaneous activation of multiple buckling modes), we performed computational modeling to predict the buckling modes of a cellular structure with a higher aspect ratio than the ones previously considered here (Fig. 5d). The deformations corresponding to the buckling modes 3 (i.e., rotation) and 4 (i.e., a wavy-shaped deformation pattern) were then summed up to create a geometrical imperfection that was used to pre-dispose the cellular structure (Fig. 5d). Our experiments clearly showed that the specimen designed using this approach deforms under a combination of the buckling modes 3 and 4 (Fig. 5d). This is an important conclusion, because it confirms that the deformations resulting from multiple modes of buckling could be combined with each other to program very complex deformation patterns into the soft cellular mechanisms proposed here.

The work presented here clearly shows the importance of form-freedom as well as freedom in the spatial distribution of multiple materials when trying to design buckling-driven soft materials. Predictive computational models are an important part of the rational design process too. When taken full advantage of, these three components enable the design of soft materials and mechanisms that are highly programmable not only in terms of the actuation force and actuation amplitude but, more importantly, in terms of the actuation mode. Of vital importance to the generality of the approach is the possibility to activate the higher modes of instability. The higher instability modes are usually so rich in geometry that they should be able to provide the basis for any practically relevant actuation mode either individually or in combination with each other. Purposeful introduction of imperfections into the metamaterial design could also be used for improving the reliability of actuation. Even when the intention is to activate the metamaterials through their first instability mode, another mode (e.g. second or third modes) may be actuated particularly when the critical loads of those modes are too close to that of the first one. Relatively small irregularities caused by the manufacturing process could then cause the metamaterial to actuate another (undesired) mode. Purposeful imperfections ensure that only the desired mode is activated.

The rational design process advocated here means that the actuation pattern and actuation characteristics could be programmed into the fabric of the metamaterials, thereby eliminating the need for an interconnected network of distributed actuators, sensors, and controllers that are usually needed for achieving complex actuations.^43,44 Buckling-driven metamaterials could have important medical applications in external prosthetic devices and wearable soft robotics such as exoskeletons and exosuits.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Dr Mukunda Bharatheesha (Department of Cognitive Robotics, TUDelft) for his help with the setting up of the robotic experiments. We also thank Dr Daniel Fan (Micro and Nano Engineering group, Department of Precision and Microsystems Engineering, TUDelft) for fabrication of the submicron structure using two photon polymerization apparatus.

References

1. J. N. Grima and R. Caruana-Gauci, Mechanical metamaterials: Materials that push back, Nat. Mater., 2012, 11, 565–566.
2. T. Buckmann, N. Stenger, M. Kadic, J. Kaschke, A. Frolich and T. Kennerknecht, et al., Tailored 3D mechanical metamaterials made by dip-in direct-laser-writing optical lithography, Adv. Mater., 2012, 24, 2710–2714.
3. A. A. Zadpoor, Mechanical meta-materials, Mater. Horiz., 2016, 3, 371–381.
4. J. H. Lee, J. P. Singer and E. L. Thomas, Micro-/nanostructured mechanical metamaterials, Adv. Mater., 2012, 24, 4782–4810.
5. R. Lakes, Foam Structures with a Negative Poisson's Ratio, Science, 1987, 235, 1038–1040.
6. K. Bertoldi, P. M. Reis, S. Willshaw and T. Mullin, Negative Poisson's ratio behavior induced by an elastic instability, Adv. Mater., 2010, 22, 361–366.
7. J. N. Grima, S. Winczewski, L. Mizzi, M. C. Grech, R. Cauchi and R. Gatt, et al., Tailoring graphene to achieve negative Poisson's ratio properties, Adv. Mater., 2015, 27, 1455–1459.
8. Q. Wang, J. A. Jackson, Q. Ge, J. B. Hopkins, C. M. Spadaccini and N. X. Fang, Lightweight Mechanical Metamaterials with Tunable Negative Thermal Expansion, Phys. Rev. Lett., 2016, 117, 175901.
9. J. Qu, M. Kadic, A. Naber and M. Wegener, Micro-Structured Two-Component 3D Metamaterials with Negative Thermal-Expansion Coefficient from Positive Constituents, Sci. Rep., 2017, 7, 40643.
10. R. Lakes, Cellular solids with tunable positive or negative thermal expansion of unbounded magnitude, Appl. Phys. Lett., 2007, 90, 221905.
11. Z. G. Nicolaou and A. E. Motter, Mechanical metamaterials with negative compressibility transitions, Nat. Mater., 2012, 11, 608–613.
12. E. B. Duoss, T. H. Weisgraber, K. Hearon, C. Zhu, W. Small and T. R. Metz, et al., Three-Dimensional Printing of Elastomeric, Cellular Architectures with Negative Stiffness, Adv. Funct. Mater., 2014, 24, 4905–4913.
13. T. A. Hewage, K. L. Alderson, A. Alderson and F. Scarpa, Double-Negative Mechanical Metamaterials Displaying Simultaneous Negative Stiffness and Negative Poisson's Ratio Properties, Adv. Mater., 2016, 28, 10323–10332.
14. X. Zheng, H. Lee, T. H. Weisgraber, M. Shusteff, J. DeOtte and E. B. Duoss, et al., Ultralight, ultrastiff mechanical metamaterials, Science, 2014, 344, 1373–1377.
15. L. R. Meza, S. Das and J. R. Greer, Strong, lightweight, and recoverable three-dimensional ceramic nanolattices, Science, 2014, 345, 1322–1326.
16. L. R. Meza, A. J. Zelhofer, N. Clarke, A. J. Mateos, D. M. Kochmann and J. R. Greer, Resilient 3D hierarchical architected metamaterials, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 11502–11507.
17. M. Kadic, T. Bückmann, N. Stenger, M. Thiel and M. Wegener, On the practicability of pentamode mechanical metamaterials, Appl. Phys. Lett., 2012, 100, 191901.
18. G. W. Milton and A. V. Cherkaev, Which Elasticity Tensors are Realizable?, J. Eng. Mater. Technol., 1995, 117, 483–493.
19. S. Babaee, J. Shim, J. C. Weaver, E. R. Chen, N. Patel and K. Bertoldi, 3D soft metamaterials with negative Poisson's ratio, Adv. Mater., 2013, 25, 5044–5049.
20. S. H. Kang, S. Shan, A. Kosmrlj, W. L. Noorduin, S. Shian and J. C. Weaver, et al., Complex ordered patterns in mechanical instability induced geometrically frustrated triangular cellular structures, Phys. Rev. Lett., 2014, 112, 098701.
21. J. Shim, S. C. Shan, A. Kosmrlj, S. H. Kang, E. R. Chen and J. C. Weaver, et al., Harnessing instabilities for design of soft reconfigurable auxetic/chiral materials, Soft Matter, 2013, 9, 8198–8202.
22. C. Coulais, D. Sounas and A. Alu, Static non-reciprocity in mechanical metamaterials, Nature, 2017, 542, 461–464.
23. J. T. B. Overvelde, S. Shan and K. Bertoldi, Compaction Through Buckling in 2D Periodic, Soft and Porous Structures: Effect of Pore Shape, Adv. Mater., 2012, 24, 2337–2342.
24. S. Janbaz, H. Weinans and A. A. Zadpoor, Geometry-based control of instability patterns in cellular soft matter, RSC Adv., 2016, 6, 20431–20436.
25. D. Pihler-Puzovic, A. L. Hazel and T. Mullin, Buckling of a holey column, Soft Matter, 2016, 12, 7112–7118.
26. S. I. Rich, R. J. Wood and C. Majidi, Untethered soft robotics, Nat. Electron., 2018, 1, 102–112.
27. M. Schaffner, J. A. Faber, L. Pianegonda, P. A. Ruhs, F. Coulter and A. R. Studart, 3D printing of robotic soft actuators with programmable bioinspired architectures, Nat. Commun., 2018, 9, 878.
28. M. Cianchetti, C. Laschi, A. Menciassi and P. Dario, Biomedical applications of soft robotics, Nat. Rev. Mater., 2018, 3, 143–153.
29. S. Kim, C. Laschi and B. Trimmer, Soft robotics: a bioinspired evolution in robotics, Trends Biotechnol., 2013, 31, 287–294.
30. T. van Manen, S. Janbaz and A. A. Zadpoor, Programming the shape-shifting of flat soft matter, Mater. Today, 2018, 21, 144–163.
31. D. S. Engstrom, B. Porter, M. Pacios and H. Bhaskaran, Additive nanomanufacturing – A review, J. Mater. Res., 2014, 29, 1792–1816.
32. A. R. Studart, Additive manufacturing of biologically-inspired materials, Chem. Soc. Rev., 2016, 45, 359–376.
33. A. A. Zadpoor and J. Malda, Additive Manufacturing of Biomaterials, Tissues, and Organs, Ann. Biomed. Eng., 2017, 45, 1–11.
34. S. Janbaz, M. McGuinness and A. A. Zadpoor, Multimaterial Control of Instability in Soft Mechanical Metamaterials, Phys. Rev. Appl., 2018, 9, 064013.
35. T. Frenzel, M. Kadic and M. Wegener, Three-dimensional mechanical metamaterials with a twist, Science, 2017, 358, 1072–1074.
36. X. Ren, J. H. Shen, P. Tranc, T. D. Ngo and Y. M. Xie, Design and characterisation of a tuneable 3D buckling-induced auxetic metamaterial, Mater. Des., 2018, 139, 336–342.
37. D. Schaeffer and M. Golubitsky, Boundary-Conditions and Mode Jumping in the Buckling of a Rectangular Plate, Commun. Math. Phys., 1979, 69, 209–236.
38. B. Florijn, C. Coulais and M. van Hecke, Programmable mechanical metamaterials, Phys. Rev. Lett., 2014, 113, 175503.
39. N. D. Dolinski, Z. A. Page, E. B. Callaway, F. Eisenreich, R. V. Garcia and R. Chavez, et al., Solution Mask Liquid Lithography (SMaLL) for One-Step, Multimaterial 3D Printing, Adv. Mater., 2018, 30, e1800364.
40. F. Mayer, S. Richter, J. Westhauser, E. Blasco, C. Barner-Kowollik and M. Wegener, Multimaterial 3D laser microprinting using an integrated microfluidic system, Sci. Adv., 2019, 5, eaau9160.
41. S. Babaee, P. Wang and K. Bertoldi, Three-dimensional adaptive soft phononic crystals, J. Appl. Phys., 2015, 117, 244903.
42. Z. Liu, H. Du, J. Li, L. Lu, Z. Y. Li and N. X. Fang, Nano-kirigami with giant optical chirality, Sci. Adv., 2018, 4, eaat4436.
43. R. Hedayati, M. J. Mirzaali, L. Vergani and A. A. Zadpoor, Action-at-a-distance metamaterials: Distributed local actuation through far-field global forces, APL Mater., 2018, 6, 036101.
44. M. J. Mirzaali, A. Caracciolo, H. Pahlavani, S. Janbaz, L. Vergani and A. A. Zadpoor, Multi-material 3D printed mechanical metamaterials: Rational design of elastic properties through spatial distribution of hard and soft phases, Appl. Phys. Lett., 2018, 113, 241903.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9mh00125e

---