Handedness-controlled and solvent-driven actuators with twisted fibers†
Abstract
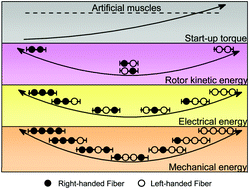
Plenty of biological materials are constructed from repeated unit cells with handed configurations, wherein the hierarchical self-assembly of handed units confers optimized mechanical properties and environmental adaptability to bulk biological materials. Inspired by biological handed architectures, we propose handedness-controlled and solvent-driven actuators by programming twisted fibers, such as twisted graphene oxide fibers (TGFs), with mirrored handedness, mechanical robustness and superb flexibility. The large twists (beyond 4800 turns per meter), hair-like diameter (down to 63 μm), large tensile strain (29%) and light weight (1.49 g cm−3) of TGFs enable them to provide a large start-up torque of 2.7 × 10−7 N m, and to deliver a record rotor kinetic power of 89.3 W kg−1 when stimulated by polar solvents such as acetone and water. By assembling handed TGF units, we achieve precise outputting of rotor kinetic energy (from 0.78 W kg−1 to 12.5 W kg−1), controllable harvesting of electrical energy (from 2.37 W kg−1 to 11.5 W kg−1), and free handling of a heavy object. The activeness, inertness and operation of all the actuating systems are well controlled by the handedness of TGF units. They are highly stable and reversible, and maintain a high energy output efficiency over multiple operation cycles. These handedness-controlled systems are also extended to hybrid twisted fibers containing nanocomposites and polymers, indicating their general practicability. Handedness-controlled actuators open an alternative avenue for fabricating energy harvesters, responsive textiles, electronic skins and soft robots.


 Please wait while we load your content...
Please wait while we load your content...