Open Access Article
Open Access ArticleAdvances in designs and mechanisms of semiconducting metal oxide nanostructures for high-precision gas sensors operated at room temperature
Zhijie
Li
 a,
Hao
Li
a,
Zhonglin
Wu
a,
Mingkui
Wang
a,
Hao
Li
a,
Zhonglin
Wu
a,
Mingkui
Wang
 b,
Jingting
Luo
c,
Hamdi
Torun
b,
Jingting
Luo
c,
Hamdi
Torun
 d,
PingAn
Hu
d,
PingAn
Hu
 e,
Chang
Yang
e,
Chang
Yang
 f,
Marius
Grundmann
f,
Marius
Grundmann
 f,
Xiaoteng
Liu
d and
YongQing
Fu
f,
Xiaoteng
Liu
d and
YongQing
Fu
 *da
*da
aSchool of Physics, University of Electronic Science and Technology of China, Chengdu, 610054, P. R. China
bWuhan National Laboratory for Optoelectronics, Huazhong University of Science and Technology, Luoyu Road 1037, Wuhan 430074, P. R. China
cShenzhen Key Laboratory of Advanced Thin Films and Applications, College of Physics and Energy, Shenzhen University, 518060 Shenzhen, China
dFaculty of Engineering and Environment, Northumbria University, Newcastle Upon Tyne, NE1 8ST, UK. E-mail: richard.fu@northumbria.ac.uk
eKey Laboratory of Micro-systems and Micro-structures Manufacturing of Ministry of Education, Harbin Institute of Technology, Harbin 150080, P. R. China
fFelix-Bloch-Institut für Festkörperphysik, Universität Leipzig, Linnéstr. 5, 04103 Leipzig, Germany
First published on 11th December 2018
Abstract
High-precision gas sensors operated at room temperature are attractive for various real-time gas monitoring applications, with advantages including low energy consumption, cost effectiveness and device miniaturization/flexibility. Studies on sensing materials, which play a key role in good gas sensing performance, are currently focused extensively on semiconducting metal oxide nanostructures (SMONs) used in the conventional resistance type gas sensors. This topical review highlights the designs and mechanisms of different SMONs with various patterns (e.g. nanoparticles, nanowires, nanosheets, nanorods, nanotubes, nanofilms, etc.) for gas sensors to detect various hazardous gases at room temperature. The key topics include (1) single phase SMONs including both n-type and p-type ones; (2) noble metal nanoparticle and metal ion modified SMONs; (3) composite oxides of SMONs; (4) composites of SMONs with carbon nanomaterials. Enhancement of the sensing performance of SMONs at room temperature can also be realized using a photo-activation effect such as ultraviolet light. SMON based mechanically flexible and wearable room temperature gas sensors are also discussed. Various mechanisms have been discussed for the enhanced sensing performance, which include redox reactions, heterojunction generation, formation of metal sulfides and the spillover effect. Finally, major challenges and prospects for the SMON based room temperature gas sensors are highlighted.
1. Introduction
Various types of hazardous gases, such as H2S, CO, NO2, NH3, H2, CH4, toluene, acetone, ethanol, methanol and benzene, are routinely and daily released from industrial and agriculture processes, or emitted as vehicle exhaust emissions. Some of them, such as H2 and CH4, are explosive when exposed to air, whereas the others, such as NO2 and toluene, are harmful for human health and the environment, when their concentrations are above a critical threshold, sometimes as low as at parts-per-million (ppm) levels. Therefore, development of high-precision gas sensors with high sensitivity, fast response, good selectivity, low limit of detection (LOD), as well as in situ and real-time monitoring capabilities is paramount.1,2 For this purpose, various types of gas sensors have been developed, mainly including resistive,3–5 optical,6–9 ultrasonic and acoustic wave,10–12 thermoelectric13,14 and electrochemical15–17 ones.Among these gas sensors, the resistive gas sensor is one of the most popular types, and is simple and easy to fabricate using cost effective processes. The transduction mechanism of resistive gas sensors is based on the change in resistance of a sensing layer upon adsorption and reaction with the target gas molecules. The sensing layer usually determines the sensitivity and selectivity. Therefore, the sensing materials and the structures of the sensing layer are highly critical to their sensing performance. The sensing materials used in these resistive gas sensors are mainly semiconducting metal oxide nanostructures (SMONs),18–21 carbon materials22–26 and organic semiconductors.27–30 Compared to the carbon materials and organic semiconductors, SMONs generally have higher sensitivity, faster response/recovery speed, better reversibility and stability, and they are cost-effective with simple fabrication processes.18–20 SMONs have large specific surface areas with numerous active sites, which facilitate fast adsorption and reaction of target gases, thus enhancing their sensing performance. They have been used to detect various hazardous gases for different applications as shown in Fig. 1. These SMON sensing materials mainly include ZnO,31,32 CuO,33–36 SnO2,37–39 TiO2,40,41 Fe2O3,42,43 In2O3,44–47 Co3O448–50 and WO3.18,51 For further improvement of sensing performance, they have been modified using noble metals,52–55 metal ions,56–60 and carbon materials.61–64 Composites of multi-phase SMONs65–67 have also been frequently reported.
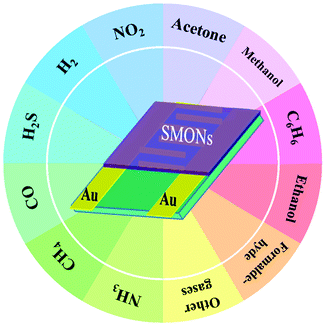 | ||
| Fig. 1 Schematic diagram of resistance-type gas sensors based on semiconducting metal oxide nanostructures for detection of various hazardous gases. | ||
SMON-based sensors are usually heated to a higher temperature (between 100 °C to 400 °C) for performance enhancement at the expense of structural complications.42–47 Operation at elevated temperature levels significantly increases the energy consumption, overall device size and cost of gas sensors. Heating up to a high temperature could lead to changes in the microstructure of the sensing nanomaterials, which can result in degradation of sensing performance. In addition, high-temperature sensing has its practical limitations. Particularly, heating is very dangerous for the detection of flammable and explosive gases, with a risk of explosion. Therefore, sensors operated at room temperature (RT) are desirable for minimizing energy consumption and cost, increasing security and stability, realizing device miniaturization and suitability for handheld operations.68,69 For these reasons, RT gas sensors based on the SMONs have received extensive attention in recent years. Different configurations of SMONs employing nanostructures have been demonstrated with desirable performance enhancements,70 regarding sensitivity, response/recovery time, selectivity, reversibility, reproducibility and long-term stability. Various SMONs have been designed and synthesized, such as nanorods,71–75 nanoparticles,76–81 nanowires,82–89 nanospheres,90 nanosheets,91–94 nanotubes,95–98 and mesoporous nanostructures.99–103
The literature on SMON-based RT gas sensing is rich and the application area is very critical. New devices have been regularly introduced. Although the merits of the SMON based RT gas sensors have already been demonstrated, currently there are still some key challenges:
(1) The sensing performance of these SMON based gas sensors is limited, when operated at RT. For example, many of these sensors exhibit insufficient sensitivities.104–108
(2) The response/recovery times of many RT gas sensors, which are crucial for rapid detection of target dangerous gases to timely trigger an alarm, are generally quite long, sometimes, up to tens of minutes.109–111
(3) Poor reversibility has been reported for some of these sensors operated at RT.101
(4) Poor selectivity is another key limitation for the RT gas sensors. Selectivity of many SMON based RT gas sensors needs to be improved to avoid interference and cross-talks.112
The aim of this topical review is to critically evaluate the design and structure of SMON-based gas sensors that may help guide the design of new devices. The performance of these SMON based gas sensors operated at RT could be improved significantly by modifying the SMONs using noble metal nanoparticles,113–116 metal ions,117–119 composites of multiple SMONs120–123 and carbon nanomaterials.124–126 In addition, not only the quantity of chemisorbed oxygen species,127 defects128 and element compositions129,130 on the surface of SMONs, but also the structural properties, i.e., porosity,131 heterojunction properties132–134 and conductivity135,136 can affect the RT gas sensing performance. Therefore, understanding the relationship between the sensing properties and structures of SMONs is crucial to design gas sensing materials with good sensing performance operated at RT.
Several review papers have been published on gas sensors based on different SMON sensing materials, including n-type oxide semiconductors such as ZnO,20,137 Fe2O3,138 SnO2,39,139,140 p-type oxide semiconductors,141 metal oxide-based heterojunctions,142 noble metal/metal oxide semiconductors143,144 and graphene–metal oxide nanohybrids.145 However, these review papers discuss the sensing properties of the sensors which are generally operated at higher working temperatures above RT.146–150 Others about the RT gas sensors are focused more on certain types of SMONs based on RT sensors, such as nanostructured ZnO based RT gas sensors.151 However, there is no comprehensive review which is focused on the recent progress in various SMONs for high-precision gas sensors operated at RT. Therefore, this review will comprehensively summarize and discuss the recent developments of the RT gas sensors based on single phase SMONs, noble metal and metal ion modified SMONs, composites of SMONs with other metal oxides, and composites of SMONs with carbon nanomaterials, as shown in Fig. 2. In addition, we will discuss the effect of UV light stimulation on enhancing the performance of SMON based RT gas sensors, and mechanically flexible RT gas sensors based on SMONs.
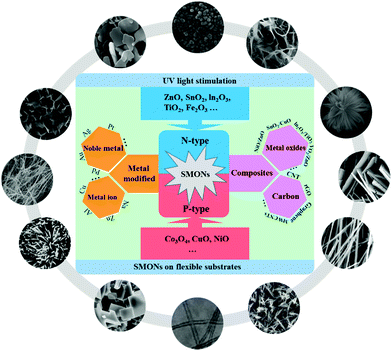 | ||
| Fig. 2 Schematic diagram of various semiconducting metal oxide nanostructures used for RT gas sensors presented in this review. | ||
2. Room temperature gas sensors based on single phase semiconducting metal oxide nanostructures
2.1 N-type semiconducting metal oxide nanostructures and gas sensors
N-type SMONs are the most reported sensing materials for RT resistive gas sensors, and they include ZnO,152–156 SnO2,157–160 In2O3,161 WO3,162 TiO2,163–166 Fe2O3,167–169 MoO3,170 VO2171 and CeO2.172 Various forms of nanostructures including nanoparticles, nanorods, nanowires, nanoflowers, nanosheets, nanofilms, nanotubes, porous structures and hierarchical nanostructures have been employed to detect various types of gases including H2S,99,101 NO2,157 H2,173 NH3,174 acetone,175 alcohol,106 HCHO,176 liquefied petroleum gas (LPG), etc.Table 1 summarizes some of the reported RT sensors using the n-type SMONs.| Material | Structure | Synthesis method | Target gas | C (ppm) | Response | t res/trec | LOD | Ref. |
|---|---|---|---|---|---|---|---|---|
| C = concentration; tres/trec = response time/recovery time; LOD = limit of detection; response is defined as Ra/Rg (for reducing gases) or Rg/Ra (for oxidizing gases), Ra: resistance of the sensor exposed to the reference, Rg: resistance of the sensor exposed to the target.a Here the response is defined as ΔR/Rg (for reducing gases) or ΔR/Ra (for oxidizing gases), ΔR: the change in resistance.b Here the response is defined as (ΔR/Rg) × 100% (for reducing gases) or (ΔR/Ra) × 100% (for oxidizing gases). | ||||||||
| ZnO | Combs | CVD | H2S | 4 | 6 | 22/540 s | 100 ppb | 152 |
| ZnO | Dendritic | Vapor-phase transport | H2S | 500 | 26.4 | 20/50 s | 10 ppm | 153 |
| ZnO | Nanorods | Hydrothermal | H2S | 1 | ∼35 | ∼20/— min | 0.05 ppm | 109 |
| ZnO | Quantum dots | Colloidal process | H2S | 50 | 113.5 | 16/820 s | 10 ppm | 177 |
| ZnO | Nanorods | Vapor-phase transport | H2S | 1 | 296 | 320/3592 s | 0.5 ppm | 71 |
| ZnO | Thin films | Thermal evaporation | Ethanol | 100 | 3 | — | — | 178 |
| ZnO | Tetrapod network | Thermal oxidation | Ethanol | 1000 | ∼4.5 | 300/— s | ∼10 ppm | 179 |
| ZnO | Nanorods | Laser ablation | Ethanol | 250 | 14 | — | ∼1 ppm | 154 |
| ZnO | Nanorods | Electrospinning | Ethanol | 100 | 23 | 26/43 s | ∼1 ppm | 180 |
| ZnO | Nanowires | Electrospinning | Ethanol | 100 | 78 | 9/12 s | ∼1 ppm | 82 |
| ZnO | Nanorods | Wet chemical route | NH3 | 200 | 24.1 | 239/398 s | ∼50 ppm | 181 |
| ZnO | Nanowires | AAO template | NH3 | 50 | 68b | 28/29 s | ∼10 ppm | 83 |
| ZnO | Thin films | Spray pyrolysis | NH3 | 25 | 233 | 20/25 s | 5 ppm | 182 |
| ZnO | Thin films | Magnetron sputtering | NH3 | 100 | 304 | 92/113 s | 5 ppm | 112 |
| ZnO | Nanowalls | Solution | NO2 | 50 | ∼6.2 | 23/11 s | ∼5 ppm | 91 |
| ZnO | Nanowires | Drop-cast | NO2 | 20 | 32 | 72/69 s | ∼5 ppm | 183 |
| ZnO | Nanorods | Wet chemical route | NO2 | 1 | 100b | ∼5/∼20 min | ∼1 ppm | 110 |
| ZnO | Nanowires | CVD | NO | 10 | 46b | — | 1.5 ppm | 184 |
| ZnO | Nanocombs | CVD | CO | 250 | 7.22 | 200/50 s | — | 185 |
| ZnO | Nanorod arrays | Microwave hydrolysis | CO | 100 | 81.1b | —/2.5 min | 10 ppm | 72 |
| ZnO | Nanorods | Chemical deposition | H2 | 150 | ∼2b | 50–80/— s | — | 186 |
| ZnO | Nanorods | Hydrothermal | H2 | 200 | ∼4b | 30 s/50–90 s | ∼1 ppm | 187 |
| ZnO | Nanowires | CVD | H2 | 121 | 8b | 29/— s | — | 108 |
| ZnO | Nanotubes | Aqueous chemical | H2 | 500 | 29.6b | — | — | 188 |
| ZnO | Thin films | Spray pyrolysis | H2 | 150 | 63 | 320/200 s | — | 189 |
| ZnO | Nanorods | RF magnetron sputtering | H2 | 1000 | 91b | 18.8/∼130 s | 0.2 ppm | 173 |
| ZnO | Nanorod arrays | Atomic layer deposition | H2 | 500 | 162 | 30/— s | 5 ppm | 190 |
| ZnO | Nanorod arrays | Chemical deposition | H2 | 1000 | 500b | 176/116 s | — | 191 |
| MoO3 | Nanoribbons | Hydrothermal | H2 | 1000 | 90b | 14.1/— s | 0.5 ppm | 192 |
| SnO2 | Nano-films | Sol–gel | H2 | 1000 | 2570b | 192/95 s | — | 193 |
| SnO2 | Nanotubes | Electrospinning | NOx | 9.7 | 89.2b | 6/218 s | 9.7 ppb | 95 |
| SnO2 | Nanocrystals | Chemical precipitation | NO2 | 11 | 33a | 100/250 s | ∼3 ppm | 76 |
| SnO2 | Thin films | Pulsed laser deposition | NO2 | 4 | 7730 | 3/176 s | ∼4 ppm | 157 |
| SnO2 | Thin films | Sol–gel | Ozone | 0.5 | 3.1 | 15/12 min | — | 194 |
| SnO2 | Nanorods | Microwave | O2 | 10 | ∼16.5a | ∼200/∼50 s | ∼1 ppm | 73 |
| SnO2 | Nanoporous | Hydrothermal | Acetone | 100 | 14.64a | 30/20 s | ∼10 ppm | 99 |
| SnO2 | Nanocrystals | Sol–gel | NH3 | 50 | 694.4b | 175/210 s | — | 158 |
| SnO2 | Nanowires | Precipitation | Ethanol | 6000 | 8000 | — | — | 88 |
| In2O3 | Nanowires | CVD | H2S | 20 | 2 | 48/56 s | 1 ppm | 84 |
| In2O3 | Whiskers | Carbothermal | H2S | 10 | 30b | 4/120 min | 200 ppb | 104 |
| In2O3 | Nanotubes | Electrospinning | H2S | 20 | 167 | 287/636 s | ∼1 ppm | 161 |
| In2O3 | Nanotubes | Electrospinning | H2S | 50 | 320.14 | 45/127 s | 200 ppb | 100 |
| In2O3 | Porous thin films | Template | H2S | 50 | 240![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
140/— s | 1 ppm | 101 |
| In2O3 | Microcrystallites | Thermal oxidation | NH3 | 1000 | 92b | 100/60 s | ∼250 ppm | 195 |
| In2O3 | Nanotubes | Precipitation | NH3 | 20 | 2500 | <20/20 s | ∼5 ppm | 111 |
| In2O3 | Octahedra | Sol–gel | NO2 | 200 | ∼70 | ∼500/∼500 s | 0.1 ppm | 196 |
| In2O3 | Mesoporous nanocrystals | Hydrothermal | NOx | 97 | 158.7a | 96/— s | 970 ppb | 102 |
| In2O3 | Cubic crystals | Hydrothermal | Ethanol | 100 | 1.4 | 5/3 s | ∼10 ppm | 105 |
| WO3−x | Quantum dots | Solvothermal | HCHO | 100 | 1.6 | 2/3 min | 1.5 ppm | 77 |
| WO3 | Nanocolumns | Hydrothermal | Isopropanol | 200 | 6.7 | 53/274 s | 1 ppm | 162 |
| WO3 | Nano-films | Thermal evaporation | Ethanol | 30 | 35b | ∼300/300 min | ∼10 ppm | 106 |
| TiO2 | Thin films | Anodic oxidation | NH3 | 100 | 0.32a | <2/2 min | ∼50 ppm | 107 |
| TiO2 | Quantum dots | Hydrolysis method | NH3 | 0.2 | 2.13 | 88/23 s | 0.2 ppm | 164 |
| TiO2 | Nano-films | Sol–gel | NH3 | 50 | 35b | 4/6 min | ∼10 ppm | 163 |
| TiO2 | Nano-films | Magnetron sputtering | NH3 | 100 | 7857 | 34/90 s | 5 ppm | 174 |
| TiO2 | Nanoparticles | Sol–gel | NH3 | 100 | 10080.8 | 35.5/59 s | ∼1 ppm | 78 |
| TiO2 | Nanotubes | Electrochemical anodization | CHCl3 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
∼0.76 | ∼3/— min | 1000 ppm | 167 |
| TiO2 | Nanorods | Acid vapor oxidation | O2 | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
1.68 | 40/75 s | 1000 ppm | 74 |
| TiO2 | Thin films | Magnetron sputtering | CH3NH2 | 10 | 11.3b | 200/260 s | ∼2 ppm | 197 |
| TiO2 | Nanodots | Nano-oxidation | NO | 10 | 31b | 91/184 s | ∼5 ppm | 165 |
| TiO2 | Nanotube arrays | Electrochemical anodization | HCHO | 50 | ∼37b | 3/— min | 0.04 ppm | 176 |
| TiO2 | Nanotubes | Electrochemical anodization | Methanol | 1000 | 60b | 34/130 s | 10 ppm | 96 |
| TiO2 | Nanotubes | Electrochemical | Acetone | 100 | 70.18b | 19/14 s | ∼10 ppm | 97 |
| TiO2 | Nanoparticles | Hydrothermal | NO2 | 40 | 1093 | 48/52 s | 0.02 ppm | 79 |
| TiO2 | Nanorods | Hydrothermal | CH4 | 60 | 6028 | — | 5 ppm | 166 |
| Fe2O3 | Nanoparticles | Hydrothermal | H2S | 100 | 38.4 | ∼180/∼3700 s | 50 ppb | 80 |
| Fe2O3 | Nanonails | Screen printing | LPG | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
51 | 120/150 s | 5000 ppm | 168 |
| MoO3 | Thin films | Magnetron sputtering | NO | 200 | 92b | 30/1500 s | 5 ppm | 170 |
| VO2 | Nanorods | CVD | NO2 | 5 | 2.42 | 59/86 s | ∼1 ppm | 171 |
| VO2 | Nanorods | Thermal evaporation | CH4 | 500 | 35a | 75/158 s | ∼100 ppm | 75 |
| V2O5 | Nanoneedles | Vapor deposition | Acetone | 1.7 | 1.025 | 73/— s | 941 ppb | 175 |
| CeO2 | Nanowires | Hydrothermal | H2S | 0.05 | 1.11 | 24/15 s | 50 ppb | 86 |
The operation temperature of gas sensors determines the types of chemisorbed oxygen ions. For example, they are mainly O2− when the temperature is below 100 °C. When the working temperature is increased between 100 °C and 300 °C, the O2− ions will capture electrons and then transform into O− ions. The O− can be converted into O2− ions at a higher working temperature above 300 °C. The formation process of oxygen ions can be summarized using the following equations:42,43
| O2(gas) ↔ O2(ads) | (1) |
| O2(ads) + e− ↔ O2−(ads) (<100 °C) | (2) |
| O2−(ads) + e− ↔ 2O−(ads) (100–300 °C) | (3) |
| O−(ads) + e− ↔ O2−(ads) (>300 °C) | (4) |
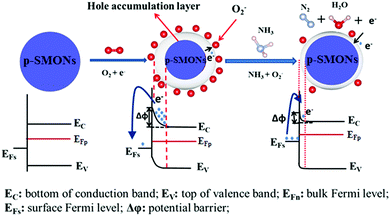
If the target gases are reducing gases, such as H2S, H2, NH3, HCHO, or C2H5OH, the chemical reaction releases electrons, which are reinjected back to the electron depletion layer (see Fig. 3, the schematic diagram for H2S gas sensing mechanism). This results in the reduction of the electron depletion layer and reduces the potential barrier energy (Δϕ). As a result, the surface resistance of SMONs is decreased. In contrast, if the target gases are oxidizing gases, such as NO, NO2, Cl2 and O3, the reaction with the chemisorbed oxygen ions will capture the electrons, which will widen the electron depletion layer, resulting in an increase of the potential barrier energy (Δϕ). Accordingly, the surface resistance of the SMONs is increased.
 | ||
| Fig. 3 Schematic diagram of the sensing mechanism of n-type semiconducting metal oxide nanostructures for reducing gas of H2S. | ||
There are generally three definitions for the response values of n-type SMON based gas sensors, which are Ra/Rg, (Ra − Rg)/Rg and ((Ra − Rg)/Rg) × 100% for the target reducing gases, respectively (where Rg and Ra are the resistance of sensors in the target gas and air, respectively). However, for the oxidizing gases, Ra and Rg need to be inter-changed in the above three definitions.196 The time from the injection of the target gas to the time of reaching 90% of the final response is defined as the response time, and the time from the extraction of the gas to the time of reaching 10% of the final response is defined as the recovery time.
Generally, formation of chemisorbed oxygen ions determines the sensing performance. However, the gas sensing mechanism is sometimes attributed to the formation of new compounds as a result of reactions between the target gas and the surface of the SMONs. For example, H2S gas molecules can react with ZnO to form ZnS at RT.71,109 Formation of such type of conductive metal sulfide significantly decreases the resistance of the SMON-based sensors, which accounts for high sensitivities of n-type SMON-based sensors for H2S.
Chemical and electronic sensitization of the SMONs can be realized by adding noble metals on their surface and thus can remarkably enhance their sensing properties. Surface modifications and introduction of defects on the surfaces and interfaces such as introduction of heterojunctions134 and vacancies117 influence the sensing performance of SMON sensing materials. Addition of carbon nanomaterials on the surface of SMONs can also significantly improve their conductivity and enhance their sensitivities at RT.135 In addition, an alkaline center129 and hydroxide radicals198 on the surfaces of SMONs have also been reported to affect the sensing properties, which will be discussed further.
| 2H2S(g) + O2−(ads) ↔ 2H2O(g) + 2SO2(g) + 3e− | (5) |
| ZnO + H2S(ads) → ZnS + H2O | (6) |
| In2O3 + 3H2S(ads) → In2S3 + 3H2O | (7) |
The reaction of metal sulfides in the sensing process and the transformation of metal sulfides back to metal oxides in the recovery process are sometimes very slow at RT. Therefore, for the RT H2S gas sensors, the response time and especially the recovery time are often relatively long, sometimes as long as several hours.71,109 Furthermore, the sensors may not fully recover at RT.101 The sensor should often be heated to a relatively higher temperature (e.g. 200 °C to 300 °C) in the recovery process for a complete recovery or shortening of the recovery time down to minute-scales.109
Hosseinia et al.71 prepared vertically aligned ZnO rods with a diameter of 300–500 nm and a length of 1–9.5 μm using a vapor phase transport method. The nanorods are grown along the c-axis or (0002) planes perpendicularly to the substrate surface as shown in Fig. 4a. The porous network of vertically aligned ZnO rods forms directional channels, which facilitates the mobility of gas molecules. As shown in Fig. 4b, the sensor based on the vertically aligned ZnO rods shows a much higher response to H2S at 26 °C than that at 250 °C, and its response value for H2S at RT is almost 600 times larger than those for other gases, such as CH4, CO, H2S, methanol, ethanol, acetone, H2 and He. However, at 250 °C, it is less than twice the original value. The response and recovery times of this sensor are very long, which are 320 s and 3592 s for 1 ppm H2S as shown in Fig. 4c. ZnO nanorods were also grown using a hydrothermal method with diameters of 70–110 nm and lengths of 0.2–1.3 μm and then used for H2S sensing.109 These sensors exhibit a high response (about 35 to 1 ppm H2S) and a very low LOD (50 ppb). However, its response time is longer than 20 min, and the sensor is difficult to recover at RT. Response and recovery rates of RT H2S gas sensors can be improved using dendritic ZnO nanostructures prepared using a vapor-phase transport method with Cu as the catalyst at 930 °C.153 The multilevel branches of ZnO have well-oriented nanorods with diameters of 60 to 800 nm. The response/recovery times are 20/50 s, which make this sensor the fastest SMON-based H2S sensor at RT reported so far. The sensor exhibits a high response of 26.4 to 500 ppm H2S and good selectivity against various gases including H2S, NH3, H2 and NO2 in dry air at RT. The large degree modulation of the contact energy barriers due to the H2S gas in ZnO dendrites is the key reason for their excellent sensing performance at RT.
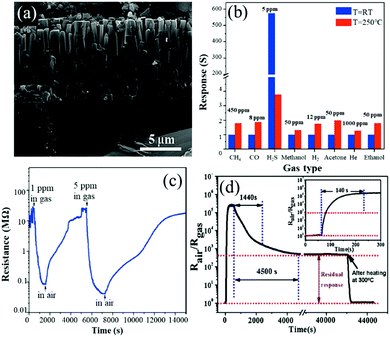 | ||
| Fig. 4 (a) Cross-section SEM image of vertically aligned ZnO rods; (b) selectivity of the sensor at 25 °C and 250 °C; (c) response/recovery curves to 1 and 5 ppm H2S at room temperature.71 Copyright 2015, Elsevier. (d) The response/recovery curve at 50 ppm H2S gas at room temperature.101 Copyright 2017, Elsevier. | ||
Nanostructured In2O3 is another widely studied material for H2S sensing. Apart from reactions of H2S gas with oxygen ions on the surface of In2O3, the formation of In2S3 is another key factor for the sensor's high response at RT. Remarkably, the response value of the In2O3 nanostructure can reach 240![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for 50 ppm of H2S at RT101 as shown in Fig. 4d. The micro/nanostructured porous In2O3 film was synthesized onto an Al2O3 ceramic tube using a self-assembly method,101 which has an ordered porous structure with a thickness of 200 nm. Although the sensor does not fully recover to its baseline at RT, it can be rapidly and completely recovered at 300 °C. Using a conventional electrospinning process, Duan et al.100 prepared In2O3 thick walled toruloid nanotubes. Owing to their larger surface areas, the nanotubes have more active sites among them, which results in enhanced responses to H2S gas. The sensors based on the In2O3 nanotubes exhibit high response values of 320.14 to 50 ppm H2S and fast response/recovery times of 45/127 s at the RT. In addition, good selectivity and a very low LOD with a value of 100 ppb have been demonstrated.100 Porous In2O3 nanotubes with a cubic phase have been prepared using the electrospinning method,161 and a high response value of 166.6 to 20 ppm H2S has been demonstrated. However, the response/recovery times are quite long (287/636 s).
000 for 50 ppm of H2S at RT101 as shown in Fig. 4d. The micro/nanostructured porous In2O3 film was synthesized onto an Al2O3 ceramic tube using a self-assembly method,101 which has an ordered porous structure with a thickness of 200 nm. Although the sensor does not fully recover to its baseline at RT, it can be rapidly and completely recovered at 300 °C. Using a conventional electrospinning process, Duan et al.100 prepared In2O3 thick walled toruloid nanotubes. Owing to their larger surface areas, the nanotubes have more active sites among them, which results in enhanced responses to H2S gas. The sensors based on the In2O3 nanotubes exhibit high response values of 320.14 to 50 ppm H2S and fast response/recovery times of 45/127 s at the RT. In addition, good selectivity and a very low LOD with a value of 100 ppb have been demonstrated.100 Porous In2O3 nanotubes with a cubic phase have been prepared using the electrospinning method,161 and a high response value of 166.6 to 20 ppm H2S has been demonstrated. However, the response/recovery times are quite long (287/636 s).
Other n-type SMONs such as α-Fe2O380 and CeO286 have also been reported as good sensing materials for H2S sensing at RT. For example, porous α-Fe2O3 nanoparticles with a diameter of 34 nm and pore sizes from 2 nm to 10 nm were obtained after annealing a FeOOH nanoparticle precursor.80 The sensor based on these porous α-Fe2O3 nanoparticles exhibits a high sensitivity (38.4 for 100 ppm H2S) with a low LOD (50 ppb). In addition, it has good selectivity to H2S against the other gases (e.g., C2H5OH, CO, H2 and NH3) and shows good reproducibility. The response time is fast with a value of 180 s. However, the recovery time is very long with a value of 3750 s for 100 ppm H2S. CeO2 nanowires86 were also synthesized using a facile hydrothermal process and they show fast response/recovery times with values of 24/15 s for 50 ppb H2S.
For the α-Fe2O3 and CeO2 nanostructure-based H2S gas sensors, the main sensing mechanism is the interactions of the H2S molecules with the oxygen ions on their surface. Accordingly, the sensing is much faster than those sensors based on ZnO and In2O3, although their response to H2S is much lower.80,86
| NO2(gas) + e− ↔ NO2−(ads) | (8) |
| NO2−(ads) + O2−(ads) + 2e− ↔ NO(gas) + 2O2−(ads) | (9) |
One of the outstanding features of SMON-based RT NO2 gas sensors is their fast response speeds due to the strong oxidation of NO2 molecules. Kodu et al.157 reported NO2 sensors based on granular SnO2 thin films with a thickness of ∼90 nm deposited using a pulsed laser deposition method. The sensor exhibits not only a remarkably high response value of 7730 to 4 ppm NO2, but also a very fast response time of 3 s at RT. Wei et al.76 prepared SnO2 nanocrystals by annealing Sn(OH)4 precursor powders at 550 °C in both vacuum and ambient air environments, respectively. The vacuum-annealed SnO2 and air-annealed SnO2 nanocrystals have different particle diameters of 7.2 nm and 10.3 nm as shown in Fig. 5a. The response value of the vacuum-annealed SnO2 sensor at RT is ∼2.4 to 5 ppm of NO2, which is higher than that of air-annealed SnO2 (∼0.35). This is mainly because the increased oxygen vacancies on the surface of the vacuum-annealed SnO2 are much more than those on the air-annealed SnO2 nanocrystals, which can be identified by X-ray photoelectron spectroscopy (XPS) analysis as shown in Fig. 5b and c.
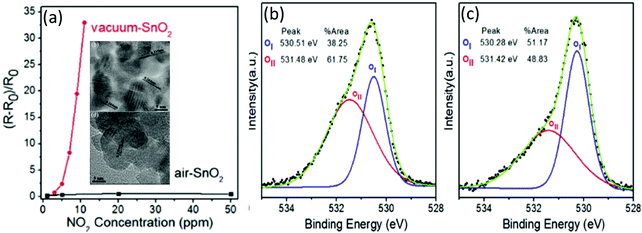 | ||
| Fig. 5 (a) Response of vacuum-annealed SnO2 compared to air-annealed SnO2 nanocrystals to different concentrations of NO2 at room temperature; the inset shows the TEM images of two types of nanocrystals; (b) and (c) deconvolution of the O 1s peaks of X-ray photoelectron spectra (XPS) for vacuum–SnO2 and air–SnO2 (the peaks with red color belong to adsorbed O ions).76 Copyright 2016, Elsevier. | ||
Yu et al.91 prepared ZnO nanowalls with uniformly distributed and cross-linked nanowalls of ∼20 nm using a solution method. The cross-linked nanowalls have a porous structure with pore sizes from 200 nm to 500 nm. The sensor exhibits a high response value (6.4) and fast response/recovery times (23/11 s) towards 50 ppm NO2 at RT with good repeatability. Based on the analysis from fluorescence emission spectrum, it was identified that the key factors for effective NO2 sensing are (1) the presence of oxygen vacancies in the ZnO nanowall nanostructures, and (2) a delicate balance between oxygen vacancy defects and porosity.
TiO2 and In2O3 are two other frequently reported nanomaterials for NO2 sensing. Tshabalala et al.79 prepared TiO2 nanoparticles with an average particle size of 6.5 nm using a hydrothermal method. The fluffy and porous TiO2 layer has a pore volume of 0.4170 cm3 g−1 and a large surface area of 80.3 m2 g−1.79 The porous nanostructures, high concentration of oxygen vacancies and the interstitial defect states on the surface are crucial for the efficient adsorption and desorption of NO2 gas molecules. Therefore, the sensor made of these nanostructures exhibits a high response (1093 to 40 ppm NO2), fast response/recovery times of 48/52 s and a low LOD of 0.02 ppm at RT. However, the selectivity of this sensor is poor with its relatively high responses to many other gases such as H2, NH3 and CH4. In2O3 octahedra have also been prepared using the sol–gel technique for NO2 sensing,102 and the sensor using these In2O3 octahedra has a response value of 63 to 200 ppm NO2 at RT, with good selectivity to NO2 against CO, H2 and NH3.
| NH3(gas) → NH3(ads) | (10) |
| 4NH3(ads) + 3O2− → 2N2 + 6H2O + 3e− | (11) |
The majority of the single phase n-type SMONs without modifications by other elements can be used for NH3 gas sensors, including ZnO,210–212 In2O3,111 SnO2,213 SnS2,214 MoO3,215 WO3216 and TiO2.217 They have good RT performance for NH3 sensing with high responses and fast response/recovery. Among these, the sensors based on In2O3 and TiO2 exhibit ultra-high responses and response/recovery times. For example, a RT sensor based on TiO2 nanoparticles has an ultra-high response of 10080.8 to 100 ppm of NH3 and fast response/recovery times of 35.5/59 s.78
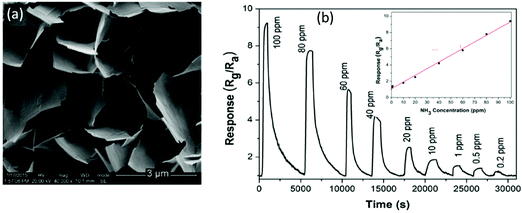
Du et al.111 reported a RT NH3 gas sensor using porous In2O3 nanotubes. This gas sensor exhibits an ultra-high response value of 2500 and good reproducibility with response and recovery times less than 20 s, both of which are better than those of the sensors made of In2O3 nanowires or nanoparticles. The performance enhancement is attributed to the porous structure and ultra-high surface-to-volume ratio of the porous In2O3 nanotubes, which can adsorb more oxygen molecules. Another gas sensor made of TiO2 films prepared using a reactive magnetron sputter method also exhibits an excellent response with a value of 7857 to 100 ppm of NH3, fast response/recovery times of 34/90 s and a low LOD of ∼5 ppm.174 Kumar et al.83 used an anodic aluminum oxide template route to prepare highly ordered ZnO nanowire arrays as the sensing layer for detection of NH3. The diameters of these nanowires are in the range of 60 to 70 nm and their length is about 11 μm as shown in Fig. 6a. At RT, the sensor exhibits 68% of response value (defined as (ΔR/Rg) × 100%) to 50 ppm NH3 and fast response/recovery times (28/29 s) (see Fig. 6b).83 Another NH3 sensor made of nanostructured ZnO thin films112 synthesized using a magnetron sputtering technique shows a high response with a value of 304 to 100 ppm NH3 with response/recovery times of 92/113 s.
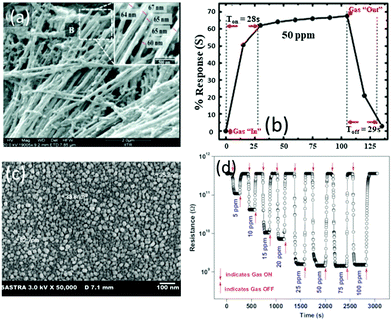 | ||
| Fig. 6 (a) SEM images of the ZnO nanowire array; (b) response/recovery curves of the ZnO nanowire array for 50 ppm NH3.83 Copyright 2014, Royal Society of Chemistry. (c) SEM image of nanostructured ZnO thin films on glass substrates; (d) response/recovery curves of the nanostructured ZnO thin film-based sensor for NH3.182 Copyright 2013, Elsevier. | ||
Mani et al.182 reported a sensor made of a nanostructured ZnO thin film (shown in Fig. 6c) using a spray pyrolysis technique. As shown in Fig. 6d, the sensor using this thin film exhibits a high response with a value of 233 to 25 ppm of NH3 at RT, and fast response and recovery times of 20/25 s. It has good selectivity to ammonia gas against other VOC gases (i.e. ethanol, methanol, benzyl alcohol, 2-propanol and acetone). Moreover, the sensor is insensitive to relative humidity. However, the sensor becomes saturated when the concentration of NH3 is above 20 ppm, indicating that the LOD is about from 5 ppm to 25 ppm. In brief, high responses, fast response/recovery, and superior LOD have been achieved for the n-type SMON-based RT NH3 gas sensors.
| CH3CH2OH(gas) → CH3CH2OH(ads) | (12) |
| C2H5OH + 3O2−(ads) → 2CO2 + 3H2O + 3e− | (13) |
The RT ethanol gas sensors based on the n-type SMONs usually exhibit rapid response and recovery. For example, a sensor based on In2O3 cubic crystals105 prepared using a hydrothermal method exhibits very fast response/recovery (3/5 s). However, the response is poor with a value of only 1.4 to 100 ppm ethanol vapors. Fast response/recovery times together with high responses have been reported for a sensor made of ZnO nanowires.82,180 Shankar et al.82 reported an ethanol sensor made of ZnO nanowires (see Fig. 7a) prepared using electrospinning. Self-assembled ZnO nanowires with two different molecular weights of poly(vinyl alcohol) (PVA), e.g., 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 140
000 and 140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1, were prepared using an electrospinning technique, and then heat-treated to transform them into ZnO nanospheres and nanowires at a temperature of 600 °C. These nanostructures have good selectivity to ethanol compared to other VOCs including ethanol, methanol, acetaldehyde, and acetone when operated at RT. The nanowire based sensors have a higher ethanol response (78 to 100 ppm) than those based on the nanoparticles (about 48 to 100 ppm).76 The nanowire-based ones also show fast response/recovery times of 9/12 s. Furthermore, the nanowire-based sensor has excellent repeatability.
000 g mol−1, were prepared using an electrospinning technique, and then heat-treated to transform them into ZnO nanospheres and nanowires at a temperature of 600 °C. These nanostructures have good selectivity to ethanol compared to other VOCs including ethanol, methanol, acetaldehyde, and acetone when operated at RT. The nanowire based sensors have a higher ethanol response (78 to 100 ppm) than those based on the nanoparticles (about 48 to 100 ppm).76 The nanowire-based ones also show fast response/recovery times of 9/12 s. Furthermore, the nanowire-based sensor has excellent repeatability.
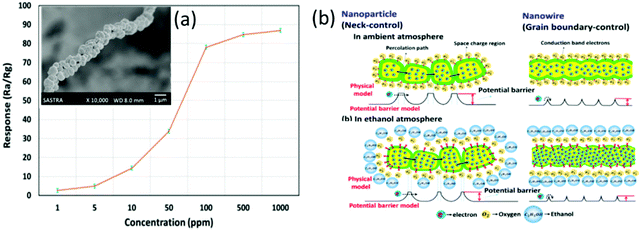 | ||
| Fig. 7 (a) Responses of the ZnO nanowire sensor to different concentrations of ethanol at room temperature; the inset shows the SEM image of ZnO nanowires; (b) the schematic diagram of the ethanol sensing mechanism.82 Copyright 2017, American Chemical Society. | ||
Fig. 7b shows a schematic diagram of the ethanol sensing mechanism for the ZnO-based sensor.82 The chemisorption of oxygen molecules on the sensor surface results in the formation of a space charge region on the surface of ZnO, which can act as a barrier for electron transport in the ZnO sensing layer.82 Due to the formation of double-spaced charge layers from the intergranular contacts of nanoparticles, the potential barrier energy is increased, which results in the broadening of the percolation path and hinders the electron transport. This further influences the adsorption–desorption rate and the sensing properties towards ethanol. However, the intergranular contact resistance will be reduced in the ZnO nanowires, which decreases the potential barrier energy, thus enhancing the sensing performance.
Similarly, TiO2 nanotubes96 prepared using an electrochemical anodization method and TeO2 nanowires85 prepared using thermal evaporation also show good responses to ethanol.85,96 However, the selectivity is poor as they are also sensitive to methanol and propanol.
| 2H2 + O2−(ads) → 2H2O + e− | (14) |
From the literature, sensors made from ZnO films189 and ZnO nanorods191 show high responses to H2, but long response/recovery times (see Fig. 8).
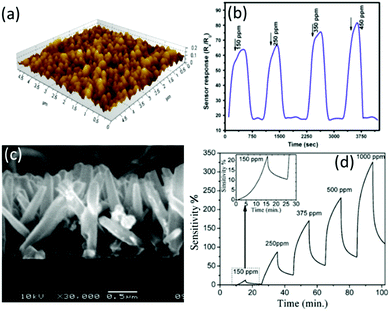 | ||
| Fig. 8 (a) AFM image of the ZnO films and (b) response/recovery curves of a ZnO film-based gas sensor to different concentrations of H2.189 Copyright 2014, Springer Nature. (c) Cross section SEM image of the ZnO nanorods and (d) response/recovery curves of a ZnO nanorod-based gas sensor to different concentrations of H2.191 Copyright 2013, Elsevier. | ||
Using anodized aluminum oxides as nano-templates, Lim et al.190 synthesized vertical ZnO nanorods (see Fig. 9a) using atomic layer deposition, and a highly sensitive and fast response/recovery H2 gas sensor was fabricated using these vertical ZnO nanorods. A response value of 162 for 500 ppm H2 and a response time of 30 s were demonstrated (see Fig. 9b).190 A faster response H2 gas sensor was also reported using [001]-oriented α-MoO3 nanoribbons (see Fig. 9c)192 with a response time of 14.1 s for 1000 ppm of H2 and a low LOD of 500 ppb (see Fig. 9d).192 It has good reproducibility and high selectivity against ethanol, CO and acetone.
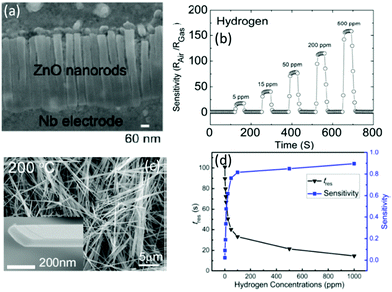 | ||
| Fig. 9 (a) TEM image of vertical ZnO nanorods; (b) response/recovery curves of a vertical ZnO nanorod-based gas sensor versus different concentrations of H2.190 Copyright 2012, Elsevier. (c) SEM images of α-MoO3 nanoribbons; (d) response values and times of an α-MoO3 nanoribbon-based gas sensor versus different concentrations of H2.192 Copyright 2015, American Chemical Society. | ||
In brief, RT gas sensors based on n-type SMONs can detect most of the hazardous gases, with advantages such as easy preparation, low cost, simple post-treatment and good stability of structure. Various morphologies of nanostructures for n-type SMONs have been synthesized and used in gas sensors operated at the RT. These sensors have been widely used to detect various gases and some good sensing properties have been achieved. However, it should be addressed that for most of these n-type SMON-based RT gas sensors, their sensitivity at RT is much lower than that at a higher working temperatures. Their responses and recovery times are quite long, and sometimes these sensors cannot be fully recovered at RT. In addition, at RT, the sensing performance is seriously affected by various environmental factors, such as humidity and external light source. To enhance their sensing properties at RT, modification of these n-type SMONs should be adopted, which will be discussed in Section 3.
2.2 P-type semiconducting metal oxide nanostructures and gas sensors
Up to now, the major p-type SMONs used in RT gas sensing have been CuO,223–225 Co3O492,103 and NiO,94,226 and the main target gases include NH3,98,103 H2S224,225 and NO2,226 as listed in Table 2. Apart from the sensing mechanism which is based on the reaction of target gases with the oxygen ions on the surface of SMONs, the formation of metal sulfides is another key reason for H2S sensing, especially for CuO nanostructures.93,225| Material | Structure | Synthesis method | Target gas | C (ppm) | Response | t res/trec | LOD | Ref. |
|---|---|---|---|---|---|---|---|---|
| C = concentration; tres/trec = response time/recovery time; LOD = limit of detection; response is defined as Ra/Rg (for reducing gases) or Rg/Ra (for oxidizing gases), Ra: resistance of the sensor exposed to the reference, Rg: resistance of the sensor exposed to the target.a Here the response is defined as ΔR/Rg (for reducing gases) or ΔR/Ra (for oxidizing gases), ΔR: the change in resistance.b Here the response is defined as (ΔR/Rg) × 100% (for reducing gases) or (ΔR/Ra) × 100% (for oxidizing gases). | ||||||||
| CuO | Nanosheets | Hydrothermal | H2S | 0.01 | 1.25 | 234/76 s | 10 ppb | 93 |
| CuO | Flowers | Hydrothermal | H2S | 1 | 2.1 | 240/1341 s | 0.1 ppm | 225 |
| CuO | Nanofibers | Electrospinning | H2S | 100 | 2.23 | 4.3/— s | 1 ppm | 227 |
| CuO | Tubes | Biotemplate | H2S | 5 | ∼41 | 29/41 s | 2 ppb | 98 |
| CuO | Thin films | Thermal evaporation | H2S | 5 | ∼250b | 60/90 s | 100 ppb | 224 |
| CuO | Nanorectangles | Hydrothermal | NH3 | 5 | ∼0.25a | 90/120 s | 5 ppm | 223 |
| CuO | Nanoparticles | Sol–gel-combustion | NH3 | 100 | 0.99a | 30/— s | — | 228 |
| CuO | Nanoparticles | Sol–gel-combustion | NH3 | 100 | 9.83a | ∼150/∼500 s | — | 81 |
| CuO | Microspheres | Reflux method | NOx | 97 | 64.93b | 5.33/— s | 0.97 ppm | 90 |
| CuxO | Virus-like | Chemical solution | NO2 | 4 | 28.1 | 22/42 s | 1 ppm | 229 |
| CuO | Nanoplatelets | Sonochemical method | NO2 | 40 | 53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 737 737 |
— | — | 230 |
| CuO | Nanowires | Thermal oxidation | Ethanol | 100 | 202 | 0.19/0.19 s | ∼10 ppm | 36 |
| CuO | Nanoribbons | Wet chemical | Ethanol | 100 | 210b | 8/25 s | 20 ppm | 231 |
| NiO | Nanosheets | Microwave synthesis | NO2 | 10 | 0.56 | — | — | 232 |
| NiO | Nanosheets | Hydrothermal | NO2 | 60 | 3.05a | ∼200/∼300 s | ∼5 ppm | 94 |
| NiO | Nanosheets | Hydrothermal | NO2 | 60 | 1.8a | ∼250/∼250 s | ∼7 ppm | 226 |
| NiO | Dendritic-like | Electrolytic | NH3 | 30 | 19b | 40/1500 s | — | 233 |
| Co3O4 | Nanosheets | Hydrothermal | NH3 | 100 | 9.5 | 9/134 s | 0.2 ppm | 92 |
| Co3O4 | Porous structure | Template | NH3 | 100 | 146b | 2/— s | 0.5 ppm | 103 |
| Co3O4 | Nanosheets | Hydrothermal | CO | 50 | — | 15/20 s | — | 234 |
| Co3O4 | Nanoparticles | Thermal treatment | NOx | 100 | 52.1b | — | 100 ppb | 235 |
| Cr2O3 | Nanospheres | Hydrothermal | Ethanol | 40 | 9a | — | 5 ppm | 236 |
| Cr2O3 | Mesoporous | Impregnation | Ethanol | 1000 | 13.0 | — | 10 ppm | 237 |
| α-MnO2 | Nanospheres | Self-assembly | NH3 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
0.2 | — | — | 238 |
| MnO2 | Nanofibers | Chemical solution | NH3 | 100 | 20b | — | 1 ppm | 239 |
| β-MnO2 | Thin films | Spray pyrolysis | CH3COH | 10 | 89b | 60/11 s | 10 ppm | 240 |
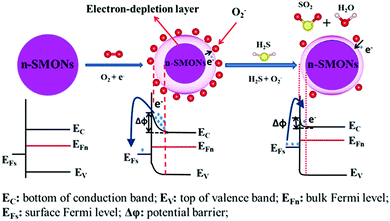
The sensing mechanism of the p-type SMONs to the reducing gas of NH3 is schematically shown in Fig. 10. When the reducing gas molecules (such as NH3) are adsorbed on the surface of SMONs, the reaction between the NH3 and O2− ions will release electrons, which will combine with the holes, resulting in an increase in the Fermi level and reduction of the hole accumulation layer. Consequently, the conductivity of the SMON layer is decreased. However, for the oxidizing gases, more free electrons are captured from the surface of the p-type SMONs. For example, the NO2 molecules adsorbed on the sensor surface can capture electrons from the p-type SMONs to form NO2− as listed in the reaction eqn (8). This significantly increases the concentrations of hole carriers, thus resulting in the increase in conductivity of the p-type SMON-based gas sensors. In summary, the resistance of p-type SMON based sensors will be increased in the presence of the reducing gases, whereas their resistance will be decreased in the presence of the oxidizing gases.
Fig. 11 shows schematic diagrams of the sensing mechanism for CuO-based H2S sensors. H2S molecules can react with CuO to form CuS on the surface at RT, based on the following reactions:93,225
| H2S(g) + CuO(s) → CuS(s) + H2O(g) | (15) |
| CuS(s) + O2(g) → CuO(s) + SO2(g) | (16) |
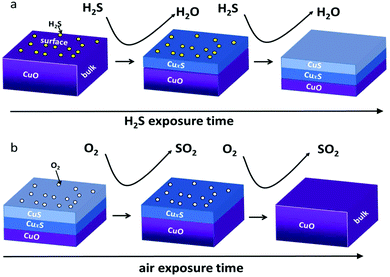 | ||
| Fig. 11 Schematic diagrams of the sensing mechanism of CuO: (a) response process in H2S and (b) recovery process in air.93 Copyright 2016, American Chemical Society. | ||
CuS is a metallic-like conductor. Formation of CuS on the SMON's surface will dramatically decrease the resistance of the sensor. Consequently, although H2S is a reducing gas, the response of the sensors exhibits a decrease in resistance. The RT H2S gas sensors are highly selective owing to this unique interaction between H2S and CuO. However, their recovery times are relatively long at RT due to the requirement for the transformation from CuS to CuO.
This H2S sensing mechanism has been proved from different studies. For example, Li et al.93 reported a H2S sensor based on porous CuO nanosheets with a thickness of about 60 nm on alumina tubes, prepared using a hydrothermal method. The sensor based on these porous CuO nanosheets has excellent selectivity to H2S. It exhibits high response values to H2S, but no apparent responses to NH3, CO, NO, NO2, H2, and C2H5OH.93 The sensor has a superior LOD as low as 10 ppb and good reproducibility at RT. The sensing mechanism based on the transformation from CuO into CuS on the surface of nanosheets has been verified using XPS analysis. As seen from the XPS spectra in Fig. 12, after the CuO is exposed to H2S gas, a new peak of the Cu 2p3/2 state at 930.8 eV appears which is attributed to CuS, and the S 2p3/2 and S 2p1/2 states at 162.3 and 163.4 eV can be identified. Similarly, nanostructures of hierarchical flower-like CuO nanostructures225 have been prepared, and the sensors made of these nanostructured CuO exhibit high sensitivity, good reproducibility and high sensing selectivity to H2S at RT. Zhang et al.98 prepared tube-like CuO nanostructures using pomelo flesh as a bio-template. The unique tube-like CuO nanostructures enhance the diffusion of H2S molecules and promote the rapid formation of CuS. The H2S sensor based on the tube-like CuO nanostructures has good selectivity to H2S, compared to gases such as gasoline, formaldehyde, CH4, H2, acetone, CO, toluene, and ethanol. The response/recovery times are lower than 60 s for the H2S in a wide range of 10 ppb–10 ppm. In addition, the sensor demonstrates a stable detection performance at RT over 3 months.
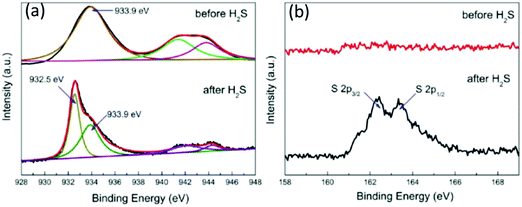 | ||
| Fig. 12 (a) Cu 2p3/2 and (b) S 2p XPS spectra of porous CuO nanosheets before and after exposure to H2S.93 Copyright 2016, American Chemical Society. | ||
Co3O4 nanostructures92 have also been found to be effective for NH3 detection with fast response speeds at RT. Fig. 13a shows an image of a Co3O4 nano-sheet array network deposited on an alumina tube prepared using a hydrothermal method. The average sheet thickness of the Co3O4 nano-sheet is 39.5 nm. NH3 molecules react with the surface chemisorbed O2− ions and form N2 and H2O. As shown in Fig. 13b, the response time for the gas sensor is as short as 9 s for 0.2 ppm NH3 at RT. The sensor responds linearly to the concentrations of NH3 within a range between 1–100 ppm. It also exhibits good performance in terms of reproducibility, stability and selectivity to NH3 (compared to H2, CO, H2S and C2H5OH). 3D hierarchical porous Co3O4 nanostructures103 were synthesized by Wu et al. using polystyrene spheres as the template. The average particle size is 20 nm and the specific surface area is 58.75 m2 g−1. The structures have macro-size pores, mesopores and plenty of irregular structural defects. The sensor made of these porous Co3O4 nanostructures exhibits a sensitivity of 146% (defined as (ΔR/Rg) × 100%) to 100 ppm NH3, and has a fast response time of 2 s. However, the recovery time is very long, e.g., longer than 1000 s.103
 | ||
| Fig. 13 (a) SEM image of network Co3O4 nano-sheet arrays; (b) response/recovery curves of the network Co3O4 nano-sheet array based sensor to different concentrations of H2S at room temperature (the inset shows the response value).92 Copyright 2016, Elsevier. | ||
Apart from CuO and Co3O4 nanostructures, NiO233,238 and MnO2239 were also used to make RT NH3 gas sensors, although the response was found to be very slow. Applying special nanostructures can improve the responses of the sensors. For example, the hierarchical hollow nanospheres of α-MnO2 composed of densely aligned nanowires were reported to exhibit an improved NH3 gas sensing sensitivity, and faster response and recovery compared with the standard α-MnO2 nanowires.238 Doping with metal ions such as Al doped NiO was also reported as an effective route for improving the sensitivity and responses of the sensor operated at RT.233
| NOx(gas) ↔ NOx−(ads) + h+ | (17) |
| NO(gas) + O2−(ads) ↔ NO2−(ads) + O−(ads) + h+ | (18) |
| NO2(ads) + O2−(ads) ↔ NO3−(ads) + 2O−(ads) + h+ | (19) |
Self-assembled mesoporous CuxO virus-like microspheres229 exhibited a high response of 28.4 and response/recovery times of 22/42 s to 4 ppm NO2 gas measured at RT. The good sensing performance of this special microstructure is attributed to the formation of hierarchical 3D nanostructures, micropores and large surface area for effective gas diffusion, the abundant surface oxygen vacancies and the heterojunctions at the interfaces between CuO and Cu2O. The RT NO2 gas sensors were also made using unique chain Co3O4 structures235 and self-assembled polycrystalline hexagonal NiO nanosheets.226 Because of the reduced grain boundaries, which minimizes the carriers’ scattering at the interfaces during the chemisorption of NO2, these special Co3O4 nanostructures showed much better responses to NO2 than those made of the Co3O4 and NiO nanoparticles.
Apart from detecting H2S, NH3 and NO2, the RT sensors based on the p-type SMONs have also been used for detecting other types of gases. For example, a sensor made of MnO2 shows good sensing performance for acetaldehyde vapor,240 and at ambient temperature, β-MnO2 thin films were reported to have good sensing responses and fast response/recovery. The sensitivity was found to be 89% for sensing 10 ppm acetaldehyde vapor, and the response and recovery times were found to be of 60 s and 11 s, respectively. This sensor also showed good selectivity to acetaldehyde gas, compared with the other reducing gases such as acetone, benzene, diethylamine, ethanol, dimethylamine, 2-propanol, monomethylamine and ammonia.240 Sensors made of Co3O4 nanosheets were also reported to have very fast response and recovery of 15/20 s to 50 ppm CO and CH4.234
The p-type Cr2O3 based gas sensor is normally operated at higher temperatures above 100 °C, and there are few reports about the Cr2O3 based RT gas sensors. However, 3D cubic mesoporous Cr2O3 nanostructures were recently prepared and the sensor made of this nanostructure exhibits an enhanced sensitivity for detecting ethanol vapor at room temperature, which is much better than those of the dense Cr2O3 film.237 The response of the 3D cubic mesoporous Cr2O3 sensor is 13.0 to 1000 ppm ethanol, whereas it is only 2.0 for the dense Cr2O3 film.
Although there are some reports on using the p-type SMONs in gas sensors operated at high temperature, these are much fewer compared to those on using n-type SMONs. The sensitivity of p-type SMON sensors is generally not as high as that of the n-type SMON sensors. Modification of the p-type SMONs using noble metal nanoparticles or metal ions is an effective route to further enhance the sensing performance, which will be discussed in Section 3.
3. Room temperature gas sensors based on modified and composite semiconducting metal oxide nanostructures
3.1 Metal modified semiconducting metal oxide and gas sensors
| Material | Structure | Synthesis method | Target gas | Concentration (ppm) | Response value | t res/trec | LOD | Ref. |
|---|---|---|---|---|---|---|---|---|
| C = concentration; tres/trec = response time/recovery time; LOD = limit of detection; response is defined as Ra/Rg (for reducing gases) or Rg/Ra (for oxidizing gases), Ra: resistance of the sensor exposed to the reference, Rg: resistance of the sensor exposed to the target.a Here the response is defined as ΔR/Rg (for reducing gases) or ΔR/Ra (for oxidizing gases), ΔR: the change in resistance.b Here the response is defined as (ΔR/Rg) × 100% (for reducing gases) or (ΔR/Ra) × 100% (for oxidizing gases). | ||||||||
| Pt/ZnO | Nanowires | Vapor–liquid–solid | CO | 0.1 | 1.02 | 120/180 s | 100 ppb | 114 |
| ZnO | 0 | — | — | |||||
| Au/ZnO | Nanostars | Hydrothermal | CO | 50 | 55.3 | 10/12 s | 5 ppm | 113 |
| ZnO | 1000 | 0 | — | — | ||||
| Au/ZnO | Nanowires | Hydrothermal | H2S | 5 | 79.4 | —/170 s | ∼1 ppm | 242 |
| ZnO | 5 | —/860 S | — | |||||
| Au/ZnO | Nanorods | Vapor phase transport | H2S | 3 | ∼475 | 11/20 min | ∼0.5 ppm | 257 |
| ZnO | ∼125 | 10/13 min | ||||||
| Au/ZnO | Core–shells | Sol–gel | HCOH | 5 | 10.57 | 138/104 s | 500 ppb | 258 |
| ZnO | Shells | 1.91 | 332/736 s | — | ||||
| Pd/ZnO | Nanoparticles | Sol–gel | NO2 | 50 | 45.2b | 67/250 s | 10 ppm | 251 |
| Pt/SnO2 | Porous | Solvothermal | CO | 100 | 64.5 | 144/882 s | ∼50 ppm | 115 |
| Au/SnO2 | Nanoparticles | Sputtering | NO2 | 50 | 90b | 70/— s | 600 ppb | 243 |
| SnO2 | ∼25b | — | — | |||||
| Au/In2O3 | Nanorods | Aqueous solution | CO | 100 | 9 | 30/30 s | ∼50 ppm | 244 |
| In2O3 | 0 | — | — | |||||
| Au/TiO2 | Core–shells | Sol–gel | O3 | 2.5 | 3.27 | 5/24 s | 0.4 ppm | 259 |
| TiO2 | Shells | 1.36 | 32/76 s | — | ||||
| Ag/TiO2 | Nanoparticles | Sol–gel | Ethanol | 5 | 4.35 | 52/61 s | 0.15 ppm | 247 |
| TiO2 | 1.54 | 112/136 s | — | |||||
| Pd/TiO2 | Nanofiber array | Electrospinning | NH3 | 100 | 6.97 | 3/150 s | ∼0.1 ppm | 260 |
| TiO2 | 0 | — | — | |||||
| Ag/TiO2 | Nanorods | Wet chemical | Ethanol | 50 | 11.98a | 3/73 s | ∼5 ppm | 116 |
| TiO2 | 8.15a | 6/213 s | ||||||
| Au/VO2 | Nanowires | CVD/Ion sputtering | NO2 | 5 | 3.22 | ∼50/∼600 s | ∼0.5 ppm | 130 |
| VO2 | CVD | ∼1 | — | — | ||||
| Pt/VOx | Thin films | Magnetron sputtering | CH4 | 500 | 18.2b | ∼1000/∼2000 s | ∼500 ppm | 261 |
| Au/VO2 | Nanosheets | CVD | CH4 | 500 | ∼70b | ∼50/∼100 s | ∼100 ppm | 262 |
| VO2 | ∼35b | — | ||||||
| Pd/Ga2O3 | Nanowires | Thermal evaporation | NO2 | 100 | 41.44b | 200/70 s | ∼10 ppm | 263 |
| Ga2O3 | 0 | — | — | |||||
| Pd/ZnO | Nanorods | Aqueous solution | H2 | 1000 | 91.2b | 18.8/— s | 0.2 ppm | 264 |
| ZnO | ∼20b | — | — | |||||
| Pd/ZnO | Nanowires | CVD | H2 | 4000 | 1017.9b | 36/50 s | 20 ppm | 265 |
| Pd/ZnO | Nanowires | Electrochemical deposition | H2 | 100 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
6.4/7.4 s | — | 252 |
| Pd/SnO2 | Nanofibers | Electrospun | H2 | 1000 | 12.09 | 4/3 s | 0.02 ppm | 266 |
| SnO2 | ∼3 | 2/— s | ||||||
| Pt/SnO2 | Nanoparticles | Aqueous solution | H2 | 1000 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
20/— s | — | 249 |
| SnO2 | 0 | — | ||||||
| Pd/SnO2 | Nanoparticles | Thermal vaporization | H2 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0000b 0000b |
2/— s | 40 ppm | 253 |
| Pd/TiO2 | Nanotubes | Sputtering | H2 | 8000 | 92.05b | 3.8/43.3 s | — | 255 |
| TiO2 | 5000 | 54.6b | 73.8/103.8 s | |||||
| Pt/TiO2 | Nanocomposites | Pressing and sintering | H2 | 1000 | 6000 | 10/20 s | — | 267 |
| Pd/WO3 | Nanocomposites | Hydrothermal | H2 | 1000 | 34 | 24/— s | — | 268 |
| WO3 | Nanoplates | ∼0 | — | |||||
| Pt/Nb2O5 | Porous ceramics | Pressing and sintering | H2 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
165 | 7/39 s | 200 ppm | 269 |
| Nb2O5 | 0 | — | — | |||||
| Au/In2O3 | Nanofibers | Electrospinning | Ethanol | 100 | 11.12 | 47/351 s | 20 ppm | 270 |
| In2O3 | 5.4 | — | — | |||||
| Pt/In2O3 | Nanocubes | Hydrothermal | H2 | 15000 | ∼20 | 33/66 s | — | 241 |
At RT, some gases such as CO and H2 are very difficult to detect using the sensors made of pristine SMONs. However, this problem might be solved by modifying the surface of these SMONs using noble metal nanoparticles. For example, Arunkumar et al.113 prepared ZnO nanostar features using a hydrothermal route and then decorated these nanostars using Au nanoparticles with an average size of ∼5–6 nm as shown in Fig. 14a. The ZnO nanostars decorated with 3 wt% gold nanoparticles can enhance the response (∼15 for 50 ppm CO) and achieve very fast response/recovery times (∼8/15 s) at 35 °C.113 The selectivity of the sensor for Co sensing is excellent against the other interfering gases including methanol, ethanol, acetone and hydrogen. Fig. 14b shows the energy band diagrams of ZnO and Au/ZnO nanostars before and after CO exposure. Due to the spillover effect, a nanoscale depletion region is formed at the interface between Au nanoparticles and ZnO as a result of strong electronic interactions, thus altering the height of the Schottky barrier. Therefore, the enhanced performance of the sensor operated at RT is attributed to the spillover effect.113
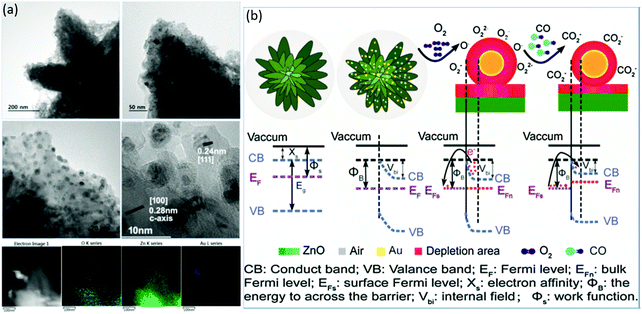 | ||
| Fig. 14 (a) TEM images and element mapping of Au/ZnO nanostars; (b) energy band diagrams of ZnO and Au/ZnO nanostars before and after CO exposure.113 Copyright 2017, Elsevier. | ||
Choi et al.114 grew a network of ZnO nanowires using a vapor–liquid–solid method and then these nanowires were functionalized with Pd nanodots using a γ-ray radiolysis method, and the sensor made of these decorated nanowires shows an improvement of the sensing performance. This improvement is attributed to the electronic and chemical sensitizations from the Pd nanodots.114 Wang et al.115 reported a highly sensitive RT CO sensor based on Pt/SnO2 porous nanostructures. The porous SnO2 nanostructures were synthesized using a solvothermal method, and Pt nanoparticles were then decorated onto the SnO2 using hexachloro-platinic acid. The sensor exhibits a good response with a value of 64.5 to 100 ppm CO at RT. It also shows good selectivity, compared to the other gases including CO, H2, N(CH3)3, NH3 and CH4. Similarly, a RT CO gas sensor made of Au/In2O3 composite nano-rods was fabricated, and showed a high response and fast response/recovery times (30/30 s to 100 ppm CO).244
Modification of SMONs by noble metals can not only enhance the sensitivity, but also significantly improve the selectivity and response/recovery speed. For example, a ZnO nanowire-based sensor modified with Pd nanoparticles exhibits both ultra-high sensitivity and very fast response and recovery.252,265 A Pd-modified ZnO nanowire-based RT nanosensor was prepared using electrochemical deposition by Lupan et al.,252 and it exhibits very fast response/recovery times of 6.4/7.4 s and a super-high response value of 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 to 100 ppm H2 as shown in Fig. 15a and b. This H2 sensor shows very good selectivity against the other gases such as CO, CH4, ethanol and acetone. The sensor can be operated at very low current levels with ultra-low power consumption.252
100 to 100 ppm H2 as shown in Fig. 15a and b. This H2 sensor shows very good selectivity against the other gases such as CO, CH4, ethanol and acetone. The sensor can be operated at very low current levels with ultra-low power consumption.252
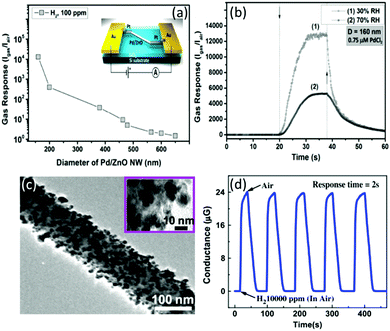 | ||
| Fig. 15 (a) Responses of nanosensors based on single Pd/ZnO nanowires with different diameters to 100 ppm of H2 at RT and 30% RH (the inset shows the schematic of the nanosensor device structure); (b) response of the Pd/ZnO nanowire based sensor to 100 ppm of H2 at 30% and 70% RH at RT.252 Copyright 2018, Elsevier. (c) TEM image of 30 at% Pd/SnO2 nanofiber; (d) the response/recovery curves of the 30 at% Pd/SnO2 nanofiber based sensor for H2 gas.253 Copyright 2010, Elsevier. | ||
Ultra-sensitive RT hydrogen gas sensors based on noble metal modified SnO2 have also been reported. For example, the sensor based on Pt/SnO2 nanoparticles exhibits a super-high response (e.g., 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 to 1000 ppm H2) at RT.249 Lee et al.253 reported a RT hydrogen sensor made of Pd/SnO2 nanowires (as shown in Fig. 15c) prepared using a thermal evaporation method, and the sensor shows an ultra-high sensitivity of about 120
500 to 1000 ppm H2) at RT.249 Lee et al.253 reported a RT hydrogen sensor made of Pd/SnO2 nanowires (as shown in Fig. 15c) prepared using a thermal evaporation method, and the sensor shows an ultra-high sensitivity of about 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000% (defined as (ΔR/Rg) × 100%) to 10
000% (defined as (ΔR/Rg) × 100%) to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm H2 and a fast response time of 2 s as shown in Fig. 15d. The Pd/SnO2 nanofibers266 were also synthesized using an electrospinning method, and the sensor made of these nanofibers exhibits super-fast response/recovery times to H2 (4/3 s to 1000 ppm H2) and an ultra-low LOD of 20 ppb. The response of a sensor made of Pt/TiO2 nanocomposites to 1000 ppm H2 in N2 was also reported as high as 6000 at RT, with short response/recovery times of only 10/20 s.267
000 ppm H2 and a fast response time of 2 s as shown in Fig. 15d. The Pd/SnO2 nanofibers266 were also synthesized using an electrospinning method, and the sensor made of these nanofibers exhibits super-fast response/recovery times to H2 (4/3 s to 1000 ppm H2) and an ultra-low LOD of 20 ppb. The response of a sensor made of Pt/TiO2 nanocomposites to 1000 ppm H2 in N2 was also reported as high as 6000 at RT, with short response/recovery times of only 10/20 s.267
Apart from the chemical sensitization and electronic sensitization, there are other mechanisms to enhance the sensing performance of the SMONs: for example, the formation of nano-scale Schottky type junctions between Au nanoparticles and ZnO nanorods and Au sulfidation with high concentrations of H2S.257 Hosseini et al.257 prepared ZnO nanorods using a vapor phase transport method, and found that H2S sensing performance has been significantly enhanced at RT after the modification of the surface of ZnO nanorods with Au nanoparticles (see Fig. 16a). As shown in Fig. 16b and c, both high response (1270 to 6 ppm of H2S) and good H2S selectivity of the Au/ZnO nanorods have been achieved, which are much better than those of the pristine ZnO nanorods.
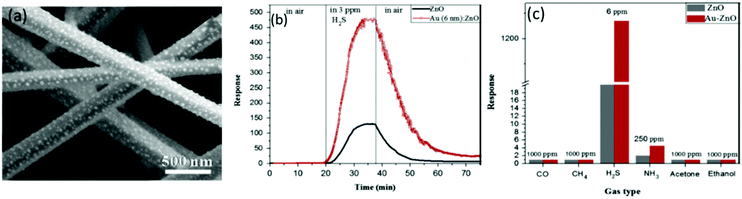 | ||
| Fig. 16 (a) SEM image of Au/ZnO nanorods; (b) response/recovery curves of the Au/ZnO nanorod-based sensor and pristine ZnO nanorod-based sensor to 3 ppm H2S at room temperature; (c) responses of the Au/ZnO nanorod-based sensor and pure ZnO nanorod-based sensor to different gases.257 Copyright 2015, Elsevier. | ||
In summary, due to the combined effects of chemical sensitization and electronic sensitization, noble metal nanoparticles and other nanostructures are suitable to be used to modify the SMONs in order to improve the sensing performance of the RT gas sensors. One significant improvement is the shortening of the response and recovery times, along with the enhanced response values and selectivity.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 280 and Sb5+.281 The recent key sensing applications of RT gas sensors using this method are summarized in Table 4.
280 and Sb5+.281 The recent key sensing applications of RT gas sensors using this method are summarized in Table 4.
| Material | Structure | Synthesis method | Target gas | C (ppm) | Response | t res/trec | LOD | Ref. |
|---|---|---|---|---|---|---|---|---|
| C = concentration; tres/trec = response time/recovery time; LOD = limit of detection; response is defined as Ra/Rg (for reducing gases) or Rg/Ra (for oxidizing gases), Ra: resistance of the sensor exposed to the reference, Rg: resistance of the sensor exposed to the target.a Here the response is defined as ΔR/Rg (for reducing gases) or ΔR/Ra (for oxidizing gases), ΔR: the change in resistance.b Here the response is defined as (ΔR/Rg) × 100% (for reducing gases) or (ΔR/Ra) × 100% (for oxidizing gases). | ||||||||
| Al/NiO | Nanosheets | Solvent-thermal | NO2 | 10 | 2.77a | 50/200 s | 250 ppb | 117 |
| Cu/Cu2O | Hollow spheres | Hydrothermal | NO2 | 10 | 6.27 | 34/— s | — | 282 |
| Sb/WO3 | Nanoparticles | Chemical solution | NO2 | 10 | 51 | ∼150/∼200 s | ∼1 ppm | 209 |
| Zn/NiO | Dendritic crystals | Electrolytic | NH3 | 30 | 0.2a | 5/30 s | 5 ppm | 119 |
| Co/CuCo2O4 | Nanoplatelets | Hydrothermal | NH3 | 400 | 7.9b | —/14 min | ∼25 ppm | 273 |
| Cu/ZnO | Nanorods | Hydrothermal | NH3 | 20 | 31.1b | 15/48 s | ∼10 ppm | 118 |
| Ce0.94Zr0.06O2 | Nanosheets | Sol-hydrothermal | NH3 | 100 | 87 | — | 100 ppb | 127 |
| Mg/ZnO | Thin films | Spray pyrolysis | NH3 | 100 | 769 | 34/28 s | ∼1 ppm | 283 |
| Sb/SnO2 | Nanoparticles | Sol–gel | NH3 | 50 | 4316b | 70/— s | — | 284 |
| SnO2:Sb | Nanowires | CVD | Ethanol | 300 | 1.3 | 10/87 s | 40 ppm | 285 |
| Al/ZnO | Nanowires | Electrodeposition | Ethanol | 1000 | 1.7 | 10/30 s | — | 286 |
| Al/ZnO | Hexagonal facets | Sol–gel | Ethanol | 300 | 94b | 68/50 s | — | 271 |
| Co/TiO2 | Nanoparticles | Sol–gel | Ethanol | 500 | ∼105b | — | — | 277 |
| Fe/WO3 | Microspheres | Spray pyrolysis | Ethanol | 400 | ∼140 | ∼10/∼40 s | ∼100 ppm | 279 |
| Ni/ZnO | Nanorods | Electrodeposition | Acetone | 100 | 1.6 | — | — | 275 |
| Na/ZnO | Nanoflowers | Solution route | Acetone | 100 | 3.35 | 18/63 s | 0.2 ppm | 287 |
| Mg/ZnO | Nanorods | Frequency sputtering | H2 | 200 | 30 | 85/70 s | — | 288 |
| Nb/TiO2 | Nanotubes | Annealing | H2 | 1000 | 30.9b | 100/— s | — | 289 |
| Mg/ZnO | Film | Rf sputtering | H2 | 200 | 35–40 | 75/54 s | — | 280 |
| Cd/ZnO | Nanowires | Electrodeposition | H2 | 100 | 274b | 14/11 s | — | 89 |
| Co/TiO2 | Mesoporous | Self-assembly | H2 | 1000 | 4082 | 66/— s | 50 ppm | 278 |
| Sb/SnO2 | Nanoribbons | Thermal evaporation | H2S | 100 | ∼18 | ∼500/∼500 s | 100 ppb | 281 |
| Zn/ZnO | Nanotetrapods | Thermal evaporation | H2S | 4 | 38b | ∼200/∼1000 s | 1 ppm | 290 |
| Zn/In2O3 | Nanowires | CVD | CO | 5 | ∼57b | 20/10 s | ∼1 ppm | 274 |
| Sb/SnO2 | Nanoporous films | Sol–gel | Cl2 | 3 | 500a | 60/120 s | ∼1 ppm | 291 |
The amount of dopant Al3+ ions was found to significantly affect the gas sensing properties of NiO nanosheets.117 Al3+ doped NiO nanosheets have introduced many new oxygen vacancies due to aliovalent ion doping. Superoxide complexes such as Ni2+–O2− are easily formed on the surface of the NiO due to the existence of oxygen vacancies. As they are very active, they can significantly increase the sensitivity of the NiO nanosheets. Compared with those of the pure NiO nanosheets, the response of the Al doped NiO nanosheet based sensor to NO2 was enhanced up to 35 times at RT. Doping with metal ions including Sb, Cd, and Ce has also been proved to enhance the sensing properties of the WO3 nanoparticles to NO2 gas at RT.209 Among these, Sb-doped WO3 nanoparticles exhibit a 6.8 times higher response and much better selectivity than those of the undoped WO3 (as shown in Fig. 17). The enhancement mechanisms have been identified to be the increase in the number of oxygen vacancies on the surface of metal doped WO3 based on the analysis results from photoluminescence, Raman spectroscopy and XPS.209
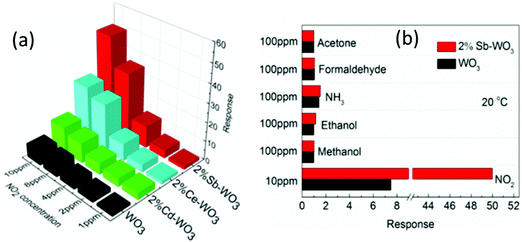 | ||
| Fig. 17 (a) Responses of sensors made of 2%-Sb-WO3, 2%-Ce-WO3 and 2%-Cd-WO3 to different concentrations of NO2; (b) responses of sensors made of 2%-Sb-WO3 to different gases.209 Copyright 2017, American Chemical Society. | ||
The responses and recovery speeds of the sensor can be significantly improved by doping of metal ions into the SMONs, which is important for practical applications of the RT gas sensors. For example, a Zn-doped NiO dendritic nanostructure119 exhibits faster responses (5–8 times) and faster recovery (30–50 times) rates than those of the pure NiO dendritic crystals. A sensor based on Mg-doped ZnO thin films on glass substrates deposited through a spray pyrolysis process283 shows a much higher response (796 towards 100 ppm of NH3) and faster response/recovery speeds (34/28 s) than those of the pure ZnO film measured at RT. The sensor based on Sb doped SnO2 nanowires prepared using a chemical vapor deposition (CVD) method285 shows a typical p-type behavior, and a fast response time of about 10 s to 300 ppm ethanol at RT.
Adsorption of water vapor on the SMON surfaces is sometimes enhanced by metal ion doping, which seems a bad news for a gas sensor. However, for RT NH3 gas sensors, this is especially beneficial as the NH3 molecules react with the absorbed H2O to form the NH4+ and OH− as is schematically shown in Fig. 18a. The electrolytic conductivity of NH4+ and OH− can significantly improve the sensitivity of sensors at RT.127,198 Porous Ce0.94Zr0.06O2 nano-sheets (see Fig. 18b) with an average thickness of 8 nm were prepared using a sol-hydrothermal process.127 Doping of Zr4+ ions into the CeO2 nanosheets enlarges the specific surface areas (185.4 m2 g−1) and increases the pore volumes (0.51 cm3 g−1). These modifications result in a much higher sensitivity (e.g. 87 to 100 ppm NH3) at RT (see Fig. 18c), better selectivity and a very low LOD of 100 ppb.
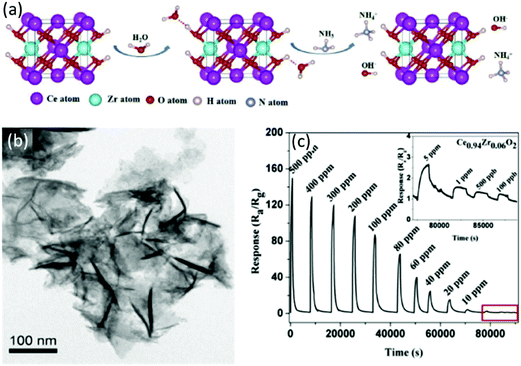 | ||
| Fig. 18 (a) Schematic diagrams of the NH3 reaction mechanism on the surface of Ce0.94Zr0.06O2 nano-sheets; (b) TEM image of porous Ce0.94Zr0.06O2 nano-sheets; (c) response/recovery curves of the porous Ce0.94Zr0.06O2 nanosheet based sensor to NH3.127 Copyright 2018, Elsevier. | ||
The H2 sensors made of metal ion doped SMONs were reported to exhibit high responses, although their response/recovery times were also reported to be longer than those made of the noble ion modified SMON-based RT H2 gas sensors.278,280,288,289 For example, Co-doped TiO2 sensors exhibit an ultra-high response with a value of 4082 to 1000 ppm H2 gas, although the response time is 66 s, which is quite slow for detection of highly explosive H2.278
In summary, compared to those sensors made of noble metal nanoparticle modified SMONs, the improved effects of gas sensors made of the metal ion modified SMONs are not as significant. However, the SMONs can be modified simultaneously by both metal ions and noble metal nanoparticles, which will combine the advantages of both metal ions and noble metal nanoparticles.
3.2 Composites of semiconducting metal oxide nanostructures and gas sensors
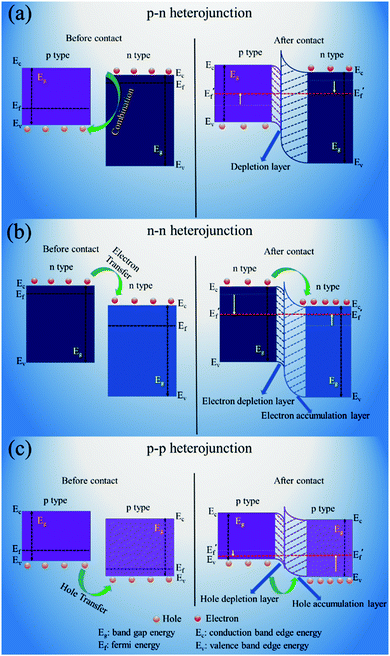 | ||
| Fig. 19 Schematic illustrations of the energy band structures at heterojunction interfaces of different types of heterojunctions: (a) p–n junction, (b) n–n junction and (c) p–p junction. | ||
For the n–n heterojunction, the electrons will be transported at the interfaces between different materials due to the differences in their conduction band states. As a result, a depletion layer forms at the surface of n-type SMONs with higher-energy conduction band states due to the loss of electrons. At the same time, an accumulation layer forms at the surface of n-type SMONs with lower-energy conduction band states due to the accumulation of electrons.
For the p–p heterojunction, the major charge carriers are holes. Due to the differences of valence band energies of different SMONs, the charge carriers are transported from one p-type SMON (which has a higher energy valence band state) to the other p-type SMON (which has a lower-energy valence band state). Therefore, a hole depletion region is formed at the surface of the first SMONs (with higher energy valence band state) and a hole accumulation region is formed at the surface of the second SMONs (with a lower energy valance band state) as shown in Fig. 19.
These formed heterojunctions can effectively accelerate the transport of electrons. On the other hand, these heterojunctions can also enhance oxygen adsorption, therefore, abundant oxygen vacancies are formed on the surfaces of the SMON composites, which can provide new active sites for sensing reactions. In addition, the composites of SMONs often contain numerous mesopores, which are beneficial to the adsorption and desorption of gas molecules. All of these effects will improve the sensitivity and response rates of the RT gas sensors made of composites of the SMONs.
Table 5 summarizes the recently reported RT gas sensors made of composite oxides of the SMONs and/or other metal oxides. For these composite oxides, a number of oxygen vacancies are formed on both the surfaces and interfaces, which provides many active sites for the gas sensing reactions. Plenty of defects will also be formed at the interfaces of nanostructures in different metal oxide nanoparticles. In addition, the heterojunctions are usually formed at the interfaces of different metal oxides, which can effectively accelerate the electron transfer between different particles, thus accelerating the response speed of the sensor. Besides, the composite oxides often contain lots of mesoporous structures due to the accumulation of nanoparticles, which are beneficial to the adsorption and desorption of gas molecules. These factors can improve the sensing performance of the sensor made of these composite oxides, especially for the sensitivity and response speed. Most sensors made of the composite oxides exhibit very fast response times at RT. For example, the gas sensor based on the nanocomposite of CuO/TiO2121 shows a very fast response time of 2 s at RT, and the sensor based on plate-like NiO/WO3 nanocomposites295 exhibits excellent sensitivity and ultrafast response/recovery times (2.5/1.1 s) to NO2 at RT.
| Material | Structure | Synthesis method | Target gas | C (ppm) | Response | t res/trec | LOD | Ref. |
|---|---|---|---|---|---|---|---|---|
| C = concentration; tres/trec = response time/recovery time; LOD = limit of detection; response is defined as Ra/Rg (for reducing gases) or Rg/Ra (for oxidizing gases), Ra: resistance of the sensor exposed to reference, Rg: resistance of the sensor exposed to target.a Here the response is defined as ΔR/Rg (for reducing gases) or ΔR/Ra (for oxidizing gases), ΔR: the change in resistance.b Here the response is defined as (ΔR/Rg) × 100% (for reducing gases) or (ΔR/Ra) × 100% (for oxidizing gases). | ||||||||
| ZnO/SnO2 | Thin films | Hydrothermal | NH3 | 20 | 1.1 | 300/— s | 5 ppm | 293 |
| In2O3/CuO | Nanofibers | Electrospinning | NH3 | 100 | 1.9a | 2/— s | 0.3 ppm | 122 |
| Cr2O3/ZnO | Thick films | Screen-printing | NH3 | 300 | 13.7a | 25/75 s | — | 298 |
| NiO/ZnO | Nanocones | Hydrothermal | NH3 | 50 | 42b | 27/150 s | ∼15 ppm | 120 |
| CuO/TiO2 | Nanoparticles | Sol–gel | NH3 | 50 | 97b | 2/55 s | ∼5 ppm | 121 |
| CuO/MNO2 | Flowers/sheets | Hydrothermal | NH3 | 100 | 135b | 120/600 s | 20 ppm | 299 |
| Silica/CeO2 | Nanoparticles | Hydrothermal | NH3 | 80 | 3244b | 750/— s | 0.5 ppm | 198 |
| Fe2O3/ZnO | Nanorods | Sol–gel | NH3 | 0.4 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
20/20 s | — | 292 |
| NiO/WO3 | Plates | Annealing | NO2 | 30 | 4.8 | 2.5/1.1 s | 5 ppm | 295 |
| NiO/SnO2 | Nanosheets | Annealing | NO2 | 60 | ∼7.5a | — | ∼5 ppm | 300 |
| NiO/CuO | Flower-like | Hydrothermal | NO2 | 100 | 77.16b | 2 s/— | 1 ppm | 131 |
| CaO/SnO2 | Rod-like | Electrospinning | NOx | 97 | 6.63a | — | 10 ppb | 297 |
| In2O3/SnO2 | Nanorods | Electrospinning | NOx | 100 | 8.98a | 4.67/— s | 0.1 ppm | 134 |
| In2O3/TiO2 | Nanofibers | Electrospinning | NOx | 97 | 41.1b | 3/— s | 97 ppb | 301 |
| Al2O3/TiO2 | Nanotubes | Induction | NOx | 97 | 88.04b | ∼8/∼8 s | 0.97 ppm | 302 |
| K2O/In2O3 | Nanowires | Template | NOx | 97 | 151.78a | 12/— s | 48.5 ppb | 129 |
| NiO/In2O3 | Nanofibers | Electrospinning | H2S | 3 | 6 | 14/22 s | 3 ppm | 303 |
| CuO/ZnO | Nanorods | Pulsed laser deposition | H2S | 0.5 | 25b | 180/15 s | ∼0.5 ppm | 304 |
| SnO2/NiO | Thin films | RF sputtering | H2S | 10 | 440 | — | 100 ppb | 123 |
| In2O3/ZnO | Core–shells | Hydrothermal | H2S | 700 | 925b | — | 20 ppm | 305 |
| Cu2O/Co3O4 | Heteroarrays | Electrodeposition | H2S | 20 | ∼2600 | ∼100/∼100 s | ∼0.1 ppm | 296 |
| SnO2/CuO | Heterojunctions | Screen printing | H2S | 1 | 3672a | 15/— s | 10 ppm | 306 |
| NiO/Nb2O5 | Nanoparticles | Hydrothermal | H2 | 500 | 1.68 | 100.42/524.84 s | — | 307 |
| Cr2O3/Nb2O5 | Nanoparticles | Hydrothermal | H2 | 200 | 5.24 | 40/— s | — | 308 |
| ZnO/CuO | Nanoparticles | Hydrothermal | Alcohol | 20 | 3.32 | 62/83 s | ∼150 ppm | 309 |
| VO2/ZnO | Heteronanostructures | Heteroepitaxial | Acetone | 100 | 4.51 | 8/18 s | ∼10 ppm | 310 |
| ZnO/SnO2 | Heterojunctions | Hydrothermal | Ozone | 0.06 | 12 | 13/90 s | 20 ppb | 311 |
| CuO/ZnO | Thick film | Screen-printing | Cl2 | 300 | 195a | 18/50 s | — | 312 |
| α-Fe2O3/ZnO | Nanowires | Piezo-surface coupling | Ethanol | 700 | 706.8b | — | ∼100 ppm | 313 |
The composite of mesoporous In2O3/CuO multijunction nanofibers122 was prepared using an electrospinning method by Zhou et al. The composite is composed of the In2O3 nanoparticles and CuO nanoparticles (with a molar ratio of Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) In of 100
In of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5). The TEM images shown in Fig. 20a and b indicate that the composite has many mesoporous structures with diameters from 1.9 to 22.9 nm and large specific surface areas (48.7 m2 g−1). The In2O3 nanoparticles are surrounded by the CuO nanoparticles to form numerous p–p homojunctions and p–n heterojunctions.122 XPS analysis indicates that the ratio of oxygen defect/vacancy on its surface is as high as 45.4%. Due to the existence of larger specific and mesoporous surface areas and the availability of chemisorbed oxygen and the formation of heterojunctions, the sensor has a much higher response to NH3 than that of a CuO nanostructured sensor. The response time is also very short with a value lower than 8 s for NH3 from 0.3 to 100 ppm (see Fig. 20c). The selectivity and LOD are also significantly improved due to the addition of In2O3.
5). The TEM images shown in Fig. 20a and b indicate that the composite has many mesoporous structures with diameters from 1.9 to 22.9 nm and large specific surface areas (48.7 m2 g−1). The In2O3 nanoparticles are surrounded by the CuO nanoparticles to form numerous p–p homojunctions and p–n heterojunctions.122 XPS analysis indicates that the ratio of oxygen defect/vacancy on its surface is as high as 45.4%. Due to the existence of larger specific and mesoporous surface areas and the availability of chemisorbed oxygen and the formation of heterojunctions, the sensor has a much higher response to NH3 than that of a CuO nanostructured sensor. The response time is also very short with a value lower than 8 s for NH3 from 0.3 to 100 ppm (see Fig. 20c). The selectivity and LOD are also significantly improved due to the addition of In2O3.
 | ||
| Fig. 20 (a) TEM and (b) HRTEM images of mesoporous In2O3/CuO composite multijunction nanofibers, (c) response values and times of the sensor to different concentrations of NH3.122 Copyright 2018, Elsevier. (d and e) TEM images of composite of In2O3/SnO2 nanorod heterostructures; (f) response/recovery curves of the sensor to different concentrations of NOx.134 Copyright 2015, Royal Society of Chemistry. | ||
Xu et al.134 prepared composites of In2O3/SnO2 nanorod heterostructures (see Fig. 20d and e) using electrospinning to improve the oxygen deficiency and carrier density of SnO2. The SnO2 nanoparticles are distributed along with the In2O3 to form numerous heterojunctions and defects at their interfaces. The availability of oxygen vacancies on the surface and at the interface has been verified using XPS.134 Compared with pure SnO2 nanorods, In2O3/SnO2 nanorods (with the atom ratio of 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.3 of Sn
0.3 of Sn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) In) exhibit 11 times higher response to NOx with a very faster response time of 4.67 s and a lower LOD with a value of 0.1 ppm (see Fig. 20f).
In) exhibit 11 times higher response to NOx with a very faster response time of 4.67 s and a lower LOD with a value of 0.1 ppm (see Fig. 20f).
NiO/CuO nanocomposites with a NiO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CuO molar ratio of 1
CuO molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 have been synthesized using a hydrothermal method,131 and the nanocomposites are consisted of CuO nanoparticles and NiO nanoplates with lots of mesoporous structures. The p–p heterojunctions formed at the interfaces of NiO and CuO accelerate the electron transfers from NiO to CuO, thus resulting in a faster response. The mesoporous hierarchical nanostructures with much larger surface areas facilitate effective adsorption and desorption of gas molecules on the surface. Thus, the sensor exhibits an ultra-fast response speed (2 s to 100 ppm NO2) to NO2 at RT.
1 have been synthesized using a hydrothermal method,131 and the nanocomposites are consisted of CuO nanoparticles and NiO nanoplates with lots of mesoporous structures. The p–p heterojunctions formed at the interfaces of NiO and CuO accelerate the electron transfers from NiO to CuO, thus resulting in a faster response. The mesoporous hierarchical nanostructures with much larger surface areas facilitate effective adsorption and desorption of gas molecules on the surface. Thus, the sensor exhibits an ultra-fast response speed (2 s to 100 ppm NO2) to NO2 at RT.
Kaur et al.123 prepared a SnO2/NiO thin film using a sputtering method and then fabricated a RT H2S sensor. As shown in Fig. 21a, the sensor exhibits a high response with a value of 440 to 10 ppm H2S, which is 9 and 415 times higher than those made of pure SnO2 and NiO films, respectively. Selectivity has also been improved using the SnO2/NiO thin film (see Fig. 21b). The formation of p–n heterojunctions using the p-type NiO and n-type SnO2 semiconductors apparently changes the resistance of the composite film. The enhanced response of the SnO2:NiO nanocomposite sensor is mainly due to the modifications of p–n junctions resulted from the conversion of NiO to metallic NiS. However, the recovery time is quite long (>20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s, see Fig. 21c).
000 s, see Fig. 21c).
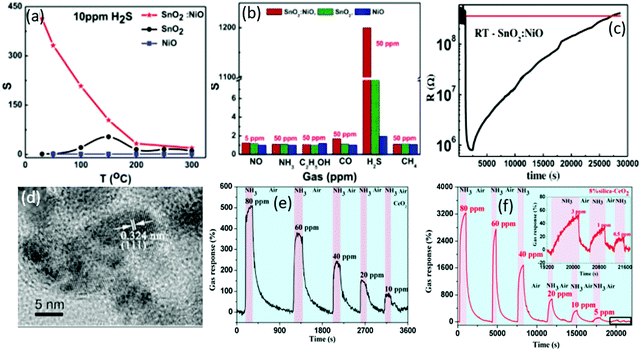 | ||
| Fig. 21 (a) Response histogram of a SnO2/NiO thin film-based room temperature gas sensor to different gases; (b) response values of the SnO2/NiO thin film-based RT gas sensor to different concentrations of H2S; (c) response/recovery curve to 100 ppm H2S.123 Copyright 2017, Elsevier. (d) TEM image of 8% silica-CeO2; (e) response/recovery curves of the pure CeO2-based sensor to NH3; (f) response/recovery curves of the 8% silica-CeO2-based sensor to NH3.198 Copyright 2017, Elsevier. | ||
Wang et al.198 reported a composite oxide sensor using 8% silica modified CeO2 nanomaterials (see Fig. 21d) synthesized using a sol-hydrothermal route. The addition of silica increases the specific surface areas (83.75 m2 g−1) and decreases the crystal sizes. Due to the existence of silica, lots of OH− species are formed on the surface of the sensor, which facilitate the adsorption of water, and the water molecules react with NH3 to generate NH4+ and OH− and decrease the electrical resistance of the sensor. As shown in Fig. 21e and f, the NH3 gas sensing performance of the sensor is significantly enhanced as compared to that of pure CeO2 at RT. Its response value reaches 3244% (defined as (ΔR/Rg) × 100%) for 80 ppm of NH3 gas.
The composites of alkali metal oxide and SMONs have also been reported as an effective way to enhance the sensitivity for sensing acidic gases, such as NOx.129 As shown in the gas sensing mechanism of mesoporous K2O–In2O3 nanowires in Fig. 22 the alkali metal oxides on the surfaces can serve as the alkaline center, which is beneficial to the adsorption and diffusion of acidic gases. Using mesoporous Santa Barbara Amorphous Material-16 (SBA-16) as a template, Rehman et al.129 prepared highly crystalline mesoporous K2O–In2O3 nanowires with diameters of 4–8 nm and pore sizes of 3–5 nm. The composite nanowires possess numerous chemisorbed oxygen and alkaline centers on their surfaces. The gas sensing performance of the mesoporous K2O–In2O3 composite nanowires has been significantly improved with the addition of K2O. Its response is 151.78 to 97 ppm of NOx, the response time is decreased to 12 s, and the LOD is as low as 48.5 ppb at RT.129
 | ||
| Fig. 22 Gas sensing mechanism to NOx of mesoporous K2O–In2O3 nanowires.129 Copyright 2016, Elsevier. | ||
Most reported composite SMON sensors exhibit higher response values and faster response time than those of the single phase SMONs. Many active sites can be generated in the composite SMONs, such as oxygen vacancies, heterojunctions, defects and mesopores, which can effectively enhance the sensing performance. The composite SMON can be further modified by noble metal nanoparticles, which takes advantage of the chemical sensitization and electronic sensitization of noble metal nanoparticles on the composite SMONs.
Table 6 summarizes the RT sensing properties of some composite nanostructures of the SMONs and carbon nanomaterials. Among these carbon materials, the composites of reduced graphene oxide (rGO) and SMONs are the most investigated ones for gas sensor applications. rGO has been used to combine with various types of SMONs for enhancing the gas sensing properties, and these SMONs include Fe2O3,315 In2O3,316 ZnO,317,318 Fe3O4,319 SnO2,320–324 WO3,325 NiO/SnO2326 and Pd/TiO2.327
| Material | Structure of SMONs | Synthesis method of SMONs | Target gas | C (ppm) | Response | t res/trec | LOD | Ref. |
|---|---|---|---|---|---|---|---|---|
| C = concentration; tres/trec = response time/recovery time; LOD = limit of detection; response is defined as Ra/Rg (for reducing gases) or Rg/Ra (for oxidizing gases), Ra: resistance of the sensor exposed to the reference, Rg: resistance of the sensor exposed to the target.a Here the response is defined as ΔR/Rg (for reducing gases) or ΔR/Ra (for oxidizing gases), ΔR: the change in resistance.b Here the response is defined as (ΔR/Rg) × 100% (for reducing gases) or (ΔR/Ra) × 100% (for oxidizing gases). | ||||||||
| NiO/rGO | Nanosheets | Hydrothermal | NO2 | 0.25 | 0.04a | 576/121 s | ∼0.25 ppm | 328 |
| WO3/MWCNTs | Nanoparticles | Metal organic decomposition | NO2 | 0.1 | 0.25a | 10.5/20 min | 100 ppb | 125 |
| Ag/SnO2/rGO | Nanoparticles | Hydrothermal | NO2 | 5 | 2.17 | 49/339 s | 1 ppm | 329 |
| SnO2/rGO | Nanoparticles | Hydrothermal | NO2 | 1 | 3.8 | 14/190 s | 50 ppb | 330 |
| α-Fe2O3/rGO | Nanoparticles | Hydrothermal | NO2 | 5 | 3.86 | 76/946 s | 0.1 ppm | 126 |
| Cu2O/rGO | Nanoparticles | Chemical solution | NO2 | 1 | 5.2 | 29.2/76.8 s | 100 ppb | 331 |
| ZnO/graphene | Spheres | Solvothermal | NO2 | 50 | 8b | 132/164 s | ∼10 ppm | 332 |
| Co3O4/rGO | Thin sheets | Hydrothermal | NO2 | 800 | ∼8b | 1.5/1 min | 60 ppm | 333 |
| In2O3/rGO | Nanosheets | Hydrothermal | NO2 | 30 | 8.25 | 4/24 min | ∼5 ppm | 334 |
| SnO2/graphene | Nanoparticles | Sol–gel | NO2 | 20 | ∼9.5 | <1/5 min | 5 ppm | 124 |
| ZnO/rGO | Nanowalls | Solution | NO2 | 50 | 9.61 | 25/15 s | ∼5 ppm | 135 |
| CuO/rGO | Nanosheets | Chemical solution | NO2 | 1 | 14 | 66/34 s | 60 ppb | 335 |
| SnO2/S/rGO | Nanoparticles | Hydrothermal | NO2 | 5 | 20.31b | 40 s/357 s | 1ppm | 336 |
| CeO2/rGO | Bilayer | Spray | NO2 | 10 | 20.5b | 92/— s | ∼1 ppm | 337 |
| SnO2/rGO | Nanoparticles | Hydrothermal | NO2 | 1000 | 22.87b | 100/— s | 1 ppm | 338 |
| Fe3O4/graphene | Nanoparticles | Hydrothermal | NO2 | 400 | 24.2b | 275/738 s | ∼30 ppm | 339 |
| ZnO/rGO | Nanorods | Oriented growth | NO2 | 1 | 119b | 75/132 s | 50 ppb | 340 |
| WO3/S/rGO | Nanorods | Hydrothermal | NO2 | 20 | 149.5b | 6 s/56 s | 0.25 ppm | 341 |
| α-Fe2O3/rGO | Nanospheres | Hydrothermal | NO2 | 90 | 150.63b | –/1648 s | 0.18 ppm | 342 |
| In2O3/rGO | Layers | Reflux | NOx | 97 | 1.45a | 25/— s | 970 ppb | 343 |
| CeO2/graphene | Nanosheets | Solvothermal | NOx | 300 | 12.76b | 1.3/— s | 5 ppm | 344 |
| CuxO/graphene | Nanoflowers | Reflux | NOx | 97 | 95.1b | 9.6/— s | 97 ppb | 345 |
| VO2/CNT | Nanocomposites | Hydrothermal | NH3 | 45 | 0.04a | 290/1800 s | 20 ppb | 346 |
| SnO2/rGO | Nanorods | Hydrothermal | NH3 | 200 | 1.3 | 8/13 s | 20 ppm | 347 |
| Cu2O/rGO | Nanorods | Hydrothermal | NH3 | 200 | 2.04 | 28/206 s | ∼100 ppm | 348 |
| TiO2/rGO | Microspheres | Hydrothermal | NH3 | 30 | ∼3.5b | ∼10/∼10 min | 5 ppm | 349 |
| Pd/SnO2/rGO | Nanoparticles | Chemical solution | NH3 | 5 | 7.6b | 7 min/50 min | ∼5 ppm | 350 |
| Pd/TiO2/rGO | Nanorods | One-pot polyol | NH3 | 50 | 14.9b | 184 s/81 s | 2.4 ppm | 351 |
| ZnO/GrO | Nanosheets | Chemical solution | NH3 | 1 | 24b | 6/2–3 s | 1 ppm | 352 |
| SnO2/MWCNTs | Nanocomposites | Microelectronic | NH3 | 200 | 26 | <5/5 min | ∼40 ppm | 136 |
| SnO/graphene | Hybrid films | CVD | NH3 | 100 | 35b | ∼10/— s | ∼5 ppm | 353 |
| ZnO/CNT | Networks | Flame | NH3 | 100 | 330 | 18.4/35 s | 200 ppb | 354 |
| SnO2/MWCNT | Nanofibers | Electrospinning | CO | 50 | 1.29 | — | 47 ppm | 355 |
| CuO/rGO | Nanocomposites | Hydrothermal | CO | 1 | 2.56b | 70/160 s | 0.25 ppm | 356 |
| Pd/SnO2/rGO | Nanoparticles | Hydrothermal | CO | 1600 | 9.5b | 2 min/2 min | ∼50 ppm | 357 |
| Au/SnO2/CNT | Nanotubes | Chemical solution | CO | 2500 | 70 | — | — | 358 |
| SnO2/F-MWCNTs | Networks | Sputtering | H2 | 500 | 5.4b | —/9 s | — | 359 |
| CuO/rGO/CuO | Sandwich | Hydrothermal | H2 | 1500 | ∼12b | 80/60 s | 10 ppm | 360 |
| ZnO/graphene | Nanotubes | Hydrothermal | H2 | 100 | 28.08b | 30/∼150 s | 10 ppm | 361 |
| Pd/SnO2/rGO | Nanoparticles | Chemical solution | H2 | 10000 | 50b | — | 100 ppm | 362 |
| TiO2/rGO | Nanosheets | Spray method | HCOH | 0.5 | 0.4b | 70/126 s | ∼0.1 ppm | 363 |
| SnO2/graphene | Nanohybrids | Electrochemical deposition | HCOH | 5 | 4.6b | 46/95 s | 0.02 ppm | 364 |
| Pd/TiO2/RGO | Nanotubes | Electrochemical anodization | Methanol | 700 | ∼70b | — | — | 365 |
| TiO2/rGO | Nanotubes | Hydrothermal | Methanol | 800 | 96.93b | 18/61 s | 10 ppm | 366 |
| Pd/SnO2/rGO | Nanoparticles | Hydrothermal | Methane | 4000 | 2.07b | 10 min/— | — | 367 |
| SnO2/rGO | Hybrid films | Hydrothermal | Acetone | 10 | 2.1b | 107/95 s | ∼10 ppm | 368 |
| ZnO/MWNTs | Nanorods | Hydrothermal | Ethanol | 50 | 4.5b | 7/11 s | ∼5 ppm | 369 |
| SnO2/Ni-graphene | Nanoparticles | Chemical solution | NO | 40 | 15 | — | — | 370 |
| SnO2/rGO | Quantum wires | Spin coating | H2S | 50 | 33 | 2/292 s | 43 ppb | 4 |
The RT NO2 sensor fabricated using rGO/α-Fe2O3126 exhibits a response value of 3.86 to 5 ppm NO2, which is better than that of pure rGO, whose response is 1.38. In addition, it has significantly shorter response/recovery times of 32/1432 s, compared with those of the sensors made of pure rGO (2059 s, 40130 s). Dong et al.342 reported a nanocomposite combining α-Fe2O3 nanospheres and reduced graphene oxide nanosheets as shown in Fig. 23a. The α-Fe2O3 nanospheres with a diameter from 40 to 50 nm were grown on the surface of graphene nanosheets using a hydrothermal method, and the improved sensing performance of the sensor made of this composite was attributed to the synergistic effect of a-Fe2O3/rGO and large specific surface areas. In addition to the interaction of NO2 with O2− on the surface of a-Fe2O3, NO2 molecules also capture the electrons from the rGO to form NO2−, thus resulting in an increased hole density, and a decreased resistance of rGO. Therefore, the a-Fe2O3/rGO nanocomposites exhibit a much higher response to NO2 at RT than that of either the pure rGO or a-Fe2O3 nanospheres. Its LOD for the NO2 gas is as low as 0.18 ppm (see Fig. 23b), and good selectivity has been demonstrated against CO, HCHO, H2S, NH3 and C2H5OH (see Fig. 23c).
 | ||
| Fig. 23 (a) TEM image of the α-Fe2O3/rGO composite; (b) response values of the sensor based on α-Fe2O3/rGO at different NO2 concentrations; (c) response histogram of the sensor to different gases.342 Copyright 2014, Royal Society of Chemistry. (d) Band gap diagrams of SnO2-nanorods/reduced graphene oxide nanostructures before and after combination.347 Copyright 2017, Elsevier. (e) TEM image of the ZnO/rGO composite; (f) response/recovery curves to 50 ppm NO2 of the sensor based on a-ZnO/rGO or ZnO.135 Copyright 2017, Elsevier. | ||
Besides the good conductivity of carbon materials, the improved interfacial electron transfer is another key factor for improving the SMONs’ sensing performance by adding carbon nanomaterials. For example, an RT NH3 gas sensor was fabricated using SnO2 nanorods/rGO composite nanostructures,347 and the sensor shows fast response/recovery with times of 8/13 s to 200 ppm NH3 at RT. Fig. 23d shows the band gap diagrams of SnO2-nanorods/rGO nanostructures before and after the combination of two nanostructures. The p–n heterojunctions are formed at the interface between the rGO and SnO2 as rGO is a p-type semiconductor. The Fermi energy of rGO is higher than that of SnO2, so electrons can be transported to SnO2 from rGO, which can further enhance the adsorption of NH3 molecules to improve the gas sensing performance.
Formation of heterojunction structures was found to contribute to the sensing performance of the ZnO nanowall/rGO nanocomposite,135 in which the ZnO nanowalls were vertically grown on the rGO thin film using a soft solution process to obtain a heterojunction structure as shown in Fig. 23e. At the interfaces between the rGO and ZnO nanowalls of the p–n heterostructures, the Fermi energy of rGO is higher than that of ZnO. Therefore, the charge transfer from rGO layers to the conduction band of ZnO enhances the adsorption of NO2 molecules. If compared with the sensor made of pure ZnO nanowalls, the sensor made of the ZnO/rGO heterojunction shows a higher response and shorter response/recovery times to NO2 at RT (see Fig. 23f).135
Another key mechanism for the improved gas sensing performance for the SMONs/rGO composite is the increased oxygen vacancy on the SMONs, such as in the SnO2–rGO composite.330 Due to the p–n heterojunction formed at the interfaces between n-type SnO2 and p-type rGO, electrons can easily transfer from the SnO2 into the rGO to form abundant oxygen vacancies on the surface of SnO2. These oxygen vacancies are the electronic charge carriers to increase the conductivity of the composite, and they can adsorb oxygen molecules to form more active sites, which will capture electrons from SnO2 and form the oxygen ions to react with target gas molecules. The oxygen vacancy also facilitates the fast adsorption of the NO2 molecules onto the surface of SnO2. All these factors contribute to the excellent sensing properties of SnO2/rGO composite based sensors to NO2 gas at RT.
However, the recovery of these composites of SMONs with carbon materials is very slow, although UV-light illumination can be used to enhance a fast and complete recovery. For example, rGO-CeO2 hybrids were synthesized by anchoring small CeO2 nanocrystals onto rGO nanosheets using a solvothermal method, and the RT NO2 gas sensor made of this hybrid showed a full recovery time of several hours.371 However, the recovery time can be significantly reduced to within 258 s with the aid of UV-light illumination. This UV light enhancement will be further discussed in Section 3.3.
Fig. 24a shows that an ultra-fast response time for sensing of H2S gas (which is the fastest reported in the literature with a value of 2s to 50 ppm of H2S) can be achieved using a sensor made of SnO2 quantum wires/rGO nanosheets.4 The electronic interactions of SnO2 quantum wires and rGO nanosheets can enhance the electron transport,4 and increase the response and recovery speed. In addition, the sensor made of the SnO2 quantum wires/rGO nanosheets shows a response of 33 with an excellent selectivity against other types of gases including NH3, SO2, NO2 and ethanol at RT as shown in Fig. 24b. In this composite material, the ultrathin and one-dimensional microstructure of SnO2 quantum wires is effective in providing large surface areas for gas adsorption and reactions.
 | ||
| Fig. 24 (a) TEM image of the SnO2 quantum wires/rGO nanosheets, the inset shows the response/recovery of the sensor based on SnO2 quantum wires/rGO nanosheets for different H2S concentrations; (b) response histogram of the SnO2 quantum wires/rGO nanosheet based sensor to different gases.4 Copyright 2016, American Chemical Society. (c) Response values at different concentrations of NH3 gas for 2%CNTs/ZnO networks (the inset presents the sensor structure); (d) long-time stability of the RT gas sensors to 100 ppm of NH3 at 30% RH.354 Copyright 2017, American Chemical Society. | ||
The sensors made of composites integrating the rGO with p-type SMONs (such as CuO and Co3O4) also show enhanced sensing performance. The RT gas sensor based on the CuO/rGO nanohybrids can detect a low-concentration of NO2 with a highly sensitive response (14 to 1 ppm NO2) and fast response/recovery times (66/34 s), mainly due to the formation of large surface areas and enhanced carrier transfers between the CuO and NO2 molecules.335 Furthermore, Ding et al. reported that the integration of chemically functionalized three-dimensional graphene oxide hydro-gels with metal–organic framework derived Co3O4 nanostructures achieved ultra-high response, short response time and distinct cross-selectivity.372
The composite of SMONs with carbon nanotubes (CNT) such as SWCNTs/SnO2373 and CNT/SnO2374–377 can also improve the sensing performance.378 The p–n junctions formed between the SMONs and p-type MWCNTs are responsible for their enhanced gas sensing responses. For example, Srivastava et al.124 reported an RT NO2 gas sensor based on multi-walled carbon nanotubes/SnO2. The sensor exhibits a much higher response to NO2 than the pure SnO2 based sensor operated at RT. Due to the good conductivity of the CNTs and the high porosity of the ZnO networks,354 the response value of 2%CNTs/ZnO networks has been increased from 37 to 330 when the sensor was exposed to 100 ppm NH3 at RT (see Fig. 24c). The response/recovery times are decreased from 58/61 s to 18/35 s, respectively. The sensor also displays good stability at RT over a duration of one month (see Fig. 24d). In addition, the CNTs can serve as acceptors for the released electrons, which are injected into the SMONs from the target gases. A H2S gas sensor made of nanocomposites of SnO2 quantum dots/MWCNTs reported by Liu et al.379 exhibited a high response value of 108 to 50 ppm H2S with fast response/recovery times of 23/44 s.
Adding noble metal nanoparticles into the composite is another method to further improve the gas sensing performance of SMONs/rGO composites. Being good catalysts, these noble metal nanoparticles can enhance the catalytic efficiency by creating extra new sites to promote fast adsorption of gas molecules and decrease the reaction temperatures by lowering the activation energy of the gas sensing reactions. For example, Shojaee et al.357 reported that the nanocomposites of Pd loaded SnO2 and partially reduced graphene oxide showed good performance to detect CO from 50 to 1600 ppm with fast response and recovery times at 26 °C. The Pd/SnO2/rGO based H2 sensor362 and Pd/TiO2/rGO based NH3 sensor351 prepared using a chemical solution method exhibited higher sensitivity and faster response time than those of the SnO2/rGO and TiO2/rGO sensors. In addition to Pd nanoparticles, Ag nanoparticles were also used to improve the RT sensing performance of SnO2–rGO hybrids for detection of NO2. The Ag/SnO2/rGO hybrid composites exhibit much shorter response time and recovery time (49 s and 339 s) to 5 ppm NO2 at RT than the SnO2–rGO hybrids (415 s and 740 s) 329.
Similar to those cases for the rGO/SMON composites, modifications of the CNT/SMON composites using noble metal nanoparticles can also improve their gas sensing properties. For example, CNT/Au/SnO2 composites were synthesized by homogeneously coating SnO2 and Au nanocrystals onto the CNTs, and then applied to detect CO gas at RT.358 The sensor made of the CNT/Au/SnO2 composites shows better selectivity to CO than that made of the CNT/SnO2 composite. It has a high sensitivity of 70 when exposed to 2500 ppm of CO, and shows higher sensitivity values to CO gases with different concentrations varying from 500 to 2500 ppm when compared with those of the Au/SnO2 composites.
In brief, due to the high conductivity of carbon nanomaterials and the formation of heterojunctions, the response/recovery times of the composites of SMONs with carbon nanomaterials are much shorter than those from the pure SMONs, although it seems that the increase of response values achieved using these composites might be less significant.
3.3 Room temperature photoactivated gas sensors based on semiconducting metal oxide nanostructures
Generally, many of the SMON-based gas sensors are needed to heat up for the best gas sensing performance, which is inconvenient in many situations. Instead, UV light can be used to activate and enhance the gas sensing performance of SMONs operated at RT.380 The reported SMONs whose sensing properties can be improved by UV light are mainly ZnO,381–385 In2O3,386,387 TiO2388,389 and SnO2,390,391 which have been summarized in Table 7. The SMONs can absorb UV light to produce photo-generated electrons and holes. The photo-generated electrons on the surface can enhance the chemisorption of oxygen molecules to form more O2− as listed in eqn (20) and (21),392 thus can enhance the sensitivity and response/recovery times of the SMONs under UV light.| hν → h+ + e− | (20) |
| O2 + e−(hν) → O2−(hν) | (21) |
| Material | Structure | Synthesis method | Target gas | C (ppm) | Response | t res/trec | LOD | Ref. |
|---|---|---|---|---|---|---|---|---|
| C = concentration; tres/trec = response time/recovery time; LOD = limit of detection; response is defined as Ra/Rg (for reducing gases) or Rg/Ra (for oxidizing gases), Ra: resistance of the sensor exposed to the reference, Rg: resistance of the sensor exposed to the target.a Here the response is defined as ΔR/Rg (for reducing gases) or ΔR/Ra (for oxidizing gases), ΔR: the change in resistance.b Here the response is defined as (ΔR/Rg) × 100% (for reducing gases) or (ΔR/Ra) × 100% (for oxidizing gases). | ||||||||
| ZnO | Nanorods | Hydrothermal | HCHO | 110 | 11.5a | 14/0.5 min | 1.8 ppm | 383 |
| ZnO | Nanofibers | Electrospinning | HCHO | 100 | 12.3 | 32/17 s | ∼5 ppm | 384 |
| ZnO | Nanoparticles | Hydrothermal | NO2 | 20 | 85a | 26/16 s | ∼1 ppm | 393 |
| ZnO | Microwires | Surface etching | NO2 | 20 | 411b | 221/118 s | ∼10 ppm | 381 |
| ZnO | Nanowires | Wet-chemical | C2H5OH | 700 | 85b | — | ∼100 ppm | 382 |
| In2O3 | Nanostructures | Arc-discharge | NO | 50 | 41.7 | ∼10/— min | ∼2 ppm | 386 |
| In2O3 | Nanoporous particles | Nanocasting | Ozone | 0.22 | 200 | 2.5/— min | 50 ppb | 387 |
| TiO2 | Thin films | Rf-sputter | NO2 | 250 | ∼1.8b | 100/210 s | 100 ppm | 389 |
| TiO2 | Hollow microspheres | Hydrothermal | HCHO | 5 | ∼40 | 40/55 s | 124 ppb | 388 |
| SnO2 | Nanowires | — | NO2 | 10 | ∼85b | 10/15 min | ∼0.1 ppm | 390 |
| SnO2/TiO2 | Hollow spheres | Thermal evaporation | Ethanol | 100 | 160 | 50/150 s | — | 394 |
| ZnO/SnO2 | Nanorods | Wet chemical | NO2 | 0.5 | 1266a | 7/8 min | ∼200 ppb | 395 |
| Ag/ZnO | Nanorods | Hydrothermal | HCHO | 40 | 119.8b | — | 5 ppm | 396 |
| NiO/TiO2 | Microspheres | Hydrothermal | NH3 | 100 | 140b | ∼400/∼400 s | ∼10 ppm | 397 |
With the assistance of a UV LED (photon energy of 2.5 mW), the RT gas sensor made of mesoporous hollow TiO2 microspheres388 exhibited a high response to formaldehyde with faster response/recovery (40/50 s) and good selectivity. Higher response has also been reported using the sensor made of ZnO/SnO2 composite materials395 to detect NO2 under UV light illumination at RT. After the sensing materials are exposed to NO2 gas, the NO2 molecules will collect the photo-generated electrons to form NO and O2− as shown in eqn (22),393 which results in an increase in the resistance of the sensor.
| 2NO2(g) + e−(hν) → 2NO(hν) + O2−(hν) | (22) |
Simultaneously, a heterojunction is formed at the interfaces between ZnO and SnO2. The photogenerated electrons are transferred from ZnO to SnO2 due to the higher Fermi energy level of ZnO than that of SnO2 (see Fig. 25a). The efficient charge separation increases charge concentrations on the surface of SnO2, which remarkably improves the sensitivity under UV light stimulation at RT as shown in Fig. 25b.
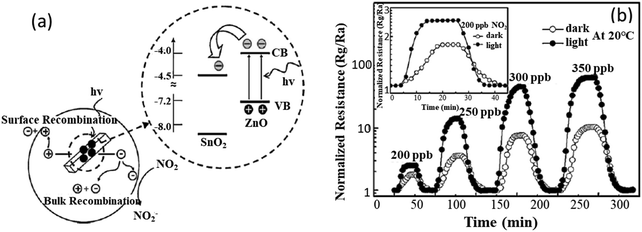 | ||
| Fig. 25 (a) Schematic diagram of the carrier transport under UV light and the electron–hole pair separation on heterostructure of ZnO/SnO2 composite; (b) response/recovery of ZnO/SnO2 composites at different concentrations of NO2 with and without UV light stimulation at room temperature.395 Copyright 2011, Elsevier. | ||
Apart from the UV light, visible light (including blue light and white light) assisted RT gas sensors with enhanced performance have also been reported.387,398–400 Klaus et al.387 reported a blue light (460 nm) activated ozone gas sensor based on nanoporous In2O3 particles, which showed a high response value of 200 and a low LOD of 50 ppb at RT. Geng et al.399 reported that a sensor made of CuxO1−y/ZnO1−α nanocomposites showed enhanced NO2 sensing properties at RT with high response and good selectivity after being illuminated with white light. Similarly, infrared (IR) light should also be beneficial for the improvement in the sensing performance.
Although the photoactivated SMON gas sensors could achieve the improved gas sensing performance operated at RT, the light-emitting diodes, UV source, or infrared light, as well as optical power detection devices are necessary to be used, which will increase the size and production cost of the sensor device. The integration and shrinkage of the devices along with mass production capabilities are challenges. In addition, for the application of the gas sensors in a real environment, the gas sensor will be exposed to air for real-time monitoring. Sunlight will severely influence the gas sensing response.
4. Mechanically flexible gas sensors based on semiconducting metal oxide nanostructures
Mechanically flexible gas sensors are in great demand due to their promising applications in wearable electronic devices. SMONs with a potentially higher carrier mobility and mechanical robustness are good candidates for the realization of stretchable and flexible sensors.223 The mechanically flexible and wearable RT gas sensors based on SMONs have been an active research area recently as listed in Table 8. Compared with those on the rigid substrates, the wearable devices need substrates which are flexible, light weight, transparent, transportable, with a small volume, and low cost.401 Due to their excellent dielectric properties, and thermal and chemical stability, many plastic substrates have been used as flexible substrates for the RT gas sensors including polyethylene terephthalate (PET),223,402–404 polypropylene (PP),405,406 polyimide (PI),264,407,408 polyvinyl acetate (PVA)105 and nylon.409| Material | Structure | Substrate | Synthesis method | Target gas | C (ppm) | Response | t res/trec | LOD | Ref |
|---|---|---|---|---|---|---|---|---|---|
| C = concentration; tres/trec = response time/recovery time; LOD = limit of detection; response is defined as Ra/Rg (for reducing gases) or Rg/Ra (for oxidizing gases), Ra: resistance of the sensor exposed to the reference, Rg: resistance of the sensor exposed to the target.a Here the response is defined as ΔR/Rg (for reducing gases) or ΔR/Ra (for oxidizing gases), ΔR: the change in resistance.b Here the response is defined as (ΔR/Rg) × 100% (for reducing gases) or (ΔR/Ra) × 100% (for oxidizing gases). | |||||||||
| ZnO | Nanowires | PET | Hydrothermal | H2 | 1000 | 5b | ∼600/— s | — | 402 |
| Ga/ZnO | Nanorods | PI | Hydrothermal | H2 | 1000 | 91b | ∼18.8/— s | 0.2 ppm | 264 |
| Pd/ZnO | Nanorods | PI/PET | Hydrothermal | H2 | 1000 | 91.2b | ∼18.8/— s | 0.2 ppm | 173 |
| ZnO | Nanorods | Nylon | Hydrothermal | H2 | 500 | 109b | 149/122 s | — | 409 |
| CuO | Nanorectangles | PET | Hydrothermal | NH3 | 5 | ∼0.25a | 90/120 s | 5 ppm | 223 |
| SnO2/SnS2 | Nanotubes | PET | Hydrothermal | NH3 | 100 | 2.48 | 21/110 s | 1 ppm | 403 |
| Polyaniline/WO3 | Flowerlike | PET | Polymerization | NH3 | 10 | 7 | 13/49 s | 500 ppb | 410 |
| ZnO | Nanoparticles | Cotton fabrics | Sol–gel | NH3 | 100 | 9 | 39/34 s | — | 411 |
| Au/In2O3/Polyaniline | Nanospheres | PI | Hydrothermal | NH3 | 100 | 46 | 118/144 s | — | 412 |
| CeO2/CuBr | Nanoparticles | PI | Electron beam evaporation | NH3 | 5 | 68 | 112/74 s | 20 ppb | 413 |
| Polyaniline/α-Fe2O3 | Fiber network | PET | Sol–gel | NH3 | 100 | 72b | 50/1575 s | 2.5 ppm | 414 |
| Polyaniline/CeO2 | Thin films | PI | Self-assembly | NH3 | 50 | 262.7b | 14/6 min | 16 ppb | 415 |
| In/Ga/Zn/Oxide | Thin-Films | PI | CVD | NO2 | 5 | ∼1.3 | — | 2 ppm | 407 |
| ZnO1−x | Sheet-like | PP | Suspension flame spraying | NO2 | 1 | 2.568a | 60/230 min | 0.25 ppm | 405 |
| MWCNTs/WO3 | Nanoparticles | PET | Hydrothermal | NO2 | 5 | 14b | 10/27 min | 0.1 ppm | 416 |
| WO3/MWCNT/rGO | Nanoparticles | PI/PET | Hydrothermal | NO2 | 5 | 17b | 7/15 min | 1 ppm | 417 |
| SWNT/Fe2O3 | Composites | PP | CVD | NO2 | 100 | 18.3b | — | ∼1 ppm | 406 |
| PdO/Co3O4 | Nanocubes | PI | Chemical precipitation | NO2 | 20 | 27.33b | — | 1 ppm | 408 |
| Cellulose/Fe2O3 | Nanoparticles | PET | Hydrothermal | NO2 | 200 | ∼1100b | 50/30 s | 1 ppm | 418 |
| WO3−δ | Films | PI | Granule spray | NO2 | 10 | 18500b | 17/25 s | 1.88 ppm | 419 |
| In2O3 | Cubic crystals | PVA | Hydrothermal | Ethanol | 100 | ∼1.4 | 5/3 s | 10 ppm | 105 |
| rGO/WO3 | Nanoneedles | PET | Hydrothermal | Isopropanol | 200 | ∼8.5 | 60/— s | 1 ppm | 404 |
| Ag/ZnO | Nanorods | PI | Hydrothermal | C2H2 | 1000 | 26.2 | 66/68 s | 3 ppm | 420 |
For many of these flexible RT gas sensors, a sensitive layer such as ZnO nanorods is often used to deposit onto the device, for example, ZnO nanorods/nylon,409 Ga-ZnO nanorods/PI,264 Pd–ZnO nanorods/PI/PET.173 The aqueous solution method to prepare these ZnO nanorod layers on the polymer substrate is facile with advantages of low growth temperature and easy modifications. For example, Mohammad et al.409 prepared well-aligned ZnO nanorods on a thin nylon substrate with a thickness of 15 μm using a hydrothermal process, and then made a H2 gas sensor. There are many contact points among ZnO nanorods which form paths of electric carriers and result in the improvement of electron transport. The mechanically flexible hydrogen gas sensor exhibited a good response value of 109% (defined as (ΔR/Rg) × 100%) with fast response/recovery.
Rashid et al.173 prepared vertically aligned ZnO nanorods on the PI substrate using a hydrothermal method, and then made the sensors for hydrogen detection at RT. Pd nanoparticles with 10 nm size were further sputtered on the surface of ZnO nanorods using RF magnetron sputtering. After being bent for 103 cycles, there were no cracks or breaks on the ZnO nanorod film (see Fig. 26a). Such flexible hydrogen sensors had a response value of ∼91% (defined as (ΔR/Rg) × 100%) for 1000 ppm hydrogen with good repeatability and stability, and a low LOD of 0.2 ppm at RT. The gas sensing performance at different bent angles from 0°, to 90° did not exhibit apparent changes (see Fig. 26b). Even after the sensor was bent to a curvature angle of 90° for 105 cycles, the sensing performance of this flexible H2 sensor did not show any degradation (see Fig. 26c). The vertically well-aligned ZnO nanorods with the Pd catalyst on Ga-modified ZnO seed layer on flexible PI substrates also showed good H2 sensing properties and good mechanical flexibility at RT with good repeatability, stability and a low LOD of 0.2 ppm, even after being bent at a curvature angle of 90°.264
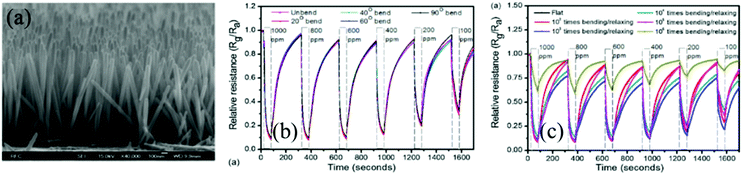 | ||
| Fig. 26 (a) SEM images of Pd/ZnO nanorods after 103 times bending/relaxing. (b) Response/recovery curves of the flexible sensor to H2 at different bending angles, (c) the reliability test of the flexible sensor.173 Copyright 2013, Elsevier. | ||
In addition to being directly grown onto the plastic substrates, the ZnO nanowires were also transferred onto plastic substrates of PET to fabricate a flexible gas sensor using various methods, including slide transfer, roll transfer and heat transfer.402 A 2D sheet-like ZnO layer was deposited onto the flexible polypropylene papers using a suspension flame spraying method, and the prepared ZnO flexible sensor exhibited good responses and stability to sub-ppm level of NO2 at RT under white LED light illumination.405
Other types of SMONs have also been applied for making flexible RT gas sensors, and these include WO3, SnO2, CeO2, Co3O4, In2O3, etc. For example, Ryu et al.419 fabracted flexible RT NO2 gas sensors based on a WO3-δ film on a plastic substrate of polyimide (PI) using the granule spray method with a vacuum process. The sensor has a repsonse of up to 18500% to 10 ppm NO2 with fast response/recovery times of 17/25 s and reliable flexibility after 4000 bending/extending cycles. As another example, a nanocompsite of polyaniline and nanoflower-like WO3 synthesized using a facile chemicaloxidation polymerization process was prepared on a PET substrate to fabricate a NH3 flexible sensor, which shows a high response and fast response/recovery times (13/49 s) to 10 ppm NH3 at RT.410
Modifying the SMONs using polyaniline (PANI) can effectivly enhance the sensing performance and stability of the flexible gas sensors, such as PANI–CeO2, PANI/α-Fe2O3 and PANI/WO3. The morphology and sensing performance of flexible RT NH3 gas sensors based on PANI–CeO2 nanocomposite thin films are stable after being bent/cycled for 500 times.415 Furthermore, adding noble metals into the SMON/PANI composites can further improve their RT sensing performance. For example, after adding Au nanoparticles, the response of the RT NH3 gas sensor made of the composite of mesoporous In2O3 nanospheres/polyaniline has been increased up to 4 times higher.412
Graphene and carbon nanotubes have excellent performance during severe plastic deformation, thus the composite integrating these carbon nanomaterials with the SMONs can achieve excellent sensing performance and mechanical flexibility. For example, a flexible isopropanol sensor was fabricated using a mixture of WO3·0.33H2O nano-needles and rGO on PET substrates (see Fig. 27a).404 Compared with the sensor made of pure WO3·0.33H2O nano-needles, the 5%rGO/WO3·0.33H2O based sensor showed better selectivity and a superior response (4.96 to 100 ppm to isopropanol) (see Fig. 27b), with good performance after repeated bending for many cycles. Similarly, SWNT–Fe2O3 composite films were prepared using the CVD method and then transferred onto the flexible PP polymer substrate.406 Compared with that fabricated using the single SWNTs, the flexible gas sensor of the SWNT–Fe2O3 composite film exhibited an improved response to H2S at RT. Under repeated bending to large angles (such as 90° and 180°) for 16 times as shown in Fig. 27c, the flexible sensor exhibited stable sensing response values to H2S. As another example, hydrothermally synthesized WO3 nanoparticles were mixed with MWCNTs (see Fig. 27d), and then cast onto a PET substrate to fabricate a flexible NO2 gas sensor.416 This sensor not only shows good sensing performance, but also has excellent mechanical flexibility (see Fig. 27e). There was no significant degradation of response values after bending/relaxing for 106 cycles, demonstrating the excellent mechanical robustness of the MWCNTs/WO3 composite layers on the flexible gas sensors (see Fig. 27f).
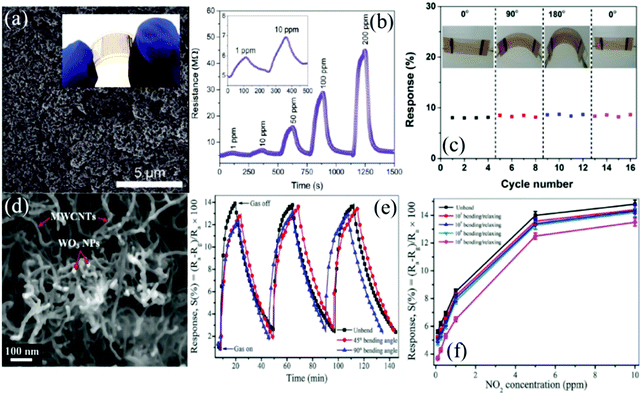 | ||
| Fig. 27 (a) SEM images of 5%rGO/WO3·0.33H2O deposited on polyethylene terephthalate; the inset is the photograph of the flexible gas sensor, (b) response/recovery curves to isopropanol with different concentrations.404 Copyright 2018, Royal Society of Chemistry. (c) Responses of the SWNT/Fe2O3 gas sensor to 20 ppm H2S under different bending angles from 0° to 180° and back to 0°.406 Copyright 2017, Elsevier. (d) SEM images of the MWCNTs/WO3 composite, (e) response curves to 5 ppm NO2 at RT under different bending angles, (f) responses to different NO2 concentrations at RT after bending/relaxing several times (90° angle).416 Copyright 2015, Elsevier. | ||
Cotton fabrics are also reported to be used as a good substrate for flexible RT gas sensors, for example, a flexible NH3 gas sensor was made by growing nanostructured ZnO onto cotton fabrics.411 Flexible nanowires of the SMONs can also be isostatically pressed into a thin paper, and then the nanowire paper is cut into small pieces to directly fabricate a flexible gas sensor. Based on this idea, a-MoO3 nanowire paper421 has been fabricated and a flexible gas sensor was made to detect hydrogen gas. The sensor shows fast response and recovery speeds (3.0 and 2.7 s toward 1.5% H2), good selectivity, and high sensitivity at RT. Wei et al.422 also reported a flexible gas sensor based on cellulose/TiO2/PANI composite nanofibers, which showed excellent ammonia gas sensing performance at RT. Similarly, a stretchable ZnO nano-accordion structure has also shown good applications in flexible RT gas sensors.423
In summary, flexible RT gas sensors can be fabricated using SMONs as the sensing materials on a mechanically flexible platform, and the sensors have demonstrated excellent mechanical robustness and can maintain good sensing performance at RT after bending/recovering many times. Furthermore, the composite of SMONs with graphene or CNT can achieve better mechanical robustness for the flexible gas sensor. However, so far, excellent sensing performance and reliability and stability have not been achieved in the case of flexible RT gas sensors compared with their rigid counterparts.
5. Conclusions and outlook
In this paper, we have summarized the recent progress in designs and mechanisms of RT gas sensors based on different SMONs. Our emphasis has been on the critical review of different structures of SMON-based gas sensors that may help the design of new devices. The key topics covered in this paper include single phase n-type SMONs, single phase p-type SMONs, noble metal nanoparticle modified SMONs, metal ion modified SMONs, SMON composites with multiple metal oxides, and SMON composites with carbon nanomaterials. The different nanostructures of these SMONs include nanoparticles, nanowires, nanofibers, nanorods, nanosheets, nanotubes etc. The sensing performance of these SMON based RT sensors has been reviewed for detecting various toxic or flammable gases, such as hydrogen disulfide, nitrogen dioxide, ammonia, carbon monoxide and hydrogen, as well as organic gases of formaldehyde, acetone, methanol and ethanol, etc. In addition, photoactivated RT gas sensors and flexible RT gas sensors based on SMONs are also summarized.Availability of numerous surface chemisorbed oxygen species of O2− at RT was identified to be the key reason for the high sensitivity of these RT gas sensors. These oxygen species react with the target molecules to change the electronic resistance of the sensor. However, many RT H2S sensors are exceptional as the sensing mechanism is dominated by the formation of metallic conducting metal sulfide.
Noble metal nanoparticles on the surface of SMONs can stimulate the adsorption of oxygen molecules to form oxygen ions by reduction processes. These oxygen ions spill onto the surface of SMONs to improve the concentration of oxygen ions on the surface of SMONs for sensing reactions. In addition, noble metal nanoparticles can accelerate the transfer of electrons to SMONs. Therefore, both the chemical sensitization and electronic sensitization enhance the sensitivity and speed of the SMON-based sensors. Doping of metal ions in the SMONs can increase the number of active sites and defects on the surface of SMON nanocrystals, and thus enhance the amount of oxygen species and increase the adsorbed gas molecules on the sensor surface. Heterojunctions can form at the interfaces of different metal oxides or at the interfaces between the SMONs and carbon nanomaterials. These can effectively accelerate the transformation of electrons and enhance oxygen adsorption, and are beneficial to improve the sensitivity and response rates in application of RT gas sensors. The sensing performance also depends significantly on the nanostructures of the SMONs. Large specific surfaces are beneficial to the formation of more oxygen species, and porous nanostructures facilitate the adsorption and desorption of target gases, thus achieving fast response and recovery.
Generally, the RT SMON based gas sensors show high response values and low LODs; however, their response and recovery times could be too long. Modifications of the SMON sensors using various methods can improve their sensing performance, which include using noble metal modified SMONs; metal ion doped SMONs, composite SMONs, and composites with carbon nanomaterials. The key conclusions are summarized below:
(1) Surface modifications of the SMONs using noble metal nanoparticles can effectively enhance their sensitivity, response/recovery speeds, selectivity and LODs through both chemical sensitization and electronic sensitization.
(2) Metal ion doped SMONs have increased number of active sites and more defects on their surfaces, which can enhance the oxygen species for sensing reactions and improve the adsorption of gas molecules.
(3) SMON composites can form abundant oxygen vacancies on their surfaces, thus providing many active sites. Heterojunctions can be formed at the interfaces of different metal oxides, which can effectively accelerate the transformation of electrons between different particles, thus improving the response rates. The composite SMONs often contain numerous mesopores which are beneficial to the adsorption and desorption of gas molecules. Hence, sensors based on the majority of reported composite oxides exhibit a high response value and very fast response.
(4) Because of the high conductivity of carbon nanomaterials, the composites of SMONs combined with carbon nanomaterials can achieve fast response/recovery.
(5) The photo-generated electrons on the surfaces of SMON sensing materials can enhance the chemisorption of oxygen molecules to form more O2−, which can enhance the sensitivity and response/recovery speed of the SMONs.
(6) RT flexible gas sensors based on the sensing layer of the SMON sensing materials have excellent mechanical robustness and can maintain good sensing performance after repeated bending/recovering.
Although there has been significant progress in developing novel SMONs for gas sensing at RT, there are still many challenges and problems towards achieving high response, fast response/recovery speed, good selectivity and long-term stability:
(1) One of the key challenges is the durability and long-term stability of the sensors for application under varying environmental conditions, such as different humidity levels and different temperatures, which could have significant influences on the sensing properties of many RT gas sensors. This is especially important for RT NH3 sensing, as high humidity seriously affects the sensitivity and the response time. Light exposure, especially ultraviolet and infrared light, and even visible light, all influence the response of the RT SMON sensors. In the literature, the performance of sensors has been normally characterized based on experiments conducted in a well-controlled laboratory environment. However, in a practical setting with variable environmental conditions, the sensing performance may be altered with light exposure. Therefore, the sensing properties under different environmental conditions should be systematically investigated in order to establish the relationship between environmental conditions and sensing properties, which are then used to correct the sensing results.
(2) Interfering gases often affect the sensing performance, resulting in a drastically reduced response. Lack of good selectivity is still the most serious problem hindering the wide applications of these RT gas sensors. There are few reports on specific gas sensors which only respond to a target gas but not all the other gases. Because the resistive gas sensors rely on their changes in resistance upon adsorption of gas molecules, it can distinguish between the reducing gases and oxidizing gases based on the increase or decrease of resistance; however, it is difficult to discriminate a group of gases which can produce similar changing trends of resistance values.
Therefore, selectivity is particularly important for multiple-agent gas sensors. To solve this problem, arrays of different sensing materials can be fabricated such that forming an array of gas sensors, which could obtain good selectivity by analyzing and comparing data from the different single sensors.424 For example, Zhang et al.425 reported a method to detect multiple VOCs using an array of gas sensors based on Ag doped LaFeO3 (ALFO). The device was optimized for the detection of acetone, benzene, methanol and formaldehyde to monitor air quality. The selectivity of ALFO can be altered using a molecular imprinting technique towards specific targets. Responsivity values of individual sensing elements vary between 14 and 21 while the values to other VOCs are lower than 4. The response and recovery times are on the order of 10 s and 100 s levels. Flitti et al.426 reported a micromachined 4 × 4 array of sensors for multiple target detection. The sensing film for individual elements is based on SnO2 and the elements are post-treated using metal catalysts of Pt, Pd, and Au and ions implanted using B, P, and H. The basic post-treatment methods are effective in selectively detecting gases of CO, CH4, ethanol, CH4–CO, ethanol–CO, and ethanol–CH4 using an algorithm based on vector angle similarity. Recognition accuracy higher than 95% is reported in this study.427 This method has been demonstrated being capable of forming 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 virtual sensors using dedicated temperature modulations. Sensing networks will be the future trends.
000 virtual sensors using dedicated temperature modulations. Sensing networks will be the future trends.
(3) The sensing mechanism of the SMONs is mainly based on the interaction between the target gas molecules and chemisorbed oxygen species, such as O2−, O− and O2− ions. However, other oxygen groups such as OH− can also react with the target gas molecules. More effective analysis and theory development of the surface groups is urgently needed to assess their effect on the sensing properties, and the surface modification methods should be developed to minimize this influence.
(4) Many gas sensing mechanisms of SMON based materials with various sizes and morphologies have been presented to explain their sensing properties. However, it is not clearly elucidated why the same SMON based materials with similar sizes and morphologies show markedly different sensing properties. Therefore, in situ characterization techniques and theory development for the sensing mechanisms are necessary.
(5) Response times of many RT gas sensors are very long, which cannot meet the need for timely triggering of the alarm. Exploring novel SMON based sensing materials for rapid response at RT is still necessary. 3-D nano-arrays of SMONs facilitate gas diffusion, which might be promising to shorten the response time.
(6) Flexible wearable RT gas sensors are in great demand due to their promising applications. SMONs with the potential of higher carrier mobility and mechanical robustness are among the good candidates for making stretchable and flexible gas sensors. For RT gas sensors, there are still challenges regarding their manufacturing technologies, and cracking and spalling problems of SMON layers on the flexible substrates usually happen, which need to be solved to achieve reliable RT flexible gas sensors. Therefore, finding new low-cost SMON based sensing materials with excellent sensing performance and mechanical robustness is still the major challenge.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Key Research and Development Program of China (Grant no. 2016YFB0402705), the National Natural Science Foundation of China (NSFC, 21711530211, 61390502, 21673091), the Foundation for Innovative Research Groups of the National Natural Science Foundation of China (Grant No. 51521003) and by Self-Planned Task (No. SKLRS201607B) of State Key Laboratory of Robotics and System (HIT), Shenzhen Science & Technology Project (Grant no. JCYJ20170817100658231), the Natural Science Foundation of Hubei Province (No. 2015CFA125), UK Engineering Physics and Science Research Council (EPSRC EP/P018998/1 and EP/P026435/1) and Newton Mobility Grant (IE161019) through Royal Society and NFSC, as well as Royal Academy of Engineering UK-Research Exchange with China and India.References
- M. Jerrett, D. Donaire-Gonzalez, O. Popoola, R. Jones, R. C. Cohen, E. Almanza, A. de Nazelle, I. Mead, G. Carrasco-Turigas, T. Cole-Hunter, M. Triguero-Mas, E. Seto and M. Nieuwenhuijsen, Environ. Res., 2017, 158, 286–294 CrossRef CAS PubMed.
- Z. A. Barakeh, P. Breuil, N. Redon, C. Pijolat, N. Locoge and J.-P. Viricelle, Sens. Actuators, B, 2017, 241, 1235–1243 CrossRef CAS.
- D. Sett and D. Basak, Sens. Actuators, B, 2017, 243, 475–483 CrossRef CAS.
- Z. Song, Z. Wei, B. Wang, Z. Luo, S. Xu, W. Zhang, H. Yu, M. Li, Z. Huang, J. Zang, F. Yi and H. Liu, Chem. Mater., 2016, 28, 1205–1212 CrossRef CAS.
- H. Ren, C. Gu, S. W. Joo, J. Zhao, Y. Sun and J. Huang, Sens. Actuators, B, 2018, 266, 506–513 CrossRef CAS.
- G. Tuerdi, P. Nizamidin, N. Kari, A. Yimit and F. Wang, RSC Adv., 2018, 8, 5614–5621 RSC.
- A. Paliwal, A. Sharma, M. Tomar and V. Gupta, Sens. Actuators, B, 2017, 250, 679–685 CrossRef CAS.
- B. Gong, T. Shi, W. Zhu, G. Liao, X. Li, J. Huang, T. Zhou and Z. Tang, Sens. Actuators, B, 2017, 245, 821–827 CrossRef CAS.
- R. Kitture, D. Pawar, C. N. Rao, R. K. Choubey and S. N. Kale, J. Alloys Compd., 2017, 695, 2091–2096 CrossRef CAS.
- M. Asad and M. H. Sheikhi, Sens. Actuators, B, 2014, 198, 134–141 CrossRef CAS.
- S.-H. Wang, C.-Y. Shen, H.-M. Huang and Y.-C. Shih, Sens. Actuators, A, 2014, 216, 237–242 CrossRef CAS.
- L. Rana, R. Gupta, M. Tomar and V. Gupta, Sens. Actuators, B, 2017, 252, 840–845 CrossRef CAS.
- T. Goto, T. Itoh, T. Akamatsu, N. Izu and W. Shin, Sens. Actuators, B, 2016, 223, 774–783 CrossRef CAS.
- L. Sun, W. L. Luan, T. C. Wang, W. X. Su and L. X. Zhang, Nanotechnology, 2017, 28, 075501 CrossRef CAS PubMed.
- H. Liang, X. Zhang, H. Sun, H. Jin, X. Zhang, Q. Jin, J. Zou, H. Haick and J. Jian, ACS Sens., 2017, 2, 1467–1473 CrossRef CAS PubMed.
- G. Jiang, M. Goledzinowski, F. J. E. Comeau, H. Zarrin, G. Lui, J. Lenos, A. Veileux, G. Liu, J. Zhang, S. Hemmati, J. Qiao and Z. Chen, Adv. Funct. Mater., 2016, 26, 1729–1736 CrossRef CAS.
- E. Menart, V. Jovanovski and S. B. Hočevar, Sens. Actuators, B, 2017, 238, 71–75 CrossRef CAS.
- S. S. Shendage, V. L. Patil, S. A. Vanalakar, S. P. Patil, N. S. Harale, J. L. Bhosale, J. H. Kim and P. S. Patil, Sens. Actuators, B, 2017, 240, 426–433 CrossRef CAS.
- Y. Li, N. Chen, D. Deng, X. Xing, X. Xiao and Y. Wang, Sens. Actuators, B, 2017, 238, 264–273 CrossRef CAS.
- R. Kumar, O. Al-Dossary, G. Kumar and A. Umar, Nano-Micro Lett., 2014, 7, 97–120 CrossRef PubMed.
- A. Dey, Mater. Sci. Eng., B, 2018, 229, 206–217 CrossRef CAS.
- S. W. Lee, W. Lee, Y. Hong, G. Lee and D. S. Yoon, Sens. Actuators, B, 2018, 255, 1788–1804 CrossRef CAS.
- H. Wu, Z. Chen, J. Zhang, F. Wu, C. He, Y. Wu and Z. Ren, J. Mater. Chem. A, 2017, 5, 24493–24501 RSC.
- S. Park, M. Park, S. Kim, S.-G. Yi, M. Kim, J. Son, J. Cha, J. Hong and K.-H. Yoo, Appl. Phys. Lett., 2017, 111, 213102 CrossRef.
- S. W. Lee, W. Lee, D. Lee, Y. Choi, W. Kim, J. Park, J. H. Lee, G. Lee and D. S. Yoon, Sens. Actuators, B, 2018, 266, 485–492 CrossRef CAS.
- N. Joshi, T. Hayasaka, Y. Liu, H. Liu, O. N. Oliveira, Jr. and L. Lin, Mikrochim. Acta, 2018, 185, 213 CrossRef PubMed.
- Y. Li, M. Jiao, H. Zhao and M. Yang, Sens. Actuators, B, 2018, 264, 285–295 CrossRef CAS.
- J. Cai, C. Zhang, A. Khan, C. Liang and W.-D. Li, RSC Adv., 2018, 8, 5312–5320 RSC.
- H. J. Park, W.-J. Kim, H.-K. Lee, D.-S. Lee, J.-H. Shin, Y. Jun and Y. J. Yun, Sens. Actuators, B, 2018, 257, 846–852 CrossRef CAS.
- H. T. Hien, H. T. Giang, N. V. Hieu, T. Trung and C. V. Tuan, Sens. Actuators, B, 2017, 249, 348–356 CrossRef CAS.
- V. L. Patil, S. A. Vanalakar, P. S. Patil and J. H. Kim, Sens. Actuators, B, 2017, 239, 1185–1193 CrossRef CAS.
- M. Jiao, N. V. Chien, N. V. Duy, N. D. Hoa, N. V. Hieu, K. Hjort and H. Nguyen, Mater. Lett., 2016, 169, 231–235 CrossRef CAS.
- D. N. Oosthuizen, D. E. Motaung and H. C. Swart, Sens. Actuators, B, 2018, 266, 761–772 CrossRef CAS.
- X. Liu, M. Hu, Y. Wang, J. Liu and Y. Qin, J. Alloys Compd., 2016, 685, 364–369 CrossRef CAS.
- A. Umar, J.-H. Lee, R. Kumar, O. Al-Dossary, A. A. Ibrahim and S. Baskoutas, Mater. Des., 2016, 105, 16–24 CrossRef CAS.
- O. Lupan, V. Postica, V. Cretu, N. Wolff, V. Duppel, L. Kienle and R. Adelung, Phys. Status Solidi RRL, 2016, 10, 260–266 CrossRef CAS.
- S. Xu, H. Zhao, Y. Xu, R. Xu and Y. Lei, ACS Appl. Mater. Interfaces, 2018, 10, 13895–13902 CrossRef CAS PubMed.
- I. Cho, K. Kang, D. Yang, J. Yun and I. Park, ACS Appl. Mater. Interfaces, 2017, 9, 27111–27119 CrossRef CAS PubMed.
- Y. Zhao, W. Zhang, B. Yang, J. Liu, X. Chen, X. Wang and C. Yang, Nanotechnology, 2017, 28, 452002 CrossRef PubMed.
- X. Tong, W. Shen, X. Chen and J.-P. Corriou, Ceram. Int., 2017, 43, 14200–14209 CrossRef CAS.
- W. Guo, Q. Feng, Y. Tao, L. Zheng, Z. Han and J. Ma, Mater. Res. Bull., 2016, 73, 302–307 CrossRef CAS.
- Z. Li, Y. Huang, S. Zhang, W. Chen, Z. Kuang, D. Ao, W. Liu and Y. Fu, J. Hazard. Mater., 2015, 300, 167–174 CrossRef CAS PubMed.
- Z. Li, Z. Lin, N. Wang, Y. Huang, J. Wang, W. Liu, Y. Fu and Z. Wang, Mater. Des., 2016, 110, 532–539 CrossRef CAS.
- D. Han, L. Zhai, F. Gu and Z. Wang, Sens. Actuators, B, 2018, 262, 655–663 CrossRef CAS.
- J. Hu, Y. Sun, Y. Xue, M. Zhang, P. Li, K. Lian, S. Zhuiykov, W. Zhang and Y. Chen, Sens. Actuators, B, 2018, 257, 124–135 CrossRef CAS.
- S. C. Zhang, Y. W. Huang, Z. Kuang, S. Y. Wang, W. L. Song, D. Y. Ao, W. Liu and Z. J. Li, Nanosci. Nanotechnol. Lett., 2015, 7, 455–461 CrossRef.
- Z. Li, S. Yan, Z. Wu, H. Li, J. Wang, W. Shen, Z. Wang and Y. Fu, Int. J. Hydrogen Energy, 2018, 43, 22746–22755 CrossRef CAS.
- T. Zhou, T. Zhang, J. Deng, R. Zhang, Z. Lou and L. Wang, Sens. Actuators, B, 2017, 242, 369–377 CrossRef CAS.
- S. F. Shen, M. L. Xu, D. B. Lin and H. B. Pan, Appl. Surf. Sci., 2017, 396, 327–332 CrossRef CAS.
- Z. Zhang, L. Zhu, Z. Wen and Z. Ye, Sens. Actuators, B, 2017, 238, 1052–1059 CrossRef CAS.
- S. Poongodi, P. S. Kumar, D. Mangalaraj, N. Ponpandian, P. Meena, Y. Masuda and C. Lee, J. Alloys Compd., 2017, 719, 71–81 CrossRef CAS.
- H. Kim, Y. Pak, Y. Jeong, W. Kim, J. Kim and G. Y. Jung, Sens. Actuators, B, 2018, 262, 460–468 CrossRef CAS.
- R. Sankar Ganesh, M. Navaneethan, V. L. Patil, S. Ponnusamy, C. Muthamizhchelvan, S. Kawasaki, P. S. Patil and Y. Hayakawa, Sens. Actuators, B, 2018, 255, 672–683 CrossRef CAS.
- X. Hu, Z. Zhu, C. Chen, T. Wen, X. Zhao and L. Xie, Sens. Actuators, B, 2017, 253, 809–817 CrossRef CAS.
- L. Xiao, S. Xu, G. Yu and S. Liu, Sens. Actuators, B, 2018, 255, 2002–2010 CrossRef CAS.
- V. S. Bhati, S. Ranwa, S. Rajamani, K. Kumari, R. Raliya, P. Biswas and M. Kumar, ACS Appl. Mater. Interfaces, 2018, 10, 11116–11124 CrossRef CAS PubMed.
- V. S. Bhati, S. Ranwa, M. Fanetti, M. Valant and M. Kumar, Sens. Actuators, B, 2018, 255, 588–597 CrossRef CAS.
- V. V. Ganbavle, S. I. Inamdar, G. L. Agawane, J. H. Kim and K. Y. Rajpure, Chem. Eng. J., 2016, 286, 36–47 CrossRef CAS.
- X. Kou, N. Xie, F. Chen, T. Wang, L. Guo, C. Wang, Q. Wang, J. Ma, Y. Sun, H. Zhang and G. Lu, Sens. Actuators, B, 2018, 256, 861–869 CrossRef CAS.
- Q. Zhou, W. Chen, L. Xu, R. Kumar, Y. Gui, Z. Zhao, C. Tang and S. Zhu, Ceram. Int., 2018, 44, 4392–4399 CrossRef CAS.
- C. Zhao, H. Gong, W. Lan, R. Ramachandran, H. Xu, S. Liu and F. Wang, Sens. Actuators, B, 2018, 258, 492–500 CrossRef CAS.
- H. W. Kim, H. G. Na, Y. J. Kwon, S. Y. Kang, M. S. Choi, J. H. Bang, P. Wu and S. S. Kim, ACS Appl. Mater. Interfaces, 2017, 9, 31667–31682 CrossRef CAS PubMed.
- P. Tyagi, A. Sharma, M. Tomar and V. Gupta, Sens. Actuators, B, 2017, 248, 980–986 CrossRef CAS.
- B. Zhang, M. Cheng, G. Liu, Y. Gao, L. Zhao, S. Li, Y. Wang, F. Liu, X. Liang, T. Zhang and G. Lu, Sens. Actuators, B, 2018, 263, 387–399 CrossRef CAS.
- S. Park, S. Kim, H. Kheel, S. K. Hyun, C. Jin and C. Lee, Mater. Res. Bull., 2016, 82, 130–135 CrossRef CAS.
- D. Li, L. Qin, P. Zhao, Y. Zhang, D. Liu, F. Liu, B. Kang, Y. Wang, H. Song, T. Zhang and G. Lu, Sens. Actuators, B, 2018, 254, 834–841 CrossRef CAS.
- H. Gao, L. Zhao, L. Wang, P. Sun, H. Lu, F. Liu, X. Chuai and G. Lu, Sens. Actuators, B, 2018, 255, 3505–3515 CrossRef CAS.
- I. Eisele, T. Doll and M. Burgmair, Sens. Actuators, B, 2001, 78, 19–25 CrossRef CAS.
- S. Stegmeier, M. Fleischer, A. Tawil, P. Hauptmann, K. Egly and K. Rose, Sens. Actuators, B, 2011, 154, 270–276 CrossRef CAS.
- A. I. Ayesh, J. Nanomater., 2016, 2016, 1–17 CrossRef.
- Z. S. Hosseini, A. I. Zad and A. Mortezaali, Sens. Actuators, B, 2015, 207, 865–871 CrossRef CAS.
- T. Sin Tee, T. Chun Hui, C. Wu Yi, Y. Chi Chin, A. A. Umar, G. Riski Titian, L. Hock Beng, L. Kok Sing, M. Yahaya and M. M. Salleh, Sens. Actuators, B, 2016, 227, 304–312 CrossRef.
- A. Azam, S. S. Habib, N. A. Salah and F. Ahmed, Int. J. Nanomed., 2013, 8, 3875–3881 CrossRef PubMed.
- H. Wang, Q. Sun, Y. Yao, Y. Li, J. Wang and L. Chen, Ceram. Int., 2016, 42, 8565–8571 CrossRef CAS.
- W. Li, J. Liang, J. Liu, L. Zhou, R. Yang and M. Hu, Mater. Lett., 2016, 173, 199–202 CrossRef CAS.
- Y. Wei, C. Chen, G. Yuan and S. Gao, J. Alloys Compd., 2016, 681, 43–49 CrossRef CAS.
- Y. Li, Q. Zhang, X. Li, H. Bai, W. Li, T. Zeng and G. Xi, RSC Adv., 2016, 6, 95747–95752 RSC.
- S. Mohamed Sali, S. Joy, N. Meenakshisundaram, R. K. Karn, C. Gopalakrishnan, P. Karthick, K. Jeyadheepan and K. Sankaranarayanan, RSC Adv., 2017, 7, 37720–37728 RSC.
- Z. P. Tshabalala, D. E. Motaung, G. H. Mhlongo and O. M. Ntwaeaborwa, Sens. Actuators, B, 2016, 224, 841–856 CrossRef CAS.
- Y. Huang, W. Chen, S. Zhang, Z. Kuang, D. Ao, N. R. Alkurd, W. Zhou, W. Liu, W. Shen and Z. Li, Appl. Surf. Sci., 2015, 351, 1025–1033 CrossRef CAS.
- R. K. Bedi and I. Singh, ACS Appl. Mater. Interfaces, 2010, 2, 1361–1368 CrossRef CAS.
- P. Shankar and J. B. B. Rayappan, ACS Appl. Mater. Interfaces, 2017, 9, 38135–38145 CrossRef CAS PubMed.
- N. Kumar, A. K. Srivastava, R. Nath, B. K. Gupta and G. D. Varma, Dalton Trans., 2014, 43, 5713–5720 RSC.
- Z. Zeng, K. Wang, Z. Zhang, J. Chen and W. Zhou, Nanotechnology, 2009, 20, 045503 CrossRef PubMed.
- Y. Shen, S. Zhao, J. Ma, X. Chen, W. Wang, D. Wei, S. Gao, W. Liu, C. Han and B. Cui, J. Alloys Compd., 2016, 664, 229–234 CrossRef CAS.
- Z. Li, X. Niu, Z. Lin, N. Wang, H. Shen, W. Liu, K. Sun, Y. Q. Fu and Z. Wang, J. Alloys Compd., 2016, 682, 647–653 CrossRef CAS.
- O. Lupan, V. Postica, R. Adelung, F. Labat, I. Ciofini, U. Schürmann, L. Kienle, L. Chow, B. Viana and T. Pauporté, Phys. Status Solidi RRL, 2018, 12, 1700321 CrossRef.
- Y. L. Wang, X. C. Jiang and Y. N. Xia, J. Am. Chem. Soc., 2003, 125, 16176–16177 CrossRef CAS PubMed.
- O. Lupan, L. Chow, T. Pauporté, L. K. Ono, B. Roldan Cuenya and G. Chai, Sens. Actuators, B, 2012, 173, 772–780 CrossRef CAS.
- W. Song, H. Wu, J. Wang, Y. Lin, J. Song, Y. Xie, L. Li and K. Shi, Aust. J. Chem., 2015, 68, 1569 CrossRef CAS.
- L. Yu, F. Guo, S. Liu, B. Yang, Y. Jiang, L. Qi and X. Fan, J. Alloys Compd., 2016, 682, 352–356 CrossRef CAS.
- Z. Li, Z. Lin, N. Wang, J. Wang, W. Liu, K. Sun, Y. Q. Fu and Z. Wang, Sens. Actuators, B, 2016, 235, 222–231 CrossRef CAS.
- Z. Li, N. Wang, Z. Lin, J. Wang, W. Liu, K. Sun, Y. Q. Fu and Z. Wang, ACS Appl. Mater. Interfaces, 2016, 8, 20962–20968 CrossRef CAS PubMed.
- J. Zhang, D. Zeng, Q. Zhu, J. Wu, Q. Huang and C. Xie, J. Phys. Chem. C, 2016, 120, 3936–3945 CrossRef CAS.
- C. Jiang, G. Zhang, Y. Wu, L. Li and K. Shi, CrystEngComm, 2012, 14, 2739 RSC.
- A. Hazra, K. Dutta, B. Bhowmik, P. P. Chattopadhyay and P. Bhattacharyya, Appl. Phys. Lett., 2014, 105, 081604 CrossRef.
- B. Bhowmik, A. Hazra, K. Dutta and P. Bhattacharyya, IEEE Trans. Device Mater. Reliab., 2014, 14, 961–967 CAS.
- J. Z. Zhang and Y. Yan, J. Mater. Sci., 2017, 52, 13711–13718 CrossRef CAS.
- S. Shao, H. Wu, S. Wang, Q. Hong, R. Koehn, T. Wu and W.-F. Rao, J. Mater. Chem. C, 2015, 3, 10819–10829 RSC.
- H. Duan, L. Yan, Y. He, H. Li, L. Liu, Y. Cheng and L. Du, Mater. Res. Express, 2017, 4, 095022 CrossRef.
- Y. Wang, G. Duan, Y. Zhu, H. Zhang, Z. Xu, Z. Dai and W. Cai, Sens. Actuators, B, 2016, 228, 74–84 CrossRef CAS.
- J. Gao, H. Wu, J. Zhou, L. Yao, G. Zhang, S. Xu, Y. Xie, L. Li and K. Shi, New J. Chem., 2016, 40, 1306–1311 RSC.
- B. Wu, L. Wang, H. Wu, K. Kan, G. Zhang, Y. Xie, Y. Tian, L. Li and K. Shi, Microporous Mesoporous Mater., 2016, 225, 154–163 CrossRef CAS.
- M. Kaur, N. Jain, K. Sharma, S. Bhattacharya, M. Roy, A. K. Tyagi, S. K. Gupta and J. V. Yakhmi, Sens. Actuators, B, 2008, 133, 456–461 CrossRef CAS.
- M. Seetha, P. Meena, D. Mangalaraj, Y. Masuda and K. Senthil, Mater. Chem. Phys., 2012, 133, 47–54 CrossRef CAS.
- R. Senthilkumar, G. Ravi, C. Sanjeeviraja, M. Arivanandhan and Y. Hayakawa, Solid State Phys., 2013, 1512, 648–649 CAS.
- D. F. Rodriguez, P. M. Perillo, C. A. Rinaldi, A. Lamagna and P. Gouma, AIP Conf. Proc., 2011, 1362, 199–200 CrossRef CAS.
- M. N. Cardoza-Contreras, J. M. Romo-Herrera, L. A. Rios, R. Garcia-Gutierrez, T. A. Zepeda and O. E. Contreras, Sensors, 2015, 15, 30539–30544 CrossRef CAS PubMed.
- C. Wang, X. Chu and M. Wu, Sens. Actuators, B, 2006, 113, 320–323 CrossRef CAS.
- Y. Xia, J. Wang, X. Li, X. Dan, D. Zhou, L. Xiang and S. Komarneni, Ceram. Int., 2016, 42, 15876–15880 CrossRef CAS.
- N. Du, H. Zhang, B. D. Chen, X. Y. Ma, Z. H. Liu, J. B. Wu and D. R. Yang, Adv. Mater., 2007, 19, 1641–1645 CrossRef CAS.
- P. Dhivya and M. Sridharan, J. Electron. Mater., 2014, 43, 3211–3216 CrossRef.
- S. Arunkumar, T. Hou, Y.-B. Kim, B. Choi, S. H. Park, S. Jung and D.-W. Lee, Sens. Actuators, B, 2017, 243, 990–1001 CrossRef CAS.
- S.-W. Choi and S. S. Kim, Sens. Actuators, B, 2012, 168, 8–13 CrossRef CAS.
- K. Wang, T. Zhao, G. Lian, Q. Yu, C. Luan, Q. Wang and D. Cui, Sens. Actuators, B, 2013, 184, 33–39 CrossRef CAS.
- P. P. Subha, K. Hasna and M. K. Jayaraj, Mater. Res. Express, 2017, 4, 105037 CrossRef.
- S. Wang, D. Huang, S. Xu, W. Jiang, T. Wang, J. Hu, N. Hu, Y. Su, Y. Zhang and Z. Yang, Phys. Chem. Chem. Phys., 2017, 19, 19043–19049 RSC.
- G. H. Mhlongo, K. Shingange, Z. P. Tshabalala, B. P. Dhonge, F. A. Mahmoud, B. W. Mwakikunga and D. E. Motaung, Appl. Surf. Sci., 2016, 390, 804–815 CrossRef CAS.
- J. Wang, L. Wei, L. Zhang, J. Zhang, H. Wei, C. Jiang and Y. Zhang, J. Mater. Chem., 2012, 22, 20038 RSC.
- J. Wang, P. Yang and X. Wei, ACS Appl. Mater. Interfaces, 2015, 7, 3816–3824 CrossRef CAS PubMed.
- P. Chaudhari and S. Mishra, Measurement, 2016, 90, 468–474 CrossRef.
- J. Zhou, M. Ikram, A. U. Rehman, J. Wang, Y. Zhao, K. Kan, W. Zhang, F. Raziq, L. Li and K. Shi, Sens. Actuators, B, 2018, 255, 1819–1830 CrossRef CAS.
- M. Kaur, B. K. Dadhich, R. Singh, K. Ganapathi, T. Bagwaiya, S. Bhattacharya, A. K. Debnath, K. P. Muthe and S. C. Gadkari, Sens. Actuators, B, 2017, 242, 389–403 CrossRef CAS.
- V. Srivastava and K. Jain, Mater. Lett., 2016, 169, 28–32 CrossRef CAS.
- P.-G. Su and T.-T. Pan, Mater. Chem. Phys., 2011, 125, 351–357 CrossRef CAS.
- H. Zhang, L. Yu, Q. Li, Y. Du and S. Ruan, Sens. Actuators, B, 2017, 241, 109–115 CrossRef CAS.
- Z. Li, J. Wang, S. Zhang, S. Yan, B. Cao, W. Shen, Z. Wang and Y. Q. Fu, J. Alloys Compd., 2018, 742, 712–720 CrossRef CAS.
- V. Inderan, M. M. Arafat, S. Kumar, A. Haseeb, Z. T. Jiang, M. Altarawneh and H. L. Lee, Nanotechnology, 2017, 28, 265702 CrossRef PubMed.
- A. U. Rehman, J. Zhang, J. Zhou, K. Kan, L. Li and K. Shi, Microporous Mesoporous Mater., 2017, 240, 50–56 CrossRef CAS.
- J. Liang, K. Zhu, R. Yang and M. Hu, Ceram. Int., 2018, 44, 2261–2268 CrossRef CAS.
- H. Xu, J. Zhang, A. U. Rehman, L. Gong, K. Kan, L. Li and K. Shi, Appl. Surf. Sci., 2017, 412, 230–237 CrossRef CAS.
- D. Liu, L. Lin, Q. Chen, H. Zhou and J. Wu, ACS Sens., 2017, 2, 1491–1497 CrossRef CAS PubMed.
- Y. Wang, Y. Zhou, C. Meng, Z. Gao, X. Cao, X. Li, L. Xu, W. Zhu, X. Peng, B. Zhang, Y. Lin and L. Liu, Nanotechnology, 2016, 27, 425503 CrossRef PubMed.
- S. Xu, J. Gao, L. Wang, K. Kan, Y. Xie, P. Shen, L. Li and K. Shi, Nanoscale, 2015, 7, 14643–14651 RSC.
- Z. Liu, L. Yu, F. Guo, S. Liu, L. Qi, M. Shan and X. Fan, Appl. Surf. Sci., 2017, 423, 721–727 CrossRef CAS.
- N. Van Hieu, L. T. B. Thuy and N. D. Chien, Sens. Actuators, B, 2008, 129, 888–895 CrossRef CAS.
- N. Tiwale, Mater. Sci. Technol., 2015, 31, 1681–1697 CrossRef CAS.
- A. Mirzaei, B. Hashemi and K. Janghorban, J. Mater. Sci.: Mater. Electron., 2015, 27, 3109–3144 CrossRef.
- G. Korotcenkov and B. K. Cho, Sens. Actuators, B, 2014, 196, 80–98 CrossRef CAS.
- S. Das and V. Jayaraman, Prog. Mater. Sci., 2014, 66, 112–255 CrossRef CAS.
- H.-J. Kim and J.-H. Lee, Sens. Actuators, B, 2014, 192, 607–627 CrossRef CAS.
- D. R. Miller, S. A. Akbar and P. A. Morris, Sens. Actuators, B, 2014, 204, 250–272 CrossRef CAS.
- G. Korotcenkov, V. Brinzari and B. K. Cho, Microchim. Acta, 2016, 183, 1033–1054 CrossRef CAS.
- P. Rai, S. M. Majhi, Y.-T. Yu and J.-H. Lee, RSC Adv., 2015, 5, 76229–76248 RSC.
- S. Gupta Chatterjee, S. Chatterjee, A. K. Ray and A. K. Chakraborty, Sens. Actuators, B, 2015, 221, 1170–1181 CrossRef CAS.
- M. Gardon and J. M. Guilemany, J. Mater. Sci.: Mater. Electron., 2012, 24, 1410–1421 CrossRef.
- P. T. Moseley, Meas. Sci. Technol., 2017, 28, 082001 CrossRef.
- Y. F. Sun, S. B. Liu, F. L. Meng, J. Y. Liu, Z. Jin, L. T. Kong and J. H. Liu, Sensors, 2012, 12, 2610–2631 CrossRef CAS PubMed.
- H. Gu, Z. Wang and Y. Hu, Sensors, 2012, 12, 5517–5550 CrossRef CAS PubMed.
- A. Mirzaei, S. G. Leonardi and G. Neri, Ceram. Int., 2016, 42, 15119–15141 CrossRef CAS.
- L. Zhu and W. Zeng, Sens. Actuators, A, 2017, 267, 242–261 CrossRef CAS.
- A. D. Faisal, Bull. Mater. Sci., 2017, 40, 1061–1068 CrossRef CAS.
- N. Zhang, K. Yu, Q. Li, Z. Q. Zhu and Q. Wan, J. Appl. Phys., 2008, 103, 104305 CrossRef.
- T. Kondo, Y. Sato, M. Kinoshita, P. Shankar, N. N. Mintcheva, M. Honda, S. Iwamori and S. A. Kulinich, Jpn. J. Appl. Phys., 2017, 56, 080304 CrossRef.
- Y. Li, S. Wang, P. Hao, J. Tian, H. Cui and X. Wang, Sens. Actuators, B, 2018, 273, 751–759 CrossRef CAS.
- A. Beniwal, P. K. Sahu and S. Sharma, J. Sol–Gel Sci. Technol., 2018, 88, 322–333 CrossRef CAS.
- M. Kodu, T. Avarmaa, A. Floren and R. Jaaniso, J. Eur. Ceram. Soc., 2013, 33, 2335–2340 CrossRef CAS.
- K. Khun Khun, A. Mahajan and R. K. Bedi, J. Appl. Phys., 2009, 106, 124509 CrossRef.
- T. Yang, M. Zhu, K. Gu, C. Zhai, Q. Zhao, X. Yang and M. Zhang, New J. Chem., 2018, 42, 13612–13618 RSC.
- D. Hanft, M. Bektas and R. Moos, Materials, 2018, 11, 1342 CrossRef PubMed.
- L. Xu, B. Dong, Y. Wang, X. Bai, Q. Liu and H. Song, Sens. Actuators, B, 2010, 147, 531–538 CrossRef CAS.
- T. M. Perfecto, C. A. Zito and D. P. Volanti, CrystEngComm, 2017, 19, 2733–2738 RSC.
- X. W. Huang, X. B. Zou, J. Y. Shi, J. W. Zhao, Y. Li, L. Hao and J. Zhang, Anal. Chim. Acta, 2013, 787, 233–238 CrossRef CAS PubMed.
- H. Liu, W. Shen, X. Chen and J.-P. Corriou, J. Mater. Sci.: Mater. Electron., 2018, 29, 18380–18387 CrossRef CAS.
- L. Y. Hong and H. N. Lin, Beilstein J. Nanotechnol., 2016, 7, 1044–1051 CrossRef CAS PubMed.
- Z. P. Tshabalala, K. Shingange, B. P. Dhonge, O. M. Ntwaeaborwa, G. H. Mhlongo and D. E. Motaung, Sens. Actuators, B, 2017, 238, 402–419 CrossRef CAS.
- P. M. Perillo and D. F. Rodríguez, Sens. Actuators, B, 2014, 193, 263–266 CrossRef CAS.
- B. C. Yadav, S. Singh and A. Yadav, Appl. Surf. Sci., 2011, 257, 1960–1966 CrossRef CAS.
- X. Song, Q. Xu, T. Zhang, B. Song, C. Li and B. Cao, Sens. Actuators, B, 2018, 268, 170–181 CrossRef CAS.
- Y. X. Li, Z. X. Song, F. Jiang, Q. Sun, F. Ma, H. R. Wang and K. Chen, Ceram. Int., 2016, 42, 18318–18323 CrossRef CAS.
- J. Liang, W. Li, J. Liu and M. Hu, J. Alloys Compd., 2016, 687, 845–854 CrossRef CAS.
- C. A. Zito, T. M. Perfecto and D. P. Volanti, New J. Chem., 2018, 42, 15954–15961 RSC.
- T.-R. Rashid, D.-T. Phan and G.-S. Chung, Sens. Actuators, B, 2013, 185, 777–784 CrossRef CAS.
- P. Dhivya, A. K. Prasad and M. Sridharan, Ceram. Int., 2014, 40, 409–415 CrossRef CAS.
- S. A. Hakim, Y. Liu, G. S. Zakharova and W. Chen, RSC Adv., 2015, 5, 23489–23497 RSC.
- S. Lin, D. Li, J. Wu, X. Li and S. A. Akbar, Sens. Actuators, B, 2011, 156, 505–509 CrossRef CAS.
- B. Zhang, M. Li, Z. Song, H. Kan, H. Yu, Q. Liu, G. Zhang and H. Liu, Sens. Actuators, B, 2017, 249, 558–563 CrossRef CAS.
- W. Ponhan, S. Phadungdhitidhada and S. Choopun, Mater. Today, 2017, 4, 6342–6348 CrossRef.
- M. Thepnurat, T. Chairuangsri, N. Hongsith, P. Ruankham and S. Choopun, ACS Appl. Mater. Interfaces, 2015, 7, 24177–24184 CrossRef CAS PubMed.
- P. Shankar and J. B. B. Rayappan, J. Mater. Chem. C, 2017, 5, 10869–10880 RSC.
- N. Van Quy, V. A. Minh, N. Van Luan, V. N. Hung and N. Van Hieu, Sens. Actuators, B, 2011, 153, 188–193 CrossRef CAS.
- G. K. Mani and J. B. B. Rayappan, Sens. Actuators, B, 2013, 183, 459–466 CrossRef CAS.
- X. Pan, X. Zhao, J. Chen, A. Bermak and Z. Fan, Sens. Actuators, B, 2015, 206, 764–771 CrossRef CAS.
- V. P. Verma, S. Das, S. Hwang, H. Choi, M. Jeon and W. Choi, Mater. Sci. Eng., B, 2010, 171, 45–49 CrossRef CAS.
- X. Pan and X. Zhao, Sensors, 2015, 15, 8919–8930 CrossRef CAS PubMed.
- O. Lupan, G. Chai and L. Chow, Microelectron. J., 2007, 38, 1211–1216 CrossRef CAS.
- O. Lupan, G. Chai and L. Chow, Microelectron. Eng., 2008, 85, 2220–2225 CrossRef CAS.
- B.-R. Huang and J.-C. Lin, Appl. Surf. Sci., 2013, 280, 945–949 CrossRef CAS.
- K. Vijayalakshmi and D. Gopalakrishna, J. Mater. Sci.: Mater. Electron., 2014, 25, 2253–2260 CrossRef CAS.
- Y. T. Lim, J. Y. Son and J. S. Rhee, Ceram. Int., 2013, 39, 887–890 CrossRef CAS.
- J. J. Hassan, M. A. Mahdi, C. W. Chin, H. Abu-Hassan and Z. Hassan, Sens. Actuators, B, 2013, 176, 360–367 CrossRef CAS.
- S. Yang, Z. Wang, Y. Hu, X. Luo, J. Lei, D. Zhou, L. Fei, Y. Wang and H. Gu, ACS Appl. Mater. Interfaces, 2015, 7, 9247–9253 CrossRef CAS PubMed.
- I. H. Kadhim and H. Abu Hassan, J. Electron. Mater., 2016, 46, 1419–1426 CrossRef.
- M. Belaqziz, M. b. Amjoud, A. Gaddari, B. Rhouta and D. Mezzane, Superlattice Microstruct., 2014, 71, 185–189 CrossRef CAS.
- A. Kaur Bal, A. Singh and R. K. Bedi, Phys. B, 2010, 405, 3124–3128 CrossRef CAS.
- X. Mu, C. Chen, L. Han, B. Shao, Y. Wei, Q. Liu and P. Zhu, J. Alloys Compd., 2015, 637, 55–61 CrossRef CAS.
- L. Yanxiao, Z. Xiao-bo, H. Xiao-wei, S. Ji-yong, Z. Jie-wen, M. Holmes and L. Hao, Biosens. Bioelectron., 2015, 67, 35–41 CrossRef PubMed.
- J. Wang, Z. Li, S. Zhang, S. Yan, B. Cao, Z. Wang and Y. Fu, Sens. Actuators, B, 2018, 255, 862–870 CrossRef CAS.
- Z. Li, S. Yan, S. Zhang, J. Wang, W. Shen, Z. Wang and Y. Q. Fu, J. Alloys Compd., 2019, 770, 721–731 CrossRef CAS.
- C. Zhang, X. Geng, H. Liao, C.-J. Li and M. Debliquy, Sens. Actuators, B, 2017, 242, 102–111 CrossRef CAS.
- R. Chen, J. Wang and L. Xiang, Sens. Actuators, B, 2018, 270, 207–215 CrossRef CAS.
- Y. Wu, M. Hu and Y. Tian, Chin. Phys. B, 2017, 26, 020701 CrossRef.
- V. Annapureddy, Y. Kim, G.-T. Hwang, H. W. Jang, S.-D. Kim, J.-J. Choi, B. Cho and J. Ryu, Adv. Mater. Interfaces, 2018, 5, 1700811 CrossRef.
- L. Han, C. Chen, Y. Wei, B. Shao, X. Mu, Q. Liu and P. Zhu, J. Alloys Compd., 2016, 656, 326–331 CrossRef CAS.
- M. Hu, D.-L. Jia, Q.-L. Liu, M.-D. Li and P. Sun, Chin. Phys. B, 2013, 22, 068204 CrossRef.
- W. Liu, L. Xu, K. Sheng, C. Chen, X. Zhou, B. Dong, X. Bai, S. Zhang, G. Lu and H. Song, J. Mater. Chem. A, 2018, 6, 10976–10989 RSC.
- S. S. Kim, H. G. Na, Y. J. Kwon, H. Y. Cho and H. W. Kim, Met. Mater. Int., 2015, 21, 415–421 CrossRef CAS.
- X. Gou, R. Li, G. Wang, Z. Chen and D. Wexler, Nanotechnology, 2009, 20, 495501 CrossRef PubMed.
- S. Bai, Y. Ma, X. Shu, J. Sun, Y. Feng, R. Luo, D. Li and A. Chen, Ind. Eng. Chem. Res., 2017, 56, 2616–2623 CrossRef CAS.
- A. Wei, Z. Wang, L.-H. Pan, W.-W. Li, L. Xiong, X.-C. Dong and W. Huang, Chin. Phys. Lett., 2011, 28, 080702 CrossRef.
- H. Abdollahi, M. Samkan and M. M. Hashemi, Microsyst. Technol., 2018, 24, 3741–3749 CrossRef CAS.
- R. S. Ganesh, G. K. Mani, R. Elayaraja, E. Durgadevi, M. Navaneethan, S. Ponnusamy, K. Tsuchiya, C. Muthamizhchelvan and Y. Hayakawa, Appl. Surf. Sci., 2018, 449, 314–321 CrossRef CAS.
- A. El Bouari, A. Gaddari, M. Amjoud, F. Berger, J. B. Sanchez, M. Lahcini, B. Rhouta, D. Mezzane, C. Mavon, R. El Ouatib, H. Hannache, S. Krimi, M. Lamire, I. Mansouri, R. Moussa and A. Aboulayt, MATEC Web of Conferences, 2013, 5, 04010 CrossRef.
- Y. Xiong, W. Xu, D. Ding, W. Lu, L. Zhu, Z. Zhu, Y. Wang and Q. Xue, J. Hazard. Mater., 2018, 341, 159–167 CrossRef PubMed.
- S. Yang, Y. Liu, W. Jin, Y. Qi, G. S. Zakharova and W. Chen, Ferroelectrics, 2015, 477, 112–120 CrossRef CAS.
- Y. Xiong, Z. Zhu, T. Guo, H. Li and Q. Xue, J. Hazard. Mater., 2018, 353, 290–299 CrossRef CAS PubMed.
- E. Zampetti, A. Macagnano and A. Bearzotti, J. Nanopart. Res., 2013, 15, 1566 CrossRef.
- C. Shao, Y. Chang and Y. Long, Sens. Actuators, B, 2014, 204, 666–672 CrossRef CAS.
- M. Chitra, K. Uthayarani, N. Rajasekaran, N. Neelakandeswari, E. K. Girija and D. P. Padiyan, Chin. Phys. Lett., 2015, 32, 078101 CrossRef.
- E. Wongrat, W. Ponhan and S. Choopun, Ceram. Int., 2017, 43, S520–S524 CrossRef CAS.
- L. Hou, C.-M. Zhang, P. Ma, L. Li, K.-K. Zhu, X.-F. Kang and W. Chen, Chin. J. Anal. Chem., 2018, 46, E1854–E1862 Search PubMed.
- A. P. Sharma, P. Dhakal, D. K. Pradhan, M. K. Behera, B. Xiao and M. Bahoura, AIP Adv., 2018, 8, 095219 CrossRef.
- B. Sakthivel, L. Manjakkal and G. Nammalvar, IEEE Sens. J., 2017, 17, 6529–6536 CAS.
- N. S. Ramgir, S. K. Ganapathi, M. Kaur, N. Datta, K. P. Muthe, D. K. Aswal, S. K. Gupta and J. V. Yakhmi, Sens. Actuators, B, 2010, 151, 90–96 CrossRef CAS.
- Z. Li, J. Wang, N. Wang, S. Yan, W. Liu, Y. Q. Fu and Z. Wang, J. Alloys Compd., 2017, 725, 1136–1143 CrossRef CAS.
- J. Zhang, D. Zeng, Q. Zhu, J. Wu, K. Xu, T. Liao, G. Zhang and C. Xie, J. Phys. Chem. C, 2015, 119, 17930–17939 CrossRef CAS.
- J. Zhou, M. Ikram, A. U. Rehman, J. Wang, Y. Zhao, K. Kan, W. Zhang, F. Raziq, L. Li and K. Shi, Sens. Actuators, B, 2018, 255, 1819–1830 CrossRef CAS.
- I. Singh and R. K. Bedi, Solid State Sci., 2011, 13, 2011–2018 CrossRef CAS.
- S. Li, M. Wang, C. Li, J. Liu, M. Xu, J. Liu and J. Zhang, Sci. China Mater., 2018, 61, 1085–1094 CrossRef.
- D. N. Oosthuizen, D. E. Motaung and H. C. Swart, Sens. Actuators, B, 2018, 266, 761–772 CrossRef CAS.
- Z. Wang, F. Li, H. Wang, A. Wang and S. Wu, J. Mater. Sci.: Mater. Electron., 2018, 29, 16654–16659 CrossRef CAS.
- S. Wang, D. Huang, S. Xu, W. Jiang, T. Wang, J. Hu, N. Hu, Y. Su, Y. Zhang and Z. Yang, Phys. Chem. Chem. Phys., 2017, 19, 19043–19049 RSC.
- J. Wang, L. Wei, L. Zhang, J. Zhang, H. Wei, C. Jiang and Y. Zhang, J. Mater. Chem., 2012, 22, 20038–20047 RSC.
- B. Geng, F. Zhan, C. Fang and N. Yu, J. Mater. Chem., 2008, 18, 4977–4984 RSC.
- X. Zhang, J. Wang, L. Xuan, Z. Zhu, Q. Pan, K. Shi and G. Zhang, J. Alloys Compd., 2018, 768, 190–197 CrossRef CAS.
- S. Li, F.-L. Li, S.-M. Zhou, P. Wang, K. Cheng and Z.-L. Du, Chin. Phys. B, 2009, 18, 3985–3989 CrossRef CAS.
- H. Liu, X. Du, X. Xing, G. Wang and S. Z. Qiao, Chem. Commun., 2012, 48, 865–867 RSC.
- W. Zhang, C. Zeng, M. Kong, Y. Pan and Z. Yang, Sens. Actuators, B, 2012, 162, 292–299 CrossRef CAS.
- R. Kumar, R. Kumar, N. Kushwaha and J. Mittal, IEEE Sens. J., 2016, 16, 4691–4695 CAS.
- S. Balamurugan, A. Rajalakshmi and D. Balamurugan, J. Alloys Compd., 2015, 650, 863–870 CrossRef CAS.
- Y. Wang, B. Liu, D. Cai, H. Li, Y. Liu, D. Wang, L. Wang, Q. Li and T. Wang, Sens. Actuators, B, 2014, 201, 351–359 CrossRef CAS.
- N. S. Ramgir, P. K. Sharma, N. Datta, M. Kaur, A. K. Debnath, D. K. Aswal and S. K. Gupta, Sens. Actuators, B, 2013, 186, 718–726 CrossRef CAS.
- Q. A. Drmosh, Z. H. Yamani, A. K. Mohamedkhair, A. H. Y. Hendi, M. K. Hossain and A. Ibrahim, Mater. Lett., 2018, 214, 283–286 CrossRef CAS.
- H. Fu, C. Hou, F. Gu, D. Han and Z. Wang, Sens. Actuators, B, 2017, 243, 516–524 CrossRef CAS.
- D. Naberezhnyi, M. Rumyantseva, D. Filatova, M. Batuk, J. Hadermann, A. Baranchikov, N. Khmelevsky, A. Aksenenko, E. Konstantinova and A. Gaskov, Nanomaterials, 2018, 8, 801 CrossRef PubMed.
- A. N. A. Anasthasiya, R. K. Kampara, P. K. Rai and B. G. Jeyaprakash, Appl. Surf. Sci., 2018, 449, 244–249 CrossRef.
- Z. Zhu, C.-T. Kao and R.-J. Wu, Appl. Surf. Sci., 2014, 320, 348–355 CrossRef CAS.
- S. Yan, Z. Li, H. Li, Z. Wu, J. Wang, W. Shen and Y. Q. Fu, J. Mater. Sci., 2018, 53, 16331–16344 CrossRef CAS.
- S. C. Wang and M. O. Shaikh, Sensors, 2015, 15, 14286–14297 CrossRef CAS PubMed.
- Q. A. Drmosh, Z. H. Yamani, A. K. Mohamedkhair, A. H. Y. Hendi and A. Ibrahim, Vacuum, 2018, 156, 68–77 CrossRef CAS.
- L. Chandra, P. K. Sahu, R. Dwivedi and V. N. Mishra, Mater. Res. Express, 2017, 4, 125017 CrossRef.
- O. Lupan, V. Postica, F. Labat, I. Ciofini, T. Pauporté and R. Adelung, Sens. Actuators, B, 2018, 254, 1259–1270 CrossRef CAS.
- J. M. Lee, J.-e. Park, S. Kim, S. Kim, E. Lee, S.-J. Kim and W. Lee, Int. J. Hydrogen Energy, 2010, 35, 12568–12573 CrossRef CAS.
- K. Vijayalakshmi, A. Renitta and A. Monamary, J. Mater. Sci.: Mater. Electron., 2018, 29, 21023–21032 CrossRef CAS.
- X. Wei, X. Yang, T. Wu, S. Wu, W. Li, X. Wang and Z. Chen, Int. J. Hydrogen Energy, 2017, 42, 24580–24586 CrossRef CAS.
- W. Lu, D. Ding, Q. Xue, Y. Du, Y. Xiong, J. Zhang, X. Pan and W. Xing, Sens. Actuators, B, 2018, 254, 393–401 CrossRef CAS.
- Z. S. Hosseini, A. Mortezaali, A. Iraji zad and S. Fardindoost, J. Alloys Compd., 2015, 628, 222–229 CrossRef CAS.
- F.-C. Chung, Z. Zhu, P.-Y. Luo, R.-J. Wu and W. Li, Sens. Actuators, B, 2014, 199, 314–319 CrossRef CAS.
- Z. Zhu, J.-L. Chang and R.-J. Wu, Sens. Actuators, B, 2015, 214, 56–62 CrossRef CAS.
- H. Wu, H. Huang, J. Zhou, D. Hong, M. Ikram, A. U. Rehman, L. Li and K. Shi, Sci. Rep., 2017, 7, 14688 CrossRef PubMed.
- J. Liang, J. Liu, W. Li and M. Hu, Mater. Res. Bull., 2016, 84, 332–339 CrossRef CAS.
- J. Liang, W. Li, J. Liu and M. Hu, Mater. Lett., 2016, 184, 92–95 CrossRef CAS.
- S. Park, H. Kim, C. Jin and C. Lee, J. Korean Phys. Soc., 2012, 60, 1560–1564 CrossRef CAS.
- T.-R. Rashid, D.-T. Phan and G.-S. Chung, Sens. Actuators, B, 2014, 193, 869–876 CrossRef CAS.
- S. Ren, G. Fan, S. Qu and Q. Wang, J. Appl. Phys., 2011, 110, 084312 CrossRef.
- Z. Wang, Z. Li, T. Jiang, X. Xu and C. Wang, ACS Appl. Mater. Interfaces, 2013, 5, 2013–2021 CrossRef CAS PubMed.
- W. P. Chen, Y. Xiong, Y. S. Li, P. Cui, S. S. Guo, W. Chen, Z. L. Tang, Z. Yan and Z. Zhang, Int. J. Hydrogen Energy, 2016, 41, 3307–3312 CrossRef CAS.
- B. Liu, D. Cai, Y. Liu, D. Wang, L. Wang, Y. Wang, H. Li, Q. Li and T. Wang, Sens. Actuators, B, 2014, 193, 28–34 CrossRef CAS.
- P. Li, Z. Xiong, S. Zhu, M. Wang, Y. Hu, H. Gu, Y. Wang and W. Chen, Int. J. Hydrogen Energy, 2017, 42, 30186–30192 CrossRef CAS.
- B. Huang, Y. Wang, Q. Hu, X. Mu, Y. Zhang, J. Bai, Q. Wang, Y. Sheng, Z. Zhang and E. Xie, J. Mater. Chem. C, 2018, 6, 10935–10943 RSC.
- M. Chitra, K. Uthayarani, N. Rajasekaran, N. Neelakandeswari, E. K. Girija and D. P. Padiyan, Surf. Rev. Lett., 2016, 23, 1550094 CrossRef CAS.
- L. Yang, L. Li, Y. Yang, G. Zhang, L. Gong, L. Jing, H. Fu and K. Shi, Mater. Res. Bull., 2013, 48, 3657–3665 CrossRef CAS.
- S. Jain, A. Patrike, S. S. Badadhe, M. Bhardwaj and S. Ogale, ACS Omega, 2018, 3, 1977–1982 CrossRef CAS.
- N. Singh, C. Yan and P. S. Lee, Sens. Actuators, B, 2010, 150, 19–24 CrossRef CAS.
- H. Ahn, Y. Wang, S. Hyun Jee, M. Park, Y. S. Yoon and D.-J. Kim, Chem. Phys. Lett., 2011, 511, 331–335 CrossRef CAS.
- M. R. Modaberi, R. Rooydell, S. Brahma, A. A. Akande, B. W. Mwakikunga and C.-P. Liu, Sens. Actuators, B, 2018, 273, 1278–1290 CrossRef CAS.
- C. Stella, D. Prabhakar, M. Prabhu, N. Soundararajan and K. Ramachandran, J. Mater. Sci.: Mater. Electron., 2015, 27, 1636–1644 CrossRef.
- Z. Li, A. A. Haidry, T. Wang and Z. J. Yao, Appl. Phys. Lett., 2017, 111, 032104 CrossRef.
- A. Renitta and K. Vijayalakshmi, Catal. Commun., 2016, 73, 58–62 CrossRef CAS.
- K. Karthick, D. Srinivasan and J. B. Christopher, J. Mater. Sci.: Mater. Electron., 2017, 28, 11979–11986 CrossRef CAS.
- J. Ma, Y. Liu, H. Zhang, P. Ai, N. Gong, Y. Wu and D. Yu, Sens. Actuators, B, 2015, 216, 72–79 CrossRef CAS.
- X. Zou, H. Fan, Y. Tian, M. Zhang and X. Yan, Dalton Trans., 2015, 44, 7811–7821 RSC.
- A. J. Kulandaisamy, J. R. Reddy, P. Srinivasan, K. J. Babu, G. K. Mani, P. Shankar and J. B. B. Rayappan, J. Alloys Compd., 2016, 688, 422–429 CrossRef CAS.
- K. Khun Khun, A. Mahajan and R. K. Bedi, Chem. Phys. Lett., 2010, 492, 119–122 CrossRef CAS.
- J. M. Wu, Nanotechnology, 2010, 21, 235501 CrossRef PubMed.
- T. Pauporte, O. Lupan, V. Postica, M. Hoppe, L. Chow and R. Adelung, Phys. Status Solidi A, 2018, 215, 1700824 CrossRef.
- R. Jaisutti, M. Lee, J. Kim, S. Choi, T. J. Ha, J. Kim, H. Kim, S. K. Park and Y. H. Kim, ACS Appl. Mater. Interfaces, 2017, 9, 8796–8804 CrossRef CAS PubMed.
- K. Vijayalakshmi and K. Karthick, Int. J. Hydrogen Energy, 2014, 39, 7165–7172 CrossRef CAS.
- H. Liu, D. Ding, C. Ning and Z. Li, Nanotechnology, 2012, 23, 015502 CrossRef PubMed.
- M. Kaur, S. Bhattacharya, M. Roy, S. K. Deshpande, P. Sharma, S. K. Gupta and J. V. Yakhmi, Appl. Phys. A: Mater. Sci. Process., 2007, 87, 91–96 CrossRef CAS.
- A. Chaparadza and S. B. Rananavare, Nanotechnology, 2008, 19, 245501 CrossRef PubMed.
- H. Tang, M. Yan, H. Zhang, S. Li, X. Ma, M. Wang and D. Yang, Sens. Actuators, B, 2006, 114, 910–915 CrossRef CAS.
- P. M. Calaque, C. J. Vergara, L. I. Ballesteros and A. Somintac, AIP Conf. Proc., 2017, 1808, 020013 CrossRef.
- T.-t. Li, R.-r. Zheng, H. Yu, L. Xia, Y. Yang and X.-t. Dong, Solid State Ionics, 2018, 325, 17–23 CrossRef CAS.
- M. Bao, Y. Chen, F. Li, J. Ma, T. Lv, Y. Tang, L. Chen, Z. Xu and T. Wang, Nanoscale, 2014, 6, 4063–4066 RSC.
- G. Cui, P. Zhang, L. Chen, X. Wang, J. Li, C. Shi and D. Wang, Sci. Rep., 2017, 7, 43887 CrossRef PubMed.
- C. Jiang, S. Xu, G. Zhang, L. Li, Y. Yang and K. Shi, CrystEngComm, 2013, 15, 2482 RSC.
- D. R. Patil, L. A. Patil and P. P. Patil, Sens. Actuators, B, 2007, 126, 368–374 CrossRef CAS.
- S. Bhuvaneshwari, S. Papachan and N. Gopalakrishnan, AIP Conf. Proc., 2017, 1832, 050126 CrossRef.
- J. Zhang, D. Zeng, Q. Zhu, J. Wu, Q. Huang, W. Zhang and C. Xie, Phys. Chem. Chem. Phys., 2016, 18, 5386–5396 RSC.
- H. Wu, K. Kan, L. Wang, G. Zhang, Y. Yang, H. Li, L. Jing, P. Shen, L. Li and K. Shi, CrystEngComm, 2014, 16, 9116–9124 RSC.
- R. Lu, W. Zhou, K. Shi, Y. Yang, L. Wang, K. Pan, C. Tian, Z. Ren and H. Fu, Nanoscale, 2013, 5, 8569–8576 RSC.
- X. Yue, T. Hong, Z. Yang and S. Huang, Chin. Sci. Bull., 2012, 58, 821–826 CrossRef.
- X. Liu, B. Du, Y. Sun, M. Yu, Y. Yin, W. Tang, C. Chen, L. Sun, B. Yang, W. Cao and M. N. Ashfold, ACS Appl. Mater. Interfaces, 2016, 8, 16379–16385 CrossRef CAS PubMed.
- W. Zang, Y. Nie, D. Zhu, P. Deng, L. Xing and X. Xue, J. Phys. Chem. C, 2014, 118, 9209–9216 CrossRef CAS.
- L. A. Patil and D. R. Patil, Sens. Actuators, B, 2006, 120, 316–323 CrossRef CAS.
- A. Mirzaei, G.-J. Sun, J. K. Lee, C. Lee, S. Choi and H. W. Kim, Ceram. Int., 2017, 43, 5247–5254 CrossRef CAS.
- S. Park, H. Kheel, G.-J. Sun, H. W. Kim, T. Ko and C. Lee, Met. Mater. Int., 2016, 22, 730–736 CrossRef CAS.
- M.-R. Yu, G. Suyambrakasam, R.-J. Wu and M. Chavali, Mater. Res. Bull., 2012, 47, 1713–1718 CrossRef CAS.
- J. Liang, R. Yang, K. Zhu and M. Hu, J. Mater. Sci.: Mater. Electron., 2017, 29, 3780–3789 CrossRef.
- L. F. da Silva, J. C. M’Peko, A. C. Catto, S. Bernardini, V. R. Mastelaro, K. Aguir, C. Ribeiro and E. Longo, Sens. Actuators, B, 2017, 240, 573–579 CrossRef CAS.
- D. R. Patil and L. A. Patil, Sens. Actuators, B, 2007, 123, 546–553 CrossRef CAS.
- D. Zhu, Y. Fu, W. Zang, Y. Zhao, L. Xing and X. Xue, Mater. Lett., 2016, 166, 288–291 CrossRef CAS.
- G. Lu, L. E. Ocola and J. Chen, Nanotechnology, 2009, 20, 445502 CrossRef PubMed.
- Y. Wang and S. Gong, J. Mater. Sci.: Mater. Electron., 2015, 26, 5024–5029 CrossRef CAS.
- W. Yang, P. Wan, X. Zhou, J. Hu, Y. Guan and L. Feng, ACS Appl. Mater. Interfaces, 2014, 6, 21093–21100 CrossRef CAS PubMed.
- S. Liu, B. Yu, H. Zhang, T. Fei and T. Zhang, Sens. Actuators, B, 2014, 202, 272–278 CrossRef CAS.
- H. Tai, Z. Yuan, W. Zheng, Z. Ye, C. Liu and X. Du, Nanoscale Res. Lett., 2016, 11, 130 CrossRef PubMed.
- Y. Yang, L. Sun, X. Dong, H. Yu, T. Wang, J. Wang, R. Wang, W. Yu and G. Liu, RSC Adv., 2016, 6, 37085–37092 RSC.
- R. Ghosh, A. K. Nayak, S. Santra, D. Pradhan and P. K. Guha, RSC Adv., 2015, 5, 50165–50173 RSC.
- S. Liu, Z. Wang, Y. Zhang, J. Li and T. Zhang, Sens. Actuators, B, 2016, 228, 134–143 CrossRef CAS.
- Z. Wang, Y. Zhang, S. Liu and T. Zhang, Sens. Actuators, B, 2016, 222, 893–903 CrossRef CAS.
- Z. Wang, T. Zhang, C. Zhao, T. Han, T. Fei, S. Liu and G. Lu, J. Colloid Interface Sci., 2018, 514, 599–608 CrossRef CAS PubMed.
- M. Shojaee, S. Nasresfahani and M. H. Sheikhi, Sens. Actuators, B, 2018, 254, 457–467 CrossRef CAS.
- T. Wang, J. Hao, S. Zheng, Q. Sun, D. Zhang and Y. Wang, Nano Res., 2017, 11, 791–803 CrossRef.
- J. Zhang, J. Wu, X. Wang, D. Zeng and C. Xie, Sens. Actuators, B, 2017, 243, 1010–1019 CrossRef CAS.
- P.-G. Su, F.-Y. Chen and C.-H. Wei, Sens. Actuators, B, 2018, 254, 1125–1132 CrossRef CAS.
- J. Zhang, D. Zeng, S. Zhao, J. Wu, K. Xu, Q. Zhu, G. Zhang and C. Xie, Phys. Chem. Chem. Phys., 2015, 17, 14903–14911 RSC.
- Z. Wang, Y. Zhang, S. Liu and T. Zhang, Sens. Actuators, B, 2016, 222, 893–903 CrossRef CAS.
- Z. Wang, T. Zhang, T. Han, T. Fei, S. Liu and G. Lu, Sens. Actuators, B, 2018, 266, 812–822 CrossRef CAS.
- J. Pan, W. Li, L. Quan, N. Han, S. Bai, R. Luo, Y. Feng, D. Li and A. Chen, Ind. Eng. Chem. Res., 2018, 57, 10086–10094 CrossRef CAS.
- X. Liu, J. Sun and X. Zhang, Sens. Actuators, B, 2015, 211, 220–226 CrossRef CAS.
- N. Chen, X. Li, X. Wang, J. Yu, J. Wang, Z. Tang and S. A. Akbar, Sens. Actuators, B, 2013, 188, 902–908 CrossRef CAS.
- F. Gu, R. Nie, D. Han and Z. Wang, Sens. Actuators, B, 2015, 219, 94–99 CrossRef CAS.
- Z. Li, Y. Liu, D. Guo, J. Guo and Y. Su, Sens. Actuators, B, 2018, 271, 306–310 CrossRef CAS.
- S. Liu, Z. Wang, Y. Zhang, J. Li and T. Zhang, Sens. Actuators, B, 2016, 228, 134–143 CrossRef CAS.
- X. Jiang, H. Tai, Z. Ye, Z. Yuan, C. Liu, Y. Su and Y. Jiang, Mater. Lett., 2017, 186, 49–52 CrossRef CAS.
- D. Zhang, J. Liu and B. Xia, J. Electron. Mater., 2016, 45, 4324–4330 CrossRef CAS.
- X. Liu, J. Li, J. Sun and X. Zhang, RSC Adv., 2015, 5, 73699–73704 RSC.
- Y. Xia, J. Wang, J. L. Xu, X. Li, D. Xie, L. Xiang and S. Komarneni, ACS Appl. Mater. Interfaces, 2016, 8, 35454–35463 CrossRef CAS PubMed.
- T. Wang, J. Hao, S. Zheng, Q. Sun, D. Zhang and Y. Wang, Nano Res., 2018, 11, 791–803 CrossRef CAS.
- Y.-l. Dong, X.-f. Zhang, X.-l. Cheng, Y.-m. Xu, S. Gao, H. Zhao and L.-h. Huo, RSC Adv., 2014, 4, 57493–57500 RSC.
- W. Fang, Y. Yang, H. Yu, X. Dong, R. Wang, T. Wang, J. Wang, Z. Liu, B. Zhao and X. Wang, New J. Chem., 2017, 41, 7517–7523 RSC.
- Y. Yang, C. Tian, L. Sun, R. Lü, W. Zhou, K. Shi, K. Kan, J. Wang and H. Fu, J. Mater. Chem. A, 2013, 1, 12742 RSC.
- Y. Yang, C. Tian, J. Wang, L. Sun, K. Shi, W. Zhou and H. Fu, Nanoscale, 2014, 6, 7369–7378 RSC.
- G. P. Evans, M. J. Powell, I. D. Johnson, D. P. Howard, D. Bauer, J. A. Darr and I. P. Parkin, Sens. Actuators, B, 2018, 255, 1119–1129 CrossRef CAS.
- Y. Chen, W. Zhang and Q. Wu, Sens. Actuators, B, 2017, 242, 1216–1226 CrossRef CAS.
- H. Meng, W. Yang, K. Ding, L. Feng and Y. Guan, J. Mater. Chem. A, 2015, 3, 1174–1181 RSC.
- X. Li, Y. Zhao, X. Wang, J. Wang, A. M. Gaskov and S. A. Akbar, Sens. Actuators, B, 2016, 230, 330–336 CrossRef CAS.
- P.-G. Su and L.-Y. Yang, Sens. Actuators, B, 2016, 223, 202–208 CrossRef CAS.
- P.-G. Su, F.-Y. Chen and C.-H. Wei, Sens. Actuators, B, 2018, 254, 1125–1132 CrossRef CAS.
- G. Singh, A. Choudhary, D. Haranath, A. G. Joshi, N. Singh, S. Singh and R. Pasricha, Carbon, 2012, 50, 385–394 CrossRef CAS.
- R. Kumar, N. Kushwaha and J. Mittal, Sens. Actuators, B, 2017, 244, 243–251 CrossRef CAS.
- F. Schutt, V. Postica, R. Adelung and O. Lupan, ACS Appl. Mater. Interfaces, 2017, 9, 23107–23118 CrossRef PubMed.
- A. Yang, X. Tao, R. Wang, S. Lee and C. Surya, Appl. Phys. Lett., 2007, 91, 133110 CrossRef.
- D. Zhang, C. Jiang, J. Liu and Y. Cao, Sens. Actuators, B, 2017, 247, 875–882 CrossRef CAS.
- M. Shojaee, S. Nasresfahani and M. H. Sheikhi, Sens. Actuators, B, 2018, 254, 457–467 CrossRef CAS.
- N. Du, H. Zhang, X. Ma and D. Yang, Chem. Commun., 2008, 6182–6184 RSC.
- S. Dhall and N. Jaggi, Sens. Actuators, B, 2015, 210, 742–747 CrossRef CAS.
- D. Zhang, N. Yin, C. Jiang and B. Xia, J. Mater. Sci.: Mater. Electron., 2016, 28, 2763–2768 CrossRef.
- D. Kathiravan, B. R. Huang and A. Saravanan, ACS Appl. Mater. Interfaces, 2017, 9, 12064–12072 CrossRef CAS PubMed.
- Y. Peng, L. Zheng, K. Zou and C. Li, Nanotechnology, 2017, 28, 215501 CrossRef PubMed.
- Z. Ye, H. Tai, T. Xie, Z. Yuan, C. Liu and Y. Jiang, Sens. Actuators, B, 2016, 223, 149–156 CrossRef CAS.
- Z. Bo, M. Yuan, S. Mao, X. Chen, J. Yan and K. Cen, Sens. Actuators, B, 2018, 256, 1011–1020 CrossRef CAS.
- S. Ghosal and P. Bhattacharyya, Microelectron. Reliab., 2017, 78, 299–306 CrossRef CAS.
- D. Acharyya and P. Bhattacharyya, IEEE Electron Device Lett., 2016, 37, 656–659 CAS.
- S. Nasresfahani, M. H. Sheikhi, M. Tohidi and A. Zarifkar, IEEE Iranian Conference on Electrical Engineering, 2016, 1014–1018 Search PubMed.
- D. Zhang, A. Liu, H. Chang and B. Xia, RSC Adv., 2015, 5, 3016–3022 RSC.
- D. Zhang, Y. e. Sun and Y. Zhang, J. Mater. Sci.: Mater. Electron., 2015, 26, 7445–7451 CrossRef CAS.
- S. G. Chatterjee, S. Dey, D. Samanta, S. Santra, S. Chatterjee, P. K. Guha and A. K. Chakraborty, J. Mater. Sci.: Mater. Electron., 2018, 29, 20162–20171 CrossRef.
- J. Hu, C. Zou, Y. Su, M. Li, X. Ye, B. Cai, E. S.-W. Kong, Z. Yang and Y. Zhang, Sens. Actuators, B, 2018, 270, 119–129 CrossRef CAS.
- D. Ding, Q. Xue, W. Lu, Y. Xiong, J. Zhang, X. Pan and B. Tao, Sens. Actuators, B, 2018, 259, 289–298 CrossRef CAS.
- B.-Y. Wei, M.-C. Hsu, P.-G. Su, H.-M. Lin, R.-J. Wu and H.-J. Lai, Sens. Actuators, B, 2004, 101, 81–89 CrossRef CAS.
- G. Lu, L. E. Ocola and J. Chen, Adv. Mater., 2009, 21, 2487–2491 CrossRef CAS.
- R. Leghrib, A. Felten, J. J. Pireaux and E. Llobet, Thin Solid Films, 2011, 520, 966–970 CrossRef CAS.
- X. Luo, H. Giessen, Y. Zhou, G. Xie, T. Xie, T. Kang and Y. Jiang, Proc. SPIE, 2014, 9285, 928509 CrossRef.
- A. Sharma, M. Tomar and V. Gupta, J. Mater. Chem., 2012, 22, 23608 RSC.
- M. Asad and M. H. Sheikhi, Sens. Actuators, B, 2016, 231, 474–483 CrossRef CAS.
- H. Liu, W. Zhang, H. Yu, L. Gao, Z. Song, S. Xu, M. Li, Y. Wang, H. Song and J. Tang, ACS Appl. Mater. Interfaces, 2016, 8, 840–846 CrossRef CAS PubMed.
- K. Anothainart, M. Burgmair, A. Karthigeyan, M. Zimmer and I. Eisele, Sens. Actuators, B, 2003, 93, 580–584 CrossRef CAS.
- L. Meng, Q. Xu, Z. Sun, G. Li, S. Bai, Z. Wang and Y. Qin, Mater. Lett., 2018, 212, 296–298 CrossRef CAS.
- P. Wang, Y. Fu, B. Yu, Y. Zhao, L. Xing and X. Xue, J. Mater. Chem. A, 2015, 3, 3529–3535 RSC.
- L. Peng, Q. Zhao, D. Wang, J. Zhai, P. Wang, S. Pang and T. Xie, Sens. Actuators, B, 2009, 136, 80–85 CrossRef CAS.
- J. Cui, L. Shi, T. Xie, D. Wang and Y. Lin, Sens. Actuators, B, 2016, 227, 220–226 CrossRef CAS.
- L. Vogel, R. Wagner, R. Moos and D. Schoenauer-Kamin, Funct. Mater. Lett., 2018, 11, 1850087 CrossRef CAS.
- N. D. Chinh, N. D. Quang, H. Lee, T. Thi Hien, N. M. Hieu, D. Kim, C. Kim and D. Kim, Sci. Rep., 2016, 6, 35066 CrossRef CAS PubMed.
- D. Klaus, D. Klawinski, S. Amrehn, M. Tiemann and T. Wagner, Sens. Actuators, B, 2015, 217, 181–185 CrossRef CAS.
- X. Li, X. Li, J. Wang and S. Lin, Sens. Actuators, B, 2015, 219, 158–163 CrossRef CAS.
- T. Xie, N. Sullivan, K. Steffens, B. Wen, G. Liu, R. Debnath, A. Davydov, R. Gomez and A. Motayed, J. Alloys Compd., 2015, 653, 255–259 CrossRef CAS PubMed.
- J. D. Prades, R. Jimenez-Diaz, F. Hernandez-Ramirez, S. Barth, A. Cirera, A. Romano-Rodriguez, S. Mathur and J. R. Morante, Sens. Actuators, B, 2009, 140, 337–341 CrossRef CAS.
- Y. Xiong, W. Lu, D. Ding, L. Zhu, X. Li, C. Ling and Q. Xue, ACS Sens., 2017, 2, 679–686 CrossRef CAS PubMed.
- H. Chen, Y. Liu, C. Xie, J. Wu, D. Zeng and Y. Liao, Ceram. Int., 2012, 38, 503–509 CrossRef CAS.
- R. Gao, Z. Ying, W. Sheng and P. Zheng, Mater. Lett., 2018, 229, 210–212 CrossRef CAS.
- J. Sun, J. Xu, Y. Yu, P. Sun, F. Liu and G. Lu, Sens. Actuators, B, 2012, 169, 291–296 CrossRef CAS.
- G. Lu, J. Xu, J. Sun, Y. Yu, Y. Zhang and F. Liu, Sens. Actuators, B, 2012, 162, 82–88 CrossRef CAS.
- J. Cui, D. Wang, T. Xie and Y. Lin, Sens. Actuators, B, 2013, 186, 165–171 CrossRef CAS.
- X. Li, N. Chen, S. Lin, J. Wang and J. Zhang, Sens. Actuators, B, 2015, 209, 729–734 CrossRef CAS.
- X. Geng, C. Zhang, Y. Luo, H. Liao and M. Debliquy, Ceram. Int., 2017, 43, 5990–5998 CrossRef CAS.
- X. Geng, C. Zhang, Y. Luo and M. Debliquy, Appl. Surf. Sci., 2017, 401, 248–255 CrossRef CAS.
- T. Wang, Q. Yu, S. Zhang, X. Kou, P. Sun and G. Lu, Nanoscale, 2018, 10, 4841–4851 RSC.
- K. Zhang, M. Peng, W. Wu, J. Guo, G. Gao, Y. Liu, J. Kou, R. Wen, Y. Lei, A. Yu, Y. Zhang, J. Zhai and Z. L. Wang, Mater. Horiz., 2017, 4, 274–280 RSC.
- W. L. Ong, C. Zhang and G. W. Ho, Nanoscale, 2011, 3, 4206–4214 RSC.
- R. Li, K. Jiang, S. Chen, Z. Lou, T. Huang, D. Chen and G. Shen, RSC Adv., 2017, 7, 52503–52509 RSC.
- T. M. Perfecto, C. A. Zito, T. Mazon and D. P. Volanti, J. Mater. Chem. C, 2018, 6, 2822–2829 RSC.
- X. Geng, C. Zhang, Y. Luo and M. Debliquy, J. Taiwan Inst. Chem. Eng., 2017, 75, 280–286 CrossRef CAS.
- C. Hua, Y. Shang, Y. Wang, J. Xu, Y. Zhang, X. Li and A. Cao, Appl. Surf. Sci., 2017, 405, 405–411 CrossRef CAS.
- S. Knobelspies, B. Bierer, A. Daus, A. Takabayashi, G. A. Salvatore, G. Cantarella, A. Ortiz Perez, J. Wollenstein, S. Palzer and G. Troster, Sensors, 2018, 18, 358 CrossRef PubMed.
- S. J. Choi, H. J. Choi, W. T. Koo, D. Huh, H. Lee and I. D. Kim, ACS Appl. Mater. Interfaces, 2017, 9, 40593–40603 CrossRef CAS PubMed.
- S. M. Mohammad, Z. Hassan, R. A. Talib, N. M. Ahmed, M. A. Al-Azawi, N. M. Abd-Alghafour, C. W. Chin and N. H. Al-Hardan, J. Mater. Sci.: Mater. Electron., 2016, 27, 9461–9469 CrossRef CAS.
- S. Li, P. Lin, L. Zhao, C. Wang, D. Liu, F. Liu, P. Sun, X. Liang, F. Liu, X. Yan, Y. Gao and G. Lu, Sens. Actuators, B, 2018, 259, 505–513 CrossRef CAS.
- D. K. Subbiah, G. K. Mani, K. J. Babu, A. Das and J. B. B. Rayappan, J. Clean. Prod., 2018, 194, 372–382 CrossRef CAS.
- S. Li, Y. Diao, Z. Yang, J. He, J. Wang, C. Liu, F. Liu, H. Lu, X. Yan, P. Sun and G. Lu, Sens. Actuators, B, 2018, 276, 526–533 CrossRef CAS.
- H.-Y. Li, C.-S. Lee, D. H. Kim and J.-H. Lee, ACS Appl. Mater. Interfaces, 2018, 10, 27858–27867 CrossRef CAS PubMed.
- D. K. Bandgar, S. T. Navale, Y. H. Navale, S. M. Ingole, F. J. Stadler, N. Ramgir, D. K. Aswal, S. K. Gupta, R. S. Mane and V. B. Patil, Mater. Chem. Phys., 2017, 189, 191–197 CrossRef CAS.
- C. Liu, H. Tai, P. Zhang, Z. Yuan, X. Du, G. Xie and Y. Jiang, Sens. Actuators, B, 2018, 261, 587–597 CrossRef CAS.
- U. Yaqoob, D.-T. Phan, A. S. M. I. Uddin and G.-S. Chung, Sens. Actuators, B, 2015, 221, 760–768 CrossRef CAS.
- U. Yaqoob, A. S. M. I. Uddin and G.-S. Chung, Sens. Actuators, B, 2016, 224, 738–746 CrossRef CAS.
- K. K. Sadasivuni, D. Ponnamma, H.-U. Ko, H. C. Kim, L. Zhai and J. Kim, Sens. Actuators, B, 2016, 233, 633–638 CrossRef CAS.
- V. Annapureddy, Y. Kim, G.-T. Hwang, H. W. Jang, S.-D. Kim, J.-J. Choi, B. Cho and J. Ryu, Adv. Mater. Interfaces, 2018, 5, 1700811 CrossRef.
- A. S. M. I. Uddin and G.-S. Chung, J. Electroceram., 2018, 40, 42–49 CrossRef.
- X. Luo, K. You, Y. Hu, S. Yang, X. Pan, Z. Wang, W. Chen and H. Gu, Int. J. Hydrogen Energy, 2017, 42, 8399–8405 CrossRef CAS.
- Z. Pang, Z. Yang, Y. Chen, J. Zhang, Q. Wang, F. Huang and Q. Wei, Colloid. Surface. A, 2016, 494, 248–255 CrossRef CAS.
- A. Bagal, E. C. Dandley, J. Zhao, X. A. Zhang, C. J. Oldham, G. N. Parsons and C.-H. Chang, Mater. Horiz., 2015, 2, 486–494 RSC.
- A. Sanaeifar, H. ZakiDizaji, A. Jafari and M. d. l. Guardia, Trac-Trend. Anal. Chem., 2017, 97, 257–271 CrossRef CAS.
- Y. Zhang, J. Zhao, T. Du, Z. Zhu, J. Zhang and Q. Liu, Sci. Rep., 2017, 7, 1960 CrossRef PubMed.
- A. B. Far, F. Flitti, B. Guo and A. Bermak, IEEE Sens. J., 2009, 9, 713–722 CAS.
- F. Flitti, A. Far, B. Guo and A. Bermak, J. Sensors, 2008, 2008, 1–6 CrossRef.
| This journal is © The Royal Society of Chemistry 2019 |