Open Access Article
Open Access ArticleBiomineralized tissue formation as an archetype of ideal grain growth
Dana
Zöllner
 and
Igor
Zlotnikov
and
Igor
Zlotnikov
 *
*
B CUBE – Center for Molecular Bioengineering, Technische Universität Dresden, Dresden, 01307, Germany. E-mail: igor.zlotnikov@tu-dresden.de
First published on 15th January 2019
Abstract
Grain size distribution is a fundamental property of polycrystalline materials and the phenomenon of grain boundary motion has major repercussions for materials processing and in a variety of technological applications. In classical models for microstructural evolution during grain boundary motion, special attention is given to the case of “ideal” grain growth defined by the seemingly unrealistic assumption of homogeneity of the physical properties of the boundaries. Whereas different models were rarely shown to demonstrate ideal microstructural evolution of selected synthetic and geological granular networks, here we present a biogenic polycrystalline material the formation of which is consistently described by all principal predictions of an ideal grain growth behaviour. We show that biomineralization of the prismatic architecture in the shell of the mollusc Atrina vexillum is fully quantified by conventional thermodynamic, kinetic and topological considerations, thus making a material formed by a living organism archetypical of ideal grain growth.
Conceptual insightsWe present an intricate 3D biomineralized architecture the formation of which is fully predicted by key thermodynamic, kinetic and topological models that were classically developed to describe an analytically ideal behavior during grain growth of man-made and geological materials. Whereas ideal grain growth was rarely shown to occur even in generic materials systems using some of the theoretical models, the morphogenesis of the prismatic assembly in the mollusc shell of Atrina vexillum is the first material that adheres perfectly to all, both qualitatively and quantitatively. Surprisingly, the polycrystalline assembly, that evaded physicists and materials scientists since the early 1950s, is found to be formed by a living organism. |
Introduction
The properties of grain networks comprising the microstructure of many polycrystalline materials systems, such as metals, alloys, ceramics and bionic composite structures have a significant impact on their physical performance.1,2 In particular, the size and shape of the grains and the properties of the boundaries that separate them are linked to numerous materials characteristics, such as mechanical behaviour and electromagnetic performance. In fact, this structure–property relationship in a polycrystalline matter is one of the most fundamental concepts in materials science. Moreover, the grain boundaries are considered to be two-dimensional defects characterized by a certain free energy. The latter introduces a driving force to the system aimed at reducing the total amount of these defects, namely, the grain boundary area. Thermal fluctuations in the atomic lattice due to elevated temperatures lead to a reduction of free energy by boundary motion and consequently, by coarsening of the grain network. This process is called grain boundary migration, in the case of individual grain boundaries, and grain growth, in the case of polycrystalline microstructures,3–6 and it is one of the most important processes in materials science.Since the early 1950s, many attempts have been made to understand and to predict polycrystalline microstructure evolution during grain growth and coarsening analytically. From a general point of view, this process is rather simple. A polycrystalline microstructure consists of many mono-crystalline grains, where the grain boundaries between two neighbouring crystals are usually slightly curved. This curvature is the result of the system striving to achieve an angle of 120 degrees between the three arms at a triple junctions, where three grains meet, necessary to maintain an energetic equilibrium.7,8 This configuration results in a curvature-driven boundary motion during which the free energy is reduced by a motion of the boundaries to the centre of their curvature. Since small grains with less than the average amount of edges tend to have convex boundaries, they shrink, whereas large grains with more than the average amount of edges tend to increase their size. As a result, the number of grains decreases and the total grain boundary area and the coupled free energy decreases, while the average grain size increases. Of course, such a transformation during production and application can be both wanted or unwanted, but in any case leads to a change of the properties of the material.
A special situation that has been drawing a majority of research efforts is the case of curvature-driven ideal grain growth, where it is assumed—mostly for reasons of simplification—that all grain boundaries in a polycrystalline network are characterized by the same physical properties.7 Specifically, by the same value of surface tension, γ, as well as by the same boundary mobility, m. Hence, any possible dependence of the boundary properties m and γ on misorientation between the associated neighbouring crystals is neglected in agreement with the uniform boundary model.5 As a result, over the years, many analytical laws have been derived to describe ideal grain growth of polycrystalline materials in two and three dimensions. Whereas large experimental evidence exists showing that different analytical theories are successful in describing microstructural evolution of a variety of structures, so far not a single materials system has been shown to obey all predictions of ideal grain growth qualitatively nor quantitatively.
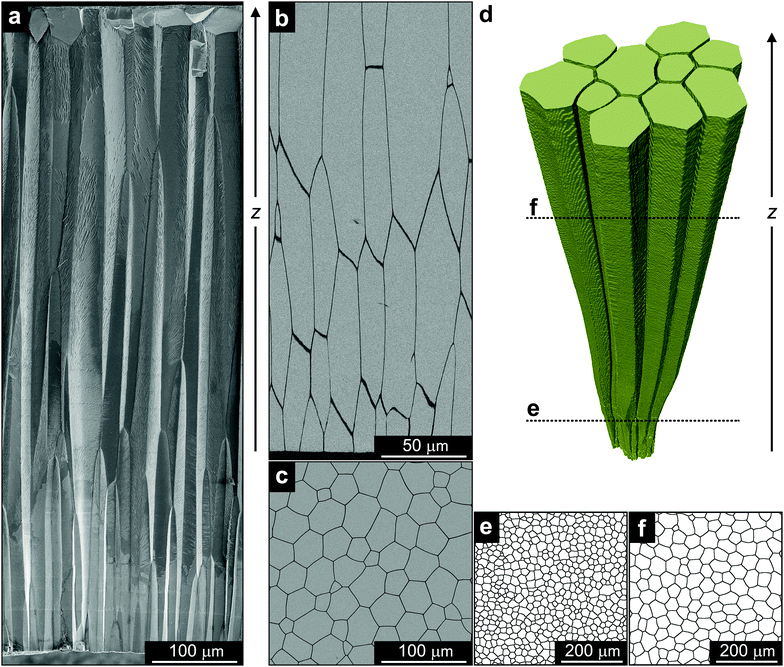
In this work, we present the first microstructure whose morphogenesis consistently fulfils a number of classical thermodynamic and kinetic relationships for ideal grain growth, both qualitatively and quantitatively. Interestingly, the different theories are shown here to converge and describe a biogenic mineralized material formed by a living organism. Namely, the growth of the prismatic architecture in the shell of the bivalve Atrina vexillum (Fig. 1). Similar to other bivalves, which are molluscs that have a shell made of two hinged valves that enclose the soft body of the animal, the shell of A. vexillum consists of two mineralized assemblies, which are arranged in layers parallel to the outer surface of the shell. One layer is called the prismatic ultrastructure composed of elongated columns made of calcite (Fig. 1a), and the other layer is a nacreous ultrastructure composed of flat platelets made of aragonite. Earlier studies were successful in demonstrating that physical models have the capacity to describe the morphogenesis of the prismatic architecture in a variety of bivalves9–11 and ideal behaviour in A. vexillum was recently suggested.12 However, ideal growth that perfectly adheres to all principal theoretical predictions has not yet been shown.
Results and discussion
Structural analysis of the prismatic layer in the shell of Atrina vexillum
The morphology and the growth process of the calcitic prismatic architecture in A. vexillum13 is reminiscent of columnar architectures formed by various vapour deposition techniques.14,15 It consists of elongated calcitic columns joined together by an organic interprismatic phase (dark boundaries in Fig. 1b). It is deposited by cellular tissue on the external organic membrane covering the entire shell (periostracum) and grows unidirectionally towards the inner part of the animal with the long axis of the columns being parallel to the direction of growth, z. In a transverse cross-section, the prismatic layer exhibits a honeycomb-like morphology characteristic of a polycrystalline material (Fig. 1c). Whereas in classic materials the grain boundaries are described by a crystallographic misorientation between two neighbouring grains, in the case of the prismatic ultrastructure the boundaries are the mineral–organic interfaces. However, in both cases, the driving force for grain growth is the reduction in the amount of boundary area. Indeed, such a coarsening of the prismatic ultrastructure with the direction of growth has already been shown in a variety of bivalve shells.9–11To obtain a complete history of microstructural evolution of the prismatic layer in A. vexillum, we performed a microtomography experiment at beamline ID19 of the European Synchrotron Radiation Facility (ESRF). The organic interfaces, having the thickness of approximately 1 μm, were easily resolved using an effective voxel size of 0.649 μm. The measurement covered a total thickness of approximately 1 mm from the main body of the prismatic layer. A representative 3D segment reconstructed from these data clearly shows the coarsening behaviour of the prismatic ultrastructure along the direction of growth, z (Fig. 1d). In addition, when comparing 2D slices, taken from the microtomography data perpendicular to the direction of growth, one during the initial stage of the prismatic layer formation (closer to the periostracum) (Fig. 1e) and one at a later stage (Fig. 1f), the reduction of the amount of the boundary and the number of prisms is evident. To follow this behaviour as a function of the growth direction quantitatively, similar 2D sections throughout the entire thickness of the prismatic layer were analysed. It is important to note that in this study, the time parameter, t, that is commonly used to follow the coarsening process, was substituted with the direction of growth, z. Here we assume a linear correlation between the two and, essentially, reduce the three-dimensional growth in space into a two-dimensional temporal process.9–11
Average growth law
In the early 1950s, Burke and Turnbull16 established one of the first physically inspired models for grain growth that describes the change of the average grain radius, 〈R〉, as a function of annealing time, t, such that 〈R〉1/n ∝ t. Ever since, it has been shown that this correlation works for different materials, such as zone-refined tin with a growth exponent of n = 0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17 or polycrystalline ice with growth exponents of n = 0.25 and n = 0.30.18 In particular, an exponent n = 0.5 represents ideal grain growth.
17 or polycrystalline ice with growth exponents of n = 0.25 and n = 0.30.18 In particular, an exponent n = 0.5 represents ideal grain growth.
Assuming that the migration of the boundaries within a grain network is driven by transport of matter under pressure because of curved interfaces between the grains, the direction of migration of a boundary is always directed towards the centre of its curvature. This leads to a reduction of the total inner interface area of the microstructure and, therefore, of the total interface energy. The associated velocity of a segment of any grain boundary is given by v = mγκ, thus, introducing the curvature κ. The velocity is always directed to the centre of curvature. In ideal growth, assuming that all boundaries are characterized by a unique value of surface tension, γ, and mobility, m, and that a grain can be described in average by a spherical shape, the curvature relates directly to a corresponding average radius, 〈R〉, calculated as a grain-volume-equivalent sphere resulting in κ ∝ 〈R〉−1.
Recently, the subsequent relation for the change of the average grain size with annealing time, t, was derived with the same result but using a completely different ansatz:19
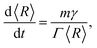 | (1) |
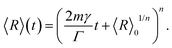 | (2) |
In the prismatic ultrastructure of A. vexillum, the average grain size indeed follows the well-known growth law, eqn (2), in terms of 〈R〉 = 〈R〉(z) (Fig. 2a) and the growth exponent is n = 0.4976 ± 0.0027. Here, the calculations were performed every 20 sections, corresponding to a step size of 12.98 μm and the area of each section is 973.5 μm × 973.5 μm (1500 pixels × 1500 pixels). The radii were calculated as prism-area-equivalent circles using R = √(A/π), where A is the measured prism area. The growth factor is b = 2mγ/Γ = 0.2369 ± 0.0011 μm, from which the reduced mobility, mγ, can be calculated under the assumption that the growth constant is the same as in the above mentioned case for ideal grain growth with Γ = 6.8639 resulting in mγ = 0.8130 ± 0.0038 μm.
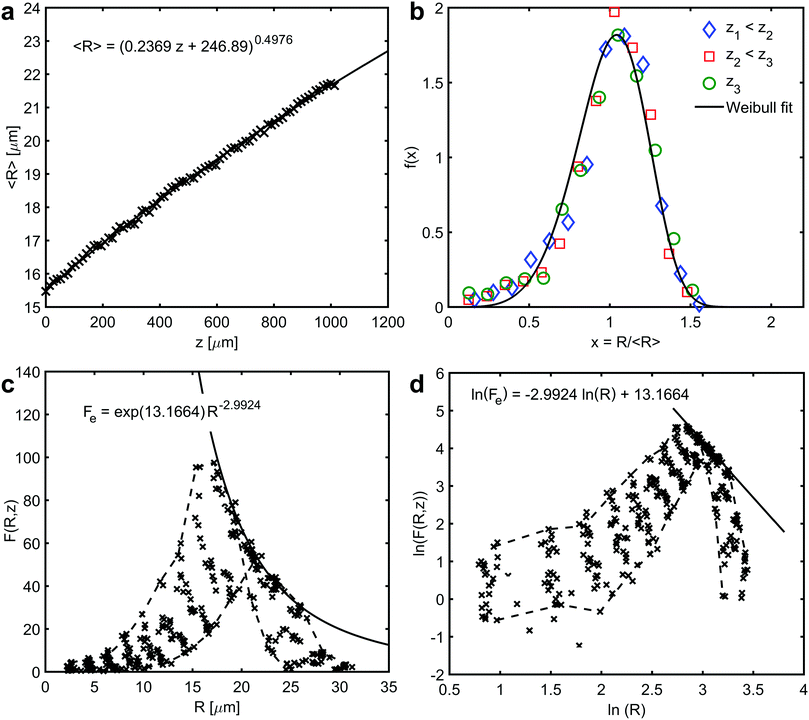 | ||
| Fig. 2 Average growth law and self-similarity. (a) The relationship between average prism radii, 〈R〉, and the growth direction, z. The curve represents a fit to eqn (2) – average growth law (the regression coefficient R2 is 0.9985). (b) Scaled prism size distributions showing self-similarity at three different sections, z1 < z2 < z3, along the growth direction of the prismatic layer. The curve represents a fit to Weibull distribution function (the regression coefficient R2 is 0.9345). (c) and (d) Prism size distribution and a corresponding natural double logarithmic plot of different sections along the growth direction, respectively. Solid curves represent a fit to the envelope of the numerical data (the regression coefficient R2 is 0.8822). Dashed curves outline the first and the last data set along the direction of growth. The data have been put into 13 bins. | ||
Self-similar size distributions
Curvature driven ideal grain growth follows not only a growth law in terms of eqn (2), but the underlying coarsening process is in a quasi-stationary state that demonstrates statistical self-similarity.21,22 This means that the grain size distribution function, F(R,t), can be written in a scaling form:| F(R,t) = g(t)f(x). | (3) |
The time-dependent function that follows from volume conservation yields g(t) = N/〈R〉 ∝ 〈R〉−(d+1),23 where the dimension of the structure is d ∈ {2,3} and N = N(t) is the number of grains, which decreases with time. In contrast, the function f(x) is time-independent function that scales the grain radii of all the grains in the microstructure by the average radius such that x = R/〈R〉 and 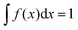 .
.
Time-independence of f(x) and therefore, self-similarity of the prismatic ultrastructure in A. vexillum is shown in Fig. 2b. Identical scaled size distributions are obtained at three randomly selected sections along the direction of growth, in z1 = 25.96 μm, z2 = 376.42 μm and z3 = 726.88 μm. The evolution of the distribution function F(R,z) is presented in Fig. 2c and also in Fig. 2d in a double-logarithmic plot showing the changes of the distribution with the direction of growth every 60 sections (corresponding to a step size of 38.94 μm). In both figures, the data points of the first and the last size distribution are connected by dashed lines. The linear least squares fit in Fig. 2d represents an envelope to the numerical data.24 In Fig. 2c, this unique curve, Fe(R), touches every single size distribution in exactly one point. It is very interesting to note that theoretically the envelope Fe(R) is proportional to R−(d+1). In the present case, the exponent is −2.9924 ± 0.0838, which represents a two-dimensional microstructure (d = 2). Moreover, the Weibull distribution function, which was previously proposed to describe two-dimensional grain growth, perfectly describes the scaled size distribution (Fig. 2b).25 Although the Weibull distribution is not physically motivated, it fits the numerical data of 2D grain growth.20,25
Aboav–Weaire-law
The self-similar state of ideal grain growth can be described by additional time-independent relationships. The Aboav–Weaire-law, derived in the early 1970s, offers a purely topological correlation between neighbouring crystals showing how grains in a polycrystalline network are arranged in space.26–28 It was successfully shown to describe a variety of cellular systems, such as nanocrystalline metals,29 colloidal soap froth structures30 and vegetable tissues.31The law states that the number of edges, n, of a grain is related to the average number of edges of all neighbouring grains, ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) , by the approximation
, by the approximation ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) ·n = 5n + 8. Based on Euler's theorem for planar graphs,32 Weaire27 extended this consideration taking the central second moment of the neighbour distribution, μ2 = 〈n2〉 − 〈n〉2, into account, thus yielding
·n = 5n + 8. Based on Euler's theorem for planar graphs,32 Weaire27 extended this consideration taking the central second moment of the neighbour distribution, μ2 = 〈n2〉 − 〈n〉2, into account, thus yielding ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) ·n = 5n + (6 + μ2). This extension takes into account that every two-dimensional cellular network can be characterized by its own distribution of the number of edges. Further studies formed what is known today as the Aboav–Weaire-law:28
·n = 5n + (6 + μ2). This extension takes into account that every two-dimensional cellular network can be characterized by its own distribution of the number of edges. Further studies formed what is known today as the Aboav–Weaire-law:28
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) ·n = (〈n〉 − α)n + (〈n〉α + μ2). ·n = (〈n〉 − α)n + (〈n〉α + μ2). | (4) |
In the present case, the predicted linear relation between the product of the average number of edges of all neighbouring prisms, ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) , and the number of edges of the corresponding central prism, n, versus n is indeed fulfilled in the three different sections (z1,z2,z3) in the prismatic layer (Fig. 3a). A linear least squares fit of the data from the section at z1 to eqn (4) yields α = 1.2028 ± 0.0217 and α = 1.2039 ± 0.0264 extracted from the first and the second term, respectively. This result is perfectly consistent considering that the two terms were fitted independently. Furthermore, the obtained average number of edges is 〈n〉 = 5.9930 ± 0.0217, which is again fully consistent with ideal growth.
, and the number of edges of the corresponding central prism, n, versus n is indeed fulfilled in the three different sections (z1,z2,z3) in the prismatic layer (Fig. 3a). A linear least squares fit of the data from the section at z1 to eqn (4) yields α = 1.2028 ± 0.0217 and α = 1.2039 ± 0.0264 extracted from the first and the second term, respectively. This result is perfectly consistent considering that the two terms were fitted independently. Furthermore, the obtained average number of edges is 〈n〉 = 5.9930 ± 0.0217, which is again fully consistent with ideal growth.
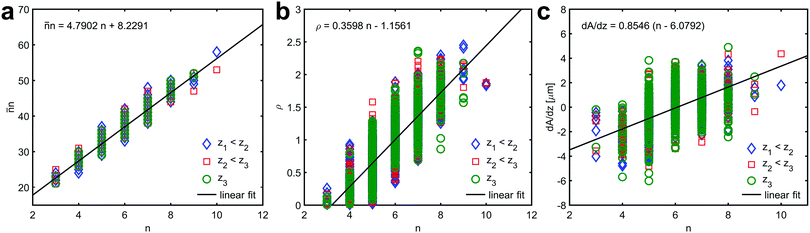 | ||
Fig. 3 Aboav–Weaire-law, Lewis-law and von Neumann–Mullins-law. (a) The relationship between the average number of edges in all neighbouring prisms, ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) , the number of edges, n, of the central prism at three different sections, z1 < z2 < z3, along the growth direction of the prismatic layer. The curve represents a fit of the data from the section at z1 to eqn (4) – Aboav–Weaire-law (the regression coefficient R2 is 0.9210). (b) The relationship between the scaled grain area, ρ = A/〈A〉, and the number of edges, n, at three different sections, z1 < z2 < z3, along the growth direction of the prismatic layer. The curve represents a fit of the data from the section at z1 to eqn (5) – Lewis-law (the regression coefficient R2 is 0.6996). (c) The relationship between prism area change rate and the number of edges, n, at three different sections, z1 < z2 < z3, along the growth direction of the prismatic layer. The curve represents a fit of the data from the section at z1 to eqn (6) – von Neumann–Mullins-law (the regression coefficient R2 is 0.3832). It is important to note, that the deviation from the predicted behaviour observed for n = 3, 9 and 10 is due to the limitation in data size and that the small values of the obtained regression coefficients are the result of naturally occurring vertical data spread. , the number of edges, n, of the central prism at three different sections, z1 < z2 < z3, along the growth direction of the prismatic layer. The curve represents a fit of the data from the section at z1 to eqn (4) – Aboav–Weaire-law (the regression coefficient R2 is 0.9210). (b) The relationship between the scaled grain area, ρ = A/〈A〉, and the number of edges, n, at three different sections, z1 < z2 < z3, along the growth direction of the prismatic layer. The curve represents a fit of the data from the section at z1 to eqn (5) – Lewis-law (the regression coefficient R2 is 0.6996). (c) The relationship between prism area change rate and the number of edges, n, at three different sections, z1 < z2 < z3, along the growth direction of the prismatic layer. The curve represents a fit of the data from the section at z1 to eqn (6) – von Neumann–Mullins-law (the regression coefficient R2 is 0.3832). It is important to note, that the deviation from the predicted behaviour observed for n = 3, 9 and 10 is due to the limitation in data size and that the small values of the obtained regression coefficients are the result of naturally occurring vertical data spread. | ||
Lewis-law
The relationship between grain size and grain topology is likewise expected to be time-independent during self-similar grain growth. Such a correlation is known as the Lewis-law:33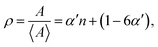 | (5) |
von Neumann–Mullins-law
In the same year in which Burke and Turnbull established their grain growth theory, von Neumann derived a fundamental equation for two-dimensional soap froth relating the rate of area change to the number of edges.34 Later Mullins generalized this idea to ideal grain growth in two dimensions35 yielding what is well-known today as the von Neumann–Mullins-law: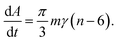 | (6) |
Conclusions
To conclude, the prismatic ultrastructure in the shell of A. vexillum is formed following thermodynamic, kinetic and topological models that were developed to describe the mechanism of ideal grain growth. The different considerations not only perfectly analytically describe the process of biomineralization of this morphology, but also independently yield similar thermodynamic parameters, such as the reduced mobility, mγ, and critical/average number of edges, 〈n〉. This consistency was never previously observed even in classical materials systems. This outcome not only provides key insights into biomineral morphogenesis, but is also of fundamental importance to the field of physics of materials. It is surprising that the epitome of a physically “ideal” construct is found in a living organism.Experimental section
Electron microscopy
Samples of the shell A. vexillum from the Caubian deep in the Philippines (purchased from Concology, Inc.) were imaged using Scios Dual Beam FIB/SEM (FEI). For fracture analysis, a segment of the shell was suspended in liquid nitrogen and then manually broken. For cross-section analysis, the samples were embedded in PMMA and then cut and diamond polished parallel and perpendicular to the direction of growth. The samples were sputtered with palladium before imaging.Synchrotron-based microtomography
The 3D spatial arrangement of the prismatic architectures was imaged by synchrotron-based microtomography at beamline ID19 of the ESRF in Grenoble (France). A part taken from the main body of the shell was grinded into a 3 mm long cylinder with a diameter of approximately 1 mm. The cylinder was mounted inside the measurement chamber with the long axis of the prisms co-aligned with the rotation axis of the stage, perpendicular to the incident X-ray beam. The samples were scanned using an X-ray photon energy of 34 keV at a sample-detector distance of 91 mm. A total of 5000 radiographic projection images were recorded over 180 degrees with an exposure time of 0.1 s and an effective pixel size of 0.649 μm. ESRF in-house code (PyHST2) was used to reconstruct the data. Prism boundaries were enhanced by means of Paganin-based filtering with a delta/beta ratio of 300.Image analysis
Two-dimensional microtomography sections were analysed using MatLab. The digital images were converted into binary images using a watershed algorithm separating the grains from the boundary network. The areas of the prisms as well as the number of edges and neighbouring prisms were measured using an in-house MatLab code. The code can be made available upon request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
I. Z. acknowledges the financial support provided by Bundesministerium für Bildung und Forschung (BMBF) through grant 03Z22EN11. We acknowledge Dr Alexander Rack (ID19, ESRF, Grenoble, France) and Dr Vanessa Schoeppler (B CUBE – Center for Molecular Bioengineering, Technische Universität Dresden, Germany) for their support during microtomography measurements and Dr Elke Reich (B CUBE – Center for Molecular Bioengineering, Technische Universität Dresden, Germany) for her support in electron microscopy. We acknowledge the European Synchrotron Radiation Facility for beamtime allocation on beamline ID19.Notes and references
- W. D. Callister and D. G. Rethwisch, Materials science and engineering, Wiley, New York, 2014 Search PubMed.
- S. M. Allen and E. L. Thomas, The structure of materials, Wiley, New York, 1999 Search PubMed.
- D. Zöllner, Reference Module in Materials Science and Materials Engineering, 2016 Search PubMed.
- F. J. Humphreys, Acta Mater., 1997, 45, 4231–4240 CrossRef CAS.
- G. Gottstein and L. S. Shvindlerman, Grain boundary migration in metals, CRC Press, Boca Raton, 1999 Search PubMed.
- C. V. Thompson, Solid State Physics, 2001, vol. 55, pp. 269–314 Search PubMed.
- H. V. Atkinson, Acta Metall., 1988, 36, 469–491 CrossRef CAS.
- C. S. Smith, Metall. Rev., 1964, 9, 48 Search PubMed.
- B. Bayerlein, P. Zaslansky, Y. Dauphin, A. Rack, P. Fratzl and I. Zlotnikov, Nat. Mater., 2014, 13, 1102–1107 CrossRef CAS PubMed.
- D. Zöllner, E. Reich and I. Zlotnikov, Cryst. Growth Des., 2017, 17, 5023–5027 CrossRef.
- I. Zlotnikov and V. Schoeppler, Adv. Funct. Mater., 2017, 1700506 CrossRef.
- E. Reich, V. Schoeppler, R. Lemanis, E. Lakin, E. Zolotoyabko, D. Zöllner and I. Zlotnikov, Acta Biomater., 2019, 85, 272–281 CrossRef PubMed.
- N. A. J. M. Sommerdijk and M. Cusack, Nat. Mater., 2014, 13, 1078–1079 CrossRef CAS PubMed.
- C. V. Thompson, Annu. Rev. Mater. Sci., 1990, 20, 245–268 CrossRef CAS.
- K. Barmak, E. Eggeling, D. Kinderlehrer, R. Sharp, S. Ta’asan, A. D. Rollett and K. R. Coffey, Prog. Mater. Sci., 2013, 58, 987–1055 CrossRef CAS.
- J. Burke and D. Turnbull, Prog. Met. Phys., 1952, 3, 220 CrossRef CAS.
- E. L. Holmes and W. C. Winegard, Acta Metall., 1959, 7, 411–414 CrossRef CAS.
- H. H. G. Jellinek and V. K. Gouda, Phys. Status Solidi, 1969, 31, 413–423 CrossRef CAS.
- P. Streitenberger and D. Zöllner, Acta Mater., 2011, 59, 4235–4243 CrossRef CAS.
- D. Zöllner, Comput. Mater. Sci., 2016, 118, 325–337 CrossRef.
- J. E. Burke, Trans. Metall. Soc. AIME, 1949, 180, 73–91 Search PubMed.
- W. W. Mullins, J. Appl. Phys., 1986, 59, 1341 CrossRef CAS.
- O. Hunderi and N. Ryum, J. Mater. Sci., 1980, 15, 1104–1108 CrossRef.
- P. Streitenberger and D. Zöllner, Acta Mater., 2015, 88, 334–345 CrossRef CAS.
- W. Fayad, C. V. Thompson and H. J. Frost, Scr. Mater., 1999, 40, 1199–1204 CrossRef CAS.
- D. A. Aboav, Metallography, 1970, 3, 383–390 CrossRef CAS.
- D. Weaire, Metallography, 1974, 7, 157–160 CrossRef.
- D. A. Aboav, Metallography, 1980, 13, 43–58 CrossRef.
- D. Zöllner, Comput. Mater. Sci., 2013, 79, 759–762 CrossRef.
- S. J. Mejía-Rosales, R. Gámez-Corrales, B. I. Ivlev and J. Ruiz-García, Phys. A, 2000, 276, 30–49 Search PubMed.
- J. C. M. Mombach, M. A. Z. Vasconcellos and R. M. C. D. Almeida, J. Phys. D: Appl. Phys., 1990, 23, 600–606 CrossRef.
- D. B. West, Introduction to graph theory, Prentice Hall, 1996 Search PubMed.
- F. T. Lewis, Anat. Rec., 1931, 50, 235–265 CrossRef.
- J. von Neumann, in Metal Interfaces, ed. C. Smith, American Society forMetals, Clevelend, Ohio, 1952 Search PubMed.
- W. W. Mullins, J. Appl. Phys., 1956, 27, 900–904 CrossRef.
| This journal is © The Royal Society of Chemistry 2019 |