Making metals linear super-elastic with ultralow modulus and nearly zero hysteresis

Abstract

We demonstrate a novel materials design approach to achieve unprecedented properties by utilizing nanoscale chemo-mechanical coupling. In particular, by using computer simulations we demonstrate how to engineer ultralow modulus (12 GPa), nearly hysteresis-free, and linear super-elastic metals with a giant elastic strain limit (2.7%) by creating appropriate concentration modulations (CMs) at the nanoscale in the parent phase and by pre-straining to regulate the stress-induced martensitic transformation (MT). The nanoscale CMs created via spinodal decomposition produce corresponding phase stability modulations, suppress autocatalysis in nucleation, impose nano-confinements on growth, and hinder long-range ordering of transformation strain during the MT, which changes the otherwise sharp first-order transition into a smeared, macroscopically continuous transition over a large stress range. The pre-straining generates retained martensitic particles that are stable at the test temperature after unloading and act as operational nuclei in subsequent load cycles, eliminating the stress–strain hysteresis and offering an ultralow apparent Young's modulus. Materials with a high strength and an ultralow apparent Young's modulus have great potential for application in orthopaedic implants.

---

Conceptual insights

An ideal orthopaedic implant should have an elastic modulus similar to that of natural bones to ensure remodeling of the latter under physiological conditions. However, the current generation of orthopaedic implants, such as the Ti-alloys, have a much higher modulus and, as a consequence, much of the load is transmitted through the implants rather than through the natural bones surrounding them, leading to bone degradation. On the other hand, the current generation of shape memory alloy actuators such as TiNi based alloys suffer from low efficiency and a lack of precise position control caused by large hysteresis and strongly non-linear elasticity. In this study, we demonstrated a novel materials design concept to achieve a combination of unprecedented properties, including an ultralow-modulus matching that of natural bones and almost zero hysteresis and linear super-elasticity, by intentionally creating nanoscale composition modulations via spinodal decomposition, that help stabilize but also confine the growth and limit the retreat of stress-induced martensitic domains. The compositional wavelength and amplitude are tuned such that after “training”, the martensite nuclei can march and retreat in an ordered fashion upon loading/unloading, and do not have to be nucleated a new each time.

Reducing the modulus of the current generation of metallic orthopaedic implants (such as the Ti-alloys) to match that of natural bones (∼20 GPa) is critical for avoiding the long standing “stress shielding” problem in bone implant applications,^1–3 but it imposes a great challenge to physical metallurgy.^4–6 According to Frenkel,⁴ the ideal strength of a ductile material is about 10% of the Young's modulus and most metals yield at a hundredth of their ideal strength. The typical yield strength of Ti-alloys is in the order of 1000 MPa. Thus, a 20 GPa modulus would imply that the alloy would yield at approximately 50% of its ideal strength.

Besides true elasticity, however, an alternative recoverable-strain carrier in materials, which is free from such limits, is the pseudo- or super-elasticity related to reversible stress-induced structural phase transformations, such as martensitic transformations (MTs) in ferroelastic materials.^7–9 Several breakthroughs have been made recently^10–14 in reducing the apparent modulus of metallic alloys using these structural phase transformations. For example, the so-called Gum Metals,¹² while having a strength of approximately 1200 MPa, show a modulus as low as ∼56 GPa, with a large recoverable strain limit of ∼2.5%. The other example is NICSMA¹³ (nanowire in situ composite with shape memory alloy), that has a strength of ∼1650 MPa, but shows a modulus of ∼28 GPa. Although these apparent moduli are still higher than that of natural bones, and NICSMA is not suitable for orthopaedic applications owing to the toxic Ni element, these studies^13,15–19 have demonstrated a true opportunity to engineer super-strong, almost hysteresis-free and linear super-elastic, and ultralow-modulus materials through MTs. In addition, MTs also offer many other novel physical and functional properties that are absent in non-transforming materials, including the shape memory effect²⁰ and Invar and Elinvar anomalies.^12,17 These extraordinary properties open up new avenues, not only for biomedical applications, but also for many other important technological fields such as space sciences,⁷ aviation and transportation,²¹ micro-electro-mechanical systems,²² and so forth.

Being first-order in nature, MTs usually exhibit a large hysteresis in stress–strain (SS) curves, consisting of an intrinsic linear elasticity of the parent phase with a high Young's modulus, followed by a stress-plateau before reaching the intrinsic linear elasticity of the martensitic phase. This large hysteresis is the origin of low efficiency (less than 1%) of shape memory alloy (SMA) actuators, and the strong non-linearity makes precise position control of SMA actuators difficult.²² Obviously this SS behaviour is completely opposite to the ultralow-modulus, hysteresis-free and linear super-elastic properties desired. Extensive efforts have been made in recent years to alter the characteristics of MTs to achieve desirable mechanical responses. For example, it has been shown that the hysteresis and nonlinearity of the pseudo-elasticity of ferroelastic materials could be reduced by cold-working,^{12,14,23–28} reducing the structural anisotropy of the martensitic phase,²⁹ introducing elastic and inelastic strain matching in a nanocomposite,¹³ introducing nano-precipitates in the parent phase,^30–33 suppressing the MTs into the so-called strain glass transitions,^34,35 improving the geometrical compatibility between the parent and martensitic phases through alloying,³⁶ and by using transformation pathway engineering.^37,38 Although the hysteresis and nonlinearity of pseudo-elasticity are reduced effectively through these efforts, the apparent Young's modulus is still significantly higher than that of the natural bone, the SS hysteresis loops are still far from vanishing, and materials that can satisfy the cofactor condition are rather limited. It should be noted that to distinguish the combined intrinsic elasticity and pseudo-elasticity from the intrinsic elasticity, we refer to the elastic modulus associated with the former as the apparent Young's modulus.

We have noticed that miscibility gaps widely exist in ferroelastic systems, including Ti–Nb,¹⁸ Mn–Cu,³⁹ Ti–V,⁴⁰ and Fe–Mn,⁴¹ in which spinodal decompositions in the parent phase produce concentration modulations (CMs) at nanoscale (with wavelengths ranging from several to several hundreds of nanometres). Based on the fact that the MTs starting temperature (M_s) is a strong function of the alloy composition,^42,43 we hypothesize that the nanoscale CMs produced by spinodal decomposition in the parent phase would behave like a three-dimensional (3D) interpenetrating multi-layer “nanocomposite” (see Fig. 1b and 2(a2)) with a systematic variation in the M_s and, hence, would effectively impose a nano-confinement to the martensitic transformation (MT) and significantly alter its characteristics. As a matter of fact, our recent computer simulations⁴⁴ have shown that the overall MT characteristics can be tuned effectively from a typically first-order transition to a high-order like continuous transition by a concentration modulation (CM) produced by spinodal decomposition, and recent experimental observations^18,39 also seem to support this hypothesis. However, the SS curves obtained in the previous study⁴⁴ are far from linear, the hysteresis is far from zero and the apparent Young's modulus (for a single crystal) is limited to 29.3 GPa (see Fig. S2, ESI†). In this study, we demonstrate how to simultaneously achieve an ultralow apparent Young's modulus (12 GPa), almost zero hysteresis and linear super-elasticity with a large elastic strain limit (see Fig. S2 for comparison, ESI†) by taking advantage of a synergic effect between the CM and pre-straining, that is, by adjusting the CM to introduce pre-existing martensitic nuclei via pre-straining to circumvent the nucleation events during the MT.

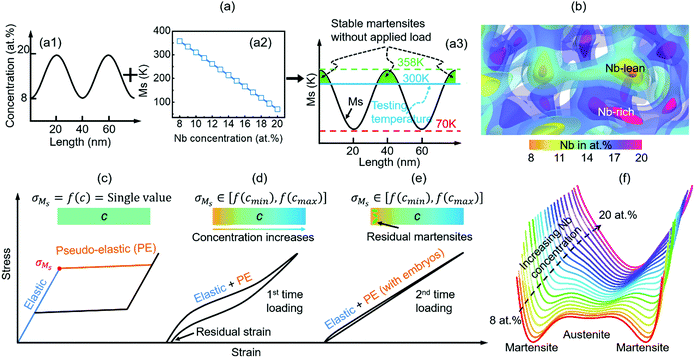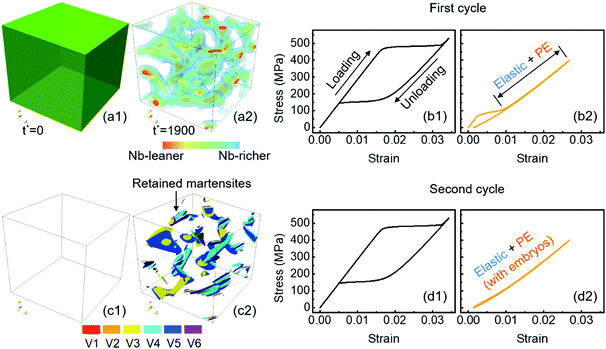
Fig. 1 Design of the nanoscale concentration modulated ferroelastic material (CMFM) and the effect of pre-straining. (a1) Schematic drawing of the nanoscale concentration variation in a CMFM. (a2) Dependence of M_s on the Nb concentration. (a3) Schematic drawing of the M_s modulation in the CMFM. Regions with M_s above the testing temperature are highlighted in green, within which martensite is thermodynamically stable. (b) Iso-surface Nb concentration contours of a local region in the computational cell shown in Fig. 2(a2), revealing an onion-like CM structure. Schematic drawing of the SS curves for: (c) a ferroelastic system having a uniform Nb concentration; (d) CMFM; and (e) pre-strained CMFM. (f) The Landau free energy curves as function of Nb concentration.

Fig. 2 Comparison of the characteristics of MTs in Ti2448 single crystals having (a1) a uniform and (a2) a modulated Nb concentration. The Nb concentration modulation shown in (a2) (represented by four iso-surface concentration contours marked by different colours) is obtained by spinodal decomposition in the parent phase at 773 K for a reduced time of 1900. (b1 and b2) The corresponding first loading–unloading SS curves under uniaxial tension along [001]. (c1 and c2) The corresponding microstructures after the unloading of the first loading–unloading cycle shown in (b1) and (b2). (d1 and d2) The corresponding SS curves of the second loading–unloading cycle of the two systems. The first loading–unloading cycle is referred to as pre-straining in the present study.

The model alloy system considered in this demonstration is the same as that considered in our previous study,⁴⁴ that is, Ti2448 (short for Ti–24Nb–4Zr–8Sn–0.1O in wt%) and the concentration dependent critical stress, σ_Ms, for the stress-induced MT and stress-free transformation strains (SFTS) are available in the literature^43,45–49 and are shown in Fig. S3 (ESI†). CMs in the parent phase of Ti2448 produced by spinodal decomposition have been reported in recent studies.^18,50 According to these experimental studies, we first designed the amplitudes and wavelengths of the CMs by controlling the ageing temperature and the time duration of the spinodal decomposition to: (i) produce a 3D interconnected, onion-like layered structure (as shown in Fig. 1b) at nanoscale in the parent phase; and (ii) ensure a small fraction of the parent phase has a M_s above the testing temperature, as illustrated in Fig. 1a and b. The alloy of such a nonuniform composition will no longer have a single value of σ_Ms (see Fig. S3, ESI†) and the corresponding Landau free energy surface is shown schematically in Fig. 1f. The stress-induced MT will start from the layer having the lowest value of σ_Ms and spread gradually to the adjacent layers as the applied load increases. Thus, the stress-induced MT is expected to take place continuously over a broad range of stress, which is in sharp contrast to the characteristics of MTs in systems having a uniform composition and thus a single-value of σ_Ms, as shown in Fig. 1c. Furthermore, the transformed layers will shed the load incrementally onto the un-transformed layers during loading, realizing the elastic strain limits of the parent phase far beyond that at the yield point of a bulk counterpart that has the same, but a uniform composition. This is similar to the transformation strain–elastic strain matching achieved in NICSMA.¹³ In this way, the SS curve will show an integrated elastic and pseudo-elastic characteristic, as illustrated in Fig. 1d.

Furthermore, if the minimum value of σ_Ms could be further reduced, the elastic and pseudo-elastic deformation will occur simultaneously at the onset of loading and, thus, the SS curve will become linear and hysteresis-free, and be accompanied by an ultralow apparent Young's modulus. This goal may be achieved if martensitic particles pre-exist in the alloy and serve as operational nuclei (i.e., over the critical nucleus size) and are ready to grow when an external load is applied. This is because the critical stress required for growth (e.g., the Peierls stress for glissile interface migration⁵¹) is much lower than that required for nucleation. Such pre-existing martensitic particles could be introduced by: (i) ensuring a small fraction of the compositional nanodomains in the parent phase have a M_s above the testing temperature (as illustrated in Fig. 1a and b); and (ii) pre-straining (similar to the pre-straining effect on NICSMA¹³) to help these domains to overcome their metastability and become stable operating martensitic nuclei in subsequent loading–unloading cycles. Fig. 1e schematically shows the SS curve of a pre-strained and CM sample, exhibiting an ultralow modulus, a linear pseudo-elasticity and an almost zero hysteresis.

To test the above hypothesis, phase field simulations were carried out for a multifunctional β TiNb-base alloy, Ti2448, in which the β parent phase (BCC, point group m3̄m) transforms into an α′′ martensite (orthorhombic, point group mmm) under stress.⁵² A large miscibility gap exists in the Ti–Nb system, with a spinodal range between ∼10 to ∼90 at% of Nb.⁵³ In particular, a concentration modulation of Nb between 8 and 20 at% has been observed experimentally in Ti2448.¹⁸ Fig. S3 (ESI†) shows the concentration dependences of σ_Ms and the SFTS of Ti2448,^54,55 in which the amplitude of the Nb CM is obtained from the experimental measurements.¹⁸ Parameters in the free energy models, including the expansion coefficients in the Landau free energy for the MT and in the chemical free energy of the parent phase for the spinodal decomposition, are determined by fitting the simulation results of: (i) the SS curve of a homogeneous system; and (ii) the CMs produced by the spinodal decomposition to the corresponding experimental observations (see ESI† for the development of the phase field model based on the combination of Landau theory,⁵⁶ gradient thermodynamics,⁵⁷ and Khachaturyan–Shatalov's microelasticity theory⁵⁸).

Fig. 2(a1 and a2) show the Nb concentration in an initially homogenous (before decomposition) and spinodally decomposed Ti2448 single-crystal computational cell (with a size of 128 × 128 × 128 nm), respectively. In the latter the CM corresponds to the spinodal decomposition in Ti2448 taking place at 773 K for a reduced time of t* = 1900. The SS curve of the uniform system at room temperature obtained by uniaxial tension along [001] is shown in Fig. 2(b1), which is characterized by a typical hysteresis with a stress plateau that is frequently observed in experiments.⁵⁹ In CMFM (Fig. 2(a2)), the Nb-lean and Nb-rich regions form a typical interpenetrating domain network from the spinodal decomposition. Owing to the CM in the parent phase, the hysteresis associated with the stress-induced MT is reduced drastically, as shown in Fig. 2(b2), indicating that the mechanical behaviour of the alloy depends strongly on the CM. An interesting observation in Fig. 2(b2) is that the SS curve, after the stress plateau, becomes almost linear and hysteresis-free. This finding implies that an almost linear pseudo-elasticity in the entire stress or strain range could be achieved if the initial hysteresis could be eliminated. We demonstrate below that this can be achieved by pre-straining.

From Fig. 2(c1 and c2) and Fig. S4 (ESI†), we find a key difference between the microstructures after the unloading of the first loading cycle in the compositionally homogeneous and modulated systems, that is, there are abundant retained martensitic particles in the latter, as shown in Fig. 2(c2) and Fig. S4 (ESI†). Furthermore, the amount of retained martensite after the first loading–unloading cycle increases with increasing ageing time held for the spinodal decomposition in the parent phase. This is because the martensitic phase is more stable in the Nb-lean regions, as indicated in Fig. S3 (ESI†) and Fig. 1f, and the volume fraction of the Nb-lean regions increases with increasing ageing time (see Fig. S5 and S6, ESI†). A greater amount of retained martensite corresponds to a larger irrecoverable strain during the first loading–unloading cycle, as shown in Fig. 2(b2) and 3a. However, if we use the first loading–unloading cycle as pre-straining (or training), then the retained martensitic particles will serve as operational nuclei and grow directly in subsequent loadings and, hence, eliminate the initial large hysteresis. This is exactly what we have observed from the SS curves obtained during the second loading–unloading cycle shown in Fig. 2(d2) and 3b. For example, these SS curves are almost hysteresis-free and almost linear. Moreover, the SS curves exhibit large elastic strains, for example, 2.7% at 400 MPa as shown in Fig. 2(d2). The stress-free transformation strain in the loading direction for a compositionally homogeneous system is 2.9% (see Fig. 2(b1)). The elastic strain limit of the CM system is expected to be even higher because, as mentioned earlier, the onion-like layered nanocomposite should be able to realize elastic strain limits far exceeding that of the bulk counterpart that has a uniform composition.

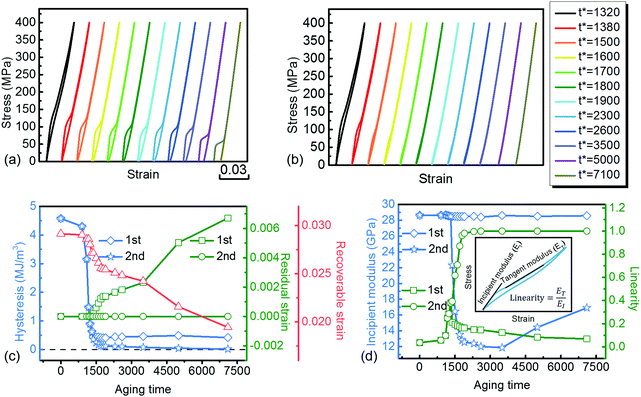Fig. 3 Mechanical properties of CM Ti2448 systems obtained with different ageing times used for the spinodal decomposition heat treatment of the parent phase. SS curves of the various CM systems obtained for: (a) the first and (b) the second load cycle. The detailed shapes of the concentration waves in 1D obtained for all of the ageing times can be found in Fig. S5 (ESI†). (c) The hysteresis area, residual strain and recoverable strain and (d) the incipient modulus and linearity index found in the various CM systems. These properties are obtained from quantitative analyses of the SS curves presented in (a) and (b) for the first and second loading–unloading cycles. The incipient modulus and linearity are defined in the inset of (d). Note that the incipient modulus and tangent modulus describe the modulus of different parts of the non-linear SS curves. When the SS curves are linear, these two moduli become the same and are equal to the apparent Young's modulus.

Fig. S7(b1–b10) and S8(c1–c10) (ESI†) show the microstructure evolutions corresponding to the loading and unloading points marked on the first and second loading–unloading SS curves of Fig. S7a and S8a (ESI†), respectively, for an alloy that has an average CM wavelength of ∼44 nm after ageing at 773 K for t* = 1900. The detailed shapes, including the wavelengths and amplitudes of the concentration waves in 1D obtained for all of the ageing times can be found in Fig. S6a (ESI†). The Supplementary Movie (ESI†) shows the entire evolution process of the microstructure corresponding to the SS curves. As we can see from these figures and the Supplementary Movie (ESI†), the almost linear pseudo-elasticity is associated with gradual growth (by both extension of the existing disks of individual martensitic variants) and addition of more disks in self-accommodation configurations (as shown in Fig. S8(e1–e4) and (e5–e8), ESI†), and shrinkage (in the opposite manner) of the self-accommodating multi-variant martensitic domains upon loading and unloading, respectively. Comparing Fig. S7(b4, b5) and S8(c3–c5) with Fig. S7(b6, b7) and S8(c6–c8) (ESI†), we can see that the microstructures corresponding to the five points on the unloading curves are almost the same as those corresponding to the five points on the loading curves (Fig. S7a and S8a, ESI†). Upon loading there is always a retained parent phase, while upon unloading there is always a retrained martensite. This reversible evolution of the microstructure underlies the almost hysteresis-free linear pseudo-elasticity. The hysteresis and nonlinearity seen in the first loading–unloading cycle are caused by the initial irreversible evolution of the microstructure (see, for example, the retained martensite in Fig. S7(b10) and S8(c1), which does not exist in Fig. S7(b1), ESI†).

Fig. 3a and b show the SS curves obtained during the first and second loading–unloading cycle, respectively, for systems aged for different times during the spinodal decomposition, and Fig. 3c and d show the corresponding quantitative analyses of the SS curves, including the hysteresis area, residual strain, recoverable strain, incipient modulus (see inset in Fig. 3d for the definition), and linearity. After the first load cycle (i.e., the pre-straining), the hysteresis area reduces dramatically (by one order of magnitude), and the residual strain drops to zero. The residual strain increases rapidly as the ageing time (or CM amplitude and wavelength) increases. The systems remain super-elastic, although the recoverable strain gradually decreases with increasing ageing time. Ageing at 773 K for t* = 3500 (with an approximate wavelength of 50 nm) brings about the lowest incipient modulus of 12 GPa. Comparison of the modulus, elastic strain limit, hysteresis area and linearity of the super-elasticity between the predictions from the current study with those from state-of-the-art systems reported in the literature is shown in Fig. 4. It is readily seen that the CMFM outperforms the material systems reported in existing studies in terms of the ultralow modulus, small hysteresis area and linearity of the super-elasticity. The elastic strain limit of CMFM is smaller than those of the Ti–Ni SMAs, NICSMA and NCATB because the CMFM, being a TiNb-based SMA, has a smaller SFTS, as indicated by the difference in the super-elasticity between the Ti–Nb and Ti–Ni alloys shown in Fig. 4a. It is noteworthy that the CMFM exhibits a perfect combination of ultralow modulus, almost zero hysteresis and linear super-elasticity.

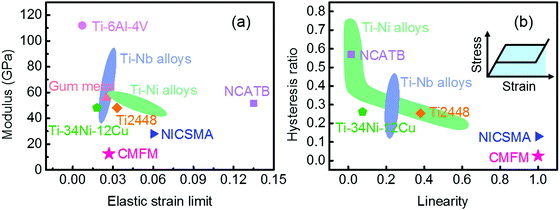Fig. 4 (a) Comparison of the modulus and elastic strain limit between predictions from the current study with those from state-of-the-art systems reported in the literature. Ti2448²³ is short for Ti–24Nb–4Zr–8Sn in wt%, NICSMA¹³ refers to nanowire in situ composite with SMA and NCATB⁶⁸ represents Fe–28Ni–17Co–11.5Al–2.5Ta–0.05B in at%. (b) Comparison of the hysteresis ratio and linearity. The definition of the hysteresis ratio is the ratio between the area encircled by the SS loop and the area under the SS curve, which is highlighted in blue in the inset of (b). The properties of CMFM are determined from the SS curve shown in Fig. 2(d2).

It should be noted that these simulation results were obtained for a single crystal with a tensile axis parallel to [001]. For polycrystalline systems, the incipient modulus will be higher. In a single crystal of Ti2448 considered in the current study, the pseudo-elastic strains (i.e., the transformation strains) along the [100], [110], and [111] directions are 1.4%, 2.2% and 0.8%, respectively.⁵⁹ The intrinsic elastic strains along these directions are 1.38%, 0.72%, and 0.46%, respectively, when loaded to 400 MPa.⁵⁹ Then, the apparent Young's moduli in these directions are 14.3 GPa, 13.7 GPa, and 31.7 GPa, respectively. Based on the rule of mixtures, the apparent Young's modulus of a polycrystal of CM Ti2448 can be estimated via the average of these three moduli of a single crystal and it is approximately 19.9 GPa. Ti2448 alloys with such a low modulus may have great potential for use in biomedical applications. It should be noted that the incipient modulus and tangent modulus are used to describe the elastic/pseudo-elastic modulus of different parts of the non-linear SS curves. They become the same and can be simply termed as the apparent Young's modulus when the SS curves become linear (see Fig. 3b).

To examine the stability of the pre-strained (trained) alloy, the third loading–unloading SS curve obtained for the alloy aged for t* = 1900 is shown in Fig. 5a, together with the SS curves from the first two load cycles. The SS curve of the third cycle coincides with that of the second one (see the inset in Fig. 5a), indicating that the mechanical behaviour of the alloy is stable after the pre-straining (i.e., the first load cycle). Microstructures at various loading–unloading states in the third cycle can be found in Fig. S8(d1–d10) (ESI†). When comparing the microstructures in Fig. S8(d1–d10) with those in Fig. S8(c1–c10) (ESI†), we found that the microstructures corresponding to the same points on the SS curves of the third and second loading–unloading cycles are almost identical. This observation is consistent with the quantitative comparison of the microstructure evolution processes obtained for the third and second load cycles shown in Fig. 5b, in which the volume fraction versus stress curve of the third load cycle coincides with that of the second cycle.

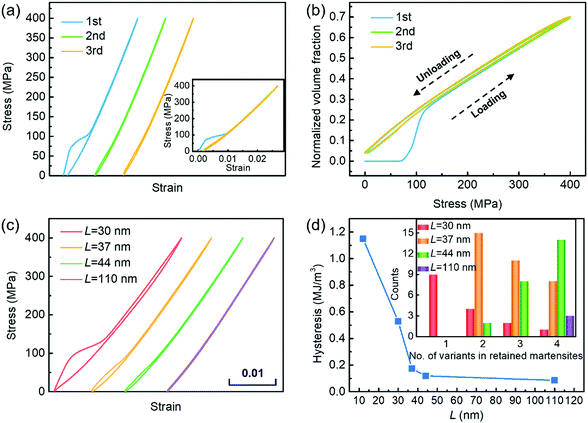Fig. 5 The stability of the pre-strained system and the influence of the CM wavelength. (a) SS curves and (b) normalized volume fraction of martensite during the first, second and third cyclic loading–unloading obtained for the CM system having a wavelength of ∼44 nm. The inset in (a) shows these SS curves without the horizontal offset. (c) SS curves of the concentration modulated systems with different wavelengths L obtained during the second loading cycle. (d) Variation of the hysteresis area of the SS curves shown in (c). The inset of (d) shows the distributions of martensitic domains having different numbers of variants in the pre-strained CM systems with different wavelengths L. CM in systems with different wavelength are shown in Fig. S11 (ESI†), and the concentration waves in the 1D version of these systems can be found in Fig. S10 (ESI†). These CMs having different wavelength are obtained by changing the gradient coefficients in the free energy model for the spinodal decomposition in the parent phase.

The retained martensitic particles shown in Fig. 2(c2) (and also Fig. S4, ESI†) consist of multi-variants in self-accommodating configurations. The degree of self-accommodation among different variants, determined by the number of variants that can be packed effectively in a given size of space, determines the stability of these martensitic particles and the hysteresis of the loading–unloading cycles. The interconnected Nb-rich nanodomain network (having a high σ_Ms) imposes a strong confinement on the MT in the Nb-lean regions (having a low σ_Ms). If the confinement is too small, then single-variant martensitic particles⁶⁰ may dominate the microstructure because, in this case, it is too costly to form a multi-variant configuration with inter-variant boundaries (domain walls).⁶¹ This is what was observed in a system with a spinodal CM wavelength ∼12 nm (see Fig. S9a, ESI†) and larger stresses are required for the formation of such non-self-accommodating, single-variant martensitic particles (compared to the SS curves shown in Fig. S8a and S9b, ESI†). The single-variant martensitic particles are able to induce the formation of self-accommodating twin variants only when the applied stress reaches a certain level, meaning that the size of the domains with σ_Ms below the applied stress becomes sufficiently large. This leads to a relatively large hysteresis (Fig. 5d and Fig. S9b, ESI†).

By systematically varying the CM wavelengths (e.g., from 12 to 110 nm, see Fig. S10, ESI†) (which can be easily realized in the experiment by controlling the aging temperature and time duration of the spinodal decomposition), we found that the configurations of the dominant martensitic particles retained after unloading during the first cycle change from a single-variant to a multiple-variant (inset of Fig. 5d) and that they are stable after unloading. The hysteresis of the corresponding SS curves (Fig. 5c) during the second loading–unloading cycle (i.e., after pre-straining) decreases monotonically towards zero (Fig. 5d) in the system with L ∼ 110 nm. It is interesting to note that only the self-accommodated 4-variant martensitic particles with herringbone structures are found in such a system (see the structure enclosed by a red circle in Fig. S11, ESI†). This is because a 4-variant herringbone configuration (Fig. S11, ESI†) has the highest geometric compatibility in this system^52,62 (see ESI,† Geometric Compatibility Analysis), and all of the Nb-lean regions are large enough to accommodate the 4-variant particles. Thus, different CMs will have different spatial confinements in terms of both the size (CM wavelength) and strength (CM amplitude) and are able to accommodate martensitic particles with different degrees of geometrical compatibilities, offering the flexibility to control the size of the hysteresis loop. Furthermore, as the CMs set up the spatial partitioning of the martensitic domains and the same partition repeats itself in the loading–unloading cycles after pre-straining, in principle we could precisely control this “seeding” process with well-ordered CM patterns produced by spinodal decomposition⁶³ to form “strain crystals” for the design of ferroelastic metamaterials.

It should be noted that the above simulations were carried out without considering the effects of other extended defects such as dislocations and grain boundaries. These defects may also contribute to the broadly smeared characteristics and reversibility of the MT. In addition, the Peierls stress (from lattice friction) for the migration of interfaces during the MT is ignored, which may make an additional contribution to the stress hysteresis when the interfaces are thin relative to the lattice spacing.⁹

Conclusions

In conclusion, we have demonstrated a novel approach to simultaneously achieve ultralow apparent Young's modulus, nearly hysteresis-free and linear super-elasticity with a large elastic strain limit in ferroelastic materials via regulating the martensitic transformation (MT) through nanoscale concentration modulations (CMs) generated by spinodal decomposition in the parent phase and pre-straining. In addition to the spinodal decomposition, nanoscale CM could be achievable by many other means, including multi-layer thin film processing techniques⁶⁴ for films, the accumulative roll-bonding process⁶⁵ for bulk materials, and the additive manufacturing technique,⁶⁶ for example, 3D printing, for components that have arbitrary and complicated shapes. Specifically, magnetron sputtering can generate films with a controllable CM along the thickness direction (i.e., 1D CM), and the thickness of each layer ranges from nanometres to microns. It is anticipated that a carefully designed 1D nanoscale CM would work equally well as the 3D CMs shown in this study in tuning the characteristics of the MT and the corresponding mechanical properties. Accumulative roll-bonding could be used to develop bulk CM materials by accumulatively rolling a set of sheets with different compositions. 3D printing produces naturally CM components because of its extremely high cooling rate and severe solute segregation in the inter-dendritic regions during solidification.

As ferroelectric⁶⁷ and ferromagnetic¹⁷ transitions share many common characteristics with the ferroelastic MTs, the approach demonstrated in the current study may open up a new avenue for the design of ferroelectric and ferromagnetic materials as well for unprecedented properties.

The ultralow apparent Young's modulus achieved in the present study may have a great potential for solving the long standing “stress shielding” problem in orthopaedic applications, which is the main factor slowing the recovery of patients and limiting the service life of the orthopaedic implants. Bones undergo constant remodelling under physiological conditions, which is carried out by osteoblast and osteoclast cells. Bone remodelling will not work properly if the bone is not under normal levels of load. The much higher modulus of the current generation of bone implants means that most of the load is transmitted through the implant material rather than through the natural bones surrounding it, leading to bone degradation. The elastic modulus estimated for this CM Ti2448 alloy, ∼20 GPa, match exactly to that of natural bones and, thus, could eliminate completely this stress-shielding problem.

Finally, the linear super-elasticity with a large elastic strain limit is attractive in a rich variety of applications, including sensors and high-efficiency and high-precision actuators.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

YG and YW acknowledge the financial support of the US Natural Science Foundation, Grant No. DMR-1410322, and the US Department of Energy, Grant No. DE-SC0001258; JL acknowledges support by NSF DMR-1410636; TY Zhang acknowledges the financial support of research grants (No. 15DZ2260300 and No. 16DZ2260600) from the Science and Technology Commission of Shanghai Municipality. D Wang acknowledges the National Key Research and Development Program of China (Grants No. 2016YFB0701302, 2014CB644003), the National Natural Science Foundation of China (Grants No. 51671156) and the Innovative Research Team in the University (Grants No. IRT13034). The work was also supported by the 111 project (No. D16002) from the State Administration of Foreign Experts Affairs, PRC.

References

1. M. Long and H. Rack, Biomaterials, 1998, 19, 1621–1639.
2. M. Niinomi and M. Nakai, Int. J. Biomater., 2011, 2011, 1–10.
3. M. Geetha, A. K. Singh, R. Asokamani and A. K. Gogia, Prog. Mater. Sci., 2009, 54, 397–425.
4. J. Frenkel, Z. Phys., 1926, 37, 572–609.
5. S. Ogata, Science, 2002, 298, 807–811.
6. J. Li, MRS Bull., 2007, 32, 151–159.
7. K. Otsuka and C. M. Wayman, Shape memory materials, Cambridge University Press, Cambridge, UK, 1998.
8. J. W. Christian, G. B. Olson and M. Cohen, Le J. Phys. IV, 1995, 5, C8-3–C8-10.
9. E. K. H. Salje, Annu. Rev. Mater. Res., 2012, 42, 265–283.
10. D. Kuroda, M. Niinomi, M. Morinaga, Y. Kato and T. Yashiro, Mater. Sci. Eng., A, 1998, 243, 244–249.
11. M. Niinomi, JOM, 1999, 51, 32–34.
12. T. Saito, T. Furuta, J.-H. Hwang, S. Kuramoto, K. Nishino, N. Suzuki, R. Chen, A. Yamada, K. Ito, Y. Seno, T. Nonaka, H. Ikehata, N. Nagasako, C. Iwamoto, Y. Ikuhara and T. Sakuma, Science, 2003, 300, 464–467.
13. S. Hao, L. Cui, D. Jiang, X. Han, Y. Ren, J. Jiang, Y. Liu, Z. Liu, S. Mao, Y. Wang, Y. Li, X. Ren, X. Ding, S. Wang, C. Yu, X. Shi, M. Du, F. Yang, Y. Zheng, Z. Zhang, X. Li, D. E. Brown and J. Li, Science, 2013, 339, 1191–1194.
14. S. Guo, Q. Meng, X. Zhao, Q. Wei and H. Xu, Sci. Rep., 2015, 5, 14688.
15. J. P. Cui, Y. L. Hao, S. J. Li, M. L. Sui, D. X. Li and R. Yang, Phys. Rev. Lett., 2009, 102, 1–4.
16. D. Wang, Y. Wang, Z. Zhang and X. Ren, Phys. Rev. Lett., 2010, 105, 205702.
17. D. Y. Cong, Y. D. Zhang, Y. D. Wang, M. Humbert, X. Zhao, T. Watanabe, L. Zuo and C. Esling, Acta Mater., 2007, 55, 4731–4740.
18. Y. L. Hao, H. L. Wang, T. Li, J. M. Cairney, A. V. Ceguerra, Y. D. Wang, Y. Wang, D. Wang, E. G. Obbard, S. J. Li and R. Yang, J. Mater. Sci. Technol., 2016, 32, 705–709.
19. R. J. Talling, R. J. Dashwood, M. Jackson and D. Dye, Acta Mater., 2009, 57, 1188–1198.
20. J. W. Christian, The Theory of Transformations in Metals and Alloys, Pergamon Press, Oxford, UK, 3rd edn, 2002.
21. D. J. Hartl and D. C. Lagoudas, Proc. Inst. Mech. Eng., Part G, 2007, 221, 535–552.
22. J. Mohd Jani, M. Leary, A. Subic and M. A. Gibson, Mater. Des., 2014, 56, 1078–1113.
23. Y. L. Hao, S. J. Li, S. Y. Sun, C. Y. Zheng and R. Yang, Acta Biomater., 2007, 3, 277–286.
24. T. Waitz, V. Kazykhanov and H. P. Karnthaler, Acta Mater., 2004, 52, 137–147.
25. T. Waitz, K. Tsuchiya, T. Antretter and F. D. Fischer, MRS Bull., 2009, 34, 814–821.
26. A. Ahadi and Q. Sun, Acta Mater., 2015, 90, 272–281.
27. H. Matsumoto, S. Watanabe and S. Hanada, Mater. Trans., 2005, 46, 1070–1078.
28. X. Zhang, W. Shyy and A. Marie Sastry, J. Electrochem. Soc., 2007, 154, A910.
29. W.-F. Rao, M. Wuttig and A. G. Khachaturyan, Phys. Rev. Lett., 2011, 106, 105703.
30. Y. Ji, X. Ding, T. Lookman, K. Otsuka and X. Ren, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 104110.
31. G. S. Bigelow, A. Garg, S. A. Padula II, D. J. Gaydosh and R. D. Noebe, Scr. Mater., 2011, 64, 725–728.
32. C. Chluba, W. Ge, R. Lima de Miranda, J. Strobel, L. Kienle, E. Quandt and M. Wuttig, Science, 2015, 348, 1004–1007.
33. L. Kovarik, F. Yang, A. Garg, D. Diercks, M. Kaufman, R. D. Noebe and M. J. Mills, Acta Mater., 2010, 58, 4660–4673.
34. X. Ren, in Disorder and Strain-Induced Complexity in Functional Materials, ed. T. Kakeshita, T. Fukuda, A. Saxena and A. Planes, Springer, Berlin, 2012, pp. 201–225.
35. X. Ren, Phys. Status Solidi, 2014, 251, 1982–1992.
36. R. D. James, Z. Zhang, R. D. James and Z. Zhang, in Magnetism and Structure in Functional Materials, ed. A. Planes, L. Manosa and A. Saxena, Springer, Berlin, 2005, pp. 159–175.
37. Y. Gao, L. Casalena, M. L. Bowers, R. D. Noebe, M. J. Mills and Y. Wang, Acta Mater., 2017, 126, 389–400.
38. Y. Gao, S. A. Dregia and Y. Wang, Acta Mater., 2017, 127, 438–449.
39. K. Tsuchiya, H. Sato, S. Edo, K. Marukawa and M. Umemoto, Mater. Sci. Eng., A, 2000, 285, 353–356.
40. J. L. Murray, Bull. Alloy Phase Diagrams, 1981, 2, 48–55.
41. F. Findik, Mater. Des., 2012, 42, 131–146.
42. J. Frenzel, E. P. George, A. Dlouhy, C. Somsen, M. F. X. Wagner and G. Eggeler, Acta Mater., 2010, 58, 3444–3458.
43. K. Otsuka and X. Ren, Prog. Mater. Sci., 2005, 50, 511–678.
44. J. Zhu, Y. Gao, D. Wang, T.-Y. Zhang and Y. Wang, Acta Mater., 2017, 130, 196–207.
45. H. Y. Kim, J. I. Kim, T. Inamura, H. Hosoda and S. Miyazaki, Mater. Sci. Eng., A, 2006, 438–440, 839–843.
46. E. W. Collings, A Sourcebook of Titanium Alloy Superconductivity, Springer US, Boston, MA, 1983.
47. H. H. Wu, A. Pramanick, Y. B. Ke and X. L. Wang, J. Appl. Phys., 2016, 120, 183904.
48. S. G. Cao, Y. Li, H. H. Wu, J. Wang, B. Huang and T. Y. Zhang, Nano Lett., 2017, 17, 5148–5155.
49. H.-H. Wu, J. Zhu and T.-Y. Zhang, Nano Energy, 2015, 16, 419–427.
50. H. L. Wang, Y. L. Hao, S. Y. He, K. Du, T. Li, E. G. Obbard, J. Hudspeth, J. G. Wang, Y. D. Wang, Y. Wang, F. Prima, N. Lu, M. J. Kim, J. M. Cairney, S. J. Li and R. Yang, Scr. Mater., 2017, 133, 70–74.
51. R. Peierls, Proc. Phys. Soc., 1940, 52, 34–37.
52. J. Zhu, H. Wu, D. Wang, Y. Gao, H. Wang, Y. Hao, R. Yang, T.-Y. Zhang and Y. Wang, Int. J. Plast., 2017, 89, 110–129.
53. D. L. Moffat and U. R. Kattner, Metall. Trans. A, 1988, 19, 2389–2397.
54. H. Y. Kim, Y. Ikehara, J. I. Kim, H. Hosoda and S. Miyazaki, Acta Mater., 2006, 54, 2419–2429.
55. T. Inamura, J. I. Kim, H. Y. Kim, H. Hosoda, K. Wakashima and S. Miyazaki, Philos. Mag., 2007, 87, 3325–3350.
56. L. D. Landau and E. M. Lifshitz, Statistical physics, Pergamon Press, Oxford, 1980.
57. J. W. Cahn and J. E. Hilliard, J. Chem. Phys., 1958, 28, 258.
58. A. G. Khachaturyan, Theory of Structural Transformations in Solids, John Wiley & Sons, New York, 1983.
59. Y. W. Zhang, S. J. Li, E. G. Obbard, H. Wang, S. C. Wang, Y. L. Hao and R. Yang, Acta Mater., 2011, 59, 3081–3090.
60. L. Liu, X. Ding, J. Li, T. Lookman and J. Sun, Nanoscale, 2014, 6, 2067–2072.
61. G. B. Olson and A. L. Roitburd, in Martensite: a tribute to Morris Cohen, ed. G. B. Olson and W. S. Owen, ASM International, Materials Park, OH, 1992, pp. 149–174.
62. K. Bhattacharya, Microstructure of Martensite: Why It Forms and How It Gives Rise to the Shape-Memory Effect, Oxford University Press, Oxford, 2003.
63. Y. Wang, L.-Q. Chen and A. G. Khachaturyan, Acta Metall. Mater., 1993, 41, 279–296.
64. P. J. Kelly and R. D. Arnell, Vacuum, 2000, 56, 159–172.
65. Y. Saito, H. Utsunomiya, N. Tsuji and T. Sakai, Acta Mater., 1999, 47, 579–583.
66. D. C. Hofmann, J. Kolodziejska, S. Roberts, R. Otis, R. P. Dillon, J.-O. Suh, Z.-K. Liu and J.-P. Borgonia, J. Mater. Res., 2014, 29, 1899–1910.
67. R. Xu, S. Liu, I. Grinberg, J. Karthik, A. R. Damodaran, A. M. Rappe and L. W. Martin, Nat. Mater., 2015, 14, 79–86.
68. Y. Tanaka, Y. Himuro, R. Kainuma, Y. Sutou, T. Omori and K. Ishida, Science, 2010, 327, 1488–1490.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8mh01141a

---