How to quantify isotropic negative thermal expansion: magnitude, range, or both?†
Chloe S.
Coates
and
Andrew L.
Goodwin
 *
*
Department of Chemistry, University of Oxford, Inorganic Chemistry Laboratory, South Parks Road, Oxford OX1 3QR, UK. E-mail: andrew.goodwin@chem.ox.ac.uk; Tel: +44 1865 272137
First published on 4th October 2018
Abstract
Negative thermal expansion (NTE) is the useful and counterintuitive material property of volume contraction on heating. Isotropic NTE is the rarest and most useful type, and is known to occur in a variety of different classes of materials. In this focus article we ask the simple question of how best to compare NTE behaviour amongst these different systems? We summarise the two main mechanisms for isotropic NTE, and illustrate how these favour alternatively NTE magnitude and NTE range. We argue in favour of a combined metric of NTE capacity, which balances both effects and allows unbiased identification of the most remarkable NTE materials, irrespective of the underlying microscopic mechanism at play. By organising known NTE materials according to these various metrics, we find intuitive trends in behaviour that help identify key materials for specific NTE applications.
Introduction
Negative thermal expansion (NTE) is a counterintuitive phenomenon whereby a material shrinks, rather than expands, with increasing temperature.1–5 It is allowed thermodynamically whenever a decrease in material volume couples to an increase in entropy.5,6 The main applications of NTE—be they in dental fillings,7,8 cooker hobs,9 or high-precision optics10—rely on exploiting this thermal volume contraction to counteract the much more usual positive thermal expansion (PTE) of ordinary materials. Consequently there is a strong drive within the field to discover systems with increasingly extreme NTE characteristics—the argument being that the stronger the NTE, the easier it is to compensate PTE within these composite materials.11–13What does it mean to say that NTE in one material is stronger than in another? Thermal expansion is usually quantified by the coefficient of thermal expansion
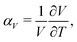 | (1) |
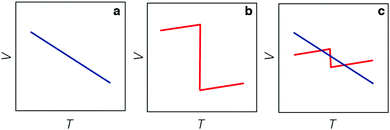
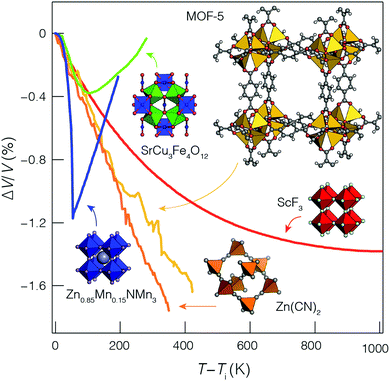
But the notion of comparing thermal expansion characteristics in terms of a volume derivative (1) becomes meaningless wherever NTE occurs across a first-order phase transition. In such cases, there is a discontinuity in the V(T) equation of state such that 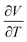 —and hence αV—diverges at some critical temperature Tc [Fig. 1]. By measuring molar volumes at sufficiently fine temperature intervals in the proximity of Tc it becomes possible to calculate values of αV of arbitrarily large magnitude. So αV alone cannot be a universal measure of the strength of NTE behaviour.
—and hence αV—diverges at some critical temperature Tc [Fig. 1]. By measuring molar volumes at sufficiently fine temperature intervals in the proximity of Tc it becomes possible to calculate values of αV of arbitrarily large magnitude. So αV alone cannot be a universal measure of the strength of NTE behaviour.
In practice, there are two key considerations when comparing the NTE performance of different materials. The first (and most frequently reported) is NTE magnitude as given by αV and outlined above. But the second is the temperature range ΔT over which NTE is observed. This range is important because different applications will demand fundamentally different thermal operating windows for NTE. The high-precision optics on satellites, for example, experience repeated thermal cycling between −75 and +135 °C.16,17 Whereas tooth enamel, by contrast, is exposed only to a substantially narrower temperature range around 37 °C.
Fig. 2 shows some of the variety of thermal expansion behaviour observed experimentally for different types of NTE materials. Some systems, such as the antiperovskite Zn0.85Mn0.15NMn3, show very abrupt NTE effects with a narrow ΔT. While others, such as ScF3, show a much more gradual effect that nonetheless persists over a very broad temperature range. How should we understand such variety, and how should we best compare the NTE characteristics of these ostensibly very different systems?
 | ||
| Fig. 2 Temperature-dependent volume strains in a variety of NTE materials: the magnetic antiperovskite Zn0.85Mn0.15NMn3 (blue points);18 the charge-transfer ceramic SrCu3Fe4O12 (green points);19 the metal–organic framework MOF-5 (yellow points);20 anticuprite structured Zn(CN)2 (orange points);21 and the A-site-deficient perovskite ScF3 (red points).22 Data are given for temperatures relative to the onset temperature Ti of NTE. | ||
There are, in practice, two fundamental mechanisms responsible for NTE that divide these various materials into two classes.5,13,23,24 In the first class are materials for which NTE is driven by phonons; in the second are those for which NTE results from an electronic transition involving e.g. magnetic or charge order. In this focus article we survey key materials in both groups, with the objective of comparing the magnitude and range of NTE in different systems. Our focus is entirely on crystalline materials with isotropic NTE—i.e. systems with cubic crystal symmetry. This choice facilitates comparison amongst different compounds, and also allows us to cast aside the role of elastic anisotropy that is crucial whenever NTE arises from elastic coupling to PTE in other directions (e.g. in ferroelectrics and/or across ferroelastic phase transitions).13,25,26 We will come to show that (i) phonon NTE mechanisms maximise ΔT, (ii) electronic-transition NTE mechanisms maximise the magnitude of αV (albeit at the expense of ΔT), and (iii) an Ashby-style analysis27,28 of various NTE materials partitions these systems naturally according to their underlying chemistry, with the most important NTE candidates emerging as those for which the product of −αV and ΔT is largest.
Maximising range: phonon-mediated NTE
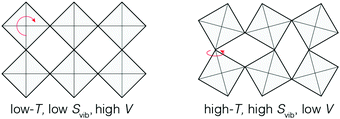
Phonon-mediated NTE is the dominant mechanism amongst network materials; i.e. open structures with directional covalent bonding.5,23 The canonical system of this type is ZrW2O8.3,29 On the very simplest level, its NTE is driven by transverse vibrations of Zr–O–W linkages: displacement of the O atom away from the Zr⋯W axis reduces the distance between Zr and W atoms, and hence the overall volume. This local mechanism is sometimes called the ‘tension effect’,30 and is implicated in one form or another in nearly all phonon-mediated NTE materials. In the case of ZrW2O8, local transverse displacements couple together to give a particularly complex set of NTE phonons,31–33 such that the collective mechanism for NTE involves a combination of translations, rotations, and deformations of ZrO6 and WO4 polyhedra towards a denser state.34,35 A simpler but conceptually-related mechanism operates in ScF3, where the key NTE phonons involve correlated rotations of connected ScF6 octahedra [Fig. 3].Whatever their particular form, NTE phonons have a clear thermodynamic signature in that their associated Grüneisen parameter36
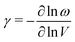 | (2) |
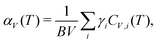 | (3) |
Some of the earliest examples of phonon-mediated NTE materials include families of transition-metal oxides, which display moderate NTE of a similar magnitude to conventional positive thermal expansion materials. The structures of these various systems tend to consist of corner-sharing polyhedra: for example, corner-sharing tetrahedra in the β-cristobalite polymorph of SiO2 (αV = −6.9(6) MK−1),39 octahedra in ReO3 (αV = −3(3) MK−1),40,41 and a combination of the two in ZrW2O8 (αV = −26.1 MK−1).34,42 As we have already seen, the fluoride perovskite ScF3 is structurally similar, and its NTE (αV = −12.3 MK−1) persists from 10 to 1000 K.22 Zeolites—with their open network structures assembled from corner-linked AlO4 and SiO4 tetrahedra—are another relevant family of this type, and many of these technologically important materials do indeed show NTE.43,44 The key point here is that many open-framework oxide/fluoride frameworks tend to show moderate NTE (αV ≃ −10 MK−1; the moderacy itself reflecting the stiffness of metal–O/F interactions and thus a larger B), but this NTE can be sustained over a large temperature range, with 〈ΔT〉 = 375 K.
There are two important ramifications of replacing the monatomic M–O/F–M linkages of these ceramic NTE materials with molecular anionic linkers, such as in Zn(CN)2 or the broad family of metal–organic frameworks (MOFs). The first is that the number of phonon modes with NTE characteristics increases; this has the effect of amplifying the sum in eqn (3). The second is that molecular frameworks tend to contain more open space, and as such are more flexible; this has the effect of reducing the elastic stiffness as measured by B. Both effects make αV increasingly negative, and so one anticipates increasingly strong NTE behaviour in molecular framework materials with open structures.
This expectation is indeed borne out in practice. A good example is that of Zn(CN)2, the diamondoid structure of which is closely related to that of β-cristobalite.21,45–47 Whereas NTE modes in the latter involve only counter-rotation of neighbouring tetrahedra,48,49 the former has access to a broad spectrum of NTE modes extending well beyond the cristobalite modes to include same-sense-rotations and rigid-unit translations.21,50–52 This difference in density of NTE modes translates to an order-of-magnitude increase in |αV|.53 Further enhancement occurs in the series of solid solutions of ZnxCd1−x(CN)2. Here, the larger mass of Cd serves lowers the NTE phonon energies, which in turn increases the CV,i, and hence the magnitude of αV.54–56 The related family of Prussian Blue analogues (PBAs) represents the molecular framework analogue of A-site-deficient perovskites such as ScF3.57,58 Again, NTE in PBAs is well documented;59–64 by varying composition it is possible to obtain coefficients of thermal expansion that vary between −4.41 MK−1 for FeCo(CN)6 and as much as −120(18) MK−1 in Zn3[Fe(CN)6]2.59,64 Such extreme values are accessed by including a substantial fraction of site vacancies, a strategy that is known to enhance further the density of NTE modes.41,53
MOFs are an excellent example of open-framework materials with large void fractions and low bulk moduli;65 indeed systems with fractional pore volumes as large as ∼90% are not unknown.66,67 So it is perhaps unsurprising that the canonical MOF-5 shows pronounced NTE (αV = −39.3(3) MK−1) which persists over its entire stability window 80 ≤ T ≤ 500 K [Fig. 2].20 Or that a number of other high-symmetry MOFs (e.g. MOF-14,68 HKUST-1,69 and UiO-6670,71) also show the effect—either experimentally20,68,69,71 or as determined computationally using e.g. ab initio calculations.72–74 Again the concept of tuning NTE via defect engineering has been demonstrated for MOFs, except that in the case of UiO-66 it appears (bizarrely) that increasing vacancy contributions lead to a reduction in magnitude of NTE. Whatever the mechanism for this may be, an important general corollary of the weaker bonding in MOFs that can limit their usefulness as NTE materials is their inherent instability with respect to phase transitions (e.g. low shear moduli) and/or their tendency to decompose thermally.75–77 So, although the magnitude of αV is usually enhanced in these systems relative to the ceramics discussed above, the temperature window for NTE is often reduced.
Maximising magnitude: NTE from electronic transitions
The limiting case of increasing the magnitude of αV at the expense of the NTE temperature window ΔT is one where volume contraction occurs on heating through a phase transition [Fig. 1(b)]. As we (and others12,13,78) have already flagged, the value of αV necessarily diverges—irrespective of whether the transition is first- or second-order—and at the same time ΔT becomes infinitesimally small. A key requirement for such a transition is the stabilisation of a distinct high entropy, low-volume phase [Fig. 4]. Here we consider briefly the two primary examples of such a transition in the NTE literature: magnetic-order-driven volume expansion on cooling, on the one hand, and charge-transfer transitions, on the other hand.13,79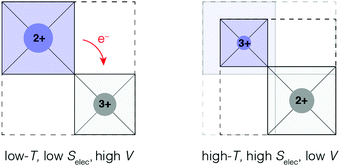 | ||
| Fig. 4 A simplified representation of charge-transfer-mediated NTE in systems such as LaCu3Fe4O12. The high-temperature low-volume state is stabilised by an increased electronic entropy. | ||
Magnetostriction
In certain magnetic materials, there is a volume expansion associated with the onset of magnetic ordering on cooling.80,81 Known as the magnetovolume effect (MVE),81–83 this coupling between magnetic and lattice degrees of freedom may even be exploitable in magnetic refrigeration technologies.84 Perhaps the most widely studied family of MVE/NTE materials is that based on the antiperovskite manganese nitrides, ANMn3; here A is usually a transition metal, metalloid or rare-earth metal.85,86 The structure consists of corner-sharing NMn6 octahedra with the A metal occupying the A-site of conventional perovskites [Fig. 2]. In many of these systems—including e.g. AgNMn3—the first-order magnetic transition that occurs on cooling (possibly ferro- or antiferromagnetic depending on the nature of A) is accompanied by a marked isotropic volume expansion. Such behaviour is understood in terms of the competition between itineracy at high temperatures (large electronic entropy, increased orbital overlap from smaller Mn⋯Mn distances) and magnetism at low temperatures (low entropy, stronger electron localisation from larger Mn⋯Mn distances).87–92These magnetostriction-driven NTE systems are typified by extremely large, and even ‘colossal’ values of αV over fairly narrow temperature ranges. For example, thermal expansion data for Zn0.85Mn0.15NMn3 are shown in blue in Fig. 2; for this system αV = −174.6 MK−1 between 94 and 155 K.18 The phase transition window associated with NTE can be extended at the expense of αV by diluting the magnetic ions with a non-magnetic species (or, alternatively, by introducing competing ferromagnetic interactions as in ref. 93).92,94 In the specific case of Zn1−xMnxNMn3, increasing x to 0.3 allows ΔT to be broadened to 98 K, with a threefold reduction in the coefficient of thermal expansion (αV = −49.5 MK−1). A similar strategy employed in related systems is to substitute N for either C or B.85,95 Chemical doping can even change the nature of the phase transition itself. For example, in the La(Fe/Co,Si/Al)13 family, exchange of Fe for Co or of Si for Al gradually shifts the phase transition type from second-order antiferromagnetic to first-order ferromagnetic.96,97 This has the effect in La(Fe1−xCox)11.4Al1.6 of extending ΔT from 152 to 190 K while αV is reduced in magnitude from −50 to −39 MK−1.97
Charge-transfer materials
Phase transitions involving the redistribution of valence electrons can also give rise to conceptually similar NTE effect. Such transitions might include localised charge transfer between metal centres19,98–100 or valence transitions in rare-earth compounds.101–103 In both cases, volume contraction on heating is caused by changes in equilibrium bond lengths of the different valence states. For example, LaCu3Fe4O12 exhibits a first-order charge-transfer transition on cooling:104,105| 3Cu2+ + 4Fe3.75+ → 3Cu3+ + 4Fe3+. |
Valence-state charge transfer transitions can also drive NTE in a conceptually similar manner. For example, in YbInCu4 the variation in formal f-electron count at 66.9 K gives rise to a large molar volume at low temperatures (localised electrons, formal Yb charge 2.9+, longer bonds) than at temperatures above 67 K (delocalised electrons, formal Yb charge 3.0+, shorter bonds). Experimental lattice-parameter measurements across the transition give αV = −57.9 MK−1 across the temperature range (8 ≤ T ≤ 90 K).101 In the related material Sm1−xYxS—a ‘heavy fermion’ Kondo insulator—αV reaches −96.9 MK−1 between 9 and 250 K for x = 0.33. The Sm electrons gradually localise from the conduction band on cooling as Sm3+→ Sm2+, leading to expansion of the unit cell.102
Magnitude and range: NTE capacity
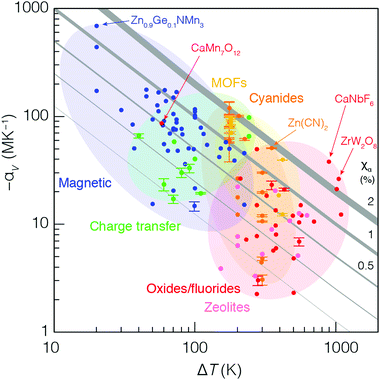
So we have seen that electronic-transition-mediated NTE materials tend to have larger values of |αV| but smaller ΔT than phonon-mediated systems. But is either mechanism intrinsically better? Hence we return to the initial question we had hoped to address: how might we hope to meaningfully compare these different behaviours?In Fig. 5 we present an ‘Ashby plot’ of the relationship between experimental values of −αV and ΔT for the large number of isotropic NTE materials studied to date.27 These data fall naturally along a diagonal, reflecting the observation that the product of the two parameters −αVΔT is mostly preserved even amongst this large collection of very different systems. This product has a clear physical meaning: it is a dimensionless quantity that corresponds to the relative volume contraction −ΔV,V exhibited by a material over the temperature range for which it exhibits NTE. By analogy to the ‘compressibility capacity’ metric χK introduced in the context of negative linear compressibility (NLC) materials,28 we suggest the term ‘NTE capacity’ and the symbol χα to denote this value. Evidently, for the vast majority of NTE materials—irrespective of underlying mechanism or system chemistry—the value of αV falls between 0.1 and 1.0%. At the extreme of large −αV lie the dense phase-transition-type NTE materials; at the other extreme, with large values of ΔT, lie the phonon-driven NTE materials with their open framework structures. Even amongst these framework systems, one observes a sensible trend in terms of pore fraction and bonding strength, reflecting the various differences in αV and ΔT rationalised above for MOFs vs. cyanides vs. oxides.
A particular success of this representation is its ability to help distinguish the truly remarkable NTE compounds within ostensibly different families: they are the materials for which the value of χα is maximised—i.e. they tend toward the top-right corner of the plot in Fig. 5. So, for instance, amongst the MVE antiperovskite nitrides, Zn0.9Ge0.1NMn3 is clearly exceptional, not just because its measured coefficient of thermal expansion is so large and negative, but because it exhibits a total volume contraction of 1.4%, which is larger than that of the vast majority of other NTE materials.106 Likewise, canonical NTE systems long known to be important in the field—such as ZrW2O8 and Zn(CN)2—are easily identifiable in terms of their large NTE capacities.3,21,46
We make three further observations regarding the data in Fig. 5. First, the value of ΔT for a given system is often limited by the variable-temperature capabilities of experimental tools at hand. This is a particularly relevant point for phonon-mediated NTE in MOFs and cyanides, which is historically studied over the temperature range 100–295 K: these are the temperatures most readily accessed by in-house single-crystal X-ray diffraction measurements. Note the large number of MOF and cyanide data points with the same ΔT ≃ 195 K. In nearly all cases, these systems would be expected to show NTE both to lower and to higher temperatures than probed experimentally so far, and so more extensive measurements would likely translate these data points further to the right of the plot; i.e. their NTE capacities are likely underestimated in our analysis. The second point concerns the effect of substitutional ‘broadening’ of NTE behaviour in magnetic and electronic-transition-driven systems.95 Here one finds that a substitutional family lies along a single diagonal, with the parent compound at the top-left, and its substituted derivatives progressively arranged towards the bottom-right direction. In other words, substitution has very little effect on χα, but allows the chemist to navigate the constant-capacity diagonals in Fig. 5. And, finally, we argue it is possible to identify anomalous assignments of NTE mechanisms in existing studies. Take, for instance, the compound CaMn7O12, which is thought to exhibit NTE via a phonon-mediated mechanism;107 its location within the Ashby plot suggests that a magnetic or electronic instability is the more likely mechanism. Perhaps this system deserves revisiting?
Concluding remarks
While the phenomenology and underlying mechanisms of NTE have been reviewed excellently many times previously4,5,11,13,23,24,78,108–110—and certainly in much greater depth than we achieve here—we feel our key contribution in this focus article the compilation of data in Fig. 5; the numerical values used to generate this plot are provided as ESI.† Our hope, of course, is that this representation will help the community identify a number of key compounds or classes of materials for future investigations. Ashby plots, such as ours, are especially useful in selecting materials optimised for a particular application. For example, if ΔT is required for some specific exploitation of NTE, then clearly phonon-mediated systems are the systems of choice. By contrast, MVE materials are the best candidates for extreme NTE localised within a narrow temperature window. We suggest that the most exciting area for future research is the region of the Ashby plot for which χα is maximised: those systems for which both −αV and ΔT are maximal. Our data suggest that MOFs and cyanide frameworks are the currently-known systems most likely to occupy this space, especially if experimental measurements are extended to wider temperature ranges.Years ago, we suggested (somewhat tongue-in-cheek, and in the context of anisotropic NTE materials) that systems with α < −100 MK−1 might be termed ‘colossal’ NTE materials.61 The arguments we develop here—as others have elsewhere13,78—expose the inevitable futility of such a definition. What is obviously more meaningful is to highlight systems with particularly large NTE capacities, say χα ≥ 2%. Certainly, extremely few such systems are known to date, and those that are known are excellent representatives of the extreme physics accessible to a particular NTE mechanism or material chemistry. But the NTE community should presumably also set its sights high for the future: can we ever make a (gargantuan?) NTE material with χα > 10%? Such a material would clearly have to be fundamentally different to those NTE systems identified so far, driven by an entirely new type of NTE physics. Whatever this physics may be, what seems likely is that any such material is most likely to be discovered by seeking to optimise at once both NTE magnitude and NTE range.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge financial support from the Leverhulme Trust (Grant No. RPG-2015-292), and thank A. B. Cairns (Imperial College London) and H. H. M. Yeung (Oxford) for useful discussions.References
- M. Blackman, Philos. Mag., 1958, 3, 831–838 CrossRef CAS.
- C. N. Chu, N. Saka and N. P. Suh, Mater. Sci. Eng., 1987, 95, 303–308 CrossRef CAS.
- T. A. Mary, J. S. O. Evans, T. Vogt and A. W. Sleight, Science, 1996, 272, 90–92 CrossRef CAS.
- J. S. O. Evans, J. Chem. Soc., Dalton Trans., 1999, 19, 3317–3326 RSC.
- M. T. Dove and H. Fang, Rep. Prog. Phys., 2016, 79, 066503 CrossRef PubMed.
- M. J. Klein and R. D. Mountain, J. Phys. Chem. Solids, 1962, 23, 425–427 CrossRef.
- A. Versluis, W. H. Douglas and R. L. Sakaguchi, Dent. Mater., 1996, 12, 290–294 CrossRef CAS PubMed.
- M. B. Jakubinek, C. O’Neill, C. Felix, R. B. Price and M. A. White, Dent. Mater., 2008, 24, 1468–1476 CrossRef CAS PubMed.
- W. Pannhorst, J. Non-Cryst. Solids, 1997, 219, 198–204 CrossRef CAS.
- D. A. Fleming, D. W. Johnson and P. J. Lemaire, Article Comprising a Temperature Compensated Optical Fiber Refractive Index Grating, U.S. Pat., 5694503, 1997 Search PubMed.
- C. P. Romao, K. J. Miller, C. A. Whiteman and M. A. White, Negative thermal expansion (thermomiotic) materials, Elsevier, Amsterdam, 2013 Search PubMed.
- K. Takenaka, Sci. Technol. Adv. Mater., 2012, 13, 013001 CrossRef PubMed.
- J. Chen, L. Hu, J. Deng and X. Xing, Chem. Soc. Rev., 2015, 44, 3522–3567 RSC.
- P. Hidnert, J. Res. Natl. Bur. Stand., 1943, 30, 101–105 CrossRef CAS.
- G. Ernst, C. Broholm, G. R. Kowach and A. P. Ramirez, Nature, 1998, 396, 147–149 CrossRef CAS.
- D. Zhengchun, Z. Mengrui, W. Zhiguo and Y. Jianguo, Compos. Struct., 2016, 152, 693–703 CrossRef.
- R. Jassemi-Zargani and J. F. Simard, 2nd CanSmart Workshop, 1999.
- J.-C. Lin, P. Tong, W. Tong, Y.-M. Zou, C. Yang, F. Zhu, X.-K. Zhang, L.-F. Li, M. Wang, Y. Wu, S. Lin, W. Song, X. Zhu and Y. Sun, Scr. Mater., 2018, 152, 6–10 CrossRef CAS.
- I. Yamada, K. Tsuchida, K. Ohgushi, N. Hayashi, J. Kim, N. Tsuji, R. Takahashi, M. Matsushita, N. Nishiyama, T. Inoue, T. Irifune, K. Kato, M. Takata and M. Takano, Angew. Chem., Int. Ed., 2011, 50, 6579–6582 CrossRef CAS PubMed.
- N. Lock, Y. Wu, M. Christensen, L. J. Cameron, V. K. Peterson, A. J. Bridgeman, C. J. Kepert and B. B. Iversen, J. Phys. Chem. C, 2010, 114, 16181–16186 CrossRef CAS.
- A. L. Goodwin and C. J. Kepert, Phys. Rev. B, 2005, 71, 140301 CrossRef.
- B. K. Greve, K. L. Martin, P. L. Lee, P. J. Chupas, K. W. Chapman and A. P. Wilkinson, J. Am. Chem. Soc., 2010, 132, 15496–15498 CrossRef CAS PubMed.
- R. Mittal, M. Gupta and S. Chaplot, Prog. Mater. Sci., 2018, 92, 360–445 CrossRef CAS.
- W. Miller, C. W. Smith, D. S. Mackenzie and K. E. Evans, J. Mater. Sci., 2009, 44, 5441–5451 CrossRef CAS.
- I. M. Shmyt’ko, N. S. Afonikova and V. I. Torgashev, Phys. Solid State, 2002, 44, 2309–2317 CrossRef.
- J. Chen, X. Xing, R. Yu and G. Liu, J. Am. Ceram. Soc., 2005, 88, 1356–1358 CrossRef CAS.
- M. F. Ashby, Materials selection in mechanical design, Butterworth-Heinemann, Cambridge, 5th edn, 2016 Search PubMed.
- A. B. Cairns and A. L. Goodwin, Phys. Chem. Chem. Phys., 2015, 17, 20449–20465 RSC.
- J. S. O. Evans, T. A. Mary, T. Vogt, M. A. Subramanian and A. W. Sleight, Chem. Mater., 1996, 8, 2809–2823 CrossRef CAS.
- T. H. K. Barron and K. J. Rogers, Mol. Simul., 1989, 4, 27–35 CrossRef.
- J. N. Hancock, C. Turpen, Z. Schlesinger, G. R. Kowach and A. P. Ramirez, Phys. Rev. Lett., 2004, 93, 225501 CrossRef PubMed.
- V. Gava, A. L. Martinotto and C. A. Perottoni, Phys. Rev. Lett., 2012, 109, 195503 CrossRef CAS PubMed.
- A. Sanson, Chem. Mater., 2014, 26, 3716–3720 CrossRef CAS.
- A. K. A. Pryde, K. D. Hammonds, M. T. Dove, V. Heine, J. D. Gale and M. C. Warren, J. Phys.: Condens. Matter, 1996, 8, 10973 CrossRef CAS.
- M. Baise, P. M. Maffettone, F. Trousselet, N. P. Funnell, F.-X. Coudert and A. L. Goodwin, Phys. Rev. Lett., 2018, 120, 265501 CrossRef PubMed.
- E. Grüneisen, Ann. Phys., 1912, 344, 257–306 CrossRef.
- R. H. Baughman, J. Chem. Phys., 1973, 58, 2976–2983 CrossRef CAS.
- T. H. K. Barron, J. G. Collins and G. K. White, Adv. Phys., 1980, 29, 609–730 CrossRef CAS.
- E. Bourova and P. Richet, Geophys. Res. Lett., 1998, 25, 2333–2336 CrossRef CAS.
- T. Chatterji, P. F. Henry, R. Mittal and S. L. Chaplot, Phys. Rev. B, 2008, 78, 134105 CrossRef.
- E. E. Rodriguez, A. Llobet, T. Proffen, B. C. Melot, R. Seshadri, P. B. Littlewood and A. K. Cheetham, J. Appl. Phys., 2009, 105, 114901 CrossRef.
- M. G. Tucker, A. L. Goodwin, M. T. Dove, D. A. Keen, S. A. Wells and J. S. O. Evans, Phys. Rev. Lett., 2005, 95, 255501 CrossRef PubMed.
- P. Lightfoot, D. A. Woodcock, M. J. Maple, L. A. Villaescusa and P. A. Wright, J. Mater. Chem., 2001, 11, 212–216 RSC.
- K. D. Hammonds, V. Heine and M. T. Dove, J. Phys. Chem. B, 1998, 102, 1759–1767 CrossRef CAS.
- B. F. Hoskins and R. Robson, J. Am. Chem. Soc., 1990, 112, 1546–1554 CrossRef CAS.
- D. J. Williams, D. E. Partin, F. J. Lincoln, J. Kouvetakis and M. O’Keeffe, J. Solid State Chem., 1997, 134, 164–169 CrossRef CAS.
- I. P. Swainson and M. T. Dove, Phys. Chem. Miner., 1995, 22, 61–65 CrossRef CAS.
- I. P. Swainson and M. T. Dove, Phys. Rev. Lett., 1993, 71, 193–196 CrossRef CAS PubMed.
- S. A. Wells, M. T. Dove, M. G. Tucker and K. Trachenko, J. Phys.: Condens. Matter, 2002, 14, 4645–4657 CrossRef CAS.
- K. W. Chapman, P. J. Chupas and C. J. Kepert, J. Am. Chem. Soc., 2005, 127, 15630–15636 CrossRef CAS PubMed.
- S. J. Hibble, A. M. Chippindale, E. Marelli, S. Kroeker, V. K. Michaelis, B. J. Greer, P. M. Aguiar, E. J. Bilbé, E. R. Barney and A. C. Hannon, J. Am. Chem. Soc., 2013, 135, 16478–16489 CrossRef CAS PubMed.
- H. Fang, M. T. Dove, L. H. N. Rimmer and A. J. Misquitta, Phys. Rev. B, 2013, 88, 104306 CrossRef.
- A. L. Goodwin, Phys. Rev. B, 2006, 74, 134302 CrossRef.
- V. E. Fairbank, A. L. Thompson, R. I. Cooper and A. L. Goodwin, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 104113 CrossRef.
- P. Ding, E. J. Liang, Y. Jia and Z. Y. Du, J. Phys.: Condens. Matter, 2008, 20, 275224 CrossRef PubMed.
- J. W. Zwanziger, Phys. Rev. B, 2007, 76, 052102 CrossRef.
- J. Brown, Philos. Trans., 1724, 33, 17–24 CrossRef.
- M. B. Zakaria and T. Chikyow, Coord. Chem. Rev., 2017, 352, 328–345 CrossRef CAS.
- S. Margadonna, K. Prassides and A. N. Fitch, J. Am. Chem. Soc., 2004, 126, 15390–15391 CrossRef CAS PubMed.
- A. L. Goodwin, K. W. Chapman and C. J. Kepert, J. Am. Chem. Soc., 2005, 127, 17980–17981 CrossRef CAS PubMed.
- A. L. Goodwin, D. A. Keen, M. G. Tucker, M. T. Dove, L. Peters and J. S. O. Evans, J. Am. Chem. Soc., 2008, 130, 9660–9661 CrossRef CAS PubMed.
- K. W. Chapman, P. J. Chupas and C. J. Kepert, J. Am. Chem. Soc., 2006, 128, 7009–7014 CrossRef CAS PubMed.
- T. Matsuda, J. E. Kim, K. Ohoyama and Y. Moritomo, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 172302 CrossRef.
- S. Adak, L. L. Daemen, M. Hartl, D. Williams, J. Summerhill and H. Nakotte, J. Solid State Chem., 2011, 184, 2854–2861 CrossRef CAS.
- J. C. Tan and A. K. Cheetham, Chem. Soc. Rev., 2011, 40, 1059–1080 RSC.
- H. Furukawa, N. Ko, Y. B. Go, N. Aratani, S. B. Choi, E. Choi, A. Ö. Yazaydin, R. Q. Snurr, M. O’Keeffe, J. Kim and O. M. Yaghi, Science, 2010, 329, 424–428 CrossRef CAS PubMed.
- J. K. Schnobrich, K. Koh, K. N. Sura and A. J. Matzger, Langmuir, 2010, 26, 5808–5814 CrossRef CAS PubMed.
- Y. Wu, V. K. Peterson, E. Luks, T. A. Darwish and C. J. Kepert, Angew. Chem., Int. Ed., 2014, 53, 5175–5178 CAS.
- Y. Wu, A. Kobayashi, G. J. Halder, V. K. Peterson, K. W. Chapman, N. Lock, P. D. Southon and C. J. Kepert, Angew. Chem., Int. Ed., 2008, 47, 8929–8932 CrossRef CAS PubMed.
- M. J. Cliffe, W. Wan, X. Zou, P. A. Chater, A. K. Kleppe, M. G. Tucker, H. Wilhelm, N. P. Funnell, F.-X. Coudert and A. L. Goodwin, Nat. Commun., 2014, 5, 4176 CrossRef CAS PubMed.
- M. J. Cliffe, J. A. Hill, C. A. Murray, F.-X. Coudert and A. L. Goodwin, Phys. Chem. Chem. Phys., 2015, 17, 11586–11592 RSC.
- D. Dubbeldam, K. S. Walton, D. E. Ellis and R. Q. Snurr, Angew. Chem., Int. Ed., 2007, 46, 4496–4499 CrossRef CAS PubMed.
- F.-X. Coudert, Chem. Mater., 2015, 27, 1905–1916 CrossRef CAS.
- S. R. G. Balestra, R. Bueno-Perez, S. Hamad, D. Dubbeldam, A. R. Ruiz-Salvador and S. Calero, Chem. Mater., 2016, 28, 8296–8304 CrossRef CAS PubMed.
- J. C. Tan, B. Civalleri, C.-C. Lin, L. Valenzano, R. Galvelis, P.-F. Chen, T. D. Bennett, C. Mellot-Draznieks, C. M. Zicovich-Wilson and A. K. Cheetham, Phys. Rev. Lett., 2012, 108, 095502 CrossRef PubMed.
- A. U. Ortiz, A. Boutin, A. H. Fuchs and F.-X. Coudert, Phys. Rev. Lett., 2012, 109, 195502 CrossRef PubMed.
- P. Küsgens, M. Rose, I. Senkovska, H. Fröde, A. Henschel, S. Siegle and S. Kaskel, Microporous Mesoporous Mater., 2009, 120, 325–330 CrossRef.
- K. Takenaka, Front. Chem., 2018, 6, 267 CrossRef PubMed.
- M. Azuma, K. Oka and K. Nabetani, Sci. Technol. Adv. Mater., 2015, 16, 034904 CrossRef PubMed.
- C. E. Guillaume, C. R. Acad. Sci., 1897, 125, 235–238 Search PubMed.
- G. Hausch, Phys. Status Solidi A, 1973, 18, 735–740 CrossRef CAS.
- R. J. Weiss, Proc. Phys. Soc., 1963, 82, 281–288 CrossRef.
- A. Katsuki and K. Terao, J. Phys. Soc. Jpn., 1969, 26, 1109–1114 CrossRef CAS.
- S. Fähler and V. K. Pecharsky, MRS Bull., 2018, 43, 264–268 CrossRef.
- T. Hamada and K. Takenaka, J. Appl. Phys., 2011, 109, 07E309 CrossRef.
- T. Peng, W. Bo-Sen and S. Yu-Ping, Chin. Phys. B, 2013, 22, 067501 CrossRef.
- P. L’Heritier, D. Boursier and R. Fruchart, Mater. Res. Bull., 1981, 16, 1511–1519 CrossRef.
- B. Y. Qu and B. C. Pan, J. Appl. Phys., 2010, 108, 113920 CrossRef.
- K. Kodama, S. Iikubo, K. Takenaka, M. Takigawa, H. Takagi and S. Shamoto, Phys. Rev. B, 2010, 81, 224419 CrossRef.
- D. Tahara, Y. Motome and M. Imada, J. Phys. Soc. Jpn., 2007, 76, 013708 CrossRef.
- S. Iikubo, K. Kodama, K. Takenaka, H. Takagi and S. Shamoto, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 020409 CrossRef.
- K. Takenaka, M. Ichigo, T. Hamada, A. Ozawa, T. Shibayama, T. Inagaki and K. Asano, Sci. Technol. Adv. Mater., 2014, 15, 015009 CrossRef PubMed.
- X. Guo, P. Tong, J. Lin, C. Yang, K. Zhang, S. Lin, W. Song and Y. Sun, Front. Chem., 2018, 6, 75 CrossRef PubMed.
- J. C. Lin, P. Tong, W. Tong, S. Lin, B. S. Wang, W. H. Song, Y. M. Zou and Y. P. Sun, Appl. Phys. Lett., 2015, 106, 082405 CrossRef.
- K. Takenaka and H. Takagi, Appl. Phys. Lett., 2005, 87, 261902 CrossRef.
- R. Huang, Y. Liu, W. Fan, J. Tan, F. Xiao, L. Qian and L. Li, J. Am. Chem. Soc., 2013, 135, 11469–11472 CrossRef CAS PubMed.
- Y. Zhao, R. Huang, S. Li, W. Wang, X. Jiang, Z. Lin, J. Li and L. Li, Phys. Chem. Chem. Phys., 2016, 18, 20276–20280 RSC.
- I. Yamada, S. Marukawa, M. Murakami and S. Mori, Appl. Phys. Lett., 2014, 105, 231906 CrossRef.
- I. Yamada, S. Marukawa, N. Hayashi, M. Matsushita and T. Irifune, Appl. Phys. Lett., 2015, 106, 151901 CrossRef.
- I. Yamada, K. Shiro, N. Hayashi, S. Kawaguchi, T. Kawakami, R. Takahashi and T. Irifune, J. Asian Ceram. Soc., 2017, 5, 169–175 CrossRef.
- B. Kindler, D. Finsterbusch, R. Graf, F. Ritter, W. Assmus and B. Lüthi, Phys. Rev. B, 1994, 50, 704–707 CrossRef CAS.
- P. A. Alekseev, J.-M. Mignot, E. V. Nefeodova, K. S. Nemkovski, V. N. Lazukov, N. N. Tiden, A. P. Menushenkov, R. V. Chernikov, K. V. Klementiev, A. Ochiai, A. V. Golubkov, R. I. Bewley, A. V. Rybina and I. P. Sadikov, Phys. Rev. B, 2006, 74, 035114 CrossRef.
- J. Arvanitidis, K. Papagelis, S. Margadonna and K. Prassides, Dalton Trans., 2004, 3144–3146 RSC.
- Y. W. Long, N. Hayashi, T. Saito, M. Azuma, S. Muranaka and Y. Shimakawa, Nature, 2009, 458, 60–63 CrossRef CAS PubMed.
- W.-T. Chen, Y. Long, T. Saito, J. P. Attfield and Y. Shimakawa, J. Mater. Chem., 2010, 20, 7282–7286 RSC.
- Y. Sun, C. Wang, Y. Wen, K. Zhu and J. Zhao, Appl. Phys. Lett., 2007, 91, 231913 CrossRef.
- K. Gautam, D. K. Shukla, S. Francoual, J. Bednarcik, J. R. L. Mardegan, H.-P. Liermann, R. Sankar, F. C. Chou, D. M. Phase and J. Strempfer, Phys. Rev. B, 2017, 95, 144112 CrossRef.
- A. W. Sleight, Curr. Opin. Solid State Mater. Sci., 1998, 3, 128–131 CrossRef CAS.
- G. D. Barrera, J. A. O. Bruno, T. H. K. Barron and N. L. Allan, J. Phys.: Condens. Matter, 2005, 17, R217–R252 CrossRef CAS.
- C. Lind, Materials, 2012, 5, 1125–1154 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Tabulated summary of known isotropic NTE materials and their NTE characteristics. See DOI: 10.1039/c8mh01065j |
| This journal is © The Royal Society of Chemistry 2019 |