Tipping the polaron–bipolaron balance: concentration and spin effects in doped oligo(aniline)s observed by UV-vis-NIR and TD-DFT†
Benjamin M.
Mills
 a,
Zhecheng
Shao‡
a,
Stephanie R.
Flynn
a,
Patrice
Rannou
a,
Zhecheng
Shao‡
a,
Stephanie R.
Flynn
a,
Patrice
Rannou
 b,
David M.
Lindsay
b,
David M.
Lindsay
 c,
Natalie
Fey
c,
Natalie
Fey
 *a and
Charl F. J.
Faul
*a and
Charl F. J.
Faul
 *a
*a
aSchool of Chemistry, University of Bristol, Bristol, BS8 1TS, UK. E-mail: natalie.fey@bristol.ac.uk; charl.faul@bristol.ac.uk
bUniv. Grenoble Alpes, CNRS, CEA, INAC, SyMMES, F-38000 Grenoble, France
cDepartment of Pure and Applied Chemistry, WestCHEM, University of Strathclyde, 295 Cathedral Street, Glasgow, G1 1XL, UK
First published on 4th December 2018
Abstract
The oxidation states and doped forms of oligo(aniline)s are readily interconverted, and each state has characteristic UV-vis-NIR absorptions, making this spectroscopic technique ideal for in situ analysis of oligo(aniline) behaviour. However, experimental isolation of some of these states can be challenging and quantitative agreement between experimental and calculated spectra has been poor, making it difficult to identify the exact structure(s) and properties of each state. Here we report a comprehensive study of the UV-vis-NIR spectra of all oxidation states and doped forms of a series of oligo(aniline)s of varying lengths (dimer, tetramer and octamer), using a computationally inexpensive DFT method that is particularly suited to molecules with charge-transfer character. The computational study suggests that doped oligo(aniline)s form mixtures of spin isomers (polaronic and bipolaronic forms) in solution, and we have been able to evaluate and compare the most likely electronic configurations, as well as supporting our insights experimentally, by ESR spectroscopy. This doping approach enables tuning of the spin isomer equilibrium position by varying the concentration of protonic dopant, offering a new pathway to explore the electronic structure of π-conjugated molecules more generally, and opening up new approaches to the design of spintronic materials.
Design, System, ApplicationWe describe a robust computational protocol for modelling the molecular geometries, electronic structures and absorption spectra of oligomers of the widely-used and versatile conducting polymer, poly(aniline). By comparing experimental UV-vis-NIR and EPR spectra with TD-DFT simulations, we discovered it is possible to switch reversibly between diamagnetic and paramagnetic forms (bipolaronic and polaronic states) of oligo(aniline)s in solution simply by adjusting dopant concentrations – a finding which could reinvigorate research into conduction mechanisms in poly(aniline) and related materials, as well as allowing control of material properties and functionality. Our approach will enable deeper understanding and better characterization and so will provide strategies for the optimisation and in silico design of nitrogen-containing π-conjugated materials for a wide variety of applications. Specifically, the insights into the nature of the polaronic and bipolaronic states resulting from these studies will enable the tuning of existing materials and the design of novel systems based on poly(aniline) for a variety of new applications. These new findings will enable the design and further development of the spin-switching phenomenon for use in solid-state organic electronic devices, particularly in the rapidly developing field of spintronics. |
Introduction
Poly(aniline), PANI, is an historically important and unique π-conjugated polymer.1 It has considerable potential for use in a wide range of applications,2 notably energy storage,3 optoelectronic devices4 and sensors,5 particularly where features such as low cost, biocompatibility and air- and moisture tolerance are important. However, there is significant uncertainty surrounding some of the details of PANI's optoelectronic properties, limiting the applications of this promising material. A detailed understanding of these properties is required to optimize PANI-based devices for such applications.6 Crucially, the question of whether polarons or bipolarons are the dominant charge carrier in PANI remains unresolved,7 despite decades of research.8 In addition, PANI is polydisperse,9 has a tendency for dynamic block-copolymer microphase separation behavior,10 and exhibits significant disorder in the solid state.11 These factors contribute to the difficulty in measuring its behavior on a molecular scale, and in critically evaluating its bulk properties, especially in the search for new applications. With limited or no structural data for the bulk material, computational studies become challenging; in addition, large systems continue to be problematic for electronic structure methods.Based on the challenges associated with the polymeric material, studies have considered oligomers of PANI (Scheme 1), such as the phenyl-capped dimer (DPPD, x + y = 1), tetramer (TANI, x + y = 2), and octamer (OANI, x + y = 4).12 These oligo(aniline)s have chemical properties that closely resemble those of PANI,13 such as multiple oxidation states and proton-induced onset of electronic conductivity (so-called ‘protonic doping’ or ‘acid doping’).14 In contrast to PANI, these oligomers have well-defined molecular structures that more readily pack to form bulk materials with long-range order,15 making them versatile π-conjugated building blocks for functional materials in their own right. For example, oligo(aniline)-based materials can self-assemble into well-defined nanostructures,15,16 with potential applications in organic electronics,17 data storage,18 and novel optoelectronic devices.19
 | ||
| Scheme 1 Chemical structures of phenyl-capped oligo(aniline)s and poly(aniline), including variations in oxidation state. | ||
Oligo(aniline)s have received much less attention than related π-conjugated materials, such as oligo(thiophene)s.20 For example, the question of whether polarons or bipolarons are the dominant charge carriers has been investigated in much greater depth for oligo(thiophene)s21 than for oligo(aniline)s. More broadly, the nature of oligo(aniline) spin states is of fundamental importance to conductivity, but remains underdeveloped: while some high-spin meta–para-linked22 and N-substituted13,23 oligo- and poly(aniline)s have been reported, these molecules are not as readily prepared as PANI and its oligomers, and, importantly, tend not to show the pH-dependent changes in spin and conductivity that are characteristic of linear (para–para-linked) oligo(aniline)s and PANI.
Previous experimental and theoretical studies have addressed aspects of oligo(aniline) and PANI chemistry. For example, Levon and co-workers investigated the acid doping of an oligo(aniline) with electron spin resonance (ESR) and ultraviolet-visible-near-infrared (UV-vis-NIR) spectroscopy, but did not compare their experimental results with calculations.24 On the other hand, Tadjer and co-workers reported calculated UV-vis-NIR spectra of long phenyl-capped oligo(aniline)s (8, 12 and 16-mer) using time-dependent density functional theory (TD-DFT) and compared these to the experimentally-derived spectra of PANI, but did not study the doping mechanism or key variables such as concentration effects.7c,d Recently, Kaner and collaborators provided insight into the doping mechanisms of TANI using optical and electron spin resonance data,25 but did not test the proposed electronic structures computationally. However, a comprehensive understanding, encompassing both detailed experimental and theoretical studies of the chemical and optoelectronic (solution) properties of oligo(aniline)s is still required to support continued development and new applications of these promising solution-processable functional materials.
We are particularly interested in the polaron–bipolaron balance, long-lived radical states and other related spin phenomena in linear oligo(aniline)s26 originating from the unique protonic doping behavior of aniline-based materials. This exceptional combination of proton responsiveness and spin changes could be harnessed for antimicrobial activity,27 and chemo- and bio-responsive spintronic devices,28 or be used to control the morphology of self-assembled oligo(aniline) materials, for example by magnetic field-influenced crystallization.29 Insights gained from these oligomeric derivatives could also be applied to PANI-based materials.
With the aim of bringing our understanding of oligo(aniline) chemistry closer to the level achieved for other organic conducting materials, and of elucidating behavior relevant to device applications, we report here a wide-ranging UV-vis-NIR, ESR, and TD-DFT study into the characterization of well-defined dimeric, tetrameric and octameric oligo(aniline)s in solution. With the computational methodology used, we demonstrate very good agreement between experimental and computational results, potentially enabling the in silico design of novel materials based on oligo(aniline)s and other π-conjugated molecular architectures. We have focused on detailed characterization of the oxidation, protonation and spin states, allowing us to identify the factors affecting the polaron–bipolaron balance and propose how the spin isomer equilibrium position can be tuned by varying the concentration of protonic dopant. This approach offers a new pathway to explore the electronic structure of π-conjugated molecules more generally, using spectroscopy and computational study.
Experimental and computational details
The oligomers DPPD, TANI, and OANI were either purchased or prepared according to published procedures. Full details are available in the ESI† (p. S2 and S3).The geometries of all known oxidation states and doped forms of the oligomers were optimized using density functional theory (DFT) at the B3LYP/6-31G(d) level of theory as implemented in Gaussian 09 (see ESI† for full computational details and references), using a continuum-dielectric model of solvation (PCM) for ethanol. For those species whose geometries have been determined by X-ray crystallography, the calculated geometries compared favorably with experiment (ESI† Tables S2–S5). These optimized geometries were used for TD-DFT calculations using either the B3LYP or CAM-B3LYP density functionals as implemented in Gaussian, again with the standard 6-31G(d) basis set and PCM solvation (tetrahydrofuran).
Results and discussion
A. Computational methodology
The B3LYP density functional was employed in a previous study of TANI, but predictions using this method differed systematically from experimental results, albeit capturing the same trends.12b In contrast, the CAM-B3LYP functional has been reported to be particularly effective at modeling charge-transfer excitations and highly delocalized π-conjugated systems.30 We recently demonstrated the effectiveness of this approach, using CAM-B3LYP to assign the experimental UV-vis-NIR spectra of star-shaped oligo(aniline)s in solution.31A comprehensive range of oligo(aniline) oxidation states (30 in total – 7 for DPPD, 12 for TANI and 11 for OANI) were studied by TD-DFT. The structures and corresponding UV-vis-NIR maxima of all the oxidation states and doped forms of the oligomers that were investigated are compared in ESI† Table S7. Comparing the two functionals over the full set of oligo(aniline)s and oxidation states studied, UV-vis-NIR maxima calculated with CAM-B3LYP were in better agreement with our experimental data than those calculated with B3LYP, except in a small window around 300 nm, where the methods were comparable (Fig. 1).
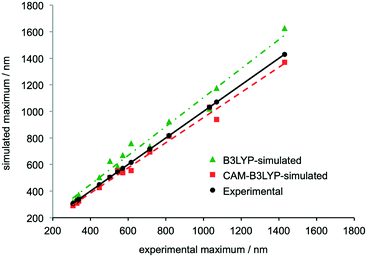 | ||
| Fig. 1 Comparison of the wavelengths of simulated and experimental UV-vis-NIR maxima associated with electronic transitions in the LEB, EB, PB, RC and ES states of DPPD, TANI and OANI species. Structures can be found in the ESI,† Fig. S2–S4 and data in Table S7. Trendlines show linear least-squares fits, R2 = 0.98 for B3LYP and 0.99 for CAM-B3LYP. See ESI† for full computational details. | ||
In extensive TD-DFT benchmarking tests, mean average errors (MAEs), i.e. the difference between experimental and theoretical transition energies, were typically around 0.25 eV for a range of functionals.32 In our study, the MAE for B3LYP was 0.25 eV and for CAM-B3LYP it was 0.11 eV (see also ESI† Fig. S50). Calculated wavelengths for these transitions were on average 74 nm higher than experiment with B3LYP and 30 nm lower with CAM-B3LYP. While some differences remain, CAM-B3LYP is therefore particularly useful for characterizing oligo(aniline) oxidation states in solution because it is accurate enough to identify which species is responsible for each peak in the UV-vis-NIR spectrum of a mixture of oligo(aniline) species, even with relatively close maxima. In contrast, B3LYP appears too unreliable to support such assignments in most cases (Fig. 1). The TD-DFT calculations also confirmed that π–π* HOMO–LUMO transitions are generally responsible for the characteristic maxima in the UV-vis-NIR spectra of oligo(aniline)s; further details are given in the ESI.†
B. DPPD doped states
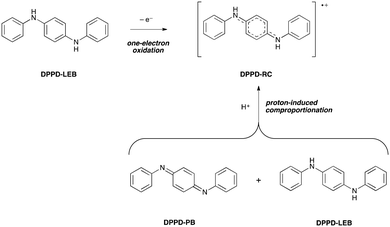
Despite their complexity, doped states are the most important forms of oligo(aniline)-based materials, as they are responsible for their electrical conductivity. As a result, we extended our studies to a detailed examination of the oligomeric doped states.The doping process varies with the length of the oligomer. The dimer, DPPD, has been reported to form a radical-cation (RC) doped state by two different mechanisms (Scheme 2): (i) directly by one-electron oxidation of the reduced, benzenoid (LEB) state,26b,c and (ii) indirectly by protonation of both of the imine nitrogen atoms of the fully oxidized, quinoid (PB) state and comproportionation with the LEB state.33a Comparison of our TD-DFT calculations with UV-vis-NIR spectra support mechanism (ii): DPPD-LEB (λmax ∼ 300 nm) and DPPD-PB (λmax ∼ 450 nm) were prepared separately and dissolved in THF, at which point the two solutions were mixed. Following addition of a protonic dopant, the maxima corresponding to DPPD-LEB and DPPD-PB were no longer present and instead a new peak indicative of DPPD-RC (λmax ∼ 700 nm) was observed instead (ESI† Fig. S42 and S43).
C. TANI doped states
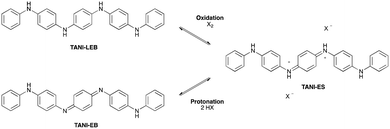
The doped states of longer oligomers such as TANI, as well as PANI itself, are often referred to as emeraldine salt (ES) states. They can be doped oxidatively, but are more commonly doped by protonation of the half-oxidized EB state (Scheme 3),12a,26b in an intermolecular analogue of DPPD's doping mechanism (ii). Further details are given in ESI† Fig. S3.We investigated the structure, spectra and spin properties of the doped ES state of TANI in detail, as an understanding of the conducting state is crucial for application-orientated studies. When TANI-EB is dissolved in THF and excess HClO4 is added, the salt TANI-ES·2ClO4·2THF crystallizes from solution. Molecular structures in related salts containing TANI-ES were reported in 1988,26a,b but full details of the crystal structure, such as atomic coordinates and packing, were not disclosed. We therefore carried out a new single-crystal X-ray diffraction structure determination (see ESI† p. S32 for details).
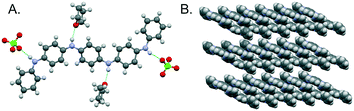
As previously reported, TANI-ES adopts a sigmoid conformation (Fig. 2A), which was calculated by DFT to be slightly more stable (∼2 kJ mol−1) and slightly closer to the experimental UV-vis-NIR maximum (by 11 nm) than the linear conformation (ESI† Table S1). It seems, therefore, that TANI-ES adopts the same conformation in solution and in the solid-state. The perchlorate counterions form hydrogen bonds with TANI-ES's outer NH groups, while the THF solvate molecules are hydrogen bonded to the inner NH groups (Fig. 2A). Molecular packing in the crystal structure consists of parallel columns of slipped π-stacked TANI-ES molecules (Fig. 2B), an arrangement that is consistent with previous reports of anisotropic electronic conductivity in related systems.16d,17a
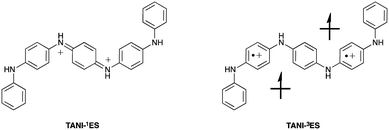
The spin state of TANI-ES is central to the currently unresolved question of bipolaronic and polaronic charge carriers in TANI-based materials. However, the molecular geometry of TANI-ES alone (ESI† Table S5) offers little insight into this issue, as it shows similarities with counterion-free DFT models of both a diamagnetic (spinless) singlet form (containing a bipolaron; TANI-1ES) and a paramagnetic triplet polaronic form (containing two separate polarons; TANI-3ES, see Fig. 3). We therefore used TD-DFT simulations in an attempt to unambiguously identify the species present during the protonic doping of TANI in solution.
TD-DFT-simulated UV-vis-NIR maxima of TANI-1ES (∼1000 nm) and TANI-3ES (∼800 nm) were in good agreement with experimental spectra of acidified solutions of TANI-EB (Fig. 4 and Table 1), showing that the 1ES and 3ES states are, therefore, both present in solution. Several other protonated TANI species were considered computationally (see ESI† for details), including the mono-protonated triplet state (TANI-3MP, with a single overall charge) as proposed by Kaner et al.25 However, these species were all ruled out as their simulated maxima did not match the experimental values (ESI† Table S7). Specifically, in the case of TANI-3MP our CAM-B3LYP calculations predicted a UV-vis-NIR maximum at 969 nm whereas experimental spectra of TANI-EB doped with HClO4 showed maxima at 818 and 1032 nm, in much better agreement with the transitions calculated for TANI-3ES and TANI-1ES respectively (Table 1). It is noteworthy that the TD-DFT assignments were in good agreement with experimental data throughout (see part A), despite the absence of counterions or explicit solvent molecules in the models (see ESI† for a brief discussion), suggesting TANI-3MP is not observed spectroscopically. A range of possible configurations for partial doping could be considered computationally, and these have been discussed in the ESI.†
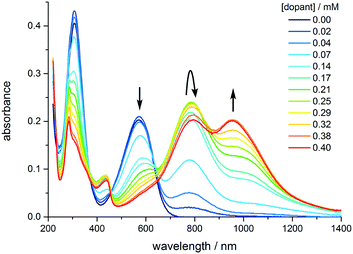 | ||
| Fig. 4 Evolution of the UV-vis-NIR spectrum of TANI as the concentration of the dopant (CSA) is increased from 0 to 0.4 mM. [TANI] = 0.15 mM in THF. | ||
The experimentally-measured spectra of TANI-ES varied with the solvent, the concentration of TANI, and the nature and concentration of the protonic dopant (ESI† Fig. S44 and S45). HClO4 causes TANI to crystallize at high concentrations, so instead we employed the common dopant DL-camphor-10-sulfonic acid (CSA), as it is more soluble in organic solvents than HClO4. As the CSA concentration was increased, TANI-EB was converted to a mixture of TANI-1ES and TANI-3ES (Fig. 5). The mixture consists mainly of TANI-3ES at intermediate dopant concentrations, but shifts in favor of TANI-1ES at higher dopant concentrations.
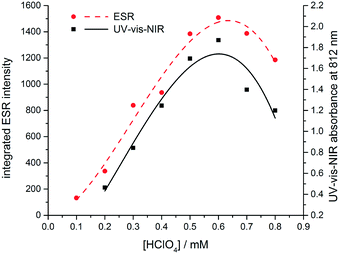 | ||
| Fig. 5 Dependence on the concentration of protonic dopant (HClO4) of the UV-vis-NIR absorbance at 812 nm (black) and integrated ESR signal at 3440 G (red). | ||
To confirm the presumed paramagnetic nature of TANI-3ES, we recorded ESR spectra of TANI over a range of dopant concentrations (Fig. S46 and S47†).24 The integrated intensity of the ESR signal is proportional to the concentration of the paramagnetic species, and showed the same dependence on dopant concentration as the UV-vis-NIR peak at 800 nm, which we assigned to TANI-3ES according to TD-DFT (Fig. 5). We note that Kaner and collaborators recently used ESR spectra to analyse the dominant electronic configurations for a range of dopants,25 but did not consider the presence of TANI-3ES in their study.
From these results we conclude that during the protonic doping of TANI in solution (with an increase of protonic dopant concentration), there is a gradual transition in electronic structure and spin state from polaronic (TANI-3ES) to bipolaronic (TANI-1ES). Molecular charge distributions calculated from DFT models (Fig. 6) show that the positive charge in TANI-1ES is concentrated at the center of the molecule, consistent with its quinoid Lewis structure (cf. Fig. S3†), whereas the charge in TANI-3ES is more evenly distributed over the whole molecule. The polaron-to-bipolaron transition might thus be due to increased electrostatic screening of the two positive charges from each other at higher dopant concentrations, stabilizing the bipolaronic form with its spatially less separated charges. As a result of these studies, we have begun, for the first time, to uncover the true nature of the spin systems in oligo(anilines).
D. OANI doped states
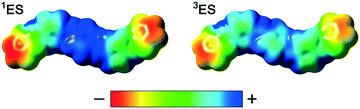
Expanding these investigations, we also explored the spin states of octa(aniline). Evidence of mixtures of analogous spin states were also found in solutions of the doped octamer OANI. Maxima consistent with a spinless bipolaronic form (OANI-1ES, ∼1400 nm) and a high spin polaronic quintet form (OANI-5ES, ∼1000 nm) were observed; however, an intermediate triplet form (OANI-3ES, expected ∼1300 nm) was not clearly detected (Table 1 and ESI† Fig. S4 and S39). In this case, there is a more appreciable difference in the calculated and experimentally-observed transitions (Table 1 and ESI† S7), which may be a result of more conformational variation resulting from the longer chain length in this system. Again, however, the transitions are sufficiently separated to allow a clear distinction of the different electronic configurations. The absence of the transitions characteristic of the triplet form from experimental spectra is the subject of further investigations. Similar to TANI, we have considered a number of protonated species and electronic configurations for OANI, and have again found their transitions in worse agreement with the experimental data (discussed in the ESI†). We note that the ESP surfaces (Fig. S10†) for the different OANI spin states show the singlet and quintet states to be more similar to each other than to the triplet state.Conclusions
A comprehensive set of DFT structural models and TD-DFT-simulated UV-vis-NIR spectra of a series of dimeric, tetrameric, and octameric aniline oligomers have been shown to agree closely with experimental data. The calculations pave the way for in silico design of oligo(aniline)s and related π-conjugated molecules for optoelectronic applications by establishing a reliable link between molecular structure, oxidation state, UV-vis-NIR spectra (i.e. color) and magnetic properties.Protonic doping of oligo(aniline)s such as TANI was found to be similar to that of PANI, in that protonation of the EB state can yield both bipolarons and polarons. In doped PANI, the polarons can form a lattice,8a which can lead to truly metallic conductivity in suitably processed samples,1b whereas this should only be possible in oligo(aniline)s if molecules pack closely enough to allow intermolecular charge transport. PANI also has a solvent-dependent conformation that affects its polaron–bipolaron balance,33 which does not apply to short oligo(aniline)s on account of their rigidity.
Here, for the first time, we have fully characterized a different type of polaron–bipolaron transition in oligo(aniline)s that depends not on conformational changes but on the concentrations of oligomer and dopant. Overall, the factors affecting the polaron–bipolaron balance that have been established here will be vital in developing similar properties in designed oligomeric materials. For example, if the polaronic form of doped TANI (the 3ES state) is particularly desired in a pure form that persists regardless of concentration, e.g. for research into the mechanisms of conductivity, for molecular wires,17b or to influence radical-mediated chemical reactions, it could be favored by the introduction of donor or acceptor substituents at suitable locations in the molecule. Subtler structural modifications could harness the spin-crossover behaviour for spintronic devices by coupling it to stimuli other than concentration.
The spin-crossover behaviour we have observed in TANI meets many of the desired criteria for molecular spin-state switches, notably reversibility, room-temperature switching, and one of the two states being diamagnetic.28b The clear spectroscopic distinction between the two spin states of TANI makes it highly suitable for further investigation, particularly as there is an urgent need for more spectroscopic scrutiny of the many theoretical models of spin-dependent electronic processes that have been proposed recently.34 In this way, oligo(aniline)s can serve as an experimentally accessible platform for investigating fundamental electronic processes in π-conjugated materials that are otherwise difficult to address.
Overall, these unprecedented observations, fully supported by TD-DFT calculations, not only provide fundamental insight into this fascinating class of materials, but present, for the first time, a way of harnessing polarons or bipolarons (and thus their magnetic properties) in oligo(aniline)s in solution by controlling the concentration of protonic dopant. The ability to tune the polaron–bipolaron ratio means that a new range of experiments, molecular architectures and applications can be envisaged for aniline oligomers and related π-conjugated molecules.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the United Kingdom Engineering and Physical Sciences Research Council (EPSRC) (grant EP/K502996/1). Mass spectrometric analysis was performed on instrumentation bought through the Core Capability for Chemistry Research – Strategic Investment in Mass Spectrometry EPSRC grant (EP/K03927X/1). ESR data were collected on an Active Spectrum extended-range benchtop Micro-ESR bought under EPSRC CDT Capital grant (EP/K035746/1). We thank Dr Natalie E. Pridmore for assistance with the X-ray crystallographic data analysis. The facilities and staff of the Mass Spectrometry service and the NMR service, as well as computing resources from the Centre for Computational Chemistry at the University of Bristol are gratefully acknowledged.Notes and references
- (a) A. J. Heeger, Angew. Chem., Int. Ed., 2001, 40, 2591–2611 CrossRef CAS; (b) K. Lee, S. Cho, S. Heum Park, A. J. Heeger, C.-W. Lee and S.-H. Lee, Nature, 2006, 441, 65–68 CrossRef CAS; (c) J. C. Michaelson, Endeavour, 1993, 17, 121–126 CrossRef CAS.
- C. O. Baker, X. Huang, W. Nelson and R. B. Kaner, Chem. Soc. Rev., 2017, 46, 1510–1525 RSC.
- L. Pan, G. Yu, D. Zhai, H. R. Lee, W. Zhao, N. Liu, H. Wang, B. C. K. Tee, Y. Shi, Y. Cui and Z. Bao, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 9287 CrossRef CAS PubMed.
- (a) A. Pron and P. Rannou, Prog. Polym. Sci., 2002, 27, 135–190 CrossRef CAS; (b) A. A. Argun, P.-H. Aubert, B. C. Thompson, I. Schwendeman, C. L. Gaupp, J. Hwang, N. J. Pinto, D. B. Tanner, A. G. MacDiarmid and J. R. Reynolds, Chem. Mater., 2004, 16, 4401–4412 CrossRef CAS.
- (a) D. T. McQuade, A. E. Pullen and T. M. Swager, Chem. Rev., 2000, 100, 2537–2574 CrossRef CAS PubMed; (b) J. Janata and M. Josowicz, Nat. Mater., 2003, 2, 19–24 CrossRef CAS PubMed.
- S. Bhadra, D. Khastgir, N. K. Singha and J. H. Lee, Prog. Polym. Sci., 2009, 34, 783–810 CrossRef CAS.
- (a) A. Varela-Alvarez, J. A. Sordo and G. E. Scuseria, J. Am. Chem. Soc., 2005, 127, 11318–11327 CrossRef CAS PubMed; (b) C. Cavazzoni, R. Colle, R. Farchioni and G. Grosso, J. Chem. Phys., 2008, 128, 234903 CrossRef PubMed; (c) J. N. Petrova, J. R. Romanova, G. K. Madjarova, A. N. Ivanova and A. V. Tadjer, J. Phys. Chem. B, 2011, 115, 3765–3776 CrossRef CAS; (d) J. Petrova, J. Romanova, G. Madjarova, A. Ivanova and A. Tadjer, J. Phys. Chem. B, 2012, 116, 6543–6552 CrossRef CAS; (e) M. Canales, J. Torras, G. Fabregat, A. Meneguzzi and C. Alemán, J. Phys. Chem. B, 2014, 118, 11552–11562 CrossRef CAS.
- (a) S. Stafström, J. L. Brédas, A. J. Epstein, H. S. Woo, D. B. Tanner, W. S. Huang and A. G. MacDiarmid, Phys. Rev. Lett., 1987, 59, 1464–1467 CrossRef PubMed; (b) W. S. Huang and A. G. MacDiarmid, Polymer, 1993, 34, 1833–1845 CrossRef CAS.
- H. S. Kolla, S. P. Surwade, X. Zhang, A. G. MacDiarmid and S. K. Manohar, J. Am. Chem. Soc., 2005, 127, 16770–16771 CrossRef CAS.
- J. Y. Shimano and A. G. MacDiarmid, Synth. Met., 2001, 123, 251–262 CrossRef CAS.
- J. Joo, S. M. Long, J. P. Pouget, E. J. Oh, A. G. MacDiarmid and A. J. Epstein, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 9567–9580 CrossRef CAS.
- (a) Z. Wei and C. F. J. Faul, Macromol. Rapid Commun., 2008, 29, 280–292 CrossRef CAS; (b) Z. Shao, P. Rannou, S. Sadki, N. Fey, D. M. Lindsay and C. F. J. Faul, Chem. – Eur. J., 2011, 17, 12512–12521 CrossRef CAS PubMed.
- T. Moll and J. Heinze, Synth. Met., 1993, 55, 1521–1526 CrossRef CAS.
- F. L. Lu, F. Wudl, M. Nowak and A. J. Heeger, J. Am. Chem. Soc., 1986, 108, 8311–8313 CrossRef CAS.
- T. G. Dane, P. T. Cresswell, G. A. Pilkington, S. Lilliu, J. E. Macdonald, S. W. Prescott, O. Bikondoa, C. F. J. Faul and W. H. Briscoe, Soft Matter, 2013, 9, 10501–10511 RSC.
- (a) Z. Wei, T. Laitinen, B. Smarsly, O. Ikkala and C. F. J. Faul, Angew. Chem., Int. Ed., 2005, 44, 751–756 CrossRef CAS PubMed; (b) Y. Wang, H. D. Tran, L. Liao, X. Duan and R. B. Kaner, J. Am. Chem. Soc., 2010, 132, 10365–10373 CrossRef CAS PubMed; (c) Y. Wang, J. Liu, H. D. Tran, M. Mecklenburg, X. N. Guan, A. Z. Stieg, B. C. Regan, D. C. Martin and R. B. Kaner, J. Am. Chem. Soc., 2012, 134, 9251–9262 CrossRef CAS; (d) Z. Shao, Z. Yu, J. Hu, S. Chandrasekaran, D. M. Lindsay, Z. Wei and C. F. J. Faul, J. Mater. Chem., 2012, 22, 16230–16234 RSC; (e) T. G. Dane, P. T. Cresswell, O. Bikondoa, G. E. Newby, T. Arnold, C. F. J. Faul and W. H. Briscoe, Soft Matter, 2012, 8, 2824–2832 RSC; (f) W. Lyu, J. Feng, W. Yan and C. F. J. Faul, J. Mater. Chem. C, 2015, 3, 11945–11952 RSC.
- (a) Y. Wang, J. A. Torres, A. Z. Stieg, S. Jiang, M. T. Yeung, Y. Rubin, S. Chaudhuri, X. Duan and R. B. Kaner, ACS Nano, 2015, 9, 9486–9496 CrossRef CAS PubMed; (b) O. A. Bell, G. Wu, J. S. Haataja, F. Brömmel, N. Fey, A. M. Seddon, R. L. Harniman, R. M. Richardson, O. Ikkala, X. Zhang and C. F. J. Faul, J. Am. Chem. Soc., 2015, 137, 14288–14294 CrossRef CAS PubMed.
- (a) B. P. Brown, L. Picco, M. J. Miles and C. F. J. Faul, Small, 2015, 11, 5054–5058 CrossRef CAS; (b) J. O. Thomas, H. D. Andrade, B. M. Mills, N. A. Fox, H. J. K. Hoerber and C. F. J. Faul, Small, 2015, 11, 3430–3434 CrossRef CAS.
- Y. Hu, B. T. Miles, Y.-L. D. Ho, M. P. C. Taverne, L. Chen, H. Gersen, J. G. Rarity and C. F. J. Faul, Adv. Opt. Mater., 2017, 5, 1600458 CrossRef.
- A. Mishra, C.-Q. Ma and P. Bäuerle, Chem. Rev., 2009, 109, 1141–1276 CrossRef CAS PubMed.
- (a) V. M. Geskin and J.-L. Brédas, ChemPhysChem, 2003, 4, 498–505 CrossRef CAS PubMed; (b) S. S. Zade, N. Zamoshchik and M. Bendikov, Acc. Chem. Res., 2011, 44, 14–24 CrossRef CAS PubMed.
- (a) M. M. Wienk and R. A. J. Janssen, J. Am. Chem. Soc., 1996, 118, 10626–10628 CrossRef CAS; (b) M. M. Wienk and R. A. J. Janssen, J. Am. Chem. Soc., 1997, 119, 4492–4501 CrossRef CAS; (c) M. P. Struijk and R. A. J. Janssen, Synth. Met., 1999, 103, 2287–2290 CrossRef CAS; (d) I. Kulszewicz-Bajer, M. Zagórska, I. Wielgus, M. Pawłowski, J. Gosk and A. Twardowski, J. Phys. Chem. B, 2007, 111, 34–40 CrossRef CAS PubMed; (e) I. Kulszewicz-Bajer, J. Gosk, M. Pawłowski, S. Gambarelli, D. Djurado and A. Twardowski, J. Phys. Chem. B, 2007, 111, 9421–9423 CrossRef CAS PubMed.
- A. Ito, D. Sakamaki, H. Ino, A. Taniguchi, Y. Hirao, K. Tanaka, K. Kanemoto and T. Kato, Eur. J. Org. Chem., 2009, 2009, 4441–4450 CrossRef.
- Q. Zhang, A. Khajo, T. Sai, I. de Albuquerque, R. S. Magliozzo and K. Levon, J. Phys. Chem. A, 2012, 116, 7629–7635 CrossRef CAS PubMed.
- C.-W. Lin, R. L. Li, S. Robbennolt, M. T. Yeung, G. Akopov and R. B. Kaner, Macromolecules, 2017, 50, 5892–5897 CrossRef CAS.
- (a) R. H. Baughman, J. F. Wolf, H. Eckhardt and L. W. Shacklette, Synth. Met., 1988, 25, 121–137 CrossRef CAS; (b) L. W. Shacklette, J. F. Wolf, S. Gould and R. H. Baughman, J. Chem. Phys., 1988, 88, 3955–3961 CrossRef CAS; (c) J. F. Wolf, C. E. Forbes, S. Gould and L. W. Shacklette, J. Electrochem. Soc., 1989, 136, 2887–2891 CrossRef CAS; (d) H. H. S. Javadi, S. P. Treat, J. M. Ginder, J. F. Wolf and A. J. Epstein, J. Phys. Chem. Solids, 1990, 51, 107–112 CrossRef CAS.
- K. Liu, Y. Liu, Y. Yao, H. Yuan, S. Wang, Z. Wang and X. Zhang, Angew. Chem., Int. Ed., 2013, 52, 8285–8289 CrossRef CAS PubMed.
- (a) S. A. Wolf, D. D. Awschalom, R. A. Buhrman, J. M. Daughton, S. von Molnár, M. L. Roukes, A. Y. Chtchelkanova and D. M. Treger, Science, 2001, 294, 1488 CrossRef CAS PubMed; (b) S. Hayami, S. M. Holmes and M. A. Halcrow, J. Mater. Chem. C, 2015, 3, 7775–7778 RSC.
- J. Potticary, L. R. Terry, C. Bell, A. N. Papanikolopoulos, P. C. M. Christianen, H. Engelkamp, A. M. Collins, C. Fontanesi, G. Kociok-Kohn, S. Crampin, E. Da Como and S. R. Hall, Nat. Commun., 2016, 7, 11555 CrossRef CAS PubMed.
- (a) T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS; (b) D. Jacquemin, E. A. Perpète, G. E. Scuseria, I. Ciofini and C. Adamo, J. Chem. Theory Comput., 2008, 4, 123–135 CrossRef CAS PubMed; (c) A. D. Laurent and D. Jacquemin, Int. J. Quantum Chem., 2013, 113, 2019–2039 CrossRef CAS; (d) M. J. G. Peach, P. Benfield, T. Helgaker and D. J. Tozer, J. Chem. Phys., 2008, 128, 044118 CrossRef PubMed; (e) M. J. G. Peach, C. R. L. Sueur, K. Ruud, M. Guillaume and D. J. Tozer, Phys. Chem. Chem. Phys., 2009, 11, 4465–4470 RSC.
- B. M. Mills, N. Fey, T. Marszalek, W. Pisula, P. Rannou and C. F. J. Faul, Chem. – Eur. J., 2016, 22, 16950–16956 CrossRef CAS PubMed.
- T. M. Maier, H. Bahmann, A. V. Arbuznikov and M. Kaupp, J. Chem. Phys., 2016, 144, 074106 CrossRef.
- (a) A. G. MacDiarmid and A. J. Epstein, Synth. Met., 1994, 65, 103–116 CrossRef CAS; (b) A. G. MacDiarmid and A. J. Epstein, Synth. Met., 1995, 69, 85–92 CrossRef CAS; (c) Y. Xia, J. M. Wiesinger, A. G. MacDiarmid and A. J. Epstein, Chem. Mater., 1995, 7, 443–445 CrossRef CAS.
- C. Boehme and J. M. Lupton, Nat. Nanotechnol., 2013, 8, 612–615 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Instrumentation, experimental details, DFT-calculated structures, charge distributions, frontier molecular orbitals, experimental and simulated UV-vis-NIR spectra, ESR spectra, analysis of computational method effects, Cartesian coordinates of computed molecular structures. CCDC 1562964. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8me00082d |
| ‡ Present address: Division of Polymer & Materials Chemistry, Lund University, Box 124, SE-221 00 Lund, Sweden. |
| This journal is © The Royal Society of Chemistry 2019 |