Controllable cell manipulation in a microfluidic pipette-tip design using capacitive coupling of electric fields

Abstract

Systems designed toward cell manipulation by electric fields are inherently challenged by energy dissipation along the electrode–electrolyte interface. A promising remedy is the introduction of high-k electrode passivation, enabling efficient capacitive coupling of electric fields into biological samples. We present the implementation of this strategy in a reusable pipette tip design featuring a 10 μl chamber volume for life science applications. Prototype validation and comparison to conductive gold-coated electrodes reveal a consistent and controllable biological effect that significantly increases the reproducibility of lysis events. The system provides precise descriptions of HEK-293 lysis dependency to variables such as field strength, frequency, and conductivity. Over 80% of cells were reversibly electroporated with minimal electrical lysis over a broad range of field settings. Successful transfection requires exponential decay pulses and showcases how modulating capacitive coupling can advance our understanding of fundamental mechanics in the field of electroporation.

---

Introduction

Electroporation describes the use of electric fields towards alteration of biological cells and tissues.¹ Depending on field parameters, the subjected cells undergo changes in size, shape and membrane uniformity.^2,3 While high electric fields lead to cell lysis (irreversible electroporation), applying moderate fields yield a reversible, non-lethal response that can be used for cell fusion or cargo delivery.⁴ The latter technique is utilized in a wide range of medical and research applications, ranging from gene delivery and stem cell isolation to electro-chemotherapy.⁵ In comparison to viral and chemical approaches for cargo- or gene transfer, electroporation has several advantages such as adaptability, high transfection rate, absence of contaminants and low immunogenicity.^6,7 In practice, one of the biggest challenges in electroporation is the limited precision of the effect which reduces cell survival or causes collateral tissue damage.^8,9

The causative effect of cellular damage is the result of various electrolytic processes that occur at the electrode interface.¹⁰ Unwanted side-effects include joule heating, pH change, bubble formation and electrode disintegration.^8,11,12 Gases formed at the solution boundary may become ionized with continuing exposure to high electric fields which in turn leads to arcing and high local temperature increase.¹¹ In sum, classic electric field application systems using metallic electrodes in direct contact with an electrolyte are always accompanied by varying degrees of adverse and unspecific side-effects which reduce cell survival, analyte integrity, reproducibility and the lifetime of electrodes.¹³

Several innovative attempts have been made to tackle this issue. Approaches include the spatial separation of electrodes and cells,⁸ fast reversal of electrochemical reactions by high frequency alternating currents¹⁴ and the introduction of nanosecond-timescale electroporation. The latter turns out to exemplify a special case for electroporation, with smaller pore sizes and substantially different effects such as organelle specificity.¹⁵ However, all three approaches require highly specialized electronic equipment regardless of their application.

Microfluidic approaches that aim to alleviate the adverse effects of electrolysis do so with varying degrees of success; persisting issues include loss of field uniformity due to complex electrode or fluidic channel geometries, elaborate flow concepts causing cell deformation and low throughput in highly miniaturized systems.^16,17 As authors and reviewers of such platforms point out, the major problem facing novel electroporation systems might be traced back to a persisting lack of mechanistic knowledge about the electropermeabilization process itself.^18,19

This study presents an attractive alternative to the above-mentioned adaptations by implementing electrodes insulated with a dielectric passivation layer. Foremost, this allows us to investigate isolated electric field effects by suppressing secondary effects that are the result of faradaic current.^20,21 The outcome is equally effective and resolves issues like electrolysis, pH change and electrode disintegration by limiting electrochemistry along the electrode interface. At the same time, the required electronic setup for pulse delivery remains simple. An efficient ohmic decoupling of electrode and liquid was previously utilized towards selective lysis of blood cells for sample preparation in a sepsis model.²¹ The TiO₂ passivation forms a biocompatible, chemically inert layer with a high dielectric constant (ε_r > 60) which is generated by thermal oxidation of titanium electrodes. This high-k coating design enables efficient capacitive coupling of the electric field into the liquid.

Capacitive coupling has a history of use in contactless dielectrophoresis, where it has successfully resolved issues associated with electrode fouling during continuous low-energy field application at high frequencies.^22,23 Here, the impact dielectric electrode coating on mammalian culture cells was assessed by lysis experiments with HEK-293 cells. Important known variables such as field strength, solution conductivity, pulse frequency and -number are addressed.

A window of opportunity exists between the pulse-field magnitude required for reversible and irreversible electroporation.^24,25 A highly specific field effect is desired for a homogeneous cell population such that a high fraction of cells are reversibly permeabilized without significant lysis. HEK-293 permeabilization experiments with propidium iodide (PI) showcase the specificity of high-k passivation by offering multiple settings to match these criteria. Subsequent experiments show that knowledge of efficient permeabilization settings can be used toward transfection of HEK-293 cells.

A further aim is to demonstrate the versatility of the material by complementing the existing flow-through design²¹ through a stationary, microfluidic pipette tip. By adapting the electric cell lysis unit (ECLU) into such a pipette tip design we present a convenient, low-throughput device optimized for life science applications. Given the small electrode distance of 81.3 μm, a battery driven version of the electroporation pipette can be envisioned for flexible and cost-effective use.

Materials and methods

Production of titanium-oxide coated prototypes

Grade 2 titanium foil (commercially pure titanium, cpTi with a purity of 99.2%) was cut in dimensions of 60 × 10 mm. Electrodes were cleaned and coated with titanium dioxide for an average thickness of 600 nm according to an optimized passivation procedure.²¹ Briefly, titanium sheets were cleaned with a series of acetone, ddH₂O and 2-propanol washes in an ultrasonic bath for 20 minutes each. Clean sheets were transferred to a muffle furnace (L 9/11P330, Schaefer & Lehmann, Germany) for thermal oxidation at 650 °C. Rise time was 2 hours and the maximum temperature sustained for 3 hours before passive cooling to room temperature.

Electroporation reservoirs were assembled using a double sided adhesive tape with defined thickness and bio-compatibility²⁶ (Adhesive Research, Arcare 90445). It provides a vertical spacing of 81.3 μm, placed 2.5 mm apart forming a channel with a volume of 12.15 μl (Scheme 1). The top 5 mm of a standard 20 μl pipette tip were removed and a short, 90° incision was made in the resulting narrow end. Electroporation tip assembly proceeded by inserting the electrode-flanked channel into the incision and sealing any edges air-tight with two-component epoxy adhesive (UHU plus Endfest 300, 45 640). The resulting tips can be used with any 20 μl pipette, set to a volume of 10 μl.

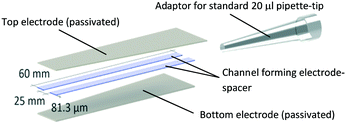Scheme 1 Prototype design and dimensions of the electroporation pipette tip. A microfluidic channel forms between the passivated titanium sheets shown on the top and bottom and flanked by double-sided adhesive tape, resulting in a channel volume of 12.15 μm. The top end of the channel was sealed to a standard 20 μl pipette-tip. With this adaptor, the channel acts as an elongation of the pipette tip and liquid can be aspirated via the open end of the channel. Images of an actual prototype are shown in Fig. 2 of the results section.

Production of gold coated prototypes

Rinsed titanium electrodes were coated with 60 nm Gold upon an adhesive layer of chrome (2–3 nm) using a vacuum coating system (Lab Coater Auto 306 with FL400 loading box, HHV). Prototype assembly was performed as described in the previous section.

Cyclic voltammetry

Buffers were prepared by dilution of PBS with Milli-Q water (Sartorius, 18 MOhm cm⁻¹) by 1 : 10 and 1 : 100. D-Sucrose (Fisher BioReagents, BP220-10) was dissolved in ddH₂O to yield a 250 mM stock solution. The buffers were aspirated into gold or titanium oxide prototype tips and connected to the impedance analyser (Metrohm Autolab B.V., μAUTOLABIII/FRA2) without reference electrode. Three cycles of current measurements were performed for voltages between +5 V_DC and −5 V_DC for all buffers and prototypes with a scan rate of 0.05 V s⁻¹ and step resolution of 2 mV. Titanium oxide coated electrode measurements include values for air (unfilled).

Leakage current measurements

Titanium oxide coated prototype tips were filled with PBS and electrodes connected to DC power supply (DP832, Rigol), and a multimeter (Fluke 289) in series. DC voltages of 5, 10, 15, 20, 25 and 30 V were applied via the DC power supply and the corresponding currents were measured by the multimeter.

Cell culture

Human embryonic kidney cells (HEK-293; ATCC CRL-1573) were cultivated at 37 °C and 5% CO₂ in DMEM (Thermo Fisher, 41965) supplemented with 10% FBS (Thermo Fisher, 10500) and 1% Pen/Strep Antibiotic-Antimycotic (Thermo Fisher, 15240). Cells were passaged by washing with PBS (1× from stock: Thermo Fisher, 70011044) followed by trypsinization (0.25%, Thermo Fisher, 25200) for 5 min at 37 °C and reconstituted in culture Medium. Any sterile protocols were processed in biological safety cabinets (Herasafe KS, Class II, Thermo Fisher, 51022488).

Sample preparation

Cells were washed with PBS, detached by trypsinization and resuspended in supplemented DMEM medium. Electroporation buffer (EPB) was prepared from autoclaved 250 mM sucrose solution. PBS was added to adjust the desired sample conductivity, which was measured using a conductivity meter (B-771 LAQUAtwin, HORIBA Advanced Techno). Cells were centrifuged for 5 min at 400 g (RT), supernatant discarded and resuspended with EPB. After two washing steps, cells were counted and adjusted to 10⁶ cells per ml with the next reconstitution. Final conductivity was recorded. If the suspension deviated more than 10 μS cm⁻¹ from the calibrated EPB, the washing step was repeated until conductivity was within this range. Cell death from sample preparation was also assessed. Only samples containing more than 85% live cells as determined by Hoechst 33342 stain were used for experiments.

Electroporation and imaging

HEK-293 cell lysis was used as a readout to analyze the biological impact of capacitive coupled electric fields on cells. Suspension of cells in EP buffer were transferred to hydrophobic parafilm in 10 μl droplets and aspirated with the electroporation tip. Electric fields were induced by applying the respective waveforms with a function generator (DG4102, Rigol) connected to a voltage amplifier (Falco WMA-300, Falco Systems, Netherlands). Voltages and currents were monitored (via a 2 Ω resistor) by an oscilloscope (DS1104B, Rigol). All indicated voltages refer to the maximum potential at the electrodes after capacitive charging is complete. When indicated, the conjectural field strength is derived by U/d = E. Both quantities refer to theoretical maxima that are proportional, but not equal to the effective electric field inside the electroporated medium.

After field application, cells were ejected onto parafilm and mixed with a 10 μg ml⁻¹ (10×) stock solution of Hoechst 33342 in PBS for a final concentration of 1 μg ml⁻¹. The sample was transferred to a hemocytometer (Thoma, Optik Labor) and imaged by a digital camera (Prosilica GT, Allied Vision) mounted on an inverted microscope (CKX41 Fluo V2, Olympus). Imaging in the hemocytometer ensures that each picture represents an equal volume of cell suspension. Bright-field images were recorded for total cell count. To identify lysed cells, Hoechst 33342 viability dye was excited at 360 nm using a UV light-source (X-Cite 120Q, Excelitas Technologies) and emission above 420 nm imaged for further analysis.

For permeabilization experiments, the cell suspension was mixed 1 : 10 with a 30 μg μl⁻¹ solution of propidium iodide prior to field exposure. The dye was prepared from dilution of a 1 mg ml⁻¹ stock with electroporation buffer to limit any conductivity change. As previously, the suspension was aspirated in the prototype channel and pulses were applied via the connected function generator. After field application, cells were directly ejected to the hemocytometer. To identify permeabilized cells, the membrane impermeable PI was excited from 480–550 nm using a UV light-source (X-Cite 120Q, Excelitas Technologies) and emission above 590 nm imaged for further analysis.

Data analysis

Lysis images were analyzed in Fiji²⁷ by adjusting the threshold to include positive cells only, isolating high-contrast live cells in bright-field and stained dead cells in fluorescence images. After converting images to binary, cell count was performed by the particle analysis function.

Results are displayed as percentage lysed, excluding the fraction of dead cells from sample preparation, which means that the control is always displayed as zero percent lysis.

PI-positive cells were counted manually from a bright-field and red fluorescence overlay. Controls were overexposed to the point where PI-negative cells remain invisible. This setting was then applied to samples subjected to electric fields. Dead cells show high-PI fluorescence, deformed or disintegrated structure in bright-field and were calculated equally as in lysis experiments. Permeabilized cells are displayed as the fraction of visibly live cells with PI fluorescence.

Transfection

Transfection requires cancellation of the inherent negative charge of the DNA molecule to allow for the formation of stable membrane-DNA complexes. This is most commonly achieved by the addition of MgCl₂ as described in the majority of standard electro-transfection protocols.²⁸ HEK-293 cells were prepared as for lysis experiments and kept in a sterile working environment. 9 μl of cell suspension was placed on hydrophobic parafilm and mixed with 1 μl vector stock solution for a final working concentration of 25 ng ml⁻¹ pTurboRFP-N (Evrogen, FP232) and 0.5 mM MgCl₂. The suspension was aspirated into the electroporation tip and exposed to 10 square wave or exponential decay pulses of 40 V at 1 kHz. They were ejected into an 8-well μ-slide (Ibidi, 80 826) and left to rest for 5 minutes. 250 μl OptiMEM (Thermo Fischer, 31 985 062) was added with gentle resuspension. Transfected cells were cultivated at 37 °C and 5% CO₂ for 48 hours and imaged by a digital camera (Prosilica GT, Allied Vision) mounted on an inverted microscope (CKX41 Fluo V2, Olympus). The fraction of cells expressing RFP was assessed from manual count of bright-field and red fluorescence overlays of at least 5 images from random positions in each respective well.

Statistics

Where applicable, n refers to the number of technical replicates with the same cell suspension and prototype. Each replicate consists of 3 imaging-replicates for lysis experiments and 5 imaging-replicates for permeabilization and transfection experiments. As such, any data point concerning lysis shows mean and standard deviation (SD) of 3 data points, in turn based upon 9 separately analysed microscopy images.

Where stated, Pearson correlation was computed between both data sets. Coefficients of variation for four different prototypes refer to the ratio of the SD to the mean. In the final section, p value was calculated using unpaired, parametric t-test (two-tailed) with Welch's correction since equal SD cannot be assumed for the different pulses applied.

Results and discussion

Electrochemical implications of high-k electrode passivation

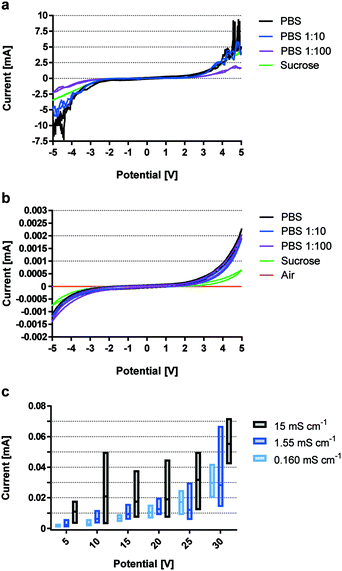
The introduction of an electrically insulating passivation leads to an ohmic decoupling of the electrode material from the liquid, limiting secondary effects of faradaic current acting on the electrolyte. This section demonstrates the advantages of using ohmic decoupling of the electrodes as compared to non-decoupled electrodes with respect to electrochemical reactions at the electrode-electrolyte interface.

Fig. 1 quantifies passivation efficiency of the metal oxide layer for different buffer conductivities. Electrodes with 60 nm Au coating reveal the faradaic current equivalents of a non-insulated system representing a standard electroporation setup. Fig. 1a shows current measurements with gold-coated titanium electrodes for potentials between −5 and 5 V_DC. Signal spikes are indicative of electrochemical reactions. Readings for higher conductivities were increasingly erratic above 4 V_DC, peaking between 2 mA and 9 mA. Electrode passivation significantly reduces the amount of current by approximately 4 orders of magnitude for all buffer dilutions (Fig. 1b). Passivated electrodes show no significant dependency on solution conductivity, as different PBS dilutions have similar current responses and peak around 2 μA. Measurements for empty electrodes (air filled) confirm that leakage current does not pass through the adhesive and was recorded at 20 nA. Due to the voltage limit of the impedance analyzer higher voltages were analyzed using a DC power source.

Fig. 1 Quantification of passivation efficiency in terms of current flow. Leakage current between +5 V_DC and −5 V_DC for pipette tip prototypes constructed with Au electrodes a) and TiO_x passivated electrodes (b and c), where c) shows results for voltages between 5 V_DC and 30 V_DC. n = 1 with 3 measurements.

Fig. 1c shows leakage currents for passivated electrodes, which remain below 10⁻⁴ A for all conductivities and voltages up to 30 V_DC. While currents for buffer conductivities of 0.160 mS cm⁻¹ and 1.55 mS cm⁻¹ remain similar, readings for 15 mS cm⁻¹ were consistently higher. Most notably, SD increased with conductivity and applied voltage, but never exceeded 72 μA even when using a highly conductive solution and 30 V_DC.

By minimizing the superimposing effects of faradaic current and thereby electrochemical reactions, high-k materials have great potential for highly reproducible and defined cell manipulation by electrical fields in microfluidic devices.

Characterization of electrode pipette tips

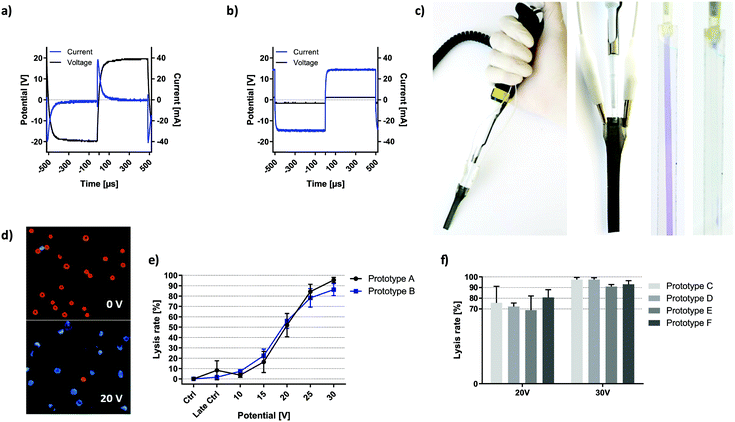
High-k materials such as titanium dioxide successfully allow for ohmic decoupling of electrode interfaces from the solution while efficient coupling of the electric field is enabled by its low capacitive reactance.

Fig. 2a and b compare the voltage and current characteristics upon application of a 20 V, 1 kHz square AC signal to a PBS-filled channel comprising Au or TiO₂ covered titanium electrodes, respectively. For the conductive Au coating, continuous current flow through the solution was observed due to direct contact between electrode material and the solution. In the case of TiO₂-coated electrodes, current flow is restricted to an initial capacitive charging of electrodes which stops when the set potential is reached, and no dynamic voltage change occurs (dU/dt = 0). This is a consequence of ohmic decoupling, the efficiency of which was quantified in detail in the previous section.

Fig. 2 Prototype description and validation. Voltage and current characteristics of prototypes using a) passivated and b) unpassivated electrodes when 20 V were applied to a PBS-filled channel at 1 kHz. c) Images of the prototype incorporated in a regular pipette configuration. Each respective electrode was contacted via alligator clamps. A flexible 2-pole cable connects the device to an amplified function generator. Transparent versions of the prototype visualize the microfluidic properties of the prototype channel. d) Overlay-image showing live (red) and dead (blue) cells at 0 V and 20 V with 6000 square waves applied at 1 kHz. Brightness and contrast have been enhanced for better visualization. e) Field dependency of HEK-293 cell lysis with two different prototypes. f = 1 kHz, σ = 260 μS cm⁻¹, exposure = 10 seconds, n = 3, error bars = SD. f) HEK-293 cell lysis at given voltage performed with 4 further prototypes. f = 1 kHz, σ = 160–171 μS cm⁻¹, exposure = 6 seconds, n = 3.

Fig. 2c shows the pipette with the electrode tip in working configuration. Electrodes were connected to the circuit via the upper lugs where the passivation layer was removed.

The channel was visualized using a blue dye in a transparent fluidic demonstrator (without the optically intransparent electrodes). The fluidic compartment was bonded to a standard pipette tip, which acted as an adapter between microfluidics and any 20 μl pipette.

Fig. 2d shows images of HEK cells without treatment and upon electric field exposure at lysis settings. Live cells are visible in the bright-field channel (visualized as red) and Hoechst 33342 viability stain shows dead cells visible in the blue channel.

To assess the reliability of prototype production, individual cell lysis curves were recorded with 6 functional electroporation pipette tips (passivated) with lysis triplicates. Fig. 2e shows lysis behaviour of HEK-293 cells exposed to 10 seconds of square wave signals with respective magnitude. The only variable was the prototype tip used. All data was standardized to the early control such that cell death from the preparation procedure was neglected in lysis values. Late control shows electric-field independent HEK-293 cell death over the course of respective experiments. Except for the data points at 30 V, all plotted values for one prototype fall within the SD of the other with a Pearson correlation of r² = 0.9817. SD is 5.5% for prototype A and 4.8% for prototype B. The highest SD was observed in the dynamic range of cell lysis (15–25 V). Similarly, Fig. 2f compares four different prototypes with respect to HEK-293 cell lysis upon 6 seconds of square wave exposure at the indicated voltage and lower solution conductivity. Application of 20 V resulted in 74.4% lysis with a combined SD of 10.0%. For individual prototypes, coefficients of variation range between 4.6% (prototype D) and 20.6% (prototype C). At 30 V lysis results were increasingly consistent, where the lysis rate of 94.7% deviated by 3.4% in total. Coefficients of variation range between 1.8% (prototype D) and 3.8% (prototype F).

The high consistency of recorded lysis events is surprising, given that sources of deviation include all passivation- and construction steps as well as randomized errors from the chosen readout. Most importantly, prototype construction is highly precise and does not represent a source of directed error in terms of HEK-293 cell lysis. This is the key prerequisite for identification of relevant lysis parameters in subsequent experiments.

Capacitive coupling dynamics are highly sensitive to cell suspension conductivity

We proceed to show the effects of electrode coating in terms of biological impact by presenting HEK-293 cell lysis dynamics at varying field strengths and buffer conductivities. Previous publications that have investigated the biological impact of solution conductivity have found contradicting correlations with respect to cell survival in response to electroporation. One study reports that lower conductivity promotes survival of DC3F cells when investigating the range between 0.01 to 10 mS cm⁻¹.²⁹ Another study finds increased survival of murine myeloma cells with increased buffer conductivity in the more narrow range between 0.8 and 3.7 mS cm⁻¹.³⁰ However, neither of the studies used a passivated or microfluidic setup and the tested conductivities included much larger changes or fall into a different range than the comparably minor changes of ±0.1 mS cm⁻¹ between 0.06 and 0.26 mS cm⁻¹ addressed here.

For mammalian cells, the threshold for low frequency electroporation is generally considered as 1 kV cm⁻¹.^7,31 Using gold-coated electrodes, onset of HEK-293 cell lysis (16.3–30.8%) was observed at 0.617 kV cm⁻¹ (Fig. 3a).

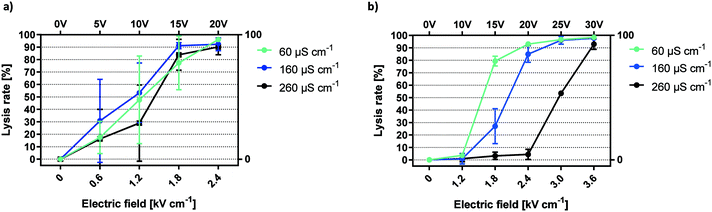Fig. 3 Conductivity dependency of electric field mediated lysis. Lysis efficiencies for HEK-293 cells using unpassivated a) and passivated electrodes b). f = 1 kHz, exposure = 6 seconds, n = 3.

Large variations for cell lysis with gold electrodes are the result of the multi-factorial nature of the lysis effect (electric field, electrolysis, electrochemistry, pH and temperature). The drawback of this combination was made clear by the difference in SD between gold and titanium oxide coated prototypes (Fig. 3a and b). The lack of reproducibility for gold electrodes was likely caused by the small electrode distance in the prototype channel. Any electrolytic activity as the result of an applied voltage will have random local distribution, thus making the fraction of affected cells unpredictable. There was no clear correlation between buffer conductivity and average cell lysis using gold-coated electrodes in this configuration.

In contrast, lysis curves for different conductivities remain distinctly separated when applying capacitively coupled electric fields (Fig. 3b). For a conductivity of 60 μS cm⁻¹, lysis began at 1.2 kV cm⁻¹ and reached a plateau at 2.4 kV cm⁻¹. Increasing the conductivity to 160 μS cm⁻¹, we observed lysis starting below 1.8 kV cm⁻¹ and peaking at 3 kV cm⁻¹. With 260 μS cm⁻¹, onset of lysis occurred at 2.4 kV cm⁻¹ and reached its maximum around 3.6 kV cm⁻¹. In sum, the lysis efficiency of HEK-293 cells was inversely proportional to buffer conductivity. This trend was highly reproducible and lysis curves are clearly distinguished by minor changes in buffer composition. The increase in the necessary field strength for cell lysis in the passivated electrode setup compared to gold electrodes was caused by a potential drop inside the passivation layer. However, due to the microfluidic setup and the high-k nature of the passivation material, high electric field-mediated lysis efficiency was reached at low voltage amplitudes. Solution conductivity must be sufficiently low for the applied voltages to influence HEK-293 cell viability. The steep correlation between lower conductivity and an increase in lysis efficiency can be attributed to ionic losses. As shown in a theoretical study of a similar system, current density is reduced by an increase in conductivity and leads to a faster decay of the electric field.¹¹

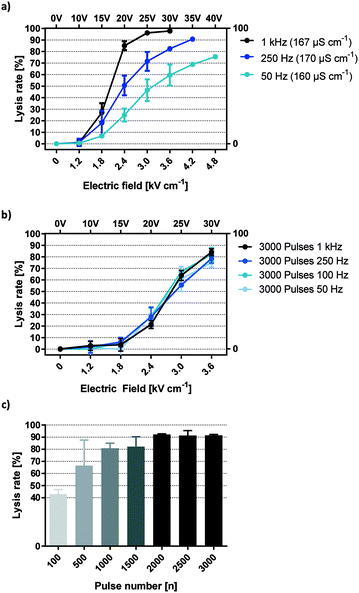
AC lysis efficiency is independent of square wave frequency and determined by pulse number

Fig. 4a shows HEK-293 cell lysis upon 6 second exposure to electric fields of rising magnitude applied by capacitive coupling. In all following descriptions, one pulse refers to a full AC square wave period. Pulses were applied in the same buffer at frequencies ranging from 50 Hz to 1 kHz. The data suggest that lysis efficiency positively correlates with both field strength and AC frequency. Because buffer conductivities were constant (165 ± 5 μS cm⁻¹), onset of lysis was observed from 1.8 kV cm⁻¹ in all cases. However, given that the total time that cells were exposed to the electric field was equal (6 seconds), the number of pulses increases with frequency. To distinguish frequency dependency from the impact of overall pulse number, total field exposure time was adjusted so that the number of pulses is equal for all frequencies (Fig. 4b). Typical for this conductivity, onset of cell disruption was seen at 1.8 kV cm⁻¹ while a plateau was reached by 3.6 kV cm⁻¹. With equal pulse numbers, lysis curves are aligned at all field strengths irrespective of frequency. This shows that coupled-field lysis dynamics are in fact frequency independent for square wave pulses when correcting exposure time for the number of pulses.

Fig. 4 Frequency dependency of electric field mediated lysis with capacitive coupling. a) Frequency dependency of HEK-293 lysis with equal field exposure time. b) HEK-293 lysis at different frequencies, exposure time adjusted to 3000 pulses. c) Lysis efficiency of different pulse numbers at 1 kHz. (a–c) σ = 160–170 μS cm⁻¹, n = 3.

Additional insights are gained by applying this information back to Fig. 4a and multiplying the indicated frequency with the total exposure time of 6 seconds. This reveals lysis information for 300 (50 Hz), 1500 (250 Hz) and 6000 (1 kHz) square wave pulses.

Notice that maximum lysis was approached for 6000 pulses at 25 V and 30 V but not for lower pulse numbers. This suggests a threshold number of 1500 to 6000 pulses required to yield a maximum electric field effect at the given voltage.

To identify the threshold pulse quantity for efficient lysis, a broader range of pulses were investigated (Fig. 4c). Field strength was set to 3.6 kV cm⁻¹ and frequency to 1 kHz. As a result, lysis efficiency increased steadily with pulse numbers up to 2000, reaching a plateau of maximum efficiency with around 90% lysis and minimal SD. We postulate that such a pulse threshold exists for any field strength high enough to cause cell lysis. This section demonstrates that HEK-293 lysis was independent of square wave frequencies between 50 Hz and 1 kHz but increases with the number of applied AC square wave pulses. This means that the lysis effect corresponds to a change in voltage (dU/dt) rather than the absolute voltage (U). In practice, this parameter is best monitored by observing the capacitive charging current which is always proportional to (dU/dt). As such, we can derive the relative electric field effect of a capacitively coupled setup simply by looking at its current plot.

If the number of times that the field direction is inversed is the only factor governing cell lysis at a specific field strength, then the time that passes between one such charge alternation and the next is also negligible in the given frequency range. In other words, it makes no difference whether the voltage is sustained for 10 ms (half-period for 50 Hz) or 0.5 ms (1 kHz) between inversions (Fig. 4b). This implies that the membrane effect that is elicited by our setup is cumulative and has a decay time longer than 10 ms.

Efficient propidium iodide delivery with limited cell death can be achieved with high and low energy pulses

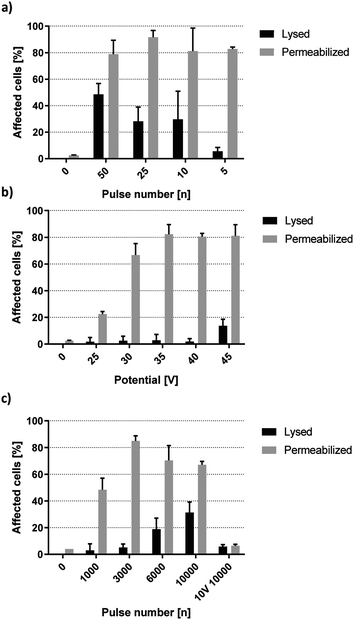
Membrane permeabilization occurs prior to cell lysis.²⁴ With knowledge of the lysis threshold of HEK-293 cells, it is possible to approximate at which setting membrane permeabilization takes place with minimal cell lysis. Fig. 5a shows lysis and PI-permeabilization of HEK-293 cells when exposed to a decreasing number of high-voltage square wave pulses. 50 pulses of 40 V lead to lysis of 48.5% of cells while PI was taken up by 78.8% of the remaining viable cells. Decreasing the number of pulses further resulted in higher viability while the fraction of live cells permeable to PI remained similar. Upon exposure to 5 square wave pulses of 40 V, 5.6% of HEK-293 cells were lysed by the electric field while 82.8% were viable and PI-positive. Fig. 5b shows further optimization of PI-delivery by changing the applied voltage. Cells were subjected to 5 square wave pulses at 1 kHz repetition rate. Viability was virtually unaltered by potentials lower than 45 V. HEK-293 cell viability was decreased by 1.8% upon application of five 25 V pulses while five 40 V pulses decreased viability by 2.5%. Because these minor viability changes do not correlate with the field increase, the recorded cell death was most likely caused by the working protocol rather than any specific field effect. Electrical cell lysis can be assumed to take place when further increasing the field to 45 V, resulting in a more significant viability reduction of 13.7%.

Fig. 5 Propidium iodide delivery with capacitive coupled electric fields. HEK-293 cell lysis and permeabilization after exposure to a) decreasing pulse number of 40 V square waves, b) 5 square wave pulses of increasing voltage and c) an increasing number of 15 V square wave pulses. Permeabilized refers to the percentage of remaining live cells. f = 1 kHz, σ = 160 μS cm⁻¹, n = 3.

Fig. 5b shows a correlation between field strength and the fraction of PI-permeable cells, yielding 22.4%, 66.7%, 82.3%, 80.5% and 81.1% for 25 V, 30 V, 35 V, 40 V and 45 V, respectively. The sharp increase between 25 V and 35 V as well as the following plateau of maximum permeabilization between 35 V and 45 V was reminiscent of dynamics observed from lysis experiments in the previous section. This implies the existence of distinct but separate energy thresholds for complete permeabilization or lysis of HEK-293 cells. Looking back at Fig. 4a reveals that onset of lysis was pulse number dependent from 15 V upward. Fig. 5c further shows that PI-permeabilization was strongly correlated with pulse number at 15 V. 1000 square wave pulses yielded 48.4% PI-positive viable HEK-293 cells, increasing up to 85.0% at 3000 pulses with minimal loss of viability. A further increase in pulse number did not improve PI delivery but rather increased the rate of electrical cell lysis. Interestingly, the permeabilization of remaining live cells did not remain at a plateau of ∼80% as was the case for high voltage pulses but decreased steadily (Fig. 5c). However, the total amount of HEK-293 cells affected by the field remained relatively stable, with the sum of lysed or permeabilized cells being 85.8%, 76.0% and 77.4% for 3000, 6000 and 10 000 pulses, respectively (not shown). As such, these numbers do not account for a difference in field penetration at different voltages but rather indicate the cumulative biological effect of this specific field magnitude. Additionally, cells exposed to 10 000 pulses of 10 V were not affected by the electric field. This indicates the existence of a minimum threshold for HEK-293 specific membrane permeabilization between 10 V and 15 V corresponding to a theoretical field strength between 1.2 and 1.8 kV cm⁻¹.

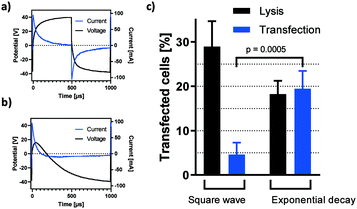
Mammalian cell transfection is feasible with high-k passivated electrodes

Given the efficiency of small molecule transfer observed in the previous section, we proceeded to assess if these settings may be applied towards gene delivery. According to Fig. 5b, high-energy pulses yield the largest window of opportunity for high-efficiency permeabilization. Consequently, square wave pulses of 40 V were chosen for initial transfection experiments. Fig. 6c shows HEK-293 cells expressing TurboRFP 48 hours after electro-transfection with pTurboRFP-N plasmid. The application of 10 square wave pulses resulted in average transfection efficiencies of 4.6%. This seems surprisingly low, given that the field thresholds required for PI and plasmid delivery are known to be similar.³² However, it was shown that efficient transfection by electric fields is improved by a unidirectional electrophoretic component that facilitates DNA movement.^7,32,33 Remembering the insights about capacitively coupled pulse dynamics revealed by their frequency independency (Fig. 4a and b), we find that each period of a square wave has two equal and opposite peaks which fail to provide net DNA movement (Fig. 6a). To achieve a unidirectional, electrophoretic force component with capacitive coupling, the slopes of the voltage plot need to be asymmetric. One example is the use of an exponential decay function in which ΔU/dt is maximised in one direction and sufficiently reduced in the other (Fig. 6b). In this case, the applied voltage rises instantly and drops exponentially from +40 V to −40 V over the course of one 20 ms period. As revealed by the current plot, a significant electric field effect occurs exceedingly in the positive direction. Fig. 6c shows that such exponential decay pulses result in a significant increase of plasmid delivery events to 19.5% of cells. This confirms the impact of an electrophoretic component on the complex process of DNA delivery and shows how capacitive coupling can be utilized for gene transfer. As can be expected from the corresponding current plots (Fig. 6a and b), the impact on cell lysis is reduced by the exponential decay pulse (Fig. 6c).

Fig. 6 Transfection by capacitive coupling. Pulse characteristics of EPB subjected to a) square wave and b) exponential decay pulses of 40 V at 1 kHz. σ = 160 μS cm⁻¹ c) capacitively coupled, electric field mediated transfection of HEK-293 cells with pTurboRFP-N plasmid. Bars show the percentage of cells lysed (black bars, n = 3) or expressing RFP 48 hours after field exposure as detected and quantified by fluorescence microscopy (blue bars). f = 1 kHz, σ = 161 μS cm⁻¹, square wave: n = 3, exponential decay: n = 8.

We propose that a modified high-k passivation layer with increased capacity allows for higher net movement of plasmid DNA per pulse application and thereby increases the rate of transfection.

Conclusion

The introduction of electrode passivation with high-k material for capacitive coupling of electric fields drastically increases the consistency of electroporation events, offers superior control of relevant variables and thereby allows for the detailed assessment of parameter changes. This was achieved by the reduction of faradaic current across the working solution at biologically relevant voltages. The implementation of titanium dioxide coated electrodes in a stationary design demonstrates the versatility and applicability of this concept in microfluidic devices. Both the passivation- and assembly procedures are simple, cost efficient and yield prototypes that have a consistent biological outcome. The necessity of electrode passivation in this microfluidic design was showcased by experiments with unpassivated electrodes, which do not allow for an indicative readout of the parameter changes. Experiments with HEK-293 cells reveal clear and distinct dependencies between experimental parameters and biological outcome in terms of both lysis and permeabilization. Most notably, manual prototype assembly has less impact on cell lysis than any other tested variable.

In summary, this system offers the unique opportunity to study the impact of alternating electrical fields on biological suspensions by excluding the superimposing effects of electrochemistry. We demonstrate its applicability towards cell lysis, cargo transfer and transfection. The efficiency of transfection is expected to increase with further optimization of the presented platform in terms of current and passivation layer characteristics.

Author contributions

TW, JRP, EKE and KJW are responsible for conceptualization of the idea. TW conducted data curation and formal analysis. KJW is responsible for funding acquisition. TW is responsible for investigation and specifically performed experiments and data acquisition. TW, EKE and KJW developed the methodology. EKE and KJW are responsible for administration, resources and supervision. TW is responsible for validation. TW, JRP, EKE and KJW are responsible for visualization, preparation, creation and presentation of the published work. TW wrote the original draft. TW, JRP, EKE and KJW are responsible for review and editing. All authors have read and approved the manuscript.

Conflicts of interest

We declare that the authors Terje Wimberger, Johannes R. Peham and Klemens J. Wassermann have filed a patent application (date: 12.12.2018; application number: EP18211969.3) on behalf of the Austrian Institute of Technology which includes the following aspects of the manuscript: the passivation strategy, stationary prototype design and their application towards cell lysis, permeabilization and transfection. Eva-Kathrin Ehmoser has no conflicts of interest to declare.

Acknowledgements

The authors would like to acknowledge the Austrian Institute of Technology GmbH as the source of funding for this project. We wish to thank Seta Küpcü from the Department of Nanobiotechnology at BOKU University for considerations that went into choosing HEK-293 cells as a model for this article. Special thanks go to Christina Bliem for her assistance in the graphical design of the prototype in Scheme 1.

References

1. J. C. Weaver, IEEE Trans. Plasma Sci., 2000, 28, 24–33.
2. R. S. Son, K. C. Smith, T. R. Gowrishankar, P. T. Vernier and J. C. Weaver, J. Membr. Biol., 2014, 247, 1209–1228.
3. J. C. Weaver, K. C. Smith, A. T. Esser, R. S. Son and T. R. Gowrishankar, Bioelectrochemistry, 2012, 87, 236–243.
4. V. Dimitrov, S. Kakorin and E. Neumann, Phys. Chem. Chem. Phys., 2013, 15, 6303–6322.
5. H. M. Eppich, R. Foxall, K. Gaynor, D. Dombkowski, N. Miura, T. Cheng, S. Silva-Arrieta, R. H. Evans, J. A. Mangano, F. I. Preffer and D. T. Scadden, Nat. Biotechnol., 2000, 18, 882–887.
6. L. Lambricht, A. Lopes, S. Kos, G. Sersa, V. Préat, G. Vandermeulen and Expert Opin, Drug Delivery, 2016, 13, 295–310.
7. C. Rosazza, S. H. Meglic, A. Zumbusch, M.-P. Rols and D. Miklavcic, Curr. Gene Ther., 2016, 16, 98–129.
8. J. A. Kim, K. Cho, M. S. Shin, W. G. Lee, N. Jung, C. Chung and J. K. Chang, Biosens. Bioelectron., 2008, 23, 1353–1360.
9. J. A. Kim, K. Cho, Y. S. Shin, N. Jung, C. Chung and J. K. Chang, Biosens. Bioelectron., 2007, 22, 3273–3277.
10. P. Turjanski, N. Olaiz, F. Maglietti, S. Michinski, C. Suarez, F. V. Molina and G. Marshall, PLoS One, 2011, 6, e17303.
11. A. Meir and B. Rubinsky, RSC Adv., 2014, 4, 54603–54613.
12. A. Ainla, S. Xu, N. Sanchez, G. D. M. Jeffries and A. Jesorka, Lab Chip, 2012, 12, 4605–4609.
13. N. Jokilaakso, E. Salm, A. Chen, L. Millet, C. D. Guevara, B. Dorvel, B. Reddy, A. E. Karlstrom, Y. Chen, H. Ji, R. Sooryakumar and R. Bashir, Lab Chip, 2013, 13, 336–339.
14. D. Zhao, D. Huang, Y. Li, M. Wu, W. Zhong, Q. Cheng, X. Wang, Y. Wu, X. Zhou, Z. Wei, Z. Li and Z. Liang, Sci. Rep., 2016, 6, 18469.
15. L. Chopinet and M.-P. Rols, Bioelectrochemistry, 2015, 103, 2–6.
16. H. Lu, M. A. Schmidt and K. F. Jensen, Lab Chip, 2005, 5, 23–29.
17. L. Nan, Z. Jiang and X. Wei, Lab Chip, 2014, 14, 1060–1073.
18. T. Geng and C. Lu, Lab Chip, 2013, 13, 3803–3821.
19. A. Rolong, E. M. Schmelz and R. V. Davalos, Integr. Biol., 2017, 9, 979–987.
20. T. S. Santra, C.-W. Chen, H.-Y. Chang and F.-G. Tseng, RSC Adv., 2016, 6, 10979–10986.
21. K. J. Wassermann, S. Barth, F. Keplinger, C. Noehammer and J. R. Peham, ACS Appl. Mater. Interfaces, 2016, 8, 21228–21235.
22. H. Shafiee, J. L. Caldwell, M. B. Sano and R. V. Davalos, Biomed. Microdevices, 2009, 11, 997–1006.
23. M. B. Sano, J. L. Caldwell and R. V. Davalos, Biosens. Bioelectron., 2011, 30, 13–20.
24. T. Kotnik, A. Macek-Lebar, D. Miklavcic and L. M. Mir, BioTechniques, 2000, 28, 921–926.
25. M. Bonakdar, P. M. Graybill and R. V. Davalos, RSC Adv., 2017, 7, 42811–42818.
26. S. R. A. Kratz, C. Eilenberger, P. Schuller, B. Bachmann, S. Spitz, P. Ertl and M. Rothbauer, Sci. Rep., 2019, 9, 9287.
27. J. Schindelin, I. Arganda-Carreras, E. Frise, V. Kaynig, M. Longair, T. Pietzsch, S. Preibisch, C. Rueden, S. Saalfeld, B. Schmid, J.-Y. Tinevez, D. J. White, V. Hartenstein, K. Eliceiri, P. Tomancak and A. Cardona, Nat. Methods, 2012, 9, 676–682.
28. S. Li, Cold Spring Harbor Prot., 2006, http://cshprotocols.cshlp.org/content/2006/1/pdb.prot4449.abstract.
29. G. Pucihar, T. Kotnik, M. Kanduser and D. Miklavcic, Bioelectrochemistry, 2001, 54, 107–115.
30. C. S. Djuzenova, U. Zimmermann, H. Frank, V. L. Sukhorukov, E. Richter and G. Fuhr, Biochim. Biophys. Acta, Biomembr., 1996, 1284, 143–152.
31. M.-P. Rols and J. Teissié, Biophys. J., 1998, 75, 1415–1423.
32. M. Pavlin and M. Kandušer, Sci. Rep., 2015, 5, 9132.
33. M. M. Sadik, M. Yu, M. Zheng, J. D. Zahn, J. W. Shan, D. I. Shreiber and H. Lin, Biophys. J., 2014, 106, 801–812.

---