 Open Access Article
Open Access ArticleRotating magnetic particles for lab-on-chip applications – a comprehensive review
C. P.
Moerland
 ,
L. J.
van IJzendoorn
and
M. W. J.
Prins
,
L. J.
van IJzendoorn
and
M. W. J.
Prins
 *
*
Department of Applied Physics, Department of Biomedical Engineering, Institute for Complex Molecular Systems, Eindhoven University of Technology, Eindhoven, The Netherlands. E-mail: m.w.j.prins@tue.nl
First published on 20th February 2019
Abstract
Magnetic particles are widely used in lab-on-chip and biosensing applications, because they have a high surface-to-volume ratio, they can be actuated with magnetic fields and many biofunctionalization options are available. The most well-known actuation method is to apply a magnetic field gradient which generates a translational force on the particles and allows separation of the particles from a suspension. A more recently developed magnetic actuation method is to exert torque on magnetic particles by a rotating magnetic field. Rotational actuation can be achieved with a field that is uniform in space and it allows for a precise control of torque, orientation, and angular velocity of magnetic particles in lab-on-chip devices. A wide range of studies have been performed with rotating MPs, demonstrating fluid mixing, concentration determination of biological molecules in solution, and characterization of structure and function of biomolecules at the single-molecule level. In this paper we give a comprehensive review of the historical development of MP rotation studies, including configurations for field generation, physical model descriptions, and biological applications. We conclude by sketching the scientific and technological developments that can be expected in the future in the field of rotating magnetic particles for lab-on-chip applications.
Introduction
Magnetic nano- and micro-particles (MPs) can be actuated in fluids using applied magnetic fields. Their large surface-to-volume ratio and the availability of a wide range of particle types and methods for surface functionalization have enabled the application of MPs as carriers (e.g. for biomolecule and cell extraction), as labels (e.g. for biomolecule detection) and as probes in biophysical studies (e.g. to quantify mechanical properties of molecules and cells). Several reviews have discussed principles and applications of magnetic actuation, see e.g. Gijs et al. 2010 (MPs in microfluidics),1 Van Reenen et al. 2014 (lab-on-chip biosensing),2 Schrittwieser et al. 2016 (homogeneous bioassays)3 and Munaz et al. 2018 (magnetophoresis).4The most well-known method to actuate MPs is by applying a magnetic field gradient that generates a translational force on the MPs. A characteristic property of gradient-based actuation is a non-uniform force on the magnetic particles. A more recently developed magnetic actuation method is to rotate particles by applying a magnetic field of which the direction and/or amplitude varies over time. Rotational actuation can be achieved with a field that is uniform in space and it allows for a precise control of torque, orientation, and angular velocity of MPs in lab-on-chip devices. In the past years a wide range of studies have been performed with rotating MPs, demonstrating applications such as fluid mixing, concentration determination of biological molecules in solution and torsional characterization of biomolecules at the single-molecule level.
This review starts with a brief description of the basic physical principles of rotational actuation of MPs and categorizes the experimental configurations. Then a detailed description is given of the internal structure of MPs, how this underlies their magnetic properties and the torque generated by an applied field, and an overview is given of field-generating setups reported in the literature. Finally we discuss a number of lab-on-chip studies with rotating MPs that exemplify the field and we give an outlook into future scientific and technological developments.
Physical principles and basic configurations
In this section the physical origin of magnetic particle rotation will be addressed and the main experimental configurations found in literature will be categorized.The rotational force on an object, the torque, is represented with symbol ![[small tau, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1ca.gif) and is expressed in the unit N m (Newton times meter). A magnetic object that is placed in a magnetic field, experiences a torque of magnetic origin given by:
and is expressed in the unit N m (Newton times meter). A magnetic object that is placed in a magnetic field, experiences a torque of magnetic origin given by:
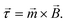 | (1) |
In eqn (1)![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) is the magnetic moment of the object and
is the magnetic moment of the object and ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) the magnetic flux density caused by the applied external field.
the magnetic flux density caused by the applied external field.
The torque tends to rotate the object so that the magnetic moment and the magnetic field become aligned; and when they are aligned, the torque reduces to zero. Note that this equation does not contain the gradient of the magnetic field, so a magnetic field that is spatially completely uniform can generate a torque. This is in contrast to the magnetic force, ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) = ∇(
= ∇(![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) ·
·![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) ), which is nonzero only in a spatially non-uniform magnetic field, i.e. the application of force requires the presence of a gradient in the magnetic field.
), which is nonzero only in a spatially non-uniform magnetic field, i.e. the application of force requires the presence of a gradient in the magnetic field.
Many different MPs are used in research and technology. They can be nanometer sized and consist of a single-domain magnetic crystal or consist of a few fused or agglomerated magnetic crystals. In this paper we will refer to such nano-crystals as “cores”. Larger magnetic particles ranging in size from approximately 200 nm to several micrometers can contain up to tens of thousands of cores embedded in a non-magnetic polymer or glassy matrix. The MPs have a total magnetic moment ![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) with a magnitude and orientation that depends on the internal magnetic structure of the MP and on the applied magnetic field.
with a magnitude and orientation that depends on the internal magnetic structure of the MP and on the applied magnetic field.
Every individual core has a magnetic moment of which the orientation can be perturbed by thermal energy (kBT), by an applied magnetic field (Um = ![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) core·
core·![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) ), and by core–core interactions. Re-magnetization of each individual core occurs when the perturbation energy is larger than the internal energy barrier for re-magnetization. The magnitude of the barrier depends on the magnetic anisotropy of the core, which has several contributions like its volume and shape. These mechanisms lead to the appearance of magnetic torque in the particle, a topic that is further detailed in section ‘Magnetic cores and magnetic particles’.
), and by core–core interactions. Re-magnetization of each individual core occurs when the perturbation energy is larger than the internal energy barrier for re-magnetization. The magnitude of the barrier depends on the magnetic anisotropy of the core, which has several contributions like its volume and shape. These mechanisms lead to the appearance of magnetic torque in the particle, a topic that is further detailed in section ‘Magnetic cores and magnetic particles’.
The torque and rotation of magnetic particles in a lab-on-chip device can be controlled by applying a magnetic field of which the direction and/or amplitude varies over time. We refer to “uniaxial field actuation” when the amplitude of the field changes over time but not the direction of the field; in literature this is also referred to as AC fields (alternating current). We refer to “rotating field actuation” when the direction of the field changes over time. See Dieckhoff et al.5 for a discussion on the effects of the types of driving field (uniaxial or rotating).
Fig. 1 sketches five experimental configurations in which rotational actuation of MPs is exploited for different functionalities, namely for mixing (Fig. 1A), for determining the concentration of biological molecules (Fig. 1B and C) or for biophysical characterization of cells or molecules (Fig. 1D and E). In the following paragraphs we will summarize the main application areas based on these experimental configurations, addressing the physical measurement principles, the magnetic properties of the involved particles, and the magnetic actuation devices used in these experiments. A more extensive description of the application areas can be found in the section “Applications of rotating MPs”.
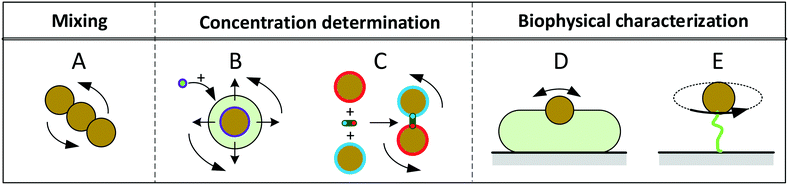 | ||
| Fig. 1 Schematic overview of experimental configurations that have been studied with rotating magnetic MPs. Related literature is indicated in Table 2. Panel A: Chains of MPs are rotated and used for mixing of fluids or to increase the molecular capturing rate for biosensor applications. Panel B: MPs capture target molecules from solution, which changes the hydrodynamic radius of the MPs. The hydrodynamic radius is determined by rotational actuation, detecting the magnetic or optical scattering response in a time varying magnetic field. Panel C: The concentration of target molecules is determined via target-induced formation of clusters of MPs. The clusters are measured by rotational actuation, detecting the magnetic or optical scattering response in a time varying magnetic field. Panel D: Magnetic particles are attached to cells and are rotated by an applied field. The MPs probe the mechanical compliance of the cell and its membrane. Panel E: Mechanical properties of single biological molecules (DNA/protein/enzyme) are probed by sandwiching the molecule between a substrate and a rotating magnetic particle. | ||
Mixing of fluid can be effectuated by applying a rotating field to a chain of MPs2,6–15 (Fig. 1A). The chains are formed due to attractive magnetic dipole–dipole forces between the particles. The resulting chains of magnetic particles have a strong shape anisotropy that causes them to align along the applied magnetic field, so that a rotating field causes rotation of the chains and locally mixes the fluid.
A second functionality of rotating MPs is to determine the concentration of target molecules in a solution (Fig. 1B and C). One technique is to detect a change in hydrodynamic size when target molecules bind to the MPs16–29 (Fig. 1B). The binding is made target-specific by coupling capture molecules to the particles, e.g. antibodies or aptamers. Preferably small particles are used (40–400 nm diameter) so that the relative volume change induced by the targets is significant. The hydrodynamic size of a MP can be measured via the rotational hydrodynamic drag that scales with the volume of the particle. A change of the hydrodynamic size of MPs can be detected by optical or magnetic signals. Optical detection of rotating particles requires an optical asymmetry. Alternatively, one can magnetically measure the rotational response of particles, which requires a magnetic moment that is physically coupled to the orientation of the particle, i.e. when the magnetic moment is a remnant moment. An early publication by Chung et al.17 in 2004 describes a measurement of hydrodynamic size by magnetic detection under uniaxial field actuation (AC fields), where a slower response speed was observed when target proteins were present in solution.
Another way to measure the concentration of target molecules is by a cluster assay. Here MPs are provided with capture molecules and form clusters in the presence of target molecules30–46 (Fig. 1C). The clusters can be detected by optical or by magnetic signals. Optical detection exploits the modulation of scattering due to the elongated shape of clusters compared to single particles, by measuring the amplitude or the frequency of the oscillations in the scattered light. An early publication by Baudry8 describes the dependence of the amplitude of the oscillations on the formation of particle clusters.
A third functionality of rotating MPs is to probe mechanical properties of single cells (Fig. 1D) or single molecules (Fig. 1E). In cell studies, the cells are immobilized on a substrate and MPs are attached to the cell membrane. The mechanical properties of the membrane and underlying cell structure are probed by applying a uniaxial or a rotating magnetic field, also called magnetic twisting cytometry.47–60 The deformation of the cell can be determined by measuring the magnetic response of ensembles of MPs, or by tracking the movement and rotation of single particles in an optical microscope. The anisotropy of cellular rigidity60 as well as influence of the binding mechanism of the MP to the cell51 was investigated.
Studies on the mechanical properties of single molecules have focused on macromolecules like DNA and proteins61–89 (Fig. 1E). The molecules are sandwiched between a magnetic particle and the surface of a fluid cell. A mechanical torque is applied by magnetic fields and the rotation of individual particles is tracked using an optical microscope. Experiments have shown that the macromolecules behave as torsional springs, that DNA has supercoiling behavior, and that the influence of proteins and enzymes binding to DNA can be studied.
In the following sections we will discuss how torque is generated in MPs, the magnetic field actuation systems that have been used, and subsequently we will review lab-on-chip studies based on application and control of torque and rotation.
Magnetic cores and magnetic particles
The magnetic content of a magnetic particle typically consists of ferro- or ferri-magnetic nano-crystals. These nano-crystals consist of a single-crystalline domain with strong internal magnetic coupling, so that they represent a single magnetic domain that is magnetized along an easy axis of magnetic anisotropy. Such nano-crystals are referred to as cores. When an external magnetic field is applied, the moment of the core tends to align with the field. The reorientation time of a single magnetic moment depends on the size, shape and atomic structure of the core. In 1949 Louis Néel developed a theory that relates the thermal magnetic relaxation time (in the absence of an applied field) of a single core to its volume: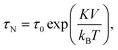 | (2) |
Core–core interactions such as dipolar and/or exchange interactions are not taken into account in the Néel model, but these can also have a strong influence on the magnetic relaxation time.93 The core–core interactions are defined by the mesoscopic structure of the MP. Three types of mesoscopic structures can be distinguished. The simplest case is a single nanocrystal that behaves as a single magnetic domain (Fig. 2A). The second type consists of multiple fused single crystals that behave as a single magnetic entity due to the strong magnetic (exchange) coupling (Fig. 2B). The third type consists of an agglomerate of single nanocrystals that do not have exchange coupling but do have strong dipolar interactions due to their close proximity (Fig. 2C). Such nanocrystal-based particles are used in many applications, including hyperthermia and magnetic particle imaging.94 Reviews on the synthesis methods of magnetic nanoparticles have been written by Willard et al. in 2004 (ref. 95) and more recently by Wu et al. in 2015.96 Classifications of magnetic nanoparticles, synthesis methods and analysis methods have been reviewed and summarized by Bogren et al. in 2015 (ref. 97) and the standardization has been described by Wells et al. in 2017.98
 | ||
| Fig. 2 Magnetic cores and magnetic particle. (A) TEM image of a single-nanocrystal core (CSIC11 produced by Consejo Superior de Investigaciones Científicas, Spain). (B) TEM image of a core consisting of fused crystals (FeraSpin-L produced by nanoPET, Germany). (C) TEM image of a multi-nanocrystal agglomerate (MM06 produced by MicroMod, Germany). (D) Example of an architecture of a bio-functional MP:98 (1) magnetic cores in brown, (2) core aggregate, (3) non-magnetic shell in gray, and (4) biofunctional layer in green. The particles shown in panels A–C were synthesized in the NanoMag FP7 project (http://nanomag-project.eu). | ||
Fig. 2D shows the architecture of a multi-core MP that is typically used in lab-on-chip applications. The magnetic cores (brown) are fixed within a non-magnetic material (gray) and the outer surface of the MP is bio-functionalized (green).
In 1976 John Ugelstad et al.99 described an emulsion polymerization process to produce porous monodisperse micrometer-sized polystyrene particles in which magnetic cores can be fixed. The cores are distributed quite homogenously throughout the particle.100 The creation of these MPs was a major breakthrough in the field. The particles show strong magnetic properties due to the large number of nanometer sized cores inside the particle.
A MP that is placed in a magnetic field can respond by internally changing its magnetization direction, called Néel relaxation, or by changing its physical orientation, called Brownian relaxation.101 Both processes lower the magnetic energy by orienting the magnetic moments of the cores toward the external field. There are two limiting cases of Néel relaxation, namely fast relaxation for superparamagnetic particles and slow relaxation for magnetically blocked particles (particles with a barrier for re-magnetization that exceeds the thermal energy). In the superparamagnetic limit the re-magnetization barrier of the cores is smaller than the thermal energy so the magnetic relaxation time is short, i.e. shorter than the timescale of the lab-on-chip experiment. The magnetization of an ensemble of superparamagnetic cores in thermal equilibrium can be modeled like atomic paramagnets, only with a significantly larger magnetic moment. This implies that the magnetic moment of the MP is zero in absence of an external field. For the small field regime (B typically <50 mT) the magnetization is approximately linear with the external field and occurs on a timescale that is short compared to the timescale of the experiment. One of the first to use the term “superparamagnetism” were Bean and Livingston in 1959.102 In the same year they also reported on the possibility to apply a torque to a powder of aligned magnetic nanoparticles.103 Due to the magnetic anisotropy of the cores, the magnetic susceptibility, χ, is anisotropic and torque is generated when the field is not aligned with the easy axis.104 For blocked particles, the re-magnetization barrier of the cores is larger than the thermal energy and the MP has a remnant magnetic moment, with a magnetic relaxation time that is much longer than the experimental timescale. To apply a torque on ferromagnetic MPs they are typically magnetized by applying a short (<1 s) strong (>100 mT) magnetic pulse.53,105 The pulse creates a remnant moment that is constant over time during the measurement. When the resulting remnant moment is placed in a field that is small (much smaller than the original pulse, i.e. <100 mT), and misaligned with the moment, then a torque is exerted.
For an ensemble of MPs, the total remnant moment can be measured using a commercially available magnetometer, for example a superconducting quantum interference device (SQUID) or a vibrating sample magnetometer (VSM). For an individual MP, the remnant moment can be quantified via the magnetic torque by tracking the rotation of a single particle in an optical microscope.106 For a particle that is not attached and that can freely rotate in solution at the same frequency as the applied magnetic field, the torque on the particle is approximately equal to its rotational hydrodynamic drag. The hydrodynamic drag of a smooth sphere with radius R in a fluid with dynamic viscosity η, is given by the Stokes equation, which together with eqn (1) gives the following equation for the angular motion of the particle:
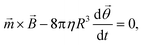 | (3) |
![[small theta, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c8.gif) is the angular orientation of the particle.107 Inertial forces have been ignored since these can be neglected for small particles (between 10 nm and 10 μm).106 When a particle is bound to a substrate via a cell or a molecular complex (cf.Fig. 1D and E), the rotational motion is restricted by the elastic properties of the biological matter. A general analytical expression is not available for the torsional elasticity of biological matter due to its complex structure. In case of small deformations of a biological macromolecule, the response can be approximated by a linear torsional spring,
is the angular orientation of the particle.107 Inertial forces have been ignored since these can be neglected for small particles (between 10 nm and 10 μm).106 When a particle is bound to a substrate via a cell or a molecular complex (cf.Fig. 1D and E), the rotational motion is restricted by the elastic properties of the biological matter. A general analytical expression is not available for the torsional elasticity of biological matter due to its complex structure. In case of small deformations of a biological macromolecule, the response can be approximated by a linear torsional spring, ![[small tau, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1ca.gif) = −k
= −k![[small theta, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c8.gif) , where typically τ < 1 pN μm (i.e. 1 pN using a 1 μm arm).70
, where typically τ < 1 pN μm (i.e. 1 pN using a 1 μm arm).70
Superparamagnetic micrometer-sized multicore MPs, like the ones invented by John Ugelstad et al.,99 typically contain tens of thousands of non-remnant nanometer-sized cores fixed in a non-magnetic matrix. If these cores are randomly oriented, one would expect an isotropic magnetic susceptibility and thus it would be impossible to generate a magnetic torque. However experiments have shown that a torque can be exerted on a single multicore superparamagnetic particle.106,108 The torque of single superparamagnetic particles with a diameter of 2.8 μm has been calibrated in small fields (<5 mT on Dynal M-280 particles106) as well as in larger fields (10–100 mT on Dynal M-270 particles108). For the small fields, the magnetic torque was calibrated based on the known hydrodynamic drag of a smooth sphere, which revealed a linear dependence of the torque on the applied field. This linear dependence of the torque was attributed to a small remnant moment in the superparamagnetic particles.106 For larger magnetic fields (10–100 mT), the angular thermal motion of surface-coupled particles was recorded to calibrate the magnetic torque. A quadratic scaling of the magnetic torque with field was found,108 indicating that there is a net anisotropy in the MP,103 or in other words, an easy-axis and a hard-axis.104
A quadratic scaling of torque with field was also found for two-particle clusters of superparamagnetic particles. Clusters of particles have a non-spherical shape and thus a magnetic shape anisotropy. For such clusters a quadratic scaling of torque with field was observed, also for small fields,41 caused by the shape anisotropy of the clusters. The torque of clusters of particles depends only on the magnetic moment and diameter of the particles. In contrast, the magnetic torque of single particles depends on the size distribution and arrangement of nanocrystals within the particle, which can vary strongly between particles.109,110 The torque varies by 30–60% between particles of the same type and even more, up to a factor 100, between particles of different types.27
Systems for magnetic torque actuation
In this section we discuss various systems to generate magnetic fields for rotational actuation of magnetic particles in lab-on-chip applications. Two main categories can be distinguished: permanent-magnet actuators and electromagnetic actuators. The geometry and type of magnetic actuator depends on the required field strength, field frequency, and sometimes the need for an additional field gradient. An instrument that can control the field direction and magnitude in two or three dimensions is typically referred to as magnetic torque tweezers (MTT),111 a term that was introduced around the year 2000. A fundamental difference between magnetic tweezers and for instance optical- or mechanical tweezers, is that magnetic fields tend to spread out in space and therefore typically many particles are actuated at the same time. The torque that can be generated in a MTT system is comparatively large. Values for the torque generated in a MTT system using micrometer-sized MPs are between 1 and 100 pN μm.84,106,108 In optical torque tweezers the torque is between 0.1 and 1 pN μm;84,112,113 higher torques could in principle be achieved using stronger optical fields, but limiting factors are the optical power, the generated heat inside the particles and heat that biological systems can withstand.Fig. 3 sketches three main classes of MTT systems. Panels A and B sketch MTTs based on permanent magnets (pMTT) and panel C a MTT system with electromagnets (eMTT). The system of panel A uses two parallel linear magnets with opposite magnetic orientations. Generally a space is left open between the two magnets to allow for optical imaging through the gap.114 The field gradient creates a large force oriented toward the magnet. The field strength and force are varied by changing the distance between magnets and substrate. A torque is applied by mechanically rotating the magnet. The pMTT system with circular magnet in panel B creates a field at the position of the particle with a field component perpendicular to the substrate. A torque is applied by adding a small linear magnet at one side of the circular magnet. The main advantage of the circular-magnet pMTT with respect to the linear-magnet pMTT is that the MP is pulled to the side, so that its rotation can be optically tracked by recording the xy-position of the particle rather than the angle of the particle itself.64 This removes the need to add a label to the particle for angular tracking. Typical in-plane field strengths are between 5 and 500 mT (ref. 108) with an out-of-plane gradient between 10 and 1000 T m−1.114 The magnitude of the field strength and the gradient are coupled by the design of the magnet. The maximum speed of field rotation is rather limited (typically ∼0.5 Hz) because the magnet needs to be physically rotated. pMTTs65,115 are typically used for single-molecule experiments on DNA (Fig. 1E) since these do not require high frequency actuation. Furthermore, in these experiments the coupling between the out-of-plane gradient and the in-plane field magnitude is not an issue as the DNA molecule typically needs to be stretched.
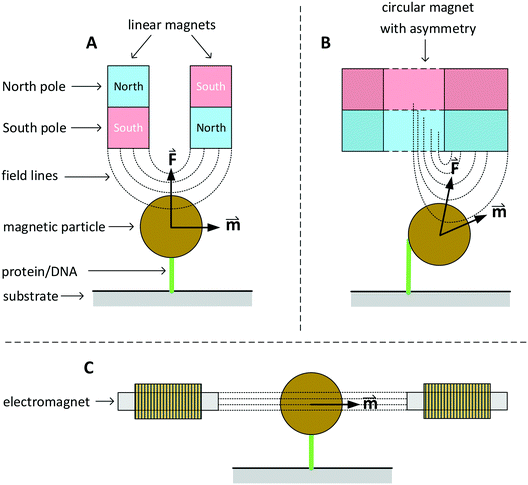 | ||
Fig. 3 Sketches of three main classes of MTT systems, for actuation of particles in solution or particles coupled to a substrate (not to scale). North and south poles of permanent magnets are sketched in red and blue respectively. Electromagnets are sketched with coils. Dotted lines represent lines of the magnetic field. The field-induced magnetic moments (![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) ) of the particles and gradient-induced forces ( ) of the particles and gradient-induced forces (![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) ) are indicated. Panel A sketches a pMTT system (p = permanent magnet) with two linear magnets.80 Panel B sketches a cross-section of a pMTT system with a circular magnet.80 Both pMTT systems generate a large gradient-induced force on the particle. Panel C sketches an eMTT system (e = electromagnet) with cores of soft magnetic material.116–119 The eMTT system has an in-plane field orientation and no field gradient in the middle of the magnetic system. ) are indicated. Panel A sketches a pMTT system (p = permanent magnet) with two linear magnets.80 Panel B sketches a cross-section of a pMTT system with a circular magnet.80 Both pMTT systems generate a large gradient-induced force on the particle. Panel C sketches an eMTT system (e = electromagnet) with cores of soft magnetic material.116–119 The eMTT system has an in-plane field orientation and no field gradient in the middle of the magnetic system. | ||
Electromagnetic MTT systems (eMTT) generate fields using current-carrying coils in combination with optional soft-magnetic materials. eMTTs typically have smaller fields than pMTTs, but eMTTs are much more flexible for modulating the magnitude-, orientation-, and frequency of the field. eMTT systems were already used three decades ago in magnetic twisting cytometry experiments (Fig. 1D). Uniaxial fields (AC fields) were used to apply mechanical stress on cell membranes.54,55 Later, eMTTs were also used to study single biological molecules.70 Typically a single coil or a set of two coils is used to control the magnetic field amplitude along a single axis. By adding pairs of coils, field control is extended to two or three spatial dimensions. The systems are typically designed to have a homogenous, gradient free, magnetic field in the center of the system. Fig. 3C sketches an example with a single pair of coils. The coils can be equipped either with or without a soft-magnetic material inside the coil. Rotating fields are created by applying phase-shifted currents through orthogonal sets of coils in the system. No physical movement is needed to create field modulation or field rotation, therefore high frequencies can be achieved (>100 Hz without a soft magnetic material inside the coils). For creating high frequency fields, a limiting factor is the currents and heating induced by time varying fields, due to Faraday’s law of induction and eddy currents.
For creating high amplitude fields the limiting factors are the Joule heating of the coils and/or the electric current that the power supply can deliver. The maximum field strengths for coils without a soft-magnetic material are in the order of a few milli Tesla at the sample location. If larger magnetic fields are required active cooling of the coils is needed. Another approach to enhance the field strength is to add a soft-magnetic material inside the coils.116,119 This enhances the field strength significantly (approximate 50 times) due to the high magnetic susceptibility of the soft-magnetic material. A disadvantage is that soft-magnetic materials have a remnant moment, typically 0.5–5% of the saturation magnetization, limiting the accuracy and the maximum frequency at which the field can be changed. Depending on the pole tip geometry, fields of 10 to 100 mT can be reached, with almost no field gradient. Table 1 summarizes the typical magnetic fields and rotation frequencies that can be achieved with the different magnetic systems. Typical values for the torque generated by an MTT and micrometer sized MPs are between 0 and 100 pN μm.84,106,108
| Typical field (mT) | Typical frequency (Hz) | Field gradient | |
|---|---|---|---|
| pMTT | 100 | 1 | Large, out of plane |
| eMTT with core | 10 | 10 | Small, in plane |
| eMTT without core | 1 | 1000 | Small, in plane |
Applications of rotating MPs
In this section we highlight early works and recent publications describing applications of rotating MPs as sketched in Fig. 1. We will discuss (1) the physical measurement principles, (2) the used detection methods (magnetic or optical), (3) the used types of particles (ferro- or superparamagnetic, size), (4) the used magnetic systems (eMTT or pMTT), and (5) we give examples of the physical systems that have been studied. An overview of this section is given in Table 2.| Application | Cluster or single particle | Magnetic Particle (type & size range) | Magnetic tweezer | Detection method | Studied system | Measurement principle | Early publication | More recent works |
|---|---|---|---|---|---|---|---|---|
| Mixing (Fig. 1A) | Cluster | SP μm | eMTT | n.a. | n.a. | n.a. | 2003 Vuppu6 | 2009 Bruls11 actuation of clusters increases mixing at a surface |
| 2014 Gao15 actuation of clusters enhances mixing and capture in solution | ||||||||
| 2014 Van Reenen2 review paper | ||||||||
| Concentration detection (Fig. 1B) | Single | FP nm | eMTT | Magnetic | Protein | Out-of-phase field component | 2004 Astalan16 | 2008 Fornara24 antibody concentration in undiluted serum |
| SP/FP nm and μm | eMTT | Optical scattering or transmission | Cell/protein | Oscillation frequency or phase lag | 2007 McNaughton22 | 2017 Schrittwieser21 protein detection in diluted serum and saliva | ||
| Concentration detection (Fig. 1C) | Cluster | SP μm | eMTT | Optical scattering or transmission | Protein | Oscillation frequency or amplitude | 2006 Baudry8 | 2012 Ranzoni43 PSA in undiluted blood plasma |
| 2016 Uddin38 Lab on a disc | ||||||||
| 2018 Van Vliembergen124 inter-particle distance | ||||||||
| FP nm | eMTT | Magnetic | Protein | In-phase component | 2007 Hong31 | 2010 Chieh40 VEGF in buffer, measured using a SQUID | ||
| Biophysical characterization (Fig. 1D) | Single | FP μm | pMTT and eMTT | Magnetic | Cell | Oscillation frequency | 1987 Valberg47 | 2001 Puig-De-Morales57 frequency demodulation to measure mechanical cell properties |
| SP/FP μm | eMTT | Optical microscopy | Cell | Spatial position and/or angular position | 1993 Berg48 | 2008 del Alamo50 anisotropy in mechanical properties of cells | ||
| 2012 Irmscher51 torsional and translational mechanical properties of cell membranes | ||||||||
| Biophysical characterization (Fig. 1E) | Single | SP μm | pMTT | Optical microscopy | DNA | Distance to surface or angular position | 1996 Strick61 | 2000 Strick83 DNA–protein interactions |
| 2005 Koster86 enzyme-induced uncoiling of DNA | ||||||||
| 2012 Bryant65 review | ||||||||
| 2016 Berghuis79 high-throughput probing of DNA–protein interactions | ||||||||
| SP μm | eMTT | Optical microscopy | Protein | Angular position | 2013 Van Reenen70 | 2016 Gutiérrez-Mejía81 conformation changes in cardiac troponin | ||
Mixing
Fluid mixing is important in lab-on-chip devices because a homogeneous composition of fluid ensures efficient reactions with low variability. However, mixing on a micrometer scale is difficult due to the low Reynolds numbers. Magnetic particles can be used to induce mixing in a lab-on-chip system (cf.Fig. 1A) by applying rotating gradient-free magnetic fields to particles in solution. Chains of particles are formed due to dipole–dipole interactions between the MPs. These chains align themselves along the field lines due to the large shape anisotropy of the self-assembled chains.When the magnetic field is rotated the chains act as rotors in the fluid. The average size of the rotors can be controlled by the magnitude of the field. Due the absence of a gradient the rotors remain in the same position and induce local mixing. Studies have shown that rotational chain mixing can enhance the capturing rate of molecular targets by about a factor 4.10,13,15 An early publication describing the use of self-assembled chains for mixing was written by Vuppu et al. in 2003,6 based on superparamagnetic MPs in combination with a motorized permanent magnet.
One year later the same group published a paper showing that these rotating magnetic particle chains can be used to capture biological molecules.9 This principle has been extensively studied in the years thereafter11 and was used in many bio-sensing applications35,37,38,42,43 (Fig. 1B and C) to significantly shorten assay times, typically from 60–120 min to 15–30 min. In later studies by Gao et al. an octopole magnetic tweezer was developed (Fig. 4A).15 The system can create 3D rotating magnetic fields with and without field gradient, which can for example be used to create particle chains, pull these to a substrate (Fig. 4B), and subsequently redisperse the chains to achieve distributed single particles14 (Fig. 4C). A more recent trend is to integrate magnetic micro-mixers on a chip, which gives compact systems for fluid mixing in very small volumes.7
 | ||
| Fig. 4 Example of a magnetic system for mixing of fluids using MPs. (A) Octopole electromagnet developed by Gao et al.15 (B) Particle chains formed by a rotating field. (C) Redispersion of the particles, achieving single particles distributed over a substrate.120,121 | ||
Biomarker detection and concentration determination
An important application field of MPs in lab-on-chip applications is the detection and concentration determination of biomarkers for point-of-care medical diagnostic purposes. Typically the biomarkers to be measured are captured onto MPs and thereafter a secondary process is applied to detect the captured substance. Commonly chemiluminescent labels and reagents are used for detection2 but a disadvantage of this method is that additional reagents and fluidic processing steps are needed.To simplify the assay and allow direct detection in solution,3 measurement concepts are being studied based on particle rotation. One method is to measure a change of the hydrodynamic size of magnetic particles, as in Fig. 1B. The surface of the particles is functionalized with specific capture molecules, e.g. antibodies or aptamers that target the antigen or bacteria of interest. There are two ways to detect a change of the hydrodynamic size of magnetic particles; the first is via the magnetic response and the second by optical scattering.
In 2003 two groups16,17 showed how the AC magnetic susceptibility (magnetization in a field with alternating amplitude) as a function of the driving field frequency can be used to measure the concentration of target proteins via the hydrodynamic size of the particles, see Fig. 5A. The theoretical concept of this measurement method was proposed by Connolly and St Pierre in 2001.122 Driving fields were used in the range between kHz to MHz, generated using eMTTs without magnetic cores. The field causes the MPs to align their magnetic moments with the field, by magnetic relaxation, called Néel relaxation, or by physical reorientation, called Brownian relaxation.101 Small (20–100 nm) ferromagnetic MPs were used, with τN ≫ 1 second. For these ferromagnetic MPs the dominant relaxation mechanism is Brownian, i.e. physical reorientation, which depends on the hydrodynamic volume. The method has been refined by optimizing the magnetic particles, see Fornara et al. in 2007.24 They were able to measure a dose–response curve of a target antibody in undiluted serum.
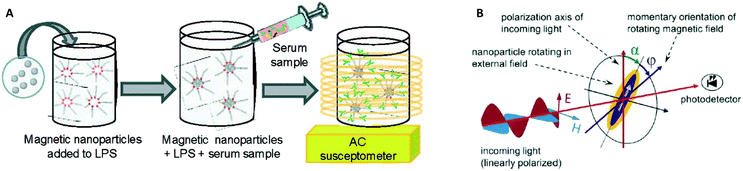 | ||
| Fig. 5 Methods to detect biological molecules via a change of hydrodynamic size of MPs, cf. the measurement principle shown in Fig. 1B. (A) Schematic representation of the experiment by A. Fornara et al.24 Ferromagnetic nanoparticles were provided with specific capture molecules. The functionalized nanoparticles were mixed with a biological sample and the magnetic relaxation of the mixture was measured. (B) Schematic illustration of the measurement principle designed by Schrittwieser et al.19 Nanoprobes follow the rotating external magnetic field at a certain phase lag ϕ, which depends on their hydrodynamic volume and increases upon analyte binding. The angle ϕ follows from the measured transmission, which depends on the orientation of the nanoprobe’s long axis with respect to the polarization direction of the incoming light (i.e., the angle α). | ||
In 2014 Dieckhoff et al. measured the phase lag of the magnetic moment using a rotating field instead of an AC field.20 By tuning the driving frequency they were able to measure the concentration of antibodies in buffer using only one field frequency. They found a limit of detection on the order of 0.1 nM. Schrittwieser et al. proposed to measure the change in hydrodynamic size of hybrid plasmonic-ferromagnetic rods by optically measuring the phase lag between the oscillations in the transmitted light and the rotating driving field, as shown in Fig. 5B.19 In a recent paper they reported experiments with non-plasmonic nanorods and were also able to measure this phase lag.21
An alternative rotation-based detection technique makes use of the scattering signal of optically anisotropic MPs in an AC- or rotating magnetic field. One of the first to use this optical detection technique was McNaughton et al. in 2007.22 They showed how the growth of a cell attached to a micrometer sized MP could be monitored via the scattered light. In these experiments a rotating field was used with a frequency such that the maximum magnetic torque was smaller than the hydrodynamic drag, i.e. the field rotates faster than the particle. This can be achieved by using small fields (1–5 mT) and relatively fast rotation speeds (10–100 Hz) in combination with micrometer sized superparamagnetic particles. This technique is referred to as asynchronous magnetic bead rotation (AMBR). If the hydrodynamic drag increases due to the growth of the cell, the average particle rotation frequency decreases.22 By tracking the rotation frequency over time the effect of anti-bacterial drugs could be tested by looking at the change in rotation frequency.25,28
The abovementioned techniques involve a change of hydrodynamic radius. Another approach for measuring the concentration of biological molecules makes use of the analyte-induced formation of clusters of particles, as in Fig. 1C. In these assays the number of clusters or the cluster size depends on the concentration of target. The clusters are detected via a change in magnetic response or optical scattering.
In 2006 two publications reported the detection of biological targets via the magnetic response of clusters of MPs. Hong et al.30 made use of the change of AC magnetic susceptibility caused by the formation of clusters of particles. They applied a mixed frequency driving field (see Fig. 6A) and measured the AC magnetic susceptibility at a sum frequency to suppress the magnetic noise from the driving field. Using a SQUID to measure the magnetic signal instead of a pickup coil, Chieh et al. achieved a limit of detection in the pg ml−1 range.40 A SQUID is more sensitive than coils, but requires cryogenic temperatures, which complicates system miniaturization.
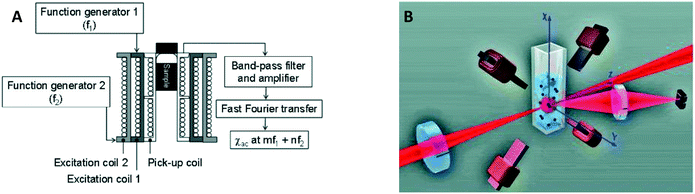 | ||
| Fig. 6 Magnetic and optical detection of clusters of MPs to detect concentrations of biological molecules in fluid. (A) Sketch of the setup used by Hong et al.30,31 The sample is placed in three concentric coils, where the two outer coils generate the driving field and the inner coil picks up the magnetic response of the sample. (B) Sketch of the setup used by Ranzoni et al.42,43 The sample is placed in a quadrupole electromagnet that generates a rotating magnetic field. The sample is illuminated using a laser and the scattered light from the particles is recorded using a photodiode. | ||
In 2006 Baudry et al. showed the detection of a biological target by optically measuring the change of the rotational Brownian relaxation speed of clusters of MPs.8 A magnetic field was applied to form chains of MPs and the redispersion time of particles was measured upon removal of the magnetic field. The redispersion time is larger when target-induced clusters are present than when such biochemically-formed clusters are absent, due to the slower Brownian motion of clusters compared to single particles. The cluster assay was accelerated by the magnetic chain formation, to a time on the order of 5 min. The formation of chains can also be measured by recording the modulation of scattered light in a rotating magnetic field, as demonstrated around 2010 by Park et al.123 and Donolato et al.36,38 who monitored the transmission of light, and by Ranzoni et al.41–43 who monitored the scattered light under an angle (see Fig. 6B). In these experiments spherical 100–1000 nm superparamagnetic MPs where used. Only clusters or chains of particles cause the scattered light to fluctuate in a rotating magnetic or AC field, because single particles possess no optical anisotropy. The magnitude of the oscillations of the scattered or transmitted light is proportional to the number of clusters, which in turn depends on the target concentration. The transmission-based measurement principle in combination with AC actuation along the optical axis, as demonstrated by Donolato et al., led in 2013 to the creation of BluSense Diagnostics, a spin-out company from the Technical University of Denmark.
BluSense combines magnetic actuation with existing blu-ray technology, where the rotational motion of a disk-shaped cartridge gives microfluidic actuation and optical detection is used to measure cluster formation.38 With a detection angle of the scattered light at 90 degrees, Ranzoni et al.43 demonstrated that the concentration of PSA in undiluted blood plasma could be measured in the low picomolar range, by recording the amplitude of the 2f signal (at twice the driving frequency). Vliembergen et al.124,125 have extended the optical detection method by analyzing the rotation-angle dependent scattering signals. Sharp peaks in the spectrum allowed them to measure nanometer-scale inter-particle distances within the clusters. The results show that particle roughness is an important factor in the data. In the future this approach can lead to novel ways to distinguish between specific and non-specific binding in lab on chip cluster assays.
Biophysical characterization
The study of single proteins and single cells is of importance for understanding the basic properties of biological systems and for the development of bioanalytical tools. One subfield in this research area is force spectroscopy, where single molecules and cells are studied under different force conditions. The forces can be applied to the biological systems in a variety of ways, including the use of sharp tips (e.g. atomic force microscopy) and particles (e.g. optical tweezers and magnetic tweezers). A review comparing the different methods has been written by Neuman et al. in 2008.111 Here we focus on the use of rotating MPs and gradient-free magnetic fields.One of the first applications of rotating MPs was for studying the mechanical properties of cell membranes (Fig. 1D), by so-called magnetic twisting cytometry (MTC).47 An experiment done by Valberg et al. in 1987 is shown in Fig. 7. Typically ferromagnetic MPs were used in combination with an AC field generated by an eMTT. The magnetic relaxation time of these ferromagnetic MPs is chosen to be significantly longer than the mechanical relaxation times of the cells. The experiments start by attaching magnetic particles to the cell surface, for instance using antibodies. Next a strong magnetic pulse (typically 100 mT) is applied to magnetize all MPs in a selected direction. Thereafter a weak magnetic field (weak enough to not change the particle magnetization) is applied along another direction, which applies a magnetic torque to the cell membrane. Using a flux gate the field is measured giving information about the orientation of the magnetic particles.56 By rotating the magnetic field with respect to the sample the storage (G′(ω)) and loss modules (G′′(ω)) are resolved for different frequencies.57,59 All magnetic measurements are ensemble averages and do not provide information about cell-to-cell variations or spatial anisotropy in the cell mechanical response.
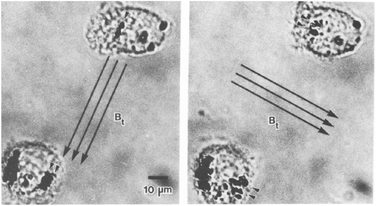 | ||
| Fig. 7 Study of mechanical properties of cells using rotating MPs. Shown are two lung macrophages, from experiments by Valberg et al. in 1987.47 The dark spots are aggregates of magnetic nanoparticles. The direction of the applied field is indicated with the arrows. Small arrow heads indicate the reorientation of the magnetic aggregates. | ||
In later work, researchers switched from detecting the magnetic signal to optically tracking the spatial position and/or angular orientation of individual particles. Both ferromagnetic and superparamagnetic particles, typically larger than 1 μm, have been used in these experiments. An example of early work using optical detection was a study on the torque generated by a flagellar motor of Escherichia coli by Berg et al. in 1993.48 They tracked the rotation speed of the particle and compared it for different magnetic field strengths.
Another example was the tracking of the spatial xy-position of a MP relative to a cell, giving the local deformation of the cell.60 In another study the three-dimensional Euler angles as well as the spatial position of a superparamagnetic MP bound to cell surface were tracked, while applying a rotating field using an eMTT.51 This allowed to determine the storage and loss modules as a function of the spatial and angular orientations. Strong differences were observed in the storage modules between the different angular orientations.
Rotating MPs are also well-suited for studying the torsional properties of biological systems at the single-molecule level69,80 (Fig. 1E). Typically, a molecular system is captured between a planar substrate and a MP, and the rotation of the MP is recorded using optical microscopy. The first molecule to be studied was double-stranded DNA (dsDNA), where the molecule was stretched by force as well as torsionally actuated by the MP.61,62,73 Stretching requires relatively high forces, so a pMTT system and micrometer-sized superparamagnetic particles were used. The torsional properties of the dsDNA were studied by measuring the height change of the MP (for instance via the optical diffraction pattern) as a function of the number of rotations of the particle.79,82,88 In these experiments the angular orientation of the MP was not tracked directly. Due to the large magnetic field and torque (10−17 Nm), it could be assumed that the number of rotations of the magnet corresponded to the number of rotations of the MP, and thus the number of windings of the dsDNA. The technique has allowed studies on the structure of over-wound and supercoiled dsDNA,73 the effect of DNA-binding proteins,89 enzymatic uncoiling of supercoiled dsDNA,83 and the speed of enzymatic uncoiling compared to cleaving.86
Later studies involved direct tracking of the angular orientation of the MP. Angular tracking can be achieved by attaching an optical marker that breaks rotational symmetry, e.g. a small non-magnetic particle. One solution is to attach a small nonmagnetic bead as marker to the DNA molecule itself. This labelling technique has allowed for studying the local structure, sequence specific effects and dynamical effects in supercoiled DNA.71 Another technique to track MP rotation is by using a circular magnet, as in Fig. 3B. The magnet creates a displacement of the center of the MP with respect to the anchoring point of the DNA in the fluid cell. As a consequence, rotation of the MP becomes related to the off-center spatial position of the MP. This technique has been used to monitor changes in the twist of nucleic acids at minimal torque.64 If required the DNA can be torsionally actuated by adding a set of coils or a small linear magnet.63,66
More recently the torque properties of proteins have been studied using MPs. The mechanical properties of proteins are very different from DNA: proteins are globular molecules (rather than filaments) with a size of around 10 nm. This gives a number of important differences: (i) there is no need to apply a stretching force when studying proteins, (ii) proteins are small and stiff, so angular and spatial displacements of the MP are small, and (iii) in the experiment the MP is close to the substrate, so artefacts due to particle–surface interactions need to be carefully ruled out. Janssen et al. developed an eMTT system with minimal field gradients.131,132 The system was used to study the torsional properties of proteins as a function of the angle of rotation70 and as a function of the concentration of surfactants.77 Fluorescent nanoparticles were attached to the MP for angular tracking, see Fig. 8. Panel C shows a microscopy image of an MP with a single fluorescent marker. By applying a continuously rotating magnetic field and recording the maximum angular deformation, the torsional rigidity of protein G-IgG and IgG–IgG complexes could be quantified.70 This technique has also been used to study the torsional rigidity of a heterotrimeric protein complex, namely the cardiac troponin complex that regulates muscle contraction of the heart. Using antibody targeting of specific protein domains, the calcium-induced conformational change of the protein complex could be recorded via a change of torsional rigidity.81 The work paves the way for nanomechanical mapping of native proteins and their conformational changes, using available libraries of monoclonal antibodies.
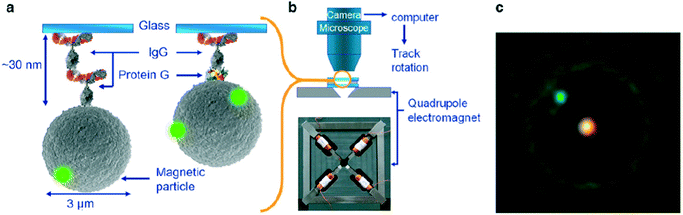 | ||
| Fig. 8 Study of single protein molecules using rotating MPs in an eMTT, by A. van Reenen et al.70 (a) MPs are bound to a glass substrate by via a molecular complex. (b) Inside a fluid cell, the particles are actuated by a rotating magnetic field generated by a quadrupole electromagnet. (c) The particle orientation is visualized by means of attached small green fluorescent spheres. The bright spot in the center of the particle is caused by the excitation light. | ||
Conclusions and outlook
Nanometer and micrometer sized magnetic particles combined with gradient-free magnetic fields allow for the generation of well-defined mechanical torques and rotations in lab on a chip devices. Foundations of the field were laid in the previous century, when superparamagnetic behavior of magnetic particles was observed and monodisperse micrometer-sized superparamagnetic particles were developed. More recently, lab on chip functionalities have been studied with rotating magnetic particles, ranging from fluid mixing, detection of biomolecules, to biophysical studies of molecules and cells. These applications could be developed due to the large and well-controlled torques and rotation, the inherent spatial uniformity, and the bio-orthogonal nature of magnetic fields.The mixing functionality (Fig. 1A) has been well-developed in terms of experiments as well as theory. Many basic studies have been performed and fluid-mechanical models exist to describe the development of flow by rotating particles. Biomarker quantification (Fig. 1B and C) is being studied using rotation of single particles as well as clusters of particles. These applications involve biofunctionalization of the particles, capture of target molecules by the particles, and readout via magnetic or optical signals. An advantageous feature is that the detection is performed in solution, without a fluidic washing process or other separation steps, which strongly simplifies assay integration into lab on chip devices. Further developments can be expected, particularly in the field of cluster assays (Fig. 1C), to achieve high analytical performance in a wide range of assays, by designing new particles, biofunctionalizations and assay implementations, with the prospect to enable affinity-based biosensing that is fast, reliable, integrated, cost-effective, and broadly applicable.
Another approach that has seen strong development is the biophysical probing of biomolecules and cells using rotating MPs (Fig. 1D and E). Methodologies were first developed for studying cells, but in recent years the focus has shifted completely to studying single molecules. Single-molecule studies (Fig. 1E) have given unique insights into the properties and function of macromolecules such as DNA, DNA–protein interactions, and also native protein complexes.
Single-molecule techniques are important for answering scientific questions but the methodologies also penetrate into bioanalytical sciences. Commercial analytical instruments are now available based on earlier academic studies on single-molecule methodologies for the quantitation of proteins126,127 and for DNA sequencing.128,129 The same trend can be expected for sensing based on magnetic rotation and torque, when the single-molecule methods will become suited to test unknown biological samples. As an example, the rotation-based methodologies based on target capturing by affinity molecules such as aptamers or antibodies81 will enable the detection and characterization of native proteins in biological samples. Due to the fact that unmodified native proteins are measured, the methods can have impact beyond research only. Proteins and their functional response can be characterized straight from industrial processes (for biotechnological process monitoring) and from patient samples (for diagnostics and patient monitoring). We foresee that this paves the way for biomarker response fingerprinting at the single-molecule level, with the prospect to lead to lab-on-chip systems with high specificity and high sensitivity, e.g. particle-based point-of-care testing devices2 and devices for continuous biomarker monitoring.130
In summary, the controlled application of torque and rotation to magnetic particles has developed strongly and steadily over the past decades, delivering a range of unique actuation and probing functionalities of fluids, molecules and cells in lab on chip systems. The field is set to further develop innovative approaches for characterizing biomolecular and biological systems as well as for integrating lab on chip functionalities into advanced bioanalytical tools.
Conflicts of interest
There are no conflicts to declare.References
- M. A. M. Gijs, F. Lacharme and U. Lehmann, Chem. Rev., 2010, 110, 1518–1563 CrossRef CAS PubMed
.
- A. van Reenen, A. M. de Jong, J. M. J. den Toonder and M. W. J. Prins, Lab Chip, 2014, 14, 1966–1986 RSC
.
- S. Schrittwieser, B. Pelaz, W. Parak, S. Lentijo-Mozo, K. Soulantica, J. Dieckhoff, F. Ludwig, A. Guenther, A. Tschöpe and J. Schotter, Sensors, 2016, 16, 828 CrossRef PubMed
.
- A. Munaz, M. J. A. Shiddiky and N.-T. Nguyen, Biomicrofluidics, 2018, 12, 031501 CrossRef PubMed
.
- J. H. Dieckhoff, T. Yoshida, K. Enpuku, M. Schilling and F. Ludwig, IEEE Trans. Magn., 2012, 48, 3792–3795 CAS
.
- A. K. Vuppu, A. A. Garcia and M. A. Hayes, Langmuir, 2003, 19, 8646–8653 CrossRef CAS
.
- Q. Xiong, C. Y. Lim, J. Ren, J. Zhou, K. Pu, M. B. Chan-Park, H. Mao, Y. C. Lam and H. Duan, Nat. Commun., 2018, 9, 1743 CrossRef PubMed
.
- J. Baudry, C. Rouzeau, C. Goubault, C. Robic, L. Cohen-Tannoudji, A. Koenig, E. Bertrand and J. Bibette, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 16076–16078 CrossRef CAS PubMed
.
- A. K. Vuppu, A. A. Garcia, M. A. Hayes, K. Booksh, P. E. Phelan, R. Calhoun and S. K. Saha, J. Appl. Phys., 2004, 96, 6831–6838 CrossRef CAS
.
- K. Tanaka and H. Imagawa, Talanta, 2005, 68, 437–441 CrossRef CAS PubMed
.
- D. M. Bruls, T. H. Evers, J. A. H. Kahlman, P. J. W. van Lankvelt, M. Ovsyanko, E. G. M. Pelssers, J. J. H. B. Schleipen, F. K. de Theije, C. A. Verschuren, T. van der Wijk, J. B. A. van Zon, W. U. Dittmer, A. H. J. Immink, J. H. Nieuwenhuis and M. W. J. Prins, Lab Chip, 2009, 9, 3504 RSC
.
- Y. Gao, M. Hulsen and J. M. J. den Toonder, in 14th International Conference on Miniaturized Systems for Chemistry and Life Science, 2010, pp. 1055–1057 Search PubMed.
- J.-T. Lee, L. Sudheendra and I. M. Kennedy, Anal. Chem., 2012, 84, 8317–8322 CrossRef CAS PubMed
.
- Y. Gao, A. van Reenen, M. A. Hulsen, A. M. de Jong, M. W. J. Prins and J. M. J. den Toonder, Lab Chip, 2013, 13, 1394 RSC
.
- Y. Gao, A. van Reenen, M. A. Hulsen, A. M. de Jong, M. W. J. Prins and J. M. J. den Toonder, Microfluid. Nanofluid., 2014, 16, 265–274 CrossRef
.
- A. P. Astalan, F. Ahrentorp, C. Johansson, K. Larsson and A. Krozer, Biosens. Bioelectron., 2004, 19, 945–951 CrossRef CAS PubMed
.
- S. H. Chung, A. Hoffmann, S. D. Bader, C. Liu, B. Kay, L. Makowski and L. Chen, Appl. Phys. Lett., 2004, 85, 2971–2973 CrossRef CAS
.
- J. Dieckhoff, M. Schilling and F. Ludwig, Appl. Phys. Lett., 2011, 99, 112501 CrossRef
.
- S. Schrittwieser, F. Ludwig, J. Dieckhoff, K. Soulantica, G. Viau, L.-M. Lacroix, S. M. Lentijo, R. Boubekri, J. Maynadié, A. Huetten, H. Brueckl and J. Schotter, ACS Nano, 2012, 6, 791–801 CrossRef CAS PubMed
.
- J. Dieckhoff, A. Lak, M. Schilling and F. Ludwig, J. Appl. Phys., 2014, 115, 024701 CrossRef
.
- S. Schrittwieser, B. Pelaz, W. J. Parak, S. Lentijo-Mozo, K. Soulantica, J. Dieckhoff, F. Ludwig and J. Schotter, Sci. Rep., 2017, 7, 4752 CrossRef PubMed
.
- B. H. McNaughton, R. R. Agayan, R. Clarke, R. G. Smith and R. Kopelman, Appl. Phys. Lett., 2007, 91, 224105 CrossRef
.
- K. Ērglis, Q. Wen, V. Ose, A. Zeltins, A. Sharipo, P. A. Janmey and A. Cēbers, Biophys. J., 2007, 93, 1402–1412 CrossRef PubMed
.
- A. Fornara, P. Johansson, K. Petersson, S. Gustafsson, J. Qin, E. Olsson, D. Ilver, A. Krozer, M. Muhammed and C. Johansson, Nano Lett., 2008, 8, 3423–3428 CrossRef CAS PubMed
.
- B. H. McNaughton, P. Kinnunen, R. G. Smith, S. N. Pei, R. Torres-Isea, R. Kopelman and R. Clarke, J. Magn. Magn. Mater., 2009, 321, 1648–1652 CrossRef CAS
.
- Q. Wei, H.-M. Song, A. P. Leonov, J. A. Hale, D. Oh, Q. K. Ong, K. Ritchie and A. Wei, J. Am. Chem. Soc., 2009, 131, 9728–9734 CrossRef CAS PubMed
.
- P. Kinnunen, I. Sinn, B. H. McNaughton and R. Kopelman, Appl. Phys. Lett., 2010, 97, 223701 CrossRef PubMed
.
- I. Sinn, P. Kinnunen, T. Albertson, B. H. McNaughton, D. W. Newton, M. A. Burns and R. Kopelman, Lab Chip, 2011, 11, 2604 RSC
.
- P. Kinnunen, I. Sinn, B. H. McNaughton, D. W. Newton, M. A. Burns and R. Kopelman, Biosens. Bioelectron., 2011, 26, 2751–2755 CrossRef CAS PubMed
.
- C.-Y. Hong, C. C. Wu, Y. C. Chiu, S. Y. Yang, H. E. Horng and H. C. Yang, Appl. Phys. Lett., 2006, 88, 212512 CrossRef
.
- C.-Y. Hong, W. S. Chen, Z. F. Jian, S. Y. Yang, H. E. Horng, L. C. Yang and H. C. Yang, Appl. Phys. Lett., 2007, 90, 074105 CrossRef
.
- A. Hecht, P. Commiskey, N. Shah and R. Kopelman, Biosens. Bioelectron., 2013, 48, 26–32 CrossRef CAS PubMed
.
- M. Donolato, P. Antunes, T. Z. G. de la Torre, E.-T. Hwu, C.-H. Chen, R. Burger, G. Rizzi, F. G. Bosco, M. Strømme, A. Boisen and M. F. Hansen, Biosens. Bioelectron., 2015, 67, 649–655 CrossRef CAS PubMed
.
- P. Antunes, D. Watterson, M. Parmvi, R. Burger, A. Boisen, P. Young, M. A. Cooper, M. F. Hansen, A. Ranzoni and M. Donolato, Sci. Rep., 2015, 5, 16145 CrossRef CAS PubMed
.
- D. Ramiandrisoa, E. Brient-Litzler, A. Daynes, E. Compain, J. Bibette and J. Baudry, New Biotechnol., 2015, 32, 467–472 CrossRef CAS PubMed
.
- J. Yang, M. Donolato, A. Pinto, F. G. Bosco, E.-T. Hwu, C.-H. Chen, T. S. Alstrøm, G.-H. Lee, T. Schäfer, P. Vavassori, A. Boisen, Q. Lin and M. F. Hansen, Biosens. Bioelectron., 2016, 75, 396–403 CrossRef CAS PubMed
.
- B. Tian, J. Ma, T. Zardán Gómez de la Torre, Á. Bálint, M. Donolato, M. F. Hansen, P. Svedlindh and M. Strömberg, ACS Sens., 2016, 1, 1228–1234 CrossRef CAS
.
- R. Uddin, R. Burger, M. Donolato, J. Fock, M. Creagh, M. F. Hansen and A. Boisen, Biosens. Bioelectron., 2016, 85, 351–357 CrossRef CAS PubMed
.
- W. U. Dittmer, T. H. Evers, W. M. Hardeman, W. Huijnen, R. Kamps, P. de Kievit, J. H. M. Neijzen, J. H. Nieuwenhuis, M. J. J. Sijbers, D. W. C. Dekkers, M. H. Hefti and M. F. W. C. Martens, Clin. Chim. Acta, 2010, 411, 868–873 CrossRef CAS PubMed
.
- J. J. Chieh, S.-Y. Yang, H.-E. Horng, C. Y. Yu, C. L. Lee, H. L. Wu, C.-Y. Hong and H.-C. Yang, J. Appl. Phys., 2010, 107, 074903 CrossRef
.
- A. Ranzoni, X. J. A. Janssen, M. Ovsyanko, L. J. van IJzendoorn and M. W. J. Prins, Lab Chip, 2010, 10, 179–188 RSC
.
- A. Ranzoni, J. J. H. B. Schleipen, L. J. van IJzendoorn and M. W. J. Prins, Nano Lett., 2011, 11, 2017–2022 CrossRef CAS PubMed
.
- A. Ranzoni, G. Sabatte, L. J. van IJzendoorn and M. W. J. Prins, ACS Nano, 2012, 6, 3134–3141 CrossRef CAS PubMed
.
- P. Kinnunen, B. H. McNaughton, T. Albertson, I. Sinn, S. Mofakham, R. Elbez, D. W. Newton, A. Hunt and R. Kopelman, Small, 2012, 8, 2477–2482 CrossRef CAS PubMed
.
- C. H. Chang, Z. X. Lai, H. L. Lin, C. C. Yang, H. H. Chen, S. Y. Yang, H. E. Horng, C. Y. Hong, H. C. Yang and H. C. Lin, Int. J. Nanomed., 2012, 7, 4335–4340 CAS
.
- S. H. Liao, H. C. Yang, H. E. Horng, J. J. Chieh, K. L. Chen, H. H. Chen, J. Y. Chen, C. I. Liu, C. W. Liu and L. M. Wang, Appl. Phys. Lett., 2013, 103, 243703 CrossRef
.
- P. A. Valberg and H. A. Feldman, Biophys. J., 1987, 52, 551–561 CrossRef CAS PubMed
.
- H. C. Berg and L. Turner, Biophys. J., 1993, 65, 2201–2216 CrossRef CAS PubMed
.
- A. Cēbers and M. Ozols, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 021505 CrossRef PubMed
.
- J. C. del Alamo, G. N. Norwich, Y.-s. J. Li, J. C. Lasheras and S. Chien, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 15411–15416 CrossRef CAS PubMed
.
- M. Irmscher, A. M. de Jong, H. Kress and M. W. J. Prins, Biophys. J., 2012, 102, 698–708 CrossRef CAS PubMed
.
- M. L. Rodriguez, P. J. McGarry and N. J. Sniadecki, Appl. Mech. Rev., 2013, 65, 060801 CrossRef
.
- N. Wang and D. E. Ingber, Biophys. J., 1994, 66, 2181–2189 CrossRef CAS PubMed
.
- N. Wang, E. Planus, M. Pouchelet, J. J. Fredberg and G. Barlovatz-Meimon, Am. J. Physiol., 1995, 268, C1062–C1066 CrossRef CAS PubMed
.
- N. Wang and D. E. Ingber, Biochem. Cell Biol., 1995, 73, 327–335 CrossRef CAS PubMed
.
- B. Fabry, G. N. Maksym, R. D. Hubmayr, J. P. Butler and J. J. Fredberg, J. Magn. Magn. Mater., 1999, 194, 120–125 CrossRef CAS
.
- M. Puig-De-Morales, M. Grabulosa, J. Alcaraz, J. Mullol, G. N. Maksym, J. J. Fredberg and D. Navajas, J. Appl. Physiol., 2001, 91, 1152–1159 CrossRef CAS PubMed
.
- H. Huang, C. Y. Dong, H.-S. Kwon, J. D. Sutin, R. D. Kamm and P. T. C. So, Biophys. J., 2002, 82, 2211–2223 CrossRef CAS PubMed
.
- V. M. Laurent, S. Hénon, E. Planus, R. Fodil, M. Balland, D. Isabey and F. Gallet, J. Biomech. Eng., 2002, 124, 408 CrossRef PubMed
.
- S. Hu, L. Eberhard, J. Chen, J. C. Love, J. P. Butler, J. J. Fredberg, G. M. Whitesides and N. Wang, Am. J. Physiol., 2004, 287, C1184–C1191 CrossRef CAS PubMed
.
- T. R. Strick, J.-F. Allemand, D. Bensimon, A. Bensimon and V. Croquette, Science, 1996, 271, 1835–1837 CrossRef CAS PubMed
.
- J. D. Moroz and P. Nelson, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 14418–14422 CrossRef CAS
.
- J. Lipfert, J. W. J. Kerssemakers, T. Jager and N. H. Dekker, Nat. Methods, 2010, 7, 977–980 CrossRef CAS PubMed
.
- J. Lipfert, M. Wiggin, J. W. J. Kerssemakers, F. Pedaci and N. H. Dekker, Nat. Commun., 2011, 2, 439 CrossRef PubMed
.
- Z. Bryant, F. C. Oberstrass and A. Basu, Curr. Opin. Struct. Biol., 2012, 22, 304–312 CrossRef CAS PubMed
.
- X. J. A. Janssen, J. Lipfert, T. Jager, R. Daudey, J. Beekman and N. H. Dekker, Nano Lett., 2012, 12, 3634–3639 CrossRef CAS PubMed
.
- F. C. Oberstrass, L. E. Fernandes and Z. Bryant, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 6106–6111 CrossRef CAS PubMed
.
- C. Brème and F. Heslot, PLoS One, 2013, 8, e55154 CrossRef PubMed
.
- S. Forth, M. Y. Sheinin, J. Inman and M. D. Wang, Annu. Rev. Biophys., 2013, 42, 583–604 CrossRef CAS PubMed
.
- A. van Reenen, F. Gutiérrez-Mejía, L. J. van IJzendoorn and M. W. J. Prins, Biophys. J., 2013, 104, 1073–1080 CrossRef CAS PubMed
.
- F. C. Oberstrass, L. E. Fernandes, P. Lebel and Z. Bryant, Phys. Rev. Lett., 2013, 110, 178103 CrossRef PubMed
.
- J. Lipfert, G. M. Skinner, J. M. Keegstra, T. Hensgens, T. Jager, D. Dulin, M. Kober, Z. Yu, S. P. Donkers, F.-C. Chou, R. Das and N. H. Dekker, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 15408–15413 CrossRef CAS PubMed
.
- J. F. Allemand, D. Bensimon, R. Lavery and V. Croquette, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 14152–14157 CrossRef CAS
.
- J. C. Cordova, D. K. Das, H. W. Manning and M. J. Lang, Curr. Opin. Struct. Biol., 2014, 28, 142–148 CrossRef CAS PubMed
.
- E. J. Banigan and J. F. Marko, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 062706 CrossRef PubMed
.
- R. S. Bejhed, T. Z. G. de la Torre, M. Donolato, M. F. Hansen, P. Svedlindh and M. Strömberg, Biosens. Bioelectron., 2015, 66, 405–411 CrossRef CAS PubMed
.
- F. Gutiérrez-Mejía, L. J. van IJzendoorn and M. W. J. Prins, New Biotechnol., 2015, 32, 441–449 CrossRef PubMed
.
- D. Dulin, T. J. Cui, J. Cnossen, M. W. Docter, J. Lipfert and N. H. Dekker, Biophys. J., 2015, 109, 2113–2125 CrossRef CAS PubMed
.
- B. A. Berghuis, M. Köber, T. van Laar and N. H. Dekker, Methods, 2016, 105, 90–98 CrossRef CAS PubMed
.
- J. Lipfert, M. Lee, O. Ordu, J. W. J. Kerssemakers and N. H. Dekker, J. Visualized Exp., 2014, 19, 1–18 Search PubMed
.
-
F. A. Gutiérrez-Mejía, PhD thesis, Eindhoven University of Technology, 2016 Search PubMed
.
- F. Mosconi, J. F. Allemand, D. Bensimon and V. Croquette, Phys. Rev. Lett., 2009, 102, 078301 CrossRef PubMed
.
- T. R. Strick, V. Croquette and D. Bensimon, Nature, 2000, 404, 901–904 CrossRef CAS PubMed
.
- G. Romano, L. Sacconi, M. Capitanio and F. Pavone, Opt. Commun., 2003, 215, 323–331 CrossRef CAS
.
- Y. Harada, Sci. Technol. Adv. Mater., 2004, 5, 709–713 CrossRef CAS
.
- D. A. Koster, V. Croquette, C. Dekker, S. Shuman and N. H. Dekker, Nature, 2005, 434, 671–674 CrossRef CAS PubMed
.
- A. Celedon, I. M. Nodelman, B. Wildt, R. Dewan, P. Searson, D. Wirtz, G. D. Bowman and S. X. Sun, Nano Lett., 2009, 9, 1720–1725 CrossRef CAS PubMed
.
- D. Klaue and R. Seidel, Phys. Rev. Lett., 2009, 102, 028302 CrossRef PubMed
.
- J. Lipfert, S. Klijnhout and N. H. Dekker, Nucleic Acids Res., 2010, 38, 7122–7132 CrossRef CAS PubMed
.
- R. Řezníček, V. Chlan, H. Štěpánková, P. Novák and M. Maryško, J. Phys.: Condens. Matter, 2012, 24, 055501 CrossRef PubMed
.
- J. Carrey, B. Mehdaoui and M. Respaud, J. Appl. Phys., 2011, 109, 083921 CrossRef
.
- A. Aharoni, Phys. Rev. B: Solid State, 1973, 7, 1103–1107 CrossRef
.
- S. Mørup, M. F. Hansen and C. Frandsen, Beilstein J. Nanotechnol., 2010, 1, 182–190 CrossRef PubMed
.
- Q. A. Pankhurst, J. Connolly, S. K. Jones and J. Dobson, J. Phys. D: Appl. Phys., 2003, 36, R167–R181 CrossRef CAS
.
- M. A. Willard, L. K. Kurihara, E. E. Carpenter, S. Calvin and V. G. Harris, Int. Mater. Rev., 2004, 49, 125–170 CrossRef CAS
.
- W. Wu, Z. Wu, T. Yu, C. Jiang and W.-S. Kim, Sci. Technol. Adv. Mater., 2015, 16, 023501 CrossRef PubMed
.
- S. Bogren, A. Fornara, F. Ludwig, M. del Puerto Morales, U. Steinhoff, M. Hansen, O. Kazakova and C. Johansson, Int. J. Mol. Sci., 2015, 16, 20308–20325 CrossRef CAS PubMed
.
- J. Wells, O. Kazakova, O. Posth, U. Steinhoff, S. Petronis, L. K. Bogart, P. Southern, Q. Pankhurst and C. Johansson, J. Phys. D: Appl. Phys., 2017, 50, 383003 CrossRef
.
- J. Ugelstad and F. K. Hansen, Rubber Chem. Technol., 1976, 49, 536–609 CrossRef CAS
.
- G. Fonnum, C. Johansson, A. Molteberg, S. Mørup and E. Aksnes, J. Magn. Magn. Mater., 2005, 293, 41–47 CrossRef CAS
.
- J. Dieckhoff, D. Eberbeck, M. Schilling and F. Ludwig, J. Appl. Phys., 2016, 119, 043903 CrossRef
.
- C. P. Bean and J. D. Livingston, J. Appl. Phys., 1959, 30, S120–S129 CrossRef
.
- J. D. Livingston and C. P. Bean, J. Appl. Phys., 1959, 30, S318–S319 CrossRef
.
- K. Kurosawa, M. Miura and S. Saito, J. Phys. C: Solid State Phys., 1980, 13, 1521–1527 CrossRef CAS
.
- D. Cohen and I. Nemoto, IEEE Trans. Biomed. Eng., 1984, 31, 261–273 CAS
.
- X. J. A. Janssen, A. J. Schellekens, K. van Ommering, L. J. van IJzendoorn and M. W. J. Prins, Biosens. Bioelectron., 2009, 24, 1937–1941 CrossRef CAS PubMed
.
- R. I. Ovseenko and Y. G. Ovseenko, Fluid Dyn., 1971, 3, 78–82 CrossRef
.
- M. M. van Oene, L. E. Dickinson, F. Pedaci, M. Köber, D. Dulin, J. Lipfert and N. H. Dekker, Phys. Rev. Lett., 2015, 114, 218301 CrossRef PubMed
.
- D. R. Baselt, G. U. Lee, M. Natesan, S. W. Metzger, P. E. Sheehan and R. J. Colton, Biosens. Bioelectron., 1998, 13, 731–739 CrossRef CAS PubMed
.
- J. Xu, K. Mahajan, W. Xue, J. O. Winter, M. Zborowski and J. J. Chalmers, J. Magn. Magn. Mater., 2012, 324, 4189–4199 CrossRef CAS PubMed
.
- K. C. Neuman and A. Nagy, Nat. Methods, 2008, 5, 491–505 CrossRef CAS PubMed
.
- A. La Porta and M. D. Wang, Phys. Rev. Lett., 2004, 92, 190801 CrossRef PubMed
.
- S. Bayoudh, T. A. Nieminen, N. R. Heckenberg and H. Rubinsztein-dunlop, J. Mod. Opt., 2003, 50, 1581–1590 CrossRef
.
- Z. Yu, D. Dulin, J. Cnossen, M. Köber, M. M. van Oene, O. Ordu, B. A. Berghuis, T. Hensgens, J. Lipfert and N. H. Dekker, Rev. Sci. Instrum., 2014, 85, 123114 CrossRef PubMed
.
- D. Kilinc and G. U. Lee, Integr. Biol., 2014, 6, 27–34 CrossRef CAS PubMed
.
- C. Jiang, T. A. Lionberger, D. M. Wiener and E. Meyhofer, Rev. Sci. Instrum., 2016, 87, 084304 CrossRef PubMed
.
- F. Mosconi, J. F. Allemand and V. Croquette, Rev. Sci. Instrum., 2011, 82, 034302 CrossRef PubMed
.
- L. Sacconi, G. Romano, R. Ballerini, M. Capitanio, M. De Pas, M. Giuntini, D. Dunlap, L. Finzi and F. S. Pavone, Opt. Lett., 2001, 26, 1359 CrossRef CAS PubMed
.
- S. Schuerle, S. Erni, M. Flink, B. E. Kratochvil and B. J. Nelson, IEEE Trans. Magn., 2013, 49, 321–330 Search PubMed
.
- A. van Reenen, A. M. de Jong and M. W. J. Prins, Lab Chip, 2015, 15, 2864–2871 RSC
.
-
A. van Reenen, PhD thesis, Eindhoven University of Technology, 2014 Search PubMed
.
- J. Connolly and T. G. St Pierre, J. Magn. Magn. Mater., 2001, 225, 156–160 CrossRef CAS
.
- S. Y. Park, H. Handa and A. Sandhu, Nano Lett., 2010, 10, 446–451 CrossRef CAS PubMed
.
- R. W. L. van Vliembergen, L. J. van IJzendoorn and M. W. J. Prins, Langmuir, 2018, 34, 179–186 CrossRef CAS PubMed
.
- R. W. L. van Vliembergen, L. J. van IJzendoorn and M. W. J. Prins, Opt. Express, 2016, 24, A123 CrossRef CAS PubMed
.
- J. Todd, B. Freese, A. Lu, D. Held, J. Morey, R. Livingston and P. Goix, Clin. Chem., 2007, 53, 1990–1995 CrossRef CAS PubMed
.
- D. M. Rissin, C. W. Kan, T. G. Campbell, S. C. Howes, D. R. Fournier, L. Song, T. Piech, P. P. Patel, L. Chang, A. J. Rivnak, E. P. Ferrell, J. D. Randall, G. K. Provuncher, D. R. Walt and D. C. Duffy, Nat. Biotechnol., 2010, 28, 595–599 CrossRef CAS PubMed
.
- D. Branton, D. W. Deamer, A. Marziali, H. Bayley, S. A. Benner, T. Butler, M. Di Ventra, S. Garaj, A. Hibbs, X. Huang, S. B. Jovanovich, P. S. Krstic, S. Lindsay, X. S. Ling, C. H. Mastrangelo, A. Meller, J. S. Oliver, Y. V. Pershin, J. M. Ramsey, R. Riehn, G. V. Soni, V. Tabard-Cossa, M. Wanunu, M. Wiggin and J. A. Schloss, Nat. Biotechnol., 2008, 26, 1146–1153 CrossRef CAS PubMed
.
- J. Eid, A. Fehr, J. Gray, K. Luong, J. Lyle, G. Otto, P. Peluso, D. Rank, P. Baybayan, B. Bettman, A. Bibillo, K. Bjornson, B. Chaudhuri, F. Christians, R. Cicero, S. Clark, R. Dalal, A. DeWinter, J. Dixon, M. Foquet, A. Gaertner, P. Hardenbol, C. Heiner, K. Hester, D. Holden, G. Kearns, X. Kong, R. Kuse, Y. Lacroix, S. Lin, P. Lundquist, C. Ma, P. Marks, M. Maxham, D. Murphy, I. Park, T. Pham, M. Phillips, J. Roy, R. Sebra, G. Shen, J. Sorenson, A. Tomaney, K. Travers, M. Trulson, J. Vieceli, J. Wegener, D. Wu, A. Yang, D. Zaccarin, P. Zhao, F. Zhong, J. Korlach and S. Turner, Science, 2009, 323, 133–138 CrossRef CAS PubMed
.
- E. W. A. Visser, J. Yan, L. J. van IJzendoorn and M. W. J. Prins, Nat. Commun., 2018, 9, 2541 CrossRef PubMed
.
- X. J. A. Janssen, A. van Reenen, L. J. van IJzendoorn, A. M. de Jong and M. W. J. Prins, Colloids Surf., A, 2011, 373, 88–93 CrossRef CAS
.
- X. J. A. Janssen, J. M. van Noorloos, A. Jacob, L. J. van IJzendoorn, A. M. de Jong and M. W. J. Prins, Biophys. J., 2011, 100, 2262–2267 CrossRef CAS PubMed
.
| This journal is © The Royal Society of Chemistry 2019 |



