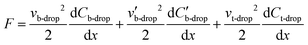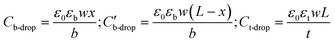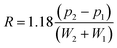Digital microfluidics and nuclear magnetic resonance spectroscopy for in situ diffusion measurements and reaction monitoring

Abstract

In recent years microcoils and related structures have been developed to increase the mass sensitivity of nuclear magnetic resonance spectroscopy, allowing this extremely powerful analytical technique to be extended to small sample volumes (<5 μl). In general, microchannels have been used to deliver the samples of interest to these microcoils; however, these systems tend to have large dead volumes and require more complex fluidic connections. Here, we introduce a two-plate digital microfluidic (DMF) strategy to interface small-volume samples with NMR microcoils. In this system, a planar microcoil is surrounded by a copper plane that serves as the counter-electrode for the digital microfluidic device, allowing for precise control of droplet position and shape. This feature allows for the user-determination of the orientation of droplets relative to the main axes of the shim stack, permitting improved shimming and a more homogeneous magnetic field inside the droplet below the microcoil, which leads to improved spectral lineshape. This, along with high-fidelity droplet actuation, allows for rapid shimming strategies (developed over decades for vertically oriented NMR tubes) to be employed, permitting the determination of reaction-product diffusion coefficients as well as quantitative monitoring of reactive intermediates. We propose that this system paves the way for new and exciting applications for in situ analysis of small samples by NMR spectroscopy.

---

1 Introduction

Nuclear magnetic resonance is a powerful spectroscopic technique that can be used to probe chemical structure and interaction,¹ to measure physicochemical properties,² and to study complex environmental processes,³ all while being non-destructive to the sample. Unfortunately, NMR spectroscopy comes with one major limitation—low mass sensitivity compared to other analytical techniques. One solution to the mass sensitivity limitation is dynamic nuclear polarization;^4–6 another (and arguably more general) solution is the use of sub-mm (or “micro”) NMR detectors, including micro-solenoids,^7–9 planar microcoils,^10–15 microslots,^16,17 microstriplines,^18–20 and magnetic lenses.^21,22 Micro-NMR detectors provide increased mass sensitivity,²³ a function of favorable scaling of induced current in the sensor relative to resistive noise,²⁴ as well as improved sample-sensor proximity. One of the more interesting practical effects of miniaturization of the sensor is the extension of NMR spectroscopy to samples such as single cells^25–27 and other tiny biological specimens.^28,29

A natural problem that arises from the use of micro-NMR detectors in NMR spectroscopy is the quandary of how to deliver the sample to be tested to the detection volume of the sensor. The most popular solution has been to interface the sensors with capillary tubes or microchannels. As with other sample-handling methods in NMR, the magnetic susceptibility mismatch between the sample, the microchannel or capillary material, and the surrounding media can lead to broadening of the peaks caused by the development of magnetic field inhomogeneities. Given the small scale of micro-NMR detector/microchannel systems, these inhomogeneities can be challenging to compensate using the native shimming coils of the spectrometer, as the latter are designed to smooth the field at larger length scales. One promising strategy to overcome this issue is to mindfully engineer void chambers around the microchannel which provide physical compensation for the inhomogeneities, leading to better peak resolution.^30,31

In place of microchannels or capillaries, in this work we describe a different microfluidic paradigm known as digital microfluidics for interfacing small sample volumes with micro-NMR detectors. There have been two previous reports of combining DMF and NMR. The first was by Lei et al.^32,33 who interfaced digital microfluidics with a low-field nuclear magnetic resonance relaxometer, used to detect a change in the T2 relaxation of water in a sample when biotin-coated iron nanoparticles aggregated in the presence of avidin. While this technique is useful for portable applications, the low magnetic fields reduce sensitivity, making conventional NMR spectroscopy (for applications such as biofluid-screening or chemical structure analysis) nearly impossible. The second report of a DMF-NMR system³⁴ described an interface between a so-called “one-plate” DMF device with a planar microcoil used in a conventional high-field NMR spectrometer. In that “proof of concept” work, it was shown that DMF could be used to move samples to and away from the microcoil, and to initiate and monitor chemical reactions within the spectrometer. As acknowledged in this previous report,³⁴ the one-plate DMF manipulation scheme (which is incapable of supporting droplet dispensing or splitting) imposed severe limits on the fluidic operations that could be achieved, and in addition the resulting spectra were not well resolved.

Here we report a significant advance over the previous DMF-high-field NMR technique.³⁴ Specifically, we describe critical improvements that make it possible to switch from the one-plate DMF device configuration to a two-plate device, which offers far more flexibility and operability to the user. In particular, the two-plate system allows for convenient manipulation of sample droplet shape, which can lead to a significant enhancement in the resolution of the resulting spectra. The switch from the one- to a two-plate DMF device configuration also allows for more complex chemical analyses than have been described previously for DMF-NMR, including the determination of analyte diffusion coefficients as well as quantitative monitoring of reactive intermediates and reaction progress. We propose that the system described here represents an important milestone that may eventually enable a wide range of previously impossible chemical analyses in small samples by NMR spectroscopy.

2 Theory

2.1 Two-to-one-plate DMF device transition

Two-plate DMF devices manipulate droplets that are sandwiched between a top-plate (bearing a contiguous counter-electrode) and a bottom-plate (bearing driving electrodes covered with a dielectric layer). When an electric potential is applied between the (top-plate) counter-electrode and a (bottom-plate) destination-electrode, the droplet is made to move until it completely covers the destination-electrode. In the alternate one-plate DMF device configuration, droplets are positioned on top of a single substrate (the “bottom plate”) bearing driving and counter-electrodes. When an electric potential is applied between adjacent (bottom-plate) destination- and counter-electrodes, the droplet is made to move until it straddles the region between the two electrodes.³⁵ One-plate systems can in fact have a “top plate,” as in the DMF-NMR system reported previously³⁴ (bearing an NMR microcoil), but this top plate does not have a DMF counter-electrode and does not contribute to the DMF driving circuit.

Here we report a new DMF-NMR system with a critical advance relative to what was reported previously,³⁴ in that the new system can be operated in “two plate” mode. Like conventional two-plate DMF systems, the top plate bears a counter-electrode to allow for droplet movement (in addition to supporting an embedded microcoil for NMR analysis). But unlike conventional two-plate DMF systems, in the devices described here, the entire top plate (including the microcoil and the DMF counter-electrode) is coated with a protective insulating layer. This configuration is more complex than conventional two-plate DMF systems (in which the counter-electrode is not insulated), necessitating study of what we term the “two-plate-to-one-plate transition.”

As an aide to understanding the two-plate-to-one-plate transition, an electromechanical model^36,37 of a DMF device was developed and is presented in Fig. 1(a). In this model, we make a simplifying (and common) assumption that the droplet is conductive, such that it is equipotential and therefore acts as a short in the circuit. Fig. 1(b) illustrates the equivalent circuit model of this system and is separated into three key sections. The first section, shown in the green box, encompasses the capacitance of the entire system (C_eq-tot). The capacitances contributed by the air-elements are small in comparison to the remainder of the circuit, such that C_eq-tot can be approximated by the second section, encompassed in the brown box, C_eq. Finally, a third section is encompassed in the blue box . As per Fig. 1(c), for a droplet moving from an origin-electrode to a destination-electrode (both with length L) such that it penetrates distance x over the destination electrode, the driving force F on the droplet is equal to the total change in capacitive energy, given by,

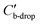where C_b-drop is the capacitance of the portion of the destination electrode covered by the droplet, v_b-drop is the voltage drop across C_b-drop, is the capacitance of the portion of the origin electrode covered by the droplet, and is the voltage drop across . These elements can be further expressed as follows,


where is the parallel combination of and C_t-drop, is the voltage drop across 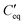, ε₀ is the permittivity of free space, ε_b is the relative permittivity the bottom-plate dielectric, b is the thickness of the bottom-plate dielectric layer, ε_t is the permittivity of top-plate dielectric, t is the thickness of the top-plate dielectric layer, w is the width of the electrode, and V is the applied voltage.

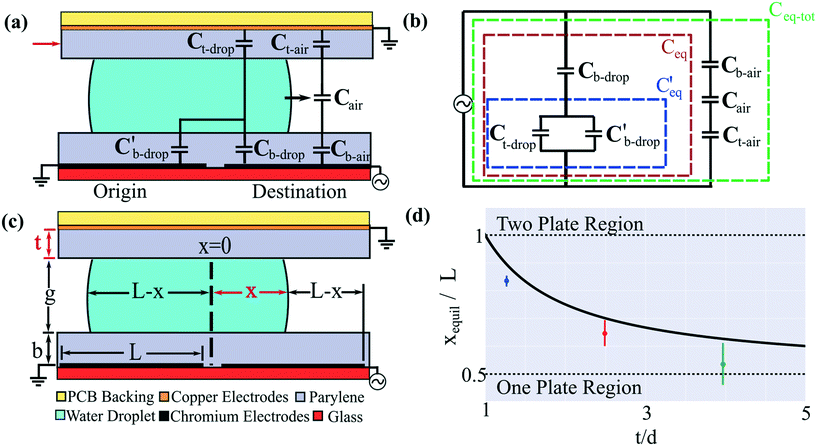Fig. 1 Two-to-one-plate digital microfluidic device transition. (a) Schematic of the unique two-plate DMF system used here, in which a droplet (turquoise) is sandwiched between a PCB-backing top-plate (yellow) bearing a copper counter-electrode (orange) and NMR microcoil (not shown) coated with a Parylene-C insulator (gray), and a glass bottom-plate (red), bearing a chromium origin-electrode and destination-electrode (black) coated with a Parylene-C insulator (gray). Most two-plate DMF systems do not have the top-plate insulator (red arrow). The droplet is moving onto the destination electrode (black arrow). Superimposed on the schematic is an electromechanical model of a DMF driving circuit, including top-plate dielectric-layer capacitances over the droplet C_t-drop and over the surrounding medium (air) C_t-air, capacitance of the surrounding medium C_air, and bottom-plate dielectric layer capacitances under the droplet and over the origin-electrode , under the droplet and over the destination-electrode C_b-drop, and under the surrounding medium and over the destination-electrode C_b-air. (b) Equivalent circuit representation of the DMF device with the elements comprising the total equivalent capacitance C_eq-tot encompassed by the green box, the elements comprising the droplet-covered equivalent capacitance C_eq encompassed by the brown box, and a third sub-circuit encompassed by the blue box. (c) Geometric properties of the system including electrode length L, droplet penetration depth over the destination-electrode x, top-plate dielectric thickness t, inter-plate spacer-height g, and bottom-plate dielectric thickness b. (d) Plot (from eqn (1) in the Theory section) of the ratio of the predicted equilibrium distance for droplet movement x_equil to electrode length (black curve) as a function of the ratio of top-plate to bottom-plate dielectric thickness. Two-plate behavior (with x_equil = L) is predicted for t ≤ b, and one-plate behavior (with x_equil = L/2) is predicted for t ≫ b (dashed horizontal black lines). Experimental results are shown for devices with top plate dielectric thickness t = 6.7 μm (blue), 13.2 μm (red), and 21.0 μm (green), all paired with a bottom plate dielectric thickness b = 5.3 μm. Error bars represent ±1 st. dev. for three replicates per condition.

The important question to be answered is how does the (unusual) protective dielectric layer on the top plate with thickness t effect droplet movement to position x. In particular, we propose that it is useful to consider the equilibrium position x_equil at which the droplet will cease moving if the origin-electrode is grounded and the destination-electrode is potentiated (at a level sufficient to cause the droplet to move, initially) for infinite time. At this position, F = 0, as per the following relationship, noting that the top-dielectric capacitance does not depend on x.

Note that solving for F = 0 is an approximation (a more accurate expression would solve for F equal to the particular force required to maintain droplet motion in a moving droplet), but is sufficient for purposes here, which are simply to predict the behaviour at the extremes of the two-plate-to-one-plate transition. Substitution for the relevant voltages gives the following expression.

Noting the two differentials are equal and opposite to each other, one obtains the following relationship.

And finally, though substitution the desired relationship between x_equil and t is obtained, shown in eqn (1).

Eqn (1) is plotted in Fig. 1(d) for the case with ε_b = ε_t. Consider two important solutions to the equation: (i) with top-plate and bottom plate dielectric having the same thickness (i.e. t = b), or (ii) with an infinitely thick top-plate dielectric (t → ∞). For the first case, the equilibrium position is equal to the length of the electrode, indicating that the droplet should move completely onto the actuated electrode [the top region in Fig. 1(d)]. Therefore at any top-plate dielectric thickness equal to or less than the bottom-plate dielectric thickness, the device should behave like the familiar two-plate DMF device. For the second case, as the thickness of the top dielectric is increased to infinity [the bottom region in Fig. 1(d)], eqn (1) predicts that the equilibrium position is halfway between the destination and source electrode, i.e. x_equil = L/2. As shown in Fig. 1(d), for intermediate conditions between these two cases, as the top dielectric layer is increased to a thickness greater than the bottom dielectric layer, eqn (1) predicts that the droplet will move to positions x_equil < L, eventually transitioning to the one-plate case where the droplet stops when it is midway between the origin and destination electrodes. The predicted trend is also observed in experimental measurements (as per Fig. S1 in the online ESI†). This framework is illustrative for the current work (in which we expect “two-plate” behavior because t < b), and we propose that it may be useful for other applications that could benefit from the presence of a protective, insulating layer on the top plate.

2.2 Simulation of magnetic flux density

An important factor in this work is how analyte molecules in sample-droplets respond to being placed in the external magnetic field in an NMR spectrometer. If the magnetic field within the droplet was completely uniform, the spins within the sample would precess at a singular Larmour frequency given by the following relationship,

ω = −γB₀

where ω is the Larmour frequency, γ is the gyromagnetic ratio for the spins of interest, and B₀ is the magnitude of the magnetic flux density. In real-world systems, however, the magnetic flux density varies within the sample because of magnetic-susceptibility mismatches between materials. It is important to understand this phenomenon because field inhomogeneities within the droplet cause significant line broadening of the resultant NMR spectra.

The NMR spectrometer provides an initial magnetization field H, which in the case of the 500 MHz spectrometer used here is 11.74 T. Any sample within the spectrometer will produce an additional magnetization M in response to the field according the constitutive relationship,

M = χ_iH

where χ_i is the magnetic susceptibility of the material in the system. The susceptibilities of the materials used in this work are copper (χ_Cu = −9.6 × 10⁻⁶), SU-8 (χ_SU-8 = 22 129.7 × 10⁻⁶), water (χ_H2O = −9.05 × 10⁻⁶), silicon dioxide (χ_SiO2 = −11.0 × 10⁻⁶), and air (χ_air = +0.36 × 10⁻⁶). This magnetization is then added to the original field to give the magnetic flux density B₀,

B₀ = μ₀(H + M)

where μ₀ is the permeability of free space and can vary significantly over the volume depending on the geometry of the system. To determine how the magnetic flux density varies in the droplets, simulations were performed using 3D COMSOL Multiphysics (COMSOL Inc., Burlington, MA, accessed via license obtained through CMC microsystems, Kingston, ON).

A COMSOL model was developed and was used to carry out two studies, the first using the magnetic fields, no currents module to determine the magnetic flux density of the droplet and surrounding environment. As there are no currents in any of the volumes of interest, Ampère's law states that the magnetization field is as shown.

∇ × H = 0

As a non-rotating field is conservative, one can describe H as gradient of a scalar magnetic potential V_m, which combined with the fact that the divergence of the magnetic flux density above is zero gives eqn (2).

−∇·(μ₀∇V_m + μ₀χ_i∇V_m) = 0 (2)

Eqn (2) is the governing equation that was used to simulate the magnetic flux density within the droplet and the surrounding DMF device. A 11.74 T magnetic flux density boundary was applied to the top of the model domain and a zero magnetic scalar potential was applied to the bottom of the model domain. All other exterior surfaces were given a magnetic insulation boundary condition.

In the second study, the magnetic fields module was used to estimate the relative field strength in the droplet that is produced by the microcoil. Knowing the field strength is important, as how much a particular spin will contribute to the signal is dependent on the field strength that the receiver coil produces at the position of that spin. The magnetic field that produced by the planar microcoil was calculated using the general form of Ampère's law,

∇ × H = J_e

where J_e is the current running though the receiver coils which in the simulation was 1 A mm⁻¹.

3 Experimental

3.1 Materials and reagents

Unless otherwise indicated, reagents were purchased from Sigma-Aldrich (Oakville, ON). Glass slides coated with chromium (100 nm) and AZ1500 photoresist (530 nm) were purchased from Telic Inc. (Santa Clarita, CA). AP7156E Pyralux double-sided copper-clad polyimide films were obtained from DuPont Electronic Materials (Research Triangle Park, NC). Parylene-C was from Specialty Coating Systems (Indianapolis, IN). FluoroPel PFC 1101V was purchased from Cytonix, LLC (Beltsville, MD). Microposit MF-312 developer was from Rohm and Haas (Marlborough, MA), AZ 300T stripper was from AZ Electronic Materials (Somerville, NJ), and CR-4 Cr etchant was from Cyantek (Freemont, CA). All solutions used to obtain NMR spectra were prepared in 99.9% deuterium oxide.

3.2 Microcoil and NMR spectrometer

Custom multi-turn copper microcoils were provided by Bruker BioSpin (Billerica, MA and Fällanden, Switzerland). Briefly, as received, each coil was mounted on a glass substrate, and had an inner diameter of 0.5 mm, 4 turns and an outer diameter of 0.98 mm. The wire-traces in the coil had a height of 0.04 mm, a width of 0.03 mm, and gaps-between-traces of 0.03 mm. Each microcoil was isolated from and surrounded by a separate copper feature (approximately 15 × 30 mm, with a cut-out for the coil) that served as the DMF counter-electrode. All spaces between copper features on the substrate were filled with SU-8 to planarize the surface, and the entire substrate (including the microcoil, the SU-8, and the DMF counter-electrode) was coated with a protective layer of Parylene-C (∼200 nm thick). A small section at the edge of the substrate was left bare to allow the DMF counter-electrode to be connected to ground. Finally, the entire substrate was coated with FluoroPel (see the following sections for details) and served as the “top” plate for a DMF device, bringing the total dielectric thickness on the top plate to around 1 μm. The microcoil substrate was mounted on a PEEK coil-holder that was interfaced to a micro-05 Broadband 2-channel H-X NMR probe (Bruker GmbH, Rheinstetten, Germany). Experiments were carried out in a Bruker Avance III spectrometer operating at 500.28 MHz ¹H frequency. The 90° ¹H radio frequency pulse was calibrated on each sample and was typically 7 μs at 0.1 W. Samples were evaluated by NMR as described below, all with no purge gas flow.

3.3 DMF device fabrication and operation

DMF bottom plates were fabricated at the Toronto Nanofabrication Centre (TNFC) at the University of Toronto (UT). Photoresist-coated, chromium-coated glass slides (50 mm × 75 mm) were exposed for 10 seconds through photomasks [printed using a Heidelberg uPG 501 mask writer (Heidelberg Instruments Mikrotechnik GmbH, Germany) at the UT Centre for Microfluidic Systems], and then were developed in Microposit MF-312 for 30–45 seconds until the electrode pattern was visible. The slides were then etched using CR-4 for 5–8 minutes, and finally stripped using AZ 300T stripper. Each slide was divided into three 15 mm × 75 mm devices using a Disco DAD3220 Automatic Dicing Saw, and then the devices were rinsed with acetone, isopropanol, and water before being blown dry with N₂ gas. When complete, each device bore 20 square DMF driving electrodes (2.25 × 2.25 mm), two reservoir electrodes (6.6 × 16 mm) and two dispensing electrodes (2.25 × 4.1 mm), and each electrode was connected to a contact-pad at the edge of the substrate. A layer of Parylene-C (approximately 5 μm) was deposited using SCS 2010 Parylene Coater (Specialty Coating Systems), followed by a layer of Fluoropel PFC 1101V, deposited via spin coating at 2000 rpm for 30 seconds and post-baking at 110 °C (forming a layer approx. 50 nm thick); the contact-pad region was not coated.

Each DMF bottom-plate was assembled with a top-plate bearing a microcoil (as described below). Bottom-plate and top-plate electrodes were connected to an open-source DropBot control system.³⁸ Droplets were controlled by applying driving voltages (155 V_RMS, 10 kHz) between driving electrodes on the bottom plate and the counter-electrode on the top plate, with droplet position determined by capacitative sensing. All non-actuated electrodes on the bottom plate were grounded.

3.4 DMF-NMR interface

The DMF-NMR interface comprises four elements—a DMF electrical manifold, the DMF device top-plate/microcoil, the DMF bottom-plate, and a mechanical housing, each described below.

The first element, the electrical manifold (re-used for multiple experiments) [Fig. 2(a)], was formed from a custom printed circuit board (PCB) bearing two connected sets of 24 vias, arranged into two 4 × 6 electrode-arrays separated by 10 cm (Pentalogix, Portland, OR). One of the arrays was modified by soldering 24 pogo-pins (one per electrode), and the other array was modified by soldering 24 wires (around 3 m in length each, one per electrode). The wires (with the addition of one extra wire designated for connecting to the DMF top-plate counter-electrode, as described below) were bundled into a cable terminated by a connector designed to interface with a DropBot control system.³⁸ Prior to each experiment, the cable was threaded through the bore of the NMR spectrometer, with the DropBot connector at the top and the PCB dangling below.

Fig. 2 Two plate DMF-NMR interface. (a) Picture of DMF electrical manifold. (b) Picture of DMF top-plate bearing a 500 μm radius planar microcoil, and (b′) close-up picture of the microcoil surrounded by a copper feature that serves as the DMF counter-electrode (highlighted by a red/dashed border). (c) Picture of DMF bottom-plate mated to a 3D printed mechanical housing. (d) Picture of a fully assembled DMF-NMR interface, and (d′) close-up picture of the DMF bottom-plate electrode array, overlaid with cartoons illustrating the position of a 4.2 μL droplet (blue) oriented parallel relative to the direction of the external field B₀, and the position of the microcoil (green). (e) Picture of DMF-NMR interface mated with the 2-channel NMR probe, covered with gradient coil. (f) Hybrid schematic and picture illustrating the position of DMF-NMR assembly and probe inside the spectrometer. Wires connected to DMF driving electrodes were fed through the top of the spectrometer to connect to a DropBot control system for remote operation.

The second element, the DMF device top-plate/microcoil (re-used for multiple experiments) [Fig. 2(b) and (b′)], was prepared for experiments in a four-step procedure. First, 1 mL of FluoroPel PFC 1101V solution was pipetted onto the surface of the top-plate/microcoil and then gently wiped with a Kimwipe. Second, a 0.5 × 2.5 cm strip of Pyralux double-sided copper-clad polyimide film was affixed to the exposed edge of the DMF-counter-electrode via M970312 conductive adhesive (3 M, St. Paul, MN). Third, 1 mL of FluoroPel PCV 1101V solution was pipetted onto the surface of the top-plate/microcoil, the excess was allowed to flow off into a reservoir, and then the piece was allowed to air dry for 10–20 minutes (the thickness of the FluoroPel layer formed in this manner is approx. 800 nm). Fourth, two 1 × 10 mm spacers were affixed to the right- and left-most edges of the DMF counter-electrode. Each spacer comprised two or three pieces of double-sided tape (3 M, St. Paul, MN) covered with a piece of fluorinated ethylene propylene (FEP) film (CSHyde Company, Lake Villa, IL), resulting in a final thickness of approximately 0.18 mm or 0.28 mm (for spacers formed from 2 or 3 pieces of double-sided tape, respectively).

A fresh third element, a DMF bottom-plate, was used for each experiment, mated to the fourth element, a cylindrical (17 mm diameter, 10 cm length) mechanical housing (re-used for multiple experiments) [Fig. 2(c)]. The housing was constructed using a Form 2 3D printer (Formlabs Somerville, Massachusetts, United States) and bears slots for elements 1–3 arranged such that the electrical manifold pogo-pins align with the contact-pads on the DMF bottom plate, and the microcoil on the top plate aligns with the center of the array of driving electrodes on the DMF bottom plate.

A typical experiment was initiated in five steps. First, the DMF bottom plate was inserted into the housing. Second, aliquots of reagents and analytes were pipetted onto the top-plate/microcoil, which was then inserted into the housing. Third, the DMF-device portion of the housing was wrapped with Teflon tape (Home Depot, Toronto, ON). Fourth, the electrical manifold (dangling from the bottom of the spectrometer) was inserted into the housing, making electrical connections to the DMF driving electrodes on the bottom plate via the pogo-pins. The counter-electrode on the top-plate was also connected to the dedicated wire in the cable (see above). Fifth, the fully assembled housing [Fig. 2(d) and (d′)] was mounted on a 2-channel NMR probe [Fig. 2(e)], and the cable at the top of the spectrometer was gently pulled to lift it into place inside the spectrometer. Finally, the connector at the end of the cable was interfaced with the DropBot control system [Fig. 2(f)].

3.5 Simulation geometry and mesh

Numerical simulations of the microcoil and its surrounding environment were generated using COMSOL Multiphysics as described in the Theory section. The total domain of the model measured 24.75 mm × 24.75 mm × 30.2 mm and was sub-divided vertically into 3 major subdomains representing the top plate, the inter-plate gap, and the bottom plate of a DMF device. The top domain (representing the device top plate) had dimensions of 24.75 mm × 24.75 mm × 15 mm and was assigned the magnetic susceptibility of SU-8 (for regions other than the coil). At the center of this domain were 4 concentric circular wires (assigned the magnetic susceptibility of copper) that approximated the microcoils used in this work, with each wire having a height of 0.04 mm and a width of 0.03 mm. The outer diameter of the largest circular wire was 1 mm, and there was a 0.03 mm spacing between each wire. The middle domain (representing the inter-plate gap) measured 24.75 mm × 24.75 mm × 0.2 mm, and was assigned the magnetic susceptibility of air (for regions other than the droplet). At the center of this domain was a droplet (assigned the magnetic susceptibility of water). Two droplet volumes were modeled, both rectangular with rounded corners, and radius of curvature in the vertical dimension of 0.2 mm. A 1.6 μL droplet measured 2.25 mm × 2.25 mm × 0.2 mm, and a 4.2 μL droplet measured 2.25 mm × 6.75 mm × 0.2 mm. A 1 mm diameter by 0.2 mm cylindrical volume in the droplet directly below the microcoil employed a mesh using a minimum element size of 0.0001 mm, a maximum element size of 0.015 mm, an element growth rate of 1.05, a resolution of curvature of 0.1, and a resolution of narrow regions of 1. Finally, the bottom domain (representing the device bottom plate) measured 24.75 mm × 24.75 mm × 15 mm and was assigned the magnetic susceptibility of SiO₂. Most domains had a free tetrahedral mesh with a minimum element size of 0.00495 mm, a maximum element size of 0.495 mm, an element growth rate of 1.3, a resolution of curvature of 0.2, and a resolution of narrow regions of 1.

3.6 Droplet volume and orientation

The effect of droplet volume and orientation with respect to the applied magnetic field B₀ was tested using devices with a 0.19 mm inter-plate gap. In typical experiments, a single 1.6 μL or 4.2 μL droplet of a 0.5 M sucrose solution (in 90% D₂O, 10% H₂O) was loaded into a device by pipette, and the device was assembled and loaded into the spectrometer (as described above). The droplet was then translated such that it was centered under the microcoil and was made to adopt the desired orientation relative to B₀. Specifically, 1.6 μL droplets covered a single DMF driving electrode and thus were symmetric with respect to B₀ in any orientation, but 4.2 μL droplets were made to stretch into a linear “bus” shape (rectangular with rounded corners) along three driving electrodes, and thus were made to orient either perpendicular or parallel with respect to B₀. The driving potential was kept “on” while the sample was shimmed (∼5 min) and then a scan was acquired using 16 384 time domain points over a 10 kHz spectral width. The data were Fourier transformed without apodization and zero-filled by a factor of 2.

To estimate spectral resolutions, peaks in the 4.12–4.23 ppm region were deconvolved using Mestre NOVA (MNOVA) v. 12.01 (Mestrelab Research, Spain) to find the underlying peak positions p_i and the peak half height widths W_i. The resolution R of each overlapping peak-pair was then calculated using the following expression, and the means of the resolutions for each condition (n = 3) were evaluated for significance using a two tailed t-test and the assumption of unequal variances.

3.7 DOSY of sucrose and cyclodextrin

Diffusion ordered spectroscopy (DOSY) experiments were carried out using devices with a 0.19 mm inter-plate gap. In typical experiments, a single 4.2 μL droplet of either a 0.5 M sucrose or a 0.125 M γ-cyclodextrin solution (in 90% D₂O, 10% H₂O) was loaded into a device by pipette and the device was assembled and loaded into the spectrometer (as described above). The droplet was translated such that it was centered under the microcoil and then was stretched to be parallel with respect to B₀. The driving potential was kept “on” while the sample was shimmed (∼5 min), and then data were acquired. Briefly, a pulsed-field gradient (PFG) stimulated-echo (STE) sequence using a spoil gradient (stebpgp1s) was used. A 1.1 ms sine-shaped encoding/decoding gradient pulse was ramped from 6 to 294 gauss per cm in 16 linear increments using a Diff-30 diffusion gradient. 16 scans and 8 dummy scans were collected at 298 K with a diffusion time of 80 ms and 16 384 time domain points. Solvent suppression was achieved by presaturating the water resonance at 0.00001 W during the 2 s recycle delay. DOSY spectra were processed using Bruker Topspin™ v.3.2 with up to mono-exponential fitting to each data point, a noise sensitivity factor of 1, and a spike suppression factor of 4. The 16 slices were processed with 16 384 points in the F2 (chemical shift) dimension and the diffusion axis included 128 points in the F1 dimension. Stacked plots were analysed using MNOVA.

3.8 Decarboxylation of glycine by N-bromosuccinimide

Decarboxylation reaction experiments were carried out using devices with a 0.28 mm inter-plate gap. In typical experiments, four 2.1 μL droplets were loaded onto a device by pipette: two of 0.1 M glycine and two of 0.08 M N-bromosuccinimde (NBS) (in D₂O). The device was assembled and loaded into the spectrometer (as described above) and a “dummy” pair of reagents (one droplet each of glycine and NBS) was made to merge and mix by translating the merged droplet in a circular pattern for 10 s. The merged dummy-droplet was then translated such that it was positioned directly under the microcoil and stretched parallel with respect to B₀. The driving potential was kept “on” while the sample was shimmed (∼5 min), and then the dummy droplet was translated away from the coil. The “true” reaction was then initiated by merging and mixing the other pair of glycine and NBS droplets (as above). The merged true-droplet was then translated such that it was centered under the microcoil and stretched parallel with respect to B₀. The driving potential was kept “on” while spectra were collected every 25 s for 900 s (note: a new shim was typically not required for the true-reaction; if necessary, it was typically accomplished in <30 s). In each measurement, 32 scans were collected along 8 dummy scans. The time domain points were reduced to 8192 and a recycle delay of 0.2 s was applied such that each scan lasted 0.6 s. Thus, a full 32-scan dataset required 20 s to acquire (25 s including the dummy scans). The data were zero-filled by a factor of 2 and processed using an exponential function corresponding to a 1 Hz line broadening in the transformed spectrum. The peak areas associated with the non-exchangeable protons of each reactant and product species found in the spectrum were normalized to the combined peak area of the methylene protons of N-bromosuccinimide and succinimide, and these normalized areas were then plotted as a function of time to evaluate the reaction progress.

4 Results and discussion

4.1 Two-plate DMF-NMR

The one example of a high-field DMF-NMR system reported previously³⁴ used the one-plate digital microfluidic format. This configuration is fine for proof of principle but has significant limitations; the most compelling applications for DMF (including dried blood spot analysis,³⁹ 3D cell culture,⁴⁰ and portable, point-of-case disease diagnostics⁴¹) use the much more powerful two-plate device format. In recognition of this challenge, we developed a two-plate DMF-NMR system featuring a custom “top plate” that houses both an embedded NMR microcoil and a DMF counter-electrode. The system introduced here is similar to other two-plate DMF systems with one exception—in the new system, the top plate is covered by a protective insulating layer (a feature required for repeated NMR measurements). This (unique) configuration has the potential to degrade the “two-plate” behavior of the system as a result of what we call the “two-plate-to-one-plate transition”. As described in the Theory section, we have derived a simple model for this phenomenon that relates the thickness of the top-plate dielectric to the equilibrium position at which droplet movement is predicted to cease moving onto a charged electrode. We have not seen this type of analysis in the literature, and propose that it may be useful for others to consider.

Figures associated with the “two-plate-to-one-plate” transition model are outlined in Fig. 1(a–c), featuring the critical parameters of top-plate dielectric thickness t (as well as bottom-plate dielectric thickness b) and droplet position x as it moves onto a destination electrode (with length L). As shown in Fig. 1(d) (and as described in detail in the Theory section), the model (shown as a black line) predicts that when t is small relative to b, the device will behave as a true “two plate” digital microfluidic system, such that the equilibrium droplet position at which the droplet ceases moving when x_equil is equivalent to L. On the other hand, when t is large relative to b, the device will (undesirably) behave as a one-plate system (with x_equil = L/2). Experimental results [collected as described in the online ESI† and plotted in Fig. 1(d) as coloured markers] confirm the trend predicted by the model, with a slight bias to smaller x_equil. In the system described here, t and b are approximately 1.0 μm (including both the Parylene-C and FluoroPel layers) and 5.0 μm, respectively, such that this system is predicted to fall comfortably in the two-plate regime (which matches experimental observation).We propose that this framework may be useful in the future for characterizing the performance of other DMF devices may benefit from a protective top-plate insulator.

In work leading up to the results reported here, a number of different device, microcoil, and probe geometries were considered and tested. The final, optimized system is depicted in Fig. 2 and consists of four key parts: (1) an electrical manifold [Fig. 2(a)], (2) the DMF top-plate bearing an embedded 1 mm outer diameter NMR microcoil [Fig. 2(b) and (b′)], and (3) a DMF bottom-plate and (4) a mechanical housing [Fig. 2(c)]. The four parts slot together [Fig. 2(d) and (d′)] and this assembly mates with a standard 2-channel NMR probe [Fig. 2(e)]. Finally, the probe is loaded into the spectrometer and the cabling is connected to the open-source DropBot control-system³⁸ [Fig. 2(f)]. From assembly to insertion the entire process can be completed within 2 minutes. As shown, the DMF device in this system is oriented vertically (with respect to gravity) rather than the more common “horizontal” orientation. Despite this oddity, droplets of various volumes were easily manipulatable in the device within the spectrometer, and their positions were stable, with no observations of unpredictable displacements caused by gravity or other forces.

4.2 Two-plate DMF-NMR: droplet volume and orientation

The two-plate device geometry introduced here represents a critical advance for DMF-NMR, as it allows for much more reproducible droplet translation than in the one-plate DMF-NMR system reported previously.³⁴ This increased fidelity enabled us to explore the effect of droplet volume and orientation on spectral resolution.

Two droplet volumes and orientations were explored. A 1.6 μL droplet-volume occupies roughly the area of a single driving electrode (with width ∼2.25 mm), while a 4.2 μL droplet-volume can be made to stretch into a bus-shaped volume covering three driving electrodes (with width and length ∼2.25 mm and ∼6.75 mm, respectively). As depicted in Fig. 3(a), the former (green) is symmetric with respect to the applied magnetic field B₀, while the latter can be aligned such that its long axis is perpendicular (red) or parallel (blue) with respect to B₀ [note that the 4.2 μL-parallel case is the size and orientation of the droplet depicted in Fig. 2(d′)]. In all cases, the precise control afforded by two-plate operation made it straightforward to shape the droplet and center it under the microcoil.

Fig. 3 Effect of droplet size and orientation on spectral resolution in two-plate DMF-NMR. (a) 3D models depicting the orientations and positions of a 1.6 μL droplet (green) and two 4.2 μL droplets (red and blue). Each droplet is centered relative to the microcoil, with a zx-cutplane highlighted that bisects the droplet and coil. Black arrows indicate the direction of B₀, such that the long axes of the red and blue droplets are oriented perpendicular and parallel with respect to the field, respectively. (b) Numerical simulations in the zx-cutplanes from (a) of magnetic flux density inhomogeneities [heat map of ΔB/B₀ from red = B_min (the minimum flux density in the droplet) to blue = B_min + 0.30 ppm] and the x–y components of the radiofrequency fields produced by the microcoil B_1xy (contours representing the magnitude of normalized magnetic flux density from at 80%, 50%, 20%, 10%, and 1% generated by a 1 A mm⁻² current running through the coil), for a 1.6 μL droplet (left, outlined in green), a 4.2 μL droplet oriented perpendicular with respect to B₀ (center, outlined in red), and a 4.2 μL droplet oriented parallel with respect to B₀ (right, outlined in blue). (c) Representative NMR spectra of 0.5 M solutions of sucrose generated from a 1.6 μL droplet (green), a 4.2 μL droplet oriented perpendicular with respect to B₀ (red), and a 4.2 μL droplet oriented parallel with respect to B₀ (blue). The inset shows a magnification of the region containing the signal from the 3 carbons in the fructose sub-unit of sucrose. The red and blue spectra were artificially shifted in the y-axis for clarity.

Numerical simulations of the applied field B₀ and the field sensed by the microcoil B₁ were generated for each of the cases above. A z–x cutplane of the simulation for each case (with z parallel to B₀ and x parallel to the normal of the plane containing the microcoil) is shown in Fig. 3(b). We first consider B₁—the relevant part of the radiofrequency field strength is the portion that is projected onto the x and y axes (B_1xy), as the signal is proportional to the time rate of change of the dot product of B₁ with the magnetic moment, meaning only the x and y components are significant. This property (normalized to the maximum intensity observed within the droplet) is represented by the contour lines in in Fig. 3(b). As shown, the B_1xy field is high in the portion of the droplet directly over the microcoil, but it rapidly drops below 1% of the maximum near the outer edge of the microcoil and continues to fall off exponentially. Therefore, it is reasonable to focus our attention on how the field inhomogeneities vary in the droplet in a restricted “active volume” directly below the microcoil, as molecules in this region are responsible for most of the NMR signal that is measured.

Next we consider variations in applied magnetic field that arise from the mismatch in magnetic susceptibility at the droplet-air and droplet-device interfaces. This property is quantified in terms of a ratio relative to the applied field, ΔB/B₀ (measured in parts per million, ppm), which is plotted as a heat map in Fig. 3(b). While previous work highlighted the importance of droplet volume (with respect to microcoil size) for this property,³⁴ a brief inspection of the simulations in Fig. 3(b) suggests that droplet orientation may be more important than droplet volume. Consider first the cases of the 1.6 μL droplet (left) and the 4.2 μL droplet oriented perpendicularly relative to B₀ (center). These samples have similar field distributions despite their very significant differences in volume. That is, the field strength experienced by molecules in the active volumes of these droplets varies by almost 0.3 ppm, which should impose limits on the eventual spectral resolution that can be achieved. In contrast, the molecules in the active volume of the 4.2 μL droplet oriented with long axis parallel to B₀ (right) experience a field variation of around 0.03 ppm—a much more homogeneous field. A potential explanation for this prediction can be envisioned by imagining the incurred current-density at the boundary between the droplet and surrounding media as being a solenoid coil. If the solenoid is long and thin, then the field inside the solenoid (i.e. the droplet) will be homogeneous. However, if the solenoid is short relative to its width, then the field inside the solenoid (i.e. the droplet) would be heterogeneous. Therefore, we expect that droplets with the shape of a long thin solenoid (i.e. droplets with parallel orientation relative to B₀) should have a relatively uniform field, while droplets in the shape of a short stubby solenoid should have a relatively non-uniform field inside the droplet.

The simulations in Fig. 3(b) represent, of course, an ideal; in actual experiments, the two-plate DMF system allows for fine control of droplet orientation, but it is likely that “perfect” droplet alignments relative to B₀ may be impossible. With this in mind, it is remarkable that the predictions in Fig. 3(b) are borne out by experimental observation. That is, in spectra [Fig. 3(c)] collected from droplets of sucrose with (our best experimental approximation of) the indicated volumes and orientations, the spectral resolutions R follow the trend predicted by the simulation. This effect was estimated quantitatively by deconvolving each set of overlapping peaks at around 4.2 ppm to determine the average resolution for each condition. Specifically, the resolutions of the 1.6 μL case, the 4.2 μL horizontal case, and the 4.2 μL parallel case were found to be R = 0.57 ± 0.12, R = 0.62 ± 0.09, and R = 0.89 ± 0.09, respectively (all reported as the mean ± st. dev. for n = 3 per condition). The resolutions estimated for the former two conditions were not statistically different (p = 0.539), while the resolution for the latter condition (4.2 μL parallel case) was statistically higher than that of the 1.6 μL case (p = 0.022) and the 4.2 μL horizontal case (p = 0.023).

In summary, the unique capacity to manipulate sample orientation to enhance spectral resolution is an exciting new feature of two-plate DMF-NMR that may be useful for a wide range of applications in the future. Further, the effects of droplet orientation on resolution suggest that it may be useful to experiment with non-circular coils (e.g., racetrack-geometry NMR sensors). In this work, all of the remaining experiments were conducted using droplets that were oriented parallel to B₀.

4.3 Two-plate DMF-NMR: applications

The new system was applied to two applications. The first was an exploration of compatibility with diffusion ordered spectroscopy (DOSY). In DOSY, the nuclear spins of molecules in the sample are spatially encoded by introducing a linearly varying field strength along the z-direction of the sample. After waiting for the molecules to diffuse, the spins are decoded by reversing the linear gradient field. If molecules have not moved in the z-axis, they will be completely refocused and the signal intensity will theoretically be the same. However, if the molecules moved along the z-direction (into a different part of the gradient field), the signals are not focused, and the signal intensity decreases in proportion to how far the molecules have moved. By ramping the gradient encoding strength in an array of experiments, the diffusion coefficient D can be estimated using the following equation,

I = I₀e^{−DΔ′(g_diffγδ)2}

where I and I₀ are the intensities in the presence and absence of a gradient pulse, Δ′ is the diffusion time corrected for the effects of finite gradient pulse width, g_diff and δ are the amplitude and duration of the gradient pulses, and γ is the gyromagnetic ratio. The equation is commonly fit using an approximation of the inverse Laplace transform, or via mono/multi-exponential fitting of the data.⁴² The resulting DOSY spectrum is a correlation of the ¹H chemical shift as a function of D.

To evaluate the feasibility of using DMF-NMR for DOSY analysis of diffusion, we evaluated droplets containing model analytes sucrose (M.W. = 343.3 g mol⁻¹) and γ-cyclodextrin (M.W. = 1297.1 g mol⁻¹). Fig. 4(a) and (b) show the raw NMR data; as expected, the peak intensities for the lighter sucrose molecules decrease more rapidly with increasing field strength than those for γ-cyclodextrin. After fitting, the diffusion coefficients can be extracted from the DOSY data [Fig. 4(c) and (d)]. The value of 10^−9.28 ≈ 5.25 × 10⁻¹⁰ m² s⁻¹ determined from the DMF-NMR analysis of sucrose is a close match for what has been reported in the literature.⁴³ The value of 10^−9.78 ≈ 1.66 × 10⁻¹⁰ m² s⁻¹ determined from the DMF-NMR analysis of γ-cyclodextrin is lower than the value of 10^−9.56 m² s⁻¹ reported previously⁴⁴ for extremely dilute solutions of this analyte. One potential source of variations in diffusion coefficient is variations in temperature; however, the electrode sizes and DMF driving potentials and frequencies used here are in a regime that was reported previously to not cause measurable heating,⁴⁵ leading us to assume that there are no (unwanted) heating effects in the current system. We propose that the difference in diffusion coefficient measured here for γ-cyclodextrin is more likely a consequence of the increased viscosities of such solutions at high concentrations [for example, the diffusion coefficients for dextrins measured in a 100 mg mL⁻¹ solution were reported to be slowed by approximately 10^−0.2–10^−0.24 m² s⁻¹ relative to those measured at 1 mg mL⁻¹ (ref. 42)]. Thus, the value of 10^−9.78 m² s⁻¹ determined here for γ-cyclodextrin (in a viscous 0.125 M solution) is approximately what we would expect for this concentration [i.e. 10^{−9.56–0.22} = 10^−9.78 m² s⁻¹].

Fig. 4 Two-plate DMF-NMR for diffusion ordered spectroscopy (DOSY). (a and b) Molecular structures (top) and representative stacks of raw NMR spectra (bottom) collected from aqueous 4.2 μL droplets in DMF devices oriented parallel to B₀ containing (a) 0.5 M sucrose or (b) 0.125 M γ-cyclodextrin. The DOSY encoding strength in each spectrum is indicated in a colour-scheme from red (low) to brown (high). (c) Fitted DOSY spectrum of the data in (a) indicating a diffusion coefficient of 10^−9.28 m² s⁻¹. (d) Fitted DOSY spectrum of the data in (b) showing a diffusion coefficient of 10^−9.78 m² s⁻¹.

As far as we are aware, DOSY has never before been demonstrated in a microfluidic device of any format. We chose to examine it here because it is a powerful tool that is used routinely to study non-covalent associations,⁴² molecular aggregation,⁴³ and the relationship between molecular size/shape and drug–protein binding;⁴⁶ the latter application is particularly important in drug discovery. In the future, we envision the development of DMF-NMR devices that can rapidly exchange droplets containing potential drugs and their protein targets over microcoils, with DOSY-NMR used to screen for interactions to identify leads and drug candidates.

A second application for DMF-NMR was selected—evaluation of the feasibility of using NMR for reaction-progress monitoring. A potential advantage of using DMF for this application is that each experiment requires only the volume of sample in each droplet. This stands in contrast to flow systems, which typically require large dead volumes (i.e. long sections of tubing connected to pumps that often must be located outside the spectrometer's 5 Gauss line⁴⁷) to achieve similar goals. Large dead volumes can be especially problematic for expensive reagents, precious samples, or highly reactive analytes that are only available in limited quantities. Furthermore, the inert (Teflon-based) surfaces and atmospheric pressures of DMF make it attractive for handing reagents and analytes that are not compatible with the materials or pressures in systems relying on standard HPLC-style pumps.

To allow for the analysis of rapid reactions, a dummy reaction strategy was developed, illustrated in Fig. 5(a). This strategy takes advantage of the fact that if the device is not moved, the shims require no or only slight readjustment between droplets that are brought to the microcoil. As shown, in this method, two sets of reagents are loaded, a first reaction is initiated, and this dummy-mixture is brought to the microcoil for shimming. After shimming is complete, the dummy reaction is removed from the microcoil and a second set of reagents is mixed and delivered to the microcoil. Spectra can thus be collected nearly immediately—in practice, we were able to evaluate the first set of reaction data ∼40 s after its initiation. Decarboxylation of glycine [Fig. 5(b), top] was chosen as a model reaction because of its rapid kinetics. Representative spectra collected after 40 s, 200 s, and 620 s of reaction in a two-plate DMF-NMR device are shown in Fig. 5(b), bottom. As indicated by colour-coding, the non-exchangeable proton peaks for glycine (blue), NBS (red), and succinimide (green) are found at around 3.55 ppm, 2.95 ppm, and 2.75 ppm, respectively. The shift in the glycine peak is associated with an increase of the pH caused by the production of ammonia. As shown in Fig. 5(c), normalized peak areas from spectra generated throughout a typical reaction can be arranged to produce a typical reaction time course. Note that the reaction proceeds rapidly at early stages and is ∼60% complete within the first 5 minutes. This type of time-resolution was not achievable using the DMF-NMR system reported previously,³⁴ as one-plate DMF is not capable of precise control of droplet shape and position (features that are required for the dummy-reaction strategy).

Fig. 5 Two-plate DMF-NMR for monitoring chemical reaction dynamics. (a) Series of schematics (from left to right) illustrating the two-plate DMF-NMR reaction protocol. (i) Two pairs of reagent droplets (blue and red) are loaded into the two-plate DMF-NMR interface (with gray DMF driving electrodes and orange microcoil). (ii) One set of dummy reagents is mixed (green) and driven to the microcoil for shimming. (iii) The other set of reagents is mixed and (iv) driven to the microcoil for analysis. (b) Reaction scheme (top) and representative two-plate DMF-NMR spectra (bottom) for glycine decarboxylation collected from recently mixed droplets in DMF devices oriented parallel to B₀ after shimming on dummy droplets. The relevant protons are color-coded in the reaction scheme for glycine (blue), N-bromosuccinimide (red) and succinimide (green), and correspond to peaks in the spectra at around 3.50, 2.95, and 2.75 ppm, respectively. The three spectra correspond to reaction times of 40 s (small dash), 200 s (thick dash), and 620 s (solid line). (c) Reaction progress as a function of time estimated from normalized non-exchangeable proton peak areas for glycine (blue), N-bromosuccinimide (red) and succinimide (green).

5 Conclusions

We report a new two-plate digital microfluidic interface for nuclear magnetic resonance spectroscopy which has significant advantages relative to the one-plate interface described previously. The two-plate configuration was enabled by embedding a standard microcoil within a DMF counter-electrode. A simple electrical model was developed to determine an appropriate dielectric layer thickness for this unique system, that could protect the coil but still allow for two-plate device operation. It was observed that the move to a two-plate device configuration allowed for more reliable droplet movement and positioning, and it was shown both theoretically and experimentally that by elongating a droplet in the direction of the static magnetic field, spectral resolution is improved. Finally, it was demonstrated that the improved fidelity of droplet movement and positioning makes the new technique compatible with sophisticated applications such as diffusion-ordered spectroscopy and the analysis of short-lived reactions. We propose that these improvements open the door for future DMF-NMR systems capable of performing complex, multi-step regimens including pre-concentration, sample work-up/clean up, protein recovery, and cell culture within the spectrometer.

Author contributions

I. S. designed and fabricated the DMF devices and interfaces (with assistance from S. v. d. E.), performed the experiments (with assistance from S. v. d. E., B. W., A. J., and R. S.), designed and ran the simulations, evaluated the data (with assistance from A. J. S. and A. R. W.), and prepared the figures (with assistance from A. J. S. and A. R. W.). F. B., D. S., T. F., and F. V. designed and fabricated the custom microcoil substrates and probe (with assistance from I. S.). H. J. S., F. B., A. J. S., and A. R. W. coordinated and supervised the work. I. S. and A. R. W. wrote and edited the manuscript. All authors provided feedback on the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Dr. Michael Fey, Dr. Dieter Gross, and Dr. Oliver Gruschke (Bruker BioSpin), as well as Prof. Marcel Utz (Southampton University) for fruitful conversations. We thank the National Science and Engineering Research Council (NSERC) of Canada for funding. A. R. W. thanks the Canada Research Chairs (CRC) Association for a CRC.

Notes and references

1. A. Mittermaier and L. E. Kay, Science, 2006, 312, 224–228.
2. Y. Cohen, L. Avram and L. Frish, Angew. Chem., Int. Ed., 2005, 44, 520–554.
3. A. J. Simpson, D. J. McNally and M. J. Simpson, Prog. Nucl. Magn. Reson. Spectrosc., 2011, 3, 97–175.
4. J. H. Ardenkjær-Larsen, B. Fridlund, A. Gram, G. Hansson, L. Hansson, M. H. Lerche, R. Servin, M. Thaning and K. Golman, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 10158–10163.
5. M. E. Merritt, C. Harrison, C. Storey, F. M. Jeffrey, A. D. Sherry and C. R. Malloy, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 19773–19777.
6. M. Mompeán, R. M. Sánchez-Donoso, A. Hoz, V. Saggiomo, A. H. Velders and M. V. Gomez, Nat. Commun., 2018, 9, 108.
7. M. Kakuta, D. A. Jayawickrama, A. M. Wolters, A. Manz and J. V. Sweedler, Anal. Chem., 2003, 75, 956–960.
8. R. A. Kautz, W. K. Goetzinger and B. L. Karger, J. Comb. Chem., 2005, 7, 14–20.
9. R. Kautz, P. Wang and R. W. Giese, Chem. Res. Toxicol., 2013, 26, 1424–1429.
10. R. M. Fratila, M. V. Gomez, S. Sýkora and A. H. Velders, Nat. Commun., 2014, 5, 3025.
11. M. V. Gomez, A. M. Rodriguez, A. de la Hoz, F. Jimenez-Marquez, R. M. Fratila, P. A. Barneveld and A. H. Velders, Anal. Chem., 2015, 87, 10547–10555.
12. K. Ehrmann, N. Saillen, F. Vincent, M. Stettler, M. Jordan, F. M. Wurm, P.-A. Besse and R. Popovic, Lab Chip, 2007, 7, 373–380.
13. H. Wensink, F. Benito-Lopez, D. C. Hermes, W. Verboom, H. J. Gardeniers, D. N. Reinhoudt and A. van den Berg, Lab Chip, 2005, 5, 280–284.
14. H. Lee, E. Sun, D. Ham and R. Weissleder, Nat. Med., 2008, 14, 869.
15. H. Ryan, S.-H. Song, A. Zaß, J. Korvink and M. Utz, Anal. Chem., 2012, 84, 3696–3702.
16. Y. Maguire, I. L. Chuang, S. Zhang and N. Gershenfeld, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 9198–9203.
17. M. Gogiashvili, A. Telfah, J. Lambert and R. Hergenröder, Anal. Bioanal. Chem., 2017, 409, 2471–2475.
18. A. J. Oosthoek-de Vries, J. Bart, R. M. Tiggelaar, J. W. Janssen, P. J. M. van Bentum, H. J. Gardeniers and A. P. Kentgens, Anal. Chem., 2017, 89, 2296–2303.
19. G. Finch, A. Yilmaz and M. Utz, J. Magn. Reson., 2016, 262, 73–80.
20. J. Bart, A. J. Kolkman, A. J. Oosthoek-de Vries, K. Koch, P. J. Nieuwland, H. Janssen, J. van Bentum, K. A. Ampt, F. P. Rutjes and S. S. Wijmenga, et al. , J. Am. Chem. Soc., 2009, 131, 5014–5015.
21. T. Meier, N. Wang, D. Mager, J. G. Korvink, S. Petigirard and L. Dubrovinsky, Sci. Adv., 2017, eaao5242.
22. N. Spengler, P. T. While, M. V. Meissner, U. Wallrabe and J. G. Korvink, PLoS One, 2017, 12, e0182779.
23. V. Badilita, R. C. Meier, N. Spengler, U. Wallrabe, M. Utz and J. G. Korvink, Soft Matter, 2012, 8, 10583–10597.
24. T. L. Peck, R. L. Magin and P. C. Lauterbur, J. Magn. Reson., Ser. B, 1995, 108, 114–124.
25. J. B. Aguayo, S. J. Blackband, J. Schoeniger, M. A. Mattingly and M. Hintermann, Nature, 1986, 322, 190.
26. J. Schoeniger, N. Aiken, E. Hsu and S. Blackband, J. Magn. Reson., Ser. B, 1994, 103, 261–273.
27. S.-C. Lee, J.-H. Cho, D. Mietchen, Y.-S. Kim, K. S. Hong, C. Lee, D. Kang, K. D. Park, B.-S. Choi and C. Cheong, Biophys. J., 2006, 90, 1797–1803.
28. I. Fugariu, R. Soong, D. Lane, M. Fey, W. Maas, F. Vincent, A. Beck, D. Schmidig, B. Treanor and A. Simpson, Analyst, 2017, 142, 4812–4824.
29. M. Grisi, F. Vincent, B. Volpe, R. Guidetti, N. Harris, A. Beck and G. Boero, Sci. Rep., 2017, 7, 44670.
30. H. Ryan, A. Smith and M. Utz, Lab Chip, 2014, 14, 1678–1685.
31. W. Hale, G. Rossetto, R. Greenhalgh, G. Finch and M. Utz, Lab Chip, 2018, 18, 3018–3024.
32. K.-M. Lei, P.-I. Mak, M.-K. Law and R. P. Martins, Analyst, 2014, 139, 6204–6213.
33. K.-M. Lei, P.-I. Mak, M.-K. Law and R. P. Martins, Analyst, 2015, 140, 5129–5137.
34. I. Swyer, R. Soong, M. D. Dryden, W. E. Fey, M. Maas, A. Simpson and A. Wheeler, Lab-on-a-Chip, 2016, 16, 4424–4435.
35. M. Abdelgawad, P. Park and A. R. Wheeler, J. Appl. Phys., 2009, 105, 094506.
36. T. B. Jones, Langmuir, 2002, 4437–4443.
37. D. Chatterjee, H. Shepherd and R. L. Garrell, Lab Chip, 2009, 9, 1219–1229.
38. R. Fobel, C. Fobel and A. R. Wheeler, Appl. Phys. Lett., 2013, 102, 193513.
39. S. C. Shih, H. Yang, M. J. Jebrail, R. Fobel, N. McIntosh, O. Y. Al-Dirbashi, P. Chakraborty and A. R. Wheeler, Anal. Chem., 2012, 84, 3731–3738.
40. I. A. Eydelnant, B. B. Li and A. R. Wheeler, Nat. Commun., 2014, 5, 3355.
41. A. H. Ng, R. Fobel, C. Fobel, J. Lamanna, D. G. Rackus, A. Summers, C. Dixon, M. D. Dryden, C. Lam and M. Ho, et al. , Sci. Transl. Med., 2018, 10, eaar6076.
42. A. J. Simpson, Magn. Reson. Chem., 2002, 40, S72–S82.
43. B. Lam and A. J. Simpson, Environ. Toxicol. Chem., 2009, 28, 931–939.
44. G. M. Pavlov, E. V. Korneeva, N. A. Smolina and U. S. Schubert, Eur. Biophys. J., 2010, 39, 371–379.
45. S. H. Au, R. Fobel, S. P. Desai, J. Voldman and A. R. Wheeler, Integr. Biol., 2013, 5, 1014–1025.
46. L. H. Lucas and C. K. Larive, Concepts Magn. Reson., Part A, 2004, 20, 24–41.
47. L. Bliumkin, R. D. Majumdar, R. Soong, A. Adamo, J. P. Abbatt, R. Zhao, E. Reiner and A. J. Simpson, Environ. Sci. Technol., 2016, 50, 5506–5516.

---

Footnote

† Electronic supplementary information (ESI) available: Descriptions of and data resulting from experimental measurements of the two-plate-to-one-plate device transition. See DOI: 10.1039/c8lc01214h

---