Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Antiscattering X-ray fluorescence analysis for large-area samples†
Wenyang
Zhao
 ab,
Keiichi
Hirano
c and
Kenji
Sakurai
ab,
Keiichi
Hirano
c and
Kenji
Sakurai
 *ab
*ab
aUniversity of Tsukuba, 1-1-1, Tennodai, Tsukuba, Ibaraki 305-0006, Japan. E-mail: sakurai@yuhgiri.nims.go.jp
bNational Institute for Materials Science, 1-2-1, Sengen, Tsukuba, Ibaraki 305-0047, Japan
cInstitute of Materials Structure Science, High Energy Accelerator Research Organization, 1-1, Oho, Tsukuba, Ibaraki 305-0801, Japan
First published on 24th September 2019
Abstract
Polarized X-rays have been utilized for many years to reduce the scattering background and optimize the signal-to-background ratio in the measurement of X-ray fluorescence spectra. It is vital to set a small solid angle in the direction of polarization for collecting fluorescence X-rays and scattering X-rays from a sample. Conventionally, this is realized by employing a large sample-to-detector distance and limiting the size of the probing area on the sample and the opening area of the detector. In this work, a collimator plate that assembles many parallel straight hollow capillaries is inserted between the sample and the detector. This can improve the signal-to-background ratio by tens of times when the primary X-rays have a high degree of polarization. The probing area on the sample is as large as 13.3 × 13.3 mm, making it convenient to survey trace elements dispersed in large-area environmental samples and industrial products. The sample-to-detector distance is as short as 3 mm, making the instrument compact and applicable to low-Z elements. The present polarization-collimator experimental scheme can exhibit its maximum potential in combination with strong and highly polarized synchrotron radiation with a reasonably large beam size.
1. Introduction
X-ray fluorescence (XRF) has been used for several decades to detect trace-level contaminants in environmental samples1,2 and industrial products.3,4 It is also a promising probe for directly inspecting the behavior of trace elements in biological tissues.5,6 In these studies, the signal of fluorescence X-rays from the target trace elements was weak, whereas the background of scattering X-rays from the entire sample matrix was much stronger. To increase the signal-to-background ratio (SBR), a general method is to perform experiments using linearly polarized X-rays.7–11The physical explanation is as follows: while fluorescence X-rays spread isotropically, the intensity of scattering X-rays has an angular distribution, and a sharp minimum occurs in the direction of polarization of the primary X-rays. Therefore, the SBR can be greatly increased by collecting X-rays at a small solid angle in the direction of polarization. So far, this is realized in a conventional scheme: illuminating a small probing area on the sample, opening a small active area on the detector, and arranging a large sample-to-detector distance. However, sometimes the probing area needs to be enlarged to study the elements dispersed in large-area samples.
In this case, the sample-to-detector distance has to be increased greatly to ensure that the detector is still roughly in the polarization direction with respect to every part on the sample. This is sometimes unacceptable owing to the size limitations of instruments or the strong absorption of low-energy fluorescence X-rays in a long air path.
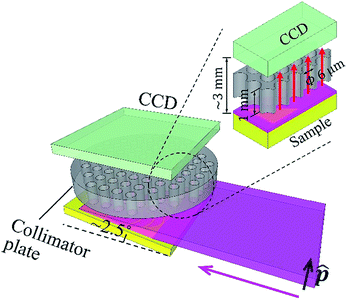
In this work, we propose the insertion of a collimator plate between the sample and detector. The collimator plate assembles many parallel straight hollow capillaries. It only passes X-rays that move parallel to the capillary axis. The allowed angular divergence is determined by the radius-to-length ratio (RLR) of the capillaries. In an experiment, the capillary axis is aligned parallel to the polarization of the primary X-rays. When the radius of the capillaries is at the micron level, the length of the capillaries, i.e., the thickness of the collimator plate, can be 1 mm. In this way, the sample-to-detector distance can be as short as 2 to 3 mm.
In addition, as all detected scattering X-rays are always guided by the capillaries, the probing area on the sample has no size limitation as long as the collimator plate and XRF detector are large enough. In this work, a conventional CCD camera sensor is utilized as an energy-dispersive XRF spectrometer owing to its large sensor. Then, the effective probing area on the sample is equivalent to the CCD sensor area, which is greater than 170 mm2.
A smaller RLR of the capillaries leads to a smaller solid angle for collecting scattering X-rays and consequently increases the SBR in the XRF spectra. However, this also decreases the efficiency of accumulating XRF signals. Calculations in this work show that there exists a critical value at which a further reduction in the RLR of the capillaries can no longer improve the SBR. This critical value of the RLR depends on the degree of polarization (DOP) of the primary X-rays. The calculation result here provides guidance for choosing an optimum collimator plate for a practical experiment to obtain the maximum counting rate under the premise of achieving the best SBR. Experiments in this work verify that trace elements of a few ppm in several certified reference materials (CRMs) can be successfully detected with using the smallest RLR of capillaries. The possible amount of reduction of the scattering intensity is also discussed.
2. Experimental
The experiment was carried out at the vertical wiggler beamline, BL-14B,12 Photon Factory, High Energy Accelerator Research Organization (KEK), Japan. Fig. 1 shows a schematic illustration of the experimental setup. The primary synchrotron X-ray beam was monochromatized by the crystal monochromator, and then the beam size was expanded in the perpendicular direction to the polarization vector, by using an asymmetric-cut crystal13 (Si 220 reflection with a miscut angle of 18°, leading to 19.62 times expansion at 9.53 keV). The beam size was 15 (H) × 0.6 (V) mm. It was linearly polarized in the vertical direction. The DOP was 0.95. The full-beam intensity was on the order of 109 counts per second. In the experiment, the sample was horizontally mounted. It was slightly tilted to make the angle between its surface and the primary X-ray beam approximately 2.5°.Thus, a wide area of approximately 15 × 14 mm on the sample was illuminated. A conventional CCD camera was placed above the sample, facing downward. The width of the gap between the sample surface and CCD sensor was approximately 3 mm. A collimator plate14–16 was inserted in the gap. It was fabricated inside the camera housing. The thickness of the collimator plate was 1 mm. The radius of each capillary was 3 μm. The overall opening ratio of the collimator plate was 0.58. The collimator plate was made of glass. The inner surfaces of the capillaries were coated with thin gold films to prevent X-ray transmission.
The CCD sensor (CCD47-10, produced by e2V) utilized here was a conventional one. It was designed for visible light. Its thickness was 10 μm and pixel size was 13 × 13 μm. The pixel resolution was 1024 × 1024. The active area of the sensor was 13.3 × 13.3 mm. The collimator plate parallelly projected X-rays from the sample to the sensor, and the probing area on the sample (13.3 × 13.3 mm) could be fully illuminated by the primary X-ray beam. During the experiment, the inside of the camera housing was a vacuum, and the sensor was cooled to −30 °C. To serve as an energy-dispersive XRF spectrometer, the CCD camera was operated in the single-photon counting mode, and a unique filtering method was adopted to process the charge-sharing problem in photon energy reconstruction. Further details of the camera operation and performance have been published elsewhere.17 In this work, the energy resolution in the XRF spectra was 150 eV at 5.9 keV.
In order to demonstrate how much the scattering intensity was reduced by the present synchrotron polarized experiment, one controlled trial was performed with unpolarized X-rays in the laboratory. The same samples were measured again. The primary X-rays came from a sealed-type copper X-ray tube. A crystal monochromator [graphite (002)] was employed to obtain monochromatic copper Kα X-rays (8.05 keV). The beam size was 1 (H) × 5 (V) mm. The full-beam intensity was on the order of 108 counts per second.
Because of the diffraction at the monochromator, the primary X-rays were slightly polarized with a DOP of 0.05, but the contribution to the observed scattering intensity is almost negligible. The sample was vertically mounted. The angle between the sample surface and primary X-ray beam was 3°. A Si-PIN detector (X-123 from Amptek) was placed in the same horizontal plane as the primary X-ray beam and the sample. The distance from the sample surface to the detector top was 80 mm. The active area of the detector sensor was 6 mm2. The sensor thickness was 500 μm.
3. Results and discussion
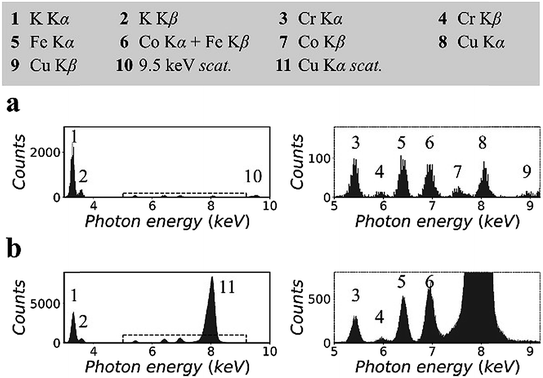
Fig. 2 shows the XRF spectra of a lithium borate pellet that includes 100 ppm chromium, iron, cobalt, and copper. The spectra in Fig. 2(a) were measured in the synchrotron polarized experiment. The live time to accumulate the spectra was 4 h. The spectra in Fig. 2(b) were measured in the laboratory unpolarized experiment. The live time to accumulate the spectra was 10 min. Details of the spectra were enlarged and attached on the right side. Information for all spectral lines was tabulated at the top of the figure.On the basis of the two spectra, it was estimated that the sample contained more than 1% potassium, which might be introduced during sample preparation. In addition, a trace amount of nickel was detected. This was an unexpected contaminant, and its concentration was estimated to be less than 50 ppm. It was noted that the relative intensities of the Kα lines of trace elements in the two spectra were different. This was due to the thickness difference between the CCD sensor and the Si-PIN sensor, which resulted in different detection efficiencies for these spectral lines. In Fig. 2(a), the scattering peak was located at 9.53 keV. Its intensity, including coherent scattering and Compton scattering, was on the same order of magnitude as the intensities of the Kα lines of the trace elements. In Fig. 2(b), copper K lines were not excited. The scattering peak (8.05 keV) was even stronger than that of potassium Kα when the concentration of potassium was greater than 1%.
This significant difference in the scattering intensity was due to the co-contribution of the polarization of the primary X-rays and the utilization of a collimator plate. For quantitative information, when two spectra were normalized by their respective iron Kα intensities, the intensity of scattering, which was inversely proportional to the SBR, was reduced to 1/15 from Fig. 2(b) to (a). It is worth noting that this quantitative comparison excluded the influence of the difference of the primary X-ray energies and detection efficiencies in the two experiments.
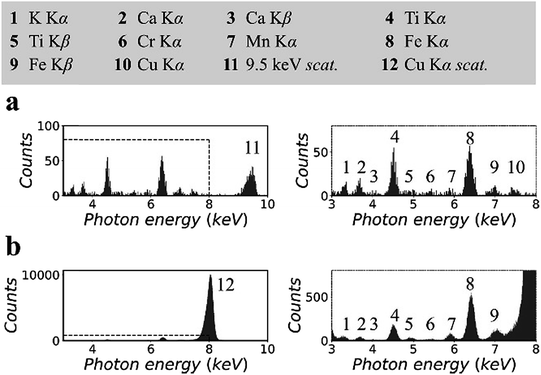
Fig. 3 shows the XRF spectra of a CRM, NIST 81a, glass sand.18 To prepare the sample, the original material was mixed with cellulose powder at a mass fraction of 30%, following which the mixture was pressed into a pellet with a density of 1.5 g cm−3. The spectra in Fig. 3(a) were measured in the synchrotron polarized experiment. The live time was 2 h. The spectra in Fig. 3(b) were measured in the laboratory unpolarized experiment. The live time was 10 min. On the basis of previous certified composition reports, the pellet sample was inferred to contain 147 ppm titanium, 7 ppm chromium, and 172 ppm iron, the K lines for which could be detected in the XRF spectra.
Other elements, i.e., potassium, calcium, manganese, and copper, were detected. The concentrations of these elements were not reported previously. In this experiment, their concentrations were estimated to be a few ppm to tens of ppm. In Fig. 3(a), owing to the low background intensity contributed by the small scattering intensity, the K lines of these trace elements can be detected despite the low counting statistics of the XRF spectra. In addition, the arrangement of spectral lines in Fig. 3(b) showed good agreement with that in Fig. 3(a), except that the cobalt K lines overlapped with the huge scattering peak, and the copper K lines were not excited by the 8.05 keV primary X-rays.
Two additional CRMs, NIST 1515 (ref. 19 and 20) and JSAC 0615,21 were tested to verify the performance of the present experimental scheme in detecting trace elements in different sample matrices. The results are included in the ESI.†
In this work, the accumulation efficiency of the XRF spectra in the synchrotron polarized experiment was low. One reason was that the primary synchrotron beam was weakened owing to beam manipulation. More important, the capillaries on the collimator plate in this work had a small RLR. The radius of the capillaries was 3 μm, and the length of the capillaries was 1 mm. The resulting effective solid angle was only 2.8 × 10−5 sr. Such a small RLR was designed for collecting X-rays at a small angular divergence with respect to the direction of polarization, but it certainly worsened the measurement efficiency as it blocked fluorescence X-rays in other directions.
Nevertheless, it is often unnecessary to use such a small RLR of capillaries. When the angular distribution of the scattering intensity has an invariant component in the direction of polarization, the SBR cannot be optimized infinitely by reducing the RLR of the capillaries ceaselessly. In other words, there exists a critical value of the RLR at which its further reduction can no longer improve the SBR. In an experiment, the RLR of the capillaries should be designed at this critical value so that it can collect X-rays as much as possible under the premise of achieving the best SBR. When the primary X-rays are not perfectly polarized, the critical value of the RLR is dependent on the DOP of the primary X-rays.
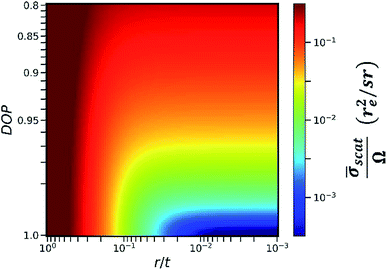
In this work, we calculated the relationship between the detected scattering intensity and the RLR of the capillaries under different DOP conditions (see Section II in the ESI†). The calculation here only considered the differential cross section of coherent scattering and Compton scattering from an electron22 because this physical process determines the fact that the angular distribution of the scattering intensity has a sharp minimum in the direction of polarization. In the calculation, the primary X-ray energy was set as 9.53 keV. The calculation result is shown in the color map in Fig. 4. The x-axis was plotted on a log scale since it represents the RLR of the capillaries. Here, r denotes the capillary radius, and t denotes the thickness of the collimator plate, i.e., the capillary length.
The y-axis was plotted on a square-root scale since it represents the DOP of the primary X-rays. The intensity in the color map indicates the detectable average scattering cross section ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) scat, which was subsequently normalized by the effective solid angle Ω. For the same sample, as the detectable fluorescence intensity is proportional to the effective solid angle Ω,
scat, which was subsequently normalized by the effective solid angle Ω. For the same sample, as the detectable fluorescence intensity is proportional to the effective solid angle Ω, ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) scat/Ω was considered to be inversely proportional to the SBR in the XRF spectra. It is worth noting that in an actual experiment, other factors including the atomic form factor, incoherent scattering function,23 and absorption in the sample matrix should also be considered. However, when r/t is small, these factors do not significantly distort the contour of the color map in the same experiment. Therefore, they were not included in the calculation model for simplicity.
scat/Ω was considered to be inversely proportional to the SBR in the XRF spectra. It is worth noting that in an actual experiment, other factors including the atomic form factor, incoherent scattering function,23 and absorption in the sample matrix should also be considered. However, when r/t is small, these factors do not significantly distort the contour of the color map in the same experiment. Therefore, they were not included in the calculation model for simplicity.
As indicated in Fig. 4, at a specific DOP, the reduction of ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) scat/Ω terminates at a critical value of r/t. This critical value depends on the DOP. For example, when the thickness of the collimator plate is 1 mm and the DOP is 0.9, 0.95, 0.99, and 0.999, the corresponding critical radii of the capillaries are 30 μm, 25 μm, 14 μm, and 6 μm, respectively. In this way, Fig. 4 provides guidance for choosing an optimum collimator plate for a practical experiment when the DOP of the primary X-rays is known.
scat/Ω terminates at a critical value of r/t. This critical value depends on the DOP. For example, when the thickness of the collimator plate is 1 mm and the DOP is 0.9, 0.95, 0.99, and 0.999, the corresponding critical radii of the capillaries are 30 μm, 25 μm, 14 μm, and 6 μm, respectively. In this way, Fig. 4 provides guidance for choosing an optimum collimator plate for a practical experiment when the DOP of the primary X-rays is known.
In addition, it is noted that even when the primary X-rays are perfectly polarized, the reduction of ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) scat/Ω still terminates at r/t = 0.003. This is related to the fact that the differential cross section of Compton scattering does not vanish in the direction of polarization. The value of 0.003 is the smallest RLR of the capillaries in the present polarization-collimator scheme. The experiments in this work verified that trace elements of a few ppm can be detected even when using capillaries with the smallest RLR.
scat/Ω still terminates at r/t = 0.003. This is related to the fact that the differential cross section of Compton scattering does not vanish in the direction of polarization. The value of 0.003 is the smallest RLR of the capillaries in the present polarization-collimator scheme. The experiments in this work verified that trace elements of a few ppm can be detected even when using capillaries with the smallest RLR.
In this work, the probing area on the sample was 13.3 × 13.3 mm, making it convenient to survey trace elements dispersed in large-area environmental samples and industrial products. Meanwhile, the sample-to-detector distance was always approximately 3 mm, which was independent of the probing area size. Such a small distance reduces the absorption of low-energy fluorescence X-rays in air and is consequently favorable for the detection of low-Z elements such as sulfur and chlorine.
On the other hand, if a collimator plate is not utilized, the optimum sample-to-detector distance becomes much longer. For example, assuming that the probing area on the sample is Φ 10 mm and the active area on the detector is Φ 6 mm, in order to achieve a similar ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) scat/Ω value to the critical value in the collimator-plate experiment, the necessary sample-to-detector distance is 16 cm, 18 cm, 32 cm, and 70 cm when the DOP of the primary X-rays is 0.9, 0.95, 0.99, and 0.999, respectively. The advantage of using a collimator plate is clear.
scat/Ω value to the critical value in the collimator-plate experiment, the necessary sample-to-detector distance is 16 cm, 18 cm, 32 cm, and 70 cm when the DOP of the primary X-rays is 0.9, 0.95, 0.99, and 0.999, respectively. The advantage of using a collimator plate is clear.
In order to clarify how much the scattering intensity can be reduced by the present polarization-collimation experimental scheme, a set of XRF spectra were generated using Monte Carlo simulation software XMI-MSIM.24 In the simulation, the sample was a cellulose pellet that included 100 ppm iron. The geometrical parameters were set the same as in the experiments in this work, either for the model of the synchrotron polarized experiment or for the model of the laboratory unpolarized experiment. For ease of comparison, in the two models, the primary X-ray energy was set the same as 9.53 keV, and the detector sensor thickness was set the same as 500 μm. The final simulated XRF spectra are included in the ESI.† It was found that when using polarized primary X-rays and the collimator plate in this work, the SBR improves by more than 10 times when the DOP is 0.90, 30 times when the DOP is 0.95, and 60 times when the DOP is 0.99.
Improving the SBR in XRF spectra makes it easy to analyze trace elements. One major concern is the minimum detectable limit (MDL). This limit is determined by the statistical fluctuations of the background beneath a given XRF peak. Therefore, the accumulated counts of the background play an important role, and the signal-to-noise ratio (SNR) is more crucial than the SBR in this discussion. Approximate equations of the SNR and the MDL are given as
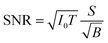 | (1) |
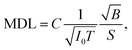 | (2) |
For example, in this work, the I0 in the laboratory experiment was on the order of 108 counts per second. The corresponding T was 600 seconds and Ω was 9.4 × 10−4 sr. Meanwhile, the I0 in the synchrotron experiment was on the order of 109 counts per second. The corresponding T was about 104 seconds and Ω was 2.8 × 10−5 sr. Such a small Ω significantly reduced the accumulation efficiency of the XRF spectra. As a result, the signal counts obtained in the synchrotron experiment were even lower than those obtained in the laboratory experiment considering the lower X-ray detection efficiency of the CCD sensor. On the other hand, nowadays, the I0 in most 3rd generation synchrotron facilities exceeds 1011 counts per second, whereas the saturation of most XRF detectors is below 106. For this reason, the strong primary X-rays are often weakened and wasted in trace-element analysis to avoid the saturation of XRF detectors. In this case, utilizing the collimator plate is adequate to fully use the strong primary X-rays and to improve the MDL.
The present experimental scheme can work in either a vacuum or air. In this work, the sample-to-detector distance was 2–3 mm. It can become up to tens of millimeters for the ease of sample alignment. When the primary X-rays are strong enough, the present experimental scheme can be combined with the total-reflection XRF (TXRT) technique to improve the MDL further. It can also be applied to handheld XRF setups if a wide polarized X-ray beam is produced using Soller slits and a scatterer. When the elements in the sample are excited by electron beam rather than by the polarized X-rays, the background in the spectra is mostly composed of bremsstrahlung X-rays, the intensity of which has no sharp minimum in the angular distribution. Thus, the use of a collimator plate in electron probe energy dispersive X-ray spectroscopy is unnecessary. The collimator plate can be replaced with other X-ray collimation components such as 2D Soller slits. The detector can be a cooled CCD/CMOS sensor, a silicon PIN diode detector, a silicon drift detector, or any other XRF detector. However, a large active area on the detector sensor is essential. In this work, we used a CCD sensor because of its large sensor area of greater than 170 mm2, while such a large area is still uncommon for ordinary XRF detectors.
The present experimental scheme was developed for antiscattering XRF analysis of large-area samples. It is suitable for many practical applications such as the survey of elemental impurities in pharmaceuticals27 and heavy metal contaminants in soil,28,29 agriculture products,30 and marine products.31 The technique of XRF analysis is adopted for easy sample preparation and rapid sample screening. As the concentration of target elements is often below 1 ppm and they are dispersed in sample matrices, utilizing strong and polarized synchrotron X-rays is necessary. In addition, as the distribution of the trace elements in the sample matrices is often inhomogeneous, it is better to probe a large area on samples to eliminate the influence of inhomogeneity.
4. Conclusions
In this work, a collimator plate that assembles many parallel straight hollow capillaries was inserted between the sample and detector in XRF measurements. The plate can improve the SBR in the XRF spectra by tens of times when the primary X-rays have a high DOP. The probing area on the sample was as large as 13.3 × 13.3 mm, making it convenient to survey trace elements dispersed in large-area environmental samples and industrial products. The sample-to-detector distance was as short as 3 mm, making the instruments compact and applicable to low-Z elements. The present polarization-collimator experimental scheme can exhibit the maximum potential when it is combined with strong and highly polarized synchrotron radiation. In addition, as the combination of the collimator plate and the CCD detector can give one-to-one correspondence between the specific sample position and the specific pixel in the detector, the present experimental scheme can be applied to highly sensitive full-field XRF imaging,15–17,25,26 while its performance simply in antiscattering XRF analysis with the use of a conventional CCD camera and polarized X-rays is already sufficiently attractive.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank Mr H. Kobayashi (University of Tsukuba) for his participation and assistance during the experiment. This work was performed with the approval of the Photon Factory Program Advisory Committee (No. 2017G063 and 2018G030). This work was partly supported by JSPS KAKENHI (grant No. JP18J12732).References
- R. C. Ragaini, H. R. Ralston and N. Roberts, Environmental Trace Metal Contamination in Kellogg, Idaho, Near a Lead Smelting Complex, Environ. Sci. Technol., 1977, 11(8), 773–781, DOI:10.1021/es60131a004.
- M. Otsuka, T. Itai, K. A. Aasante, M. Muto and S. Tanabe, Trace Element Contamination around the E-Waste Recycling Site at Agbogbloshie, Accra City, Ghana, Interdisciplinary Studies on Environmental Chemistry – Environmental Pollution and Ecotoxicology, 2012, 6, 161–167 Search PubMed.
- L. Perring and D. Andrey, ED-XRF as a Tool for Rapid Minerals Control in Milk-Based Products, J. Agric. Food Chem., 2003, 51(15), 4207–4212, DOI:10.1021/jf034158p.
- S. Arzhantsev, X. Li and J. F. Kauffman, Rapid Limit Tests for Metal Impurities in Pharmaceutical Materials by X-Ray Fluorescence Spectroscopy Using Wavelet Transform Filtering, Anal. Chem., 2011, 83(3), 1061–1068, DOI:10.1021/ac1028598.
- B. S. Twining, S. B. Baines, N. S. Fisher, J. Maser, S. Vogt, C. Jacobsen, A. Tovar-Sanchez and S. A. Sañudo-Wilhelmy, Quantifying Trace Elements in Individual Aquatic Protist Cells with a Synchrotron X-Ray Fluorescence Microprobe, Anal. Chem., 2003, 75(15), 3806–3816, DOI:10.1021/ac034227z.
- A. Carmona, P. Cloetens, G. Devès, S. Bohic and R. Ortega, Nano-Imaging of Trace Metals by Synchrotron X-Ray Fluorescence into Dopaminergic Single Cells and Neurite-like Processes, J. Anal. At. Spectrom., 2008, 23(8), 1083–1088, 10.1039/b802242a.
- H. Aiginger, P. Wobrauschek and C. Brauner, Energy-Dispersive Fluorescence Analysis Using Bragg-Reflected Polarized X-Rays, Nucl. Instrum. Methods, 1974, 120(3), 541–542, DOI:10.1016/0029-554X(74)90027-5.
- T. G. Dzubay, B. V. Jarrett and J. M. Jaklevic, Background Reduction in X-Ray Fluorescence Spectra Using Polarization, Nucl. Instrum. Methods, 1974, 115(1), 297–299, DOI:10.1016/0029-554X(74)90459-5.
- A. Iida, K. Sakurai, T. Matsushita and Y. Gohshi, Energy Dispersive X-Ray Fluorescence Analysis with Synchrotron Radiation, Nucl. Instrum. Methods Phys. Res., Sect. A, 1985, 228(2–3), 556–563, DOI:10.1016/0168-9002(85)90304-3.
- J. M. Jaklevic, R. D. Giauque and A. C. Thompson, Quantitative X-Ray Fluorescence Analysis Using Monochromatic Synchrotron Radiation, Nucl. Instrum. Methods Phys. Res., Sect. B, 1985, 10–11(Part 1), 303–308, DOI:10.1016/0168-583X(85)90257-5.
- K. Sakurai, A. Iida and Y. Gohshi, Analysis of Signal to Background Ratio in Synchrotron Radiation X-Ray Fluorescence, Anal. Sci., 1988, 4(1), 3–7, DOI:10.2116/analsci.4.3.
- M. Ando, Y. Satow, H. Kawata, T. Ishikawa, P. Spieker and S. Suzuki, Design of beamline 14 for the PF vertical wiggler and its operation, Nucl. Instrum. Methods Phys. Res., Sect. A, 1986, 246, 144–148, DOI:10.1016/0168-9002(86)90062-8.
- K. Hirano, Y. Yamashita, Y. Takahashi and H. Sugiyama, Development of variable-magnification X-ray Bragg optics, J. Synchrotron Radiat., 2015, 22, 956–960, DOI:10.1107/S1600577515008802.
- T. Wroblewski, An X-ray Camera, Synchrotron Radiation News, 1996, 9, 14–19, DOI:10.1080/08940889608602867.
- K. Sakurai, Total-Reflection X-Ray Fluorescence Imaging, Spectrochim. Acta, Part B, 1999, 54(10), 1497–1503, DOI:10.1016/S0584-8547(99)00071-3.
- K. Sakurai and H. Eba, Micro X-Ray Fluorescence Imaging without Scans: Toward an Element-Selective Movie, Anal. Chem., 2003, 75(2), 355–359, DOI:10.1021/ac025793h.
- W. Zhao and K. Sakurai, CCD Camera as Feasible Large-Area-Size X-Ray Detector for X-Ray Fluorescence Spectroscopy and Imaging, Rev. Sci. Instrum., 2017, 88(6), 063703, DOI:10.1063/1.4985149.
- https://www-s.nist.gov/srmors/view_detail.cfm?srm=81a .
- https://www-s.nist.gov/srmors/view_detail.cfm?srm=1515 .
- I. O. Olabanji, E. A. Oluyemi and E. I. Obianjuwa, Nondestructive Analysis of Dumpsite Soil and Vegetable for Elemental Composition, J. Environ. Chem. Ecotoxicol., 2015, 7(1), 1–10, DOI:10.5897/jece2014.0335.
- K. Nakano, T. Nakamura, I. Nakai, A. Kawase, M. Iimai, M. Hasegawa, Y. Ishibashi, I. Inamoto, K. Sudou, M. Kozaki, S. Tsuruta, H. Homma, A. Ono, K. Kakita and M. Sakata, Plastic Certified Reference Materials JSAC 0611-0615 for Determination of Hazardous Constituents Using X-Ray Fluorescent Analysis, Bunseki Kagaku, 2006, 55(7), 501–507, DOI:10.2116/bunsekikagaku.55.501.
- L. Vincze, K. Janssens, F. Adams, M. L. Rivers and K. W. Jones, A General Monte Carlo Simulation of ED-XRF Spectrometers. II: Polarized Monochromatic Radiation, Homogeneous Samples, Spectrochim. Acta, Part B, 1995, 50(2), 127–147, DOI:10.1016/0584-8547(94)00124-E.
- J. H. Hubbell, W. J. Veigele, E. A. Briggs, R. T. Brown, D. T. Cromer and R. J. Howerton, Atomic Form Factors, Incoherent Scattering Functions, and Photon Scattering Cross Sections, J. Phys. Chem. Ref. Data, 1975, 4(3), 471–538, DOI:10.1063/1.555523.
- T. Schoonjans, L. Vincze, V. A. Solé, M. Sanchez Del Rio, P. Brondeel, G. Silversmit, K. Appel and C. Ferrero, A General Monte Carlo Simulation of Energy Dispersive X-Ray Fluorescence Spectrometers – Part 5: Polarized Radiation, Stratified Samples, Cascade Effects, M-Lines, Spectrochim. Acta, Part B, 2012, 70, 10–23, DOI:10.1016/j.sab.2012.03.011.
- K. Sakurai and M. Mizusawa, X-Ray Diffraction Imaging of Anatase and Rutile, Anal. Chem., 2010, 82(9), 3519–3522, DOI:10.1021/ac9024126.
- H. Eba, H. Ooyama and K. Sakurai, Combination of Projection-Based XRF, XAFS and XRD Imagings for Rapid Spatial Distribution Analysis of a Heterogeneous Material, J. Anal. At. Spectrom., 2016, 31(5), 1105–1111, 10.1039/c6ja00024j.
- V. Balaram, Recent Advances in the Determination of Elemental Impurities in Pharmaceuticals – Status, Challenges and Moving Frontiers, TrAC, Trends Anal. Chem., 2016, 80, 83–95, DOI:10.1016/j.trac.2016.02.001.
- B. Wei and L. Yang, A Review of Heavy Metal Contaminations in Urban Soils, Urban Road Dusts and Agricultural Soils from China, Microchem. J., 2010, 94(2), 99–107, DOI:10.1016/j.microc.2009.09.014.
- F. Zeng, W. Wei, M. Li, R. Huang, F. Yang and Y. Duan, Heavy Metal Contamination in Rice-Producing Soils of Hunan Province, China and Potential Health Risks, Int. J. Environ. Res. Public Health, 2015, 12(12), 15584–15593, DOI:10.3390/ijerph121215005.
- P. N. Williams, M. Lei, G. Sun, Q. Huang, Y. Lu, C. Deacon, A. A. Meharg and Y.-G. Zhu, Occurrence and Partitioning of Cadmium, Arsenic and Lead in Mine Impacted Paddy Rice: Hunan, China, Environ. Sci. Technol., 2009, 43(3), 637–642, DOI:10.1021/es802412r.
- P. Sivaperumal, T. V. Sankar and P. G. V. Nair, Heavy Metal Concentrations in Fish, Shellfish and Fish Products from Internal Markets of India Vis-a-Vis International Standards, Food Chem., 2007, 102(3), 612–620, DOI:10.1016/j.foodchem.2006.05.041.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ja00220k |
| This journal is © The Royal Society of Chemistry 2019 |