Open Access Article
Open Access ArticleA laboratory-based double X-ray spectrometer for simultaneous X-ray emission and X-ray absorption studies
Wojciech
Błachucki
 *a,
Joanna
Czapla-Masztafiak
*a,
Joanna
Czapla-Masztafiak
 b,
Jacinto
Sá
b,
Jacinto
Sá
 *ac and
Jakub
Szlachetko
*ac and
Jakub
Szlachetko
 *b
*b
aInstitute of Physical Chemistry, Polish Academy of Sciences, 44/52 Kasprzaka Street, 01-224 Warsaw, Poland. E-mail: wojciech.blachucki@ichf.edu.pl; jacinto.sa@kemi.uu.se
bInstitute of Nuclear Physics, Polish Academy of Sciences, 152 Radzikowskiego Street, 31-342 Kraków, Poland. E-mail: jakub.szlachetko@ifj.edu.pl
cDepartment of Chemistry, Uppsala University, Lägerhyddsvägen 1, 75120 Uppsala, Sweden
First published on 22nd May 2019
Abstract
X-ray spectroscopy studies are usually performed using synchrotron radiation sources, which offer bright, coherent, energy-tuneable and monochromatic light. However, the application of synchrotron-based X-ray emission spectroscopy (XES) and X-ray absorption spectroscopy (XAS) is directly constrained by the limited, infrequent access to central facilities. With the advent of new technological solutions in the field of X-ray sources, optics and detectors, the development of efficient and compact laboratory X-ray spectroscopy systems is possible. A permanent laboratory-based setup offers the advantages of low cost and easy accessibility and, therefore, more flexibility in the preparation and scheduling of measurements. Herein, we report a laboratory X-ray setup allowing simultaneous XES and XAS measurements. The double von Hámos spectrometer performances are demonstrated by concurrent Kβ XES and K-edge XAS measurements done for 3d elements.
1 Introduction
1.1 X-ray methods in material and electronic structure determination
Nowadays researchers routinely use X-ray radiation in structural studies on complex systems. So far a variety of approaches have been developed allowing structural studies in chemistry, biology and materials science both in laboratories and at large scale facilities. For example, in X-ray diffraction (XRD) the investigated material is irradiated with an X-ray beam and the elastically scattered photons are detected.1 The measured dependence of the scattered photons' intensity on the scattering angle is used to determine the spatial distribution of electron density in the sample, and thus the structure of the material. The electronic structure may be probed with X-ray photoelectron spectroscopy (XPS), a surface-sensitive method where the sample is excited with X-ray radiation and the ejected photoelectrons' spectral energy distribution is measured.2 XPS data enable elemental identification as well as characterization of the sample's chemical state.X-ray spectroscopy is the ensemble of approaches dedicated to determination of the energy distribution of the atomic electrons' quantum states under different conditions.3 It is traditionally split into X-ray emission spectroscopy (XES), focused on the study of the radiation emitted from matter through X-ray fluorescence (XRF) and resonant X-ray scattering, and X-ray absorption spectroscopy (XAS) aiming at measuring the dependence of X-ray absorption in materials on the radiation energy. Owing to the penetrating properties of X-ray radiation, X-ray spectroscopy methods are bulk-sensitive. There are, however, approaches allowing enhancement of the surface signal through either reducing the detection scope to a sample's thin layer (grazing emission X-ray fluorescence, GEXRF) or inducing X-ray emission uniquely in a thin layer of the sample (total reflection X-ray fluorescence, TXRF, and grazing incidence X-ray fluorescence, GIXRF).4–6 The use of XES and XAS in chemical analysis is routinely focused on the determination of the density of states (DOS) of atomic electrons as a function of their energy in the vicinity of the Fermi level or, in other words, on probing of the valence and conduction bands of the material under study. This discipline is extensively applied in many research fields such as chemistry, medicine, biology and materials sciences (see, e.g., ref. 7–11).
Among X-ray spectroscopy instrumentation techniques researchers commonly distinguish the so-called energy-dispersive spectrometry (EDS) and wavelength-dispersive spectrometry (WDS).12–15 EDS is based on the use of detectors (such as gas counters, scintillators and solid state detectors) for detection of photons and for analysis of their energy. EDS devices are characterized by a broad energy range of detection in a single measurement (from a few keV to tens of keV) and short photon collection times. EDS is frequently used for XRF detection to determine complex samples' chemical compositions but because of its poor energy resolution it is not able to be used to precisely study the electronic structure. WDS instruments, X-ray spectrometers, cover a much narrower energy range in a single measurement (up to about 200 eV) and are less efficient and more difficult to operate than EDS detectors. In WDS, however, an analysing X-ray crystal is used for spatial dispersion of photons of different energies and an X-ray detector is used only for photon counting and photon energy discrimination which makes X-ray spectrometers' energy resolution far beyond those of the EDS devices. WDS allows precise electronic structure determination and until recently its laboratory use was focused only on fundamental research.16,17
1.2 Challenges of application of X-ray spectroscopy at the laboratory scale
Use of X-ray spectroscopy in applied sciences is governed by three technical factors: access to X-ray sources, availability of X-ray spectrometers and characteristics of the investigated sample. These factors ensure that most analytical studies are executed at central facilities like synchrotrons, highly specialized large scale facilities developed for production of very bright, coherent, energy-tuneable and monochromatic electromagnetic radiation. They are nowadays equipped with sophisticated X-ray detection systems that enable high energy resolution of detection and high data collection rates. They also provide tools for sample preparation and manipulation. However, access to synchrotrons is not straightforward as each experimental proposal is subjected to an evaluation procedure, which requires time and does not guarantee a priori the granting of beam time. In addition to granted access, the experiments are often limited by the access time, often a few days. Moreover, many experiments require complicated and fragile sample environments that cannot be easily shipped and/or accommodated at large scale facilities. The same is valid for materials that require special safety procedures and often cannot be transported by means of public transport to foreign synchrotron centres. As a result, challenging and urgent scientific questions are addressed first at synchrotrons rather than systematic studies on dedicated subjects.Recent development of X-ray instrumentation enabled researchers to apply X-ray spectroscopy in certain analytical studies at the laboratory scale.17–19 Combination of compact polychromatic X-ray sources with X-ray focusing optics allowed the photon flux to be increased (as expressed in photons per (s cm2)) and new charge-coupled device (CCD) detectors gave a good compromise between the cost, energy resolution and data collection rate.14,20 A permanent laboratory-based setup allows the development of sophisticated sample environments and provides more flexibility in scheduling of the measurements. The main factor limiting the performance of a laboratory X-ray setup is its source's brightness which is much lower than a synchrotron's. It necessitates use of concentrated samples, which is unpractical in certain, especially biological, cases. Nevertheless, laboratory X-ray setups allow routine ground state sample characterization and fingerprinting as well as long-term measurements, ideal to follow slow changes that are inconceivable at central facilities.
1.3 Laboratory X-ray spectroscopy setups
High-energy resolution X-ray spectrometers are powerful instruments used to determine the electronic structure of matter and have found many applications in a variety of scientific areas. In general, X-ray spectrometers rely on X-ray dispersion by a crystal providing high-energy resolution for X-ray detection. In order to access detailed information about the electronic structure of matter, the energy resolution has to be around 0.1–5 eV in order to be comparable with the natural lifetimes of the studied electronic states of an atom. There are four relevant X-ray emission spectrometer geometries: von Hámos,21 Laue-type DuMond,22 Johansson,23 and Johann,24 each with specific advantages and disadvantages. Based on the available reports,18,25 the von Hámos geometry allows low-cost development of compact and versatile X-ray spectrometers.The von Hámos spectrometer is based on a cylindrically bent analyser crystal which disperses the photon energy along one axis and focuses the X-ray photons along the second axis. Bending the crystal, typically to a radius curvature of a few tens of cm, allows the detection efficiency to be increased by enhancing the solid angle of detection. It may, however, cause crystal strain and in consequence lead to the deterioration of its resolving power. For this reason, in certain applications the analyser crystal used is not bent but built up of flat crystal segments pressed onto a curved substrate.26 In the von Hámos geometry the sample is placed at the centre of the crystals' curvature and the X-rays are imaged on either a 1D strip detector or a 2D detector. This generates an emission spectrum in a single measurement without any detector or crystal motion. It has proven to be extremely useful for tracking fast chemical kinetics where a full X-ray emission spectrum can be collected on the ms timescale or faster27,28 as well as for shot-to-shot acquisition at X-ray free-electron laser facilities.29–31 The drawback to this geometry is that the collected fluorescence solid angle is dispersed over a large energy range, reducing the photon flux per eV.
X-ray emission spectroscopy (XES) has been used for a long time in laboratories to study different chemical effects32–34 and laboratory X-ray absorption spectroscopy (XAS) has already allowed absorption spectra acquisition for dilute samples in the 1990s.35 Also recently a handful of research groups have undertaken activity to develop different laboratory experimental setups for XES and XAS.17,36–38 They have shown that such setups allow synchrotron quality spectra acquisition within a few hours of measurement. However, unlike synchrotrons, such instrumentation can be developed around dedicated projects and used almost continuously over an entire year delivering experimental data and approaches that can be further used in large scale facilities. Herein, we report a new laboratory von Hámos geometry-based experimental setup for simultaneous XES and XAS measurements.
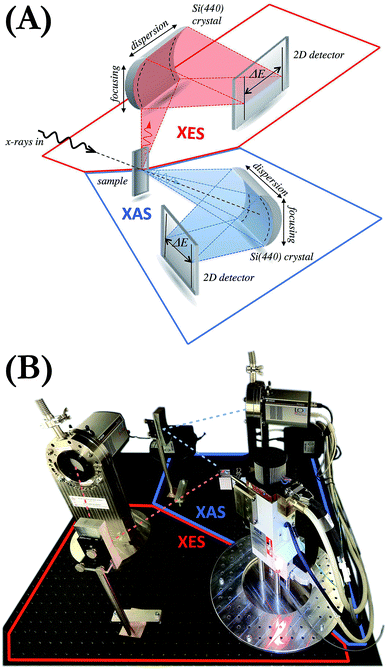
2 Laboratory setup for simultaneous XES and XAS studies
The setup is composed of an X-ray source, the sample and two von Hámos geometry-based X-ray spectrometers,21,26 one for the measurement of the radiation transmitted through the sample (XAS measurements) and another for the emitted fluorescence detection (XES measurements) (see Fig. 1). The X-ray source is an XOS X-Beam Superflux PF X-ray tube with a Mo anode and integrated focusing optics. The maximum voltage and the maximum current at which it can operate are 50 kV and 1 mA, respectively, and divergence of the beam exiting the polycapillary focusing optics is about 3°. The crystals used are two cylindrically bent Si(440) of 25 cm radius of curvature. The diffracted radiation is registered by two Andor Newton DO920P cameras equipped with 250 μm-thick Be windows and front-illuminated CCD sensors of 1024 × 256 26 μm-sized pixels. The cameras are connected through flanges to a vacuum pumping system decreasing the pressure in the sensors' proximity down to 10−7 mbar. This allows us to safely cool down the sensors to −70 °C by means of thermoelectric coolers integrated in the cameras. The apparatus is enclosed in a compact shielding box occupying a volume of about 112 (width) × 112 (depth) × 162 (height) cm3 and equipped with walls movable up and down. The entire setup is maintained in air at room conditions. We wish to emphasize that the system does not require any scanning or moving components. The setup is motor-free and the alignment is done manually. The motorized positioners can be, however, employed in cases where frequent realignment of the elements is necessary.The application of a two-dimensional (2D) position-sensitive detector in the von Hámos geometry is compatible with focusing the excitation X-ray beam to a line. Such line focusing allows the engagement of more photons in the interaction with the sample and thus increases the signal intensity. We, however, opted for the point focusing geometry as it facilitates studies with very small amounts of material (micro- to milligrams) and with sample delivery methods such as liquid jets and flow-through cells. 2D CCD cameras were used because, thanks to their capability of selecting a pixel range on the sensor, they allow much better signal-to-noise ratios to be achieved than one-dimensional detectors.
The setup was commissioned using samples of different types: solids, powders39 and liquids and the detection limit has been determined to be around 0.2 mol L−1 (i.e. 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm). In the sample preparation the target thickness is controlled in order to provide optimal signal strength from both the XES and the XAS units. The sample thickness control is also important because nonuniformity in the target's structure may alter the shape of experimental spectra. We avoid it by preparing targets of well-defined thickness by, e.g., placing liquids in cuvettes of regular shape or embedding powders in cellulose matrices. The potential sample nonuniformity or inhomogeneity is mitigated by the micrometre size of the X-ray beam.
000 ppm). In the sample preparation the target thickness is controlled in order to provide optimal signal strength from both the XES and the XAS units. The sample thickness control is also important because nonuniformity in the target's structure may alter the shape of experimental spectra. We avoid it by preparing targets of well-defined thickness by, e.g., placing liquids in cuvettes of regular shape or embedding powders in cellulose matrices. The potential sample nonuniformity or inhomogeneity is mitigated by the micrometre size of the X-ray beam.
3 Microfocusing and energy discrimination
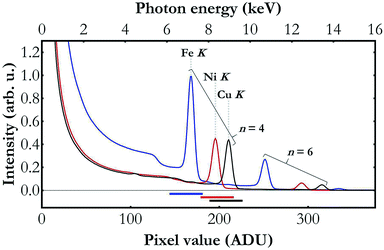
The main challenge in the setup development was establishing a compromise between sufficient X-ray source's output photon intensity with the micrometre size of the X-ray beam focus. The applied polycapillary optics reduces the primary X-ray beam intensity by a factor of 10–50 (depending on X-ray intensity) which results in an output X-ray intensity of nominally about 5 × 108 photons per s at full power in the Mo K-series X-ray lines' energy domain which is considerably lower as compared to regular low-power X-ray tubes. On the other hand, the optics allows focusing of the X-ray beam to a relatively small spot (100 × 100 μm2) and hence mitigates the effects of sample nonuniformity. Variation of the material density in the beam field may have a strong impact on the data acquired with any wavelength-dispersive detection system and may lead to measured spectral misinterpretation. Reduction of the irradiation area is in fact the only solution in many cases where preparation and adaptation of samples with uniform composition on a large area are not feasible because of insufficient amounts of sample being available or other experimental aspects.Another effect that needs to be considered when using an X-ray tube in combination with any crystal X-ray spectrometer originates from the broad spectrum of the X-ray tube's beam and the Bragg's law allowing different orders of diffraction of radiation by crystals. The Bragg's law allows diffracted photons of different energies to propagate at the same angle and the photon energies allowed in the diffraction at a given angle depend on this angle, the crystal's lattice spacing and the diffraction order which takes on values from the set of positive natural numbers. As the X-ray tube delivers a spectrum beam spanning over many kiloelectronvolts, the radiation diffracted by the crystal and registered by the detector comes effectively from different diffraction orders. This effect is demonstrated in Fig. 2 presenting low energy resolution spectra of the X-ray tube's beam diffracted by the crystal and recorded by the Andor Newton DO920P CCD camera during the Fe K, Ni K and Cu K XAS measurements. As shown, though the setup was adjusted to detect the radiation diffracted by the Si(110) crystal in the order of diffraction n = 4, the detector registered contributions of other diffraction orders as well. If the detector does not have sufficient energy resolution and the electronics does not provide the capability of adequate count discrimination based on the photon energy, the recorded signal will effectively reflect the total counts of photons diffracted at all diffraction orders and hence have very different energies. As a consequence, the XAS function, determined as −log[Itr(E)/Iinc(E)], where Iinc(E) and Itr(E) are, respectively, the spectra of the beam incident on the sample and of the transmitted one, will exhibit incorrect ratios of the spectral features.36 In the present work this problem is mitigated by using a detector of the relative energy resolution of about 4 to 5 × 10−2 and capable of lower and upper energy threshold applications. The energy spectrum of the CCD detector clearly resolves the detected photons coming from different diffraction orders and allows filtering out of only the contribution of the required diffraction order.
4 Simultaneous Kβ XES and K-edge XAS measurements
To demonstrate the capabilities of the experimental setup, simultaneous Kβ XES and K-edge XAS measurements were performed for Fe, Ni and Cu metal foils of a nominal thicknesses of 5 μm each. The X-ray tube's voltage and current were set to 40 kV and 0.9 mA, respectively, and the CCD sensors were cooled down to −40 °C. The incident beam spectrum was measured for about 10 hours with a foil out of the beam. With a sample in the beam focal point, the Kβ XES and the transmitted beam spectrum were measured simultaneously. The capability of the setup is presented in Fig. 3, where it is shown that already a 2 hour-measurement provides good quality data with statistical uncertainty at the level of 0.008 s−1 eV−1 and 0.012 eV−1 for the Kβ XES and the K-edge XAS measurements, respectively. Increasing the acquisition time to 20 hours results in the reduction of uncertainty by a factor of 3 and provides detailed information on the shape of the valence-to-core structure. Due to the fine size of the CCD pixels of 25 μm, the raw measured spectra are oversampled giving an average energy step per pixel of 0.15, 0.23 and 0.23 eV for Fe K-, Ni K- and Cu K-edge XAS measurements, respectively. Since these values are much lower than the setup's resolving power, a binning of 5 was applied to all the acquired spectra, i.e. the number of counts registered in the full pixel range was summed in groups of 5 neighbouring pixels. The energy calibration was done by fitting the positions of spectral features in the obtained spectral curves and of the corresponding ones in the reference data40–44 assuming the Bragg's-law form of the pixel-to-energy conversion function.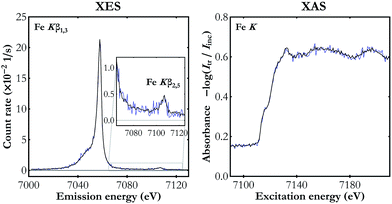 | ||
| Fig. 3 The simultaneous Fe Kβ XES and Fe K-edge XAS measurement for two acquisition times: 2 hours (blue line) and 20 hours (black line). | ||
The results of the simultaneous Kβ XES and K-edge XAS measurements on the three metal foils studied are presented in Fig. 4. Kβ features observed in the XES spectra are the main Kβ1,3 X-ray line arising from the 3p → 1s electron deexcitations and much weaker Kβ2,5 emission resulting from electron transitions from the valence band to the core 1s level. In the K-edge XAS measurements electron excitations are involved from the core 1s energy level to the valence levels (4p and the unfilled 3d) and to the continuum of states. The spectra shown in Fig. 4 demonstrate the high energy resolution of the X-ray setup and, despite the moderate count rate, ability to resolve as weak spectral features as valence-to-core emission lines.
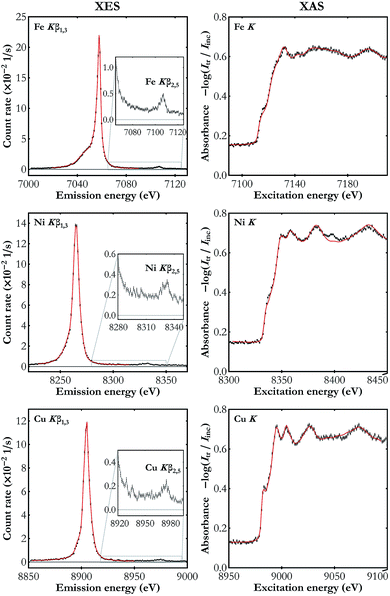 | ||
| Fig. 4 The simultaneously measured Kβ XES (left-hand side) and K-edge XAS spectra (right-hand side) for Fe, Ni and Cu foils (black dots). The reference spectra used in the energy calibration are also shown (red line).40–44 The valence-to-core emission lines are enlarged in the insets. The XAS spectra plots show the absorbance calculated using the transmitted and the incident beam spectra Itr and Iinc, respectively. The statistical uncertainty does not exceed 0.003 s−1 eV−1 and 0.008 eV−1 in all the presented XES and XAS spectra, respectively. | ||
There is a visibly better performance in the case of measurements on the Fe foil which results mainly from the smaller Bragg angle (greater solid angle covered) as well as the detectors' higher quantum efficiency in this energy domain (see Table 1). The obtained spectra are in very good agreement with the published data.40–44 Note that the published XAS spectra41,43,44 shown in Fig. 4 were acquired with synchrotron radiation and they exhibit the same features with, however, lower resolution as compared to our setup's. The superiority of the developed setup's energy resolution originates from two factors. First, due to the order of diffraction n = 4, greater than the one used in synchrotron experiments with a double-crystal monochromator (typically n = 1 or n = 2), the Darwin width is smaller. Second, following the Bragg's law, the energy resolution is proportional to the cotangent of the Bragg angle and in our setup the angles used, 46.0–66.2°, are much higher than the angle of diffraction on the synchrotron's monochromator, which is typically below 30°. Analysis of the measured XAS spectra showed that the best fit to the reference curves is achieved if the experimental data are additionally blurred with a Gaussian kernel of the full width at half maximum (FWHM) of about 1 eV. Thus the developed setup's relative energy resolution is at the level of about 1 to 2 × 10−4. The clear discrepancy in the Ni K XAS spectra around 8398 eV results from the W Lα1 emission in the X-ray tube's cathode. This signal cannot be filtered out using photon energy discrimination in the CCD detector because the W Lα1 photons are diffracted in the same diffraction order.
| Bragg angle (°) | Average registered spectral intensity (photons per (s eV)) | |
|---|---|---|
| Fe Kβ XES | 66.2 | 0.020(3) |
| Fe K XAS | 65.2 | 2.697(12) |
| Ni Kβ XES | 51.4 | 0.010(1) |
| Ni K XAS | 50.8 | 1.202(7) |
| Cu Kβ XES | 46.5 | 0.007(2) |
| Cu K XAS | 46.0 | 0.989(8) |
5 Determination of valence and conduction bands' structure
While the Fermi-level determination by coupling XES and XAS has a long history,45 the developed X-ray setup allows for the first time simultaneous XES and XAS measurements using a single X-ray source. One of the unique capabilities provided by a simultaneous XES and XAS measurement is detailed determination of the electronic structure in the atoms of interest under the very same sample conditions. This is very relevant in cases where the sample undergoes controlled transformation that cannot be reversed or the conditions cannot be easily repeated. Moreover, simultaneous measurements allow highly precise determination of the valence and conduction bands' relative positions. The XES spectra carry information on the density of occupied electronic states (valence band) while the XAS spectra depend on the density of unoccupied states (conduction band). The simultaneous XES and XAS measurement thus provides complementary information on the density of states (DOS) and allows determination of the forms of valence and conduction bands.Fig. 5 presents Cu Kβ XES and Cu K-edge XAS spectra in the vicinity of the Fermi level measured with the developed setup and calculated with FEFF software.46 As shown, the general trend of calculated spectral curves and the strength of their features are in good agreement with the shape of experimental spectra. Partial DOS calculations show that the d-states hybridized with the p-states have the strongest contribution to the valence band and the conduction band is composed mainly of the s- and p-states. Shapes of the measured XES and XAS spectra should be regarded as a projection of the p-DOS because of the dipole selection rules for transitions involving the core 1s electronic state.
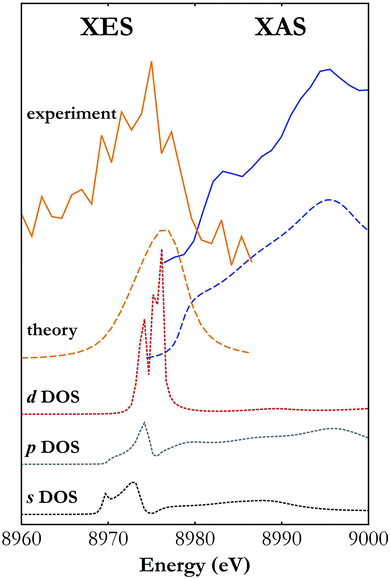 | ||
| Fig. 5 Cu Kβ XES and K-edge XAS spectra around the Fermi level measured with the developed X-ray setup (solid lines) and calculated with FEFF software (long dashed lines).46 Also shown are the contributions of the s, p and d states' densities (short dashed lines) to the valence and conduction bands. | ||
6 Conclusions
Laboratory X-ray setups are gaining popularity due to their cost effectiveness and, once built, unlimited availability as compared to beam time at any 3rd or 4th generation radiation facility. The developments are also driven by new technological solutions delivered in areas of X-ray sources, optics and detectors. Such setups allow ground state sample characterization and even slow chemical reaction tracking. This work reports on a recently constructed laboratory X-ray setup uniquely characterized by the capability of simultaneous XES and XAS measurements. The setup is composed of an X-ray tube and two X-ray spectrometers in the von Hámos geometry which makes it very compact and adaptable to different sample environments. Surrounded by a shielding box with movable walls, it does not need more space than a small lab's corner.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is financed by the Polish Ministry of Science and Higher Education from the budget allocations for science for years 2016–2019 within the IDEAS PLUS II project of number IdPII2015000164. We acknowledge the National Science Centre, Poland (NCN), for partial support under grant no. 2016/21/D/ST4/00378.Notes and references
- A. A. Bunaciu, E. G. Udriştioiu and H. Y. Aboul-Enein, Crit. Rev. Anal. Chem., 2015, 45, 289 CrossRef CAS PubMed.
- A. M. Venezia, Catal. Today, 2003, 77, 359 CrossRef CAS.
- C. Bonnelle, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 1987, 84, 201 RSC.
- J. Szlachetko and Y. Kayser, in High-resolution XAS/XES: Analyzing Electronic Structures of Catalysts, ed. J. Sá, CRC Press, Publisher Location, 1st edn, 2014, Techniques: RXES, HR-XAS, HEROS, GIXRF, and GEXRF, pp. 59–116 Search PubMed.
- J. Szlachetko, D. Banaś, A. Kubala-Kukuś, M. Pajek, W. Cao, J.-Cl. Dousse, J. Hoszowska, Y. Kayser, M. Szlachetko, M. Kavčič, M. Salome and J. Susini, J. Appl. Phys., 2009, 105, 086101 CrossRef.
- Y. Kayser, J. Szlachetko and J. Sá, Rev. Sci. Instrum., 2013, 84, 123102 CrossRef CAS PubMed.
- J. Czapla-Masztafiak, J. Szlachetko, C. J. Milne, E. Lipiec, J. Sá, T. J. Penfold, T. Huthwelker, C. Borca, R. Abela and W. M. Kwiatek, Biophys. J., 2016, 110, 1304 CrossRef CAS PubMed.
- J. Szlachetko and J. Sá, CrystEngComm, 2013, 15, 2583 RSC.
- W. Błachucki, J. Szlachetko, J. Hoszowska, J.-Cl. Dousse, Y. Kayser, M. Nachtegaal and J. Sá, Phys. Rev. Lett., 2014, 112, 173003 CrossRef PubMed.
- J. Szlachetko, J. Sá, M. Nachtegaal, U. Hartfelder, J.-Cl. Dousse, J. Hoszowska, D. L. A. Fernandes, H. Shi and C. Stampfl, J. Phys. Chem. Lett., 2014, 5, 80 CrossRef CAS PubMed.
- J. Czapla-Masztafiak, J. J. Nogueira, E. Lipiec, W. M. Kwiatek, B. R. Wood, G. B. Deacon, Y. Kayser, D. L. A. Fernandes, M. V. Pavliuk, J. Szlachetko, L. González and J. Sá, J. Phys. Chem. Lett., 2017, 8, 805 CrossRef CAS PubMed.
- K. P. Severin, in Energy Dispersive Spectrometry of Common Rock Forming Minerals, Springer Netherlands, Dordrecht, 2004, Energy Dispersive Spectrometry, pp. 1–13 Search PubMed.
- J.-Cl. Dousse and J. Hoszowska, in High-resolution XAS/XES: Analyzing electronic structures of catalysts, ed. J. Sá, CRC Press, Publisher Location, 1st edn, 2014, Crystal spectrometers, pp. 27–58 Search PubMed.
- J. Szlachetko, M. Cotte, J. Morse, M. Salomé, P. Jagodzinski, J.-Cl. Dousse, J. Hoszowska, Y. Kayser and J. Susini, J. Synchrotron Radiat., 2010, 17, 400 CrossRef CAS PubMed.
- M. Cotte, J. Szlachetko, S. Lahlil, M. Salomé, V. A. Solé, I. Biron and J. Susini, J. Anal. At. Spectrom., 2011, 26, 1051 RSC.
- J. Hoszowska, J.-Cl. Dousse, J. Kern and Ch. Rhême, Nucl. Instrum. Methods Phys. Res., Sect. A, 1996, 376, 129 CrossRef CAS.
- C. Schlesiger, L. Anklamm, H. Stiel, W. Malzer and B. Kanngießer, J. Anal. At. Spectrom., 2015, 30, 1080 RSC.
- G. T. Seidler, D. R. Mortensen, A. J. Remesnik, J. I. Pacold, N. A. Ball, N. Barry, M. Styczinski and O. R. Hoidn, Rev. Sci. Instrum., 2014, 85, 113906 CrossRef CAS PubMed.
- F. Wei, Z. W. Chen and W. M. Gibson, X-Ray Spectrom., 2009, 38, 382 CrossRef CAS.
- J. Szlachetko, J.-Cl. Dousse, J. Hoszowska, M. Berset, W. Cao and M. Szlachetko, Rev. Sci. Instrum., 2007, 78, 093102 CrossRef CAS PubMed.
- L. von Hámos, Naturwissenschaften, 1932, 20, 705 CrossRef.
- M. Szlachetko, M. Berset, J.-Cl. Dousse, J. Hoszowska and J. Szlachetko, Rev. Sci. Instrum., 2013, 84, 093104 CrossRef CAS PubMed.
- T. Johansson, Z. Phys., 1933, 82, 507 CrossRef CAS.
- H. H. Johann, Z. Phys., 1931, 69, 185 CrossRef CAS.
- J. Szlachetko, M. Nachtegaal, D. Grolimund, G. Knopp, S. Peredkov, J. Czapla-Masztafiak and C. J. Milne, Appl. Sci., 2017, 7, 899 CrossRef.
- J. Szlachetko, M. Nachtegaal, E. de Boni, M. Willimann, O. Safonova, J. Sá, G. Smolentsev, M. Szlachetko, J. A. van Bokhoven, J.-Cl. Dousse, J. Hoszowska, Y. Kayser, P. Jagodzinski, A. Bergamaschi, B. Schmitt, C. David and A. Lücke, Rev. Sci. Instrum., 2012, 83, 103105 CrossRef CAS PubMed.
- J. Szlachetko, M. Nachtegaal, J. Sá, J.-Cl. Dousse, J. Hoszowska, E. Kleymenov, M. Janousch, O. V. Safonova, C. König and J. A. van Bokhoven, Chem. Commun., 2012, 48, 10898 RSC.
- J. Szlachetko, D. Ferri, V. Marchionni, A. Kambolis, O. V. Safonova, C. J. Milne, O. Kröcher, M. Nachtegaal and J. Sá, J. Am. Chem. Soc., 2013, 135, 19071 CrossRef CAS PubMed.
- J. Szlachetko, C. J. Milne, J.-Cl. Dousse, W. Błachucki, J. Sá, Y. Kayser, M. Messerschmidt, R. Abela, S. Boutet, C. David, G. Williams, M. Pajek, B. D. Patterson, G. Smolentsev, J. A. van Bokhoven and M. Nachtegaal, Struct. Dyn., 2014, 1, 021101 CrossRef CAS PubMed.
- W. Błachucki, Y. Kayser, J. Czapla-Masztafiak, M. Guo, P. Juranić, M. Kavčič, E. Källman, G. Knopp, M. Lunberg, C. Milne, J. Rehanek, J. Sá and J. Szlachetko, Struct. Dyn., 2019, 6, 024901 CrossRef PubMed.
- J. Szlachetko, W. Błachucki and J. Sá, et al. , Sci. Rep., 2016, 6, 33292 CrossRef CAS PubMed.
- H. Hayashi, in Encyclopedia of Analytical Chemistry, ed. R. A. Meyers, John Wiley, Chichester, 2014, Chemical Effects in Hard X-ray Photon-In Photon-Out Spectra Search PubMed.
- K. Tsutsumi, H. Nakamori and K. Ichikawa, Phys. Rev. B: Solid State, 1976, 13, 929 CrossRef CAS.
- J. Kawai, E. Nakamura, Y. Nihei, K. Fujisawa and Y. Gohshi, Spectrochim. Acta, Part B, 1990, 45, 463 CrossRef.
- K. Tohji, T. Mizushima and Y. Udagawa, Jpn. J. Appl. Phys., 1990, 29, 2171 CrossRef CAS.
- Z. Németh, J. Szlachetko, É. G. Bajnóczi and G. Vankó, Rev. Sci. Instrum., 2016, 87, 103105 CrossRef PubMed.
- L. Anklamm, C. Schlesiger, W. Malzer, D. Grötzsch, M. Neitzel and B. Kanngießer, Rev. Sci. Instrum., 2014, 85, 053110 CrossRef PubMed.
- Y. Kayser, W. Błachucki, J.-Cl. Dousse, J. Hoszowska, M. Neff and V. Romano, Rev. Sci. Instrum., 2014, 85, 043101 CrossRef CAS PubMed.
- D. Giziński, W. Błachucki, A. Śrębowata, M. Zienkiewicz-Machnik, I. Goszewska, K. Matus, D. Lisovytskiy, M. Pisarek, J. Szlachetko and J. Sá, ChemCatChem, 2018, 10, 3613 CrossRef.
- Y. Ito, T. Tochio, M. Yamashita, S. Fukushima, A. M. Vlaicu, Ł. Syrocki, K. Słabkowska, E. Weder, M. Polasik, K. Sawicka, P. Indelicato, J. P. Marques, J. M. Sampaio, M. Guerra, J. P. Santos and F. Parente, Phys. Rev. A, 2018, 97, 052505 CrossRef CAS.
- Z. Guo, L. L. Henry, V. Palshin and E. J. Podlaha, J. Mater. Chem., 2006, 16, 1772 RSC.
- Y. Ménesguen, M.-C. Lépy, P. Hönicke, M. Müller, R. Unterumsberger, B. Beckhoff, J. Hoszowska, J.-Cl. Dousse, W. Błachucki, Y. Ito, M. Yamashita and S. Fukushima, Metrologia, 2018, 55, 56 CrossRef.
- D. Pan, J. K. Jian, A. Ablat, J. Li, Y. F. Sun and R. Wu, J. Appl. Phys., 2012, 112, 053911 CrossRef.
- G. Silversmit, H. Poelman, V. Balcaen, P. M. Heynderickx, M. Olea, S. Nikitenko, W. Bras, P. F. Smet, D. Poelman, R. De Gryse, M.-F. Reniers and G. B. Marin, J. Phys. Chem. Solids, 2009, 70, 1274 CrossRef CAS.
- L. G. Parratt and E. L. Jossem, Phys. Rev., 1955, 97, 916 CrossRef CAS.
- J. J. Rehr, J. J. Kas, F. D. Vila, M. P. Prange and K. Jorissen, Phys. Chem. Chem. Phys., 2010, 12, 5503 RSC.
| This journal is © The Royal Society of Chemistry 2019 |