LA-ICP-MS analyses of Fe-rich alloys: quantification of matrix effects for 193 nm excimer laser systems

Abstract

Laser-ablation inductively coupled plasma mass spectrometry (LA-ICP-MS) is increasingly used to determine major, minor and trace element concentrations in Fe-rich alloys. In the absence of matrix-matched standards, standardization is often based on silicate glass reference materials. This approach could result in significant matrix effects. Here, we quantify these matrix effects for a wide suite of volatile to refractory trace elements during ns-excimer LA-ICP-MS analyses of Fe-rich alloys by comparing measured LA-ICP-MS concentrations with results from electron microprobe analysis (EPMA). Measurements performed with LA-ICP-MS consistently overestimate the concentration of volatile elements in metals relative to concentrations measured by EPMA. In contrast, the concentrations of non-volatile and refractory elements in Fe-rich alloys are systematically underestimated with LA-ICP-MS relative to EPMA. To quantitatively describe these offsets, we consider the fractionation index (F_i) for element i, or the ratio between the EPMA- and LA-ICP-MS determined elemental concentrations. The F_i is found to be independent of concentration and type of Fe-rich alloy considered, and ranges from >0.14 for the most volatile elements to ≤1.8 for the most refractory elements. The F_i correlate positively with the 50% condensation temperature of the elements considered, suggesting the matrix effects are predominantly the result of ablation-induced evaporative and/or melting processes at the ICP site. Comparison of the results with results from previous studies obtained for metals and sulfides using similar laser systems for a smaller subset of elements generally confirms the magnitude of the observed matrix effects for metals. These results were used to quantify the effects of matrix effects on calculated metal-silicate partition coefficients (D, defined as the metal to silicate abundance ratio by weight) derived from high-pressure experiments. The comparison was done by considering uncorrected and corrected LA-ICP-MS derived metal concentrations, where ‘‘corrected’’ concentrations were obtained by multiplying uncorrected LA-ICP-MS values with the appropiate F_i values derived here. Our results show that neglecting matrix effects will result in erroneous partitioning results for many volatile and refractory elements. The matrix effects described here should therefore be taken into account in future applications of ns-LA-ICP-MS for Fe-rich metal analysis if metal standards are not available for calibration.

---

1. Introduction

Laser-ablation inductively coupled plasma mass spectrometry (LA-ICP-MS) is widely applied to quantify iron-loving (siderophile) and nominally lithophile element abundances in (extra)-terrestrial Fe-rich metals and sulfides relevant to planetary, experimental, archaeological and metallurgical geochemistry.^1–5 The ablation behavior of trace elements during LA-ICP-MS analyses in metals depends on a range of material properties, including target surface reflectivity, optical absorption coefficient, thermal diffusivity and melting/boiling temperature, which in turn affect the target surface temperature and amount of laser-induced vaporization.⁶ Elemental and isotopic fractionation of elements during ablation and sample heating can occur through (1) redistribution of elements among sub-solidus phases that are formed close to the ablation pit,⁷ (2) non-congruent evaporation of volatile elements from melts that form in the ablation pit,⁸ (3) fractional condensation of the cooling plume of sample vapor rising from the ablation site,⁹ (4) differential transport of particles of different sizes and compositions from the ablation cell to the ICP torch,¹⁰ (5) incomplete vaporization of particles larger than 150 nm, resulting in higher signal responses of more volatile elements¹¹ and (6) reduction of signal intensities for volatile elements, relative to refractory elements, due to high loading of laser-derived aerosols and corresponding effects on plasma conditions and count rates.^12,13 The relative contribution of these effects to elemental and isotopic fractionation will most likely change with changes in sample matrices. For example, laser ablation processes with metal targets are characterized by melting and associated evaporative processes,¹⁴ whereas the ablation behavior of silicate materials is characterized by more efficient evaporation. Matrix effects for silicate samples are therefore less pronounced than for Fe based samples, although they can still be significant.^13,15 The extent of matrix effects has also been shown to be affected by the ablation mechanisms.¹⁶ The ablation mechanisms of nano-second (ns) lasers are dominated by thermal effects resulting in melting of the ablated material, whereas femto-second (fs) lasers generate pulses with a much shorter plasma life time leading to evaporation rather than melting.¹⁶

Some studies have also assessed these effects for Fe-based samples for a limited set of elements and element concentrations.^6,17–26 Možná et al.¹⁸ investigated matrix and non-matrix matched calibration capabilities for the quantification of Fe-based samples while using three different types of laser systems (ns-ArF*, ns-Nd-YAG, fs-Ti-sapphire). They reported significant matrix effects for Fe-based samples while using ns-laser systems, and found that these effects are least significant for the shortest laser pulse duration systems. No significant matrix effects were observed for Fe-based samples while using the fs-Ti-sapphire laser system. Chernonozhkin et al.²³ performed bulk elemental analyses and 2D mapping of iron meteorites using a 193 ns-ArF* excimer-based LA system and observed major matrix effects for elements V, Cr, Mn, Co, Ni, As and Mo. Glaus et al.²⁰ and Diwakar et al.²² observed fractionation of Cu and Zn using fs or ns laser pulse ICP-MS analyses of brass materials, whereas Gilbert et al.²⁴ reported significant fractionation of S relative to Fe in sulfide minerals while using ns-LA due to differences in their volatility. Wohlgemuth-Ueberwasser and Jochum²⁶ analysed sulfides using three different LA systems (213 nm ns solid state; 193 nm ns excimer, and 200 nm fs laser) and found significant differences in melting between the three LA systems, resulting in different matrix effects. They reported massive melting events in sulfides during ablation with a set-up similar to that used in this study. It was found that elemental fractionation is not related to progressing ablation or deepening of the ablation crater. Danyushevsky et al.²⁷ developed a new synthetic sulfide standard and compared measured concentrations of chalcopyrite that were derived using either the synthetic sulfide standard or the NIST 612 glass as the calibration standard. They found that the use of NIST 612 glass as the calibration standard dramatically decreases the accuracy of the measured elemental concentrations, relative to using the synthetic sulfide standard.

It is clear from the above that matrix-related fractionation effects on trace element measurements are significant. Although Fe-rich metal reference materials are available for some of the elements considered here (enabling matrix-matched calibrations), such materials are often heterogeneous with respect to minor element distributions.²⁸ Many workers therefore continue to use silicate primary standards to calibrate quantitative analyses of Fe-rich alloys^29–32 and sulfides,³³ which could result in erroneous results if matrix effects are large. Although the use of fs laser systems has been shown to greatly decrease matrix effects,¹⁸ ns lasers are still the most widely used systems worldwide due to their easy implementation and because of the remaining challenges of operating fs laser systems.^34,35 It is therefore important to obtain consistent correction factors for analyses of Fe-based samples using 193 nm ns laser systems.

To quantify the effects of matrix-related fractionation effects on trace element determination in Fe-rich metals and sulfides by LA-ICP-MS for 193 nm ns laser systems, here we compile an extensive set of previously published chemical analyses of Fe-rich metals and sulfides using LA-ICP-MS and electron microprobe (EPMA).^36–41 The use of near-identical analytical conditions throughout these studies allows for direct comparison of the analytical results obtained with LA-ICP-MS and EPMA and enables a systematic quantitative assessment of the extent of matrix-related fractionation of trace elements in Fe-rich alloys and sulfides. We also compare these results with fractionation indices previously obtained for various laser systems and sample matrices, and assess whether matrix effects are similar for both Fe-rich metals and sulfides. We show it is possible to derive a consistent set of correction factors that can be applied to non-matrix-matched LA-ICP-MS analyses of metals and sulfides, yielding results that are in good agreement with EPMA analyses.

2. Methods

2.1 Synthetic Fe-based samples

Synthetic Fe-based alloys were obtained by mixing high-purity metal powders (Alpha Aesar, >99.5% purity) in variable proportions^36–41 under ethanol in an agate mortar for >30 minutes. Metal powders were combined with powdered silicate glasses and loaded into graphite or polycrystalline MgO capsules that were machined from graphite or MgO rods. For the purpose of experimental determination of trace element partition coefficients between metal and silicate phases (D^met_sil, defined as the weight ratio between the concentration of element i in metal and silicate, respectively)^36–41 samples were synthesized at high pressures (1–5 GPa) and temperatures (1473–2873 K) using piston cylinder and multi-anvil high pressure apparatus at the Vrije Universiteit Amsterdam, the University of Münster and at the Geophysical Laboratory, Carnegie Institution for Science, Washington D.C. After the experiments, the samples (consisting of clearly segregated quenched metal alloy and silicate phases) were embedded in epoxy resin and polished using various grades of Al powder and/or SiC sandpaper.

2.2 EPMA analyses

Major and trace element concentrations in experimentally synthesized metal and sulfide phases from our database^36–41 were obtained using electron microprobes at the Institute of Mineralogy at the University of Münster and at the Dutch National Geological Facility at Utrecht University. Both institutes are equipped with a JEOL JXA 8530F field emission electron microprobe. Analyses were all performed using a defocused beam because of the inevitable heterogeneous nature of the Fe-rich alloys and sulfides. Measurement points were set in lines and/or raster grids, depending of the available surface area of the analysed phases. The use of grids ensured that compositional heterogeneities in the metal were analysed and included in the average. The electron beam size was approximately equivalent to the step size (5–15 μm), while using a beam current of 15 nA and an accelerating voltage of 15 kV. Dwell times of 20–30 s on peak and 10–15 s on each background were used. At least 20 repeat analyses were performed if sufficient sample surface area was available, and usually more (N > 30), given the heterogeneity of the Fe-based samples. Care was taken to avoid analyses of areas close to the edge of phases and/or surrounding capsule materials. Standards used for metal analyses were KTiPO₅ or apatite for P, fayalite or pure Fe metal for Fe, TiO₂ or rutile for Ti, tephroite or rhodonite for Mn, pure metal or willemite for Zn, galena or Pb–Zn glass for Pb, pure metal or InAs for In, GaAs or InAs for As, pure metal or CdS for Cd, hypersthene or diopside for Si, chalcopyrite or pyrite for S, pure metal or Cr₂O₃ for Cr, pure metal or NiO for Ni, and pure metal standards for V, Co, Cu, Ge, Se, Sn, Sb, Te, Mo, W, Tl and Bi. Calibrations were considered successful when the primary standard compositions were reproduced within 1% relative deviation. Data reduction was performed using the Φ(ρZ) approach,⁴² which corrects for the decrease in X-ray density due to the distance the x-rays have to travel through the specimen before they reach the detector. In Section A.1† from the Appendix we present a full analysis of the accuracy of our analytical strategy, using analyses of the NIST 610 reference glass with the EPMA standardization that was implemented in the previous studies that are used in this work. We observe that there is generally good agreement (i.e. within 10% relative deviation) between reference and measured values (Fig. S1†), despite the low concentrations of nominally 500 ppm and the use of a moderate beam current of 15 nA due to the beam sensitive nature of silicate glasses. Several analyses of the NIST 616 glass, that contains approximately 0.5 ppm of each trace element, were also performed to assess true zero counts for the elements of interest and confirmed the accuracy and precision of our analytical approach.

2.3 LA-ICP-MS analyses

Laser ablation inductively coupled plasma mass spectrometry (LA-ICP-MS) analyses of all compiled experimental charges were conducted with a 193 nm ArF excimer laser (Analyte G2, Photon Machines) at the University of Münster. Low mass resolution ICP analyses were all performed using a repetition rate of 10 Hz, whereas the laser fluence was ∼3–4 J cm⁻² throughout each of the sampled sessions. The large majority of analyses were performed using a spot size of 50 μm diameter. In case of limited sample availability, analyses were performed using 25 or 35 μm diameter spot sizes.

Elemental analysis was performed with an Element 2 mass spectrometer (ThermoFisher). Forward power was 1300 W and reflected power <2 W, gas flow rates were 1.1 l min⁻¹ for He (carrier gas of ablated material), 0.9 l min⁻¹ and 1.2 l min⁻¹ for the Ar-auxiliary and sample gas, respectively. Cooling gas flow rate was set to 16 l min⁻¹. Before starting the analysis, the system was tuned (torch position, lenses, gas flows) on a NIST 612 glass measuring ¹³⁹La, ²³²Th and ²³²Th¹⁶O to obtain stable signals and high sensitivity, as well as low oxide rates (²³²Th¹⁶O/²³²Th <0.1%) during ablation. Isotopes of Fe and P were measured using medium and high resolution mode of the Element 2 mass spectrometer, due to polyatomic interferences of P by N, O, H and C and of Fe by Ar, O, Ca, N and H. The following isotopes were measured: ²⁴Mg, ²⁹Si, ³¹P, ⁴³Ca, ⁴⁹Ti, ⁵¹V, ⁵³Cr, ⁵⁵Mn, ⁵⁶Fe, ⁵⁹Co, ⁶⁰Ni, ⁶³Cu, ⁶⁶Zn, ⁶⁹Ga, ⁷³Ge, ⁷⁵As, ⁸²Se, ⁹⁰Zr, ⁹³Nb, ⁹⁵Mo, ¹¹¹Cd, ¹¹⁵In, ¹¹⁸Sn, ¹²¹Sb, ¹²⁵Te, ¹⁸¹Ta, ¹⁸²W, ¹⁹⁵Pt, ²⁰⁵Tl, ²⁰⁸Pb and ²⁰⁹Bi. In the medium resolution model analyses the NIST 612 reference glass was used as a calibrant for metal and sulfide phases, whereas for high resolution mode analyses the NIST 610 glass was used. USGS BIR-G1 and BCR-2G silicate reference materials were measured every ∼20–25 LA-ICP-MS analyses to assess accuracy and precision.

For metals, Ni was mostly used as the internal standard, whereas Si was used for metals with Si concentrations exceeding >0.5 wt% if Ni was not available. Sulfur-rich Fe alloys and sulfides were processed using Cu, Cr, Mn or Fe concentrations measured by EPMA as internal standards. Copper is a moderately volatile element and it is fractionated due to the use of non-matrix-matched silicate primary standards. The concentrations of Cu determined by EPMA were corrected using the empirical correction term later reported in this paper (Table 1). These corrected concentration values were used as internal standards for LA-ICP-MS data processing.

Table 1 Calculated fractionation indices

	50% cond. T^43 (K)	Fractionation index (Fi)	N	R ^2
a Number of measurements included in regression. b Coefficient of determination. c Fractionation indices for elements Ti, Ga, Nb, Ta, Tl, Bi, Th and U were calculated using the equation: Fi = 0.00109 ± 0.00013 × 50% T(K) − 0.29 0.0.15; R^2 = 0.80.
In	536	0.49 ± 0.03	80	0.77
Cd	652	0.14 ± 0.01	60	0.62
Se	697	0.72 ± 0.04	74	0.83
Sn	704	0.73 ± 0.07	33	0.75
Te	705	0.39 ± 0.03	78	0.60
Zn	726	0.24 ± 0.06	14	0.44
Pb	727	0.35 ± 0.03	73	0.56
Ge	883	1.09 ± 0.06	62	0.69
Sb	976	0.74 ± 0.04	76	0.77
Cu	1037	0.65 ± 0.03	35	0.92
As	1065	0.88 ± 0.04	77	0.82
P	1229	0.82 ± 0.05	23	0.93
Cr	1296	1.11 ± 0.03	91	0.92
Si	1302	1.09 ± 0.02	56	0.98
Ni	1348	0.95 ± 0.11	5	0.95
Co	1352	1.14 ± 0.06	42	0.87
V	1427	1.39 ± 0.07	62	0.86
Mo	1590	1.58 ± 0.10	79	0.69
W	1789	1.77 ± 0.15	79	0.52
Tl^c	532	0.29 ± 0.14	—	—
Bi	746	0.52 ± 0.17	—	—
Ga	968	0.77 ± 0.20	—	—
Nb	1559	1.41 ± 0.28	—	—
Ta	1573	1.42 ± 0.28	—	—
Ti	1582	1.44 ± 0.28	—	—
U	1610	1.47 ± 0.29	—	—
Th	1659	1.52 ± 0.29	—	—

---

3. Results

3.1 Elemental fractionation during LA-ICP-MS analyses of metals and sulfides

It was demonstrated in Appendix section A.2† that there are no systematic offsets exceeding 10% relative deviation between reference values and measured LA-ICP-MS concentrations for several silicate reference glasses. Using the previously published compiled dataset of major and minor element concentrations in Fe-rich alloys,^33–38 EPMA and LA-ICP-MS analyses for Fe-based samples were compared in the present study. Fig. 1–3 and Table 1 show a compilation of the results. Significant offsets between EPMA and LA-ICP-MS determined element concentrations are observed. These offsets are most significant for volatile (Zn, Se, Cd, In, Te, Pb) and highly refractory elements (V, Mo, W), and appear to increase linearly with increasing absolute concentration. Although the data set for sulfides is limited, it appears as if there is no significant difference in the offset between Fe-rich (S-poor) and S-rich alloys.

Fig. 1 Comparison between measured concentrations (%, in mass) of volatile elements In, Cd, Se, Sn, Te, Zn using LA-ICP-MS and EPMA.^36–41 Horizontal and vertical error bars are 2 standard errors. Coarse dashed lines are 1 : 1 identity lines plotted for reference. Finely dashed lines represent linear fits to the data (Table 1). Except for Zn, values for S-rich alloys and sulfides are plotted for comparison purposes and were not incorporated into the regressions due to the possibility of different matrix effects.

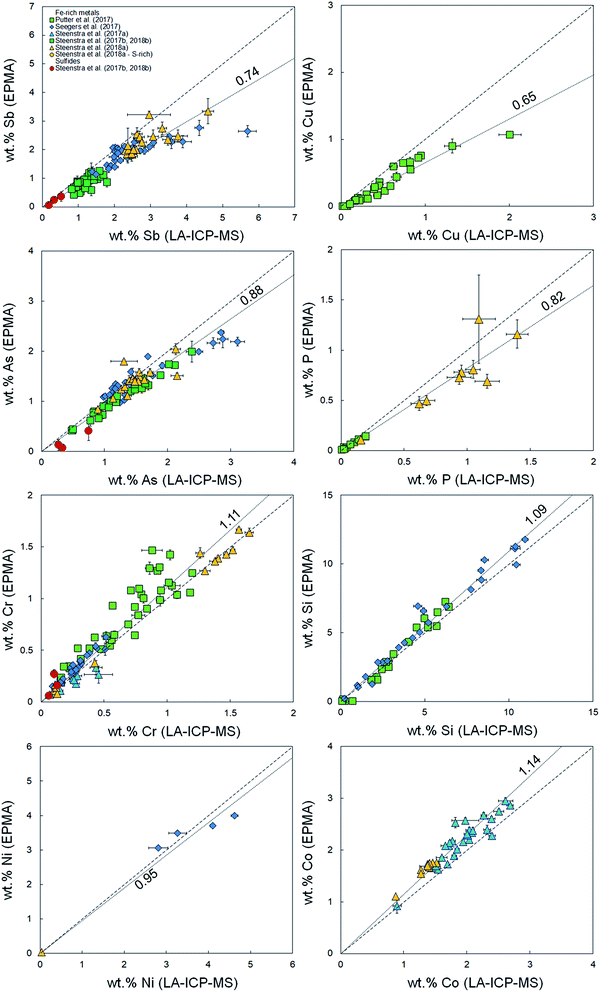Fig. 2 Comparison between measured concentrations (%, in mass) of volatile elements Pb, Ge, Sb, Cu, As, P using LA-ICP-MS and EPMA.^36–41 Horizontal and vertical error bars are 2 standard errors. Coarse dashed lines are 1 : 1 identity lines plotted for reference. Finely dashed lines represent linear fits to the data (Table 1). Values for S-rich alloys and sulfides are plotted for comparison purposes only.

Fig. 3 Comparison between measured concentrations (%, in mass) of non-volatile or refractory elements Cr, Si, Ni, Co, V, Mo and W using LA-ICP-MS and EPMA.^36–41 Horizontal and vertical error bars are 2 standard error. Coarse dashed lines are 1 : 1 identity lines plotted for reference. Finely dashed lines represent linear fits to the data (Table 1).

To quantitatively describe the offsets, we consider the fractionation index (F_i) for element i, or the ratio between the EPMA- and LA-ICP-MS determined elemental concentrations:

These indices are derived by linear regression fits of EPMA and LA-ICP-MS measurements for each element and are indicative of the relative differences between both values. A higher F_i value implies that elemental concentrations are underestimated by LA-ICP-MS and vice versa. Table 1 lists the F_i values that were calculated using this approach. EPMA and LA-ICP-MS elemental concentrations of the non-volatile or -refractory elements (Si, Cr, Co, Ni) are within 10% of each other, leading to F_i values between 0.95 and 1.09 (Table 1). The F_i ranges down to 0.14 for the most volatile element and up to 1.8 for the most refractory element. The results are graphically illustrated as a function of their volatility (approximated here as their 50% condensation temperatures^43–45) in Fig. 4. A clear positive correlation (R² = 0.80) is observed between the F_i values of an element and its 50% condensation temperatures, given by the equation: F_i = 0.00109 ± 0.00013 × 50% T(K) − 0.29 ± 0.15; which corresponds with the linear fit shown in Fig. 4. This suggests the matrix effects are the result of volatility-related fractionation processes during and/or following ablation of metal phases (see Section 4.2†), as has been previously proposed for Fe-based samples^24,25 and silicate glasses.⁴⁴ The latter equation was used to calculate the expected F_i values for elements Ti, Ga, Nb, Ta, Tl, Bi, Th and U, for which at present no EPMA and/or LA-ICP-MS data are available (Table 1).

Fig. 4 Calculated fractionation indices for the elements considered in this study as a function of their 50% condensation temperatures (based on a carbonaceous Ivuna chondritic composition at 10⁻⁴ bar (ref. 43)). Dashed line represents a linear fit to the calculated fractionation indices, defined by: F_i = 0.00109 ± 0.00013 × 50% T(K) – 0.29 0.0.15 (R² = 0.80).

4. Discussion

4.1 Comparison with previous studies and possible variability of matrix effects with metal composition

The excellent correlation between fractionation indices and 50% condensation temperatures suggest that the matrix effects observed in the present study are predominantly due to volatility-related processes, as previously observed for Fe-based samples by Gilbert et al.²⁴ and Luo et al.²⁵ for several different laser systems. To explore to which extent metal composition and the type of implemented laser system affect the extent of matrix effects, we compare our new results with those reported in these previous studies.^13,18,26,46 As illustrated in Fig. 5, our results for metals are generally within the range of previous values derived for Fe-rich samples.¹⁸ The range in volatility of the elements considered in this study is limited, prohibiting a quantitative comparison of the derived trend of F_iversus 50% condensation temperature (Fig. 5) for Fe-rich metals. As previously concluded, our comparison confirms that matrix effects are indeed much smaller for fs-LA-ICP-MS systems¹⁸ both for metals and sulfides (Fig. 5).

Fig. 5 Relative deviations between the measured concentrations and reference concentrations by using different laser systems,^13,18,26,46 as a function of relative elemental volatility⁴³ for metals and sulfides. Negative relative deviations imply measured concentrations are less than reference values and vice versa. Errors are 1 standard deviations, where reported.

For sulfides, the element set is limited to Co, Ni, Cu and Zn and refractory platinum group elements Pd, Rh and Pt.^13,26,46 Measurements of Co and Ni in sulfides^13,42 that were obtained using 193 nm ArF* laser systems in conjunction with the use of NIST 610 silicate reference materials as calibrants for sulfide measurements generally show a lack of significant fractionation. The F_i values for Co and Ni cluster between 0.80–1.05 and 0.90–1.10, respectively, which is close to or within error of the F_i values reported for metals (1.14 ± 0.06 and 0.95 ± 0.11 for Co and Ni, respectively). Only one measurement is available in the literature for Zn,¹³ obtained for the standard MASS-1, a Cu and Zn-rich sulfide (13 and 21 wt%, respectively). This value significantly deviates from the F_i value obtained for Zn for metals in this study (F_i = 0.24 ± 0.06), which at face value may suggest that the addition of significant quantities of Cu and/or Zn may result in different matrix effects due to different ablation behavior. However, this seems unlikely as concentrations for various other volatile elements (Se, Cd, In, Te) determined in this study for sulfides plot on the expected trend for metals (Fig. 1 and 2), suggesting that matrix effects are similar for both matrices. In addition, the relative deviations of Pd, Rh and Pt previously obtained using a ns 193 nm excimer laser system²⁶ are in very good agreement with the relative volatility trend observed for metals. In fact, using our new expression in conjunction with the 50% condensation temperatures reported by Lodders⁴³ yields F_i values of 1.15 ± 0.25, 1.23 ± 0.26 and 1.25 ± 0.26 which are within error with those derived for the data of Wohlgemuth-Ueberwasser and Jochum²⁶ (F_i = 1.09 ± 0.10, 1.20 ± 0.13 and 1.27 ± 0.13 for Pd, Rh and Pt, respectively). These results show that (1) our model can be likely applied to sulfides as well and (2) measurement of elemental concentrations in sulfides using a silicate glass as a reference material³⁵ will most likely result to erroneous results, as proposed for metals.

The exact processes through which the elemental fractionations occur during LA-ICP-MS analyses of Fe-rich alloys could not be identified in the present study. It should be noted that the exact ablation mechanisms and relative contribution of these processes to matrix effects are in general not well understood, complicating the interpretation of the results.⁴⁷ It would be worthwhile to address this in future work to provide more quantitative insights into the observed matrix effects and to assess if F_i values are indeed applicable across a wider compositional range, as suggested from this work.

4.2 Implications for metal-silicate partition coefficients of siderophile elements

Matrix effects may strongly affect experimentally determined metal-silicate partition coefficients (D^met_sil values), independent of the exact mechanism(s) that are responsible for these effects. The effect is likely small for quantification of the partitioning between two metal phases with different compositions^3,5,48,49 given the matrix similarities. The majority of previous published metal-silicate partitioning studies used silicate primary standards for calibration of LA-ICP-MS analyses of Fe-rich alloys.^29–32 Given the fractionation indices found in this study, neglecting matrix effects will result in erroneous results for most volatile and refractory elements. These effects are quantitatively illustrated in Fig. 6, where both uncorrected and corrected metal-silicate partition coefficients for two typical experiments are shown (for runs GG1Si-1 and GGR1Si-4b, reported by Seegers et al.³⁷ and Putter et al.,³⁶ respectively; see Table 1). The comparison was done by considering uncorrected and corrected LA-ICP-MS derived metal concentrations, where ‘‘corrected’’ concentrations were obtained by multiplying uncorrected LA-ICP-MS values with the appropiate F_i values derived here. Fig. 6 shows that experimentally determined metal-silicate partition coefficients or D^met_sil values may be overestimated by up to 0.85 log units if the described matrix effects are ignored. The importance of these matrix effects are illustrated most dramatically by the shift from siderophile (D^met_sil > 1) to lithophile (D^met_sil < 1) behavior of Cd and Pb after considering the matrix effects. The D^met_sil values for the most refractory elements may be underestimated by up to 0.25 log units (Table 1). The effects are therefore most significant for the volatile elements and these effects may, if not taken into account, result in substantial inter-laboratory offsets (Table 2).

Fig. 6 Comparison between matrix-effect-corrected and uncorrected metal-silicate partition coefficients (D^met_sil) of run GGR1Si-4b and GG1Si-1 (ref. 36 and 37) as a function of their volatility.

Table 2 Effects of matrix effects on derived metal-silicate partition coefficients (D^met_sil, defined here as the ratio between the weight concentration of element i in the metal phase and the concentration of element i in the silicate glass) reported for GG1-Si1 and GGR1Si-4b^36,37

	Uncorrected log D^metsil	Corrected log D^metsil	Offset
In	1.10	0.80	−0.30
Cd	0.57	−0.27	−0.84
Se	0.97	0.83	−0.14
Sn	1.54	1.40	−0.14
Te	1.28	0.86	−0.42
Zn	−0.61	−1.06	−0.46
Pb	0.45	−0.01	−0.46
Ge	2.77	2.80	+0.04
Sb	3.98	3.85	−0.13
Cu	1.65	1.46	−0.19
As	4.59	4.54	−0.05
P	1.47	1.38	−0.09
Cr	−0.95	−0.90	+0.05
V	−0.67	−0.52	+0.12
Mo	4.44	4.63	+0.20
W	2.83	3.08	+0.25

---

5. Conclusions

Elements in Fe-rich alloy phases are often quantified by LA-ICP-MS using non-matrix-matched silicate primary standards. We demonstrated that LA-ICP-MS-measured concentrations of volatile elements in Fe-rich alloys are significantly higher than those measured using EPMA. In contrast, refractory element concentrations are consistently underestimated by LA-ICP-MS, relative to values obtained with EPMA. In all cases offsets between EPMA and LA-ICP-MS appear to increase linearly with increasing element concentration. This confirms that significant matrix effects exist. To quantify these effects, the fractionation index (F_i) for element i, or the ratio between the EPMA- and LA-ICP-MS determined elemental concentrations were considered. The F_i, which can be used to correct LA-ICP-MS fractionation in Fe-rich alloys analysis, is found to be correlated positively with elemental volatility.

The matrix effects are therefore most pronounced for the most volatile elements investigated (Zn, Cd, In, Te, Pb). Our results suggests our model is applicable for both Fe-rich metal and sulfide matrices, given the similar F_i values derived for both phases.

It was observed that neglecting to perform a matrix correction in the LA-ICP-MS analysis can result in a shift of metal-silicate partition coefficients (D^met_sil values) by up to 0.85 log units. The matrix effects are negligible for the non-volatile and non-refractory elements such as Si, Co, Ni and Cr, confirming the suitability of these elements as internal standards in LA-ICP-MS analyses. The most refractory elements are also hampered by matrix effects, although these effects are less pronounced than they are for volatile elements, resulting in an expected maximum offset of 0.25 log units in their log D^met_sil values. These results show that matrix effects arising from application of non-matrix-matched primary standards to measurements of elements in Fe-rich alloys using LA-ICP-MS is significant for many volatile elements, and that it is possible to correct for these matrix effects by developing a large database from LA-ICP-MS and EPMA analyses of the same Fe-rich alloy matrix.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was supported financially by a Netherlands Organization for Scientific Research (N. W. O.) Vici award to W. v. W. and by SFB TRR-170. We thank three anonymous reviewers for their insightful and constructive criticism, enabling us to significantly improve the quality of this work.

References

1. V. V. Kogan, M. W. Hinds and G. I. Ramendik, Spectrochim. Acta, Part B, 1994, 49, 333–343.
2. A. J. Campbell and M. Humayun, Anal. Chem., 1999, 71, 939–946.
3. A. J. Stewart, W. van Westrenen, M. W. Schmidt and D. Günther, Earth Planet. Sci. Lett., 2009, 284, 302–309.
4. J. Siebert, A. Corgne and F. J. Ryerson, Geochim. Cosmochim. Acta, 2011, 75, 1451–1489.
5. N. Rai, S. Ghosh, M. Wälle and W. van Westrenen, Chem. Geol., 2013, 357, 85–94.
6. D. Bleiner, Z. Chen, D. Autrique and A. Bogaerts, J. Anal. At. Spectrom., 2006, 21, 910–921.
7. J. Kosler, M. Wiedenbeck, R. Wirth, J. Hovorka, P. Sylvester and J. Mikova, J. Anal. At. Spectrom., 2005, 20, 402–409.
8. R. Hergenröder, J. Anal. At. Spectrom., 2006, 21, 505–516.
9. S. M. Eggins, L. P. J. Kinsley and J. M. G. Shelley, Appl. Surf. Sci., 1998, 127–129, 278–286.
10. J. Koch, I. Feldmann, N. Jakubowski and K. Niemax, Spectrochim. Acta, Part B, 2002, 57, 975–985.
11. M. Guillong, L. Horn and D. Gunther, J. Anal. At. Spectrom., 2003, 18, 1224–1230.
12. I. Kroslakova and D. Günther, J. Anal. At. Spectrom., 2007, 22, 51–62.
13. P. Sylvester, in Laser Ablation-ICP-MS in the Earth Sciences, Current Practices and Outstanding Issues, Mineralogical Association of Canada (MAC) Short Course Series, 2008, pp. 67–78.
14. M. V. Allmen and A. Blatter, in Laser-Beam interactions with Materials, Springer, Berlin, 1995.
15. J. Kimura and Q. Chang, J. Anal. At. Spectrom., 2012, 27, 1549–1559.
16. I. Horn and F. von Blanckenburg, Spectrochim. Acta, Part B, 2007, 62, 410–422.
17. D. Bleiner and A. Bogaerts, Spectrochim. Acta, Part B, 2006, 61, 421–432.
18. V. Možná, J. Pisonero, M. Holá, V. Kanický and D. Günther, J. Anal. At. Spectrom., 2006, 21(11), 1194–1201.
19. J. J. Gonzales, C. Liu, S.-B. Wen, X. Mao and R. E. Russo, Talanta, 2007, 73(3), 567–576.
20. R. Glaus, R. Kaegi, F. Krumeich and D. Günther, Spectrochim. Acta, Part B, 2010, 65, 812–822.
21. H. Wiltsche and D. Günther, Anal. Bioanal. Chem., 2011, 399(6), 2167–2174.
22. P. K. Diwakar, S. S. Harilal, N. L. LaHaye, A. Hassanein and P. Kulkarni, J. Anal. At. Spectrom., 2013, 28, 1420–1429.
23. S. M. Chernonozhkin, S. Goderis, S. Bauters, B. Vekemans, L. Vincze, P. Claeys and F. Vanhaecke, J. Anal. At. Spectrom., 2014, 29, 1001–1016.
24. S. E. Gilbert, L. V. Danyushevsky, K. Goemann and D. Death, J. Anal. At. Spectrom., 2014, 29, 1024–1033.
25. T. Luo, Y. Wang, Z. C. Hu, D. Günther, Y. S. Liu, S. Gao, M. Li and S. H. Hu, J. Anal. At. Spectrom., 2015, 30, 941–949.
26. C. C. Wohlgemuth-Ueberwasser and K. P. Jochum, J. Anal. At. Spectrom., 2015, 30, 2469–2480.
27. L. Danyushevsky, P. Robinson, S. Gilbert, M. Norman, R. Large, P. McGoldrick and M. Shelley, Geochem.: Explor., Environ., Anal., 2011, 11, 51–60.
28. S. E. Gilbert, L. Danyushevsky, P. Robinson, C. Wohlgemuth-Ueberwasser, N. Pearson, D. Savard, M. Norman and J. Hanley, Geostand. Geoanal. Res., 2012, 37, 51–64.
29. M. A. Bouhifd, D. Andrault, N. Bolfan-Casanova, T. Hammouda and J. L. Devidal, Geochim. Cosmochim. Acta, 2013, 114, 13–28.
30. V. Clesi, M. A. Bouhifd, N. Bolfan-Casanova, G. Manthilake, A. Fabbrizio and D. Andrault, Geochim. Cosmochim. Acta, 2016, 192, 97–121.
31. Z. Wang, V. Laurenz, S. Petitgirard and H. Becker, Earth Planet. Sci. Lett., 2016, 435, 136–146.
32. C. Ballhaus, R. O. C. Fonseca, C. Münker, A. Rohrbach, T. Nagel, I. M. Speelmanns, H. M. Helmy, A. Zirner, A. K. Vogel and A. Heuser, Contrib. Mineral. Petrol., 2017, 172, 68.
33. J. Koch, S. Schlamp, T. Rosgen, D. Fliegel and D. Günther, Spectrochim. Acta, Part B, 2007, 62, 20–29.
34. J. Koch and D. Günther, Anal. Bioanal. Chem., 2007, 387, 149–153.
35. B. Gourcerol, D. J. Kontak, P. C. Thurston and J. A. Petrus, Miner. Deposita, 2018, 53, 871–894.
36. R. Putter, E. S. Steenstra, A. X. Seegers, Y. H. Lin, S. Matveev, J. Berndt, N. Rai, S. Klemme and W. van Westrenen, 48^th Lun. Planet. Sci. Conf., 2017, #1055.
37. A. X. Seegers, E. S. Steenstra, R. Putter, Y. H. Lin, J. Berndt, S. Matveev, N. Rai, S. Klemme and W. van Westrenen, 48^th Lun. Planet. Sci. Conf., 2017, #1053, https://www.sciencedirect.com/science/article/pii/S0009254113003768.
38. E. S. Steenstra, A. B. Sitabi, Y. H. Lin, N. Rai, J. Berndt, S. Matveev and W. van Westrenen W, Geochim. Cosmochim. Acta, 2017, 212, 62–83.
39. E. S. Steenstra, Y. H. Lin, D. Dankers, N. Rai, J. Berndt, S. Matveev and W. van Westrenen, Sci. Rep., 2017, 7, 14552.
40. E. S. Steenstra, Y. Fei, S. Matveev, J. Berndt, S. Klemme and W. van Westrenen, 49^th Lun. Planet. Sci. Conf., 2018, #1198.
41. E. S. Steenstra, D. Dankers, J. Berndt, S. Klemme, S. Matveev and W. van Westrenen, Icarus, 2018 DOI:10.1016/j.icarus.2018.08.020.
42. J. T. Armstrong, Microbeam Anal., 1995, 4, 177–200.
43. K. Lodders, Astrophys. J., 2003, 591, 1220–1247.
44. M. Gaboardi and M. Humayun, J. Anal. At. Spectrom., 2009, 24, 1188–1197.
45. F. E. Jenner, H. St and C. O'Neill, Geochem., Geophys., Geosyst., 2012, 13, Q03003.
46. W. E. Halter, T. Pettke and C. A. Heinrich, Contrib. Mineral. Petrol., 2004, 147, 385–396.
47. J. Fietzke and M. Frische, J. Anal. At. Spectrom., 2016, 31, 234–244.
48. N. L. Chabot, A. J. Campbell, J. H. Jones, M. Humayun and C. B. Agee, Meteorit. Planet. Sci., 2003, 38, 181–196.
49. C. M. Corrigan, N. L. Chabot, T. J. McCoy, W. F. McDonough and H. C. Watson, Geochim. Cosmochim. Acta, 2009, 73, 2674–2691.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ja00291f

---