Open Access Article
Open Access ArticleMolecules in confinement in clusters, quantum solvents and matrices: general discussion
Zlatko
Bacic
,
David
Benoit
 ,
Malgorzata
Biczysko
,
Malgorzata
Biczysko
 ,
Joel
Bowman
,
Stephen
Bradforth
,
Timothy
Burd
,
Joel
Bowman
,
Stephen
Bradforth
,
Timothy
Burd
 ,
Gilberte
Chambaud
,
David
Clary
,
Claudine
Crépin
,
Gilberte
Chambaud
,
David
Clary
,
Claudine
Crépin
 ,
Martin
Dracinsky
,
Martin
Dracinsky
 ,
Peter
Felker
,
Ingo
Fischer
,
Francesco
Gianturco
,
Majdi
Hochlaf
,
Karel
Kouril
,
Peter
Felker
,
Ingo
Fischer
,
Francesco
Gianturco
,
Majdi
Hochlaf
,
Karel
Kouril
 ,
Irena
Kratochvilova
,
ChunMei
Liu
,
Anne
McCoy
,
Jun
Miyazaki
,
Irena
Kratochvilova
,
ChunMei
Liu
,
Anne
McCoy
,
Jun
Miyazaki
 ,
Halima
Mouhib
,
Jeremy
Richardson
,
Petr
Slaviček
,
Thierry
Stoecklin
,
Krzysztof
Szalewicz
,
Ad
van der Avoird
,
Halima
Mouhib
,
Jeremy
Richardson
,
Petr
Slaviček
,
Thierry
Stoecklin
,
Krzysztof
Szalewicz
,
Ad
van der Avoird
 and
Anne
Zehnacker-Rentien
and
Anne
Zehnacker-Rentien
First published on 6th December 2018
Ingo Fischer opened a general discussion of the paper by Anne Zehnacker: You also presented data on the structure of the ionic dipeptide and discuss the relative stability of the isomers in terms of the CH–π and NH–π bonds in the ion. But in the ion you also have ion–multipole interactions. Can you comment on their role for the structure and stability of the dipeptide isomers?Anne Zehnacker-Rentien responded: Actually, the CH and NH π–bonds disappear in the ionic “folded-extended” structure. Indeed, most of the charge is borne by the extended aromatic ring. Therefore, the interaction between the charged benzene ring and the NH becomes repulsive. This is why the extended ring undergoes a rotation upon ionisation, to favour an interaction between CO and the aromatic ring. However, I agree that this interaction is probably more of a dipole/charge interaction than a CO–π interaction.
Ingo Fischer added: You point out that the NH–π bond is weaker in the c-LL isomer than in the c-LD isomer, while for the CH–π bond you observe the opposite trend. Do you have a simple picture that explains this result?
Anne Zehnacker-Rentien replied: In general, steric constraints due to the cyclic nature of the dipeptide add to chirality effects and make these effects more prominent. This is the case for example for 1-amino-2-indanol in which the (R,S) and (R,R) diastereomers show much more structural differences than linear 1,2 amino alcohols.1 In the cyclo Tyr-Tyr studied here, the cyclic nature of the peptide backbone is also responsible for the differences in interactions. Because of the different position of the extended aromatic ring in the “folded/extended” geometry of the two diastereomers (axial for L and equatorial for D), the CH–π hydrogen bond involves CaH as a donor in c-LD vs. CβH in c-LL, which is slightly weaker. The same kind of conclusion holds for the NH–π interaction. This is why these interactions are slightly stronger in c-LD.
1 A. Bouchet, J. Klyne, G. Piani, O. Dopfer and A. Zehnacker, Phys. Chem. Chem. Phys., 2015, 17, 25809–25821.
Malgorzata Biczysko said: In the analysis of the experimental spectra, you are comparing mainly with results computed at the harmonic level. Do you think that in the case of such rather complicated systems it would be helpful to also perform fully anharmonic simulations of vibrational spectra, including overtones and combination bands?
Anne Zehnacker-Rentien answered: We have calculated the fully anharmonic frequencies for related systems (cyclo Phe–Phe, please see ref. 1) and cyclo Tyr-Pro.2 We have used them for determining the scaling factors used for correcting the harmonic frequencies. Three zones can be distinguished; the fingerprint, the ν(CH), and the ν(NH)/ν(OH) regions for which the scaling factors are slightly different. In the systems mentioned above, fully anharmonic calculations reproduce well the amide I/II overtone or combination band that is experimentally observed near the ν(NH) stretch band. Anharmonic calculations limited to selected modes, namely NH and OH stretching modes, as well as amide I and II, give good agreement with both fully anharmonic frequencies and experiment. This is why anharmonic calculations with selected modes were used for the cyclo Tyr-Tyr system presented here.
1 A. Pérez-Mellor, I. Alata, V. Lepere and A. Zehnacker, J. Mol. Spectrosc., 2018, 349, 71–84.
2 A. Pérez Mellor, PhD thesis, Université Paris Saclay, 2017.
Irena Kratochvilova queried: I would like to ask about your molecules in a different solvent, such as water or some different solution, what does it mean from the perspective of studied molecular structures?
Anne Zehnacker-Rentien answered: The cyclo Tyr–Tyr molecule has been studied in solution (please see ref. 1 and 2). It seems that several structures coexist, but no clear conclusion could be drawn. Studies of cyclo dipeptides in solution often rest on NMR or electronic circular dichroism. They are usually limited to the natural LL dipeptides and do not include the LD stereoisomer. For the parent molecule cyclo Phe–Phe, which we have extensively studied, the structure seems to be the same for the solid phase3 in the neutral molecule isolated in a supersonic expansion,4 or in the protonated molecule isolated in an ion trap.5
1 K. D. Kopple and D. H. Marr, J. Am. Chem. Soc., 1967, 89, 6193–6200.
2 J. Fleischhauer, J. Grotzinger, B. Kramer, P. Kruger, A. Wollmer, R. W. Woody and E. Zobel, Biophys. Chem., 1994, 49, 141–152.
3 A. Pérez-Mellor, A. Zehnacker, Chirality, 2017, 29, 89–96.
4 Perez-Mellor, et al., J. Mol. Spectrosc., 2018, 349, 71–84.
5 I. Alata et al., J. Phys. Chem. A, 2017, 121 (38), 7130–7138.
Gilberte Chambaud commented: To obtain a better differentiation of the folded structures of your LL and LD stereoisomers you introduce hydroxyl substituents on the phenyl branches, don’t you think than you can capture one or more water molecules interacting with these hydroxyl substituents that could help the differentiation of the close structures?
Anne Zehnacker-Rentien responded: This is an excellent suggestion. Indeed, previous work on biomolecules like peptides (please see for example ref. 1) has shown that complexation with one water molecule is enough to introduce the transition from an extended structure to a folded structure. Although the formation of hydrates might be experimentally challenging, a water bridge between the two residues could help to differentiate between the LL and LD stereoisomers in related structures, by stabilizing the folded geometry in one stereoisomer and not in the other one.
1 H. S. Biswal, Y. Loquais, B. Tardivel, E. Gloaguen and M. Mons, J. Am. Chem. Soc., 2011, 133 (11), 3931–3942.
Ingo Fischer contributed: As Anne Zehnacker demonstrated in her contribution, IR/UV spectroscopy is an excellent way to characterise isomers and verify their structure. This is not only useful for biomolecules, but also for reactive intermediates, in particular when generated by pyrolysis. Therefore, the technique establishes a connection between Anne Zehnacker’s presentation and my presentation on para-xylylene. We use IR/UV ion dip spectroscopy employing the free electron laser FELIX in Nijmegen to characterise radicals, biradicals and their reaction products by mid-IR spectroscopy.1,2 Recently we conducted IR/UV ion dip spectroscopy to investigate the isomers of xylylene and showed that pyrolysis of [2,2]paracyclophan indeed generated para-xylylene.
1 K. H. Fischer, J. Herterich, I. Fischer, S. Jaeqx and A. M. J. Rijs, Phys. Chem A, 2012, 116, 8515.
2 F. Hirsch, P. Constantinidis, I. Fischer, S. Bakels, A. M. Rijs, Chem. Eur. J., 2018, 24, 7647.
Anne Zehnacker-Rentien replied: This is a follow-up of the comments of Prof. Dr. Ingo Fischer, who suggested that double resonance IR-UV experiments would be useful for probing the proton transfer at play in the systems presented by Dr. Martin Dracinsky (DOI: 10.1039/c8fd00070k). IR-UV double resonance experiments have been performed by the group of Markus Gerhards1 to detect excited-state proton transfer in jet cooled 3-hydroxyflavone/water clusters.
1 K. Bartl, A. Funk and M. Gerhards, The Journal of Chemical Physics, 2008, 129, 234306.
Majdi Hochlaf addressed Anne Zehnacker-Rentien and Malgorzata Biczysko: Once we compare the spectra, can we probe or measure the binding energy of weak interactions? Indeed, it is hard to compute accurately the NH–π interaction in electronic excited states. Can we get some insights from experiments?
Malgorzata Biczysko answered: An example of an experimental attempt to estimate the binding energy of weak interactions in excited electronic states, I am aware of, is based on the molecular beam-laser spectroscopy experiments for the neutral and positively charged anisole dimer.1
1 F. Mazzoni, M. Pasquini, G. Pietraperzia and M. Becucci, Phys. Chem. Chem. Phys., 2013, 27, 11268.
Anne Zehnacker-Rentien added: Using REMPI, we can measure the appearance threshold of the fragments and deduce from that value, and the ionisation potential of the molecule, the binding energy in the ground state. Using then the shift of the S0–S1 transition relative to the bare chromophore, we get the binding energy in the excited state. Actually, we resorted to this procedure for measuring the difference in binding energy between homochiral and heterochiral jet-cooled complexes.1 The main difficulty is that flexible molecules, as we usually study, might possess a geometry in the complex that differs from that of the isolated molecule, so that there is rearrangement of the fragments after dissociation. This introduces a bias in the measurements, which has to be carefully taken into account.
1 M. Mons et al., Phys. Chem. Chem. Phys., 2000, 2, 5065.
Majdi Hochlaf opened a general discussion of the paper by Malgorzata Biczysko: Can you apply your methodology when the electronic states are coupled?
Malgorzata Biczysko answered: This methodology does not include couplings between electronic states. However, we have recently postulated that the single-state spectra computations can still be informative in the analysis of complex experimental results, with the discrepancy between simulated sum-spectrum and experiment as a useful indication of possible vibronic couplings (see ref. 28 in the paper, DOI: 10.1039/c8fd00094h and ref. 1).
1 M. H. Palmer et al., J. Chem. Phys., 2017, 147, 074305.
Joel Bowman remarked: Please clarify your notation “HOCH” and whether that was meant to describe the high-energy isomers of H2CO?
Malgorzata Biczysko replied: We have considered only the most stable isomer of HCOH, usually denoted H2CO.
Ad van der Avoird asked: Are the complexes that you discussed actually occurring in the Earth’s atmosphere? It would be surprising, because the presence of the water dimer, a strongly hydrogen-bonded system, in the atmosphere has not yet been demonstrated.
Malgorzata Biczysko responded: Understanding the highly complex phenomena proceeding in the Earth’s atmosphere requires knowledge not only on gas-phase processes but also on reactions at boundary layers and in the condensed phase. Therefore, it is important to study the role of molecular complexes which can be considered as first-step models for the condensed phase (aerosols). The high density of the Earth’s atmosphere, as well as relatively high temperature, make formation of weakly bound complexes likely but both their abundance and lifetime are limited.1 Weakly bound species exist naturally in the atmosphere only with their more abundant monomeric precursors. Moreover, detection of such aggregates is difficult due to the fact that their spectroscopic properties are similar to those of the parent monomers. Indeed, that is demonstrated by the difficulties in detecting water dimers, however their presence has been postulated based on dedicated experiments in the NIR region.2 In this context, theoretical data obtained from high level quantum chemical calculations should be very useful for potential detection, or prediction of the possible role of complexes in atmospheric photochemistry.
1 W. Klemperer and V. Vaida, PNAS, 2006, 103, 10584–10588.
2 K. Pfeilsticker, A. Lotter, C. Peters and H. Bösch, Science, 2003, 300, 2078.
Anne McCoy queried: Can you provide more details about how the reduced dimensional vibrational perturbation theory calculations were performed?
Anne McCoy added: Did you remove the cubic and quartic terms from the expansion of the Hamiltonian prior to performing the perturbation theory or did you not use all of the calculated frequencies and anharmonicities in evaluating the energies/diagonal elements in the subsequent variational calculation?
Malgorzata Biczysko replied: Reduced dimensional vibrational perturbation theory (VPT2) calculations have been performed by initially excluding all the large amplitude motions (LAMs) and all related cubic and quartic force constants from the perturbative treatment (RedDim=Passive). So, the VPT2 computations are made in the reduced space, and any subsequent variational computations are set within the same reduced space. That approach, of course, cannot account for anharmonicities of the LAMs and is only set to reduce the problem caused by the LAMs contamination of the VPT2 treatment, which can lead to large errors even for the intense, high-frequency vibrations which are coupled to the LAMs. Some relevant examples are discussed in ref. 16. of our paper (DOI: 10.1039/c8fd00094h).
Anne Zehnacker-Rentien asked: Can you simulate the consequences of the Duschinsky effect, i.e. rotation of the normal modes upon electronic excitation, on the shape of the emission spectra, in particular reproduce the splitting of the ν = 1 to ν = 1 transition?
Malgorzata Biczysko replied: The Duschinsky effect has been taken into account in all computations reported in the discussed paper, which is referred to as the Adiabatic Hessian model (see reference 14 of our paper for details, DOI: 10.1039/c8fd00094h). This model can be also applied to the emission spectra and to include transitions originating from excited vibrational states of the initial electronic state. So it is possible to compute a ν1–ν1 transition, and for example splittings due to the isotopic effects. However, the vibronic model applied in this study (and implemented in the Gaussian suite) is set within the Born–Oppenheimer and harmonic approximations. It is possible to correct energy levels for anharmonicity (as done in the present study, http://dx.doi.org/10.1039/c8fd00094h), but other vibronic and/or anharmonic effects, as for instance excitonic or tunneling splittings are not accounted for.
Gilberte Chambaud remarked: To determine the spectra of your molecules of interest, you calculate separately the ro-vibrational levels of the lower and of the upper states. Doing so, you are in principle able to describe either emission or absorption spectra. Did the conditions of the calculations allow you to obtain spectra either in absorption or in emission.
Malgorzata Biczysko answered: Both absorption and emission spectra are computed within the Born–Oppenheimer and harmonic approximations. Anharmonicity has only be accounted for in the corrections to the vibrational levels of the lower and upper electronic states, but not to the band intensities, also rotational resolution is not considered. For spectra encompassing large energy intervals, with several electronic transitions, the total spectrum is obtained by a simple sum of single-state spectra, so vibronic coupling is not accounted for. In more general terms, the applied model can be successfully applied for semi-rigid systems where harmonic description of potential energy surfaces close to the equilibrium can be considered as a good approximation. Otherwise, temperature effects can be considered and there are no direct limitations on the system size, total number of normal modes to be included in the computations, number of modes excited simultaneously, or number of vibrational quanta to be considered.
Irena Kratochvilova commented: You have measured the internal energy relaxation process can you generalise more on what this means? Can you explain it?
Malgorzata Biczysko responded: We attempt to measure and simulate spectroscopic signatures of internal energy relaxation processes, as well as to predict experimental conditions for irradiation induced processes. Relevant examples are the excitation of OH stretching overtones by NIR irradiation allowing for conformational switching in pyruvic acid (ref. 9 in our paper, DOI: 10.1039/c8fd00094h), or electronic excitation localized on the anisole, in the anisole–phenol complex, leading to a photoinduced isomerization process.1 We investigate which of these processes could be effective in atmospheric complexes of formaldehyde and predict the most effective energy/wavelength ranges for further experimental studies.
1 G. Pietraperzia et al., J. Phys. Chem. A, 2011, 115, 9603.
Timothy Burd queried: For some of these weakly bound complexes, I can imagine there may be a large number of nearly degenerate, low energy configurations they can adopt. Here you have just considered the lowest lying one or two structures. Do you have an idea of how significant these other structures may be to your results?
Malgorzata Biczysko replied: We have done some more extensive searches for possible structures of all the complexes, and in the case of the CO–HCOH additional stable structures have been found. However, due to their stability being lower by about 8 kJ mol−1 they have not been included in the present study.
Stephen Bradforth opened a general discussion of the paper by Anne McCoy: Could you address the issue of the intensities of the various bands in the spectra and how well your calculations reproduce the relative intensities? Presumably, depending on whether the proton localizes or not, there is a large effect on the intensities of the O–H stretch and the coupled lower frequency transitions?
Anne McCoy answered: The short answer is intensities are hard to calculate accurately for such anharmonic systems that have this many vibrational degrees of freedom.
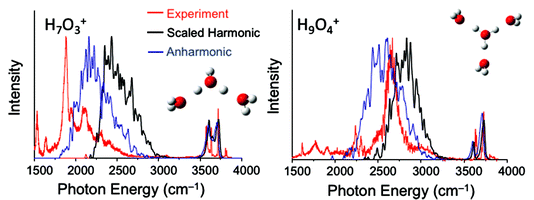
If the proton were localized then the situation would be much simpler. From a calculation standpoint, the leading source of difficulties in calculating spectra comes from the very large intrinsic intensity of the shared proton stretch vibrations, which is often an order of magnitude or more larger than the intensities of the other vibrational degrees of freedom. As couplings are introduced between the states with one quantum of excitation in these OH stretching vibrations and nearby nominally dark states, intensity borrowing leads to broadening of the OH fundamental band (as is seen in the spectrum of H9O4+), the series of transitions seen in H7O3+ or the pairs of peaks found in H5O2+. In the case of H5O2+, Meyer and co-workers1 used MCTDH approaches to reproduce the intensities as well as the frequencies of the transitions seen in the spectrum. The increased number of degrees of freedom, and accompanying higher density of vibrational states makes this much more challenging for the larger systems. Joel Bowman and his group have shown that they are able to get good agreement with experiment using the VSCF/CI approaches he described in his paper,2,3 although their calculations on D7O3+ (ref. 4) demonstrated that the calculated spectrum can be sensitive to small changes in potential surfaces. This is because small changes in the energy differences and size of the coupling between the bright OH stretches and nearby dark states can lead to significant changes to the spectral envelope.
Calculations of ions with ten or thirteen atoms, which undergo large amplitude motions are close the limit of the systems where we can calculate the vibrational energies and wave functions. As we have shown, VPT2 also provides good agreement in the frequencies and intensities for H7O3+ and D7O3+ when near degeneracies are included. While we worry about whether we are getting the ‘right answer for the right reasons’ the fact that several approaches, which make different approximations and are based on slightly different potential surfaces, give similar intensity patterns is reassuring that the results are robust.
A further complication in comparing measured and calculated spectra comes from the fact that until recently3 the experiments were performed on tagged ions (ions complexed with an argon atom, H2 molecule or other chemically inert atom or molecule). When discrepancies were found between experiment and theory, it was hard to know if the differences reflected the potential surface, approximations used to calculate frequencies and intensities or the effect of the tag.
1 O. Vendrell, F. Gatti, H.-D. Meyer, J. Chem. Phys., 2007, 127, 184303.
2 T. K. Esser, H. Knorke, K. R. Asmis, W. Schöllkopf, Q. Yu, C. Qu and J. M. Bowman, J. Phys. Chem. Lett., 2018, 9, 798–803.
3 C. H. Duong, N. Yang, P. J. Kelleher, M. A. Johnson, R. J. DiRisio, A. B. McCoy, Q. Yu, J. M. Bowman, B. V. Henderson and K. D. Jordan, Tag-Free and Isotopomer-Selective Vibrational Spectroscopy of the Cryogenically Cooled H9O4+ Cation with Two-Color, IR-IR Double Resonance: Isolating the Spectral Signature of a Single OH Group in the Hydronium Ion Core, J. Phys. Chem. A (submitted Aug 31, 2018).
4 C. H. Duong, O. Gorlova, N. Yang, P. J. Kelleher, M. A. Johnson, A. B. McCoy, Q. Yu, J. M. Bowman, J. Phys. Chem. Lett., 2017, 8, 3782–3789.
Ingo Fischer asked: To what extent does your work contribute to the long-standing discussion of whether protonated water exists as a Zundel- or Eigen-cation in solution? Is any new information derived from the computations?
Anne McCoy replied: At this stage, it is probably safest to say that protons in solution exist in a variety of environments. Depending on the solvent environment the proton may be more strongly associated with a single water molecule or shared among two. While OH stretch frequency can be used as a reporter of the environment of the shared proton, the large couplings between the shared proton stretch and other degrees of freedom make it difficult to identify a single transition that would directly report an Eigen- or Zundel-like structure in solution.
Joel Bowman commented: Identifying the dominant motif of the solvated proton as Zundel or Eigen is problematic in a room temperature liquid owing to the many different hydration conditions. This contrasts to cold size-selected clusters, where a combination of state-of-the-art experiment and theory have been able to make these identifications. Nevertheless, there is evidence, from recent theory, that there are vestiges of these motifs, albeit distorted, in the room temperature experiments.
Joel Bowman added: Anne mentioned the potential energy surface from our group that she used in DMC calculations. I just wish to elaborate a bit on this surface. It is an ab initio many-body potential consisting of 1, 2, 3-body interactions between the waters and also between hydronium and water. We also have recently developed a simply 4-body hydroinum-water-water-water interaction. This improves the relative energies of the numerous isomers of hydronium water clusters.
Zlatko Bacic asked: How are these particular ions isolated experimentally? Is it by means of mass spectroscopy?
Anne McCoy replied: The experimental details are provided by the Johnson and Duncan groups,1,2 who we have collaborated with. Broadly, the work that was the focus of our paper is based on tagged spectra in which a complex of the ion of interest and a weakly bound tag is isolated using mass spectroscopy. The spectrum of the selected ion is obtained using infrared laser photodissociation spectroscopy in which the complex is vibrationally excited and a second mass spectrometer is used to detect any untagged ions that are formed. Only if the photon is in resonance with a vibrational transition in the molecule, and the complex has sufficient internal energy to dissociate the tag will any ions be detected by the second mass spectrometer. More recently, the Johnson group have developed approaches that enable them to obtain tag-free spectra.3 In the case of H9O4+, they find that the tag introduces only minor perturbations in the spectrum.
1 D. C. McDonald, J. P. Wagner, A. B. McCoy and M. A. Duncan, J. Phys. Chem. Lett., 2018, 9, 5664–5671.
2 C. H. Duong, O. Gorlova, N. Yang, P. J. Kelleher, M. A. Johnson, A. B. McCoy, Q. Yu and J. M. Bowman, J. Phys. Chem. Lett., 2017, 8, 3782–3789.
3 C. H. Duong, N. Yang, P. J. Kelleher, M. A. Johnson, R. J. DiRisio, A. B. McCoy, Q. Yu, J. M. Bowman, B. V. Henderson and K. D. Jordan, J. Phys. Chem. A (submitted Aug 31, 2018).
Joel Bowman added: I believe that is basically correct.
David Clary commented: These are very nice spectra, but I think the spectral range considered is above 1000 cm−1. When you go to lower frequencies into the far IR region, there are more challenges for the dynamics, the potential surfaces and the experiments. Can you comment on that region?
Anne McCoy answered: Yes, the lower frequency region is interesting. Recent experiments of Asmis and co-workers reported H2-tagged spectra of H7O3+ and H9O4+ down to 250 cm−1.1 Both spectra show two dominant peaks near 250 cm−1. These have been assigned based on VSCF/VCI calculations to the hydronium core rattling in the water cage (or O–O stretching vibrations). Recently we identified these transitions in combination with the OH stretch fundamental in H9O4+ and D9O4+.2
1 T. K. Esser, H. Knorke, K. R. Asmis, W. Schöllkopf, Q. Yu, C. Qu and J. M. Bowman, J. Phys. Chem. Lett., 2018, 9, 798–803.
2 C. H. Duong, N. Yang, P. J. Kelleher, M. A. Johnson, R. J. DiRisio, A. B. McCoy, Q. Yu, J. M. Bowman, B. V. Henderson and K. D. Jordan, J. Phys. Chem. A (submitted Aug 31, 2018).
Joel Bowman added: Concerning the AIMD method, this can produce fairly accurate results (provided the potential and dipole moment surfaces are accurate) for low frequency modes. We showed this for the flanking water modes in the H7O3+ cluster in comparison with experiment from the Asmis group.
Thierry Stoecklin commented: This is beautiful work. I would like to mention a recent work we did which is going to be published in Phys. Chem. Chem. Phys. dedicated to the CO2–N2 complex: "Quantum tunneling behavior on weakly bound complexes: the case of the CO2–N2 dimer" by Miguel Lara Moreno, Thierry Stoecklin, Philippe Halvick and Majdi Hochlaf.
In this work, we find that the usual description of the fundamental bound state by a simple gaussian function does not work for this system. More generally its accurate numerical description even when using large basis sets does remain a difficult task as we identified two nodal planes while a ground state wave function is usually nodeless. This is illustrated in the left panel of Fig. 3 of this paper (DOI: 10.1039/c8fd00120k) where a 3D plot of the two equivalent A’1 and B’2 quasi-degenerate ground state wave functions are represented.
Anne McCoy replied: Thank you for sharing the results of this study.1 We have also found that on such flat potential surfaces the wave functions are often not particularly well-described by the usual Gaussian functions. The projections of the ground state probability amplitude onto various coordinates in Fig. 3 of our paper (DOI: 10.1039/c8fd00120k) show such behavior. We have been exploring approaches we can use to use the DMC ground state wave functions to gain insights into the spectra of such floppy molecules.2,3
1 M. Lara-Moreno, T. Stoecklin, P. Halvicka and M. Hochlaf, Phys. Chem. Chem. Phys., 2018, DOI: 10.1039/c8cp04465a.
2 A. B. McCoy, E. G. Diken and M. A. Johnson, J. Phys. Chem. A, 2009, 113, 7346–7352.
3 T. L. Guasco, M. A. Johnson and A. B. McCoy, J. Phys. Chem. A, 2011, 115, 5847–5858.
Petr Slavicek asked: Do you have any guesses as to what the quality of the IR spectra recorded as instantaneous harmonic spectra averaged over e.g. path integral MD trajectory or over the density calculated diffusion Monte Carlo technique would be?
Anne McCoy replied: We have explored a study similar to what you describe, and the results were not as encouraging as we had hoped. We believe the reason reflects the very specific nature of the couplings of the zero-order bright state to nearby background states. More specifically, we followed an approach based on one that was developed for studying the broad OH stretch feature in MgOH+(H2O)n and CsOH+(H2O)n systems. In that study, we sampled geometries based on the harmonic ground state probability amplitude, where the harmonic analysis was performed in internal coordinates. For each of the sampled geometries, we optimized the OH bond lengths and HOH angles of the flanking water molecules and the hydronium core. The details of these calculations are provided in Laura C. Dzugan’s PhD thesis,2 and the results are reproduced in Fig. 1, where they are compared to argon-tagged spectra. For the calculations of the OH vibrational frequencies we performed the harmonic calculations or the VPT2 in a reduced-dimensional space that only includes the coordinates that were optimized. Overall the approach roughly captures the breadth of the OH stretch features in these spectra, but the details of the spectral envelopes are not well reproduced. Additionally, there is an overall frequency shift between the calculated harmonic or VPT2 frequencies and the measured frequency. This reflects the importance of explicit couplings to the lower frequency vibrations.
 | ||
| Fig. 1 Calculated spectra obtained using the approach described in the text. Comparisons are made to the argon-tagged spectra reported in ref. 3. | ||
 | ||
| Fig. 2 Comparison of costs and of systems sizes that can be investigated using force fields and using on-the-fly calculations. | ||
1 C. J. Johnson, L. C. Dzugan, A. B. Wolk, C. M. Leavitt, J. A. Fournier, A. B. McCoy and M. A. Johnson, J. Phys. Chem. A, 2014, 118, 7590–7597.
2 L. C. Dzugan, Ph.D. thesis, The Ohio State University, 2017.
3 R. A. Relph, T. L. Guasco, B. M. Elliot, M. Z. Kamrath, A. B. McCoy, R. P. Steele, D. P. Schofield, K. D. Jordan, A. A. Viggiano, E. E. Ferguson and M. A. Johnson, Science, 2010, 327, 308–312.
Majdi Hochlaf addressed Anne McCoy and Joel Bowman: By exploring the potential energy surface of your clusters, can you have any intuitive prediction of the complex dynamical behaviors you are observing?
Anne McCoy replied: This is an excellent question. Certainly, the harmonic frequencies and barrier heights help us to understand and anticipate the spectroscopy and dynamics of these cluster ions. On the other hand, we have found that, for systems that are sampling multiple minima and some of the saddle points that connect the minima, we are able to gain more insights by exploring the projections of the ground state probability amplitude obtained using diffusion Monte Carlo. Examples of this are in Fig. 3 of our paper, DOI: 10.1039/c8fd00120k.
Joel Bowman responded: Thanks for this important question. The high dimensionality of these PESs make explorations challenging. As we know for simple A+BC reactive potentials it is common to make contour plots in two degrees of freedom and to learn a great deal by examining such plots. While we do have a full-dimensional PES for, say, the isomerizations of the eigen H9O4+ cluster we haven’t figured out yet how to visualize important regions of this PES. I think this is a major challenge for our field and one that deserves future research.
Francesco Gianturco commented: in the past, we have done quite a few calculations using simply H+, i.e. a sort of naked proton, embedded in helium clusters of various sizes and using quantum DMC calculations. We looked at the interactions, using fairly accurate ab initio potentials and found that the diffusion Monte Carlo structures showed cages around the H+. At that time we tested mainly 2-body potentials, and when we added a 3-body potential, because helium was the solvent, we found negligible effects. In your situation, which was rather different in the end, did you use a full multi-body potential in the diffusion Monte Carlo? Having thus a more complicated diffusional potential, did you have any problem with the number of walkers you used or the danger of producing biased results?
1 F. A. Gianturco and B. Balta, J. Chem. Phys., 2000, 254, 203.
2 F. A. Gianturco and B. Balta, J. Chem. Phys., 2000, 254, 215.
Anne McCoy responded: The potential used in these studies is the full many-body surface, which was developed by Joel Bowman and his group. This potential is based on accurate potentials they developed for hydronium, H5O2+ and water along with the introduction of up to four-body terms. These surfaces are more complicated than what you describe using in your studies. Indeed, there are some challenges to DMC, which appear to be increasing with system size, particularly when we consider the statistical uncertainties in the zero-point energies obtained using DMC. We believe this is due to the large number of degrees of freedom, and the weaker coupling between the intramolecular OH stretches and bends and the intermolecular hindered rotations. Based on our analysis of the projections of the probability amplitude onto various coordinates, which are averaged over 35 wavefunctions, we are confident in our results. At the same time, we are continuing to explore methods to minimize the statistical uncertainties in the energies.
Claudine Crépin remarked: Your work on protonated water clusters with multiple large amplitude motions, and especially (H5O2)+, reminds me of the case of acetylacetone. Do you think it’s possible to calculate according to your methodologies an average geometry of acetylacetone with its three coupled large amplitude motions? Do you think this could help to rationalize the results of microwave spectroscopy (see ref. 1 and Poster number 10) which conclude a C2v geometry with the other results (including ours) showing a Cs geometry for this molecule?
1 W. Caminati and J.-U. Grabow, J. Am. Chem. Soc., 2006, 128, 854.
Anne McCoy responded: With a potential surface we could use DMC to evaluate the ground state wave function and probability amplitude for acetylacetone. This approach would allow us to explore the couplings among the various degrees of freedom involved in the tautomerization. This could provide an interesting way to explore the couplings between the methyl rotors, hydrogen location and the CO/CC bond lengths as well as the CCO angles. With appropriate choices of nodal surfaces, we could also explore the various tunneling splittings. We have found that knowledge of how the molecule samples the potential in its ground state can help us to develop a better zero-order description of the molecular vibrations for other types of calculations. Although it is hard to anticipate exactly what we would learn from such a study, it seems that such insights could provide understanding of the apparent contradictory results related to the structure (C2vvs. Cs) for this molecule.
Ad van der Avoird opened a general discussion of the papers by Krzysztof Szalewicz: The quantum contributions to the virial coefficients that you found now are substantially larger than in previous calculations with a rigid-body water potential. Is this due to the flexibilty or to higher order effects?
Krzysztof Szalewicz answered: The short answer is that I am not aware of literature results with substantially lower quantum contributions than that obtained in our calculations but it depends on what the word “substantially” means. I corroborate this statement below.
The effects of higher-order quantum effects and of monomer flexibility are discussed in the paper and are as follows. From Table 1 in our paper (DOI: 10.1039/c8fd00092a), the values of B(T) for H2O at 300 K at various levels of theory are; rigid, classical −1330.1, rigid, semiclassical −1042.2, rigid, quantum −1061.2, and flexible, quantum −1085.6. The quantum contribution given in the paper, 25.3%, is the quantum effect for rigid monomers (as a fraction of the quantum rigid-monomer result). The analogous semiclassical quantum effect in the Takahshi–Imada (TI) approximation is slightly larger, 27.6%. Thus, the higher-order effects not included at the TI level are 2.3%. We have not performed classical calculations with flexible monomers, so we cannot determine flexibility effects at the classical level. However, the total monomer-flexibility plus quantum effect is 22.5% and the difference between rigid- and flexible-monomer quantum calculations is 2.2%. Thus, we may estimate that flexibility effects at the classical level are also about 2%.
The recent literature values for the discussed effects are reasonably close to those in our paper. For example, in ref. 1 Table 10, the rigid-monomer semiclassical TI quantum effect at 298.15 K is 33.5% and the total TI quantum and monomer-flexibility effect is 30.3%. The monomer-flexibility effect at the classical level is 2.4% relative to the flexible-monomer quantum result. In Bukowski et al.,2 the rigid-monomer semiclassical TI quantum effect at 298.15 K is 33% with the CC-pol potential (27% with the SAPT-5s potential). This paper also includes results with the semiclassical quantum correction in the Kirkwood–Wigner (KW) approximation, amounting to 49% and showing that TI is a much better approximation than KW. I could not find any very low values of quantum effects in the literature.
Schenter, in ref. 3, gets at 300 K 100%, 14%, and 25% contributions from quantum effects at TI level for the TIP4P, DC, and TTM2-R potentials, respectively. The value from empirical DC potential is low, but the very large value from the empirical TIP4P potential clearly shows that the values of quantum corrections computed with empirical potentials are meaningless. Millot et al.4 computed virial coefficients at the KW level with several first-principles potentials and obtained quantum corrections ranging between 17% and 24%. These values presumably would decrease in the TI approximation, so perhaps the question refers to such values.
It appears that the reason for the smaller contributions from 1998 and earlier potentials is mainly the lower accuracy of these potentials compared to modern ones.
1 P. Jankowski et al., J. Phys. Chem. A, 2015, 119, 2940.
2 R. Bukowski et al., J. Chem. Phys., 2008, 128, 094314.
3 G. K. Schenter, J. Chem. Phys., 2002, 117, 6573.
4 C. Millot et al., J. Phys. Chem. A, 1998, 102, 754.
Ad van der Avoird asked: You found in earlier calculations with quantum effects included in first order or by the Takahashi–Imada model, that the quantum contributions to the second virial coefficients are mainly due to librations. Does this also hold in higher orders and for the third virial coefficients?
Krzysztof Szalewicz responded: The contributions due to librations are easy to determine in KW or TI approximations since these approximations include an explicit term dependent on torques. There is no such term appearing in PIMC calculations of the second virial coefficient at the flexible-monomer level. However, since the difference between TI and full quantum flexible-monomer calculations is not large, the importance of librations carries to the latter level.
For the third virial coefficient, we are not aware of any equivalent of the KW or TI approximation for the terms resulting from the three-body potential. We have included in Table 4 (DOI: 10.1039/c8fd00092a) results that use TI for the two-body component and classical approximation for the three-body part.
This approximation does capture a large part of the quantum effect. However, we did not look into a separation of this approximate quantum effect into the translational and librational parts.
Francesco Gianturco commented: A rather long time ago (e.g. ref. 2 and 3) we did quantum and classical calculations of 2nd and 3rd virial coefficients. We found that the diatomic systems had minor effects on their results when going from a classical to a quantum treatment, while CH4 was better evaluated by using quantum methods. Do you think that increasing the spatial anisotropy of the interaction could be a factor in requiring a more quantized treatment of these momentum-transfer cross sections? What is your experience on this point?
1 F. A. Gianturco, Mol. Phys., 1995, 84, 481.
2 F. A. Gianturco, A.S. Dickinson and M. Venanzi, Mol. Phys., 1988, 65, 563.
Krzysztof Szalewicz responded: The main part of the quantum effect for water comes from librational motions. The latter are proportional to rotational constants and to torques which in turn depend on the anisotropy of a potential. The rotational constants are approximately 20, 5, and 2 cm−1 for the water, methane, and nitrogen molecules which correlates with quantum effects being the largest for water and smallest for Rg–N2. However, correlation with anisotropy is not so clear-cut. The water-water potential is certainly the most anisotropic of the potentials considered, so both factors contribute to the largest relative magnitude of quantum effects. However, the He–methane potential is presumably the least anisotropic, so the fact that quantum effects in this system are larger than in Rg–N2 suggests that the larger rotational constant of methane compared to nitrogen makes up for the torque effect. All of this can be checked by performing appropriate calculations at the TI level.
Jeremy Richardson asked: Can you also comment on the differences in the results obtained between a flexible and a rigid description of the water molecules?
Krzysztof Szalewicz responded: This subject is discussed in some detail in answer to the question from Professor van der Avoird above. The flexibility effect for the second virial coefficient at 300 K is 2% and it is 10% at 700 K, see also Fig. 3 in the paper (DOI: 10.1039/c8fd00092a). These findings are consistent with the fact that rigid-monomer classical simulations with accurate first-principles potentials for liquid water at ambient conditions agree reasonably well with experiments, see for example ref. 1 and 2. It is important to realize that the quality of rigid-monomer approximation depends to a large extent on the monomer geometry chosen. Jeziorska et al.3 have shown that the approximation works best if the monomer geometry averaged in the ground state vibration is used, rather than the commonly used equilibrium geometry. An even better choice is to use the potential averaged over the ground-state vibrational function.
One may add that while the size of monomer-flexibility effects found for the second virial coefficient correlates well with the analogous effect in liquid water, the same is not true for the quantum effects. While these are 25% and 250% for the second and third virial coefficients at 300 K, the quantum effects appear to be small for most properties of liquid water at ambient conditions. We discuss this issue in section 5 of our paper (DOI: 10.1039/c8fd00092a). We hypothesize that large quantum effects in virial coefficients may not affect bulk properties such as pressure since for the saturated vapor the virial coefficients reduce the pressure by only approximately 0.2% at 300 K.
1 R. Bukowski et al., J. Chem. Phys., 2008, 128, 094314.
2 O. Akin-Ojo and K. Szalewicz, J. Chem. Phys., 2013, 138, 024316.
3 M. Jeziorska et al., J. Chem. Phys., 2000, 113, 2957.
Anne McCoy said: You performed these calculations using several potential surfaces. As the expense of such calculations scale with the cost of each energy evaluation, I was wondering if you could comment on the relative expense of doing the calculations with these potential surfaces?
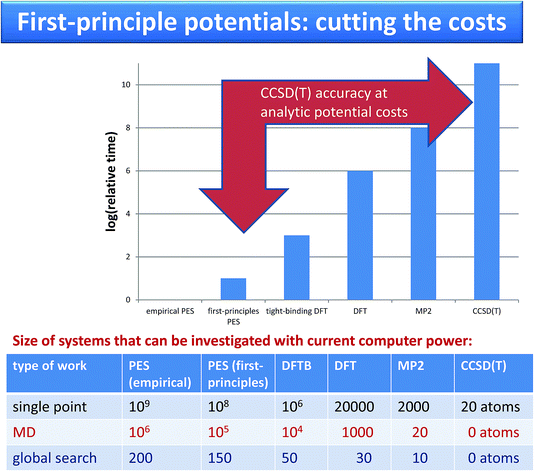
Krzysztof Szalewicz replied: Calculations with the potentials developed by our group require resources from a couple to about 100 times larger than calculations with empirical force fields such as OPLS. For large molecules, our potentials do not use off-atomic sites and similarly as empirical ones are sums of isotropic atom-atom functions. Consequently, the timings range from about the same (exactly the same if we use atom-atom functions as simple as in empirical potentials, but our functions are always at least a bit more complicated) to a few times longer for our potentials (for the most complicated functions). The timing ratio is the largest for very small monomers such as water since we aim then for very high accuracy of our potentials, 0.01 kcal/mol, and therefore use a large number of off-atomic sites. We can compare the popular TIP4P potential with a potential from our group used in the paper and called CCpol2.1 Both potentials are in the form of a sum of site-site pair functions, with the total number of sites equal to 4 in TIP4P and 25 (8 symmetry-distinct) in CCpol2. Each of our site-site pair functions takes a few times longer to compute than a TIP4P one. However, the main difference in timings comes from the number of sites as the costs are proportional to the square of this number, so the overall cost is about two orders of magnitude larger (an additional cost comes from the polarization term present in CCpol2 but not in TIP4P, but this cost is essentially the same as for polarizable empirical potentials). To put things into perspective, one should add that AIMD calculations with DFTB (DFT) are 3 (6) orders of magnitude more expensive than calculations with potentials such as CCpol2. AIMD calculations with CCSD(T) would be 11 orders of magnitude more expensive, and therefore are not doable at the present time. Thus, since our potentials are faithful representations of CCSD(T) energies, our approach amounts to 11 orders of magnitude speedup (see the Fig. 2).
1 U. Gora et al., J. Chem. Phys., 2014, 140, 194101.
David Clary asked: As we have seen, an important aspect of this Faraday Discussion is interaction between experiment and theory. As you emphasise, the virial coefficients are really important fundamental scientific quantities. But the existing experimental results you are comparing with seem to be 20–30 years old, with large error bars. Why is there a such a challenge in doing good experiments on these important quantities?
Krzysztof Szalewicz answered: First, for the second virial the experimental accuracy is quite good above approximately 400 K; for example, it is good enough to show that the small effect of monomer flexibility is necessary to obtain quantitative agreement with experiment (see Table 1 and Fig. 3, DOI: 10.1039/c8fd00092a). Experimental uncertainties grow quickly for third and higher virial coefficients, since they are higher order effects, each of which effectively requires extracting one higher order of derivative from the experimental data, making accurate theory for higher virial coefficients important.
Second, the experiments and their analysis are quite difficult for water (and mixtures containing water). At roughly 500 K and below, the adsorption of water molecules on the walls of the typical experimental apparatus is significant, requiring increasingly complicated corrections (and sometimes additional parallel experiments) in order to obtain meaningful virial coefficients. While excellent experimental determinations of virial coefficients have been made in recent years for many nonpolar gases, we know of nobody currently doing such work on aqueous systems. Another factor is that high-accuracy thermophysical property work is not a trendy topic in academia, so there is little funding for such measurements. Increasingly, only national metrology laboratories have the capability for such work, and much of their effort is focused on gases like helium, argon, and nitrogen which find more uses in metrology.
Joel Bowman asked: Does the latest version of your paper contain second and third virial coefficients of H20 using the flexible WHBB potential? If not, could you comment on those results?
Krzysztof Szalewicz replied: See the note added in proof in our paper, DOI: 10.1039/c8fd00092a.
Ad van der Avoird opened a general discussion of the paper by Claudine Crépin: The (partial) conversion of para-H2 into ortho-H2 that you saw in your spectra must also occur in the pure solid. This is known, I suppose, isn’t it? Is the conversion time of several days that you observed similar to what was observed for the pure para H2 solid?
Claudine Crépin replied: The process of intrinsic conversion (from ortho to para hydrogen) in the solid is a second order process. Its rate is estimated to 1.90%/h.1 The NSC rates that we measured have the same order of magnitude. It was therefore important to make sure that the NSC process at play in AcAc/pH2 samples was occurring within AcAc and not simply the oH2→pH2 conversion. The oH2→pH2 conversion is very sensitive to the presence of impurities. Hence, we have checked that the oH2→pH2 process is still very long in our doped samples by analyzing samples with enough oH2 to be able to monitor its amount as a function of time (only rough estimations were performed and kinetics were not studied by themselves).
1 I. F. Silvera, Rev. Mod. Phys., 1980, 52, 393–452.
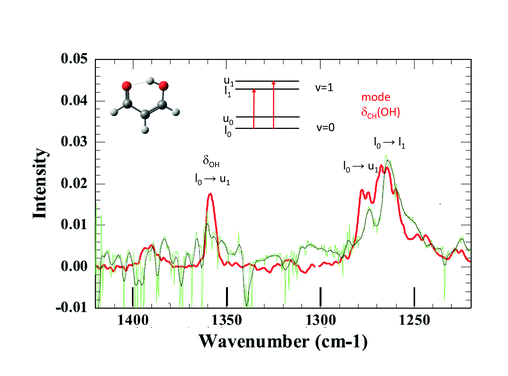
Joel Bowman said: Very interesting work. I read in your paper that you considered producing malonaldehyde in the H2 matrix. Have you made any progress on that?
Claudine Crépin answered: Thank you. Effectively, we have performed first attempts to isolate MA (malonaldehyde) in pH2, but our samples were contaminated by impurities and the observation windows of the recorded spectra were severely limited by the impurity absorption bands. However, I can show you the first results.
The tunnelling splitting of ground state free MA is quite large (21.6 cm−1)1 and at 3K in pH2, only the lowest energy level of the tunnelling doublets is significantly populated assuming a weak perturbation of this tunnelling splitting in the matrix. The infrared selection rules force indeed a much stronger transition moment toward one level of the vibrationally excited state than to the other.2 Hence, only a few vibrational bands are expected to appear as doublets in IR spectra. When looking at the IR spectrum of MA in jet experiments, there are only two clearly observed doublets assigned to transitions from the same lowest level of the ground state, one around 1660 cm−1 and the other around 1270 cm−1.3 Unfortunately, the first one lies in the range of water absorption and cannot be documented in our pH2 spectrum. This is not the case with the second spectral range where we observe two broad bands at 1264 cm−1 and 1274 cm−1 (see Fig. 3). They could correspond to the bands detected at 1267 cm−1 and 1276 cm−1 in the jet experiments, with similar relative intensities. These bands are assigned in the jet experiment to transitions toward the two tunnelling levels of the CH in-plane bending mode of the hydrogen in the OH side (see Fig. 3).3,4 Better spectra are needed for a final conclusion, but it seems that the H tunnelling occurs and is weakly perturbed by the pH2 environment.
1 T. Baba et al., J. Chem. Phys., 1999, 110, 4131.
2 J. Seliskar and R. E. Hoffmann, J. Mol. Spectrosc., 1982, 155, 146.
3 N. O. B. Lüttschwager et al., Mol. Phys., 2013, 111, 2211.
4 N. O. B. Lüttschwager et al., Phys. Chem. Chem. Phys., 2010, 12, 8201.
Jun Miyazaki said: As the reason of the increasing of “E” and “A” state splitting, the authors suggested several oH2 molecules complexed with AcAcH8 written in lines 47–50, page 7. Do you have the evidence of those complexes formed? I wonder how many oH2 molecules in pH2 are influenced to the “E” and “A” state splitting of AcAcH8.
Claudine Crépin replied: We assumed that oH2 molecules influence the “E”–“A” splitting as a working hypothesis to interpret the observed spectrum in H2 (22% oH2) and its time evolution. In our opinion, it is no more than a hypothesis that has no direct confirmation. Recent simulations by means of classical molecular dynamics indicate that AcAc should take the place of 5 or 6 Ar atoms in an argon matrix.1 Since the distance between nearest neighbors in the Ar lattice is close to that in the pH2 one, one can assume that AcAc takes the place of 5 or 6 hydrogen molecules in solid H2. In these conditions, the guest molecule has more than 20 H2 as nearest neighbors. In solid H2 samples with 22% oH2, AcAc has statistically much more than only one oH2 (more than 4) as nearest neighbors to form a kind of weakly bound complex.
1 G. Rojas-Lorenzo, M. Lara-Moreno, A. Gutiérrez-Quintanilla, M. Chevalier and C. Crépin, Low Temp. Phys., in press.
Karel Kouril said: What can be said about the kinetics of the E to A conversion? Is it just a single-exponential or do your data indicate a more complicated process? Experiments on ortho–para conversion in water endofullerene H2O@C60 indicate second-order kinetics in this system (see ref. 1).
1 S. Mamone et al., J. Chem. Phys., 2014, 140, 194306.
Claudine Crépin responded: It is an interesting point that we have not fully explored. We have not indeed enough data to extract reliable kinetics. The rates mentioned in the paper are obtained when a single-exponential decay is assumed. This single exponential behavior reproduces very well the data recorded during the first day, as reported in our previous work (ref. 11 in our paper). However, a more complex situation is apparently revealed by our recent experiments where the sample is kept in the cryostat for 5 to 7 days. For instance, the data extracted from Fig. 5 in our paper (DOI: 10.1039/c8fd00080h) can be fitted by a bi-exponential decay with constants differing by one order of magnitude (0.087/h and 0.009/h). Anyway, these long kinetics depend on the quality of the samples. Another important point is that the limit at infinite time deduced from exponential decay fits, which should give the “E”/“A” ratio at thermal equilibrium at 3 K, seems unrealistic: the extrapolated limit suggests an energy gap ∼7 cm−1 between the “E” and “A” states, i.e. a value which is higher than the energy gap between the corresponding states in the free methyl rotor in the gas phase. In short, yes, our data suggest complex kinetics.
Karel Kouril said: Is it possible to observe the “backward” spin isomer conversion from A to E states that should occur at elevated temperatures?
Claudine Crépin responded: We deduced from our data quite a large energy gap between “E” and “A” states, larger than 7 K (5 cm−1). The observation of the “backward” conversion would need to keep the sample at “high” temperatures during a very long time, which is impossible with hydrogen samples. The matrix evaporates at 6 K and totally disappears in a few hours at 5 K in our experimental conditions.
Karel Kouril commented: An inelastic neutron scattering experiment (if feasible) should give the A–E splittings in your systems. Such information would be useful for analysis of the spin isomer conversion kinetics data you have.
Claudine Crépin answered: Indeed, we would like to get a reliable “A”–”E” splitting. It would indicate the asymptote of the recorded kinetics. Inelastic neutron scattering experiments were performed on solid acetylacetone1 giving the tunnelling splitting in the two non-equivalent methyl groups, and highlighting a deuteration effect on the tunnelling in the comparison between AcAcH8 and AcAcD2. The splitting values are of course far from those expected in the gas phase or in pH2 matrices.
1 M. R. Johnson et al., J. Chem. Phys., 2002, 116, 5694.
Anne McCoy said: Can you provide us with a sense of how strongly the H2 matrix environment is perturbing the methyl rotors, and in particular how it is affecting the tunneling splittings.
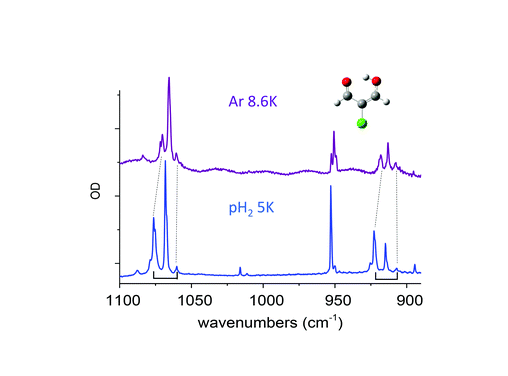
Claudine Crépin responded: Previous studies on molecules with methyl groups embedded in parahydrogen matrices, performed by Y.P. Lee and his coworkers, have addressed this important question. One concerns CH3F, with spectroscopic signatures of the methyl rotation in pH2:1 the authors estimate an energy gap of 5.5 ± 1.5 cm−1 between the K = 0 and K = 1 levels in pH2 whereas it is 6.0 cm−1 in the gas phase. Another concerns methanol, which involves a tunneling splitting between A and E species:2 the authors obtained E–A gaps for different vibrational bands very similar to those in the gas phase for most of the modes, but the splitting in the ground state was not estimated. We would like to go further in this domain by investigating a variety of molecules containing methyl rotors in the near future. I would like to add a comment related to the question of environment effects on the tunnelling splitting. In the paper (DOI: 10.1039/c8fd00080h), we described the tunnelling splitting of vibrational transitions of MACl (2-chloromalonaldehyde) trapped in pH2, with a clear detection in the spectral range shown in Fig. 7 of our paper, (DOI: 10.1039/c8fd00080h). This splitting comes from the H tunnelling in the intramolecular H-bond of MACl. We performed experiments in various cryogenic matrices and the H tunnelling splitting was detected in pH2 and Ar, providing a comparison between these two kinds of environments. Very recent results in pH2 at different temperatures had clarified the structures involving this H tunnelling. Fig. 4 below reports the IR spectrum of MACl when this molecule is isolated in pH2 at 5 K (bottom) and Ar at 8.6 K (top). The spectral range of Fig. 4 is the same as that of Fig. 7 of our paper (DOI: 10.1039/c8fd00080h) which reported the data at 2.8 K in pH2. The doublets of Fig. 7 at 2.8 K in pH2 become triplets at 5K: the third components, of lowest energies (at 1060.2 and 907 cm−1 in Fig. 4), are assigned to the infrared transitions originated from the upper level of the tunneling splitting in the ground state which is significantly populated at 5 K. Only the transitions coming from the lower level were detected in the spectrum at 2.8 K (at 1076.4 and 922.5 cm−1 in Fig. 4). The middle components (at 1068.1 and 914.7 cm−1) of these two clear “triplets” are thus assigned to the vibrational bands of the MACl–oH2 complex, following the results reported in the paper: the presence of orthohydrogen quenches the tunnelling process. The results in pH2 suggest the following assignment of the triplets in Ar: components of lowest energy assigned to transitions from the upper level of the tunnelling splitting in the ground state, components of highest energy assigned to transitions from the lower level of the tunnelling splitting in the ground state (the correspondences between these components in pH2 and Ar are underlined by dotted lines in Fig. 4), and the middle components assigned to transitions of MACl trapped in Ar sites where the tunnelling process is quenched. These results show a decrease of the tunnelling splitting from pH2 to Ar. The gap between the two components decreases from ∼16 cm−1 in pH2 to ∼10 cm−1 in Ar, reflecting a decrease of the tunneling splitting in v = 0 and v = 1 of the two vibrational modes which are discussed. The results in Ar also indicate how sensitive to the environment (to the matrix site in this case) is the tunnelling process. The complete results in pH2 will be the subject of a forthcoming work.
1 Y.-P. Lee et al., J. Chem. Phys., 2008, 129, 104502.
2 Y.-P. Lee et al., Science, 2006, 311, 365.
Zlatko Bacic commented: Among the rare-gas matrices that you were planning to use in your experiments, one was conspicuously absent — Helium matrix. He matrices have many unique properties; they are ultra cold, exceptionally “gentle”, i.e., interact very weakly with guest molecules and, because of the large zero-point energy of helium, they are highly homogeneous. Do you intend to utilize them at some point?
Claudine Crépin answered: Setups, which allows one isolating molecules in a helium environment, usually follow the HElium NanoDroplet Isolation technique. Our setup is not adapted at all for such experiments. However, you are right, a Helium environment has the unique properties you mentioned. They are approached in a certain extent by parahydrogen matrices. Our colleague, a coauthor of the paper, Jean-Michel Mestdagh has recently built with his group an experiment devoted to photophysics and photochemistry in helium droplets at LIDYL (Saclay, France). We intend to do a joint experiment with the two setups and investigate similar questions in parahydrogen matrices and helium droplets. We are presently working on molecules which carry methyl groups, looking at the effects of these soft environments on molecular rotation. Unfortunately, the laser which is available on the helium setup covers the spectral range 3000–4000 cm−1 only and does not allow us to address questions that we just raised on acetylacetone and malonaldehyde derivatives.
Ingo Fischer opened a general discussion of the papers by Claudine Crépin: I have a few rather basic questions concerning spectroscopy in para-hydrogen matrices. When you add ortho-hydrogen to the matrix, the bands (cf. Fig. 3 in your paper, DOI: 10.1039/c8fd00080h) broaden. Can you explain why the bands are sharp in a pure para-hydrogen matrix, but not when ortho-hydrogen is added?
Claudine Crépin replied: Cold parahydrogen is in the J = 0 rotational level and thus, it carries no electrostatic multipole moment. This limits a lot the possible interactions with the guest molecule. Cold orthohydrogen is in the J = 1 rotational state and has a non-zero rotationally averaged quadrupole moment. It can therefore interact via long-range intermolecular forces with the guest molecule and build complexes with it. The consequence is that the spectroscopic bands of the guest molecule are shifted when the latter forms complexes with oH2. The bands are then inhomogeneously broadened in solid hydrogen containing oH2 in small amounts. The observed spectra include the signatures of the guest in pure pH2 superimposed to signatures of the guest complexes with one or more oH2 molecules.
Ingo Fischer asked: So what would happen if you used a pure ortho-hydrogen matrix for molecular spectroscopy?
Claudine Crépin answered: In fact, we did not want to use pure ortho-hydrogen. First, a pure ortho-hydrogen matrix is much more difficult to obtain than a pure para-hydrogen matrix, since para-hydrogen is the thermodynamically stable species. Second, we use para-hydrogen to avoid “strong” host–guest interactions which can modify the guest properties. It is much easier to use a nitrogen matrix, for example, to play with an environment that has similar effects to ortho on the guest molecule.
Jeremy Richardson remarked: Can you highlight the advantages and disadvantages of studying molecules trapped in p-H2 as opposed to in the gas phase?
Claudine Crépin answered: The advantages of studying molecules trapped in p-H2 are first those common with the matrix isolation technique: 1. a large amount of molecules are concentrated in a small volume, which does not move. This contrasts with the diluted samples in gas cells or beam experiments; 2. molecules are isolated at a low and well-defined temperature. This can be useful to clarify the spectroscopy or to study specific dynamical processes. The specificity of p-H2 comes from its “quantum nature” due to a large zero point motion (close to 20% of the nearest neighbor distance) and its rotational level J = 0 (see previous reply). It allows very weak interactions with the guest molecule. As a result, almost no site effects and cage effects are observed. It thus provides an ideal tool to investigate the molecular properties at cryogenic temperatures. More details are given in ref. 1–5 of our paper (DOI 10.1039/c8fd00080h), and references therein. Nevertheless the host-guest interactions are non-rigorously zero and weak environment effects can occur (it’s actually what we want to study).
Halima Mouhib commented: The coupling between the proton tunneling and internal rotation motion in acetyl acetone is a very challenging problem in molecular physics. It has been addressed by Caminati et al.1 using molecular beam Fourier transform microwave spectroscopy (MB-FTMW), which is the method of choice to accurately quantify barrier heights of isolated molecules. However, due to the extremely low barrier of internal rotation, which causes very large splittings of the rotational transitions, as well as its coupling with the proton tunneling motion, only the A species transitions could be assigned so far. What is the estimated barrier height of acetyl acetone using quantum chemical calculations? Did you try different levels of theory to obtain a theoretical estimation of the barrier height?
1 W. Caminati, J.-U. Grabow, J. Am. Chem. Soc., 2006, 128, 854–857.
Claudine Crépin replied: We performed these estimations at two levels of theory. A rotational barrier of 32 cm−1 was obtained in DFT B3LYP/6-311++G(3df,3pd) calculations and 77 cm−1 at the MP2/6-311++G(3df,3pd) level of theory for the methyl group on the C=O side (411 and 466 cm−1 for the other methyl group at the two levels of theory, respectively) – see ref. 11 in our paper (DOI: 10.1039/c8fd00080h). Values of 87 cm−1 and 507 cm−1 were obtained at the MP2(FC)/6-311G(d,p) level of theory for the two methyl torsions in ref. 1.
1 Matanovic et al., Chem. Phys., 2004, 306, 201.
Halima Mouhib said: The accurate determination of barrier heights for the internal rotation motion of methyl groups using theoretical methods is still very inaccurate. This is a problem for the rational assignment of microwave spectra, as for low barriers (i.e., <100 cm−1) changes of only 1 cm−1 can already have a tremendous effect on the dimension of the predicted line splittings. In the case of 5-methyl furfural, where experimental values of 352.196(19) cm−1 and 358.777(51) cm−1 were determined for the two existing conformers using MB-FTMW, the theoretical values of the barrier heights (including and excluding dispersion corrections) ranged from 230 to 330 cm−1.1 The error is usually even higher for lower barriers. So, at the moment, chemical intuition and careful comparison of available systems is still inevitable to guide the experimental evaluation of a new molecule. Completely understanding the internal dynamics of acetyl acetone in future may be a breakthrough and this molecule is a great system for theoretical benchmarks.
1 R. Hakiri, N. Derbel, H.V.L. Nguyen and H. Mouhib, Phys. Chem. Chem. Phys., 2018, 20, 25577–25582.
Zlatko Bacic opened a general discussion of the papers by Anne McCoy, Krzysztof Szalewicz and Claudine Crépin: This is a general comment regarding the relationship of clusters to the bulk condensed phase. Clusters in general, and in particular neutral and protonated water clusters, are viewed as the bridge between isolated molecules and the condensed phase. It is true that because or their small size and relative simplicity, in comparison with liquid water, water clusters allow the implementation of theoretical methods for electronic structure and spectroscopic calculations at the level and with the accuracy that would not be feasible for the liquid. Moreover, the complexity can be increased gradually, with increasing cluster size. On the other hand, the clusters are formed, and studied, at temperatures far below that of liquid water. Therefore, the molecules comprising the cluster probe a range of geometries, as well as the amplitudes of the vibrations and their couplings, that have to be much smaller than those sampled by the molecules in the liquid. Consequently, while I believe that studying clusters is most valuable and essential, there must be many features of the spectroscopy and dynamics of the liquid that are not fully captured by small clusters at very low temperatures.
Anne McCoy answered: Over the years, my thinking on the idea of clusters as a “bridge” between isolated molecules and condensed phase systems has evolved. Indeed, as Prof. Bacic mentions, there are many differences between water clusters and liquid water. Specifically, the temperature, local structure and surface to volume ratios can change dramatically as the size of the system is increased. On the other hand, we have found that we can use clusters as a platform to study phenomena in the liquid phase. Examples from our recent and on-going research include:
A study of the response of the frequency of the OH/D stretch involved in an ionic hydrogen bond to the solvent environment (e.g. the solvochromatic shift). This was achieved by spectroscopic studies of tagged H+(H2O)4 clusters, complexed with either a chemically inert molecule (D2, N2 or CO) or additional water molecules. In this combined spectroscopic/computational study,1 we were able to map the evolution of spectral features to the increased delocalization of the shared proton in this interaction.
A study in which we explored the origin of a peak in tri-solvated H3O+ that appeared roughly 600 cm-1 to the blue of the bend fundamental, and the intensity relative to the bend fundamental increased with increased binding energy of the solvent molecules. The work focused on argon atoms, N2, CH4 and water molecules. Through an analysis of the spectrum, we found that the intensity came from combination bands involving the HOH bends and hindered rotation of the H3O+ in the solvent shell, and reflected higher order terms in the expansion of the dipole surface.2 These terms led to a decrease in the transition moment for the HOH bend when it is in a hydrogen bonding environment. The act of rotation within the solvent shell weakened the hydrogen bonding and led to an increase in this transition moment. In subsequent work, we showed that a similar effect can be found in neutral water clusters, and can be used to explain the absorbance in the spectrum of liquid water near 2100 cm−1.3
An on-going study in collaboration with Sotiris Xantheas and Thomas Markland’s group, in which we are exploring the origins of the correlations between OH bond lengths and vibrational frequencies and again the insights into these relationships translate from the cluster studies to condensed phase environments. In all of these examples, the clusters are viewed less as a “bridge” to the condensed phase as a controlled experimental environment within which we can probe interactions that occur in both these small cluster systems and in bulk water.
1 C. T. Wolke, J. A. Fournier, L. C. Dzugan, M. R. Fagiani, T. T. Odbadrakh, H. Knorke, K. D. Jordan, A. B. McCoy, K. R. Asmis, M. A. Johnson, Science, 2016, 354, 1131–1135.
2 A. B. McCoy, J. Phys. Chem. B, 2014, 118, 8286–8294.
3 A. B. McCoy, T. L. Guasco, C. M. Leavitt, S. G. Olesen, M. A. Johnson, Phys. Chem. Chem. Phys., 2012, 14, 7205–7214.
Joel Bowman replied: This is a good question. Depending on the system, for example liquid water, the IR spectrum is captured quite well by using “snapshots” of say an MD simulation and performing quantum calculations of each monomer or just doing classical simulations of the IR spectrum. These do bear a close relationship to the IR spectra of water clusters and their isomers. In the case of the excess proton in liquid water, the situation is more complex as proton transfer can occur at room temp whereas this is very unlikely to be seen in low temp studies of protonated water clusters. Nevertheless, there appears to be spectral signatures of either the so-called Zundel or Eigen motif in liquid 2D IR experiments. These motifs are clearly seen in low temperature protonated water clusters. The situation is still in flux and probably more theoretical work is needed.
Joel Bowman remarked: 2D IR experiments on the excess proton in liquid water are attempting to assess the relative importance of the so-called Eigen and Zundel motifs of the hydrated proton. This isn’t easy because while these motifs are clear (at least now after some controversy about the spectral signatures) in the cold size-selected clusters the signatures are blurred in the liquid at room temperature. Nevertheless, the cold cluster work, both theory and experiment have had a major impact in the interpretation of the liquid work.
Anne McCoy commented: Following up on Joel’s comment, in some of their recent work, the Tokmakoff group at Chicago has used the frequencies of the shared proton stretch and the HOH bending vibrations obtained from these types of cluster studies to provide the frequencies that they are using to identify the Eigen and Zundel forms of hydrated protons.
Joel Bowman replied: Yes, I agree completely. In fact, we (Qi Yu and myself) are collaborating with the Tokmakoff group to analyze their liquid 2d IR spectra. I should also mention the group of Pines and Elsaesser and co-workers doing similar experiments.
Zlatko Bacic commented: I am somewhat puzzled that certain features in the IR spectra of water can be interpreted with the help of the spectrum of H7O3+. The hydrogen-bonding network in water is extended and dynamic, constantly breaking up and rearranging, and it is not clear to me that a discrete entity such as H7O3+ can be recognized in it, or be helpful for confidently interpreting spectral features of the liquid.
Joel Bowman noted: Liquid simulations using classical mechanics and model empirical potentials such as TIP4P can be used to create “snapshots” that can be used in the quantum calculations of the IR spectrum of liquid water. This worked out very well by us using trajectories generated by Skinner’s group and then by us using the Local Monomer model. The agreement with experiment was very good both for H2O(l) and D2O(l). These spectra are quite broad and while a challenge to get theoretically it seems clear by now that they don’t provide details about the underlying H-bond dynamics.
Martin Dracinsky opened a generalal discussion on the paper by Karel Kouřil: In your paper, you propose two possible mechanisms of water alignment in the C60 cages: direct interaction of water molecules with the alignment medium or change of the shape of the C60 molecules. Could there be another possible mechanism based on interaction of dipole moments of water molecules in neighbouring cages?
Karel Kouřil responded: Such mechanism is unlikely in the H2O@C60 dissolved in the MBBA liquid crystal. The concentration of H2O@C60 was approximately 2–3 micromolar in our samples. This corresponds to typical cage–cage (or water–water) distance of several hundred nm – too far for the water–water dipole–dipole interactions to play a role in the alignment. Furthermore the residual couplings observed in the NMR spectra of the endohedral water follow the same temperature dependence as the order parameter of the liquid crystal solvent. The electric dipole–dipole interaction would be more relevant in solid endofullerenes where the distance between the nearest neighbour endohedral molecules is below 1 nm. At low enough temperatures it could even give rise to ordering of the dipoles. However, I am not aware of any direct observation of either the interaction or the ordering. An interaction between nearest-neighbour water molecules in solid H2O@C60 was observed indirectly: kinetics of the ortho–para conversion is second order which implies that the neighbouring water molecules do interact.1
1 S. Mamone et al., J. Chem. Phys., 2014, 140, 194306.
Peter Felker said: Do you have a picture of the sample by any chance: What the liquid crystal molecules look like and how the C60 sits in there?
Karel Kouril answered: A sketch of the MBBA molecule is in the Fig. 5 below.
1 R. S. Ruoff et al., J. Phys. Chem., 1993, 97, 3379–3383.
2 M. L. Magnuson et al., Liquid Crystals, 1995, 19, 823–832.
Anne McCoy opened a general discussion of the paper by David Benoit: One thing I found interesting, was when a rigid cage was used the three translation and three rotational levels each split into a pair of degenerate states and a non-degenerate state, while, when the relaxed cage was used, the degeneracy was broken. The latter case is consistent with the measured splittings. Can you use the results of the DMC simulations to get a sense of how the cage is responding to the presence of the H2?
David Benoit answered: Yes, it is tempting to correlate the near-degeneracy lifting, and thus better qualitative agreement with experiment, with the quantum delocalisation of the cage. However, the geometry of the static cage is not unique and as shown by Bacic and collaborators1 and the hydrogen bond network can easily reorganise to create similar but different geometries, all compatible with the overall clathrate structure. In our rigid-cage model, we used one frozen geometry (the same as taken in our previous paper) and thus the degeneracy could be the fortuitous result of the presence of minor symmetry elements. Those minor symmetry elements are then likely to be destroyed during the DMC simulation thus lifting the accidental degeneracy. To answer the second point, by examining the hydrogen density distribution shown in Fig. 2 of our paper, we see water molecules displaying a typical delocalisation pattern observed in previous studies of smaller water clusters. These patterns are consistent with water molecules preferentially interacting amongst themselves through hydrogen bonds rather than the host molecule. At a qualitative level, the delocalisation pattern appears to be quite isotropic and could explain the lifting of degeneracy. This is also in line with the degeneracy lifting shown in ref. 1.
1 A. Powers et al., J. Phys. Chem. Lett., 2016, 7, 308.
Zlatko Bacic responded: The threefold degeneracy of the J = 1 level of H2 is completely lifted already for the rigid cage, both in the paper discussed, by Benoit et al., and in our earlier papers on H2 in the small hydrate cage.1 As for the translational fundamental, the degree to which its threefold degeneracy is broken or not in the rigid cage actually varies with the H2–H2O pair potential used in the calculations. It is broken when an ab initio pair potential is employed.2
1 M. Xu et al., J. Chem. Phys., 2008, 128, 244715.
2 A. Powers et al., J. Chem. Phys., 2018, 148, 144304.
Joel Bowman commented: Very nice work. We were inspired by the work from Bacic, you and others into looking at H2 hydrate clathrate, suggesting three body interactions might be significant. We published ab initio potentials a couple of years ago for 2 and 3-body interactions of H2 with H2O (ref. 1) and noted a significant 3-b effect on the harmonic vibrational frequency of H2. We are writing up calculations using unbiased diffusion Monte Carlo calculations of the H2 frequency shift using the 2-b and the 2-b + 3-b interactions with a rigid water cage. The take-home message is the 3-body is significant and increases the magnitude of downshift by roughly 10 wavenumbers.
1 Z. Homayoon, R. Conte, C. Qu and J. M. Bowman, J. Chem. Phys., 2015, 143, 084302.
Jeremy Richardson remarked: In the Born–Oppenheimer approximation we say that electrons are fast and can therefore be adiabatically decoupled from the motions of the electrons from the slow nuclei. However, in your case, the adiabatic approximation is the other way around as you are averaging over the slow dynamics of the cage from the fast dynamics of the H2. Can you comment on the validity of this approximation?
David Benoit replied: It is true that our “adiabatic” separation is different from a traditional “fast motion–slow motion” separation (i.e. classical Born–Oppenheimer). However, for our system the coupling between the water rotational motion and the H2 translational and vibrational motion is expected to be small. Thus our approximation is likely to be valid (see answer to Anne McCoy’s question below). Zlatko Bacic’s question below also also elaborates more on this type of approach.
Zlatko Bacic addressed David Benoit and Jeremy Richardson: The use of the adiabatic, Born–Oppenheimer (BO) approximation in situations where there is no clear-cut, order(s)-of-magnitude frequency separation between the types of motions considered has a long history. For example, the early calculations of the bound states of atom-diatom van der Waals complexes invoked the BO separation between the intermolecular radial motion (taken to be slow) and large-amplitude angular motion (taken to be fast) of the complex, although their respective frequencies are not too dissimilar. See, for example, ref. 1 and 2.
1 S. L. Holmgren et al., J. Chem. Phys., 1977, 67, 4414.
2 J. M. Hutson and B. J. Howard, Mol. Phys., 1980, 41, 1123.
David Benoit replied: Coupling strength between the two types of motion ultimately validates (or invalidates) this type of approach, very similarly to what is used in electronic structure theory.
Joel Bowman responded: Adiabatically separating rotation from vibration does seem counterintuitive but it can work very well. We developed this in some detail for both scattering and vibrational applications and termed it the Adiabatic Rotation Model. It works very well, provided there isn’t strong vibration/rotation coupling, which generally there isn’t owing to the large time-scale differences between those motions.
Anne McCoy addressed Zlatko Bacic and David Benoit: If I am reading the results in Table 3 (DOI: 10.1039/c8fd00087e) correctly, the difference between the full RB-DMC and Smolyak approaches is less than 1 cm−1, which helps justify the separation of the H2 rotations and translations from the intermolecular motions of the water molecules that form a cage.
Zlatko Bacic answered: No, the RB-DMC and Smolyak calculations that Prof. McCoy refers to were both performed for the rigid clathrate cage. Therefore, neither can say anything about the validity of treating the translation-rotation (TR) motions of the guest H2 as separable from the motions of the framework water molecules. As stated in the first sentence of Section III (DOI: 10.1039/c8fd00087e), their purpose was to simply validate the accuracy of the RB-DMC approach. The fact that the TR ground-state energies of the encapsulated H2 from the two types of calculations agree to within 0.3–0.5 cm−1 testifies to the satisfactory accuracy of the RB-DMC approach for this system.
It is the results in Table 4 (DOI: 10.1039/c8fd00087e), in particular those in the last column (ΔRotating-Rigid, that shed some light on the degree of coupling between the rotational motions of the cage water molecules (with their centers of mass fixed) and the TR motions of the guest H2. From them, it is evident that the inclusion of the quantum rotations of the water molecules changes the splitting of the translational fundamental by about 10% (relative to that for the rigid cage), while the impact on the splitting of the J = 1 triplet is more pronounced.
David Benoit answered: The results reported in Table 3 (DOI: 10.1039/c8fd00087e) show the difference between RB-DMC and the Smolyak approach using a fixed cage. This was done to demonstrate the accuracy/agreement of both approaches for the zero-point energy (ZPE). A better test of adiabaticity is shown in the attached Table 1, where we used a larger replica population (6000 replicas) and a long propagation time (120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles) to obtain ZPE calculations and adiabatic PES with an average accuracy of ±7 cm−1. We observe that the difference between the fully coupled ZPE obtained through RB-DMC and the ZPE computed using an adiabatic Smolyak approach is 100 cm−1 (0.5 % of the ZPE, or about 5 cm−1 per water molecule). While the absolute difference is noticeable, in relative terms it is within the expected uncertainty of the RB-DMC approach for such large system.
000 cycles) to obtain ZPE calculations and adiabatic PES with an average accuracy of ±7 cm−1. We observe that the difference between the fully coupled ZPE obtained through RB-DMC and the ZPE computed using an adiabatic Smolyak approach is 100 cm−1 (0.5 % of the ZPE, or about 5 cm−1 per water molecule). While the absolute difference is noticeable, in relative terms it is within the expected uncertainty of the RB-DMC approach for such large system.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles with Δτ = 30 a.u. and averaging phase of 120
000 cycles with Δτ = 30 a.u. and averaging phase of 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 × 100 cycles with Δτ = 15 a.u.
000 × 100 cycles with Δτ = 15 a.u.
| Energy (cm−1) | Difference (RB-DMC–Smolyak) | |
|---|---|---|
| Minimum energy | −136228.5 | |
| E0Smolyak | −115698.7 | |
| E0RB–DMC | −115599 ± 7 | 100 ± 7 cm−1 or 0.09% |
| ZPERB–Smolyak | 20529.8 | |
| ZPERB–DMC | 20629.5 ± 7 | 100 ± 7 cm−1 or 0.48% |
David Benoit added: Given that Z. Bacic and his group have done extensive analysis of translation-rotation levels on a number of similar systems, he might be able to comment better on the nature of the mixing between translation and rotation in this case.
Zlatko Bacic answered: That the translational and rotational motions of H2 in the clathrate hydrate cage are coupled is evident from the calculated translation-rotation (TR) eigenstates.1 For example, the energies of TR levels with quanta of excitation in both translation and rotation are not simply the sum of (separate) translational and rotational excitations which they would be if the two were uncoupled. Nevertheless, the manifestations of TR coupling in hydrogen clathrate hydrates are not as pronounced as in the case of H2 inside C60, where the angular momentum coupling gives rise to very characteristic splitting patterns.2
1 M. Xu et al., J. Chem. Phys., 2008, 128, 244715.
2 M. Xu et al., J. Chem. Phys., 2008, 128, 011101.
Gilberte Chambaud opened a general discussion of the paper by Zlatko Bacic: You obtain very nice agreement for the splittings of the ro-vibrational levels of the molecules captured inside the C60 molecule. Could you clearly and unambiguously identify the more relevant and significant quantities which explain these good results?
Zlatko Bacic replied: Our studies have unambiguously established that the electrostatic, quadrupolar interaction between the guest molecule inside the central C60 and the 12 nearest-neighbor C60 cages of the solid is the main source of the symmetry breaking at low temperatures. This is supported by the fact that the J = 1 splittings (measured or calculated) scale linearly with the magnitude of the quadrupole moments of the endohedral molecules.
ChunMei Liu remarked: I would like to add a comment on not only breaking but also restoring the symmetry of the electronic structure of a small molecule by means of laser pulses: Prof. Dr. Bačić and his partners have shown that the electrostatic field of host molecules can break the symmetry of small guest molecules (DOI: 10.1039/c8fd00082d). It is well known that the electric fields of laser pulses can also break molecular symmetry, see for example ref. 1–5. Recently we have discovered a new quantum effect in atoms and small molecules, i.e. after breaking the symmetry of the electronic structure by a first laser pulse, the symmetry can be restored by a properly designed second laser pulse.6,7 Specifically, the method of ref. 6 applies one or two superimposed weak circularly polarized laser pulses with Gaussian shapes centered at time tb<0 to break the symmetry of the electronic structures of the oriented benzene molecule (D6h), or of the 87Rb atom in their ground states. Initially, (t = ti<tb) the systems are in the ground state ψg. Symmetry breaking is achieved by generating a superposition ψ(t) = cg(t)ψg + ce(t)ψe of ψg and an excited state ψe, with energies Eg and Ee, and with different irreducible representations, IRREPg ≠ IRREPe, respectively (e.g. A1g ≠ E1u in the case of benzene). Symmetry is restored by a second laser pulse that is designed as a copy of the first pulse centered at time tr = −tb. At the central time tc = (tb + tr)/2 between the pulses, the systems are in quasi field-free environment such that the coefficients evolve as cg(t) = Cgexp(i ηg − i Eg t/ħ) and ce(t) = Ceexp(i ηe − i Ee t/ħ) with real valued amplitudes Cg, Ce and phases ηg, ηe. This superposition state is non-stationary; it represents charge migration, or charge circulation (see e.g. ref. 8–14) with period T = h/(Ee − Eg) and with broken symmetry (e.g. D6h→Cs in the case of benzene). Successful symmetry restoration (e.g. Cs→D6h) depends on the phase difference Δη(t) = ηe − ηg − (Ee − Eg) t/ħ at time tc.6 For example, if the time delay td = tr − tb between the pulses is chosen such that Δη(tc) mod 2π = {0, ±2π}, then the second pulse de-excites the system finally (tf = − ti) back to the ground state, thus restoring its symmetry. For electronic processes, this phase condition must be satisfied with the precision of few attoseconds (as). This requirement is a formidable challenge to experiment. The experimental feasibility was demonstrated by means of high-contrast time-dependent Ramsey interferometry,15 with application to the 87Rb atom.6
Here we present a new scenario of breaking and restoring the symmetry of the electronic structure of a small molecule by means of two laser pulses, again with application to the oriented benzene molecule, using the model of ref. 16, as in ref. 6, 7 and 17. The results are illustrated in Fig. 6. The first laser pulse is an intense circularly right polarized π/2 pulse with Gaussian shape (panel 1a) that transfers 50% population from the ground state (IRREPg = A1g) to the excited state (IRREPe = E1u), thus Pe(tc) = Pg(tc) = 0.5 (panel 1b). For the new scenario, we redefine tr = −tb + T/2. If the second pulse (panel 1a) is fired at tr′ = tr + t′, then the population of the excited state at the final time tf′ = tf + T/2 + t′ is 7 Pe(tf′) = 2 Pg(tc) Pe(tc) [1+cos(2πt′/T)] = [1+cos(2πt′/T)]/2 where tc = (tb + tr)/2 see panels (1b) and (1c). For t′ = 0, T, 2T etc., we have Pe(tf′) = 1, i.e. the molecule is in the excited state with IRREPe (e.g. E1u for benzene), without any contamination of the ground state (panel 1c). These events coincide with special values of the phase difference, Δη(tc′) mod 2π = ±π/2, where t′c = (tb + t′r)/2 different from the previous case of symmetry restoration in the electronic ground state6,7 (compare panels (1b),(1c),(1d)). The preparation of the finally excited pure eigenstate means that the system is back to the original symmetry (e.g. D6h for benzene), even though its IRREPe (e.g. E1u) is different from the original IRREPg (e.g. A1g).
Successful symmetry breaking and restoration is illustrated by the snapshots of the electronic density shown in panels (1e),(1f),(1g), from the initial ground state with symmetry D6h (IRREPg = A1g) via the intermediate state representing charge migration/circulation with broken symmetry (Cs) to the final excited state with restored symmetry D6h (IRREPe = E1u).†
1 M. Ivanov, P. B. Corkum and P. Dietrich, Laser Phys., 1993, 3, 375.
2 T. C. Weinacht, J. Ahn and P. H. Bucksbaum, Phys. Rev. Lett., 1998, 80, 5508.
3 N. Elghobashi, L. González and J. Manz, J. Chem. Phys., 2004, 120, 8002.
4 A. S. Alnasser, M. Kübel, R. Siemering, B. Bergues, N. G. Kling, K. J. Betsch, Y. Deng, J. Schmidt, Z. A. Alahmed, A. M. Azzeer, J. Ullrich, I. Ben-Itzhak, R. Moshammer, U. Kleineberg, F. Krausz, R. de Vivie Riedle and M. F. Kling, Nature Commun., 2014, 5, 3800.
5 Y. Pertot, C. Schmidt, M. Matthews, A. Chauvet, M. Huppert, V. Svoboda, A. Conta, A. Tehlar, D. Baykusheva, J.-P. Wolf and H. J. Wörner, Science, 2017, 355, 264.
6 C. Liu, J. Manz, K. Ohmori, C. Sommer, N. Takei, J. C. Tremblay and Y. Zhang, Phys. Rev. Lett., 2018, 121, 173201.
7 C. Liu, J. Manz and J. C. Tremblay, in Progress in Ultrafast Intense Laser Science (PUILS) XIV, ed. K. Yamanouchi, P. Martin, M. Sentis, L. Ruxin, D. Normand, Springer Nature, Switzerland, DOI: 10.1007/978-3-030-03786-4_7.
8 L. S. Cederbaum and J. Zobeley, Chem. Phys. Lett., 1999, 307, 205.
9 I. Barth and J. Manz, Angew. Chem. Int. Ed., 2006, 45, 2962.
10 F. Remacle and R. D. Levine, PNAS, 2006, 103, 6793.
11 M. Kanno, H. Kono, and Y. Fujimura, Angew. Chem. Int. Ed., 2006, 45, 7995.
12 P. M. Kraus, B. Mignolet, D. Baykusheva, A. Rupenyan, L. Horny, E. F. Penka, G. Grassi, O. I. Tolstikhin, J. Schneider, F. Jensen, L. B. Madsen, A. D. Bandrauk, F. Remacle and H. J. Wörner, Science, 2015, 350, 790.
13 K. Ueda, Science, 2015, 350, 740.
14 N. V. Golubev, V. Despré and A. Kuleff, J. Mod. Opt., 2017, 64, 1031.
15 N. Takei, C. Sommer, C. Genes, G. Pupillo, H. Goto, K.Koyasu, H. Chiba, M. Weidemüller and K. Ohmori, Nat. Commun., 2016, 7, 13449.
16 I. S. Ulusoy and M. Nest, J. Am. Chem. Soc., 2011, 133, 20230–20352.
17 D. Jia, J. Manz, B. Paulus, V. Pohl, J. C. Tremblay and Y. Yang, Chem. Phys., 2017, 482, 146.
ChunMei Liu said: Our theory of symmetry breaking and symmetry restoration is general for small systems. It was not easy to do the calculation and develop the theory. If you are interested, please kindly find more details of the theory from our paper in ref. 1. Thank you.
1 C. Liu, J. Manz, K. Ohmori, C. Sommer, N. Takei, J. C. Tremblay and Y. Zhang, Phys. Rev. Lett., 2018, 121, 173201.
Karel Kouril commented: Your work explains the observed symmetry breaking in molecular endofullerenes under cryogenic conditions (where the C60 cages are static). Symmetry breaking in solid H2O@C60 has also been observed at room temperature (where the C60 cages can rotate) by solid-state NMR.1 The symmetry breaking is evidenced by 1H–1H dipole-dipole coupling of the two hydrogen nuclei in the encapsulated water molecule and by 1H chemical shift anisotropy (CSA). The CSA is too large to be explained by alignment of the encapsulated water molecules. This is a different regime from your work – the obvious question is what could be the nature of the symmetry breaking in this case?
1 M. Concistre et al., Phil. Trans. R. Soc. A, 2013, 371, 20120102.
Zlatko Bacic answered: It is a good question, to which unfortunately I do not have an answer. Once the C60 cages can rotate freely, the S6 symmetry in the solid that leads to the level splittings is lost, so that the low-temperature mechanism of symmetry breaking that we have identified no longer applies. Perhaps at these higher temperatures the distortion of the geometry of the cages does become feasible, as the endohedral H2O is excited to high-energy TR states. But it would be necessary to quantify the consequences of such a distortion, and compare them to experiment, in order to establish, or refute, the validity of this mechanism.
Zlatko Bacic commented: The coupling between the center-of-mass translational motions of the guest molecule and its rotational degrees of freedom exists, and is caused by the confining potential of the cage. It is a common feature of nanoconfined systems. This translation-rotation coupling manifests in the levels structure and complicates it. At the same time, it makes its information content richer and more interesting to study.
Zlatko Bacic said: Prior to our two recent studies in ref. 1 and DOI: 10.1039/c8fd00082d, it was largely taken for granted that the symmetry breaking observed experimentally in the endofullerenes M@C60 (M = H2, HF, H2O] had to be caused by the geometric distortion of the C60 cage away from the icosahedral symmetry. However, in order to establish, or not, the validity of this mechanism, one would have to calculate from first principles its consequences and compare them to experiment. But this would require quantum calculations of the translation-rotation eigenstates of the guest molecule fully coupled to the vibrational modes of the cage. Such calculations are not possible now, and for the foreseeable future, because of the very high dimensionality of the quantum problem, and the lack of the potential energy surface that would incorporate all the inter- and intra-molecular mode couplings. Our work has demonstrated quantitatively that symmetry breaking can be caused by an entirely different mechanism, that involves the “through-the-wall” interaction of the guest molecule with the symmetry-lowering environment. In our case these are the nearest-neighbor C60 molecules, while in your case it could be the liquid crystal environment. For the latter, it remains to be shown, by calculations, that it can reproduce the experimental observations.
1 Felker et al., Phys. Chem. Chem. Phys., 2017, 19, 31274.
Conflicts of interest
There are no conflicts to declare.Footnote |
| † Jörn Manz and Jean Christophe Tremblay also contributed to this comment. |
| This journal is © The Royal Society of Chemistry 2018 |