Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Hot electron effects during reactive scattering of H2 from Ag(111): assessing the sensitivity to initial conditions, coupling magnitude, and electronic temperature
Reinhard J.
Maurer†
 *a,
Yaolong
Zhang†
b,
Hua
Guo
*a,
Yaolong
Zhang†
b,
Hua
Guo
 c and
Bin
Jiang
c and
Bin
Jiang
 *b
*b
aDepartment of Chemistry, Centre for Scientific Computing, University of Warwick, Gibbet Hill Road, Coventry, CV4 7AL, UK. E-mail: R.Maurer@warwick.ac.uk
bHefei National Laboratory for Physical Science at the Microscale, Department of Chemical Physics, University of Science and Technology of China, Hefei, Anhui 230026, China. E-mail: bjiangch@ustc.edu.cn
cDepartment of Chemistry and Chemical Biology, University of New Mexico, Albuquerque, New Mexico 87131, USA
First published on 10th December 2018
Abstract
Low-lying electronic excitations in metals, so-called hot electrons, efficiently mediate molecule-metal energy transfer and contribute to energy loss during molecular reactions at surfaces. They furthermore play an important role in plasmon-driven chemistry. Electronic friction represents a simple and effective concept to model hot electron-induced energy loss under ambient conditions. Different methods exist that vary in their description of magnitude, coordinate and directional dependence of friction during reactive molecular scattering at metal surfaces. Using molecular dynamics simulations with electronic friction, we systematically study the effect of hot electrons on measurable state-to-state scattering probabilities of molecular hydrogen from a (111) surface of silver. We assess the ability of ab initio electronic friction methods to accurately describe hot electron-mediated energy loss as a function of initial reaction conditions and electronic temperature. We furthermore find that dynamic scattering results and the ensuing energy loss are highly sensitive to the magnitude of electronic friction. Therefore, existing approximate models of electronic friction, which exhibit inherent uncertainties with respect to the magnitude of electronic friction, may not be applicable for a quantitative prediction of plasmon driven hot electron effects in their current state. We outline a development direction to potentially overcome these limitations.
1 Introduction
Plasmonic science1 and hot electron chemistry2–4 are based on the idea of controlling the flow of energy between electronic excitations in metallic surfaces or nanostructures,5 so-called hot electrons, and molecular adsorbate degrees of freedom, such as molecular vibrations. A high level of control of this molecule–surface energy flow can facilitate chemical bond breaking events with light by funneling energy into the reaction coordinate or impair a reaction by efficiently dissipating energy away from a reaction centre.6,7 The underlying mechanism for this energy exchange is based on the efficient coupling of molecular adsorbate motion and metallic electrons due to the vanishing band-gap in metallic systems.8,9 The consequence of this coupling is a deviation from thermal chemistry as described by the Born–Oppenheimer approximation and a failure of existing methods to describe chemical reaction dynamics.10,11The proposed technological applications of hot electron effects in plasmonic sensors,12 plasmon-enhanced catalysts,13 and locally-enhanced cancer radiation treatment,14 are driven by exciting fundamental experiments that provide quantitative evidence for hot electron effects. These include molecular beam scattering experiments that explicitly measure the state-to-state scattering probability and the energy loss profile of a gas–surface reaction,15 but also the measurement of electric currents,11,16 so-called chemicurrents, that occur due to hot electrons that are generated upon adsorption, desorption, or chemical transformation of molecules.
The ability to computationally predict the molecular details that underlie hot electron-mediated processes and the intricate coupling of electrons and atomic motion is essential for the design of new devices and catalysts based on plasmonics. As such, it is imperative to develop first-principles computational simulation methods that correctly capture how molecular adsorbate motion generates hot electrons or how hot electrons affect measurable dynamical properties of chemical reactions. The intrinsic dimensionality of systems involving many hundreds of atoms and thousands of electrons make exact nonadiabatic quantum dynamics simulations close to unfeasible and therefore ask for efficient approximate mixed quantum-classical dynamics methods.17,18 Such methods are typically based on stochastic surface hopping models based on chemical master equations, where hot electron effects on the reaction dynamics are modelled as explicit electronic transitions.19,20 An alternative is the molecular dynamics with electronic friction (MDEF) method,21–23 where the classical motion of nuclei follows a single potential energy surface and hot electron effects are described as electronic friction forces that act on the adsorbate nuclei. These forces are governed by the so-called electronic friction tensor,24 which arises from nonadiabatic coupling and the resulting equations of motion follow a stochastic Langevin model. The electronic friction tensor is in general frequency-dependent and anisotropic but is often approximated to be frequency independent and spatially isotropic, i.e., nonadiabatic relaxation rates are equal in all spatial directions for rigid atomic and molecular motion. The most common is the Local Density Friction Approximation (LDFA),25,26 where nonadiabatic coupling is expressed as a simple function of the metallic electron density within which the adsorbate atom is embedded. This model is spatially isotropic for rigid molecular motion, but does account for some anisotropic effects along intramolecular degrees of freedom.26,27 Due to its simplicity and ease of computation, LDFA-based MDEF is a particularly appealing approach that, in the past, has been applied to describe hot electron-mediated dynamics in ambient28 and laser-driven conditions.29,30 However, especially for molecular scattering and light-driven plasmonics, the underlying neglect of frequency dependence and the role of molecular anisotropy of electronic friction forces and their effects on measurable observables have been the reason for exciting debates in recent literature.24,31–33
In recent work, we have achieved a description of electronic friction that captures the directional and the explicit vibrational mode dependence and tensorial nature of electronic friction using an efficient implementation of first-order time-dependent perturbation theory (TDPT) based on Density Functional Theory (DFT).24,31 On the examples of vibrational energy loss of metal-adsorbed diatomics31 and the dissociative chemisorption of molecular hydrogen on Ag(111),34 we were able to show that the overall magnitude of friction is, on average, similar to the LDFA prediction, but the directional and vibrational mode dependences and their effect on the dynamic energy loss are different. Before us, Spiering and Meyer have reached a similar conclusion for reactive scattering of H2 on Cu(111),35 where mode-dependent electronic friction forces as described by TDPT provide a measurable signature of energy loss during state-to-state scattering of vibrationally excited molecules. We have recently developed a general method to construct an analytical representation of the electronic friction tensor as a function of the adsorbate coordinates that enabled us to simulate dynamic scattering probabilities and to discuss the subtle differences in electronic friction that give rise to the observation that hot electron effects are much more pronounced during reactive scattering of H2 on Cu(111) than on Ag(111).36
In this work, we use this analytical representation of electronic friction for H2 on Ag(111) further to systematically assess the validity and robustness of the current frequency-independent MDEF method based on TDPT electronic friction. We do this by studying the sensitivity of dynamic observables such as the vibrational excitation/de-excitation probability during molecular scattering and the integrated energy loss along a specific degree of freedom as a function of various initial conditions and the type of electronic friction description. The former includes the effects of the initial and final vibrational excited states and the electronic temperature of the substrate. The latter includes a comparison between LDFA and TDPT and a discussion of their limitations and sensitivity to intrinsic numerical parameters. We find that the energy loss predicted by LDFA and TDPT shows different trends with respect to the parameters we studied and that dynamic observables are particularly sensitive to the absolute magnitude of tensorial friction. The intrinsic sensitivity of friction to numerical parameters such as the broadening width will represent a particular challenge for quantitative predictions of hot electron mediated reaction dynamics at high electronic temperatures that correspond to light-driven conditions. We therefore stress the importance of overcoming this limitation introduced by assuming frequency independence of the friction tensor. This will enable further study of the applicability of electronic friction approaches for light-driven hot electron chemistry.
2 Theory
2.1 Electronic friction based on time-dependent perturbation theory
In MDEF simulations, the nuclear dynamics are defined via a Langevin equation (LE):21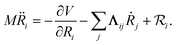 | (1) |
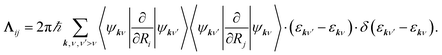 | (2) |
2.2 Neural network representation of the friction tensor
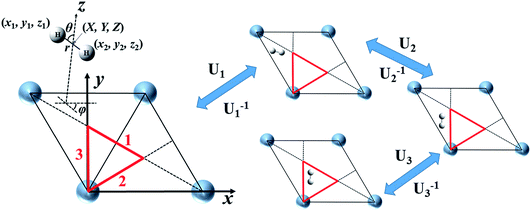
Spiering and Meyer have very recently reported an approximate NN-based representation of the 6 × 6 friction tensor for the H2 + Cu(111) system.35 They first described individual friction coefficients in terms of four symmetry independent internal coordinates, as illustrated in Fig. 1, namely X, Y, Z, and r with angular coordinates fixed (e.g., θ0 = φ0 = 90°). Since the tensorial friction (Λ) is a symmetric matrix, only the upper triangular elements Λij(i ≤ j) are to be determined in practice. This treatment avoids the complex symmetry involved in the full six-dimensional representation. Once Λ(X, Y, Z, r) with θ0 = φ0 = 90° is obtained, the friction tensor at an arbitrary configuration depending on all six internal coordinates can be approximately generated by the following transformation,35
| Λ(X, Y, Z, r, θ, φ) ≈ T(θ, φ)Λ(X, Y, Z, r)T−1(θ, φ), | (3) |
In a previous publication36 and in this present work, we propose an alternative strategy. We choose to fit the elements of the full 6 × 6 matrix form of the electronic friction tensor in Cartesian coordinates inside an irreducible triangle in the (111) surface unit cell (marked in red in Fig. 1). In this triangle, each friction tensor element is symmetry unique with a one-to-one mapping to a molecular geometry, thus posing no problems for fitting. In practice, since we have collected many data scattered inside and out the unit cell, we first move those data distributed outside this triangle into it. This can be done by first translating a data point outside the unit cell into this region, which does not change the friction tensor, followed by a series of reflections when necessary.46 For each reflection, the new Cartesian coordinate vector q′ and friction tensor Λ′ can be obtained by,
| q′ = Uq, | (4) |
| Λ′ = UTΛU, | (5) |
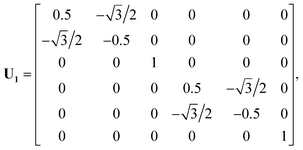 | (6) |
 | (7) |
 | (8) |
In practice, the number of reflections operated on a given point may be less than three and, in the case that the molecule is already situated inside the triangle, no transformation is necessary. It should be noted that this treatment does not account for exchange symmetry of the two H atoms. We solve this issue by ordering the positions of the two hydrogen atoms when necessary (i.e. with z1 ≤ z2) so that the related matrix elements in the friction tensor are exchanged accordingly. Similar mapping schemes have been successfully applied in constructing PESs for gas–surface systems using either NNs47–49 or the modified Shepard interpolation.46 One drawback of these PESs is that the gradients of PESs (i.e. forces) may not be continuous at the boundary, resulting in non-conservation of total energy when running classical trajectories. However, this is not a problem for the friction tensor as we only need values of friction coefficients but no gradients in eqn (1). Similar schemes can be devised for other facets of the metal surface.
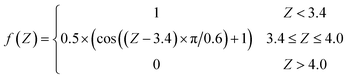 | (9) |
One should note that the NN fitting of each friction coefficient is essentially the same as that of the PES in previous works and very robust.47–49 However, for our purpose, to evaluate a friction tensor for any point outside this symmetry-unique region, we need to first find the symmetry identical geometry of that point in the irreducible triangle by the transformation described above, then calculate the NN interpolated friction tensor there, followed by inversely transforming the obtained full 6 × 6 friction tensor back to that corresponding to the original geometry.
2.3 Molecular dynamics simulations with tensorial friction
The molecular dynamics (MD) and MDEF trajectories have been computed with various initial conditions sampled in a quasi-classical way as described in our previous publication.36 The initial molecular center is chosen to be far above the Ag(111) surface (Z = 8.0 Å) with random lateral positions in the surface unit cell. The molecular internal coordinates and conjugate momenta are sampled semi-classically for given vibrational and rotational quantum numbers v and j.52 The molecular orientation is randomly selected in the polar and azimuthal angles for most cases. For those mj specific states, however, the molecular orientation is chosen randomly on a plane perpendicular to the angular momentum vector![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_i_char_006a_20d1.gif) , which forms an angle of
, which forms an angle of 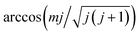 with the space-fixed Z axis (surface normal here). For the scattered molecule, the vibrational action number is determined by Einstein–Brillouin–Keller (EBK) semi-classical quantization and rotational quantum number j by the quantum mechanical expression for rotational angular momentum.53 As in ref. 35, the standard histogram binning is used to obtain the state distributions with integer quantum numbers.
with the space-fixed Z axis (surface normal here). For the scattered molecule, the vibrational action number is determined by Einstein–Brillouin–Keller (EBK) semi-classical quantization and rotational quantum number j by the quantum mechanical expression for rotational angular momentum.53 As in ref. 35, the standard histogram binning is used to obtain the state distributions with integer quantum numbers.
Given an initial condition, eqn (1) is propagated using third-order Beeman’s algorithm with a time step of 0.1 fs. The MD and MDEF with LDFA simulations are easily implemented as friction coefficients only depend on the value of the electron density of the clean substrate.25,28 The tensorial nature of the TDPT based electronic friction makes the equations of all coordinates coupled. In practice, we need to transform the coordinates and velocities into the friction eigenspace and apply the friction eigenvalues as damping coefficients onto the transformed velocities, and then transform the products back to the Cartesian space. This requires a diagonalization of the friction tensor at each time step. In addition, the random force term on the right-hand side of the Langevin equation, given a finite surface temperature (T), is described as a Gaussian white noise of zero mean and a standard deviation of 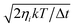 , where ηi is the ith friction eigenvalue (or simply the ith friction coefficient in LDFA) and k is the Boltzmann constant. However, we neglect surface temperature in most simulations because the contribution of the random force is typically small, except where we discuss temperature effects explicitly.
, where ηi is the ith friction eigenvalue (or simply the ith friction coefficient in LDFA) and k is the Boltzmann constant. However, we neglect surface temperature in most simulations because the contribution of the random force is typically small, except where we discuss temperature effects explicitly.
3 Results and discussion
3.1 Validation of the NN interpolation of the friction tensor
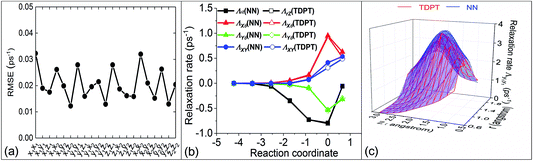
Based on our previously published analysis,54 we have further examined the quality of our NN representation of the friction tensor. Fig. 2a shows the root mean square errors (RMSEs) averaged over all data for the 21 independent friction coefficients. The overall RMSEs uniformly range from ∼0.01 ps−1 to ∼0.03 ps−1 without any outliers, which are generally comparable or smaller than those reported for the H2 + Cu(111) system.35 In Fig. 2b, we compare several large components in the TDPT friction tensor with the NN interpolated values along the minimum energy path (MEP) for H2 dissociative chemisorption, corresponding to the route for H2 dissociation over the bridge site with the H–H bond parallel to the surface and stretching to two hollow sites. Clearly, there are strong couplings between the vibration (r) and translation (Z) directions, and between parallel motion (X/Y) and rotation (θ). Although the coupling terms can be both negative and positive, their absolute values increase as the molecule approaches the transition state. It has been previously shown that our NN diagonal tensor elements agree well with TDPT ones,36 and we also find here excellent agreement between NN and TDPT off-diagonal friction coefficients. As a further validation, Fig. 2c compares two-dimensional electronic friction contour plots, as a function of Z and r along the MEP, generated from NN interpolation and direct DFT calculations, respectively. Our NN representation faithfully captures the multi-dimensional topography of the friction tensor element, even though these data points were actually not included in the training set. These results indicate that the NN representation of the friction tensor is sufficiently accurate for subsequent MDEF simulations.3.2 The physical differences between LDFA and TDPT
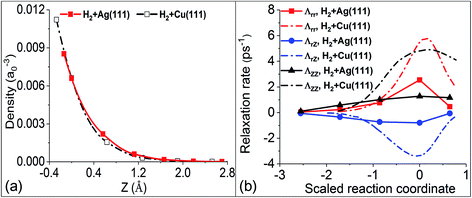
In our previous work,36 we have shown different behaviors of the electronic friction in the H2 + Cu(111) and H2 + Ag(111) systems, which can be traced back to the differences in the underlying electronic structure of the two metals. Within the framework of the independent atom LDFA method, the friction coefficient depends only on the local electron density (ρ) at the position of the adsorbate atoms, whereas TDPT accounts for the response of the electronic wave functions (and therefore the nonadiabatic density response) of the combined molecule–surface system to the adsorbate motion. In Fig. 3a, we plot the clean surface density ρ varying with the position of one of the H atoms in the molecule along the MEP (the other H atom moves almost symmetrically to the opposite and hence feels nearly the same electron density). Because the transition state structures for H2 dissociation on Cu(111) and Ag(111) appear at different distances from the surface, the comparison of ρ is best made as a function of the relative height with respect to that of the hydrogen atom at the respective transition state. Surprisingly, the embedded electron densities for H2 scattering on Ag and Cu are very similar, resulting in very close values in LDFA friction coefficients. In the case of Fermi’s golden rule, electronic friction does not depend on the density, but on the local density of states around the Fermi level and on the nonadiabatic coupling matrix elements that encode the difference in response along different directions, which sensitively depend on the underlying electronic structure and the nature of the metal. This level of difference is position and direction dependent and can be directly seen in Fig. 3b. In the following we will study how these different descriptions translate into measurable dynamic observables and how they depend on system parameters.3.3 The sensitivity of the vibrational deexcitation probability on the magnitude of friction
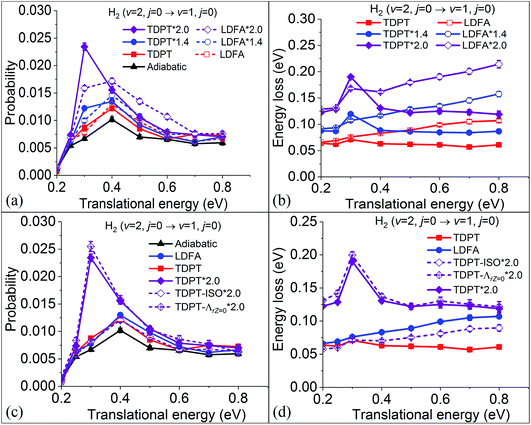
In our previous results on the vibrational deexcitation probabilities from H2 (v = 2, j = 0) to H2 (v = 1, j = 0) (i.e. P2→1) during H2 scattering on Ag(111), we found that both TDPT and LDFA yield comparable deexcitation probabilities that are slightly elevated compared to the adiabatic MD case (see Fig. 4a). This is in contrast to findings for H2 on Cu(111), where particularly the TDPT friction has been shown to lead to a significantly elevated deexcitation probability at intermediate translational incidence energies.35 This suggests that dynamic observables are highly sensitive to the absolute magnitude of electronic friction. To test this sensitivity, we monitor the P2→1 varying with the electronic friction multiplied with a scaling factor for H2 + Ag(111). We scale all tensor elements in Cartesian coordinates by the same factor. As shown in Fig. 4a, rather unsurprisingly, P2→1 increases for both TDPT and LDFA with increasing magnitude of electronic friction. When the strength of the TDPT friction tensor is doubled, corresponding to a similar magnitude as was found for the H2 + Cu(111) system, the P2→1 with TDPT becomes much more significantly increased and sharply peaks at a translational energy (Ei) of 0.3 eV. At this specific Ei, we obtain a P2→1 with TDPT that is roughly 4 (3) times larger than the adiabatic (LDFA) results, in general accord with the observation in the H2 + Cu(111) system. On the other hand, the doubly-increased LDFA friction coefficients also promote vibrational deexcitation at higher energies, yielding a greater enhancement of P2→1 at translational energies higher than 0.4 eV. The different dependence of P2→1 on translational energy with TDPT and LDFA can be understood by the corresponding mode-specific magnitude of electronic friction and nonadiabatic energy loss. As discussed in our previous work,36 the LDFA electronic friction is dominated by the component along the translational coordinate, leading to almost linearly increased energy dissipation with increasing translational energy. This behavior becomes more remarkable when the strength of the friction coefficient is doubled, as shown in Fig. 4b, giving rise to the greater enhancement at high translational energies for LDFA. On the other hand, the fact that the energy loss due to the TDPT electronic friction shows a peak at 0.3 eV is consistent with the same peak in the P2→1 distribution. This can be related to a balanced effect between the longer interaction time and smaller molecular velocity at this incidence energy.Furthermore, it is interesting to analyse whether the nonadiabatic effects stem from the anisotropy along different directions or the mode-coupling between these directions in the friction tensor. In Fig. 4c, we compare the P2→1 with TDPT electronic friction where the off-diagonal coupling between the intra-atomic coordinate and the molecule-adsorbate coordinate (TDPT) is included and where it is artificially set to zero (TDPT-ΛrZ=0). To make the comparison clearer, a factor of two is also multiplied in both cases. Although the magnitude of ΛrZ is not small as displayed in Fig. 2b, interestingly, the results with zero ΛrZ are quite close to the original ones in the entire energy range, implying the negligible effect of the mode-coupling between the translational and vibrational DOFs in this case. In addition, to study the importance of directional anisotropy, we average the three diagonal components of the TDPT friction tensor (twice in magnitude) in the Cartesian space for each atom, then assign the same friction coefficient for each atomic Cartesian coordinate in the following way,
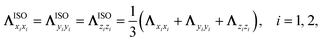 | (10) |
3.4 Dependence on initial conditions and final states
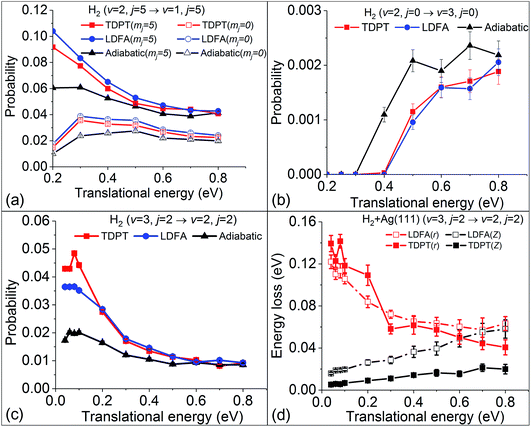
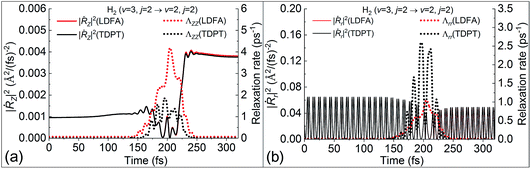
Our previous analyses suggested that the velocity profile and potential energy landscape also play a significant role in determining the nonadiabatic effects in the molecular scattering process.36 One can of course change the velocity profile by choosing various initial conditions. We first study the influence of the angular velocity by performing MDEF simulations with initially different rotational and orientational states at the same (v = 2) vibrational state. Fig. 5a compares the vibrational deexcitation probabilities for H2 (v = 2, j = 5, mj = 0/5) to H2 (v = 1, j = 5) with and without electronic friction. These two initial states correspond to the cartwheel (mj = 0) and helicopter (mj = j) orientations, respectively, which would impact the surface with similar vibrational and translational velocities but distinctly different angular velocities for a given incidence energy. Compared to previous results for the rotational ground state, the nonadiabatic energy dissipation is more important for these two states, resulting in up to an ∼80% increase of the vibrational deexcitation probability at low translational energies. Both friction methods provide similar results with small EHP-induced enhancement for the cartwheel motion and larger effects for the helicopter motion. The latter can be understood in terms of an increased residence time of the molecule and rovibrational coupling during the scattering process. Our findings show that, despite some rotational state dependence of friction, there is little change of the nonadiabatic effects on P2→1 among different product rotational states (partly shown in ref. 36), suggesting that the angular velocities only play a minor role in such cases.Following this line of thought, we show the excitation probability (P2→3) from H2 (v = 2, j = 0) to H2 (v = 3, j = 0) in Fig. 5b and deexcitation probability (P3→2) from H2 (v = 3, j = 2) to H2 (v = 2, j = 2) in Fig. 5c. Both scattering processes involve a higher vibrational state which naturally increases the molecular velocity with respect to the intramolecular stretching mode. We see much stronger nonadiabatic effects in both cases, leading to the significant decrease of P2→3 and increase of P3→2 due to electronic friction at low translational energies. In such cases, the translational velocity is low enough for the molecule to remain close to the surface for an extended time, and the vibrational velocity is high enough to cause electronic excitations. While the results with TDPT and LDFA are very similar with respect to P2→3, the former become qualitatively different from the latter in P3→2 below Ei = 0.2 eV. This interesting behavior is reflected by the nonadiabatic energy loss given in Fig. 5d, where the TDPT induced energy losses along the molecular vibration (r direction) are more significant than the LDFA ones in that range. Such a large vibrational energy loss with TDPT at low energy seems to be surprising given the similar magnitude of Λrr with TDPT and LDFA. We therefore monitor the velocity and friction coefficient profiles in the Z and r directions as a function of time for an exemplary trajectory at Ei = 0.1 eV in Fig. 6a and b. It appears that Λrr with TDPT is remarkably higher than those with LDFA in the strong interaction region, implying that the trajectory significantly departs from the MEP. Unlike our previous results (Fig. 4d in ref. 36) for H2 (v = 2 → v = 1), the H2 (v = 3) molecules do not necessarily follow the MEP. As a result, the multidimensional topography of the friction tensor determines the total nonadiabatic energy loss and thus the scattering probability. This reflects the importance of correctly capturing this tensorial topology.
3.5 Electronic temperature
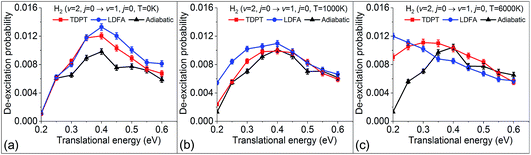
Within the electronic friction picture, plasmon driven or laser-heated hot electron effects are typically simulated via an increase of the electronic temperature that defines the heat of the electronic bath and the strength of the random force contribution. This can be done in the form of a constant elevated temperature or by simulating a time-dependent temperature profile that is coupled with a two-temperature model of the coupled lattice-electron dynamics of the metallic substrate.29,30 Electronic temperatures that arise from laser-heating a surface can reach transient temperatures up to several thousands of Kelvin. It should be noted that this approach will assume that all hot electrons are thermalised and the weak coupling assumption will neglect any possible resonant electron-nuclear coupling effects due to high-lying excitations. Furthermore, the use of a temperature ramp is not strictly valid within an equilibrium Langevin theory and corresponding implications on detailed balance need to be carefully considered. In previous work, we studied the effect of including electronic temperature in eqn (2) and found that over a range of up to 6000 K, electronic relaxation rates within our currently employed level of theory depend very weakly on temperature.31 We therefore describe the electronic friction tensor as temperature independent. However, within the dynamic formalism of eqn (1) temperature still enters the Langevin expression and it is interesting to study how dynamic state-to-state scattering is affected by varying the electronic bath temperature. Whereas previous sections studied scattering at low temperature conditions and neglected the random force, Fig. 7 shows the dependence of vibrational deexcitation as a function of different electronic temperatures (0 K, 1000 K, and 6000 K). We find that, while overall deexcitation probabilities do not significantly change for both friction models, higher temperatures lead to higher integrated energy loss and increased deexcitation probabilities for very low translational energies. For the LDFA method, this effect becomes relevant at lower temperatures than for the TDPT method. This can be related to the higher average friction magnitude of the LDFA method. The increase of deexcitation probability at low translational energies can be directly understood by the increased residence time of molecules close to the surface and the increased exposure to random force perturbations. From our results, it appears that state-to-state scattering is not strongly affected by plasmonic heating. This will, however, be different for rates of reactions such as recombinative desorption and dissociation reactions with high barriers and physisorbed precursor states where surface residence times are much larger.4 Conclusions
We have presented extensive MDEF simulations within the Markov approximation for the state-to-state scattering of molecular hydrogen from a Ag(111) surface. These simulations are enabled by the construction of neural-network based potential energy surfaces and an electronic friction tensor with data calculated from density functional theory and 1st order TDPT. We find that nonadiabatic dynamic state-to-state scattering is strongly dependent on the absolute magnitude of friction with respect to the relevant internal coordinate, whereas coupling between internal coordinates does not appear to play a significant role. Different vibrational and rotational states are affected very differently by electronic friction, however, the two different friction models did not yield drastically different results. The rotational state dependence hereby is mostly due to the changed molecular orientation and particular trajectory route with respect to the surface during impingement that boost vibrational or translational energy loss. We have furthermore shown that the inclusion of elevated electronic temperatures as they appear in plasmon-driven hot electron chemistry dominantly affects reaction probabilities at low incidence energy, where surface residence times are larger than at high incidence energies. In particular the latter finding suggests that plasmon-driven MDEF studies with electronic friction directly computed from DFT orbitals are possible and could provide a basis for further systematic improvement beyond the current state-of-the-art represented by LDFA.29,30 As guided by recent work of Novko et al.,33 a word of warning on the Markov and zero-frequency approximation is in order. Our methodology is numerically robust but suffers from the choice of a broadening parameter that, despite a weak dependence in the chosen regime, does introduce some variation of frictional magnitude. Our results have shown that this dependence can strongly affect the dynamical scattering results on a level that would, at best, allow a qualitative prediction of reaction rate trends for hot electron chemistry. We conclude from this that, to investigate the ability of MDEF to act as a predictive tool for plasmonic science, the Markov approximation needs to be overcome. This endeavor is currently under way.Conflicts of interest
There are no conflicts to declare.Acknowledgements
YZ and BJ acknowledge support by the National Key R&D Program of China (2017YFA0303500), the National Natural Science Foundation of China (91645202, 21722306, and 21573203), the Anhui Initiative in Quantum Information Technologies, and computational resources offered by the Supercomputing Center of USTC and Advanced Materials High-Performance Company. RJM acknowledges computational resources provided by the University of Warwick Scientific Computing Research Technology Platform, and the EPSRC-funded HPC Midlands Plus centre (EP/P020232/1). HG is supported by the U.S. National Science Foundation (Grant No. CHE-1462109).References
- M. L. Brongersma, N. J. Halas and P. Nordlander, Nat. Nanotechnol., 2015, 10, 25–34 CrossRef CAS PubMed.
- W. Xie and S. Schlücker, Nat. Commun., 2015, 6, 7570 CrossRef PubMed.
- J. Y. Park, S. W. Lee, C. Lee and H. Lee, Catal. Lett., 2017, 147, 1851–1860 CrossRef CAS.
- J. Y. Park, S. M. Kim, H. Lee and I. I. Nedrygailov, Acc. Chem. Res., 2015, 48, 2475–2483 CrossRef CAS PubMed.
- S. D. Forno, L. Ranno and J. Lischner, J. Phys. Chem. C, 2018, 122, 8517–8527 CrossRef.
- E. Cortés, W. Xie, J. Cambiasso, A. S. Jermyn, R. Sundararaman, P. Narang, S. Schlücker and S. A. Maier, Nat. Commun., 2017, 8, 14880 CrossRef PubMed.
- S. Mukherjee, F. Libisch, N. Large, O. Neumann, L. V. Brown, J. Cheng, J. B. Lassiter, E. A. Carter, P. Nordlander and N. J. Halas, Nano Lett., 2013, 13, 240–247 CrossRef CAS PubMed.
- A. M. Wodtke, D. Matsiev and D. J. Auerbach, Prog. Surf. Sci., 2008, 83, 167–214 CrossRef CAS.
- S. P. Rittmeyer, V. J. Bukas and K. Reuter, Adv. Phys.: X, 2018, 3, 1381574 Search PubMed.
- A. M. Wodtke, J. C. Tully and D. J. Auerbach, Int. Rev. Phys. Chem., 2004, 23, 513–539 Search PubMed.
- A. Kandratsenka, H. Jiang, Y. Dorenkamp, S. M. Janke, M. Kammler, A. M. Wodtke and O. Bünermann, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 680–684 CrossRef CAS PubMed.
- D. Sil, K. D. Gilroy, A. Niaux, A. Boulesbaa, S. Neretina and E. Borguet, ACS Nano, 2014, 8, 7755–7762 CrossRef CAS PubMed.
- P. Christopher, H. Xin and S. Linic, Nat. Chem., 2011, 3, 467–472 CrossRef CAS PubMed.
- X. Huang, P. K. Jain, I. H. El-Sayed and M. A. El-Sayed, Nanomedicine, 2007, 2, 681–693 CrossRef CAS PubMed.
- O. Bunermann, H. Jiang, Y. Dorenkamp, A. Kandratsenka, S. M. Janke, D. J. Auerbach and A. M. Wodtke, Science, 2015, 350, 1346–1349 CrossRef PubMed.
- H. Nienhaus, H. S. Bergh, B. Gergen, A. Majumdar, W. H. Weinberg and E. W. McFarland, Phys. Rev. Lett., 1999, 82, 446–449 CrossRef CAS.
- J. C. Tully, J. Chem. Phys., 2012, 137, 22A301 CrossRef PubMed.
- Y. Zhang, T. R. Nelson, S. Tretiak, H. Guo and G. C. Schatz, ACS Nano, 2018, 12, 8415–8422 CrossRef CAS PubMed.
- N. Shenvi, S. Roy and J. C. Tully, J. Chem. Phys., 2009, 130, 174107 CrossRef PubMed.
- H. Guo, P. Saalfrank and T. Seideman, Prog. Surf. Sci., 1999, 62, 239–303 CrossRef CAS.
- M. Head Gordon and J. C. Tully, J. Chem. Phys., 1995, 103, 10137–10145 CrossRef CAS.
- W. Dou and J. E. Subotnik, J. Chem. Phys., 2018, 148, 230901 CrossRef PubMed.
- B. Hellsing and M. Persson, Phys. Scr., 1984, 29, 360–371 CrossRef CAS.
- M. Askerka, R. J. Maurer, V. S. Batista and J. C. Tully, Phys. Rev. Lett., 2016, 116, 217601 CrossRef PubMed.
- J. Juaristi, M. Alducin, R. Muiño, H. Busnengo and A. Salin, Phys. Rev. Lett., 2008, 100, 116102 CrossRef CAS PubMed.
- D. Novko, M. Blanco-Rey, M. Alducin and J. I. Juaristi, Phys. Rev. B, 2016, 93, 245435 CrossRef.
- S. P. Rittmeyer, J. Meyer and K. Reuter, Phys. Rev. Lett., 2017, 119, 176808 CrossRef PubMed.
- M. Blanco-Rey, J. I. Juaristi, R. Díez Muiño, H. F. Busnengo, G. J. Kroes and M. Alducin, Phys. Rev. Lett., 2014, 112, 103203 CrossRef CAS PubMed.
- J. I. Juaristi, M. Alducin and P. Saalfrank, Phys. Rev. B, 2017, 95, 125439 CrossRef.
- I. Lončarić, M. Alducin, P. Saalfrank and J. I. Juaristi, Phys. Rev. B, 2016, 93, 014301 CrossRef.
- R. J. Maurer, M. Askerka, V. S. Batista and J. C. Tully, Phys. Rev. B, 2016, 94, 115432 CrossRef.
- D. Novko, M. Alducin, M. Blanco-Rey and J. I. Juaristi, Phys. Rev. B, 2016, 94, 224306 CrossRef.
- D. Novko, M. Alducin and J. I. Juaristi, Phys. Rev. Lett., 2018, 120, 156804 CrossRef CAS PubMed.
- R. J. Maurer, B. Jiang, H. Guo and J. C. Tully, Phys. Rev. Lett., 2017, 118, 256001 CrossRef PubMed.
- P. Spiering and J. Meyer, J. Phys. Chem. Lett., 2018, 9, 1803–1808 CrossRef CAS PubMed.
- Y. Zhang, R. J. Maurer, H. Guo and B. Jiang, Chem. Sci., 2019, 10, 1089–1097 RSC.
- S. Roy, N. A. Shenvi and J. C. Tully, J. Chem. Phys., 2009, 130, 174716 CrossRef PubMed.
- N. Shenvi, S. Roy and J. C. Tully, Science, 2009, 326, 829–832 CrossRef CAS PubMed.
- T. Olsen and J. Schiøtz, J. Chem. Phys., 2010, 133, 134109 CrossRef PubMed.
- M. Forsblom and M. Persson, J. Chem. Phys., 2007, 127, 154303 CrossRef PubMed.
- A. C. Luntz and M. Persson, J. Chem. Phys., 2005, 123, 074704 CrossRef CAS PubMed.
- V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- B. Jiang and H. Guo, Phys. Chem. Chem. Phys., 2014, 16, 24704–24715 RSC.
- B. Jiang, M. Alducin and H. Guo, J. Phys. Chem. Lett., 2016, 7, 327–331 CrossRef CAS PubMed.
- C. Crespos, M. A. Collins, E. Pijper and G. J. Kroes, J. Chem. Phys., 2004, 120, 2392–2404 CrossRef CAS PubMed.
- T. Liu, B. Fu and D. H. Zhang, Sci. China: Chem., 2014, 57, 147–155 CrossRef CAS.
- T. Liu, Z. Zhang, B. Fu, X. Yang and D. H. Zhang, Chem. Sci., 2016, 7, 1840–1845 RSC.
- X. Shen, J. Chen, Z. Zhang, K. Shao and D. H. Zhang, J. Chem. Phys., 2015, 143, 144701 CrossRef PubMed.
- Y. Zhang, X. Zhou and B. Jiang, Chin. J. Chem. Phys., 2017, 30, 727–734 CrossRef CAS.
- M. T. Hagan and M. B. Menhaj, IEEE Trans. Neural Network., 1994, 5, 989–993 CrossRef CAS PubMed.
- X. Hu, W. L. Hase and T. Pirraglia, J. Comput. Chem., 1991, 12, 1014–1024 CrossRef CAS.
- M. C. Gutzwiller, Chaos in classical and quantum mechanics, Springer, New York, 1990 Search PubMed.
- P. Shi, Y. Yang, B. Ao, P. Zhang and X. Wang, J. Phys. Chem. C, 2014, 118, 26634–26640 CrossRef CAS.
Footnote |
| † These two authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2019 |