 Open Access Article
Open Access ArticleOn the electrical operation of batch electrodialysis for reduced energy consumption
Karim M.
Chehayeb
 and
John H.
Lienhard
V
and
John H.
Lienhard
V
 *
*
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: lienhard@mit.edu
First published on 15th April 2019
Abstract
The cost of desalination using electrodialysis (ED) may be decreased by lowering the electrical energy consumption. This can be done by improving the operating conditions of ED systems. For a fixed application, the total amount of salt that needs to be transported, or the duty, is roughly fixed. For a fixed system size and a fixed duty, the optimal operation can be guided by the theorem of equipartition of entropy generation. This paper examines the improved operation of a batch ED system for the desalination of brackish water and seawater, and for the concentration of high-salinity brine. Energy consumption is compared for three operating conditions: constant applied voltage, constant current, and constant entropy generation. The work then considers the effect of improved operation on the energy consumption and on the non-pumping system costs of batch ED at various cost factors by using a simple cost model. Significant improvements to energy consumption and cost are shown to be achievable through better system operation, especially for the seawater desalination application and when fixed costs are low relative to energy costs.
Water impactDesalination systems have the potential to increase the global fresh water supply. However, sustainable desalination, in a world threatened by climate change, requires that energy consumption be minimized. This study shows how operating conditions can reduce the electricity needed to desalinate groundwater, seawater, or salty brines by electrodialysis. The methods can be applied to other desalination technologies as well. |
1 Introduction
Electrodialysis (ED) is a desalination technology which uses an electric voltage and anion-exchange and cation-exchange membranes placed in alternating order to separate low salinity water from high salinity water. To sustainably expand the use of ED systems (and other desalination technologies), their energy consumption should be minimized. In addition, reducing the energy consumption of desalination technologies can decrease the cost of water if other costs are not increased by amounts exceeding the energy savings.Multiple approaches may be used to improve the energy efficiency of an ED system. One way is to decrease local resistances to mass transfer. At any point along the direction of fluid flow in an ED system, salt and water are transported through electrochemical potential gradients, resulting in entropy generation that lowers the energy efficiency. These losses can be decreased through the use of better membranes and better system designs (e.g., thinner channels).1–3 A second way to reduce energy consumption is to increase system size and available membrane area. A larger system size allows the operation at a lower current density. The lower rate at which mass transfer occurs keeps the system closer to thermodynamic equilibrium, which reduces the irreversibilities due to transport.3,4 A third, and often overlooked, approach consists of better choosing the electrical operating conditions (e.g., applied voltage/current). In this paper, we focus on the operation of batch ED systems, and, in particular, we study how the applied voltage/current should be chosen as the salinities change with time.
Few studies in the literature have looked at the improved electrical operation of a batch ED system. Below, we consider some of these studies.
Parulekar5 studied five possible operating profiles of a batch ED system, including constant-current and constant-voltage operation. The values of the applied current and voltage were determined by minimizing the sum of the stack energy consumption and the pumping energy, such that the process time and the final diluate salinity were not held constant.
Rohman et al.6 modeled a batch ED system operating under constant current, and studied the effects of various parameters on the process time and energy consumption. In another study, Rohman and Aziz7 made use of dynamic optimization to determine the optimal processes for different objective functions.
In a study by Lee et al.,8 a batch ED system is operated under constant current until a pre-determined concentration is reached, where the operation is switched to constant voltage. Tran et al.9 used a batch ED system to treat RO concentrate, and operated the ED system at constant current density. Tanaka10 modeled a constant-voltage batch ED system and determined that it can consume less energy than reverse osmosis at low salinities. Yan et al.11 studied the effects of several parameters by operating a batch ED system under a constant voltage.
In fact, batch ED systems are commonly operated at constant voltage10–16 and at constant current.6,8,9,17 These choices usually seem to be made without a justification of which regime to operate under, and without a fair comparison between the different operating regimes.
To compare the energy consumption of different operating conditions, a fair set of constraints must first be ensured. The amount of energy consumed by a desalination system depends strongly on the inlet and outlet salinities and flow rates, which directly influence the total amount of salt (or water in technologies such as reverse osmosis) that needs to be transported, the streamwise concentration variations, and the potential difference through which this salt (or water) must be transported. As a result, comparing the energy consumption of different operating conditions while also varying the inlet and outlet salinities and flow rates results in an unfair comparison, which might lead to incorrect conclusions regarding the best operating point. To ensure a fair comparison, the systems being compared need to have the same application, which entails having the same inlet and outlet salinities and flow rates. These conditions translate roughly into a fixed amount of salt that needs to be transported from the diluate to the concentrate, or a fixed “duty”. In addition, the size of the systems being compared must be fixed so as to ensure that only the operating conditions are varied and that the fixed costs are the same in the systems being compared.
The conditions of fixed application and fixed system size, which are required to ensure a fair comparison of the energy consumption of different operating conditions, roughly correspond to those required to apply the theorem of equipartition of entropy generation. As first proposed by Tondeur and Kvaalen,18 the theorem states that, for a system of fixed duty and fixed size, the optimal process is that which minimizes the spatial and/or temporal variance of the rate of entropy generation. Tondeur and Kvaalen proved this finding for a system with a constant phenomenological coefficient, which is the proportionality constant linking the flux and the driving force. This finding was extended by Johannessen et al.19 for a system with a varying phenomenological coefficient. In a subsequent study by Johannessen and Kjelstrup,20 it was shown that the theorem of equipartition of entropy generation only strictly applies if all the driving forces can be controlled independently. However, it was shown that equipartition of entropy generation was a good approximation of the numerical optimal. This final point was also replicated in a later study by Magnanelli et al.21
In a recent study by Chehayeb et al.,4 the theorem of equipartition of entropy generation was applied to a two-stage ED system. It was shown that the voltages of the two stages that minimized the power consumption of a system of fixed duty were also those that minimized the spatial variance in the rate of entropy generation. A batch ED system can be thought of as a continuously staged system, where the applied voltage can be varied with time to result in the best energetic performance. The infinite number of degrees of freedom means that many processes can achieve the set desalination requirements. However, numerical simulation of all the possible processes is difficult, and some of these processes are difficult to run in practice. For these reasons, only certain processes are considered in this paper. Given that equipartition of entropy generation is a good approximation of the optimum when the conditions of fixed size and duty are met, and given the processes commonly used in the literature, we investigate the three following processes: a) fixed-voltage operation; b) fixed-current operation; and c) operation at fixed entropy generation.
In the first part of the paper, we study the energy consumption of the different processes at different system sizes, represented by the product of the process time and the cell-pair area. If the condition of fixed desalination application (i.e., fixed inlet and outlet salinities and flow rates) results in the requirement of a fixed duty, we expect the theorem of equipartition of entropy generation to provide a good approximation of the optimum. As a result, we expect the operation under fixed entropy generation to yield the best energetic performance at fixed area. Starting with this hypothesis, we outline cases in which a batch ED system might deviate from the conditions required by the theorem of equipartition, and we explore the energetic performance of the three processes for each of these cases. We then study how these processes affect the stack energy consumption and the non-pumping costs at various cost factors by using a simple cost model.
2 Modeling
As mentioned in section 1, when comparing the energy efficiency of different operating points, it is essential to fix the system size and the inlet and outlet flow rates and salinities. Any change in these constraints between the systems being compared results in an inconclusive comparison. A system may appear to be more efficient because it is treating water to a lesser extent or in smaller quantities, or because it is using more capital and is larger. In the case of a batch ED system, we fix the initial volume and salinity of the feed, and the final salinities and volumes of the concentrate and the diluate tanks (determined by the recovery, defined as the mass fraction of the feed that is turned into the product). The system is shown in Fig. 1.Given that the process affects the rates of osmosis and diffusion, as explained in detail in section 3.3, we do not know the initial division of the feed volume between the concentrate and diluate tanks. For this reason, the numerical simulation starts with the final state, where the volumes and concentrations are set, and solves the species balances with time until the initial state is reached. For example, for a constant-voltage process, given the application and the system size, only one voltage can result in the required salinities. Starting with the final state, a value of the voltage is guessed, and a species balance is performed at each time step until the end of the process time. The guessed value is updated until the initial feed salinity is reached. By solving in the reverse direction, we only need to guess the voltage, whereas, if we had started with the initial state, we would also have needed to guess the division of the feed volume between the two tanks that would lead to the set recovery.
At each step of the process, given the concentrations in the two tanks and the applied voltage, we can determine the species fluxes using the models detailed and validated in previous studies using experimental results.2–4,22 The major components of the models are presented briefly in the Appendix.
We assume that the stack length is small such that the concentrations do not vary with space, and only vary with time. If the size and shape of the ED stack are known, the optimal velocity at any point in time is determined by the trade-off between stack power consumption and pumping power, as was shown in a previous study.3 Given that the concentrations change with time, the velocity can be varied to minimize the total power consumption. We expect the optimal velocity in the diluate channel to increase as the concentration decreases. In this paper, however, the velocity is held constant in each application and is equal in the two channels,† so the pumping power is the same between the three processes that are compared. For this reason, and because the pumping power depends strongly on the size and shape of the stack, the pumping power is not considered in this paper, and the different processes are compared based on the stack power consumption at each system size.
When an ED system is operated in batch mode, the size of the system is determined by the product of the cell-pair area and the process time. These two quantities are equivalent because the spatial variation of the concentrations along the stack length is neglected. A system with an effective cell-pair area A1 and process time τprocess,1 has the same production rate and energy consumption as a system with area A2 and process time τprocess,2 if
| A1τprocess,1 = A2τprocess,2 |
Given that a dimension of meters-squared-second (m2 s) is not very intuitive, the system size is replaced by the following expression of the minimum average current density:
 | (1) |
Finally, when comparing the energy consumption of different operating regimes for the same application and system size, it can be said that the operating regime with the lower energy consumption is more efficient. The corresponding measure of efficiency is the second-law efficiency, which is defined as the ratio of the least work to the actual work.2
2.1 Calculating entropy generation in electrodialysis
The entropy generation due to the transport of a species is the product of the species flux, ji, and its driving force, which is the gradient of the electrochemical potential divided by the temperature, . When n species are present, the total rate of entropy generation per unit volume is the sum of the rates of entropy generation due to the transport of each species‡23,24
. When n species are present, the total rate of entropy generation per unit volume is the sum of the rates of entropy generation due to the transport of each species‡23,24 | (2) |
μi = RT ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ai + ziFΦ ai + ziFΦ | (3) |
3 Equipartition of entropy generation in batch electrodialysis
As explained in section 1, the theorem of equipartition of entropy generation, developed by Tondeur and Kvaalen,18 states that, for a system of fixed size and fixed duty, the total rate of entropy generation is minimized when the spatial and/or temporal variance of the entropy generation is minimized. However, Johannessen and Kjelstrup,20 show that the theorem only strictly applies if all the driving forces can be controlled independently. In the use of electrodialysis to desalinate (or concentrate) sodium chloride, a proxy for seawater, the driving forces and the fluxes of the three species (water, and sodium and chloride ions) are not independent, and are therefore not controlled independently. The driving force of any of the species is the gradient of the electrochemical potential of that species divided by the temperature. The electrochemical potential is a function of the concentration and the electric potential. With only two controllable independent variables (i.e., concentration and electric potential), only two of the three species driving forces can be controlled independently. And with only two independent driving forces, the three fluxes cannot be controlled independently. Therefore, the conditions for the use of the theorem of equipartition of entropy generation are not strictly met. That said, the fixed entropy generation profile is still expected to yield close-to-optimal performance.20,21In their study, Tondeur and Kvaalen18 extend the optimal conditions to also include the minimization of the variance of the flux and the variance of the driving force. This extension is possible because the phenomenological coefficient, which relates the flux to the driving force, is assumed constant. In fact, Tondeur and Kvaalen18 prove the theorem by starting with the assumption of constant phenomenological coefficient, and by using the Cauchy–Schwarz inequality.
In an ED system, the electric resistance of the stack changes because of the changing concentrations. As a result, the relationship between salt flux and driving force is not constant, which means that the variances of the flux, the driving force, and the rate of entropy generation are not minimized at the same operating point. In addition, the salt flux in ED is limited by the limiting current density, which does not have the same value throughout the process because of the changing diluate concentration. Finally, some ED applications have operation-dependent losses in the form of osmosis and back-diffusion. This places the condition of constant inlet and outlet salinities and flow rates at odds with the condition of fixed total duty. In this section, we look at how each of these points affects the improved electrical operation of ED, and we compare the operation of ED under constant voltage to better operating regimes.
3.1 Effect of having a varying phenomenological coefficient on the improved electrical operation of ED
In a batch ED system, the concentrations of the diluate and concentrate channels vary with time, which causes the stack resistance, and with it the phenomenological coefficient linking the salt flux to the driving force to vary. A varying phenomenological coefficient, L, means that the variance of the entropy generation is not minimized at the same operating points that minimize the variance of the flux and the variance of the driving force. A previous study4 showed that, in the absence of osmosis and diffusion, the power consumption is minimized when the variance of the rate of entropy generation is minimized. In this section, we investigate the effect of operation under constant entropy generation and constant current density on the performance of a batch ED system, and we compare these regimes to a constant-voltage operation. The application considered in this section is that of the desalination of brackish water from 3 g kg−1 to 0.35 g kg−1 at a recovery of 80%.Fig. 2 shows the reduction in energy consumption due to the operation at constant current and at constant entropy generation relative to a constant-voltage operation at different system sizes, where the system size can be thought of as inversely proportional to the average current density. As shown in Fig. 2, the energy consumption of a fixed-current operation is not the same as that of a fixed-entropy-generation operation. This difference arises from having a stack resistance that varies with time. In addition, operation under constant entropy generation outperforms the constant-current operation, which means that, for a system of varying phenomenological coefficient, the spatial and temporal equipartition should be that of entropy generation and not of flux. This conclusion is consistent with the mathematical proof reported by Johannessen et al.,19 which generalizes the theorem of equipartition of entropy generation to systems of varying resistance, and it is also consistent with the results reported for two-stage ED by Chehayeb et al.4 For practical purposes, the local rate of entropy generation per unit area can be estimated by that due to current flowing across a resistive loss, as shown by Chehayeb and Lienhard.2 For systems with negligible diffusion and osmosis:§
 | (4) |
Further, as shown in Fig. 2, the effect of improved operation increases with increasing system size (or decreasing current density). The reason for this observation was explained in a previous study.4 The total rate of losses can be thought of as the sum of two parts: losses due to suboptimal operation, Ṡgen,imbalance, and losses that would occur if the variance of the rate of entropy generation were zero, referred to by Thiel et al.25 as the entropy generation of the equivalent equipartitioned system, Ṡgen,equip:
| Ṡgen,total = Ṡgen,imbalance + Ṡgen,equip | (5) |
As the system size is increased, Ṡgen,equip decreases because the rate of the process (represented by the average current density) is decreased, and a larger fraction of the total rate of entropy generation is due to the variance of the rate of entropy generation. As a result, improved operation, which reduces the imbalance, has a larger effect at larger system sizes.
3.2 Effect of limiting current density on the improved electrical operation of ED
A possible constraint that might arise in the improved electrical operation of ED is that related to the limiting current density. When the diluate concentration in ED is low, concentration polarization causes the concentration at the membrane interface to reach zero, which limits the current density that can be achieved. In a constant-current batch ED system, the highest applied current density is limited by the lowest limiting current in the process, which is set by the final diluate concentration (the lowest concentration).This constraint on the highest current density sets the limit on the smallest possible system size that can be used for constant-current operation. The system sizes that allow a constant-current operation are shown using a solid line in Fig. 2, and the transition to a dashed line occurs when the smallest possible system size is reached. For the system sizes represented by a dashed line, the process can be divided into two parts. The system is initially operated at constant current. When the set current density is larger than 90% of the local limiting current density, the remainder of the process is operated at 90% of the limiting current density at each time step, where the limiting current density is estimated using the following expression:
 | (6) |
The variation of current density and entropy generation with time for the smallest simulated system size is shown in Fig. 3 for operation at constant voltage, at partially constant current, and at partially constant entropy generation.
At this small system size, constant-voltage operation outperforms the operation at partially constant current by 2% and yields a similar energy consumption as the partially constant entropy generation profile. Constant-voltage operation performs well in this case because it results in a smooth entropy generation profile, as shown in Fig. 3(b), which is made possible by the changing stack resistance. When the rate of entropy generation cannot be held constant with time, its variance should be minimized, and the partially fixed profile is not necessarily the one with the smallest variance.
3.3 Effect of osmosis and diffusion on the improved electrical operation of ED
A third point to consider in the improved operation of ED is the presence of osmosis and diffusion. Osmosis and diffusion constitute flows of water and salt, respectively, in the direction opposite that which the desalination system is attempting to achieve. The ED system consumes energy to move salt from diluate to concentrate, whereas diffusion moves salt from the concentrate to the diluate, and osmosis moves water from the diluate to the concentrate. When these “leaks” are larger, a larger amount of salt needs to be transported to achieve the required desalination.The magnitudes of osmosis and diffusion depend on the system size, and on the profiles of the diluate and concentrate concentrations, which are set by the application and by the system operation. If a batch ED system is operated differently while keeping the same inlet and outlet concentrations, the total rates of osmosis and diffusion could change. As shown in Fig. 4, a system operated under constant voltage results in the largest total difference between the two concentration profiles, followed by the constant-entropy system and the constant-current system. As a result, osmosis and diffusion, and the total amount of salt that needs to be transported, are the smallest in the constant-current operation. The total current in the constant-current operation is 0.8% lower than that in the constant-entropy-generation operation, and 3.5% lower than that in the constant-voltage operation. As a result, the condition of fixed duty is no longer satisfied when the inlet and outlet salinities and flow rates are set, and the theorem of equipartition of entropy generation cannot be used to guide the selection of operating conditions when the conditions of a fair comparison outlined in section 1 are met.
 | ||
| Fig. 4 Concentration profiles of the three processes: constant voltage, constant current, and constant entropy generation. Sfeed = 35 g kg−1, and the average current density is 164 A m−2. | ||
In fact, Fig. 5 shows that the constant-current system outperforms the constant-entropy-generation system for average current densities lower than around 164 A m−2. The difference between the energy consumption of the two increases when the average current density decreases and the system size increases because of increased osmosis and diffusion. The current density and entropy generation profiles for an average current density of 164 A m−2 are shown in Fig. 6. Even though the entropy generation rate is much better balanced when entropy generation is constant, the fact that the fixed-current operation can achieve the same application by removing 0.8% less salt results in the same total energy consumption for the two operating points. As the system size is increased, the effect of the increased duty dominates and operation at constant current outperforms the operation at constant entropy generation.
In a batch process where we can control the voltage at every point in time, there are many process paths that can achieve the set desalination requirements. These processes can be divided into equal-duty groups. In each of these groups, because the condition of fixed duty is satisfied, equipartition of entropy generation is a good approximation of the optimum. From each of these equal-duty groups, we are left with one process that approximates the optimum, which leaves us with a subset of processes, each with a different combination of duty and variance of the rate of entropy generation. All of these processes can achieve the required desalination application and use the same system size, which means that we can compare them based on their energy consumption. The best process among this subset is the one that balances between a low duty and a low variance of the rate of entropy generation as was shown in a previous study for a two-stage system.4 In this paper, however, we only consider the three processes previously outlined.
In this section, we have shown that the presence of osmosis and diffusion in ED systems with the same inlets and outlets violates the condition of fixed duty required for the use of the theorem of equipartition of entropy generation, and results in operation at fixed entropy generation being a less accurate approximation of the optimum than other operating conditions (in this example, fixed-current operation).
4 Effect of improved electrical operation on energy consumption and system cost
In this section, we look at the reductions in energy consumption and in cost that are gained by going from constant-voltage operation to operation at constant current and at constant entropy generation. The possible improvements in performance due to better operation greatly depend on the system size, with larger systems yielding larger improvements because of lower Ṡgen,equip, as explained in section 3.1. It is therefore important to determine the system sizes that are cost effective. To do this, we use the cost model introduced in a previous study.3 We assume that all the fixed costs are proportional to the system size, represented by the product of the effective cell-pair area and the process time. For a continuously operated system, we calculated the cost rate of producing a flow rate of 1 m3 s−1, which resulted in cost numbers having the unit of $ per m3. For batch systems, the process time, τprocess, is varied, and the rate of production is 1 m3/τprocess. By multiplying the previous expression of cost by the process time, which is an indicator of system size, we get the following expression for cost:| C = KmAτprocess + KeE | (7) |
 | (8) |
 | (9) |
At each value of the cost ratio, r, the optimal system size, (Aτprocess)opt, is determined for each of the processes, and at those system sizes the energy and cost savings by going from a constant-voltage process to operation at constant current and at constant entropy generation are calculated for three different applications, summarized in Table 1. In choosing the concentration of sodium chloride that is equivalent to seawater, the total salinity is held constant to fix the amount of salt that needs to be removed. This approach does not capture the exact composition of seawater, and is used as a first-order approximation.
| Application | Initial salinity [g kg−1] | Final salinity [g kg−1] | Recovery ratio [%] |
|---|---|---|---|
| Brackish-water desalination | 3 | 0.35 | 80 |
| Partial seawater desalination | 35 | 1 | 70 |
| High-salinity brine concentration | 70 | 200 | 21 |
In a previous study,3 it was determined based on data from the literature that current fixed costs and electricity prices result in a cost ratio of around 134 W m−2. As shown in Table 2, constant current and constant entropy generation cannot be achieved in brackish-water desalination at this cost ratio because of limiting current density, and, as a result, operating under a partially constant current is worse than a fixed-voltage operation, and operating under a partially constant entropy generation yields a similar performance to fixed-voltage operation. As shown in Fig. 3, the current density and entropy generation profiles for constant-voltage operation at this system size are close to linear, and yield an acceptable temporal variance compared to the partially constant current and entropy generation profiles.
| Application | Improvement in energy consumption [%] | Improvement in cost [%] | ||
|---|---|---|---|---|
| Constant i | Constant | Constant i | Constant | |
| a Partially constant current density due to the limiting current density. b Partially constant entropy generation due to the limiting current density. c Constant entropy generation calculated without osmosis and diffusion. | ||||
| Brackish-water desalination | −2a | <1b | −1a | <1b |
| Partial seawater desalination | 12.5 | 13.5 | 5 | 6 |
| High-salinity brine concentration | 1 | <1c | <1 | <1c |
Operation at fixed entropy generation yields an energy reduction of 13.5% relative to fixed-voltage operation in the seawater desalination application, and also a non-pumping cost reduction of around 6%. At this system size, operation at constant current and at constant entropy generation can be achieved without being constrained by the limiting current density. In the brine-concentration case, the improvements at this cost ratio are negligible. As shown in a previous study,4Ṡgen,equip dominates in this case, and reducing Ṡgen,imbalance does not have a large effect on the total rate of entropy generation. This is because the average current density is very high, and the dominant resistance is that of the membranes, which does not vary greatly with salinity.
A question that arises at this point is: what if ED fixed costs could be decreased? Table 3 shows the energy and cost improvements at a cost ratio of 26 W m−2, a fivefold decrease from the previously considered cost ratio. At this decreased cost ratio, significant improvements happen in seawater desalination, where energy consumption is decreased by 30%, and non-pumping costs are reduced by 15% when we move away from operating at fixed voltage. Brackish-water desalination sees a non-pumping cost improvement of 5%, which is no longer negligible, and better operation of brine concentration yields a minor cost improvement of 2%.
| Application | Improvement in energy consumption [%] | Improvement in cost [%] | ||
|---|---|---|---|---|
| Constant i | Constant | Constant i | Constant | |
| a Partially constant current density due to the limiting current density. b Constant entropy generation calculated without osmosis and diffusion. | ||||
| Brackish-water desalination | 3a | 8 | 2a | 5 |
| Partial seawater desalination | 30 | 30 | 15 | 15 |
| High-salinity brine concentration | 3 | 2b | 2 | 1b |
From the results presented in this section, we can conclude that operation under constant entropy generation or constant current is necessary in the use of ED for seawater desalination. This improved operation can yield significant energy and cost improvements, especially when the relative importance of fixed costs with respect to energy costs is decreased. The improvements seen from better operation of brackish-water desalination can also be significant at lower cost ratios, especially when operation is not constrained by the limiting current density. Better operation of high-salinity brine concentration results in minor improvements, which can be explained by the already low amount of losses due to imbalance relative to the other losses.
5 Conclusions
In this paper, we have investigated the application of the equipartition of entropy generation to batch electrodialysis (ED) systems. The cases considered were brackish-water desalination, seawater desalination, and high-salinity brine concentration. The major conclusions from this paper are the following:1. The varying stack resistance in ED causes equipartition of entropy generation to be different from equipartition of flux. In the absence of osmosis and diffusion, operation under constant entropy generation was shown to perform better than constant-current operation.
2. Osmosis and diffusion in ED are process-dependent losses. As a result, changing the operation of a fixed-size and fixed-application system where these losses are important results in a change in its duty, which means that the conditions for equipartition of entropy generation are violated. In these cases, improved electrical operation balances between the minimization of the total salt flux (i.e., the duty) and equipartition of entropy generation.
3. Significant reductions in energy consumption and cost can be achieved by optimizing the operation of ED systems if unit fixed costs are decreased relative to the cost of electricity. Between the three applications studied, seawater desalination shows the greatest room for process improvement.
In practice, control to maintain a constant rate of entropy generation may be difficult, and the practical operating modes available will likely be limited to constant-current operation or constant-voltage operation. In this paper, we have shown that constant-current operation is always energetically better than constant-voltage operation and that the difference between the two increases with system size. To achieve constant-current operation, the current density can be initially set using eqn (1), which is a function of the amount of salt that needs to be removed and the available process time and membrane area. The current density can then be adjusted to account for losses like imperfect current utilization rate, osmosis, and diffusion. When the system size is small, and the required current density is above the lowest limiting current density, constant-current operation is not possible. In such cases, constant-voltage operation might outperform operation at a partially constant current.
Appendix
Major components of the transport model
In this section, the models used are briefly introduced. For additional details, the reader is referred to past studies by the present authors,2–4,22 in which the models are fully described and validated with experimental data from the literature.The first major component of the local mass transport models used is the stagnant film model. This model assumes that the fluid is very well mixed inside the channel except for a thin layer of fluid adjacent to the membranes. The thickness of the diffusion films, δ, is determined using the correlation developed by Kuroda et al.27
Inside the diffusion films, electroneutrality is satisfied because the electric double layer is taken as part of the solution–membrane interface. In addition, the Maxwell–Stefan equations are used to determine the concentration and electric potential profiles from the bulk to the solution–membrane interface, as was done by Kraaijeveld et al.28 The Maxwell–Stefan equation for species i in a solution of n species is as follows:
 | (10) |
At the solution–membrane interface, every species that is present in both media is assumed to be in thermodynamic equilibrium, with its electrochemical potential being the same in both media. The equilibrium equation and the electroneutrality equation inside the membrane (accounting for the membrane fixed charge) allow the determination of the concentrations of the ions at either end of the membrane.
For low-salinity applications, the Maxwell–Stefan equations are also used to calculate the fluxes through the membranes. The membrane properties used are taken from the work by Kraaijeveld et al.28,29
For the high-salinity application, the model developed by Fidaleo and Moresi30 is used. The salt flux is the sum of an electromigration term and a counter-diffusion term
 | (11) |
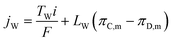 | (12) |
The final component of the model links the applied cell-pair voltage, Vcp, to the resistances and the voltage drops inside the cell pair, which are treated as part of a resistance network in series:
 | (13) |
Nomenclature
Symbols
| A | Effective cell-pair area [m2] |
| a | Activity [—] |
| C | Cost [$ per m3 product] |
| c* | Normalized cost [($ per m3 product)/($ per kW h)] |
| c | Concentration [mol m−3] |
| D | Diffusion coefficient [m2 s−1] |
| Đ ij | Maxwell–Stefan diffusion coefficient for species i and j [m2 s−1] |
| E | Energy consumption [J] |
| F | Faraday constant, 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 487 [C mol−1] 487 [C mol−1] |
| i | Current density [A m−2] |
| i lim | Limiting current density [A m−2] |
| j | Molar flux [mol m−2 s−1] |
| K e | Cost of electricity [$ per W s] |
| K m | Fixed cost per unit cell-pair area per unit time [$ per m2 s] |
| L s | Salt permeability [m s−1] |
| L w | Water permeability [mol m−2 s−1 bar−] |
| R | Universal gas constant, 8.3145 [J mol−1 K−1] |
| r | Electric resistance [Ω m2] |
| r | Cost ratio, eqn (9) [W m−2] |
| S | Salinity [g kg−1] |
| Ṡ gen | Entropy generation rate [W K−1] |
| Ṡ gen,equip | Entropy generation rate of the equivalent equipartitioned system [W K−1] |
| Ṡ gen,imbalance | Entropy generation rate due to the imbalance [W K−1] |

| Volumetric rate of entropy generation [W m−3 K−1] |

| Entropy generation rate per unit area [W m−2 K−1] |
| T | Absolute temperature [K] |
| T s | Salt transport number [—] |
| T w | Water transport number [—] |
| V | Volume [m3] |
| V | Voltage [V] |
| z | Charge number |
Greek
| Δ | Difference or change |
| δ | Diffusion layer thickness [m] |
| ∇ | Gradient |
| Φ | Electric potential [V] |
| μ i | Electrochemical potential of ion i [J mol−1] |
| π | Osmotic pressure [bar] |
| τ process | Process time [s] |
Subscripts
| C | Concentrate |
| cp | Cell-pair |
| D | Diluate |
| i | Species i |
| i | Initial |
| j | Species j |
| f | Final |
| m | At membrane interface |
| s | Salt |
| w | Water |
| min | Minimum |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank the Kuwait Foundation for the Advancement of Sciences (KFAS) for financial support through Project No. P31475EC01.References
- A. A. Sonin and M. S. Isaacson, Ind. Eng. Chem. Process Des. Dev., 1974, 13, 241–248 CrossRef CAS.
- K. M. Chehayeb and J. H. Lienhard, Desalination, 2017, 413, 184–198 CrossRef CAS.
- K. M. Chehayeb, D. M. Farhat, K. G. Nayar and J. H. Lienhard, Desalination, 2017, 420, 167–182 CrossRef CAS.
- K. M. Chehayeb, K. G. Nayar and J. H. Lienhard, Desalination, 2018, 439, 1–16 CrossRef CAS.
- S. J. Parulekar, J. Membr. Sci., 1998, 148, 91–103 CrossRef CAS.
- F. Rohman, M. Othman and N. Aziz, Chem. Eng. J., 2010, 162, 466–479 CrossRef CAS.
- F. Rohman and N. Aziz, Desalination, 2011, 275, 37–49 CrossRef CAS.
- E. G. Lee, S.-H. Moon, Y. K. Chang, I.-K. Yoo and H. N. Chang, J. Membr. Sci., 1998, 145, 53–66 CrossRef CAS.
- A. T. Tran, Y. Zhang, N. Jullok, B. Meesschaert, L. Pinoy and B. Van der Bruggen, Chem. Eng. Sci., 2012, 79, 228–238 CrossRef CAS.
- Y. Tanaka, Desalination, 2009, 249, 1039–1047 CrossRef CAS.
- H. Yan, C. Xu, W. Li, Y. Wang and T. Xu, Ind. Eng. Chem. Res., 2016, 55, 2144–2152 CrossRef CAS.
- A. Güvenç and B. Karabacakolu, Desalination, 2005, 172, 7–17 CrossRef.
- T. Sirivedhin, J. McCue and L. Dallbauman, J. Membr. Sci., 2004, 243, 335–343 CrossRef CAS.
- T. Mohammadi, A. Moheb, M. Sadrzadeh and A. Razmi, Desalination, 2004, 169, 21–31 CrossRef CAS.
- C.-V. Gherasim, J. Křivčík and P. Mikulášek, Chem. Eng. J., 2014, 256, 324–334 CrossRef CAS.
- J. M. Ortiz, J. A. Sotoca, E. Expósito, F. Gallud, V. García-García, V. Montiel and A. Aldaz, J. Membr. Sci., 2005, 252, 65–75 CrossRef CAS.
- E.-Y. Choi, J.-H. Choi and S.-H. Moon, Desalination, 2003, 153, 399–404 CrossRef CAS.
- D. Tondeur and E. Kvaalen, Ind. Eng. Chem. Res., 1987, 26, 50–56 CrossRef CAS.
- E. Johannessen, L. Nummedal and S. Kjelstrup, Int. J. Heat Mass Transfer, 2002, 45, 2649–2654 CrossRef.
- E. Johannessen and S. Kjelstrup, Chem. Eng. Sci., 2005, 60, 3347–3361 CrossRef CAS.
- E. Magnanelli, E. Johannessen and S. Kjelstrup, Ind. Eng. Chem. Res., 2017, 56, 4856–4866 CrossRef CAS.
- K. M. Chehayeb, PhD thesis, Massachusetts Institute of Technology, 2017 Search PubMed.
- A. Bejan, Advanced engineering thermodynamics, John Wiley & Sons, 3rd edn, 2006 Search PubMed.
- H. B. Callen, Thermodynamics and an introduction to thermostatistics, John Wiley & Sons, 2nd edn, 1985 Search PubMed.
- G. P. Thiel, R. K. McGovern, S. M. Zubair and J. H. Lienhard, Appl. Energy, 2014, 118, 292–299 CrossRef.
- T. W. Chapman, PhD thesis, University of California, Berkeley, 1967 Search PubMed.
- O. Kuroda, S. Takahashi and M. Nomura, Desalination, 1983, 46, 225–232 CrossRef CAS.
- G. Kraaijeveld, V. Sumberova, S. Kuindersma and H. Wesselingh, Chem. Eng. J. Biochem. Eng. J., 1995, 57, 163–176 CrossRef CAS.
- G. Kraaijeveld, PhD thesis, University of Groningen, 1994 Search PubMed.
- M. Fidaleo and M. Moresi, J. Membr. Sci., 2005, 260, 90–111 CrossRef CAS.
- R. K. McGovern, A. M. Weiner, L. Sun, C. G. Chambers, S. M. Zubair and J. H. Lienhard, Appl. Energy, 2014, 136, 649–661 CrossRef.
- R. A. Robinson and R. H. Stokes, Electrolyte solutions, Courier Corporation, 2002 Search PubMed.
- T. Shedlovsky, J. Am. Chem. Soc., 1932, 54, 1411–1428 CrossRef CAS.
- J. F. Chambers, J. M. Stokes and R. H. Stokes, J. Phys. Chem., 1956, 60, 985–986 CrossRef CAS.
- R. Mills and V. M. Lobo, Self-diffusion in electrolyte solutions, Elsevier Science, Amsterdam, Netherlands, 1989 Search PubMed.
- G. P. Thiel, E. W. Tow, L. D. Banchik, H. W. Chung and J. H. Lienhard, Desalination, 2015, 366, 94–112 CrossRef CAS.
- G. P. Thiel and J. H. Lienhard, Desalination, 2014, 346, 54–69 CrossRef CAS.
Footnotes |
| † The volumetric flow rates in the channels can be controlled by the pumps and are independent of the volume in each tank, which can change due to water flowing from the diluate to the concentrate channel. |
| ‡ Note that the systems considered in this paper are assumed isothermal, so that temperature gradients and heat fluxes are set to zero. |
| § Note that eqn (4) is only used to demonstrate a simplified relationship between current and entropy generation, and is not used in any of the calculations in this manuscript. |
| This journal is © The Royal Society of Chemistry 2019 |









