Residence times of nanoconfined CO₂ in layered aluminosilicates

Abstract

Nanoconfinement of CO₂ in layered aluminosilicates contributes to the capture and release of this greenhouse gas in soils. In this work, we show that the residence times of CO₂ in montmorillonite are lowered by 15 min for each 1 °C increment in temperature during venting. Molecular simulations showed that activation energies of release are no more than half of the experimentally derived value of 34 kJ mol⁻¹. This raised the possibility of additional processes limiting CO₂ mobility in real materials, including (chemi)sorption at reactive sites or frayed edges or defects. The residence times (∼1616 min at −50 °C to ∼6 min at 60 °C) for some of the driest (∼1.4 mmol H₂O per g) montmorillonites that can be produced at ambient temperatures are readily lowered by inclusion of additional water. They are, in turn, prolonged again as the water content and interlayer spacing become smaller through venting. These efforts showed that soil-building clay minerals will lose their propensity to dynamically exchange CO₂ as temperatures continue to rise, yet they may retain CO₂ more efficiently in cold seasons as soils will become depleted in moisture content.

---

Environmental significance

Dynamic exchange of atmospheric CO₂ with terrestrial environments includes important contributions from nanometer-thick interlayer regions of clay nanominerals. With the aim of understanding how global warming will impact soil CO₂ exchanges in the forthcoming decades, we resolved the lifetimes of this greenhouse gas under nanoconfinement in montmorillonite, a representative soil-building clay nanomineral. Our study shows that montmorillonite will lose its propensity to dynamically exchange CO₂ as soil temperatures continue to rise, yet it may retain CO₂ more efficiently in cold seasons if soils become depleted in moisture content. This study thus shines new light on the important roles that nanoparticles play in the progressively shifting biogeochemical and hydrogeological cycles of soils under a warming climate.

Introduction

Layered aluminosilicate minerals play important roles in technology and nature due to their tremendous solute and solvent exchange capacities. Those of the expandable type can readily confine gases between nanometer-thick interlamellar layers. Exchanges between these materials and CO₂ are under increasing scrutiny to follow the fate of this greenhouse gas in soils and for its deep geological storage. In particular, thawing of soils of the cryosphere is of great concern as mineral-bound and newly bio-respired CO₂ are expected to be released into the atmosphere over the next few decades.^1–3 Along these lines, a 2018 report⁴ by the Intergovernmental Panel on Climate Change highlights the devastating impact that a 1.5 °C hike in global warming could have by the end of the century.

The positive feedback to a CO₂-driven warming climate is of particular concern given that frozen soils contain about one-third of Earth's soil carbon, and that all soils contain about three times more carbon than the atmosphere.⁵ Understanding how global warming will alter land–air exchanges requires knowledge of the ability of soil-building minerals to dynamically exchange CO₂ with the atmosphere as soils begin to thaw. This is central to our ability to evaluate possibilities for geological storage of CO₂.

A primary focus on common soil-building swelling clay minerals is central because this important class of phyllosilicates entraps CO₂ between nanometre-thick layers of negatively charged aluminosilicate layers (Fig. 1).^6–11 CO₂ molecules are intercalated with their main axis parallel to the basal face (Fig. 1), either as dimers or as part of the hydration shell of interlayer cations (e.g. sodium).^12–14 Studies^9,15–20 under supercritical CO₂ conditions show that humidity facilitates uptake, and that the greatest loadings are achieved with interlayers populated with ∼1 monolayer (1W) of water. Less CO₂ can be stored at greater humidity as thicker water interlayers (>1W) suppress cation–CO₂ and CO₂–CO₂ interactions.¹² Additionally, other studies^21,22 under environmentally relevant conditions show that very high CO₂ pressures and prolonged exposure times are required to intercalate CO₂ in dehydrated clays. Seasonal and climatic variations in moisture levels – from wet to dry and from warm to cold – should therefore exert important changes in the dynamic exchanges of CO₂ with soil-building clay minerals. This can have especially important implications on the loadings and isotopic signatures of soil inorganic carbon.^23,24

Fig. 1 H₂O and CO₂ in the interlayer region of MMT taken from two separate snapshots of MD simulations. (a) Selected portion of the MMT structure showing intercalated H₂O and CO₂ between T–O–T sheets composed of Si-tetrahedra (yellow) and Al-octahedra (pink) with Mg substitutions (turquoise). (b) Selected map view of the basal plane of the T layer showing a snapshot of the distribution of interlayer Na⁺ ions (blue), H₂O (ball-and-stick white and red), and CO₂ (red oxygen, grey carbon).

To address this issue, we measured the rates of CO₂ release from the interlayer of montmorillonite (MMT), a representative soil-building swellable clay mineral. The rates were calculated from time-resolved vibration spectra of CO₂ released by venting dry and hydrated MMT over a range of temperatures well covering those of the cryosphere up to the warmest regions of the planet. Molecular simulations provided the insight needed to explain molecular interactions controlling CO₂ mobility in the interlayer region. In this study we suggest that the dynamic breathing²⁵ of CO₂ by clays will be attenuated by warming soils.

Results and discussion

CO₂ was intercalated in the interlayer of MMT upon exposure to 20 000 ppm CO₂, a representative amount in high CO₂ soils.^26,27 To uncover the intrinsic abilities of MMT to dynamically exchange CO₂, intercalation was first carried out on MMT with the lowest levels of water that can be achieved after a 30 min period of outgassing in vacuo. We note that all final water loadings were no more than 26 mg H₂O per g MMT (∼1.4 mmol H₂O per g), which is equivalent to (i) ∼23% of a 1W (∼112 mg H₂O per g MMT)²⁸ or (ii) ∼1.6 H₂O per interlayer Na⁺ if water is homogeneously distributed throughout the particles (cf. ESI† for details and Fig. S1–S5). This hydration level can therefore be regarded as one of the lowest that could be achieved by MMT in dry air at ambient temperatures. Additionally, it is responsible for maintaining a partially opened interlayer region needed to intercalate CO₂. The expanded interlayer of our samples was confirmed via mixed layer modelling of X-ray diffraction data, as discussed in the ESI† (Fig. S5).

CO₂ intercalated in Na-exchanged MMT was readily identified through a single asymmetric band of the stretching mode (ν₃) at 2343 cm⁻¹ (Fig. 2a). The 2343 cm⁻¹ band of CO₂ in this MMT was most clearly seen once free gaseous and sorbed CO₂ were evacuated from the clay (Fig. 2a and S6†). It was strongly comparable to that for supercritical CO₂ in clays^15,16 and in liquid²⁹ or solid^30,31 water, as well as in organic-based frameworks.³² The confining effects of the MMT interlayer on CO₂ are also confirmed by the absence of rotational sidebands, which are typical of gaseous CO₂ (Fig. 2a).³³ The spectra provided no other evidence of changes in water content, (bi)carbonate formation or the formation of solid CO₂ ice³⁴ (Fig. S2†).

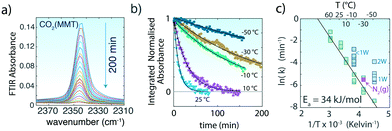Fig. 2 (a) Asymmetric (ν₃) stretching region of CO₂ of MMT (∼0W) originally exposed to CO₂(g) at −30 °C during the 200 min evacuation (<0.3 Pa). (b) Examples of loss of the normalized band area of the 2343 cm⁻¹ band during evacuation of MMT originally exposed to 20 000 ppm CO₂. Lines are generated from a first-order kinetic model. (c) Arrhenius plot of the first-order rate constants for the release of CO₂ from the interlayer region of MMT with ∼0W. The release rate of CO₂ resulting from evacuation with 101 kPa N₂(g) is shown through the pink data point at −30 °C (see Fig. S4† for data and analysis). Enhanced release rates with ∼1W and 2W at −10 °C and −50 °C, respectively, are shown in turquoise.

Intercalated CO₂ was systematically removed by prolonged exposure to vacuum, a means to simulate the action of venting on soils by displacing pore gases outside clay mineral particles. No or little changes in ∼1.4 mmol H₂O per g interlayer water took place during CO₂ release (Fig. S2†). While complete removal took place well within ∼10 min at 60 °C, it took a substantially longer time than the ∼20 min originally needed to intercalate CO₂ at lower temperatures. Consequently, this provided a first level of indication pointing to molecular forces responsible for holding CO₂ in the interlayer region.

The loss in area (a) of the 2343 cm⁻¹ band with evacuation follows first-order reaction kinetics (ln(a/a₀) = −kt, where a₀ is the band area prior to venting and k is the reaction rate), confirming that the loss of CO₂ from the interlayer region is predominantly a simple molecular desorption process (Fig. 2b). These rates revealed CO₂ residence times (τ = 1/k) ranging from τ = ∼6 min at 60 °C to ∼1616 min at −50 °C. Additionally, these rates were unchanged when CO₂ was vented by a flow of 101 kPa N₂(g) instead of vacuum (Fig. 3).

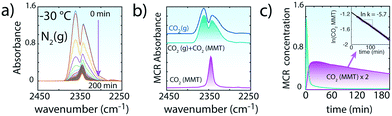Fig. 3 Evacuation of CO₂ upon flushing of 200 sccm N₂(g) to CO₂-loaded MMT (∼0.1W) at −30 °C. (a) ν₃ region of CO₂ during the ∼200 min evacuation period. In contrast to in vacuo removal, gaseous CO₂ lingers over ∼60 min in the reaction cell as MMT-bound CO₂ begins to be released to the atmosphere. The strong overlap between the spectra of free CO₂(g) and intercalated CO₂ required a multivariate curve resolution alternating least squares (MCR, version 2004)³⁵ analyses. (b) MCR spectral components for CO₂(g) + CO₂(MMT) and CO₂(MMT). (c) Concentration profiles of MCR-ALS components of (b). The values of CO₂(MMT) were used to estimate the first-order rate constant for the evacuation of CO₂ from MMT by N₂(g).

The temperature dependence of these rate constants obeys the Arrhenius relationship (ln k = ln A + E_a/RT), with an activation energy of E_a = 34 kJ mol⁻¹ (Fig. 2c). This value is ∼2.3 times larger than the one estimated for site-hopping of CO₂ within the interlayer¹³ but is most comparable to experimental desorption activation energies from bridged-bonded oxygens on TiO₂ (ref. 36) and on Mg₂SiO₄ (∼30–40 kJ mol⁻¹).³⁷ We note that the pre-exponential factor (A = 3.8 × 10⁴ min⁻¹) is seven to nine orders of magnitude lower than typical values for in vacuo desorption of CO₂ from open mineral surfaces.^36,37 We ascribe this difference to the effects of interlayer confinement, which is expected to decrease the frequency of desorption events.

In another set of experiments, CO₂ removal rates were tracked in MMT containing interlayer water at −10 °C and −50 °C (Fig. 4). The rates were generally 2–4 ln k larger than in ∼1.4 mmol H₂O per g but were also strongly coupled to the stability of interlayer water (Fig. 4b and c), which we estimate here from the O–H stretching region of water, as explained in Fig. 4 and S8.† The loss of water in 1W-bearing MMT at −10 °C was rapid within the first ∼10 min (τ = 14 min) but then slowed considerably after ∼40 min of evacuation (τ = 1213 min) (Fig. S9†). CO₂ evacuation rates followed accordingly, as highlighted by the instantaneous rates shown in Fig. 4a. In contrast, higher loadings of interlayer water were retained over longer time periods at −50 °C (Fig. 4c). High CO₂ removal rates were therefore maintained under extended periods of venting.

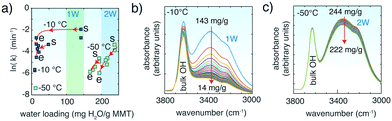Fig. 4 CO₂ release in MMT with 10–15 mg H₂O per g MMT and 1W at −10 °C and 2W at −50 °C over ∼60 min reaction time. MMT was previously loaded at the same water loadings with 20 000 ppm at −50 °C for ∼20 min. (a) Rate constants for CO₂ release. Instantaneous rates (red lines) were obtained by the first derivative of a 2nd-order polynomial function of ln(area) versus t of data (see Fig. S7† for examples). Arrows show the direction of the change in rate as water is removed from the interlayer region, from the start (‘s’) to the end (‘e’) of the evacuation period. Interlayer water loadings are estimated from the time dependence of the O–H stretching band intensities during evacuation of CO₂-loaded MMT at (b) −10 °C and (c) −50 °C. See section 1 of the ESI† and Fig. S8 and S9 for details.

Theoretical calculations of CO₂ diffusion in the interlayer region of Na-exchanged MMT added further insight into the mechanisms affecting the removal of CO₂ during venting (Fig. 5) (for basal spacing data, see Fig. S9–S11†). First, we note that simulations confirmed previous findings^19,20 showing that oxygen atoms of CO₂ at low hydration levels predominantly lie in the middle of the interlayer, with one oxygen atom above Si tetrahedra and the other over ditrigonal cavities (Fig. 1). The carbon atom interacts predominantly with the basal oxygens sharing a Si-tetrahedral edge, or occasionally with a corner sharing tetrahedral oxygen when CO₂ oxygen atoms are positioned over two corner-sharing Si tetrahedra. Under completely dehydrated conditions (0W), CO₂ molecules remain in the middle of the interlayer nanopore, but with oxygen atoms coordinating to Na⁺, which is often in ditrigonal cavities of the basal plane adjacent to sites of isomorphic substitution. Simulations also suggest that large CO₂ loadings favour dimers and clusters with a slipped plane parallel coordination.¹³ However, no such configurations could be unambiguously ascertained in the vibrational spectra (Fig. 2a) because of the strong overlap of the main 2343 cm⁻¹ band with those of dimers.^38,39

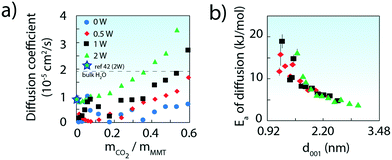Fig. 5 a) Computed diffusion coefficients of CO₂ in the interlayer region of MMT (25 °C). Values from bulk water (ref. 40) and from a comparable MD simulation of MMT at low CO₂ loadings (ref. 42) are also shown. (b) Activation energies (E_a) with d-spacing. Values were obtained from the Arrhenius relationship of diffusion coefficients obtained by molecular dynamics simulations from −10 to 50 °C.

Simulated CO₂ diffusion coefficients (Fig. 5a and S10†) were as small as 10% of bulk H₂O values^40,41 at both low CO₂ and H₂O loadings. Values were however greatly enhanced at larger CO₂ loadings, or by intercalation of greater populations of water (see full results in Tables S1–S5†). We note that our 2W value at low CO₂ loadings falls in line with another simulated value⁴² in 2W MMT.

Activation energies for diffusion (E_a), obtained by the Arrhenius relationship to computed diffusion coefficients, were also strongly loading dependent. Values were as large as ∼15–20 kJ mol⁻¹ at the lowest CO₂ loadings, and down to ∼5 kJ mol⁻¹ above 0.4 g CO₂ per g MMT (Fig. S12†). Expressed on a d-spacing basis, the trend of Fig. 5 denotes a decrease in E_a of ∼4–6 kJ mol⁻¹ per nanometer of interlayer expansion, irrespective of water loading. Expansion of the interlayer region, which can result from gains in both CO₂ and water, therefore shortens the energetic threshold of CO₂ removal during venting.

Finally, we note that the calculated E_a values are in line with previously estimated energies with site-hopping values on clays,¹³ and yet are no more than 50–60% of our experimentally derived value of 34 kJ mol⁻¹. This latter difference could point to more convoluted processes limiting the interlayer mobility of CO₂ in real materials. For instance, contributions from clay particle packing motifs, frayed particle edges,⁴³ internal defects or chemisorption could have contributed to these differences. Resolution of these and related phenomena should add further insight needed in predicting gaseous exchange involving natural soil-building materials.

Conclusions

Atmospheric exchanges of CO₂ with MMT are strongly affected by water content and temperature. MMT with low levels of resilient interlayer water (up to ∼1.4 mmol H₂O per g) stored CO₂ with residence times as long as ∼1616 min at −50 °C to ∼6 min at 60 °C. The activation energy for the release of CO₂ is 34 kJ mol⁻¹, and thus at least twice that expected from theoretical simulations on idealised MMT.

Our results suggest that as even the driest soils thaw under a warming climate, we should expect a decrease in the residence times of CO₂ of ∼15 min for each 1 °C rise in temperature. These residence times are even shorter under conditions of stable interlayer water, and especially below −10 °C, where smaller release rates of water promote CO₂ release by maintaining a large interlayer spacing in MMT. Residence times will nonetheless continue to be longer than in the warmest regions of the planet. However, considering the vast quantities of carbon stored in cold terrestrial environments, these accelerated rates are likely to result in important shifts in land–air fluxes of CO₂.

Consequently, this work suggests that exposure of CO₂-bearing soil clay minerals to increasingly longer periods of thawing will accelerate fluxes of CO₂ to the atmosphere. Conversely, exposure to cold and dry periods will increase the residence time of CO₂ in soils. Given that soil warming of the planet's cold regions is expected to be faster in the winter than in the summer months,⁴⁴ wintertime venting of soil CO₂ will likely be an increasing contributor to terrestrial emissions of CO₂ to the atmosphere in the years to come.

Experimental section

Materials

The MMT was Wyoming clay powder (SWy-2) obtained from the Clay Mineral Repository. A portion of this clay was Na-exchanged, as detailed by Schaef et al.⁴⁵ The Brunauer–Emmett–Teller specific surface area (25.3 m² g⁻¹) was calculated from 90-point adsorption/desorption N₂ gas isotherms (Micromeritics). X-ray photoelectron spectroscopy (Kratos Axis Ultra DLD electron spectrometer) was used to detect the surface compositions of Na-exchanged MMT (Na/Fe/Mg/Al/Si/O = 0.1 : 0.1 : 0.1 : 1.0 : 2.3 : 7.8) and to confirm that the particles were free of impurities, other than adventitious forms of atmospheric carbon at the 285.0 eV line.

Fourier transform infrared spectroscopy (FTIR)

Aqueous suspensions of MMT of 25 g L⁻¹ in deionized water (18.2 MΩ cm) were equilibrated for 30 min and then centrifuged at ∼2000g for 10 min. The top-to-middle portion of the centrifuged wet paste was sampled to avoid accessory minerals and then applied as a thin layer on a fine tungsten mesh (Unique wire weaving, 0.002′′ mesh diameter). Then, it was dried under N₂(g) overnight, and the mass (7–8 mg) of the resulting dry MMT film was determined. Next, the dried sample–tungsten support assembly was inserted into an electrically heated or N₂(l)-cooled copper shaft connected to a K-type thermocouple used to monitor temperature. The shaft was thereafter inserted into a transmission optical gas reaction chamber (AABSPEC #2000-A) equipped with CaF₂ windows.

The sample was dried further in vacuo (<0.3 Pa, the detection limit of the capacitance manometer; MKS, Baratron) in the reaction chamber for 30 min at 25 °C to remove atmospheric gases bound to the materials (Fig. S1†). Next, the sample was either heated or cooled to reach the desired temperature in this study (−50 °C, −30 °C, −10 °C, 10 °C, 25 °C, and 60 °C; experiments at 95 °C and 135 °C were abandoned due to excessively high rates of CO₂ release). Then, the sample was equilibrated for another 30 min. During this time, residual water contents were monitored through the O–H stretching (∼3250 cm⁻¹) and water bending (∼1630 cm⁻¹) bands. The water content in the clay was quantified using the ratio of the intensities of the 1630 cm⁻¹ (ν₃ from interlayer water) and the 1850 cm⁻¹ combination band (Si–O stretch of MMT + OH deformation),^46,47 using the water vapor binding data from Yeşilbaş et al.²⁸ A Matlab (The MathWorks, Inc.) code using this strategy is given in Table S6.†

CO₂ was intercalated in the samples upon exposure to a flow of 200 square cubic centimetres per minute (sccm) of ∼20 000 ppm CO₂. This gas mixture was prepared by mixing a 7 sccm flow of pure CO₂(g) with 193 sccm dry N₂(g) and controlled by mass-flow controllers (MKS, Baratron). A non-dispersible infrared device (Li-7000, Licor, Inc.) was used to continuously monitor the partial pressures of CO₂(g) and to ensure that the gases were free of H₂O(g). Removal of intercalated CO₂ was then observed as a function of time through the asymmetric C–O stretching band (ν₃) at 2343 cm⁻¹ upon evacuation of the reaction cell (<0.3 Pa). Repeated sessions of intercalation and evacuation showed that an exposure time of ∼20 min was sufficient to maximize the 2343 cm⁻¹ band. One experiment at −30 °C involved CO₂ removal by flushing with 200 sccm N₂(g).

All FTIR spectra of the samples were collected in transmission mode using a Bruker Vertex 70/v FTIR spectrometer equipped with a DLaTGS detector. The FTIR spectra were collected in the spectral range of 600–4000 cm⁻¹ at 4 cm⁻¹ resolution with a 10 Hz forward/reverse scanning rate. We used the Blackman–Harris three-term apodisation function with 16 cm⁻¹ phase resolution and the Mertz phase correction algorithm. Each spectrum was obtained from 100 co-added spectra and collected over an 89 s period.

Chemometrics

Multivariate curve resolution alternating least squares (MCR, version 2004)³⁵ was used to separate strongly overlapping bands of free and MMT-bound CO₂. MCR applies the Beer–Lambert law (A = εC) to extract the spectral components (ε ≥ 0) and their correlated concentrations (C ≥ 0) from a sequence of experimental absorbance (A). Calculations were performed in the computational environment of Matlab (The MathWorks, Inc.)

Molecular dynamics

Molecular dynamics simulations of CO₂-intercalated and hydrated Na⁺–MMT systems were modelled with the MD package Gromacs 2016.3.⁴⁸ Simulation cells consisted of 4 × 6 × 3 MMT unit cells with the average structural formula Na_0.66(Al_3.33Mg_0.66)(Si₈O₂₀)OH₄, corresponding to a structural charge of −0.11 C m⁻², a value typical for Wyoming montmorillonites.

The CLAYFF^19,49 force field, modified with a Morse potential for O–H vibrations,⁵⁰ was used to model clay minerals, and a flexible EPM2 model¹⁹ was used to treat CO₂ molecules. Na⁺ was modelled with the pair potentials originally optimized for the SPC/E water model.⁵¹ In this study, however, water was modelled with a flexible SPC water model.⁵² The harmonic and anharmonic terms of this model have better dielectric, vibrational and diffusive properties compared to the SPC water model used in the original parameterization of CLAYFF. CO₂ or H₂O removal from the interlayer region was mimicked through a custom-made simulation protocol allowing simulation systems to automatically generate sequentially reduced loadings. This was achieved by removing either CO₂ or H₂O molecules between production runs. Systems of fixed water populations (0–2W) were simulated with varying CO₂ content (0–10 molecules per unit cell; 0.5 g_CO2 g_clay⁻¹). Systems denoting 1.5 CO₂ and 3.0 CO₂ contained a fixed amount of 1.5 and 3.0 CO₂ molecules per MMT unit cell, and were simulated as a function of water loading by varying between 0 and 20 water molecules per MMT unit cell (0.6 g_water g_clay⁻¹).

The initial configurations with maximum loadings were equilibrated by energy minimization, a 50 ps solute restrained simulation under NVT conditions, followed by 5 ns of volume optimization under fixed NPT conditions. The production runs were performed under fixed NPT conditions for 5 ns with a 0.5 fs time step and preceded by a short equilibration step of 100 ps between the evaporative steps. Selected configurations were also simulated for an additional 10 ns using a 1 fs time step under fixed NVT conditions and individual thermostating, in order to obtain diffusion coefficients at −10 °C, 10 °C, 25 °C and 50 °C. The simulation results were analysed by computing density maps, radial distribution functions, and diffusion coefficients from the mean square displacement.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors wish to thank the insightful comments of three anonymous reviewers on an earlier version of this manuscript. This work was supported by the Swedish Research Council (2016-03808). The authors thank Eugene Ilton and Odeta Qafoku (Pacific Northwest National Laboratory) for providing the MMT samples used in this study, and the Swedish National Infrastructure for Computing (SNIC) for access to the computational facilities at the High Performance Computer Center North (HPC2N) of Umeå University and the PDC Center for High Performance Computing at KTH.

Notes and references

1. D. G. Kim, R. Vargas, B. Bond-Lamberty and M. R. Turetsky, Biogeosciences, 2012, 9, 2459–2483.
2. B. Elberling, A. Michelsen, C. Schadel, E. A. G. Schuur, H. H. Christiansen, L. Berg, M. P. Tamstorf and C. Sigsgaard, Nat. Clim. Change, 2013, 3, 890–894.
3. E. A. G. Schuur, A. D. McGuire, C. Schädel, G. Grosse, J. W. Harden, D. J. Hayes, G. Hugelius, C. D. Koven, P. Kuhry, D. M. Lawrence, S. M. Natali, D. Olefeldt, V. E. Romanovsky, K. Schaefer, M. R. Turetsky, C. C. Treat and J. E. Vonk, Nature, 2015, 520, 171.
4. IPCC, Global Warming of 1.5 °C, 2018.
5. S. A. Zimov, E. A. G. Schuur and F. S. Chapin, Science, 2006, 312, 1612–1613.
6. E. Sendula, M. Páles, B. P. Szabó, B. Udvardi, I. Kovács, P. Kónya, Á. Freiler, A. Besnyi, C. Király, E. Székely, C. Szabó and G. Falus, Energy Procedia, 2017, 114, 4934–4947.
7. J. J. Fripiat, M. I. Cruz, B. F. Bohor and J. Thomas Jr., Clays Clay Miner., 1974, 22, 22–30.
8. L. Michels, J. O. Fossum, Z. Rozynek, H. Hemmen, K. Rustenberg, P. A. Sobas, G. N. Kalantzopoulos, K. D. Knudsen, M. Janek, T. S. Plivelic and G. J. da Silva, Sci. Rep., 2015, 5, 8775.
9. Q. Rao and Y. Leng, J. Phys. Chem. C, 2016, 120, 2642–2654.
10. G. Rother, E. S. Ilton, D. Wallacher, T. Hauβ, H. T. Schaef, O. Qafoku, K. M. Rosso, A. R. Felmy, E. G. Krukowski, A. G. Stack, N. Grimm and R. J. Bodnar, Environ. Sci. Technol., 2013, 47, 205–211.
11. P. R. Jeon, J. Choi, T. S. Yun and C. H. Lee, Chem. Eng. J., 2014, 255, 705–715.
12. G. M. Bowers, H. T. Schaef, J. S. Loring, D. W. Hoyt, S. D. Burton, E. D. Walter and R. J. Kirkpatrick, J. Phys. Chem. C, 2017, 121, 577–592.
13. M. M. Sena, C. P. Morrow, R. J. Kirkpatrick and M. Krishnan, Chem. Mater., 2015, 27, 6946–6959.
14. J. J. Fripiat, in Clays and Clay Minerals: Proceedings of the Twelfth National Conference on Clays and Clay Minerals, Atlanta, Georgia, September 30, October 2, 1963, ed. W. F. Bradley, N. A. o. S. C. o. C. Minerals and N. R. Council, Symposium Publications Division. Pergamon Press, 1964.
15. J. S. Loring, E. S. Ilton, J. Chen, C. J. Thompson, P. F. Martin, P. Bénézeth, K. M. Rosso, A. R. Felmy and H. T. Schaef, Langmuir, 2014, 30, 6120–6128.
16. J. S. Loring, H. T. Schaef, R. V. F. Turcu, C. J. Thompson, Q. R. S. Miller, P. F. Martin, J. Hu, D. W. Hoyt, O. Qafoku, E. S. Ilton, A. R. Felmy and K. M. Rosso, Langmuir, 2012, 28, 7125–7128.
17. H. T. Schaef, J. S. Loring, V.-A. Glezakou, Q. R. S. Miller, J. Chen, A. T. Owen, M.-S. Lee, E. S. Ilton, A. R. Felmy, B. P. McGrail and C. J. Thompson, Geochim. Cosmochim. Acta, 2015, 161, 248–257.
18. H. T. Schaef, N. Loganathan, G. M. Bowers, R. J. Kirkpatrick, A. O. Yazaydin, S. D. Burton, D. W. Hoyt, K. S. Thanthiriwatte, D. A. Dixon, B. P. McGrail, K. M. Rosso, E. S. Ilton and J. S. Loring, ACS Appl. Mater. Interfaces, 2017, 9, 36783–36791.
19. R. T. Cygan, V. N. Romanov and E. M. Myshakin, J. Phys. Chem. C, 2012, 116, 13079–13091.
20. V. N. Romanov, Int. J. Greenhouse Gas Control, 2013, 14, 220–226.
21. L. Michels, J. O. Fossum, Z. Rozynek, H. Hemmen, K. Rustenberg, P. A. Sobas, G. N. Kalantzopoulos, K. D. Knudsen, M. Janek, T. S. Plivelic and G. J. da Silva, Sci. Rep., 2015, 5, 9.
22. H. Hemmen, L. R. Alme, J. O. Fossum and Y. Meheust, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 11.
23. E. Webb Elizabeth, A. G. Schuur Edward, M. Natali Susan, L. Oken Kiva, R. Bracho, P. Krapek John, D. Risk and R. Nickerson Nick, J. Geophys. Res.: Biogeosci., 2016, 121, 249–265.
24. S. A. Sistla, J. C. Moore, R. T. Simpson, L. Gough, G. R. Shaver and J. P. Schimel, Nature, 2013, 497, 615–618.
25. S. Ishihara, P. Sahoo, K. Deguchi, S. Ohki, M. Tansho, T. Shimizu, J. Labuta, J. P. Hill, K. Ariga, K. Watanabe, Y. Yamauchi, S. Suehara and N. Iyi, J. Am. Chem. Soc., 2013, 135, 18040–18043.
26. D. Sotomayor and C. W. Rice, J. Environ. Qual., 1999, 28, 784–793.
27. C. Kammann, L. Grunhage and H. J. Jager, Eur. J. Soil Sci., 2001, 52, 297–303.
28. M. Yeşilbaş, M. Holmboe and J.-F. Boily, ACS Earth Space Chem., 2018, 2, 38–47.
29. T. Schadle, B. Pejcic and B. Mizaikoff, Anal. Methods, 2016, 8, 756–762.
30. O. Galvez, B. Mate, V. J. Herrero and R. Escribano, Icarus, 2008, 197, 599–605.
31. M. G. Trainer, M. A. Tolbert, C. P. McKay and O. B. Toon, Icarus, 2010, 206, 707–715.
32. K. L. Kauffman, J. T. Culp, A. Goodman and C. Matranga, J. Phys. Chem. C, 2011, 115, 1857–1866.
33. P. E. Martin and E. J. Barker, Phys. Rev., 1932, 41, 209–303.
34. K. Isokoski, C. A. Poteet and H. Linnartz, Astron. Astrophys., 2013, 555, 6.
35. J. Jaumot, R. Gargallo, A. de Juan and R. Tauler, Chemom. Intell. Lab. Syst., 2005, 76, 101–110.
36. R. S. Smith, Z. J. Li, L. Chen, Z. Dohnalek and B. D. Kay, J. Phys. Chem. B, 2014, 118, 8054–8061.
37. R. S. Smith, Z. J. Li, Z. Dohnalek and B. D. Kay, J. Phys. Chem. C, 2014, 118, 29091–29100.
38. J. Norooz Oliaee, M. Dehghany, M. Rezaei, A. R. W. McKellar and N. Moazzen-Ahmadi, J. Chem. Phys., 2016, 145, 174302.
39. M. A. Walsh, T. H. England, T. R. Dyke and B. J. Howard, Chem. Phys. Lett., 1987, 142, 265–270.
40. B. Jahne, G. Heinz and W. Dietrich, J. Geophys. Res.: Oceans, 1987, 92, 10767–10776.
41. D. L. Wise and G. Houghton, Chem. Eng. Sci., 1966, 21, 999–1010.
42. G. Gadikota, B. Dazas, G. Rother, M. C. Cheshire and I. C. Bourg, J. Phys. Chem. C, 2017, 121, 26539–26550.
43. J. Wan, T. K. Tokunaga, P. D. Ashby, Y. Kim, M. Voltolini, B. Gilbert and D. J. DePaolo, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 873–878.
44. J. H. E. A. Chrisensen, in Climate Change 2013: The Physical Science Basis. Contribution of Working Group 1 to the Fifth Assessment Report of the Intergovernmental Panel on Climate Changed, Press Cambridge, U.K., and New York, 2013.
45. H. T. Schaef, E. S. Ilton, O. Qafoku, P. F. Martin, A. R. Felmy and K. M. Rosso, Int. J. Greenhouse Gas Control, 2012, 6, 220–229.
46. M. Szczerba, A. Kuligiewicz, A. Derkowski, V. Gionis, G. D. Chryssikos and A. G. Kalinichev, Clays Clay Miner., 2016, 64, 452–471.
47. A. Kuligiewicz, A. Derkowski, M. Szczerba, V. Gionis and G. D. Chryssikos, Clays Clay Miner., 2015, 63, 15–29.
48. D. van der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718.
49. R. T. Cygan, J. J. Liang and A. G. Kalinichev, J. Phys. Chem. B, 2004, 108, 1255–1266.
50. J. A. Greathouse, J. S. Durkin, J. P. Larentzos and R. T. Cygan, J. Chem. Phys., 2009, 130, 7.
51. I. S. Joung and T. E. Cheatham, III, J. Phys. Chem. B, 2008, 112, 9020–9041.
52. D. M. Ferguson, J. Comput. Chem., 1995, 16, 501–511.

---

Footnote

† Electronic supplementary information (ESI) available: Fig. S1–S11 and Tables S1–S6. See DOI: 10.1039/c8en01156g

---