Electrochemical characterization of natural organic matter by direct voltammetry in an aprotic solvent

Abstract

The complex and indeterminant composition of NOM makes characterization of its redox properties challenging. Approaches that have been taken to address this challenge include chemical probe reactions, potentiometric titrations, chronocoulometry, and voltammetry. In this study, we revisit the use of direct voltammetric methods in aprotic solvents by applying an expanded and refined suite of methods to a large set of NOM samples and model compounds (54 NOM samples from 10 different sources, 7 NOM model compounds, and 2 fresh extracts of plant materials that are high in redox-active quinonoid model compounds dissolved in DMSO). Refinements in the methods of fitting the data obtained by staircase cyclic voltammetry (SCV) provided improved definition of peaks, and square wave voltammetry (SWV), performed under the same conditions as SCV, provided even more reliable identification and quantitation of peaks. Further evidence is provided that DMSO improves the electrode response by unfolding some of the tertiary structure of NOM polymers, thereby allowing greater contact between redox active functional groups and the electrode surface. We averaged experimental peak potentials for all NOM compounds and calculated potentials in water. Average values for E_pa1, E_pc1, and E_p1 in DMSO were −0.866 ± 0.069, −1.35 ± 0.071, and −0.831 ± 0.051 V vs. Ag/Ag⁺, and −0.128, −0.613, and −0.0930 V vs. SHE in water. In addition to peak potentials, the breadth of SCV peaks was quantified as a way to characterize the degree to which the redox activity of NOM is due to a continuum of contributing functional groups. The average breadth values were 1.63 ± 0.24, 1.28 ± 0.34, and 0.648 ± 0.15 V for E_pa1, E_pc1, and E_p1 respectively. Comparative analysis of the overall dataset—from SCV and SWV on all NOMs and model compounds—revealed that NOM redox properties vary over a narrower range than expected based on model compound properties. This lack of diversity in redox properties of NOM is similar to conclusions from other recent work on the molecular structure of NOM, all of which could be the result of selectivity in the common extraction methods used to obtain the materials.

---

Environmental significance

Natural organic matter (NOM) is a major component of many important environmental processes, including carbon sequestration, primary productivity, and contaminant degradation. The role of NOM in these processes usually involves oxidation–reduction (redox) reactions, which has made the redox properties of NOM among their most widely studied characteristics. The results from this and other recent studies provide increasingly reliable redox property data for NOM, which should enable more quantitative assessments of biogeochemical redox processes that involve NOM.

1. Introduction

A defining characteristic of environmental science is that many of its grand challenges arise from the indeterminate composition of environmental materials. This is true of the mineralogical materials that comprise soils, sediments, and aquifers, but it is even more true of the natural organic matter (NOM) that is abundant in these compartments, as well as in surface waters, rain water, atmospheric aerosols, etc. Inevitably, the composition of NOM varies across these compartments, as well as spatially and temporally within compartments, due to variation in the source material and extent of diagenesis. This has led to a vast amount of research on the molecular structure and macromolecular composition of NOM,^1–19 but quantitative characterization of the diversity of NOM is complicated by its indeterminant structure.

The indeterminant composition of NOM is often dealt with by (i) fractionation to decrease structural diversity and/or (ii) fingerprinting to encompass the whole range of NOM structural diversity. The various methods for fractionation of NOM have been optimized, standardized, compared, and criticized over many years of study,^7,20–24 and during this process they have become deeply embedded in the literature on all aspects of NOM. The methods used to fingerprint NOM have expanded with advancements in the availability of high-resolution instrumentation, beginning with Fourier transform infrared spectroscopy (FTIR) and nuclear magnetic resonance (NMR),^15,25–34 then fluorescence excitation emission matrices (EEMs),^35–39 and most recently Fourier transform ion cyclotron resonance mass spectrometry (FTICR-MS).^{5,6,9,10,19,20,22,24,40–43} The increasingly wholistic characterizations of NOM obtained from fingerprinting methods have renewed concerns over the representativeness of NOM samples obtained by extraction methods,^7,21,24 and growing recognition that sample preparation for fingerprinting can introduce biases due to fractionation.^{19,20,22–24,44}

The ultimate motivation for on-going work on the characterization of NOM structure and composition is to enable new insights into its fate and effects. Currently, the main focus of this work is on the bioavailability of carbon in NOM, because of its role in the global carbon cycle, and implications for climate change.^40,45–51 The other major applications of NOM characterization are to its role in biogeochemistry,^46,52–56 and contaminant fate.^57–73 In both of these contexts, NOM participates in reactions as a ligand,^74–78 electron donor/acceptor,^{53,56,79–87} electron shuttle (i.e., electron-transfer mediator),^88–95 and/or catalyst.^91,95 Most of these are redox reactions, so the thermodynamics, kinetics, capacity, and mechanisms of redox reactions involving NOM have been studied extensively. The majority of this work has focused on probe reactions (usually involving model contaminants),^60,67 but spectroscopies such as electron paramagnetic resonance (EPR),⁹⁶ X-ray absorption spectroscopy (XAS),⁹⁷ and electrochemical methods have also proven useful.

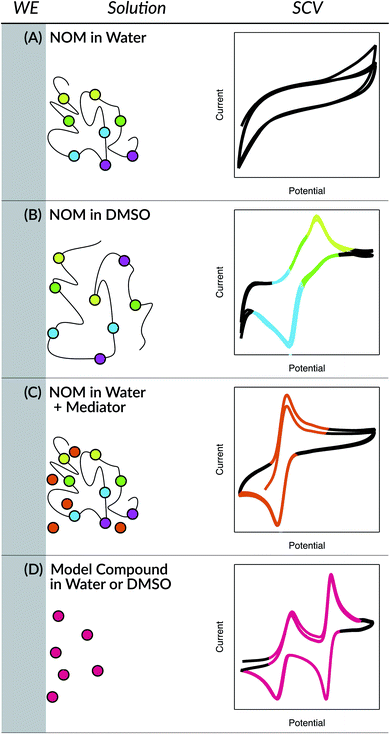
The earliest applications of electrochemical methods to the study of NOM extend back to the 1950's and include a surprisingly wide range of methods, but as late as the 1990's these methods were still not producing data that was amenable to quantitative analysis.⁹⁸ Since then, two innovations have greatly improved the resolution and quantification of electrochemical data on NOM: the use of aprotic solvents (e.g., dimethyl sulfoxide (DMSO)) and the addition of electron-transfer mediators (ETMs or electron “shuttles”). In both approaches, the key innovation (the solvent or the shuttle) is believed to improve the electrode response to NOM by facilitating interaction between the working electrode surface and redox-active functional groups in the NOM.⁹⁸ In the former approach, the solvent allows unfolding of the NOM's tertiary structure, thereby exposing protected functional groups to the electrode. In the latter approach, the size and mobility of the shuttle compounds allow it to diffuse between the protected functional groups and the electrode surface. These conceptual models are summarized in Fig. 1, with representative data from cyclic voltammetry that is explained later.

Fig. 1 Conceptual model of interactions between NOM and a working electrode (WE), with colored circles representing different moieties of electroactive functional groups. (A) NOM in water where its tertiary structure protects redox-active groups from the electrode, (B) NOM in DMSO where unfolding allows direct contact of some groups, (C) NOM in water where soluble mediators (red circles) shuttle electrons between NOM and the electrode, and (D) model or shuttle compounds in DMSO, which stabilizes one-electron transfer products. In each case, an example voltammogram is shown (right column) with sections colored to match the specific functional group markers in the cartoon.

Electron-transfer mediators have many well-established uses in electrochemistry,^99–102 but the benefits of including ETMs in the electrochemical characterization of NOM has been demonstrated only recently.^80,83,103 The most popular approach—called mediated electrochemical reduction and oxidation (MER and MEO, respectively)—involves chronoamperometry applied to aqueous solutions of NOM and an ETM (selected for solubility, reversibility, pH-independence, and E within the expected potential of the target redox couple). Constant potentials, above and below the reported analyte potentials, are applied and the resulting current or charge passed is measured and used to calculate electron donor and acceptor capacities (EDC and EAC). The use of MER/MEO to measure EDC/EAC is primarily for characterizing the capacity of NOM to serve as a reservoir of electrons in biogeochemical processes. However, mediated electrochemical methods can also been used to characterize the kinetics of electron transfer to/from NOM, if the mediator/electrode reaction is comparatively fast,⁸² or to estimate the potentials of NOM. During bulk mediated chronoamperometry, as the analyte gets reduced (or oxidized) the E_H changes, and the fraction of reduced to oxidized species increases (or decreases) with time. By using these data (change in E_H, and the fraction of reduced to oxidized species) in the Nernst equation, a coefficient can be extracted and used to calculate a theoretical potential.^83,104,105 The latter two applications of MER/MEO are indirect measures of the target properties and therefore require careful attention to the assumptions of the method in order to avoid misleading results.¹⁰⁶

Aprotic solvents have long been used in organic electrochemistry,^107–115 and also have only recently been shown to be useful for characterization of NOM redox properties.^98,116,117 This approach was rooted in recognition that NOM under aqueous conditions develops tertiary structure, which could result in protection of redox active functional groups from direct interaction with electrodes. This effect might arise if the tertiary structure of NOM had micelle-like character, which was proposed for humic substances (HS) in 1978,¹¹⁸ and has since been supported by results obtained by a variety of methods. For example, fluorescence spectroscopy using pyrene as a fluorescent probe molecule that should partition into the hydrophobic interior of a micelle and bromide as a flourescence quencher that should be excluded from the micelle.^119,120 Other evidence consistent with the micellar character of NOM include (i) the surface tension of water being lowered by HS and increasing solubility of organic compounds that are otherwise insoluble in water without HS present;¹²¹ and (ii) that addition of organic acids and observed structural changes suggested micelle type formation and hydrophobic bonding that plays a key role in aggregation.¹²² Because NOM is complex it cannot be directly compared to a surfactant that would simply form micelles, but rather has many different associations with one molecule having varying effects of coiling and folding.

A better model for the tertiary structure of NOM—and how it influences electrode response—might be the self-assembly of biological molecules such as proteins, lipids, and DNA. This analogy is justified by the similarity in H-bonding interactions between moieties in these polyelectrolytes.^18,123,124 Disassociation of H-bonds is favored by aprotic solvents like DMSO,¹²⁵ so it has long been used as a solvent for polyelectrolytes like proteins and lignin.^126–128 DMSO has also been used as a (co)solvent for NOM, where it has been found to increase the quantity of humin recovered by the standard alkaline extraction method,³¹ the diversity of organic matter obtained by alkaline extraction of soils and sediments,¹²⁹ and the quantity of hydrophobic moieties detected during structural characterization of NOM by high resolution NMR.¹²⁵ Analogous benefits from the solvency of DMSO have been reported in studies of proteins, including reducing binding affinities of proteins,¹³⁰ protein unfolding,^131,132 DMSO affecting protein charge,¹³⁰ and aiding in electron transfer.^133–135

While mediators and aprotic solvents can greatly improve the electrode response of polyelectrolytes like proteins and NOM, other advances in electrochemical methodology can also have significant benefits. One such opportunity for method refinement concerns the working electrode composition (e.g., various forms of carbon vs. noble metals) and configuration (e.g., micro vs. reticulated). Another such opportunity concerns methods of data acquisition (e.g., voltametric waveform) and analysis (various corrections and transforms). In our original work on NOM in DMSO,¹¹⁷ we gave limited attention to these opportunities, including only preliminary experiments with microelectrodes and square wave voltammetry.^98,116 Recently, we have done an extensive study of phenol redox properties (including common NOM model compounds) and demonstrated several advantages to using square wave voltammetry, and we have noted studies that have very successfully applied square wave voltammetry with analysis methods to the electrochemical characterization of the redox properties of proteins.¹³⁶ Given the analogy (noted above) between the challenges to doing electrochemistry on proteins and NOM, we hypothesized that an optimized combination of these method developments might provide a significant improvement in direct electrochemical characterization of NOM redox properties.

The objectives of this work include development of optimized methods for direct electrochemical characterization of NOM, comparison of the most promising methods to clarify ways in which the methods are complementary, demonstration of the applicability of these methods to NOM samples from a wide ranges of sources, and analysis of the data for correlations that provide new insight into the redox activity of NOM. For comparison with the results obtained with 54 samples of NOM, the same suite of electrochemical methods was applied to 7 quinonoid model compounds and 2 fresh plant abstracts. A notable overall result was the general lack of diversity in measured redox properties of NOMs (compared with the model compounds), which is interpreted as evidence that the extraction methods used to obtain most samples of NOM favor a relatively narrow range of redox-active functional groups.

2. Experimental

2.1. Materials and reagents

All of the NOM samples used in this study are listed as ESI in Table S1,† together with the available meta data on each sample's source, composition, and key references. The model compounds selected for this study are listed in Table S2,† and their molecular structures are given in Fig. S1.† The calculated values of pK_a's for each model compound in water and DMSO are given in Table S3.† Additional model compounds used during method development—including 2,2′-azino-bis(3-ethylbenzothiazoline-6-sulphonic acid)diammonium salt (ABTS), 2,6-dichloroindophenol (DCIP), and resorufin (RSZ)—were all obtained from Sigma Aldrich. These and other chemical regents including—dimethyl sulfoxide (DMSO), tetrabutylammonium hexafluorophosphate (TBAFP), potassium chloride (KCl), mono and di-potassium phosphate—were ACS reagent grade and used as received without further purification.

Two different methods were used to prepare solutions of NOM for analysis: (i) if there was sufficient loose powder of the sample for subsampling, then, preweighed portions were dissolved in DMSO to form stock solutions that could be used over multiple experiments; (ii) if sample quantity was insufficient for this, all of the sample container contents were washed into the cell with two ∼1 mL volumes of electrolyte from the background scan, and the difference in container weight before and after washing was used as the quantity of NOM. In general, the target final concentration of the NOM in the cell was 1 mg mL⁻¹, but the concentration was less for samples that did not fully dissolve or for which the total sample mass was limited. Stock solutions of NOM in DMSO were stored in amber bottles and used within three days (even though control experiments shown in Fig. S15† indicate there was not a significant effect of aging on the electrochemical results).

In a few cases, dry powders of plant material were purchased (Mountain Rose Herbs, Eugene, OR) and extracted using DMSO or H₂O. For these extractions, 500 mg of black walnut hull or pau d'arco bark (natural sources of juglone and lapachone, respectively) were dissolved in 5 mL of DMSO, or in 5 mL of ultrapure Millipore water, then left to mix for 24 h and centrifuged. The supernatant was removed and analyzed by SCV and SWV (Fig. S16†) as detailed below. For the aqueous samples, a second extraction was performed using DMSO after the powder was oven dried at ∼200 °C for 24 h.

2.2. Electrochemical methods

For the NOM samples, all square-wave voltammograms (SWVs) and staircase cyclic voltammograms (SCVs) were obtained with a Metrohm Autolab PGSTAT30. The model NOM compounds were characterized with a Princeton Applied Research VersaSTAT4, a Pine AFCBP1 Bipotentiostat, and the PGSTAT30. There were no significant differences between the data obtained using the three different potentiostats. All of the voltammograms were acquired at an amplitude of 25 mV (SWV) and with a step size of 2 mV (SWV and SCV), based on method optimizations that we performed in a previous study on the electrochemistry of phenols and anilines.¹³⁷ The effect of SWV scan rate has greater diagnostic value, so it was performed at 25, 125, and 225 mV s⁻¹ (which are designated SWVi, SWVii, and SWViii, respectively, in some figures). The SCV scan rate was always 25 mV s⁻¹ and is labelled SCVi. Most runs were performed at least in duplicate.

The peak potentials summarized in Tables S4 and S5† were obtained from voltammetry data using both Nova 2.02 (Metrohm, Herisau Switzerland) and Igor Pro 7 (Wavemetrics, Lake Oswego, OR) software. For NOM samples, peak data were determined using cubic baseline and Gaussian fit functions in Igor's multi-peak fit module, with manual adjustment of peak start and stop positions only when necessary. For the model compounds, peak data were determined using either the manual or automatic peak selection/integration tools in Nova 2.02. The results obtained by these methods were compared on selected datasets and no significant differences were found. However, data analysis with Nova generally was faster (so preferred for well-defined peaks from the model compounds), and Igor gave greater control (needed for the less-well defined peaks from most NOM samples).

All measurements were made in a three-electrode cell with a low profile 1.6 mm diameter platinum working electrode (Pine Research Instrumentation), and a 0.5 mm diameter coiled platinum wire counter electrode, and a reference electrode. For aprotic conditions, the reference electrode was a Ag/Ag⁺ reference electrode (BASi) filled with 0.1 M TBAFP and 0.010 M AgNO₃, whereas experiments in aqueous media were performed using a Ag/AgCl reference electrode (BASi) filled with 3.0 M KCl. The reference electrode for aprotic conditions had BASi's exchangeable CoralPor tip for the liquid junction, and required frequent changes (every 3 days) during continuous experiments in DMSO. For comparison, a low profile 3.0 mm glassy carbon working electrode (Pine Research Instrumentation) was used in some runs with NOM model compounds. All potentials measured in aprotic solvent are reported vs. the Ag/Ag⁺ reference electrode and those done in aqueous medium are reported vs. the Ag/AgCl reference electrode.

Before each set of electrochemical measurements, the working electrode was polished using 0.05 μm MicroPolish Alumina (Buehler), rinsed with DI water, sonicated for 2 min, and rinsed again with DI water. The electrochemical cell was prepared by adding 5 mL of 0.1 M TBAFP in DMSO, or 5 mL of 0.1 M KCl and 0.1 M phosphate buffer (pH 7.0), and purging for 15 min with N₂ (ultra-high purity), purging of the cell headspace was continued during the experiments. After deaeration, a background scan was performed and 0.5 mL of the analyte stock solution was added so the final concentration in the cell was 1.5 × 10⁻³ M for NOM model compounds (where possible, but not all of these compounds were completely soluble in either water or DMSO), or 1 mg mL⁻¹ for NOM (for the 17 samples that fully dissolved, and less for the 37 that did not). For the DMSO extracts of plant material, the concentration was 2 mg mL⁻¹. Details on how the electrochemical measurements were performed are described below under method development.

3. Results and discussion

3.1. Selection of method conditions

In preliminary experiments, various combinations of NOM and model compounds, solvents, and mediators were tested using four working electrodes: 1.6 mm platinum, 3.0 mm glassy carbon, 5.0 mm edge plane pyrolytic graphite (all macro electrodes from Pine), and a 10 μm platinum electrode (BASi). The 1.6 mm platinum electrode gave the most consistent and characteristic response (data not shown), so it was used for all subsequent experiments.

Additional preliminary experiments were done to test whether the combination of added mediators and SWV would give improved characterization of NOM under aqueous conditions. Using one type of NOM (NOM-GT) with three common ETMs (Fig. S2A†) and one mediator (ABTS) with several types of NOM (Fig. S2B†), both gave SWVs that appear to be dominated by the mediator response (Fig. S2C and D†). Based on these results, we decided not to include mediators in most experiments with NOM.

To confirm that direct voltammetry of NOM (without mediators) is best done in 100% DMSO, and that DMSO as a co-solvent in predominantly aqueous media is not as effective, we performed otherwise identical experiments on Georgetown NOM in water with and without added DMSO (Fig. S2A†), and in DMSO with and without added water (Fig. S2B†). When the primary solvent was water, the sample voltammograms contained no more well-defined features than the solvent-only control; but when DMSO was the main solvent, the sample voltammograms gave clear peaks with currents that were 2–3 times the size of any features in the control. Similar exploratory experiments with other solvents (isopropanol, acetonitrile, etc.) did not show the advantages of DMSO. Therefore, all subsequent experiments were done with 100% DMSO as the solvent. Note that no effort was made to remove traces of water from the DMSO, as is often done in applications of organic electrochemistry that require rigorously aprotic media.^111–113

3.2. Method validation using model quinones

The conditions and protocols selected for electrochemical characterization of NOM were first applied to a variety of model compounds, most of which are known to be well-behaved ETMs from prior studies of their electrochemistry.^99,138–141 Of the seven model compounds we tested (Table S2 and Fig. S1†), six were derivatives of ortho- or para-naphthoquinones and one was a para-anthraquinone. These quinones were further distinguished by hydroxyl, alkyl, or sulfonate substituents. An example of the resulting SCV and SWV data (for AQDS) can be seen in Fig. 2A and all of the model compound data are shown in Fig. S3.† In all cases, the model compounds gave SCVs and SWVs that are typical of reversible quinone-hydroquinone couples in aprotic solvents.^{107,111,117,142} In such cases, SCVs typically exhibit anodic and cathodic peaks that differ by 59/n mV, where n is the number of electrons transferred in the reaction, and the ratio of anodic to cathodic peak currents should be ∼1.¹⁴³ Also, the corresponding SWV peak potential should be the average of potentials of the anodic and cathodic SCV peaks (i.e., (E_pa + E_pc)/2). All of these conditions apply to the data obtained in this study for AQDS (Fig. 2A) and most of the other quinone model compounds (Fig. S3†).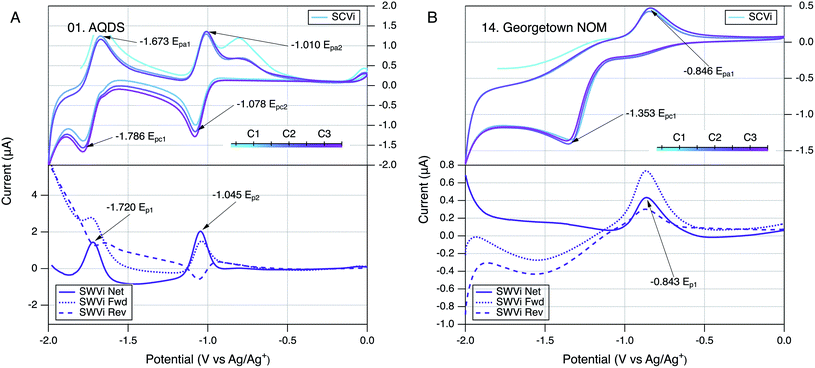

Fig. 2 Comparison of SCV (top) and SWV (bottom) for (A) AQDS and (B) Georgetown NOM. Only scan rate (i) is shown (25 mV s⁻¹), but others are given in Fig. S3.01 and S4.14.† The color gradient in the SCVs represents the potential sweep through cycles labelled C1, C2, and C3 in the legend. All runs in DMSO with a Pt working electrode.

Comparing the voltammograms for the whole set of model compounds (Fig. S3†) reveals some differences that could shed light on their relevance to redox reactions of NOM. One such comparison is between the six quinones and sphagnum acid, which is a p-alkyl substituted phenol. Like most phenols,¹³⁷ it oxidizes to a phenoxy radical, which is less stable than semiquinone radicals, resulting in irreversible peaks similar to those observed in NOM (as discussed below). Another comparison is between the quinones that give increasing current from the beginning of each anodic scan (AQDS, lawsone, menadione, and menaquinone-4) and those that show a delayed response and anodic peaks that begin only above about −1.5 mV (juglone and o-NQS). The difference between these two groups is most likely due to substituent effects. For example, sterically bulky substituents, like the one on menaquinone-4, will have a more negative redox potential than a quinone with a charged substituent, like o-NQS with its SO₃⁻ group.¹⁴⁴ Depending on the microenvironment surrounding the redox active groups in NOM, the onset and magnitude of potentials will shift accordingly. Lawsone is unique among the quinones studied in that the second peak on the anodic scan is shifted to higher potentials (∼0 mV), which likely is due to H-bonding involving the hydroxy group ortho to the quinone/semiquinone.¹⁴⁵

Another consistent characteristic of the model quinone data is that the SCVs show deviation between the first anodic potential scan and the later cycles. This type of deviation is common and reflects a variety of processes needed to develop the conditions required for stable and reversible electrode response. Since these experiments were prepared using only pure quinones, the shape of the first anodic scan is determined partly by the reduction of that starting material at the beginning of the scan, the oxidation of which then causes the anodic peaks even in the first and subsequent cycles of the SCV. This was ensured by preceding each SCV with 5 s induction period, during which −2 V was applied at the working electrode.

3.3. Method application to natural organic matter

Preliminary characterization of the overall stability of the controlling reactions during electrochemical experiments with NOM was done by comparing SCVs obtained over a sequence of three scan cycles.¹⁴³ In most of the SCV figures shown in this study (model compounds and NOMs), the progression of the scans is represented by a color gradient (teal to pink) and the cycles are labelled C1 to C3 in the corresponding legend (e.g., Fig. 2). Qualitative changes in SCV shape over multiple cycles can indicate changes in the reactions controlling the electrode response. This is commonly observed during the first scan, as was discussed above for the SCVs for model quinones included in this study. Another well defined example of this effect that can be seen in our previous work on electrochemistry of phenols and anilines, which typically showed featureless first anodic scans because the subsequent cathodic scan is needed to produce the reduction products that give electrode response in the next anodic scan.¹³⁷ In this study, the first anodic scan of SCVs with some NOMs also gave a different electrode response, but subsequent cycles were very similar for most NOMs, suggesting that the controlling interfacial reactions had stabilized (e.g., Fig. 2B).

In our original study of NOM electrochemistry in DMSO,¹¹⁷ the SCVs for most NOMs that we studied gave anodic and cathodic peaks at potentials that differed by a few hundred millivolts, which we interpreted as evidence of quasi-reversible redox couples. In the current study, the SCVs obtained with some NOM samples might also have been interpreted as containing quasi-reversible anodic–cathodic peak pairs (e.g., Fig. S4.11, 4.13, 4.14, and 4.16†), but the wide range of NOM types included in the scope resulted in relatively few SCVs that could be interpreted reliably in this way. A typical example of an NOM that does not appear to give reversible or quasi-reversible electrode response is Georgetown NOM (Fig. 2B), where the dominant anodic and cathodic peaks are well defined but not close enough in potential to be interpreted as the result of one electroactive redox couple. In these cases, the forward and reverse currents in SWV confirm this by the presence of two oxidation (or reduction) peaks in both the forward and reverse directions of the scan.

Another operational factor with diagnostic value in voltammetry is scan rate. The effects of scan rate on SCVs are confounded by multiple factors, so they were performed only at one, slow scan rate (25 mV s⁻¹, where time for decay of the capacitive current should provide more purely faradaic electrode response.^143,146). However, compared with SCV, the data obtained by SWV is less confounded with capacitive current and therefore the effect of scan rate on SWVs is better defined.¹⁴³ To explore this, we measured SWVs at three scan rates for all NOMs and model compounds and all of these data are documented in Fig. S3 and S4.† In all cases, increasing scan rate increased the net SWV current, but had negligible effect on the potentials of the major anodic peak. Therefore, only one scan rate (the slowest) was used in the quantitative analysis of SWV peak potentials presented below.

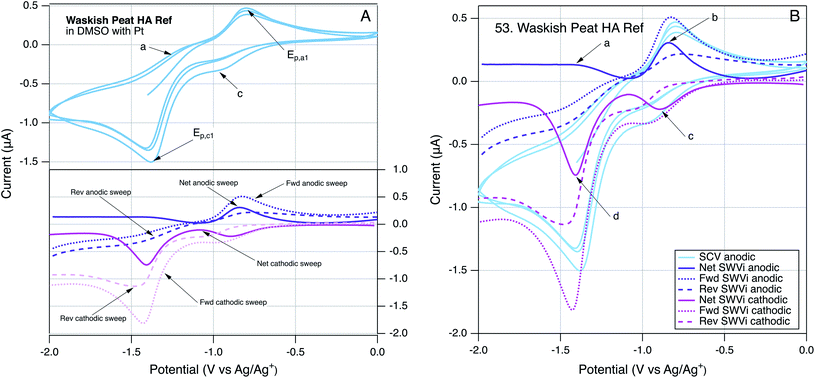
To provide further insight into the robustness of our method for direct electrochemical characterization of NOM, we took the somewhat unusual step of running SCVs and SWVs by scanning potential in the cathodic, as well as anodic, direction. Because the SCVs were identical regardless which direction the scan was initiated, only SCVs initiated in the anodic direction are reported. However, the SWVs gave different results when scanned in the anodic or cathodic direction, and these differences can be diagnostic of electrode processes.¹⁴⁷ An example of these data is given in Fig. 3, using Waskish Peat Reference Humic Acid because it was a good representation of the behavior of the majority of the NOM data. Fig. 3A shows the SCV (top, initiated anodic, three cycles, without color gradient) and SWVs (bottom) performed by scanning potential in the cathodic (pink) and anodic (purple) directions. To facilitate quantitative comparisons, all of these data are superimposed in Fig. 3B, and the SWV peaks are labeled: (a) and (b) for the anodic scan and (c) and (d) for the cathodic scan.

Fig. 3 SCV (blue) and SWV anodic (purple) and cathodic (pink) sweeps for Waskish Peat HA. For SWV, forward, reverse, and net currents are shown with dashed and solid lines. (A) SCV and SWV separated and annotated to identify each component; a and c in the SCV show anodic and cathodic analogues discussed below. (B) SCV and SWV data are superimposed for comparison. All measurements made at scan rate of 25 mV s⁻¹, 2 mV step size, and 25 mV amplitude using a Pt working electrode.

3.4. Qualitative comparison of NOM voltammograms

The main features in Fig. 3A are the two major peaks in the SCV (labelled E_pa1 and E_pc1) and the corresponding peaks (at the same potential) in the net current data for anodic and cathodic SWVs. The SCV also shows a shoulder that could be the cathodic analog to E_pa1 and hump that could be the anodic analog to E_pc1 (labelled c, and a respectively). Pairing the shoulder with E_pa1 is supported by their alignment with the potentials of the peaks in the net anodic and cathodic SWV data (Fig. 3B, peaks b and c). However, resolving the net anodic SWV data into forward and reverse components (dashed lines) shows they are roughly parallel, in constrast to the inverse relationship expected if peak b were due to a reversible electrode reaction (e.g., see E_p2 for AQDS in the bottom of Fig. 2A for AQDS). This evidence for irreversibility of the first anodic peak of NOM also can be seen in Fig. 2B, for Georgetown NOM, and most of the other NOMs studied (Fig. S4†). In contrast to the anodic results, the cathodic SWV for peak c shows net, forward, and reverse currents that are indicative of a quasi-reversible reduction reaction. The improved resolution of this feature in the SWV relative to the shoulder in the SCV could just be due to the higher sensitivity of SWV, but it could also arise because irreversible oxidation products formed during the forward scan of SCV interfere with the electrode response during that reverse scan (whereas the cathodic SWV is not preceded by an anodic scan).

The other main feature in the SCV shown in Fig. 3A is the large cathodic peak labelled E_pc1. In this case, the corresponding SWV feature is the peak in the cathodic scan that is labelled d in Fig. 3B. As with peak b, the net current that defines peak d is the result of forward and reverse components (dashed lines) that are roughly parallel, and therefore indicative of an irreversible electrode reaction. The putative anodic analog to E_pc1 is the hump labelled a in Fig. 3A, but inspection of the corresponding region of the SWV data shows no peak in oxidation current at the point labelled a, and significant peak in reduction current labelled d, which is consistent with the electrode process that causes E_pc1 being fully irreversible. This analysis of electrode processes responsible for E_pc1, and above discussion regarding E_pa1, illustrates how SWV data can be used to clarify the interpretation of otherwise ambiguous features of SCV data on complex materials such as NOM. Similar interpretations apply to the data obtained with many of the NOMs included in this study (Fig. S4†).

In addition to the four characteristic peaks and shoulders labelled (a, b, c, and d) in Fig. 3, some of the SCVs for NOM had another distinctive characteristic: a sharp increase in current from the beginning of each anodic scan, an example of which can be seen in Fig. 2B. In some cases, this feature is prominent enough to clearly define a new peak (e.g., Bemidji FA (S4.02), Kitty Hawk NOM (S4.20), Red Tussock NOM (S4.35), Rio Negro NOM (S4.36) and Suwannee River NOM (S4.50)), but in most cases it produces only a shoulder (Fig. S4†). The SCVs for model quinones do not show this feature (except possibly AQDS), but it is prominent in the SCV for the model phenol Sphagnum Acid Fig. S3.07.† This combination of results suggests that the sharp rise in current at the beginning of the anodic scan involves oxidation of species derived from phenolic moieties, which are more prevalent in NOM then quinonoid moieties. The feature is often absent from the first anodic sweep by SCV, which could indicate that it reflects oxidation of species formed during the previous cathodic scan, similar to the interpretation given in a study of analogous features in SCVs of nitrobenzene in DMSO.¹⁴⁸ However, inspection of the SWV data obtained in this study shows that when NOMs gave an analogous peak in the net SWV data (at about −1.8 V), it was mainly due to increased current in the forward scan, and there generally was no change in the SWV reverse scan. Since the former is anodic, it confirms that the sharp rise during anodic scans in the SCV data was due to oxidation. Such an oxidation of phenolic moieties is likely to lead to products via autooxidation like reactions,^140,149,150 which will tend to be irreversible, which is consistent with both the SCV and SWV data.

To codify and summarize the qualitative characteristics of the SCVs of NOM, we classified them into four types and by six features. The types include: (1) negligible response of features above background, (2) significant but somewhat featureless response, (3) sharp features similar to model compounds, and (4) combination of features characteristic of NOM. The feature characteristics of most NOM SCVs include: (i) the core, which creates “thickness” of the SCV on which other features are added, (ii) a rise in current immediately upon initiation of the anodic scan (IAR), (iii) a small inflection midway through the anodic scan (AI), (iv) the major peak during the anodic scan (MAP), (v) a small inflection near the beginning of the cathodic sweep, which is analogous to (iii) (CI), and (vi) the major peak during the cathodic peak, which is analogous to (iv) (MCP). Fig. S5† illustrates how these characteristics can generate the whole range of shapes of SCVs obtained with NOM. We scored each of the categories and features (0 for absent; 1, 2, and 3 for weak, moderate, and strong, respectively), and calculated the sum as a measure of the overall “featurefullness” of the SCVs. That data for this accounting is given in Table S6† and the results are summarized in Fig. 4, with the NOMs sorted by increasing values of the sum of scores. The data in Fig. 4A are also colorized by the sum of scores, to demonstrate that classification of the SCVs in this way gives a continuum of results with considerable range.

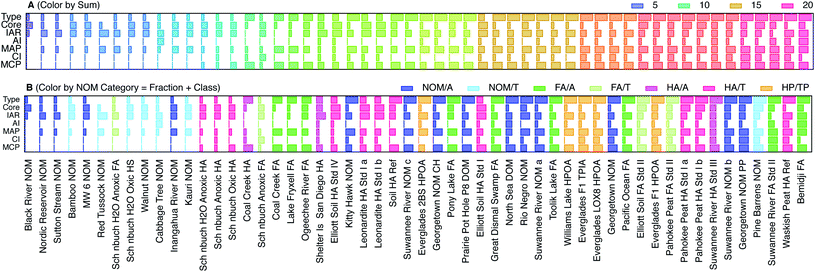Fig. 4 Comparison of scores that characterize features of the SCVs for all NOMs, ordered by increasing sum of all scores. The scores are 1–4 for type and indicate no response, mostly core, model-like, and typical NOM behavior for 1, 2, 3, and 4 respectively. The scores for characteristics within type which include, core, immediate anodic rise (IAR), anodic inflection (AI), major anodic peak (MAP), cathodic inflection (CI), and major cathodic peak (MCP) are assigned values of 0–3, where 0, 1, 2, 3 are a lack of, small, medium, and large response respectively. (A) NOMs colorized by sum of scores, and (B) NOMs colorized by category. Categories represent NOM class and fraction: e.g., aquatic fulvic acid, terrestrial humic acid, etc. Further description of sums of scores and category assignments are given in Table S6† and the fraction and class data for each NOM are given in Table S1.†

Fig. 4B shows the same data as Fig. 4A, but colorized by the NOM category, where category reflects both the fraction and class (Table S1†). This presentation shows that nominally similar NOMs (i.e., similar category) give qualitatively similar SCVs (i.e., relatively similar feature score and therefore position on the x-axis). For example, whenever two samples of the same material were included (Leonardite HA, Pahokee Peat HA), the score obtained from their SCVs plot together (with the exception of Suwannee River NOM, which may be due to the very different age of these two samples, or because NOM being less fractionated is more diverse as opposed to HA which is more fractionated and less diverse owing to more similar SCV features). Comparing the color gradients for the six features shown in Fig. 4A reveals that AI, MAP, CI, and MCP increase with overall featurefullness of the SCVs, but the Core and IAR scores appear to vary independently of the sum of scores.

To test the diagnostic value of the scoring and ordering of SCVs shown in Fig. 4A, that result can be compared with Fig. 4B, which shows the same data, but colorized by NOM category. In general, the low scores are dominated by terrestrial samples (light colors), and the high scores are mostly aquatic samples (dark colors). For example, all terrestrial NOMs except Pine Barrens have low scores (light blue) and all aquatic FAs have moderate to high scores (dark green). The most variable categories are aquatic NOM (dark blue), which are distributed about evenly across the whole range of scores, and both terrestrial (red) and aquatic humic acids (pink), which are mixed together in the middle of the range of scores. Other studies have reported a different trend in redox properties: electron accepting capacity (EAC) tends to be higher for humic acids than fulvic acids, and higher for terrestrial humic acids than aquatic humic acids.^80,85 However, EAC is more directly comparable to the cathodic peak potential breadths defined later in this study, and the trends in this aspect of our voltammetric data are more consistent with the trends in EAC. Comparison of Fig. 4B to Table S1† also reveals that most of the NOMs provided by D. Macalady scored low (with the exception of Rio Negro and Kitty Hawk) as did all of the Schönbuch Soil samples from A. Kappler, whereas most of the standard materials from IHHS gave high scores. This trend is not consistent with differences in the age of these samples, or what detail we have on differences in the extraction methods, but may be due to differences to the extent that the redox active moieties were concentrated in the samples.

3.5. Fitting of peaks in voltammetry data

In addition to the qualitative analysis of the SCV and SWV data presented above, we investigated several methods for quantitative determination of peak currents and potentials. On both the SCV and SWV data, the raw data with analyte was modified by subtracting background scans that were obtained without the analyte, but under otherwise identical conditions (solvent, electrolyte, buffer, etc.). In principle, this approach should isolate the electrochemical response of the analyte from non-faradaic effects, but we found that background subtraction produced distorted peaks in a few cases, usually where the sample signal was weak. Therefore, we used background subtraction to process the data for most materials, but when this gave problematic results, we used the raw analyte in further analysis, and include the background data for comparison. The latter group is identifiable in Fig. S4† by the presence of background scans shown in gray.

The next step on quantitative analysis was determination of peak position and size (position/height/area). To choose peak position and size: (i) a baseline was defined from the start to the end of the current response, (ii) a vertical line was drawn from the middle of this baseline to where the current response was largest. The potential at which this line crosses to the highest current response is defined as the peak potential. These values are summarized in Tables S4 and S5† and used throughout the remainder of this study. Peak height is defined by the length of the vertical line described above and is defined as the peak current. Peak areas were quantified by integrating the area under the curve bordered by the peak and defined baseline. Peak current data are not tabulated because their significance was ambiguous in many cases, for reasons elaborated below. But, we did use the better defined peak current data for a few samples to demonstrate the electrode response in our system showed the expected relationship to sample concentration. This is shown in Fig. 5 for a model ETM, AQDS, and Georgetown NOM. In both cases, peak currents show a roughly linear increased peak current with concentration (Fig. 5, insets). The result with NOM is notable because it verifies that the peaks obtained by the method developed in this study are the direct result of an electrode reaction involving NOM.

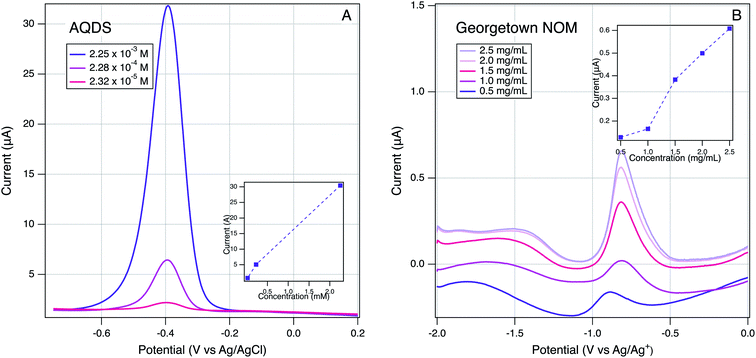Fig. 5 Effect of varying analyte concentration on SWVs: (A) AQDS in H₂O and (B) Georgetown NOM in DMSO. Scan rate of 25 mV s⁻¹, 2 mV step size, and 25 mV amplitude using a Pt working electrode.

After background subtraction, the SCVs and SWVs for the model quinones show roughly flat baselines (Fig. 2A and S3†), which made it straight-forward to define baselines for accurate measurement of peak size. However, most SCVs and SWVs for NOMs showed significantly uneven baselines, even after background subtraction (Fig. 2B and S4†). To overcome this, we investigated using the moving average baseline correction method,^136,151 which is the most common advanced method for defining the baseline of voltammograms with complex shape. The method is not easily applied to SCVs, but it gave nearly flat baselines for the SWVs of most NOMs (not shown). However, we chose not to use these results because the correction removed prominent features from the raw SWV data that might be indicative of electrochemical characteristics of NOM the could deserve further consideration. In particular, we noted that NOM usually gave SWVs with current that was significantly greater than expected background (capacitive) current over a much wider range of potentials than expected from specific peaks (e.g., compare Fig. 2A and B). Elevated faradaic current over wide potential ranges is sometimes attributed to redox reactions of species in the bulk solution that have not had time to diffuse to the electrode surface,¹⁴³ or it could arise from the combined effect of multiple redox active function groups (i.e., the “continuum” hypothesis described in the introduction). To allow us to explore the continuum hypothesis further in the analysis that follows, we did not apply baseline correction to the data. Instead, we adopted a novel set of criteria to define the broad regions of electrode response that extend beyond well defined peaks.

3.6. Quantitative comparison of characteristic potentials

Using the peak identification and fitting methods described above, two anodic and cathodic pairs of peaks were assigned for most model quinones and one anodic and one cathodic peak (unpaired) were assigned for the NOMs. These peaks are labelled (E_pa1, E_pa2, E_p1, etc.) in Fig. S3 and S4,† and the potential values are summarized in Tables S4 and S5.† Direct correlation of peak potentials obtained by SWV with those obtained by SCV—for all peak types and samples—shows the two methods gave values that agree within ∼50 mV (Fig. 6). While the overall trend in Fig. 6 suggests a 1 : 1 correlation between the two types of potentials, this is mainly due to the distribution of data for model compounds and a relatively tight cluster for most NOMs. The NOM responses, like the model compounds, make up two clusters within their respective groups. The two model compounds that form the smaller cluster are o-NQS and juglone, which as mentioned previously is most likely due to substituent effects. A quinone with a charged substituent (o-NQS) will have a more positive reduction potential. The NOM clustering is most likely to do with similar substituent effects. One implication of this result is that the quinones used as NOM model compounds have potentials that are substantially more negative than any of the NOM samples studied, which has been noted in other recent studies.⁹⁸

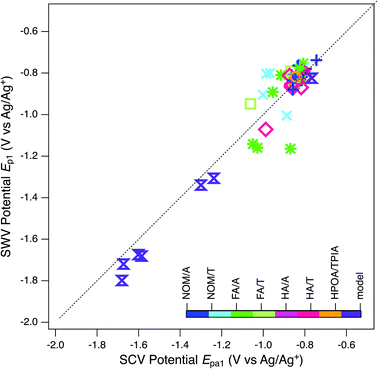Fig. 6 Comparison of potentials obtained by SWV (E_p1) and by SCV (E_pa1). Markers represent peak potentials (from Table S4†) for each NOM sample. Marker color and the legend refer to the NOM classification documented in Tables S1 and S6.† Diagonal dashed line is 1 : 1.

The clustering of peak potentials for NOMs in Fig. 6—and lack of a correlation between SCV and SWV potentials within that range of data—was surprising and led us to consider additional characteristics of the NOM voltammograms before further analysis for correlations within the peak potential data set. The main concern was that the features identified as peaks in the SCVs for NOM tend to be broader than the range of potentials expected for peaks from well-defined redox couples (which should be roughly ±120 mV about the peak,¹⁴³ as seen with the model quinones shown in Fig. S3†). For many of the NOMs, large portions of the potential scan (often about 1 Volt) exhibit current that is elevated beyond what could be non-faradaic background from the electrode or electrolyte (Fig. 2B, 3, and S4†). This result is expected if the sample is comprised of multiple electrode-active moieties with potentials that are too similar to be resolved by (conventional) SCV, such as for some quinones at high pH.¹⁴⁰ Of particular interest is the possibility that the redox-active moieties in NOM are coupled through intramolecular conduction to a sufficient degree that the sample potential is a continuum, analogous to the band gap in semiconductor materials. The continuum hypothesis has been suggested previously,^{56,79,80,98,103} but not evaluated quantitatively.

As a first step toward quantitative characterization of the hypothesized continuum of NOM electrode response, we characterized the “breadth” of each major anodic and cathodic peak from SCV and SWV by determining beginning and end potentials that were chosen with more inclusive criteria than is used in conventional analysis of peak widths.^152,153 The criteria—which are summarized together with the data in Table S7†—were necessarily subjective because the features that define the full extent of these peaks often were ambiguous, but comparison of the SCV and SWV data helped to ensure consistency. The results of this analysis are summarized in Fig. 7 and S6† (for SCV, and SWV respectively), with the peak potentials shown as black markers and the corresponding start and end potentials (colored markers) connected with a bar to represent breadth. When there was more than one anodic or cathodic peak (usually the model compounds), they are distinguished by marker shape. Note that this often resulted in overlapping breadths for SCV data, although not for SWV data. The samples (y-axis) are sorted and colorized by fraction and class (using the same category scheme defined in Table S1† for Fig. 4 and 6).

The main purpose of Fig. 7 and S6† is to provide a broad perspective on trends in the overall dataset. Starting with the peak potentials (black markers), the figure shows there is relatively little variation in the main anodic and cathodic peak potentials for NOMs, so we calculated the average and standard deviation of these values, which are −0.866 ± 0.069 V vs. Ag/Ag⁺ for E_pa1 (Fig. 7A), −1.35 ± 0.071 for E_pc1 (Fig. 7B), and −0.831 ± 0.051 for E_p1 (Fig. S6†). The similarity between average values of E_pa1 and E_p1 is consistent with Fig. 6. The low relative standard deviation on all three of these average potentials (5–8%) despite the very wide range of NOM types and sources included in the dataset, could be due to (i) selectivity in the methods used to extract NOM samples and/or (ii) a “central limit” that arises from continuum redox potentials. Both of these possibilities are discussed further in the sections that follow.

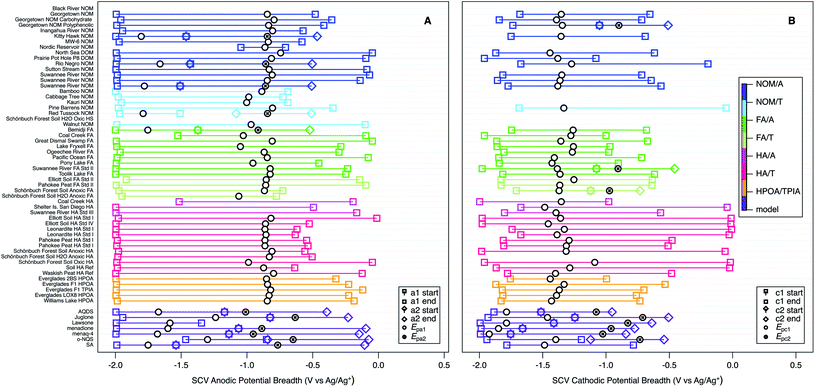Fig. 7 SCV anodic (A) and cathodic (B) potentials and peak breadths of all NOMs and model compounds. Squares indicate onset and end of current surrounding E_pa1 or E_pc1, diamonds indicate onset and end of current surrounding E_pa2 and E_pc2. Colors indicate type of NOM. For SWV breadths see Fig. S6.†

The peak breadth data (colored markers and bars in Fig. 7 and S6†), shows greater variability than the peak potentials, but some of this is likely to be due to ambiguity in the assignment of the start/end potentials, and there is no simple relationships between breadth and other factors. For example, while the breadth about E_pc1 in Fig. 7B appears to be greater for HA and less for FA and HPOA/TPIA, consistent with observations for electron accepting capacities^80,85 this pattern does not extend to E_pa1 or E_p1 (Fig. 7A and S6†), even though electron donating capacities have been shown to be affected by the molecular weight of NOMs.¹⁵⁴ Therefore, we conclude that breadths, like potentials, are largely invariant with NOM category and source. The average values of breadth are 1.63 ± 0.24 V for E_pa1 (Fig. 7A), 1.28 ± 0.34 for E_pc1 (Fig. 7B), and 0.648 ± 0.15 for E_p1 (Fig. S6†). These values are similar for E_pa1 and for E_pc1, and about twice that of E_p1, which probably just reflects the greater resolution of SWV over SCV. The average values of breadth are much greater than the standard deviation in the peak potentials (about 3- and 5-fold for SWV and SCV, respectively), which is futher evidence for the continuum hypothesis.

Evidence for redox potentials ranging over a continuum of values has been seen in electrochemical characterization of iron minerals and in electron donating capacities of microbially reduced humic substances.^83,104,105 Some of those studies modeled the larger than expected range over which electrons are accepted and donated with a Nernst equation that contained a factor (β) to account for the non-ideal behavior. When β is 1 behavior is Nernstian and when β is less than 1 the potential range is widened. This formulation originates from models developed to account for peak broadening and narrowing (non-ideal behavior) in electroactive polymer films.¹⁵⁵ Even though we experienced this in our system, using the β factor did not apply in our case due to the complex and indeterminate nature of the analyte, and ascertaining fraction of reduced to oxidized moieties to obtain the β factor is something that we did not pursue.

Comparing the peak potentials and breadths in Fig. 7 and S6† reveals that the SCVs for NOMs are asymmetrical about the corresponding potentials and skewed opposite the direction of the scan (i.e., anodic scans are negatively skewed in Fig. 7A and cathodic scans are positively skewed in Fig. 7B). This trend is the reverse of prototypical SCV peak shape (which rises sharply when a characteristic potential is reached and then decays slowly as diffusion becomes limiting)¹⁴³ and the SCV peaks obtained with most model compounds (Fig. S3†). However, this comparison may be strong evidence for the continuum hypothesis of NOM redox potentials, because that scenario should produce a gradual increase in current over an extended range of potentials. The SWV data (Fig. S6†) shows a modest positive skew for NOMs, which is slightly more consistent with the model compounds. This is expected because the breadths for the SWVs were chosen using the net potential, which subtracts the forward and reverse components, and this essentially subtracted out the effect of the rising current.

3.7. Relationship to chemical composition

The above analysis of characteristic potentials from the electrochemical measurements made in this study was interpreted mainly as evidence for the continuum hypothesis of NOM redox properties. However, this does not preclude the other possible explanation for the lack of significant trends in the peak potentials: that the methods used to obtain the samples (extraction, fraction, and concentration) were selective for some chemical components over others, thereby decreasing the diversity of chemical structure within the sample set. To investigate this possibility, it would be useful to compare the electrochemical data with chemical composition data for the whole set of test compounds. Unfortunately, the very limited quantities of some samples, and cost of performing larger numbers of structural characterizations by advanced methods (e.g., FTICR-MS) made it infeasible to fully implement this approach within the study. However, for 25 of the 54 NOM samples that we characterized electrochemically, chemical composition data were available from the suppliers, or their publications. These data were used to calculate ratios of H : C and O : C so that they could be summarized in a Van Krevelen diagram format.^19,156 Comparing the data (solid markers in Fig. 8) to regions of typical composition for component types (dashed lines, from ref. 157), shows that all of the sample data fall in just two regions on the diagram: aquatic NOMs plot as tannins, most fulvic and humic acids plot as lignins, and HPOA/TPIA straddles the tannin and lignin regions.

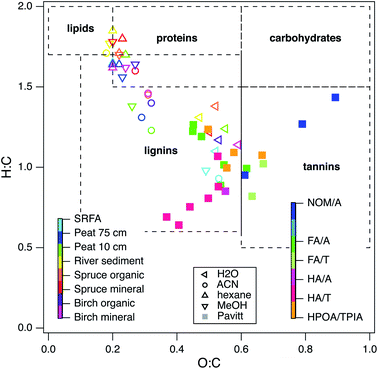Fig. 8 Van Krevelen diagram of 25 NOMs used in this study and recreated data from the following ref. 129. Colors indicate different categories of NOM. The legend in the middle and left defines the open markers (recreated data), the legend on the right defines the filled in markers (data in this study). Elemental composition data obtained from IHSS, USGS, and ref. 25.

To provide further context for interpretation of Fig. 8, data are included (open markers) from a recent study on the chemical composition of organic matter obtained by different extraction methods.¹²⁹ For these data, the source material is represented by color and the extraction method is represented by marker shape (left and middle legends, respectively). Most of the data distribute along a trend with negative slope according to the extraction method (high H : C, low O : C ratio for hexane and methanol, intermediate H : C and O : C ratio for acetonitrile and water). In contrast, solvent extraction of SRFA (light blue markers) had little influence on H : C and O : C and the data all plot in the vicinity of other source materials that were extracted with water. Unlike the other source materials, SRFA was initially obtained by the conventional alkaline extraction step, and it was concluded that this step decreased the diversity in molecular structure that was otherwise evident in the NOMs that were obtained without alkaline extraction.¹⁹

Many of the NOMs used in this study were alkaline extracted, so it is not surprising that they plot near the SRFA data in Fig. 8. Therefore, the distribution of the chemical composition of the samples used in this study is consistent with selectivity of the conventional (alkaline) extraction methods for similar redox active moieties. Similar conclusions have been drawn from other types of evidence, such as near edge X-ray absorption fine structure (NEXAFS) spectra,¹⁵⁸ collision induced dissociation coupled to FTICR MS,¹⁵⁹ solid phase extractions and FTICR MS,²² fluorescence spectroscopy coupled to PARAFAC analysis,¹⁶⁰ and statistical analysis of chemical composition data for hundreds of NOMs.^21,29 A few of the NOMs from this study distribute along a diagonal in Fig. 8 that is consistent with H : C/O : C ratio of ∼2. This type of trend in a Van Krevelen diagram can arise from a homologous series of molecules that vary only by an exact mass of a certain functional group,¹⁶¹ which could result from a consistent diagenetic history,¹⁵⁶ but this interpretation is not likely to apply to the selection of NOM samples used in this study.

For the relatively narrow range of peak potentials observed in this study to be due to the polyphenolic and quinoid moieties associated with lignin and tannin, the redox active moieties that are expected under these conditions should have peak potentials that are consistent with the peak potentials measured for NOM. A previously published survey of over one-hundred quinones shows that the potential window in DMSO for naphthoquinones and anthraquinones (∼0.6 V) is smaller than the potential window of benzoquinones (∼1.5 V).¹¹⁵ Similarly, another study compared over seventeen hundred quinones, and found that the potentials for most of them fell in a window of ∼0.6 V.¹⁶² The narrower potential range for the more conjugated quinone model compounds could be consistent with the relatively narrow range observed for NOM because NOM is thought to be a complex network of quinones and polyphenols.

3.8. Solvent effects on potential measurements

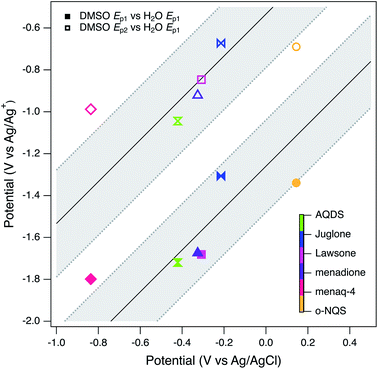
The main benefit of using DMSO as the solvent for electrochemical characterization of NOM is the improved electrode response due to increased access to the redox-active moieties, as conceptualized in Fig. 1. However, this effect also creates other challenges: for example, it will take further study to fully understand how the access to redox-active moieties created by unfolding the tertiary structure of NOM compares with the access gained by mediation with solution-phase ETMs. However, the primary issue is whether potentials measured in DMSO can be adjusted for direct, quantitative comparison with potentials measured in water or calculated from thermodynamic data. In previous work,⁹⁸ we assumed this could be done by applying a constant correction factor, obtained by measuring the potential of a suitable redox couple (commonly ferrocene¹⁶³) measured in both solvent systems. This calculation led to estimates of the redox potential of NOM in water that ranged from 0.4 to −0.3 volts vs. SHE, which overlaps with other estimates of NOM redox potential and model quinones.

However, there are additional factors that complicate the comparison of potentials made in different solvents (e.g., solvation effects on activity coefficients) that are not as easily quantified.^164,165 To investigate this issue more thoroughly than we did in previous work, all seven of the model compounds used in this study (Tables S2 and S3†) were characterized by SCV and SWV in both DMSO and in water (Fig. S3† for DMSO, not shown for water). Not all of the model compounds were fully soluble in both solvents, so the two sets of data are not directly comparable in terms of current, but modest differences in the model compound concentration should not affect the peak potentials significantly. As discussed above, the model quinones in DMSO give two pairs of peaks representing (quasi)reversible one-electron transfer, but in water they give one pair of peaks representing a two-electron transfer.^{111–113,138,140,144} The potentials corresponding to these peaks are given in Table S5† and SWV data are summarized in Fig. 9 by plotting both E_p1 and E_p2 obtained in DMSO versus E_p1 obtained in water. The two correlations are roughly linear and parallel, so we fit the data as two lines with a common slope by global regression. The resulting intercepts were −1.26 and −0.533 V for E_p1 and E_p2 respectively. We then used the E_p2 intercept to adjust our average peak potentials. We were able to disregard E_p1 by assuming that its shift from a two wave (aprotic) to a one wave (water) response was minimal in comparison to the shift of E_p2.¹¹³ This value (0.533 V) is similar to the correction factor determined previously (0.472 V) using only ferrocene.⁹⁸

Fig. 9 SWV potentials of model compounds in water vs. DMSO. Conditions in water are 0.1 M KCl, 0.1 M phosphate buffer (pH 7), Pt or GC WE, and Ag/AgCl RE. Conditions in DMSO are 0.1 M TBAFP, Pt WE, Ag/Ag⁺ RE filled with 0.1 M TBAFP, and 0.005 M AgNO₃. CE Pt coil for both DMSO and water. The slope for both lines were fixed at 1; the fitted intercepts are −1.26 ± 0.22 for E_p1 and −0.533 ± 0.26 for E_p2. Dashed lines are the 95% confidence bands about the regression lines.

Assuming that the new correction factor more accurately reflects the whole range of factors that cause differences in potentials from DMSO and water, we used this new value to adjust the average peak potentials for E_pa1, E_pc1, and E_p1 obtained from the data in Fig. 7 and S6.† The resulting estimates, for aqueous conditions vs. SHE, are −0.128, −0.613, and −0.0930 V, for E_pa1, E_pc1, and E_p1, respectively. The values for E_pa1 are in excellent agreement with values for select humic acids that were calculated from MER/MEO data.⁸³ It is important to note that these numbers should be considered a rough estimate, due to the difficulty in comparing potentials using two different reference electrodes, higher concentrations of electrolyte can alter potentials by several hundred millivolts,¹⁶⁶ and a change of electrolyte type can alter the potential significantly.¹¹³

4. Conclusions

Characterization of the properties of NOM is greatly complicated by its complex, indeterminant, and presumably variable composition. This necessitates the use of multiple, complementary characterization methods, ranging from mass spectrometry to fluorescence spectroscopy and electrochemistry. Conventional electrochemical methods generally produce poor results due to poor contact between the redox-active moieties in NOM and the working electrode surface, but that can be overcome using soluble electron transfer mediators or aprotic solvents. The latter has been shown to produce promising voltammograms for a variety of NOM samples, and that approach was refined and extended to a large range of NOMs in the study.

A major refinement to the method used in this study was the sequential use of cyclic and square-wave voltammetry (SCV and SWV), which provided complimentary information that greatly improved confidence in the interpretation of peaks and other features in terms of NOM redox processes. Most samples gave voltammograms that were dominated by one anodic and one cathodic peak, superimposed on a background of apparently faradaic current over a wide range of potentials. The peak potentials and breadths were found to be similar across all types of NOM, which contradicts the expectation that the redox properties would vary significantly with NOM source, type, etc.

The lack of differentiation in electrochemical properties of NOM may be partly due to the extraction methods commonly used to obtain NOM samples, which may result in selection for some components of NOM structure over others. This hypothesis is supported by comparison with recent results using other structural characterization methods like FTICR-MS and PARFAC. However, the similarity in NOM redox properties may also be because the redox-active moieties in NOM are coupled through intramolecular conduction to a sufficient degree that the sample potential reflects a continuum of electrode response, which would result in voltammograms with more broad and average features. This conclusion is similar to the interpretation given to the redox properties of NOM determined in other studies using coulometry.

The continuum model of NOM redox properties has broad implications for the role of NOM in biogeochemistry and contaminant fate. In both contexts, NOM may act as an electron donor or acceptor with a wide range of other redox active species, thereby mediating reactions among species with a range of redox potentials. Coupling between the redox active moieties within NOM determines the aggregate potentials measured by voltammetry, as well as the electron donor/acceptor capacities measured by coulometry. Measurement of these properties is facilitated by dissolution in DMSO, which allows unfolding of the tertiary structure of NOM and, thereby, access of redox-active groups to the electrode.

Conflicts of interest

There are not conflicts to declare.

Acknowledgements

The study was initiated for a presentation by P. Tratnyek for a symposium in honor of George Aiken at the 253^rd ACS National Meeting in San Francisco, CA, 2–6 April 2017. Initially, a goal of the study was to compare results obtained on samples of NOM acquired over several decades from George Aiken, Donald Macalady, Yo-Ping Chin, and Baohua Gu. The scope was expanded to include new NOM samples from Paul Bloom (IHSS), Joel Coates, Gordon Getzinger, Andreas Kappler, Boris Koch, Joseph Needoba, and Brett Poulin. We thank all of these colleagues for their contributions to this work. Some preliminary electrochemical experiments were performed by undergraduates Eric Sauer, Nancy Nguyen, and Nick Slenning. Nguyen and Slenning were funded by a Murdock Trust grant to Paige Osberg Hall (Univ. of Portland). This material is based on the work supported by the National Science Foundation, Environmental Chemical Sciences Program under Grant # 1506744.

References

1. T. A. Brown, B. A. Jackson, B. J. Bythell and A. C. Stenson, Benefits of multidimensional fractionation for the study and characterization of natural organic matter, J. Chromatogr. A, 2016, 1470, 84–96,  DOI:10.1016/j.chroma.2016.10.005.
2. J. Chen, B. Gu, E. J. LeBoeuf, H. Pan and S. Dai, Spectroscopic characterization of structural and functional properties of natural organic matter fractions, Chemosphere, 2002, 48, 59–68.
3. Y.-P. Chin, G. Aiken and E. O'Loughlin, Molecular weight, polydispersity, and spectroscopic properties of aquatic humic substances, Environ. Sci. Technol., 1994, 28, 1853–1858,  DOI:10.1021/es00060a015.
4. Y.-P. Chin, S. J. Traina, C. R. Swank and D. Backhus, Abundance and properties of dissolved organic matter in pore waters of a freshwater wetland, Limnol. Oceanogr., 1998, 43, 1287–1296.
5. J. Guigue, M. Harir, O. Mathieu, M. Lucio, L. Ranjard, J. Lévêque and P. Schmitt-Kopplin, Ultrahigh-resolution FT-ICR mass spectrometry for molecular characterisation of pressurised hot water-extractable organic matter in soils, Biogeochemistry, 2016, 128, 307–326,  DOI:10.1007/s10533-016-0209-5.
6. N. Hertkorn, M. Frommberger, M. Witt, B. P. Koch, P. Schmitt-Kopplin and E. M. Perdue, Natural organic matter and the event horizon of mass spectrometry, Anal. Chem., 2008, 80, 8908–8919,  DOI:10.1021/ac800464g.
7. B. P. Kelleher and A. J. Simpson, Humic substances in soils: are they really chemically distinct?, Environ. Sci. Technol., 2006, 40, 4605–4611,  DOI:10.1021/es0608085.
8. M. Kleber and M. G. Johnson, Advances in understanding the molecular structure of soil organic matter: Implications for interactions in the environment, in Advances in Agronomy, 2010, pp. 77–142,  DOI:10.1016/s0065-2113(10)06003-7.
9. B. P. Koch, K.-U. Ludwichowski, G. Kattner, T. Dittmar and M. Witt, Advanced characterization of marine dissolved organic matter by combining reversed-phase liquid chromatography and FT-ICR-MS, Mar. Chem., 2008, 111, 233–241,  DOI:10.1016/j.marchem.2008.05.008.
10. E. B. Kujawinski, P. G. Hatcher and M. A. Freitas, High-resolution Fourier transform ion cyclotron resonance mass spectrometry of humic and fulvic acids: improvements and comparisons, Anal. Chem., 2002, 74, 413–419,  DOI:10.1021/ac0108313.
11. D. L. Macalady and K. Walton-Day, Redox chemistry and natural organic matter (NOM): geochemists' dream, analytical chemists' nightmare, in Aquatic Redox Chemistry, ed. P. G. Tratnyek, T. J. Grundl and S. B. Haderlein, American Chemical Society, Washington, DC, 2011, vol. 1071, ch. 5, pp. 85–111,  DOI:10.1021/bk-2011-1071.ch005.
12. B. F. Mann, H. Chen, E. M. Herndon, R. K. Chu, N. Tolic, E. F. Portier, T. R. Chowdhury, E. W. Robinson, S. J. Callister, S. D. Wullschleger, D. E. Graham, L. Liang and B. Gu, Indexing permafrost soil organic matter degradation using high-resolution mass spectrometry, PLoS One, 2015, 10, e0130557,  DOI:10.1371/journal.pone.0130557.
13. J. Mao, N. Chen and X. Cao, Characterization of humic substances by advanced solid state NMR spectroscopy: demonstration of a systematic approach, Org. Geochem., 2011, 42, 891–902,  DOI:10.1016/j.orggeochem.2011.03.023.
14. E. C. Minor, M. M. Swenson, B. M. Mattson and A. R. Oyler, Structural characterization of dissolved organic matter: a review of current techniques for isolation and analysis, Environ. Sci.: Processes Impacts, 2014, 16, 2064–2079,  10.1039/C4EM00062E.
15. P. N. Nelson and J. A. Baldock, Estimating the molecular composition of a diverse range of natural organic materials from solid-state ¹³C NMR and elemental analyses, Biogeochemistry, 2005, 72, 1–34,  DOI:10.1007/s10533-004-0076-3.
16. T. Reemtsma, Determination of molecular formulas of natural organic matter molecules by (ultra-) high-resolution mass spectrometry: status and needs, J. Chromatogr. A, 2009, 1216, 3687–3701,  DOI:10.1016/j.chroma.2009.02.033.
17. T. Riedel and T. Dittmar, A method detection limit for the analysis of natural organic matter via Fourier transform ion cyclotron resonance mass spectrometry, Anal. Chem., 2014, 86, 8376–8382,  DOI:10.1021/ac501946m.
18. R. Sutton and G. Sposito, Molecular structure in soil humic substances: the new view, Environ. Sci. Technol., 2005, 39, 9009–9015,  DOI:10.1021/es050778q.
19. M. M. Tfaily, R. K. Chu, N. Tolic, K. M. Roscioli, C. R. Anderton, L. Pasa-Tolic, E. W. Robinson and N. J. Hess, Advanced solvent based methods for molecular characterization of soil organic matter by high-resolution mass spectrometry, Anal. Chem., 2015, 87, 5206–5215,  DOI:10.1021/acs.analchem.5b00116.
20. P. L. Brezonik, P. R. Bloom, R. L. Sleighter, R. M. Cory, A. R. Khwaja and P. G. Hatcher, Chemical differences of aquatic humic substances extracted by XAD-8 and DEAE-cellulose, J. Environ. Chem. Eng., 2015, 3, 2982–2990,  DOI:10.1016/j.jece.2015.03.004.
21. J. Burdon, Are the traditional concepts of the structures of humic substances realistic?, Soil Sci., 2001, 166, 752–769.
22. J. Raeke, O. J. Lechtenfeld, M. Wagner, P. Herzsprung and T. Reemtsma, Selectivity of solid phase extraction of freshwater dissolved organic matter and its effect on ultrahigh resolution mass spectra, Environ. Sci.: Processes Impacts, 2016, 18, 918–927,  10.1039/C6EM00200E.
23. U. J. Wünsch, J. K. Geuer, O. J. Lechtenfeld, B. P. Koch, K. R. Murphy and C. A. Stedmon, Quantifying the impact of solid-phase extraction on chromophoric dissolved organic matter composition, Mar. Chem., 2018, 207, 33–41,  DOI:10.1016/j.marchem.2018.08.010.
24. Y. Li, M. Harir, J. Uhl, B. Kanawati, M. Lucio, K. S. Smirnov, B. P. Koch, P. Schmitt-Kopplin and N. Hertkorn, How representative are dissolved organic matter (DOM) extracts? A comprehensive study of sorbent selectivity for DOM isolation, Water Res., 2017, 116, 316–323,  DOI:10.1016/j.watres.2017.03.038.
25. J. Chen, B. H. Gu, E. J. LeBoeuf, H. J. Pan and S. Dai, Spectroscopic characterization of the structural and functional properties of natural organic matter fractions, Chemosphere, 2002, 48, 59–68,  DOI:10.1016/S0045-6535(02)00041-3.
26. N. Hertkorn, A. B. Permin, I. V. Perminova, D. V. Kovalevskii, M. V. Yudov and A. Kettrup, Comparative analysis of partial structures of a peat humic and fulvic acid using one and two dimensional nuclear magnetic resonance spectroscopy, J. Environ. Qual., 2002, 31, 375–387.
27. K. A. Thorn and L. G. Cox, N-15 NMR spectra of naturally abundant nitrogen in soil and aquatic natural organic matter samples of the International Humic Substances Society, Org. Geochem., 2009, 40, 484–499,  DOI:10.1016/j.orggeochem.2009.01.007.
28. I. Kögel-Knabner, The macromolecular organic composition of plant and microbial residues as inputs to soil organic matter: fourteen years on, Soil Biol. Biochem., 2017, 105, A3–A8,  DOI:10.1016/S0038-0717(01)00158-4.
29. N. Mahieu, E. W. Randall and D. S. Powlson, Statistical analysis of published carbon-13 CPMAS NMR spectra of soil organic matter, Soil Sci. Soc. Am. J., 1999, 63, 307–319,  DOI:10.2136/sssaj1999.03615995006300020008x.
30. J. Niemeyer, Y. Chen and J. M. Bollog, Characterization of humic acids, composts, and peat by diffuse reflectance Fourier-transform infrared spectroscopy, Soil Sci. Soc. Am. J., 1992, 56, 135–140,  DOI:10.2136/sssaj1992.03615995005600010021x.
31. A. J. Simpson, G. Song, E. Smith, B. Lam, E. H. Novotny and M. H. B. Hayes, Unraveling the structural components of soil humin by use of solution-state nuclear magnetic resonance spectroscopy, Environ. Sci. Technol., 2007, 41, 876–883,  DOI:10.1021/es061576c.
32. D. Zhang, D. Duan, Y. Huang, Y. Yang and Y. Ran, Composition and structure of natural organic matter through advanced nuclear magnetic resonance techniques, Chem. Biol. Technol. Agric., 2017, 4, 8,  DOI:10.1186/s40538-017-0086-8.
33. J. Zhong, R. L. Sleighter, E. Salmon, G. A. McKee and P. G. Hatcher, Combining advanced NMR techniques with ultrahigh resolution mass spectrometry: a new strategy for molecular scale characterization of macromolecular components of soil and sedimentary organic matter, Org. Geochem., 2011, 42, 903–916,  DOI:10.1016/j.orggeochem.2011.04.007.
34. I. V. Perminova, E. A. Shirshin, A. I. Konstantinov, A. Zherebker, V. A. Lebedev, I. V. Dubinenkov, N. A. Kulikova, E. N. Nikolaev, E. Bulygina and R. M. Holmes, The structural arrangement and relative abundance of aliphatic units may effect long-wave absorbance of natural organic matter as revealed by ¹H NMR spectroscopy, Environ. Sci. Technol., 2018, 52, 12526–12537,  DOI:10.1021/acs.est.8b01029.
35. C. Romera-Castillo, M. Chen, Y. Yamashita and R. Jaffé, Fluorescence characteristics of size-fractionated dissolved organic matter: implications for a molecular assembly based structure?, Water Res., 2014, 55, 40–51,  DOI:10.1016/j.watres.2014.02.017.
36. R. M. Cory and D. M. McKnight, Fluorescence spectroscopy reveals ubiquitous presence of oxidized and reduced quinones in dissolved organic matter, Environ. Sci. Technol., 2005, 39, 8142–8149,  DOI:10.1021/es0506962.
37. U. J. Wünsch, K. R. Murphy and C. A. Stedmon, The one-sample PARAFAC approach reveals molecular size distributions of fluorescent components in dissolved organic matter, Environ. Sci. Technol., 2017, 51, 11900–11908,  DOI:10.1021/acs.est.7b03260.
38. P. Kowalczuk, J. Ston-Egiert, W. J. Cooper, R. F. Whitehead and M. J. Durako, Characterization of chromophoric dissolved organic matter (CDOM) in the Baltic Sea by excitation emission matrix fluorescence spectroscopy, Mar. Chem., 2005, 96, 273–292.
39. L. Klapper, D. M. McKnight, J. R. Fulton, E. L. Blunt-Harris, K. P. Nevin, D. R. Lovley and P. G. Hatcher, Fulvic acid oxidation state detection using fluorescence spectroscopy, Environ. Sci. Technol., 2002, 36, 3170–3175,  DOI:10.1021/es0109702.
40. H. Chen, Z. Yang, R. K. Chu, N. Tolic, L. Liang, D. E. Graham, S. D. Wullschleger and B. Gu, Molecular insights into arctic soil organic matter degradation under warming, Environ. Sci. Technol., 2018, 52, 4555–4564,  DOI:10.1021/acs.est.7b05469.
41. P. Herzsprung, W. von Tümpling, K. Wendt-Potthoff, N. Hertkorn, M. Harir, P. Schmitt-Kopplin and K. Friese, High field FT-ICR mass spectrometry data sets enlighten qualitative DOM alteration in lake sediment porewater profiles, Org. Geochem., 2017, 108, 51–60,  DOI:10.1016/j.orggeochem.2017.03.010.
42. B. P. Koch and T. Dittmar, From mass to structure: an aromaticity index for high-resolution mass data of natural organic matter, Rapid Commun. Mass Spectrom., 2016, 30, 250,  DOI:10.1002/rcm.7433.
43. A. Zherebker, I. V. Perminova, Y. Kostyukevich, A. S. Kononikhin, O. Kharybin and E. Nikolaev, Structural investigation of coal humic substances by selective isotopic exchange and high-resolution mass spectrometry, Faraday Discuss., 2019 10.1039/C9FD00002J.
44. M. H. B. Hayes, Solvent systems for the isolation of organic components from soils, Soil Sci. Soc. Am. J., 2006, 70, 986–994,  DOI:10.2136/sssaj2005.0107.
45. M. W. I. Schmidt, M. S. Torn, S. Abiven, T. Dittmar, G. Guggenberger, I. A. Janssens, M. Kleber, I. Koegel-Knabner, J. Lehmann, D. A. C. Manning, P. Nannipieri, D. P. Rasse, S. Weiner and S. E. Trumbore, Persistence of soil organic matter as an ecosystem property, Nature, 2011, 478, 49–56,  DOI:10.1038/nature10386.
46. T. Heitmann, T. Goldhammer, J. Beer and C. Blodau, Electron transfer of dissolved organic matter and its potential significance for anaerobic respiration in a northern bog, Global Change Biol., 2007, 13, 1771–1785,  DOI:10.1111/j.1365-2486.2007.01382.x.
47. C. P. Ward, S. G. Nalven, B. C. Crump, G. W. Kling and R. M. Cory, Photochemical alteration of organic carbon draining permafrost soils shifts microbial metabolic pathways and stimulates respiration, Nat. Commun., 2017, 8, 772,  DOI:10.1038/s41467-017-00759-2.
48. M. P. Waldrop, K. P. Wickland, R. White III, A. A. Berhe, J. W. Harden and V. E. Romanovsky, Molecular investigations into a globally important carbon pool: permafrost-protected carbon in Alaskan soils, Global Change Biol., 2010, 16, 2543–2554,  DOI:10.1111/j.1365-2486.2009.02141.x.
49. O. Pisani, L. H. Lin, O. O. Y. Lun, K. Lajtha, K. J. Nadelhoffer, A. J. Simpson and M. J. Simpson, Long-term doubling of litter inputs accelerates soil organic matter degradation and reduces soil carbon stocks, Biogeochemistry, 2016, 127, 1–14,  DOI:10.1007/s10533-015-0171-7.
50. G. Y. K. Moinet, J. E. Hunt, M. U. F. Kirschbaum, C. P. Morcom, A. J. Midwood and P. Millard, The temperature sensitivity of soil organic matter decomposition is constrained by microbial access to substrates, Soil Biol. Biochem., 2018, 116, 333–339,  DOI:10.1016/j.soilbio.2017.10.031.
51. E. Lipczynska-Kochany, Effect of climate change on humic substances and associated impacts on the quality of surface water and groundwater: a review, Sci. Total Environ., 2018, 640–641, 1548–1565,  DOI:10.1016/j.scitotenv.2018.05.376.
52. I. F. Creed, D. M. McKnight, B. A. Pellerin, M. B. Green, B. A. Bergamaschi, G. R. Aiken, D. A. Burns, S. E. G. Findlay, J. B. Shanley, R. G. Striegl, B. T. Aulenbach, D. W. Clow, H. Laudon, B. L. McGlynn, K. J. McGuire, R. A. Smith and S. M. Stackpoole, The river as a chemostat: fresh perspectives on dissolved organic matter flowing down the river continuum, Can. J. Fish. Aquat. Sci., 2015, 72, 1272–1285,  DOI:10.1139/cjfas-2014-0400.
53. N. Walpen, G. J. Getzinger, M. H. Schroth and M. Sander, Electron-donating phenolic and electron-accepting quinone moieties in peat dissolved organic matter: quantities and redox transformations in the context of peat biogeochemistry, Environ. Sci. Technol., 2018, 52, 5236–5245,  DOI:10.1021/acs.est.8b00594.
54. J. A. Hakala, R. L. Fimmen, Y. P. Chin, S. G. Agrawal and C. P. Ward, Assessment of the geochemical reactivity of Fe-DOM complexes in wetland sediment pore waters using a nitroaromatic probe compound, Geochim. Cosmochim. Acta, 2009, 73, 1382–1393,  DOI:10.1016/j.gca.2008.12.001.
55. E. S. Kane, M. R. Chivers, M. R. Turetsky, C. C. Treat, D. G. Petersen, M. Waldrop, J. W. Harden and A. D. McGuire, Response of anaerobic carbon cycling to water table manipulation in an Alaskan rich fen, Soil Biol. Biochem., 2013, 58, 50–60,  DOI:10.1016/j.soilbio.2012.10.032.
56. R. L. Fimmen, R. M. Cory, Y.-P. Chin, T. D. Trouts and D. M. McKnight, Probing the oxidation–reduction properties of terrestrially and microbially derived dissolved organic matter, Geochim. Cosmochim. Acta, 2007, 71, 3003–3015,  DOI:10.1016/j.gca.2007.04.009.
57. T. Borch, R. Kretzschmar, A. Kappler, P. V. Cappellen, M. Ginder-Vogel, A. Voegelin and K. Campbell, Biogeochemical redox processes and their impact on contaminant dynamics, Environ. Sci. Technol., 2010, 44, 15–23,  DOI:10.1021/es9026248.
58. A. G. Bravo, S. Bouchet, J. Tolu, E. Björn, A. Mateos-Rivera and S. Bertilsson, Molecular composition of organic matter controls methylmercury formation in boreal lakes, Nat. Commun., 2017, 8, 14255,  DOI:10.1038/ncomms14255.
59. S. Canonica and H. Laubscher, Inhibitory effect of dissolved organic matter on triplet-induced oxidation of aquatic contaminants, Photochem. Photobiol. Sci., 2008, 7, 547–551,  10.1039/B719982A.
60. F. M. Dunnivant, R. P. Schwarzenbach and D. L. Macalady, Reduction of substituted nitrobenzenes in aqueous solutions containing natural organic matter, Environ. Sci. Technol., 1992, 26, 2133–2141,  DOI:10.1021/es00035a010.
61. A. M. Graham, G. R. Aiken and C. C. Gilmour, Effect of dissolved organic matter source and character on microbial Hg methylation in Hg-S-DOM solutions, Environ. Sci. Technol., 2013, 47, 5746–5754,  DOI:10.1021/es400414a.
62. M. Haitzer, G. R. Aiken and J. N. Ryan, Binding of mercury(II) to aquatic humic substances: influence of pH and source of humic substances, Environ. Sci. Technol., 2003, 37, 2436–2441,  DOI:10.1021/es026291o.
63. H.-Y. N. Holman, K. Nieman, D. L. Sorensen, C. D. Miller, M. C. Martin, T. Borch, W. R. McKinney and R. C. Sims, Catalysis of PAH biodegradation by humic acid shown in synchrotron infrared studies, Environ. Sci. Technol., 2002, 36, 1276–1280,  DOI:10.1021/es0157200.
64. A. Höllrigl-Rosta, R. Vinken, M. Lenz and A. Schäffer, Sorption and dialysis experiments to assess the binding of phenolic xenobiotics to dissolved organic matter in soil, Environ. Toxicol. Chem., 2003, 22, 743–752,  DOI:10.1002/etc.5620220411.
65. L. E. Jacobs, R. L. Fimmen, Y.-P. Chin, H. E. Mash and L. K. Weavers, Fulvic acid mediated photolysis of ibuprofen in water, Water Res., 2011, 45, 4449–4458,  DOI:10.1016/j.watres.2011.05.041.
66. W. Jiang, Q. Cai, W. Xu, M. Yang, Y. Cai, D. D. Dionysiou and K. E. O'Shea, Cr(VI) adsorption and reduction by humic acid coated on magnetite, Environ. Sci. Technol., 2014, 48, 8078–8085,  DOI:10.1021/es405804m.
67. A. Kappler and S. B. Haderlein, Natural organic matter as reductant for chlorinated aliphatic pollutants, Environ. Sci. Technol., 2003, 37, 2714–2719.
68. M. E. Karpuzcu, A. J. McCabe and W. A. Arnold, Phototransformation of pesticides in prairie potholes: effect of dissolved organic matter in triplet-induced oxidation, Environ. Sci.: Processes Impacts, 2016, 18, 237–245,  10.1039/C5EM00374A.
69. J. W. Moreau, C. M. Gionfriddo, D. P. Krabbenhoft, J. M. Ogorek, J. F. DeWild, G. R. Aiken and E. E. Roden, The effect of natural organic matter on mercury methylation by Desulfobulbus propionicus 1pr3, Front. Microbiol., 2015, 6, 1389,  DOI:10.3389/fmicb.2015.01389.
70. B. A. Poulin, C. A. Gerbig, C. S. Kim, J. P. Stegemeier, J. N. Ryan and G. R. Aiken, Effects of sulfide concentration and dissolved organic matter characteristics on the structure of nanocolloidal metacinnabar, Environ. Sci. Technol., 2017, 51, 13133–13142,  DOI:10.1021/acs.est.7b02687.
71. P. Sharma, M. Rolle, B. Kocar, S. Fendorf and A. Kappler, Influence of natural organic matter on As transport and retention, Environ. Sci. Technol., 2011, 45, 546–553,  DOI:10.1021/es1026008.
72. P. G. Tratnyek, M. M. Scherer, B. Deng and S. Hu, Effects of natural organic matter, anthropogenic surfactants, and model quinones on the reduction of contaminants by zero-valent iron, Water Res., 2001, 35, 4435–4443,  DOI:10.1016/S0043-1354(01)00165-8.
73. J. Wenk, U. von Gunten and S. Canonica, Effect of dissolved organic matter on the transformation of contaminants induced by excited triplet states and the hydroxyl radical, Environ. Sci. Technol., 2011, 45, 1334–1340,  DOI:10.1021/es102212t.
74. P. S. Craig, T. J. Shaw, P. L. Miller, P. J. Pellechia and J. L. Ferry, Use of multiparametric techniques to quantify the effects of naturally occurring ligands on the kinetics of Fe(II) oxidation, Environ. Sci. Technol., 2009, 43, 337–342,  DOI:10.1021/es802005p.
75. C. Peng, A. Sundman, C. Bryce, C. Catrouillet, T. Borch and A. Kappler, Oxidation of Fe(II)–organic matter complexes in the presence of the mixotrophic nitrate-reducing Fe(II)-oxidizing bacterium Acidovorax sp. BoFeN1, Environ. Sci. Technol., 2018, 52, 5753–5763,  DOI:10.1021/acs.est.8b00953.
76. J. Wu and G. W. Luther, III., Complexation of Fe(III) by natural organic ligands in the Northwest Atlantic Ocean by a competitive ligand equilibration method and a kinetic approach, Mar. Chem., 1995, 50, 159–177,  DOI:10.1016/0304-4203(95)00033-n.
77. E. E. Daugherty, B. Gilbert, P. S. Nico and T. Borch, Complexation and redox buffering of iron(II) by dissolved organic matter, Environ. Sci. Technol., 2017 DOI:10.1021/acs.est.7b03152.
78. A. M. Jones, P. J. Griffin and T. D. Waite, Ferrous iron oxidation by molecular oxygen under acidic conditions: the effect of citrate, EDTA and fulvic acid, Geochim. Cosmochim. Acta, 2015, 160, 117,  DOI:10.1016/j.gca.2015.03.026.
79. M. Aeschbacher, C. Graf, R. P. Schwarzenbach and M. Sander, Antioxidant properties of humic substances, Environ. Sci. Technol., 2012, 46, 4916–4925,  DOI:10.1021/es300039h.
80. M. Aeschbacher, M. Sander and R. P. Schwarzenbach, Novel electrochemical approach to assess the redox properties of humic substances, Environ. Sci. Technol., 2010, 44, 87–93,  DOI:10.1021/es902627p.
81. C. Blodau, M. Bauer, S. Regenspurg and D. Macalady, Electron accepting capacity of dissolved organic matter as determined by reaction with metallic zinc, Chem. Geol., 2009, 260, 186–195,  DOI:10.1016/j.chemgeo.2008.12.016.
82. M. Bauer, T. Heitmann, D. L. Macalady and C. Blodau, Electron transfer capacities and reaction kinetics of peat dissolved organic matter, Environ. Sci. Technol., 2007, 41, 139–145,  DOI:10.1021/es061323j.
83. L. Klupfel, A. Piepenbrock, A. Kappler and M. Sander, Humic substances as fully regenerable electron acceptors in recurrently anoxic environments, Nat. Geosci., 2014, 7, 195–200,  DOI:10.1038/ngeo2084.
84. M. P. Lau, M. Sander, J. Gelbrecht and M. Hupfer, Solid phases as important electron acceptors in freshwater organic sediments, Biogeochemistry, 2015, 123, 49–61,  DOI:10.1007/s10533-014-0052-5.
85. D. T. Scott, D. M. McKnight, E. L. Blunt-Harris, S. E. Kolesar and D. R. Lovley, Quinone moieties act as electron acceptors in the reduction of humic substances by humics-reducing microorganisms, Environ. Sci. Technol., 1998, 32, 2984–2989,  DOI:10.1021/es980272q.
86. G. C. Wallace, M. Sander, Y.-P. Chin and W. A. Arnold, Quantifying the electron donating capacities of sulfide and dissolved organic matter in sediment pore waters of wetlands, Environ. Sci.: Processes Impacts, 2017 10.1039/C7EM00060J.
87. Z.-G. Yu, S. Orsetti, S. B. Haderlein and K.-H. Knorr, Electron transfer between sulfide and humic acid: electrochemical evaluation of the reactivity of Sigma-Aldrich humic acid toward sulfide, Aquat. Geochem., 2015, 22, 117–130,  DOI:10.1007/s10498-015-9280-0.
88. I. Bauer and A. Kappler, Rates and extent of reduction of Fe(III) and O₂ by humic substances, Environ. Sci. Technol., 2009, 43, 4902–4908,  DOI:10.1021/es900179s.
89. J. Chen, B. Gu, R. A. Royer and W. D. Burgos, The roles of natural organic matter in chemical and microbial reduction of ferric iron, Sci. Total Environ., 2003, 307, 167–178,  DOI:10.1016/S0048-9697(02)00538-7.
90. A. Kappler, M. Benz, B. Schink and A. Brune, Electron shuttling via humic acids in microbial iron(III) reduction in a freshwater sediment, FEMS Microbiol. Ecol., 2004, 47, 85–92,  DOI:10.1016/s0168-6496(03)00245-9.
91. G. Liu, S. Qiu, B. Liu, Y. Pu, Z. Gao, J. Wang, R. Jin and J. Zhou, Microbial reduction of Fe(III)-bearing clay minerals in the presence of humic acids, Sci. Rep., 2017, 7, 45354,  DOI:10.1038/srep45354.
92. D. R. Lovley, J. L. Fraga, E. L. Blunt-Harris, L. A. Hayes, E. J. P. Phillips and J. D. Coates, Humic substances as a mediator for microbially catalyzed metal reduction, Acta Hydrochim. Hydrobiol., 1998, 26, 152–157.
93. S. Rakshit, M. Uchimiya and G. Sposito, Iron(III) bioreduction in soil in the presence of added humic substances, Soil Sci. Soc. Am. J., 2009, 73, 65–71,  DOI:10.2136/sssaj2007.0418.
94. Y. Yuan, X. Cai, Y. Wang and S. Zhou, Electron transfer at microbe-humic substances interfaces: electrochemical, microscopic and bacterial community characterizations, Chem. Geol., 2017, 456, 1–9,  DOI:10.1016/j.chemgeo.2017.02.020.
95. M. Wolf, A. Kappler, J. Jiang and R. U. Meckenstock, Effects of humic substances and quinones at low concentrations on ferrihydrite reduction by Geobacter metallireducens, Environ. Sci. Technol., 2009, 43, 5679–5685,  DOI:10.1021/es803647r.
96. G. Davies, A. Fataftah, A. Cherkasskiy, E. A. Ghabbour, A. Radwan, S. A. Jansen, S. Kolla, M. D. Paciolla, L. T. Sein and W. Buermann, Tight metal binding by humic acids and its role in biomineralization, J. Chem. Soc., Dalton Trans., 1997, 4047–4060,  10.1039/A703145I.
97. S. C. B. Myneni, Soft X-ray spectroscopy and spectromicroscopy studies of organic molecules in the environment, Rev. Mineral. Geochem., 2002, 49, 485–579,  DOI:10.2138/gsrmg.49.1.485.
98. J. T. Nurmi and P. G. Tratnyek, Electrochemistry of natural organic matter, in Aquatic Redox Chemistry, ed. P. G. Tratnyek, T. J. Grundl and S. B. Haderlein, American Chemical Society, Washington, DC, 2011, vol. 1071, pp. 129–151,  DOI:10.1021/bk-2011-1071.ch007.
99. M. L. Fultz and R. A. Durst, Mediator compounds for the electrochemical study of biological redox systems: a compilation, Anal. Chim. Acta, 1982, 140, 1–18,  DOI:10.1016/S0003-2670(01)95447-9.
100. R. P. Schwarzenbach, R. Stierli, K. Lanz and J. Zeyer, Quinone and iron porphyrin mediated reduction of nitroaromatic compounds in homogeneous aqueous solution, Environ. Sci. Technol., 1990, 24, 1566–1574,  DOI:10.1021/es00080a017.
101. K. Vuorilehto, Stable, colourless and water-soluble electron-transfer mediators used in enzyme electrochemistry, J. Appl. Electrochem., 2008, 38, 1427–1433,  DOI:10.1007/s10800-008-9587-2.
102. S. Orsetti, C. Laskov and S. B. Haderlein, Electron transfer between iron minerals and quinones: estimating the reduction potential of the Fe(II)-goethite surface from AQDS speciation, Environ. Sci. Technol., 2013, 47, 14161–14168,  DOI:10.1021/es403658g.
103. M. Aeschbacher, D. Vergari, R. P. Schwarzenbach and M. Sander, Electrochemical analysis of proton and electron transfer equilibria of the reducible moieties in humic acids, Environ. Sci. Technol., 2011, 45, 8385–8394,  DOI:10.1021/es201981g.
104. C. A. Gorski, L. Klupfel, A. Voegelin, M. Sander and T. B. Hofstetter, Redox properties of structural Fe in clay minerals. 2. Electrochemical and spectroscopic characterization of electron transfer irreversibility in ferruginous smectite, SWa-1, Environ. Sci. Technol., 2012, 46, 9369–9377,  DOI:10.1021/es302014u.
105. C. A. Gorski, L. E. Klupfel, A. Voegelin, M. Sander and T. B. Hofstetter, Redox properties of structural iron in clay minerals: 3. Relationships between smectite redox and structural properties, Environ. Sci. Technol., 2013, 47, 13477–13485,  DOI:10.1021/es403824x.
106. A. Prevoteau, F. Ronsse, I. Cid, P. Boeckx and K. Rabaey, The electron donating capacity of biochar is dramatically underestimated, Sci. Rep., 2016, 6, 32870,  DOI:10.1038/srep32870.
107. N. Gupta and H. Linschitz, Hydrogen-bonding and protonation effects in electrochemistry of quinones in aprotic solvents, J. Am. Chem. Soc., 1997, 119, 6384–6391,  DOI:10.1021/ja970028j.
108. V. Gutmann, G. Gritzner and K. Danksagmuller, Solvent effects on the redox potential of hexacyanoferrate(III)-hexacyanoferrate(II), Inorg. Chim. Acta, 1976, 17, 81–86,  DOI:10.1016/S0020-1693(00)81961-1.
109. R. Lu, W. Chen, W.-W. Li, G.-P. Sheng, L.-J. Wang and H.-Q. Yu, Probing the redox process of p-benzoquinone in dimethyl sulphoxide by using fluorescence spectroelectrochemistry, Front. Environ. Sci. Eng., 2017, 11, 14,  DOI:10.1007/s11783-017-0905-y.
110. R. Petrucci, G. Marrosu, P. Astolfi, G. Lupidi and L. Greci, Cyclic voltammetry, spectroelectrochemistry and electron spin resonance as combined tools to study thymoquinone in aprotic medium, Electrochim. Acta, 2012, 60, 230–238,  DOI:10.1016/j.electacta.2011.11.055.
111. K. Sasaki, T. Kashimura, M. Ohura, Y. Ohsaki and N. Ohta, Solvent effect in the electrochemical reduction of p-quinones in several aprotic solvents, J. Electrochem. Soc., 1990, 137, 2437–2443,  DOI:10.1149/1.2086957.
112. S. L. J. Tan, M. L. Novianti and R. D. Webster, Effects of low to intermediate water concentrations on proton-coupled electron transfer (PCET) reactions of flavins in aprotic solvents and a comparison with the PCET reactions of quinones, J. Phys. Chem. B, 2015, 119, 14053–14064,  DOI:10.1021/acs.jpcb.5b07534.
113. M. E. Tessensohn, H. Hirao and R. D. Webster, Electrochemical properties of phenols and quinones in organic solvents are strongly influenced by hydrogen-bonding with water, J. Phys. Chem., 2012, 117, 1081–1090,  DOI:10.1021/jp311007m.
114. N. G. Tsierkezos, Cyclic voltammetric studies of ferrocene in nonaqueous solvents in the temperature range from 248.15 to 298.15 K, J. Solution Chem., 2007, 36, 289–302,  DOI:10.1007/s10953-006-9119-9.
115. X. Zhu and C. Wang, Accurate estimation of the one-electron reduction potentials of various substituted quinones in DMSO and CH₃CN, J. Org. Chem., 2010, 75, 5037–5047,  DOI:10.1021/jo100735s.
116. J. T. Nurmi and P. G. Tratnyek, Voltammetric investigations of natural organic matter, Proceedings of the 20th Anniversary Conference of the International Humic Substances Conference (IHSS), 21-26 July 2002, Northeastern University, Boston, MA, 2002. pp. 58–60.
117. J. T. Nurmi and P. G. Tratnyek, Electrochemical properties of natural organic matter (NOM), fractions of NOM, and model biogeochemical electron shuttles, Environ. Sci. Technol., 2002, 36, 617–624,  DOI:10.1021/es0110731.
118. W. Rochus and S. Sipos, Micelle formation by humic substances, Agrochimica, 1978, 22, 446–454.
119. R. R. Engebretson and W. R. von, Micro-organization in dissolved humic acids, Environ. Sci. Technol., 1994, 28, 1934–1941,  DOI:10.1021/es00060a026.
120. R. Von Wandruszka, The micellar model of humic acid: evidence from pyrene fluorescence measurements, Soil Sci., 1998, 163, 921–930,  DOI:10.1097/00010694-199812000-00002.
121. T. F. Guetzloff and J. A. Rice, Does humic acid form a micelle?, Sci. Total Environ., 1994, 152, 31–35,  DOI:10.1016/0048-9697(94)90548-7.
122. A. Piccolo, S. Nardi and G. Concheri, Macromolecular changes of humic substances induced by interaction with organic acids, Eur. J. Soil Sci., 1996, 47, 319–328,  DOI:10.1111/j.1365-2389.1996.tb01405.x.
123. Z. Yang, A. Kappler and J. Jiang, Reducing capacities and distribution of redox-active functional groups in low molecular weight fractions of humic acids, Environ. Sci. Technol., 2016, 50, 12105–12113,  DOI:10.1021/acs.est.6b02645.
124. M. J. M. Wells and H. A. Stretz, Supramolecular architectures of natural organic matter, Sci. Total Environ., 2019, 671, 1125–1133,  DOI:10.1016/j.scitotenv.2019.03.406.
125. A. J. Simpson, W. L. Kingery, D. R. Shaw, M. Spraul, E. Humpfer and P. Dvortsak, The application of ¹H HR-MAS NMR spectroscopy for the study of structures and associations of organic components at the solid-aqueous interface of a whole soil, Environ. Sci. Technol., 2001, 35, 3321–3325,  DOI:10.1021/es010607v.
126. D. Martin and H. G. Hauthal, Dimethyl Sulphoxide, Halsted Press, 1975.
127. T. Heinze, R. Dicke, A. Koschella, A. H. Kull, E. A. Klohr and W. Koch, Effective preparation of cellulose derivatives in a new simple cellulose solvent, Macromol. Chem. Phys., 2000, 201, 627–631,  DOI:10.1002/(SICI)1521-3935(20000301)201:6<627::AID-MACP627>3.0.CO;2-Y.
128. F. Lu and J. Ralph, Non-degradative dissolution and acetylation of ball-milled plant cell walls: high-resolution solution-state NMR, Plant J., 2003, 35, 535–544,  DOI:10.1046/j.1365-313X.2003.01817.x.
129. M. M. Tfaily, R. K. Chu, J. Toyoda, N. Tolic, E. W. Robinson, L. Paša-Tolić and N. J. Hess, Sequential extraction protocol for organic matter from soils and sediments using high resolution mass spectrometry, Anal. Chim. Acta, 2017, 972, 54–61,  DOI:10.1016/j.aca.2017.03.031.
130. D. S. H. Chan, M. E. Kavanagh, K. J. McLean, A. W. Munro, D. Matak-Vinković, A. G. Coyne and C. Abell, Effect of DMSO on protein structure and interactions assessed by collision-induced dissociation and unfolding, Anal. Chem., 2017, 89, 9976–9983,  DOI:10.1021/acs.analchem.7b02329.
131. T. Arakawa, Y. Kita and S. N. Timasheff, Protein precipitation and denaturation by dimethyl sulfoxide, Biophys. Chem., 2007, 131, 62–70,  DOI:10.1016/j.bpc.2007.09.004.
132. H. J. Sterling, J. S. Prell, C. A. Cassou and E. R. Williams, Protein conformation and supercharging with DMSO from aqueous solution, J. Am. Soc. Mass Spectrom., 2011, 22, 1178,  DOI:10.1007/s13361-011-0116-x.
133. C. Fan, J. Lu, W. Zhang, I. Suzuki and G. Li, Enhanced electron-transfer reactivity of cytochrome b5 by dimethylsulfoxide and N,N’-dimethylformamide, Anal. Sci., 2002, 18, 1031–1033,  DOI:10.2116/analsci.18.1031.
134. C. Fan, G. Wagner and G. Li, Effect of dimethyl sulfoxide on the electron transfer reactivity of hemoglobin, Bioelectrochemistry, 2001, 54, 49–51,  DOI:10.1016/S0302-4598(01)00107-6.
135. Q. Li and P. Mabrouk, Spectroscopic and electrochemical studies of horse myoglobin in dimethyl sulfoxide, JBIC, J. Biol. Inorg. Chem., 2003, 8, 83–94,  DOI:10.1007/s00775-002-0392-9.
136. B. W. Berry, M. C. Martínez-Rivera and C. Tommos, Reversible voltammograms and a Pourbaix diagram for a protein tyrosine radical, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 9739–9743,  DOI:10.1073/pnas.1112057109.
137. A. S. Pavitt, E. J. Bylaska and P. G. Tratnyek, Oxidation potentials of phenols and anilines: correlation analysis of electrochemical and theoretical values, Environ. Sci.: Processes Impacts, 2017, 19, 339–349,  10.1039/C6EM00694A.
138. S. A. Petrova, M. B. Kolodyazhny and O. S. Ksenzhek, Electrochemical properties of some naturally occurring quinones, J. Electroanal. Chem., 1990, 277, 189–196,  DOI:10.1016/0022-0728(90)85101-A.
139. R. Ojani, J. Raoof and M. Ebrahimi, A cyclic voltammetric study of the aqueous electrochemistry of some anthraquinone derivatives on carbon paste electrode, Iran. J. Chem. Chem. Eng., 2001, 20, 75–81.
140. S. I. Bailey and I. M. Ritchie, A cyclic voltammetric study of the aqueous electrochemistry of some quinones, Electrochim. Acta, 1985, 30, 3–12,  DOI:10.1016/0013-4686(85)80051-7.
141. Y. Kumagai, Y. Shinkai, T. Miura and A. K. Cho, The chemical biology of naphthoquinones and Its environmental implications, Annu. Rev. Pharmacol. Toxicol., 2012, 52, 221–247,  DOI:10.1146/annurev-pharmtox-010611-134517.
142. R. Salazar, J. Vidal, M. Martínez-Cifuentes, R. Araya-Maturana and O. Ramírez-Rodríguez, Electrochemical characterization of hydroquinone derivatives with different substituents in acetonitrile, New J. Chem., 2015, 39, 1237–1246,  10.1039/C4NJ01657B.
143. A. J. Bard and L. R. Faulkner, Electrochemical Methods. Fundamentals and Applications, Wiley, New York, 2001.
144. M. T. Huynh, C. W. Anson, A. C. Cavell, S. S. Stahl and S. Hammes-Schiffer, Quinone 1 e⁻ and 2 e⁻/2 H⁺ reduction potentials: identification and analysis of deviations from systematic scaling relationships, J. Am. Chem. Soc., 2016, 138, 15903–15910,  DOI:10.1021/jacs.6b05797.
145. M. Uchimiya and A. T. Stone, Reversible redox chemistry of quinones: impact on biogeochemical cycles, Chemosphere, 2009, 77, 451–458,  DOI:10.1016/j.chemosphere.2009.07.025.
146. A. Slowey and M. Marvin-DiPasquale, How to overcome inter-electrode variability and instability to quantify dissolved oxygen, Fe(II), Mn(II), and S(II) in undisturbed soils and sediments using voltammetry, Geochem. Trans., 2012, 13, 6,  DOI:10.1186/1467-4866-13-6.
147. M. Zelic, Reverse scan as a source of information in square wave voltammetry, Croat. Chem. Acta, 2006, 79, 49–55.
148. T. Andres, L. Eckmann and D. K. Smith, Voltammetry of nitrobenzene with cysteine and other acids in DMSO. Implications for the biological reactivity of reduced nitroaromatics with thiols, Electrochim. Acta, 2013, 92, 257–268,  DOI:10.1016/j.electacta.2013.01.047.
149. H. Hotta, H. Sakamoto, S. Nagano, T. Osakai and Y. Tsujino, Unusually large numbers of electrons for the oxidation of polyphenolic antioxidants, Biochim. Biophys. Acta, Gen. Subj., 2001, 1526, 159–167,  DOI:10.1016/S0304-4165(01)00123-4.
150. M. D. Ryan, A. Yueh and W. Y. Chen, The electrochemical oxidation of substituted catechols, J. Electrochem. Soc., 1980, 127, 1489–1495,  DOI:10.1149/1.2129936.
151. Ł. Górski, F. Ciepiela and M. Jakubowska, Automatic baseline correction in voltammetry, Electrochim. Acta, 2014, 136, 195–203,  DOI:10.1016/j.electacta.2014.05.076.
152. J. M. Saveant, Elements of Molecular and Biomolecular Electrochemistry, John Wiley & SonsNew Jersey, 2006.
153. A. L. Eckermann, D. J. Feld, J. A. Shaw and T. J. Meade, Electrochemistry of redox-active self-assembled monolayers, Coord. Chem. Rev., 2010, 254, 1769–1802,  DOI:10.1016/j.ccr.2009.12.023.
154. Y. Yuan, H. Zhang, Y. Wei, Y. Si, G. Li and F. Zhang, Onsite quantifying electron donating capacity of dissolved organic matter, Sci. Total Environ., 2019, 662, 57–64,  DOI:10.1016/j.scitotenv.2019.01.178.
155. M. E. G. Lyons, Transport and kinetics in electroactive polymers, Adv. Chem. Phys., 1996, 94, 297–624,  DOI:10.1002/9780470141533.ch5.
156. S. Kim, R. W. Kramer and P. G. Hatcher, Graphical method for analysis of ultrahigh-resolution broadband mass spectra of natural organic matter, the Van Krevelen diagram, Anal. Chem., 2003, 75, 5336–5344,  DOI:10.1021/ac034415p.
157. R. L. Sleighter and P. G. Hatcher, Molecular characterization of dissolved organic matter (DOM) along a river to ocean transect of the lower Chesapeake Bay by ultrahigh resolution electrospray ionization Fourier transform ion cyclotron resonance mass spectrometry, Mar. Chem., 2008, 110, 140–152,  DOI:10.1016/j.marchem.2008.04.008.
158. J. Lehmann, D. Solomon, J. Kinyangi, L. Dathe, S. Wirick and C. Jacobsen, Spatial complexity of soil organic matter forms at nanometre scales, Nat. Geosci., 2008, 1, 238–242,  DOI:10.1038/ngeo155.
159. M. Witt, J. Fuchser and B. P. Koch, Fragmentation studies of fulvic acids using collision induced dissociation Fourier transform ion cyclotron resonance mass spectrometry, Anal. Chem., 2009, 81, 2688–2694,  DOI:10.1021/ac802624s.
160. K. R. Murphy, S. A. Timko, M. Gonsior, L. C. Powers, U. J. Wünsch and C. A. Stedmon, Photochemistry illuminates ubiquitous organic matter fluorescence spectra, Environ. Sci. Technol., 2018, 52, 11243–11250,  DOI:10.1021/acs.est.8b02648.
161. R. L. Sleighter and P. G. Hatcher, The application of electrospray ionization coupled to ultrahigh resolution mass spectrometry for the molecular characterization of natural organic matter, J. Mass Spectrom., 2007, 42, 559–574,  DOI:10.1002/jms.1221.
162. S. Er, C. Suh, M. P. Marshak and A. Aspuru-Guzik, Computational design of molecules for an all-quinone redox flow battery, Chem. Sci., 2014, 6, 885–893,  10.1039/C4SC03030C.
163. S. E. Treimer and D. H. Evans, Electrochemical reduction of acids in dimethyl sulfoxide. CE mechanisms and beyond, J. Electroanal. Chem., 1998, 449, 39.
164. G. Gritzner, Solvent effects on half-wave potentials, J. Phys. Chem., 1986, 90, 5478–5485,  DOI:10.1021/j100412a116.
165. V. V. Pavlishchuk and A. W. Addison, Conversion constants for redox potentials measured versus different reference electrodes in acetonitrile solutions at 25^∘C, Inorg. Chim. Acta, 2000, 298, 97–102,  DOI:10.1016/S0020-1693(99)00407-7.
166. D. Bao, B. Millare, W. Xia, B. G. Steyer, A. A. Gerasimenko, A. Ferreira, A. Contreras and V. I. Vullev, Electrochemical Oxidation of Ferrocene: A Strong Dependence on the Concentration of the Supporting Electrolyte for Nonpolar Solvents, J. Phys. Chem. A, 2009, 113, 1259–1267,  DOI:10.1021/jp809105f.

---

Footnote

† Electronic supplementary information (ESI) available: The supporting information includes background, voltammograms, and peak properties for all of the materials characterized in this study. See DOI: 10.1039/c9em00313d

---