Open Access Article
Open Access ArticleUncertainty and equifinality in environmental modelling of organic pollutants with specific focus on cyclic volatile methyl siloxanes†
M. J.
Whelan
 *a,
J.
Kim
*a,
J.
Kim
 b,
N.
Suganuma
c and
D.
Mackay
d
b,
N.
Suganuma
c and
D.
Mackay
d
aSchool of Geography, Geology and the Environment, University of Leicester, Leicester, UK. E-mail: mjw72@le.ac.uk; Tel: +44 (0)116 2525215
bThe Dow Chemical Company, Midland, Michigan, USA
cThe Dow Chemical Company, Japan
dCentre for Environmental Modelling and Chemistry, Trent University, Canada
First published on 5th June 2019
Abstract
Multi-media fate and transport models (MFTMs) are invaluable tools in understanding and predicting the likely behaviour of organic pollutants in the environment. However, some parameters describing the properties of both the environmental system and the chemical pollutant under consideration are uncertain and or variable in space and time. Furthermore, model performance is often evaluated using sparse data sets on chemical concentrations in different media. This can result in equifinality – the phenomenon in which several different combinations of model parameters can result in similar predictions of environmental concentrations. We explore this idea for MFTMs for the first time using, as examples, three cyclic volatile methyl siloxanes (cVMS: D4, D5 and D6) and the QWASI lake model applied to Tokyo Bay. Monte Carlo simulation was employed with parameters selected from probability distributions representing estimated uncertainty in a large number of iterations. This generated distributions of predicted chemical concentrations in water (CW) and sediment (CS) which represent the aleatory uncertainty envelope but which also demonstrate significant equifinality. For all three compounds, the uncertainty implied in the CW was lower (coefficient of variation, CV, of the order of 20%) than for CS (CV ca. 45%), reflecting the propensity of cVMS compounds to sorb to sediment and the sensitivity of the model to KOC. Confidence intervals were particularly high for the persistence of D5 and D6 in sediment which both ranged between approximately 1.7 years and approximately 26 years for Tokyo Bay. Predicted concentration distributions matched observations well for D5 and D6 not for D4. Equifinality could be reduced by better constraining acceptable parameter sets using additional measured data from different environmental compartments.
Environmental significanceMulti-media fate and transport models (MFTMs) are invaluable tools in understanding the likely behaviour of organic pollutants in the environment. In this paper we explore, for the first time, the concept of equifinality – the phenomenon in which several different combinations of model parameters can result in similar model predictions – for MFTMs. This is illustrated using the QWASI model applied to Tokyo Bay for three cyclic volatile methyl siloxanes. These compounds are currently under regulatory scrutiny in terms of their persistence and potential to bioaccumulate. As well as highlighting the idea of equifinality in MFTMs, the paper demonstrates the utility of calculating confidence intervals for predicted concentrations and persistence – which can help underpin our confidence in model-based regulatory decisions. |
1. Introduction
Multi-media fate and transport models (MFTMs) are invaluable tools with which to explore the environmental behaviour of organic pollutants. They allow the integration of knowledge about chemical partitioning and degradation in different environmental compartments with information about physical environmental characteristics (e.g. dimensions, composition, temperature, flow rates) to predict net outcomes such as concentrations in different compartments and chemical flux rates.1–3Unlike models of some other types of environmental systems behaviour, such as in hydrology,4–6 river water quality7 and diffuse pollutant transfer,8 MFTMs are rarely calibrated. Rather, their system-specific parameters (e.g. compartment dimensions, flow rates, organic carbon concentrations, temperatures, etc.) are often estimated from independent measurements reported in the literature. Model performance is usually evaluated in terms of the match between predicted concentrations and measured data. However, the spatial and/or temporal frequency of available samples is often low. This means that formal validation can be weak (in a statistical sense) and sometimes qualitative.9,10 In addition, the possibility of “equifinality” (similar predictions of salient model outputs – such as predicted concentrations in various environmental compartments – resulting from very different combinations of model parameters11) is rarely, if ever, explored. For example, different values of sediment deposition rate, resuspension rate, burial rate and organic carbon mineralisation rate in a lake might lead to the same organic carbon content in sediment (cf. the derivation of the particulate organic carbon mass balance in CoZMo-POP12), but these combinations could have quite different implications for the predicted concentrations and residence times of organic contaminants in the sediment and water compartments. In some other fields, where measured data are more abundant (such as hydrology and diffuse pollution transfers13–17), equifinality is a widely recognised phenomenon and has been a major area of research over the last few decades. It sometimes occurs when models are poorly constrained (e.g. when measured data are available for only one predicted output variable, such as stream discharge, with other predicted internal state variables, such as soil water content or water table height, not measured and, hence, not used to constrain parameter choice or in validation). Equifinality can be important because it means that an “optimal” set of model parameters may appear to yield good predictions of the data available (in hydrology this is often the river discharge at the catchment outlet) but actually yield poor predictions for the variables which are not measured (e.g. soil water storage, groundwater levels or the specific contributions of different hydrological pathways). In other words, the model gives right results for the wrong reasons.18 Other combinations of parameters may yield similarly good predictions of the available data but better (and unknown) predictions of the unmeasured state variables.19
MFTMs are often used to investigate the implications of different physico-chemical properties for the environmental fate and transport of organic pollutants20 and in risk assessment to estimate levels of exposure in different environmental compartments resulting from a given emission scenario. However, significant uncertainties (and variability) exist in both chemical-specific parameters (such as partition coefficients and degradation rate constants) and in the parameters which are used to describe the characteristics of the receiving environment (such as inter-media mass transfer coefficients, advection rates, some system dimensions and organic carbon fluxes). Uncertainty in environmental parameters is sometimes unimportant if the aim of the modelling is to compare the relative behaviours, exposures and risks of different organic pollutants for the same environmental assumptions – as is the case in the adoption of “evaluative” unit world models.1,21 However, it becomes more important if the aim is to predict (and explain) absolute exposure in specific environmental systems – where the accuracy of the model is judged on the basis of a comparison with (often sparse) measured concentrations. Similarly, if chemicals are evaluated in terms of their environmental persistence using absolute thresholds,22 the uncertainty in both chemical-specific and media-specific properties can be important. So-called benchmarking in which persistence is defined relative to other substances23 can offer some advantages in this respect, although parameter uncertainties could potentially still impact outcomes.
The effects of uncertainty in model parameterisation can be assessed in a number of ways, including first order analysis and Monte Carlo Simulation.24 The principles are identical to sensitivity analysis and uncertainties in parameters to which model outputs are most sensitive will make larger contributions to output uncertainty than those to which outputs are insensitive. Although it is often useful to quantify the propagation of uncertainty from parameters to outputs (e.g. to estimate the spread of output values resulting from a priori uncertainties in inputs), particularly when making comparisons with measured data, this is still not common practice in applications of MFTMs (although Buser et al. [2012]25 suggest that it should be).
To illustrate and explore these ideas we adapted QWASI (Quantitative Water Air Sediment Interaction), a steady state non-equilibrium (Level III) MFTM, designed for lakes and applied it to three cyclic volatile methyl siloxanes (cVMS): octamethylcyclotetrasiloxane (D4), decamethylcyclopentasiloxane (D5) and dodecamethylcyclohexasiloxane (D6). QWASI26,27 has been previously applied to explore the fate of a range of different chemicals in different aquatic systems and its predictions have generally been shown to match observations adequately.28–32 This model has also been used to explore the behaviour of cVMS compounds in various lakes including Lake Pepin and Lake Ontario3,9 and is applied here to Tokyo Bay, Japan, where environmental monitoring for cVMS compounds has been conducted.33 Importantly, we explicitly introduce the term equifinality to the applications of MFTMs and discuss the relevance of this concept for the interpretation of model outputs – particularly in comparison with measured environmental concentrations. A secondary aim of the paper is to use an MFTM as a framework for exploring aspects of cVMS behaviour in Tokyo Bay and to discuss levels of exposure and persistence for D4, D5 and D6.
2. Methods
The work described here was conducted using a modified version of QWASI v3.1 (http://www.trentu.ca/academic/aminss/envmodel/models/models.html) implemented in MS Visual BASIC for Applications, running behind Microsoft Excel.9 As an example system, the model was applied to the Inner Tokyo Bay, Japan (Fig. 1), for which measured concentrations of cVMS have been determined in sediment.33 Tokyo Bay is a large semi-enclosed marine environment with a surface area of approximately 992 km2 and a mean depth of approximately 15–19 m.34,35 It receives wastewater from a catchment inhabited by approximately 29 million people.36 Approximately 8.7 million of these people live in Tokyo itself and the rest live in the surrounding area draining to the Bay. It is assumed that the entire population is served by good wastewater treatment.33,36 It is also assumed that there is no degradation or volatilisation of cVMS compounds discharged to rivers before these rivers reach the Bay (although we recognise that, in reality, there are likely to be losses of cVMS compounds from some discharge points where rivers are distant from the Bay). The dimensions and properties for Tokyo Bay adopted in the QWASI modelling described here are shown in Table S2.† In all cases, the concentrations of cVMS compounds were assumed to have a constant value of 10 ng m−3 in air which is consistent with measurements of D5 reported for rural Sweden.37 Emissions of D4, D5 and D6 to Tokyo Bay were assumed to be 122, 3693 and 426 kg year−1, respectively, based on the same per capita emission estimates to wastewater from ‘‘cosmetic’’ products (i.e. those products which are potentially washed off to wastewater) assumed by Brooke et al. (2008a, b, c)38–40 and used by Whelan and Breivik (2013):10 [i.e. 140, 4250 and 490 mg cap−1 year−1, respectively] but with an assumed removal in wastewater treatment of 97% for all three compounds. These per capita estimates are higher than unpublished estimates derived from average measured concentrations of D4, D5 and D6 in untreated wastewater by the Silicone Industry Association of Japan (SIAJ) i.e. 64, 1442 and 90 mg cap−1 year−1. However, given that the aim of this paper is to explore the concept of equifinality, the Brooke et al. (2008)38–40 values have been retained.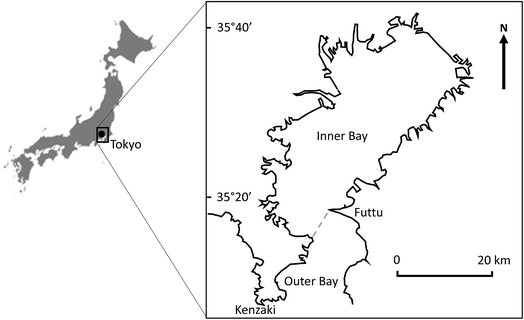 | ||
| Fig. 1 Location map of Tokyo Bay showing the boundary between the Inner and Outer Bay. The dashed line marks the division between the Inner and Outer Bays (adapted from Okada et al., 201134). | ||
2.1 Monte Carlo Simulation
In Monte Carlo Simulation (MCS), a deterministic model is run a large number of times (iterations). In each iteration, a different set of model parameter values is used with each parameter value selected randomly from pre-defined probability density functions (pdf's). A number of different pdf's can be used to describe the distribution of a parameter. If the parameter is well defined (i.e. if there are measured data on the parameter value) then it may be possible to fit a specific pdf to the measured data. More commonly, however, measured values are scarce and both the shape and the statistical parameters of the distribution must be estimated. Common pdf's employed to represent uncertain distributions include the normal (Gaussian) distribution, the log-normal distribution and the triangular distribution.41 Although many natural phenomena exhibit symmetrical (e.g. normal) distributions, it is more common for distributions to be positively skewed. The log-normal distribution is, therefore, often used.42 One significant advantage of this distribution over the normal distribution is that it does not contain values less than or equal to zero. When used in MCS, therefore, negative values (which are not physically realistic for many model parameters) are not sampled, which means that models do not need to discard some iterations. Another advantage is that the width of the distribution can be described in relative terms via the coefficient of variation (CV) where: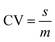 | (1) |
The resulting log-normal distribution will have parameters μ and σ given by:
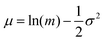 | (2) |
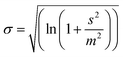 | (3) |
In the code, exceedance quantiles (0–1) are generated from a random number generator. These quantiles are then converted to standard normal deviates N using an empirical formula.43 For log-normally distributed parameters individual parameter values (G) can then be generated from
| G = exp[(N × σ) + μ] |
For normally distributed parameters with arithmetic mean, m, and standard deviation, s, values (G) are simply:
| G = (N × s) + m |
In all cases, simulated parameters were assumed to be uncorrelated41 and 5000 iterations were performed.
2.2 Sensitivity versus uncertainty
MCS is used here explicitly to quantify the uncertainty in model predictions as a consequence of the combined realistic estimates of the uncertainty in model input parameters. Unlike in sensitivity analysis, where the distribution of the parameter is not important except for defining the extent of parameter space explored by the analysis, in uncertainty analysis the parameter distributions adopted could affect the uncertainty of the predicted variables (e.g. predicted concentrations in water and sediment) – particularly when the model is sensitive to the parameter in question. It should also be noted that the distributions assumed and, in particular, their parameter values are explicitly defined in terms of uncertainty rather than variability. This is an important distinction to make because we can be highly certain about a parameter (e.g. mean annual temperature) for which the variable upon which it is based varies significantly. This distinction is made clearer in the exploration of the effects of temperature on model performance.2.3 Constructing probability distributions for key parameters
The following parameters were described using pdf's in MCS (grouped as either a chemical-specific or an environmental property). The chemical-specific properties considered were: the air water partition coefficient (KAW); the organic carbon to water partition coefficient (KOC); the chemical half life in water (HLwater); the chemical half life in sediment (HLsed); the enthalpy of phase change between air and water (ΔUAW); the enthalpy of phase change between organic carbon and water (ΔUOC) which is assumed to be identical to that between octanol and water (ΔUOW) and the Arrhenius activation energy (Ea) for degradation by hydrolysis. The same Ea value is assumed for both water and sediment because degradation in both media is assumed to be controlled exclusively by hydrolysis in the dissolved phase. The environmental properties were the water inflow and outflow rates; the sediment deposition and resuspension rates; the sediment burial rate; the water surface area and volume; the “active” sediment depth (i.e. the sediment layer which can potentially be resuspended); suspended solids concentrations in the water column and in inflow water; the organic carbon concentration on suspended solids and on sediment particles; the concentration of aerosols in the air; the sediment porosity and particle density; the rainfall rate; the aerosol dry deposition rate; the aerosol scavenging ratio; partial mass transfer coefficients for the air and water sides of the air–water interface and for the sediment–water interface and the water temperature. With the exception of temperature, all parameters were assumed to be log-normally distributed in accordance with similar work conducted on modelling cVMS compounds using QWASI.44 In the absence of good empirical evidence, the pdf parameters (μ and σ) were derived, respectively, from m and s which, in turn were assumed to be the best estimate (base) and an expert estimation of the relative spread of the distribution (CV: eqn (1)). Model parameter CVs used here were based on the parameter “dispersion factors” estimated by Mackay et al. (2014)44 who present detailed justification for their derivation. The method used for the conversion of dispersion factors to CVs is described in S1.† Details of the distributions used are given in S2.†The case of temperature deserves special mention. QWASI is a steady state model and, therefore, does not represent the (potentially important) seasonal cycles in temperature and river flows. The inclusion of temperature in the uncertainty analysis is, therefore, interpreted here primarily in terms of the uncertainty in estimating the mean temperature of the system under consideration (i.e. the sampling error) which is assumed to be relatively small (CV 0.05). However, we also explored the implications of water temperature variability on cVMS behaviour in a separate set of iterations. In this case a normal distribution with an arbitrary CV of 0.5 was assumed. We do not have data on the CV for air or water temperature in Toyko but this value is approximately consistent with typical air temperature variability reported for the continental USA.45
In addition, emission is also known to be highly uncertain. The consequences of uncertainty in emission rate were, therefore, also examined by comparing the distribution in outputs obtained from the MCS where emission was assumed to be constant and a MCS where the emission was assumed to take a log-normal distribution with an arbitrary CV of 0.5. Note that uncertainty in the concentration of cVMS in air was not investigated because the model is very insensitive to the concentration assumed for cVMS in air.9,46 This is because (i) the KAW values for cVMS are so high that exchange is always in the direction water to air for water bodies exposed to waste water (i.e. the fugacity in water is always much greater than the fugacity in air which means that net air to water diffusion will not occur) and (ii) rate of exchange (which is described using the two film resistance model) is limited almost entirely by the partial mass transfer coefficient on the water side of the interface.9
3. Results and discussion
3.1 Uncertainty analysis using MCS
Example outputs from the MCS are shown in Fig. 2 for D5 (5000 iterations). Distributions for D4 and D6 are presented in the ESI (Fig. S1 and S2).† Pertinent statistics for the predicted distributions of CW and CS are given in Table 1. In all cases, the predicted concentrations in water are lower than the limits of detection (LOD) and limits of quantification (LOQ) typically reported for cVMS in water.47 The distributions are slightly positively skewed (i.e. the mean is slightly greater than the median) with a relatively limited range (CVs of 18%, 21% and 22% for D4, D5 and D6 respectively). The predicted concentrations in sediment, on the other hand, have a pronounced positive skew and a relatively wider range (CVs of 53%, 46% and 37% for D4, D5 and D6 respectively). With the exception of CS for D4, all distributions are platykurtic (kurtosis < 3). Values between the 2.5th and 97.5th percentiles capture 95% of the distribution and can, thus, be interpreted as uncertainty confidence intervals (i.e. we are 95% confident that predicted concentrations will be between these values, given the uncertainty distributions in the individual input parameters which were assumed in the simulation). In other words, as long as the “real” (but unknown) values for the input parameters used in QWASI for Tokyo Bay lie within the uncertainty bounds set by the input distributions, we can be 95% confident that the “real” model predictions will be captured by the distributions shown in Fig. 2 and in the ESI† (i.e. that the “real” predicted concentrations lie between the 2.5th and 97.5th percentiles shown in Table 1). Please note that these estimates refer only to the “aleatory” uncertainty in model predictions (i.e. the uncertainty in predicted concentrations resulting from given uncertainties in the input parameters). They do not refer to our degree of certainty in the ability of the model to represent processes in the actual system under consideration which can be considered “epistemic” and essentially unknown.48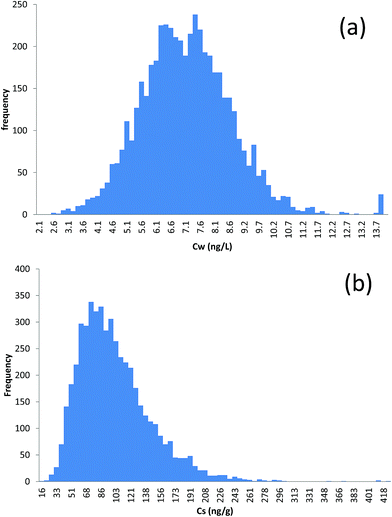 | ||
| Fig. 2 Frequency distributions of (a) predicted concentration in the water column and (b) predicted concentration in sediment (ng g−1 dry weight) for D5 in Tokyo Bay. | ||
| D4 | D5 | D6 | ||
|---|---|---|---|---|
| C W | Mean (ng L−1) | 0.032 | 7.24 | 0.864 |
| Median (ng L−1) | 0.032 | 7.22 | 0.848 | |
| Skewness | 0.681 | 0.201 | 0.539 | |
| Kurtosis | 1.35 | 0.151 | 0.374 | |
| CV (%) | 17.6 | 21.2 | 22.7 | |
| 2.5 percentile (ng L−1) | 0.023 | 4.37 | 0.526 | |
| 97.5 percentile (ng L−1) | 0.044 | 10.3 | 1.31 | |
| C S | Mean (ng g−1 dw) | 0.013 | 98.5 | 64.4 |
| Median (ng g−1 dw) | 0.011 | 90.8 | 60.8 | |
| Skewness | 1.60 | 1.16 | 0.994 | |
| Kurtosis | 4.58 | 2.23 | 2.06 | |
| CV (%) | 55.1 | 43.3 | 37.6 | |
| 2.5 percentile (ng g−1 dw) | 0.004 | 39.0 | 28.2 | |
| 97.5 percentile (ng g−1 dw) | 0.030 | 199 | 122 |
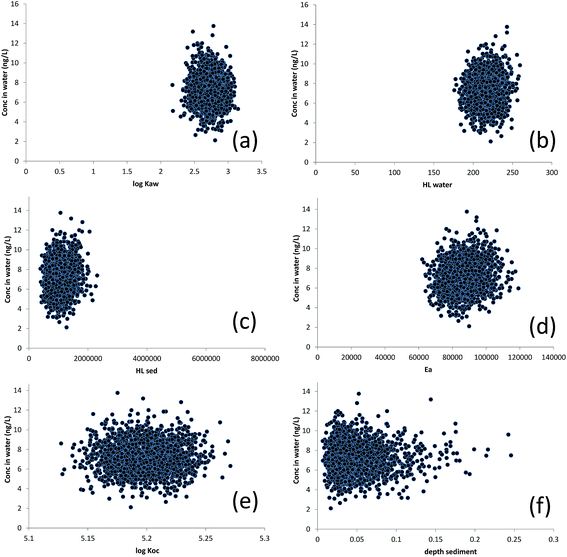
The predicted concentration of D5 in water plotted against MCS-generated values of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KAW, HLwater, HLsed, Ea, log
KAW, HLwater, HLsed, Ea, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOC and sediment depth are displayed in Fig. 3. Although there appears to be little clear relationship between any of the parameter values and CW in Fig. 3 (suggesting that each parameter, individually, exerts a relatively weak influence over CW), Spearman Rank correlations were significant (p ≤ 0.05) between CW and (inter alia) the following parameters: KAW, HLwater, HLsed, Ea, Qout (the advective outflow rate) and MTCw (the water-side partial mass transfer coefficient for water–air exchange) for D4 and D5 and kres (the sediment resuspension rate), Qout, D (the sediment deposition rate), SSC (the suspended sediment concentration) and MTCw for D6 (see ESI Section S3†). There is also a moderate range of values for each parameter which predict (in various combinations with other parameters) the same value of CW. For example, a CW of 8 ng L−1 could be predicted with any value of log
KOC and sediment depth are displayed in Fig. 3. Although there appears to be little clear relationship between any of the parameter values and CW in Fig. 3 (suggesting that each parameter, individually, exerts a relatively weak influence over CW), Spearman Rank correlations were significant (p ≤ 0.05) between CW and (inter alia) the following parameters: KAW, HLwater, HLsed, Ea, Qout (the advective outflow rate) and MTCw (the water-side partial mass transfer coefficient for water–air exchange) for D4 and D5 and kres (the sediment resuspension rate), Qout, D (the sediment deposition rate), SSC (the suspended sediment concentration) and MTCw for D6 (see ESI Section S3†). There is also a moderate range of values for each parameter which predict (in various combinations with other parameters) the same value of CW. For example, a CW of 8 ng L−1 could be predicted with any value of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KAW between approximately 2.4 and 3.1 as long as other parameters were different. This is an example of equifinality.
KAW between approximately 2.4 and 3.1 as long as other parameters were different. This is an example of equifinality.
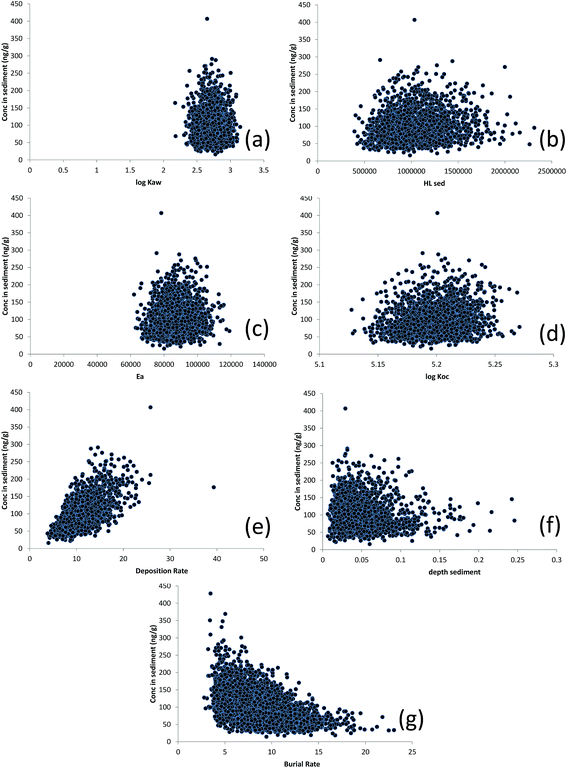
The predicted concentration of D5 in sediment plotted against Monte-Carlo-generated values of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KAW, HLsed, Ea, log
KAW, HLsed, Ea, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOC, sediment deposition rate, sediment depth and sediment burial rate are displayed in Fig. 4. Here, the relationships between the parameter values and CS appear a little stronger – particularly for the sediment deposition rate and, to a lesser extent, KOC, HLsed and the depth of the active mixed sediment layer (all positive) suggesting that these parameters, individually, can exert significant influence over the predicted value of CS. Spearman rank correlations between CS and model input parameters are also shown in Table S4† (note the particularly strong control of D). There is considerable equifinality here too but the extent of this (i.e. the range of parameter values which yield the same value of CS) varies, depending on CS. For example, a CS of 100 ng g−1 dw could arise from any value of the burial rate between 5 and 15 g m−2 d−1, provided other parameters are adjusted (from within their feasible distributions) to compensate.
KOC, sediment deposition rate, sediment depth and sediment burial rate are displayed in Fig. 4. Here, the relationships between the parameter values and CS appear a little stronger – particularly for the sediment deposition rate and, to a lesser extent, KOC, HLsed and the depth of the active mixed sediment layer (all positive) suggesting that these parameters, individually, can exert significant influence over the predicted value of CS. Spearman rank correlations between CS and model input parameters are also shown in Table S4† (note the particularly strong control of D). There is considerable equifinality here too but the extent of this (i.e. the range of parameter values which yield the same value of CS) varies, depending on CS. For example, a CS of 100 ng g−1 dw could arise from any value of the burial rate between 5 and 15 g m−2 d−1, provided other parameters are adjusted (from within their feasible distributions) to compensate.
3.2 Uncertainty in predicted environmental persistence
Frequency distributions (representing model uncertainty) of the predicted persistence of D5 in water (PW), sediment (PS) and overall (POV) are shown, for illustrative purposes in Fig. 5. Descriptive statistics for the simulated distributions of PW, PS and POV are shown in Table 2 for D4, D5 and D6. Although the spread in PW is quite narrow (the 2.5th and 97.5th percentiles were 6.5 and 16.9 days, respectively, for D5), the spreads in PS and POV are wider (the 2.5th and 97.5th percentiles for PS range from 619 to 8275 days and for POV from 47 to 686 days for D5). As in the case of predicted concentrations, the distributions are all positively skewed, with higher skewness values for PS than for PW and with the highest values for POV. The distributions for PW were all flat or platykurtic (kurtosis < 3) and were all peaky or leptokurtic (kurtosis > 3) for POV, with a mix of platykursis and leptokursis for the distributions of PS, reflecting the distribution shapes shown in Fig. 5. The predicted persistence of all three compounds in water suggest that they do not fall into a regulatory persistence category. However, there is no doubt that the predicted persistence in sediment would meet regulatory criteria – even for D4 (e.g. chemicals with a half life of over 180 days would be classified as “vP” in the EU). This is, in part, due to the fact that fairly conservative assumptions have been made with respect to hydrolysis rates in sediment. The ranges of overall persistence predictions (spanning an order of magnitude) are, instead, open to different interpretations because POV is less well established as a regulatory threshold. It is worth re-emphasising the fact that these distributions were generated using MCS employing input parameter distributions which represent feasible ranges and that the same predicted persistence could be predicted from several different combinations of parameters. For example over 300 different combinations of parameters predict a PS value of about 2000 days. Whilst many of these combinations will be similar, some could be quite different.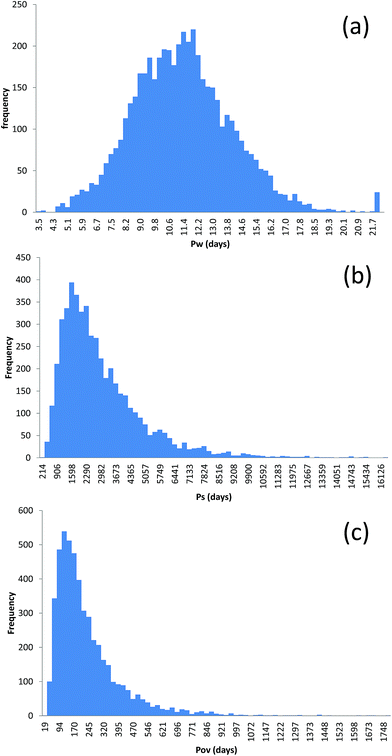 | ||
| Fig. 5 Frequency distributions of (a) predicted persistence in the water column; (b) predicted persistence in sediment and (c) predicted overall persistence for D5 in Tokyo Bay. | ||
| D4 | D5 | D6 | ||
|---|---|---|---|---|
| P W | Mean (d) | 1.41 | 11.5 | 18.5 |
| Median (d) | 1.39 | 11.4 | 18.1 | |
| Skewness | 0.750 | 0.233 | 0.528 | |
| Kurtosis | 1.70 | 0.059 | 0.371 | |
| CV (%) | 14.9 | 21.9 | 24.5 | |
| 2.5 percentile (d) | 1.06 | 6.51 | 9.61 | |
| 97.5 percentile (d) | 1.87 | 16.9 | 30.4 | |
| P S | Mean (d) | 312 | 2895 | 3102 |
| Median (d) | 301 | 2374 | 2447 | |
| Skewness | 0.896 | 1.99 | 2.91 | |
| Kurtosis | 1.44 | 6.33 | 16.0 | |
| CV (%) | 27.8 | 71.5 | 78.9 | |
| 2.5 percentile (d) | 174 | 619 | 643 | |
| 97.5 percentile (d) | 525 | 8275 | 9456 | |
| P OV | Mean (d) | 2.08 | 222 | 1222 |
| Median (d) | 1.99 | 172 | 940 | |
| Skewness | 1.45 | 2.59 | 3.06 | |
| Kurtosis | 5.29 | 11.7 | 18.7 | |
| CV (%) | 23.1 | 77.2 | 79.5 | |
| 2.5 percentile (d) | 1.37 | 47.2 | 239 | |
| 97.5 percentile (d) | 3.23 | 685 | 3883 |
3.3 Including the influence of temperature variability
In the MCS analysis conducted thus far, the uncertainty CV for the system temperature was assumed to be 5% (reflecting a relatively high certainty in the mean temperature of Tokyo Bay arising from the availability of measured data). However, if we consider the statistical distribution of system temperature – i.e. reflecting variability (CV assumed to be 50%), the results are quite different. Note that although the assumption of a Gaussian distribution for temperature is probably reasonable for the bulk of conditions experienced in Tokyo Bay, a small number of MCS samples will be selected which are outside the range of temperatures seen in this system using this assumption (e.g. some sub-zero temperatures may be simulated which are unrealistic). Results are shown in Fig. S3, S4 and S5.† The predicted mean concentrations in water and sediment are slightly lower (for D5 6.99 ng L−1 and 88 ng g−1 dw, respectively) and the CV for predicted D5 concentration in sediment was similar (44%). However, the variability in the predicted concentrations in water was higher (CV = 39%). Although there is considerable scatter, there is a clear inverse relationship between temperature and CW due to the effects of temperature on the hydrolysis rate constant, removal via sediment deposition (cVMS compounds are assumed here to become more hydrophobic with increasing temperatures on the basis of experimental data for KOW:49 see Table S3†) and (to a much lesser extent) on partitioning to air (KAW). For CS, the relationship is less clear. There appears to be a temperature (near the mean) at which concentrations in sediment tend to be highest but this may simply reflect a higher frequency of sampling at this temperature. The relationships between a number of other model parameters and CW were also more apparent with a wider range of temperatures. Of particular note were the wider ranges of KAW and KOC which were predicted as a consequence of temperature-dependent partitioning along with a wider range in half lives in water and sediment. For sediment, clear relationships between predicted concentration and parameter values are less apparent. Examples of these scatter plots are given in the ESI (Fig. S4 and S5).†3.4 Exploring the uncertainty in emission
As expected, the effect of emission uncertainty (log-normal distribution and a CV of 0.5) on CW and CS was directly proportional. Including an uncertainty in the emission value had little effect on the shape of the scatter plots generated, except to draw out the concentration scales (i.e. increasing the uncertainty in predicted concentrations). As an example, for D5, there was little effect on the mean value of CW (7.42 ng L−1), but there was an increase in the CV (58%) and the range between the 5th and 95th percentiles (2.7 and 15.4 ng L−1, respectively) was wider. The predicted mean concentration in sediment was also unaffected by introducing a distribution for emission (mean CS was 100 ng g−1 dw). However, the CV increased to 68% and the 5th and 95th percentiles were 29 and 227 ng g−1 dw, respectively (compare with data presented in Table 1 for the MCS scenario in which emission was kept constant).3.5 Implications for interpretation of measured versus modelled comparisons
The analysis presented here has some important implications for the interpretation of predicted concentrations from QWASI (and other MFTMs, by extension), particularly with respect to discrepancies between predicted and measured concentrations of cVMS compounds in sediment. Predicted steady state values of CW were 0.034, 9.61 and 1.04 ng L−1 for D4, D5 and D6, respectively, and values of CS were 0.011, 127 and 76.8 ng g−1 dw for D4, D5 and D6, respectively. The aleatory uncertainty confidence intervals for these concentrations were relatively narrow. Measured concentration data are only available for concentrations in sediment in Tokyo Bay.33 Briefly, surface sediment samples were collected from 20 locations in the Bay in a systematic grid with a sampling interval of 5 km. They are, therefore, likely to be representative of the mean conditions in the Bay as a whole. Water depths at each location ranged from 10 to 35 m. Sediments were collected with a Birge-Eckman grab sampler and sub-samples representing the upper 1 cm were extruded into stainless steel storage containers (for further details see Supplementary Information in Powell et al., 201733). Mean measured dry weight concentrations for D4, D5 and D6 were 5.9 ± 6.4, 161 ± 132 and 32 ± 23 ng g−1 dw, respectively (where the error represents the standard deviation of 20 measurements). For reference with the model predictions of CW, equivalent expected concentrations in water were derived from these dry weight sediment concentrations, assuming equilibrium partitioning with a sediment organic carbon content of 0.05 g g−1 and the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOC values reported in Table S3.† The calculated values were 7.1, 20.3 and 0.6 ng L−1 for D4, D5 and D6, respectively, which were below the LOD and LOQ typically reported for cVMS in water34 for D4 and D6 but would be detectable for D5. These values were less than a factor of ∼2 of the steady state values of CW predicted by QWASI for D5 and D6 (9.61 and 1.04 ng L−1) but a long way from the predicted D4 value (0.034 ng L−1). Comparison with the range of MCS-predicted concentrations (e.g.Fig. 2, Table 1 and Fig. S1 and S2†) suggests that the mean measured CS for D5 is close to the middle of the model envelope and that the mean measured CS for D6 is also captured by the overall model envelope (see Fig. S2†), although it is only just above the 5th percentile prediction (i.e. 28.2 ng g−1 dw), without accounting for uncertainty in emission. When uncertainty in emission is included (CV = 0.5), the 5th percentile predicted value of CS for D6 becomes 21 ng g−1 dw, which does capture the measured mean concentration of 32 ng g−1 dw. For D4, the range of model predictions, even accounting for emission uncertainty (i.e. 5th and 95th percentile concentrations of 0.003 and 0.032 ng g−1 dw, respectively) remains inconsistent with the mean measured CS (5.9 ± 6.4 ng g−1 dw n = 20). There are a number of possible reasons for this including: (i) underestimation of emission; (ii) overestimation of losses due to volatilisation or hydrolysis in wastewater treatment, the water column or the sediment and (iii) underestimation of D4 sorption. In all cases, the error(s) in parameters extend beyond the uncertainty distributions considered in the analysis hitherto. Taking these in turn: it is unlikely that the current emission assumptions were underestimated in the model because independent estimates of per capita losses to wastewater (32–134, mean 64 mg cap−1 year−1), based on measured concentrations of D4 in the influent of a wastewater treatment plant in Tokyo (unpublished industry data), were lower than the value assumed here (122 mg cap−1 year−1). It is possible, however, that the removal rate assumed (97%) was too high. In addition, it is possible that measured D4 concentrations in sediment represent a legacy from previously high emissions (D5 has replaced D4 in many applications over the last 15 years) and this should be investigated further using dated sediment coring.
KOC values reported in Table S3.† The calculated values were 7.1, 20.3 and 0.6 ng L−1 for D4, D5 and D6, respectively, which were below the LOD and LOQ typically reported for cVMS in water34 for D4 and D6 but would be detectable for D5. These values were less than a factor of ∼2 of the steady state values of CW predicted by QWASI for D5 and D6 (9.61 and 1.04 ng L−1) but a long way from the predicted D4 value (0.034 ng L−1). Comparison with the range of MCS-predicted concentrations (e.g.Fig. 2, Table 1 and Fig. S1 and S2†) suggests that the mean measured CS for D5 is close to the middle of the model envelope and that the mean measured CS for D6 is also captured by the overall model envelope (see Fig. S2†), although it is only just above the 5th percentile prediction (i.e. 28.2 ng g−1 dw), without accounting for uncertainty in emission. When uncertainty in emission is included (CV = 0.5), the 5th percentile predicted value of CS for D6 becomes 21 ng g−1 dw, which does capture the measured mean concentration of 32 ng g−1 dw. For D4, the range of model predictions, even accounting for emission uncertainty (i.e. 5th and 95th percentile concentrations of 0.003 and 0.032 ng g−1 dw, respectively) remains inconsistent with the mean measured CS (5.9 ± 6.4 ng g−1 dw n = 20). There are a number of possible reasons for this including: (i) underestimation of emission; (ii) overestimation of losses due to volatilisation or hydrolysis in wastewater treatment, the water column or the sediment and (iii) underestimation of D4 sorption. In all cases, the error(s) in parameters extend beyond the uncertainty distributions considered in the analysis hitherto. Taking these in turn: it is unlikely that the current emission assumptions were underestimated in the model because independent estimates of per capita losses to wastewater (32–134, mean 64 mg cap−1 year−1), based on measured concentrations of D4 in the influent of a wastewater treatment plant in Tokyo (unpublished industry data), were lower than the value assumed here (122 mg cap−1 year−1). It is possible, however, that the removal rate assumed (97%) was too high. In addition, it is possible that measured D4 concentrations in sediment represent a legacy from previously high emissions (D5 has replaced D4 in many applications over the last 15 years) and this should be investigated further using dated sediment coring.
Losses of D4 in the water column due to volatilisation are controlled by the value assumed for the partial mass transfer coefficient on the water side of the air–water interface.9 This affects all three compounds in a similar way and so is unlikely to explain the low D4 predictions. However, D4 is the most hydrolytically unstable of the cVMS compounds considered here, with an estimated half life in water of only 3.9 days at pH 7 and 25 °C which reduces to just 9.6 h at pH 8 and 25 °C (i.e. 2.9 days at pH 8 and 9 °C). Although hydrolysis in the model is adjusted for the fraction in the dissolved phase, rate of hydrolysis may still be overestimated – e.g. if sorption is elevated due to a higher concentration of suspended particles in the water column or if the real KOC for D4 is higher than the value assumed here. We assumed a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOC value for D4 of 4.22 (KOC = 16
KOC value for D4 of 4.22 (KOC = 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 596 L kg−1) with a CV of 0.32 (i.e. a standard deviation = 5210 L kg−1). This equates to a 95th percentile value in a log-normal distribution of 26
596 L kg−1) with a CV of 0.32 (i.e. a standard deviation = 5210 L kg−1). This equates to a 95th percentile value in a log-normal distribution of 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 412 L kg−1 (equivalent to a log
412 L kg−1 (equivalent to a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOC value of 4.42). This is still much lower than the log
KOC value of 4.42). This is still much lower than the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOC value reported by Panagopoulos et al. (2015)50 of 5.06. This would suggest that the pdf for KOC assumed here is too narrow (as was the case for D5). Furthermore, Panagopoulos et al. (2016)51 have suggested that KOC increases with salinity due to the salting out effect52 and that the slope of the relationship between KOC and salinity is steeper for D4 than it is for D5 and D6. If we assume a salinity of 0.6 mol L−1 (typical of seawater53), log
KOC value reported by Panagopoulos et al. (2015)50 of 5.06. This would suggest that the pdf for KOC assumed here is too narrow (as was the case for D5). Furthermore, Panagopoulos et al. (2016)51 have suggested that KOC increases with salinity due to the salting out effect52 and that the slope of the relationship between KOC and salinity is steeper for D4 than it is for D5 and D6. If we assume a salinity of 0.6 mol L−1 (typical of seawater53), log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOC could be as high as 5.45. The effects of assuming a mean log
KOC could be as high as 5.45. The effects of assuming a mean log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOC for D4 of 5.45 in the MCS resulted in a mean CS of 0.87 ± 0.72 ng g−1 dw (Fig. S7a†). However, this is still an order of magnitude lower than the measured data so other factors (e.g. the hydrolysis half life) may also be at play. Increasing the hydrolysis half life at 25 °C by a factor of 3 in the MCS resulted in a mean predicted CS of 2.5 ± 1.9 ng g−1 dw (Fig. S7b†).
KOC for D4 of 5.45 in the MCS resulted in a mean CS of 0.87 ± 0.72 ng g−1 dw (Fig. S7a†). However, this is still an order of magnitude lower than the measured data so other factors (e.g. the hydrolysis half life) may also be at play. Increasing the hydrolysis half life at 25 °C by a factor of 3 in the MCS resulted in a mean predicted CS of 2.5 ± 1.9 ng g−1 dw (Fig. S7b†).
3.6 General discussion
Although applied to specific chemicals in a specific environmental system, this paper is intended to illustrate some broader generic ideas about the role of uncertainty in assessing environmental exposure and persistence. We introduce, for the first time, the concept of equifinality to MFTMs – in which the same predictions of exposure and persistence can be derived using very different combinations of parameters. When model outputs are compared with measured data, “success” is often judged on the basis of the fidelity of the predictions compared with observations. However, it is important to recognise that model performance (good or poor) will, to some extent, be influenced by the parameter combinations selected. Although MFTMs are rarely calibrated in the same way as hydrological models (i.e. where some parameters are adjusted so as to optimise the model fit with observed data), a particular selection of parameters may yield apparent success in terms of the fidelity of predictions with one set of observations (e.g. measured concentrations in sediment) but may yield poor predictions of other (often unknown) end points (e.g. concentrations in water or biota). An alternative parameter set may yield good predictions for all end points and, hence, be a better description of system behaviour. In the work presented here, the Monte Carlo Simulation approach taken was similar to that employed elsewhere for sensitivity and uncertainty analysis54 – essentially estimating the uncertainty distributions for each parameter and allowing these uncertainties to propagate forwards to yield uncertainty distributions in model predictions.An alternative approach for exploring equifinality, and one frequently adopted in hydrology (e.g. in the Generalised Likelihood Uncertainty Estimation or GLUE14), is to make very few a priori assumptions about the nature of the distributions of the model parameters. In GLUE uniform distributions may be employed for all parameters, with minimum and maximum values set simply at feasible physically realistic limits. Those combinations of parameters which generate “successful” predictions of observed data (i.e. which meet certain threshold criterion or criteria) are considered to be equally plausible. However, this approach is not a particularly useful option when there is a paucity of observed data (as is often the case for environmental concentrations of organic pollutants) because the model will be poorly constrained and the number of “successful” combinations too high. One possible option for better constraining models (improving so-called model identifiability and, potentially, reducing equifinality) would be to link the simulations for several different pollutants for which measured data are available in the same system of interest and to use the combined model performance to exclude system parameter combinations which fail to predict all the measured data adequately (i.e. parameter sets which successfully predict measured concentrations for one chemical would be rejected if they fail to match the observations for the other chemicals). Although this could be problematic where major (unexplained) discrepancies arise for some chemicals (as was the case here for D4) it should, nevertheless, be explored further for more data-rich systems, such as the Great Lakes.
Measured data on both chemical properties and system properties should also be used as much as possible to constrain parameter sets so that they are consistent. For example, in the case of chemical-specific properties, additional independent measurements of KOC and its temperature dependence would be useful for better defining the parameters of the uncertainty distribution for KOC. It is pertinent to note that the assumptions made for the uncertainty in KOC (Table S3†) yield a distribution of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOC values (Fig. 3e and 4d) which is relatively narrow compared with the wide range of log
KOC values (Fig. 3e and 4d) which is relatively narrow compared with the wide range of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOC values which have been reported for D5 in the literature from ca. 5.2 (ref. 55 and 56) to ca. 6.2.50,57 Increasing the CV but maintaining a mean log
KOC values which have been reported for D5 in the literature from ca. 5.2 (ref. 55 and 56) to ca. 6.2.50,57 Increasing the CV but maintaining a mean log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOC value of 5.2 results in a wider range of simulated KOC values but too many of these values are unrealistically small. The effect of increasing the mean log
KOC value of 5.2 results in a wider range of simulated KOC values but too many of these values are unrealistically small. The effect of increasing the mean log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOC value to 5.7 and assuming a wider distribution (CV = 0.5) is illustrated in Fig. S6.† Unsurprisingly, high values of KOC tend to result in higher predicted CS concentrations – many of which are unrealistically high compared to the measured data for D5 in Tokyo Bay, although values of log
KOC value to 5.7 and assuming a wider distribution (CV = 0.5) is illustrated in Fig. S6.† Unsurprisingly, high values of KOC tend to result in higher predicted CS concentrations – many of which are unrealistically high compared to the measured data for D5 in Tokyo Bay, although values of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOC > 6 can still generate a good match with the measured data in some parameter combinations. Additional data on the magnitude of KOC for cVMS compounds would help to better-constrain this important parameter.
KOC > 6 can still generate a good match with the measured data in some parameter combinations. Additional data on the magnitude of KOC for cVMS compounds would help to better-constrain this important parameter.
For system-specific properties, sediment deposition, resuspension and burial rates should be consistent with measured sediment accumulation rates, if available, and the organic carbon balance should close (i.e. carbon storage in the sediment should be consistent with POC input and output rates). In QWASI (like most MFTMs), both state variables (e.g. the pelagic suspended solids concentration or the organic carbon concentration of suspended or settled solids) and flux parameters (e.g. the rates of sediment deposition, resuspension and burial) are defined a priori by the user. However, since the concentrations and fluxes are not linked together, they may be inconsistent with one another. For example, the user could define a high rate of net sediment deposition even if the suspended solids concentration in the water column was low. Similarly, a high concentration of organic carbon in the active sediment layer may be defined, even if the rate of net carbon deposition is insufficient to maintain such a concentration. This issue was recognised in developing CoZMo-POP v2 (Coastal Zone Model for Persistent Organic Pollutants)12 in which particulate organic carbon fluxes are defined by the user and state variables (such as the fraction of organic carbon in sediment) are calculated from these fluxes. Although this requires the user to “fit” the state variables to sensible values (e.g. based on measured fOC data) using manual trial and error iterations of the flux parameters, it does generate flux parameters and state variables which are internally consistent (although equifinality can, of course, be an issue here too). One approach for linking different observations in the model framework could be to employ some sort of recursive Bayesian estimation method in which new information results in a modification of existing beliefs (e.g. parameter combinations) and this should be explored further.
The lack of correlation in simulated parameters assumed in the work presented here is unlikely to be important for most parameters (where the uncertainty envelopes are independent) except in cases where parameters are physically connected (e.g. KOA = KOW/KAW or ΔUOW = ΔUOA + ΔUAW). In the latter case, even when the mean values are consistent, parameter combinations in individual MCS iterations may be selected which are beyond the range of statistical tolerance for consistency. The effect of this phenomenon on the output distributions is unknown but is probably not a major issue because the probabilities of selecting extreme values (which are more likely to be inconsistent) are low. Nevertheless, this could be investigated further in additional work.
4. Conclusions
This paper presents an uncertainty analysis of the QWASI model applied, as an example, to the fate of cVMS compounds in Tokyo Bay. Models like QWASI have historically been shown to generate reasonable predictions of chemical exposure and the relative importance of competing loss processes in lake.3,9,20,28–30 The purpose here is not to undermine this successful approach. Rather, MCS provides a means of enhancing point estimates of exposure and persistence, with relatively modest additional computational effort (as long as the models are relatively simple).The uncertainty in the predicted steady state values of CW and CS arising from uncertainty in the model parameters was fairly modest, even for those parameters to which the model is relatively sensitive. For all three compounds, the uncertainty implied in CW is lower (CV of the order of 12–22%) than that in CS (CV of the order of 38–55%), reflecting the propensity of cVMS compounds to sorb to sediment20,56,57 and the sensitivity of the model to sediment deposition rate and KOC.9,20,58 Predicted concentrations in sediment were more sensitive than predicted concentrations in water for the same simulations (the relative range of outputs was wider). Uncertainty in the predicted persistence of all three cVMS compounds was lower in water than in sediment, both in relative and absolute terms. The confidence intervals were particularly high for the persistence of D5 and D6 in sediment which both ranged between approximately 1.7 years and approximately 26 years. Increasing the CV for water temperature from 5% to 50% had little effect on the predicted cVMS concentrations in sediment but increased the range of predicted concentrations in water. Higher temperatures tend to be associated with lower values of CW due to an increase in the predicted hydrolysis rate and an assumed increase in the hydrophobicity of cVMS compounds with increasing temperature. The latter assumption was based on three-phase experiments49,59 in which simultaneous values for ΔUOW, ΔUAW and ΔUOA were derived. Although the value for ΔUOW was based on just two temperatures, it was consistent with sum of ΔUAW and ΔUOA. In addition values of ΔUOW for other cVMS compounds were also positive. That said, this finding has been challenged by Panagopoulos et al. (2017)60 who observed, via an indirect application of multi-media modelling to volatilisation experiments, that KOC decreased with increasing temperature. Thus, the actual temperature dependence of cVMS partitioning may differ from that assumed here.
The distribution of model predictions generated by MCS to assess model uncertainty matched observations well for D5. However, the results demonstrate significant equifinality for both CW and CS (i.e. the same predicted concentrations can be generated by different combinations of parameter values). This suggests that a unique “optimal” parameter configuration does not exist. Additional observed data (e.g. measured CW values > LOD and better emission estimates derived from measured concentrations in wastewater) could be used to constrain the possible parameter combinations which appear to yield “good” predictions (i.e. promoting the right results for the right reasons18). For D6, the measured concentrations are also captured by the uncertainty range of model predictions, particularly when uncertainty in emissions were accounted for. For D4, the range of model predictions was substantially lower than the measured concentration data. Including uncertainty in emissions (via the assumption of a log-normal distribution with a CV of 50%) and increasing the mean log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOC value resulted in an increase in both the range and mean predicted concentrations in both water and sediment which were enough to capture the measured concentrations of D4 in sediment. In addition, it is possible that the measured D4 concentrations are, at least in part, a reflection of legacy emissions. Attention in monitoring efforts should be directed at better defining current emissions of D4 to Tokyo Bay and checking the real rate of hydrolysis.
KOC value resulted in an increase in both the range and mean predicted concentrations in both water and sediment which were enough to capture the measured concentrations of D4 in sediment. In addition, it is possible that the measured D4 concentrations are, at least in part, a reflection of legacy emissions. Attention in monitoring efforts should be directed at better defining current emissions of D4 to Tokyo Bay and checking the real rate of hydrolysis.
Models can be seen as extended hypotheses which describe our current understanding of environmental system behaviour and which can be usefully employed to compare the expected behaviours and exposures of chemicals (e.g. in “evaluative” unit world models1,21). They can also be employed to make absolute predictions of exposure which can be compared to measurements. This comparison can test our understanding of chemical behaviour in environmental systems; increasing confidence in our understanding if model predictions agree with observations (e.g., here, for D5) but challenging our assumptions when they do not adequately explain all the available observed data.61 Disagreement (e.g., here for D4) can result from gaps in our conceptual understanding and how this is translated into model code (epistemic uncertainty) and/or inappropriate parameterisation (aleatory uncertainty). Incorporating uncertainty into the modelling process (e.g. via MCS) can facilitate this comparison process because it provides confidence intervals for the predictions and, hence, an envelope within which discrepancies with measured data can be tolerated. It should also be remembered that there is also often considerable uncertainty associated with measured data, which may not be representative of the system under consideration (e.g. due to low sample numbers in a variable system) or when our analytical methods are not sensitive enough to measure concentrations in some media sufficiently accurately (i.e. when concentrations are less than the limits of quantification). Explicit attempts to quantify uncertainty can also help to underpin our confidence in model-based regulatory decisions (e.g. in risk assessment and in the designation of persistence classes). For example, environmental persistence is both variable and uncertain, even for a specific environmental system. Whether a single estimate of persistence based on one set of parameters is above or below a regulatory threshold is, thus, uncertain. However, by quantifying the uncertainty distribution we can be more confident about the likelihood of exceeding this threshold. More (and better quality) data should help to reduce uncertainty (where needed) leading to increased confidence in our understanding and, thus, better-informed decision making.
An important consideration in this paper is the concept of equifinality and its use in MFTMs. Hitherto, equifinality has not been explicitly recognised by the MFTM community but it is relatively easy to identify using MCS. Does this matter? In most cases, probably not. Recognising that different combinations of parameters can generate the same predicted outcomes (or the failure to do so) will not change the utility of modelling as an extended hypothesis. However, it does add a layer of transparency to our predictions and to our understanding and interpretation of model outcomes. For example, it might be useful to be aware of the uncertainty in the relative contributions of different loss processes (e.g. volatilisation, reaction or advection) for a particular chemical and environmental system with the same predicted state (e.g. fugacity). Care may also need to be exercised when an apparently successful model for one chemical is employed to make predictions for other chemicals, if there are equifinality issues for the first chemical to which the outcome is insensitive but which are more important in the second. For example, the sediment deposition rate may not influence the predicted concentrations of a hydrophilic chemical but will be important for a hydrophobic one. Equifinality may also be a useful consideration in situations where models are used inversely to derive chemical properties50,56,57,60 such as KOC and its temperature-dependence. This should be investigated further.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the Centre Européen des Silicones (CES). The authors are grateful to the CES Modelling Task Force for useful suggestions. M. J. W. benefitted from a period of study leave granted by the University of Leicester.References
- D. Mackay, Multimedia Environmental Models: The Fugacity Approach, Lewis, New York, 2nd edition, 2001, p. 261 Search PubMed.
- M. Macleod, M. Scheringer, T. E. McKone and K. Hungerbuhler, The state of multimedia mass-balance modeling in environmental science and decision-making, Environ. Sci. Technol., 2010, 44, 8360–8364 CrossRef CAS PubMed.
- J. Kim, D. Mackay and M. J. Whelan, Predicted Persistence and Response Times of Linear and Cyclic Volatile Methylsiloxanes in Global and Local Environments, Chemosphere, 2018, 195, 325–335 CrossRef CAS PubMed.
- K. J. Beven and A. Binley, The future of distributed models: model calibration and uncertainty prediction, Hydrol. Processes, 1992, 6, 279–298 CrossRef.
- M. J. Whelan and C. Gandolfi, Modelling of Spatial Controls on Denitrification at the Landscape Scale, Hydrol. Processes, 2002, 16, 1437–1450 CrossRef.
- K. J. Beven, Rainfall-Runoff Modelling: The Primer, Wiley, Chichester, UK, 2nd edition, 2012 Search PubMed.
- M. B. Beck, Water quality modeling: A review of the analysis of uncertainty, Water Resour. Res., 1987, 23, 1393–1442 CrossRef CAS.
- S. P. Pullan, M. J. Whelan, J. Rettino, K. Filby, S. Eyre and I. P. Holman, Development and application of a catchment scale pesticide fate and transport model for use in drinking water risk assessment, Sci. Total Environ., 2016, 563–564, 434–447 CrossRef CAS PubMed.
- M. J. Whelan, Predicting the fate and behaviour of cyclic volatile methyl siloxanes in two contrasting North American lakes, Chemosphere, 2013, 91, 1566–1576 CrossRef CAS PubMed.
- M. J. Whelan and K. Breivik, Dynamic modelling of aquatic exposure and pelagic food chain transfer of cyclic volatile methyl siloxanes in the Inner Oslofjord, Chemosphere, 2013, 93, 794–804 CrossRef CAS PubMed.
- L. von Bertalanffy, General System Theory, George Braziller, New York, 1968 Search PubMed.
- F. Wania, K. Breivik, N. J. Persson and M. S. McLachlan, CoZMo-POP 2: A fugacity-based dynamic multi-compartmental mass balance model of the fate of persistent organic pollutants, Environ Model Softw., 2006, 21, 868–884 CrossRef.
- S. W. Franks, K. J. Beven, P. F. Quinn and I. R. Wright, On the sensitivity of soil-vegetation-atmosphere transfer (SVAT) schemes: Equifinality and the problem of robust calibration, Agric. For. Meteorol., 1997, 86, 63–75 CrossRef.
- K. J. Beven and J. Freer, Equifinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems using the GLUE methodology, J. Hydrol., 2001, 249, 11–29 CrossRef.
- R. Brazier, K. J. Beven, J. Freer and J. S. Rowan, Equifinality and uncertainty in physically based soil erosion models: Application of the glue methodology to WEPP - the water erosion prediction project - for sites in the UK and USA, Earth Surf. Processes Landforms, 2000, 25, 825–845 CrossRef.
- N. McIntyre, B. Jackson, A. J. Wade, D. Butterfield and H. S. Wheater, Sensitivity analysis of a catchment-scale nitrogen model, J. Hydrol., 2005, 315, 71–92 CrossRef.
- P. M. Najmaddin, M. J. Whelan and H. Balzter, Application of satellite-based precipitation estimates to rainfall-runoff modelling in a data-scarce semi-arid catchment, Climate, 2017, 5(32), 1–22 Search PubMed.
- J. Kirchner, Getting the right answers for the right reasons: Linking measurements, analyses, and models to advance the science of hydrology, Water Resour. Res., 2006, 42, W03S04 CrossRef.
- N. Kannan, S. M. White, F. Worrall and M. J. Whelan, Hydrological modelling of a small catchment using SWAT-2000-Ensuring correct flow partitioning for contaminant modelling, J. Hydrol., 2007, 334, 64–72 CrossRef.
- I. S. Krogseth, M. J. Whelan, G. N. Christensen, K. Breivik, A. Evenset and N. A. Warner, Understanding of cyclic volatile methyl siloxane fate in a high latitude lake is constrained by uncertainty in organic carbon-water partitioning, Environ. Sci. Technol., 2017, 51, 401–409 CrossRef CAS PubMed.
- T. G. Vermeire, D. T. Jager, B. Bussian, J. Devillers, K. den Haan, B. Hansen, I. Lundberg, H. Niessen, S. Robertson, H. Tyle and P. T. J. van der Zandt, European Union System for the Evaluation of Substances (EUSES). Principles and structure, Chemosphere, 1997, 34, 1823–1836 CrossRef CAS PubMed.
- R. Boethling, K. Fenner, P. Howard, T. Madsen, J. R. Snape and M. J. Whelan, Evaluating Environmental Persistence of Organic Pollutants: Guidance for Development and Review of POP Risk Profiles, Integr. Environ. Assess. Manage., 2009, 5, 539–556 CrossRef CAS PubMed.
- H. Zou, M. Radke, A. Kierkegaard, M. Macleod and M. S. McLachlan, Using chemical benchmarking to determine the persistence of chemicals in a Swedish lake, Environ. Sci. Technol., 2015, 49, 1646–1653 CrossRef CAS PubMed.
- M. Macleod, A. J. Fraser and D. Mackay, Evaluating and expressing the propagation of uncertainty in chemical fate and bioaccumulation models, Environ. Toxicol. Chem., 2001, 21, 700–709 CrossRef.
- A. M. Buser, M. MacLeod, M. Scheringer, D. Mackay, M. Bonnell, M. H. Russell, J. V. DePinto and K. Hungerbühler, Good modeling practice guidelines for applying multimedia models in chemical assessments, Integr. Environ. Assess. Manage., 2012, 8, 703–708 CrossRef CAS PubMed.
- D. Mackay, M. Joy and S. Paterson, A Quantitative Water Air Sediment Interaction (QWASI) fugacity model for describing the fate of chemicals in lakes, Chemosphere, 1983a, 12, 981–997 Search PubMed.
- D. Mackay, S. Paterson and M. Joy, A Quantitative Water, Air, Sediment Interaction (QWASI) Fugacity Model for Describing the Fate of Chemicals in Rivers, Chemosphere, 1983b, 12, 1193–1208 Search PubMed.
- D. Mackay, Modelling the Long Term Behaviour of an Organic Contaminant in a Large Lake: Application to PCBs in Lake Ontario, J. Great Lakes Res., 1989, 15, 283–297 CrossRef CAS.
- M. Diamond, D. Mackay, D. Poulton and F. Stride, Development of a Mass Balance Model of the Fate of 17 Chemicals in the Bay of Quinte, J. Great Lakes Res., 1994, 20, 643–666 CrossRef CAS.
- R. Lun, K. Lee, L. De Marco, C. Nalewajko and D. Mackay, A Model of the Fate of Polycyclic Aromatic Hydrocarbons in the Saguenay Fjord, Environ. Toxicol. Chem., 1998, 17, 333–341 CrossRef CAS.
- D. G. Woodfine, R. Seth, D. Mackay and M. Havas, Simulating the Response of Metal Contaminated Lakes to Reductions in Atmospheric Loading Using a Modified QWASI Model, Chemosphere, 2000, 41, 1377–1388 CrossRef CAS PubMed.
- D. Mackay and B. Hickie, Mass Balance Model of Sources, Transport, and Fate of PAHs in Lac Saint Louis, Quebec, Chemosphere, 2000, 41, 681–692 CrossRef CAS PubMed.
- D. E. Powell, N. Suganuma, K. Kobayashi, T. Nakamura, K. Ninomiya, K. Matsumura, N. Omura and S. Ushioka, Trophic dilution of cyclic volatile methylsiloxanes (cVMS) in the pelagic marine food web of Tokyo Bay, Japan, Sci. Total Environ., 2017, 578, 366–382 CrossRef CAS PubMed.
- T. Okada, K. Nakayama, T. Takao and K. Furukawa, Influence of freshwater input and bay reclamation on long-term changes in seawater residence times in Tokyo Bay, Japan, Hydrol. Processes, 2011, 25, 2694–2702 CrossRef.
- Y. Nakagawa, K. Nadaoka, H. Yagi, R. Ariji, H. Yoneyama and K. Shirai, Field measurement and modeling of near-bed sediment transport processes with fluid mud layer in Tokyo Bay, Ocean Dynamics, 2012, 62, 1535–1544 CrossRef.
- T. Sakurai, S. Serizawa, J. Kobayashi, K. Kodama, J. H. Lee, H. Maki, Y. Zushi, J. Beltran Sevilla-Nastor, Y. Imaizumi, N. Suzuki, T. Horiguchi and H. Shiraishi, Temporal trends for inflow of perfluorooctanesulfonate (PFOS) and perfluorooctanoate (PFOA) to Tokyo Bay, Japan, estimated by a receptor-oriented approach, Sci. Total Environ., 2015, 539, 277–285 CrossRef PubMed.
- M. S. McLachlan, A. Kierkegaard, K. M. Hansen, R. van Egmond, J. H. Christensen and C. A. Skjøth, Concentrations and Fate of Decamethylcyclopentasiloxane (D5) in the Atmosphere, Environ. Sci. Technol., 2010, 44, 5365–5370 CrossRef CAS PubMed.
- D. N. Brooke, M. J. Crookes, D. Gray and S. Robertson, Risk Assessment Report: Octamethylcyclotetrasiloxane, Environment Agency of England and Wales, Bristol, 2008a Search PubMed.
- D. N. Brooke, M. J. Crookes, D. Gray and S. Robertson, Risk Assessment Report: Decamethylcyclopentasiloxane, Environment Agency of England and Wales, Bristol, 2008b Search PubMed.
- D. N. Brooke, M. J. Crookes, D. Gray and S. Robertson, Risk Assessment Report: Dodecamethylcyclohexasiloxane, Environment Agency of England and Wales, Bristol, 2008c Search PubMed.
- D. Vose, Risk Analysis: A Quantitative Guide, John Wiley and Sons, Chichester, UK, 2008 Search PubMed.
- M. J. Whelan, C. Gandolfi and G. B. Bischetti, A simple stochastic model of point source solute transport in rivers based on gauging station data with implications for sampling requirements, Water Res., 1999, 33(14), 3171–3181 CrossRef CAS.
- M. Abramowitz and I. Stegun, Handbook of Mathematical Functions, Dover Publications, New York, 1970 Search PubMed.
- D. Mackay, L. Hughes, D. E. Powell and J. Kim, An updated Quantitative Water Air Sediment Interaction (QWASI) model for evaluating chemical fate and input parameter sensitivities in aquatic systems: Application to D5 (decamethylcyclopentasiloxane) and PCB-180 in two lakes, Chemosphere, 2014, 111, 359–365 CrossRef CAS PubMed.
- S. M. Robeson, Relationships between mean and standard deviation of air temperature: implications for global warming, Clim. Res., 2002, 22, 205–213 CrossRef.
- J. Kim, D. Mackay and D. E. Powell, Roles of steady-state and dynamic models for regulation of hydrophobic chemicals in aquatic systems: A case study of decamethylcyclopentasiloxane (D5) and PCB-180 in three diverse ecosystems, Chemosphere, 2017, 175, 253–268 CrossRef CAS PubMed.
- C. Sparham, R. Kanda, M. Whelan, R. van Egmond, S. O'Connor, C. Hastie and O. Franklin, Determination of Decamethylcyclopentasiloxane in River Water and Final Effluent by Headspace GC/MS, J. Chromatogr. A, 2008, 1212, 124–129 CrossRef CAS PubMed.
- W. L. Oberkampf, S. M. DeLand, B. M. Rutherford, K. V. Diegert and K. F. Alvin, Error and Uncertainty in Modeling and Simulation. Reliability Engineering & System Safety, 2002, Vol. 75, pp. 333–357 Search PubMed.
- S. H. Xu and G. E. Kozerski, Assessment of the Fundamental Partitioning Properties of Permethylated Cyclosiloxanes, SETAC Europe, Porto, Portugal, 2007 Search PubMed.
- D. Panagopoulos, A. Jahnke, A. Kierkegaard and M. MacLeod, Organic Carbon/Water and dissolved organic carbon/water partitioning of cyclic volatile methylsiloxanes: Measurements and polyparamter linear free energy relationships, Environ. Sci. Technol., 2015, 49, 12161–12168 CrossRef CAS PubMed.
- D. Panagopoulos, A. Kierkegaard, A. Jahnke and M. MacLeod, Evaluating the Salting-Out Effect on the Organic Carbon/Water Partition Ratios (KOC and KDOC) of Linear and Cyclic Volatile Methylsiloxanes: Measurements and Polyparameter Linear Free Energy Relationships, J. Chem. Eng. Data, 2016, 61, 3098–3108 CrossRef CAS.
- S. Endo, A. Pfennigsdorff and K.-U. Goss, Salting-out effect in aqueous NaCl solutions: trends with size and polarity of solute molecules, Environ. Sci. Technol., 2016, 46, 1496–1503 CrossRef PubMed.
- F. J. Millero, R. Feistel, D. G. Wright and T. J. McDougall, The composition of Standard Seawater and the definition of the Reference-Composition Salinity Scale, Deep Sea Res., Part I, 2008, 55, 50–72 CrossRef.
- Y. Luo and X. Yang, A multimedia environmental model of chemical distribution: Fate, transport, and uncertainty analysis, Chemosphere, 2007, 66, 1396–1407 CrossRef CAS PubMed.
- J. Durham, Soil-water Distribution of Decamethylcyclopentasiloxane (D5) Using a Batch Equilibrium Method, HES Study No. 10352e108, Health and Environmental Sciences, Dow Corning Corporation, 2007 Search PubMed.
- M. J. Whelan, D. Sanders and R. van Egmond, Effect of Aldrich humic acid on water – atmosphere transfer of decamethylcyclopentasiloxane, Chemosphere, 2009, 74(8), 1111–1116 CrossRef CAS PubMed.
- M. J. Whelan, R. van Egmond, D. Gore and D. Sanders, Dynamic multi-phase partitioning of decamethylcyclopentasiloxane (D5) in river water, Water Res., 2010, 44, 3679–3686 CrossRef CAS PubMed.
- D. Panagopoulos and M. MacLeod, A critical assessment of the environmental fate of linear and cyclic volatile methylsiloxanes using multimedia fugacity models, Environ. Sci.: Processes Impacts, 2018, 20, 183–219 RSC.
- S. Xu and B. Kropscott, Evaluation of the three-phase equilibrium method for measuring temperature dependence of internally consistent partition coefficients (KOW, KOA, and KAW) for volatile methylsiloxanes and trimethylsilanol, Environ. Toxicol. Chem., 2014, 33, 2702–2710 CrossRef CAS PubMed.
- D. Panagopoulos, A. Jahnke, A. Kierkegaard and M. MacLeod, Temperature Dependence of the Organic Carbon/Water Partition Ratios (KOC) of Volatile Methylsiloxanes, Environ. Sci. Technol. Lett., 2017, 4, 240–245 CrossRef CAS.
- J. McDonnell and K. J. Beven, Debates - The future of hydrological sciences: A (common) path forward? A call to action aimed at understanding velocities, celerities and residence time distributions of the headwater hydrograph, Water Resour. Res., 2014, 50, 5342–5350 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9em00099b |
| This journal is © The Royal Society of Chemistry 2019 |