Open Access Article
Open Access ArticleModeling the electrical double layer to understand the reaction environment in a CO2 electrocatalytic system†
Divya
Bohra
 a,
Jehanzeb H.
Chaudhry
a,
Jehanzeb H.
Chaudhry
 b,
Thomas
Burdyny
b,
Thomas
Burdyny
 a,
Evgeny A.
Pidko
a,
Evgeny A.
Pidko
 c and
Wilson A.
Smith
c and
Wilson A.
Smith
 *a
*a
aMaterials for Energy Conversion and Storage (MECS), Department of Chemical Engineering, Delft University of Technology, 2629 HZ, Delft, The Netherlands. E-mail: W.Smith@tudelft.nl; Tel: +31 15 27 87977
bDepartment of Mathematics and Statistics, University of New Mexico, 310 SMLC, Albuquerque, NM 87131, USA
cInorganic Systems Engineering (ISE), Department of Chemical Engineering, Delft University of Technology, 2629 HZ Delft, The Netherlands
First published on 1st October 2019
Abstract
The environment of a CO2 electroreduction (CO2ER) catalyst is intimately coupled with the surface reaction energetics and is therefore a critical aspect of the overall system performance. The immediate reaction environment of the electrocatalyst constitutes the electrical double layer (EDL) which extends a few nanometers into the electrolyte and screens the surface charge density. In this study, we resolve the species concentrations and potential profiles in the EDL of a CO2ER system by self-consistently solving the migration, diffusion and reaction phenomena using the generalized modified Poisson–Nernst–Planck (GMPNP) equations which include the effect of volume exclusion due to the solvated size of solution species. We demonstrate that the concentration of solvated cations builds at the outer Helmholtz plane (OHP) with increasing applied potential until the steric limit is reached. The formation of the EDL is expected to have important consequences for the transport of the CO2 molecule to the catalyst surface. The electric field in the EDL diminishes the pH in the first 5 nm from the OHP, with an accumulation of protons and a concomitant depletion of hydroxide ions. This is a considerable departure from the results obtained using reaction-diffusion models where migration is ignored. Finally, we use the GMPNP model to compare the nature of the EDL for different alkali metal cations to show the effect of solvated size and polarization of water on the resultant electric field. Our results establish the significance of the EDL and electrostatic forces in defining the local reaction environment of CO2 electrocatalysts.
Broader contextMassive reductions in anthropogenic emissions of CO2 are required to limit global warming to 1.5–2 °C and carbon capture and utilization technologies can play an important role in achieving this goal. Renewable electricity-powered electrochemical reduction of CO2 (CO2ER) to hydrocarbon molecules for the fuels and chemicals value-chain is a technological solution with potential to recycle CO2 emissions to limit their accumulation in the atmosphere. However, there remain several challenges to improve the performance of the CO2ER technology for it to be scalable and economically competitive to displace fossil-fuels based products. Optimizing the activity and selectivity of the CO2 electro-reduction process is essentially an exercise in engineering the optimal solid–liquid interface as it determines the catalyst surface properties as well as the reaction environment. In an attempt to resolve the composition of the CO2ER reaction interface, we model the electrical double layer (EDL) facing the charged catalyst surface using a continuum description including migration, diffusion and reaction processes with a excluded volume ascribed to solution species. The consideration of the EDL has significant consequences for critical performance parameters such as the transport properties of CO2, the local pH, the electric field strength and consequently the overall mechanistic understanding of the CO2ER system. |
1 Introduction
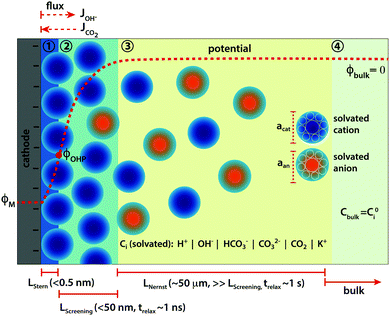
The immediate environment of the CO2 electro-reduction (CO2ER) catalyst is an extremely important handle to rationally optimize the overall performance of the system.1 The concentrations of reactive as well as non-reactive species in the vicinity of the catalyst surface, and their mutual interactions, have a direct influence on catalytic behaviour, and thus on the achievable activity and selectivity.2,3 Mass transport becomes a crucial factor for CO2ER due to the limited solubility of CO2 in aqueous electrolytes, the participation of CO2 in the buffer reactions, as well as the changes in the local environment during reaction due to the continuous consumption of CO2 and production of hydroxide (OH−) ions. Designing more favorable reaction interfaces has helped to achieve remarkable performance gains4–6 and the approach highlights the significance of mass transport as an influential optimization parameter for the CO2ER system. What constitutes the local reaction environment in such an electrocatalytic system however, is still an open question. Further understanding needs to be developed to define the physical phenomena that result in the local environment of the catalyst and that sufficiently capture the parameters most important for the performance.Although there have been several attempts to model the mass transport of solution species to the catalyst surface in CO2ER, a vast majority of the existing literature is restricted to reaction-diffusion type models introduced by N. Gupta and co-authors7 and ignore the formation of the electrical double layer (EDL) and therefore any migration of charged species in front of the catalyst surface.8–11 The presence of the electrified interface has been used however, to explain the influence of cations on experimentally observed performance.3,12 Considering the significant applied voltage under which CO2ER operates, the local environment for the catalysis is insufficiently defined without the inclusion of the electrostatic interactions of the ionic species with the charged metallic surface. These interactions, and the resulting double layer structure, can extend up to several nanometers from the catalyst surface (see Fig. 1) and are necessary to consider in order to derive physically consistent hypotheses based on experimental observations.
In this study, we resolve the species concentrations and potential profiles in the EDL of a syngas (CO and H2) producing CO2ER system by self-consistently solving the migration, diffusion and reaction phenomena in a CO2 saturated aqueous electrolyte facing a planar cathode (see schematic in Fig. 1). We do this by numerically solving the generalized modified Poisson–Nernst–Planck (GMPNP) set of equations which include the effect of volume exclusion due to the solvated size of solution species.13 Using the GMPNP equations, we demonstrate that the inclusion of migration in the mass transport of species provides a drastically different picture of the catalyst reaction environment as compared to reaction-diffusion models. By comparing with a PNP system, where molecules are considered as point species without volume, we show how inclusion of size of solvated solution species is important to derive physically consistent concentration profiles at high operating potentials. The effect of volume exclusion in the GMPNP model results in a diminishing of CO2 concentration from the EDL at high applied potentials providing strong evidence of many-body correlations playing an important role in the transport of CO2 to the catalyst surface. The resistance to the transport of CO2 to the catalyst surface through a densely packed layer of solvated cations can potentially play a role in the activation mechanism of the CO2 molecule. Yet another important consequence of the interaction of the electrostatic forces in the EDL with charged species is a considerable drop in the pH and OH− concentration for a distance of up to 5 nm from the outer Helmholtz plane (OHP). This has significant repercussions for the CO2ER system especially from a mechanistic view-point, while requiring us to provide greater definition to what is defined as the ‘local reaction environment’. Finally, we compare the properties of the EDL for different alkali metal cations and look at the results in view of the existing experimental evidence.
2 Model and simulation details
2.1 Choice of model
The Poisson–Boltzmann (PB) model, also known as the classical Gouy–Chapman model,14,15 uses dilute solution theory with point-like ionic species to model the electrical double layer which is assumed to be in equilibrium with the bulk. Similarly, the classical description from dilute solution theory of the dynamics of the double layer is given by the Poisson–Nernst–Planck (PNP) equations.16 However, it has been shown that the PB and PNP models break down dramatically at voltages much higher than the thermal voltage (≫ϕT = kBT/e = 25 mV, where kB is the Boltzmann constant, T is the temperature and e is the fundamental charge of the electron)17 which is the region of interest for electrocatalytic applications such as CO2ER.One of the primary limitations of the dilute solution theory based models has been shown to be the breaking of the steric limit of ion concentration (Csteric = a−3, where a is the effective size of the ion) close to the charged surface at high applied voltages relative to ϕT. Excluding steric effects then leads to unphysically high EDL capacitance values and inherently making the solution non-dilute in the double layer region irrespective of the concentration of the bulk solution.13,18 Therefore, in order to resolve the EDL of a CO2ER system such that its essential qualitative nature is captured, we use the generalised modified PNP (GMPNP) equations13,19–23 to resolve the concentration and potential profiles in the screening layer (zones 2 + 3) which incorporate a mean-field continuum description of steric effects to the dilute solution theory based time-dependent PNP system. This modification is in addition to the Stern layer,24,25 where the surface catalytic reactions occur (zone 1 in Fig. 1), which defines the plane of closest approach; the so-called outer-Helmholtz plane (OHP). Poisson equation is used to derive the potential profile for the Stern layer as described in the following section.
2.2 Model description
The heterogeneous reactions (1) and (2) are considered to be occurring at the planar cathode surface in the CO2ER process, where the protons are provided by water. For simplicity, we base our calculations on CO producing catalysts such as Ag and Au but the analysis can be easily extended to catalysts producing a wider range of CO2 reduction products. We do not assume a faradaic current due to the consumption of H+ in our base-case. A comparison of the base-case with the scenario where a maximum of 10% of the bulk concentration of H+ is present at the OHP (limiting H+ current case) can be found in the ESI.†| CO2(aq) + H2O + 2e− ⇌ CO(g) + 2OH− | (1) |
| 2H2O + 2e− ⇌ H2(g) + 2OH− | (2) |
A total current density (jtot) and CO faradaic efficiency (FECO, defined as the ratio of electrons consumed for the production of CO vs. H2) is assumed for the simulations and data is generated for a range of jtot and FECO values. The flux of the solution species at the surface is then given by eqn (3)–(5). Our simulations are in 1D and x = 0 is considered to be at the OHP (the boundary between the zone 1 and zone 2 in Fig. 1).
![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) i|x=0,t = 0 i = HCO3−, CO32−, K+, H+ i|x=0,t = 0 i = HCO3−, CO32−, K+, H+ | (3) |
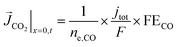 | (4) |
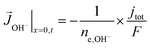 | (5) |
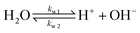 | (6) |
 | (7) |
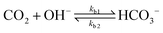 | (8) |
The values of the rate constants for the reactions (6)–(8) can be found in the ESI.† The bulk values of the concentrations of the solution species: H+, OH−, HCO3−, CO2, CO32− and K+ for a 0.1 M KHCO3 solution saturated with CO2 are assumed to be constant and are calculated by solving the transient rate equations for reactions (6)–(8) combined with the Sechenov equation26,27 (see ESI† for details). Varying the bulk concentration of KHCO3 will not change the nature of the EDL presented in this report unless either the solution volume is very small or the concentration of electrolyte is too low such that the bulk gets significantly depleted of counter-ions. However, the buffering capacity, the CO2 solubility and therefore the concentration profiles beyond the EDL will vary considerably.
The GMPNP equations used to model the mass transport of electrolyte species (for zones 2 + 3 in Fig. 1) are given by:
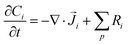 | (9) |
![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) i is the flux of species i given by:
i is the flux of species i given by: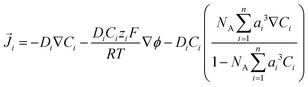 | (10) |
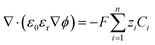 | (11) |
Our simulations assume an overall Nernst diffusion length of 50 μm. Dirichlet boundary conditions are used for the potential at the OHP (left-hand boundary) as well as for the concentration of species and potential in the bulk (right-hand boundary). Neumann boundary conditions are used for the flux of species at x = 0 as per eqn (3)–(5). The initial conditions for the concentrations are assumed to be at bulk values with ϕ = 0 V vs. PZC everywhere in the electrolyte. The scaled form of the GMPNP equations used for the numerical simulations can be found in the ESI.†
The potential at the point of zero charge (PZC, ϕσ=0) of the cathode is the potential at which the charge density of the surface is zero and no electrical double layer is therefore present in the electrolyte solution facing the electrode. The potential profile can be considered to be a flat line across the metal–electrolyte interface at the PZC thereby leading to a Dirichlet boundary condition of ϕbulk=0 at the right-hand boundary as well as an initial condition of ϕ = 0 V vs. PZC in the entire simulation domain. The ϕσ=0 is thus a natural choice for a reference for all the potential values used in this study. PZC of a metal surface depends on the crystal facet as well as on the electrolyte solution in case specific adsorption happens on the surface.28 For reference, the PZC in an aqueous solution for Ag surfaces is given in the ESI.† The range of OHP potentials considered in our simulations correspond to surface potentials of −0.10 to −0.61 V vs. PZC, which translate to −0.55 to −1.06 V vs. standard hydrogen electrode (SHE) for a Ag(111) surface and −0.80 to −1.31 V vs. SHE for a polycrystalline Ag surface. It should be noted that the PZC for a polycrystalline metallic surface is not a uniquely defined quantity but is in some cases estimated using the minimum of the measured differential capacitance. We assume only non-specific adsorption of solvent species on the cathode surface for our simulations.
The relative permittivity in eqn (11) is assumed to vary with cation concentration as given by eqn (12).29,30 The concentration terms in the eqn (12) are in mol dm−3 and Mwater is the molarity of water at room temperature taken as 55 M. The parameter wi is the total number of water molecules held by the ion i. ε0r is taken to be 80.1 equal to the relative permittivity of water at room temperature whereas εminr is the dielectric constant of water under the condition of dielectric saturation and is taken equal to 6. The model in eqn (12) is thus a summation of the contributions of bulk and cation-bounded water molecules to the relative permittivity. More advanced models such as the Booth model describe the dependence of the relative permittivity of the electrolyte medium as a function of the electric field.31,32 However, the Booth model is numerically more challenging to solve simultaneously with the GMPNP due to its non-linear nature.
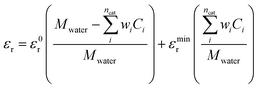 | (12) |
The potential profile in the Stern region (zone 1, Fig. 1) can be post-calculated using eqn (13) from the values of relative permittivity (εr,OHP) and electric field at the OHP obtained from the solution of the GMPNP equations for a given value of potential at the OHP. The width of the Stern layer is assumed to be 0.4 nm which is slightly larger than the radius of the largest cation considered in this study (Li+). The electric field value and the potential value at the OHP are used as Neumann and Dirichlet boundary conditions for eqn (13), respectively.
| ∇·(ε0εr,OHP∇ϕ) = 0 | (13) |
The description for the reaction-diffusion model and the PNP model used for comparison with the GMPNP model described above can be found in the ESI.†
2.3 Numerical simulations
The GMPNP (eqn (9)–(11)), PNP (eqn (S23)–(S25) in the ESI†) as well as the reaction-diffusion system (eqn (S21) and (S22) in the ESI†) are solved using the finite element method for spacial discretization and a backward Euler scheme for temporal discretization. The simulation domain in 1D is depicted in Fig. S1 in the ESI.† The backward Euler scheme, although computationally more intensive, was found to be necessary considering the stiff nature of both the PNP and GMPNP system of equations. We use the Python package FEniCS project33,34 to solve the weak Galerkin form of the transient non-linear GMPNP system such that the mass balance eqn (9) and the Poisson eqn (11) are solved self-consistently using the Newton method till a steady-state is reached.The GMPNP as well as the PNP system are highly numerically unstable at the large values of applied potentials (relative to the thermal voltage ϕT) that are relevant for CO2ER. The two most challenging aspects of numerically solving the (GM)PNP systems for the domain defined in this work are firstly, the characteristic length and time scales of the formation of the EDL are several orders of magnitude smaller than the length and time scales relevant for the homogeneous reaction and diffusion processes (see Fig. 1). To simulate such a system as a single domain implies that a variable finite element spatial mesh is needed to resolve the concentrations, both in the EDL, and in the entirety of the Nernst layer. In addition, due to numerical instability of the system very small time step sizes (1.0 × 10−5 s) are required to converge to a solution, which makes the simulation computationally expensive to reach steady-state (10 s). Secondly, there is a very strong drift of charged species close to the cathode surface due to the high applied voltage as compared to the strength of diffusive flow in this EDL region (or a high Péclet number). This makes the standard Galerkin weak form further numerically unstable and the problem is exaggerated in the PNP relative to the GMPNP due to the assumption of point species that accumulate to unphysically high concentrations at the OHP. The inclusion of species volume in the GMPNP interestingly also make the equations numerically more stable than the PNP equations. We have used the streamline upwind Petrov–Galerkin (SUPG) method to stabilize the weak form of the PNP system in order to be able to use a computationally tractable time step size.35–38 The formulation of the SUPG method used for PNP is described in detail in the ESI.†
3 Results
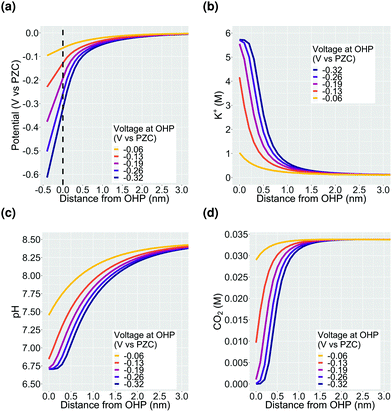
Fig. 2 shows the potential and concentration profiles in the EDL region calculated using the GMPNP model for a fixed total current density of 1 mA cm−2 with a faradaic efficiency of CO of 0.8. The boundary condition for the potential at the OHP is varied to demonstrate the build-up of potassium ions in the EDL with increasing potential. It should be noted that the EDL is comprised of both the Stern layer as well as the potential screening layer which lies beyond the OHP (zones 1 and 2 in Fig. 1). Since the concentration of solution species does not penetrate the OHP by definition, all the concentration profile plots start from the OHP (x = 0) whereas the potential profile shown in Fig. 2a starts at x = −0.4 nm which signifies the catalyst surface. As discussed previously, all voltage values are referenced against ϕσ=0 and are thus given in V vs. PZC. The concentration of K+ cations increases till the steric limit aK+−3, where aK+ is the effective size of the solvated K+ ion (Fig. 2b). Once this steric limit is reached, the EDL profile grows in thickness away from the OHP with a constant density of counter-ions (cations in this case). Therefore, at higher voltages relative to ϕT, the nature of the EDL can no longer be described as a diffuse-layer, but rather, it assumes the form of a condensed layer of counter-ions which builds in thickness with applied potential.18 We will discuss our results in the context of the impact of the condensed double layer on CO2 transport in Section 3.1 and the pH in Section 3.2. Section 3.3 discusses the impact of changing the alkali metal type in the electrolyte on the nature of the EDL.3.1 Influence of EDL on CO2
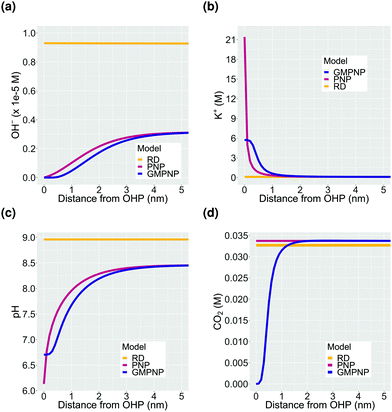
The first important aspect of the build-up of counter-ions in the EDL at higher potentials is the accessibility of the catalyst surface for the CO2 molecule. The rate at which CO2 can diffuse to the catalyst surface, puts an upper limit to the activity that is achievable through catalysis and is therefore a critical parameter for CO2ER performance. The diminishing of CO2 concentration in the EDL at high applied voltages (Fig. 2d) is a direct consequence of the steric effect incorporated in the GMPNP model. Fig. 3 shows a comparison between the concentration profiles in the EDL obtained using a reaction-diffusion model, a PNP model which solves the migration, diffusion and reaction processes self-consistently but assumes point species and a GMPNP model which corrects the PNP for steric effects. It is evident that inclusion of migration in the PNP and GMPNP models drastically influences the activity of charged species in the EDL region. The volume exclusion in the GMPNP model has important consequences for the extent of cation concentration at the OHP which, for the PNP model, reach unphysically high concentrations (significantly higher than the steric limit, Fig. 3b). Despite a very high cation accumulation at the OHP for the PNP model, the assumption of point species results in no exclusion of CO2 from the EDL region as is predicted by the GMPNP model (Fig. 3d). The minor variation between the CO2 concentration profiles derived using the RD and PNP models stems from the significant difference in the OH− concentrations (Fig. 3a) leading to the formation of bicarbonate through the homogeneous reaction (8). These results highlight the importance of considering volume-exclusion in mass transport models attempting to resolve the EDL in electrocatalytic systems such as CO2ER.According to Fig. 2d, the CO2 concentration is completely depleted at potentials more cathodic than ∼−0.2 V vs. PZC at the OHP. Since there is no experimental evidence suggesting that CO2 reduction completely terminates at high applied potentials, the result in Fig. 2d leads us to the hypothesis that the CO2 molecule diffuses to the catalyst surface at high applied potentials due to many-body correlations in the presence of the solvated cations in the EDL region, albeit with a diminished diffusivity due the condensed nature of the EDL. Complex many-body correlations arising from the mutual interaction of chemical species (including water molecules) are expected to play a role especially in the EDL with a high concentration of counter-ions and the presence of competing electrostatic and van der Waals forces. In addition, the identity of the solvated cation should also have an influence on the rate of diffusion of CO2. Cations have been shown to influence the CO2 reduction rate through numerous experimental as well as computational studies2,3,12,39–44 however, this influence has not been studied from the perspective of changing diffusion coefficient of the CO2 molecule. The modeling results presented in this study use Fick's law of diffusion with constant values of diffusion coefficients for all species (Fick diffusivity values are tabulated in the ESI†). The EDL is however a multi-component non-dilute solution where considerable deviations from the Fick's diffusivities can be expected due to non-ideal behaviour. We are currently conducting force-field molecular dynamics (MD) simulations to study the diffusion of CO2 in such an EDL environment. The effect of cation type will be discussed further in the context of Fig. 6 later in the text.
The other possibility is that the reduction of CO2 (at least the first reduction step) happens beyond the condensed layer of counter-ions at the EDL and not directly at catalyst surface. We believe that it is highly unlikely that all the CO2 reduction steps occur at the EDL as it would not be able to explain the major deviation between the CO2 reduction products amongst different metallic catalysts.45 However, the involvement of the solvated cations in the reduction of CO2 could be one of the reasons for the difference in performance of systems using different cation types. Ab initio quantum-mechanical methods need be developed to study the first CO2 reduction step in the presence of the condensed EDL to compare the energetics of the potential pathways.
3.2 Influence of EDL on pH
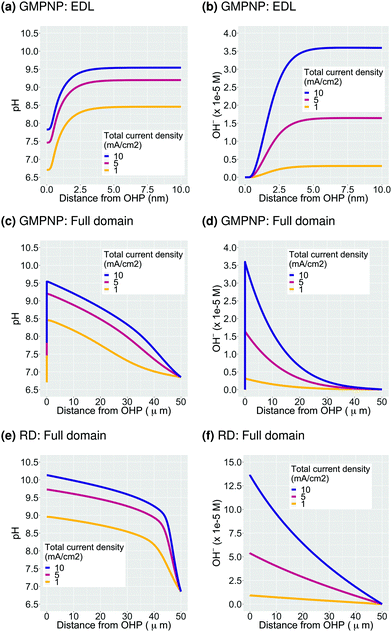
The second important consequence of the formation of the EDL is the drop in pH in the double layer region due to both, a higher concentration of positively charged H+, and a depletion of negatively charged OH− from the region measuring a few nm from the electrode surface (Fig. 2c and Fig. S2a, ESI†). The pH at the OHP drops to a threshold value and the profile extends into the double layer region at higher voltages analogous to what is observed for the accumulation of the K+ ions in Fig. 2b. Assuming point species and not considering volume exclusion within the PNP model, leads to an unphysically low pH value at the OHP (Fig. 3c). Fig. 4a–d show the pH and OH− concentration profiles for varying values of total current densities at a fixed potential and faradaic efficiency distribution computed using the GMPNP model. The results obtained using the reaction-diffusion (RD) model are shown in Fig. 4e and f for comparison. As expected, the pH at the OHP as well as at its peak value are found to be proportional to the total current density and the pH attains a maximum value beyond the EDL at a distance of ∼5 nm from the OHP (Fig. 4a and c). The RD model predicts a considerably higher pH at x = 0 and also, as expected, does not capture the drop in the pH due to migration effects very close to the electrode surface as predicted by the GMPNP model (also see Fig. 3c).Similarly, the OH− concentration calculated using GMPNP is completely depleted at the OHP at high voltages (Fig. 4b and Fig. S2a, ESI†) whereas the peak value beyond the EDL is proportional to the total current density. The RD model however, predicts a ∼4 times higher rise in OH− concentration at the electrode relative to the peak value predicted by GMPNP and does not account for its depletion due to electrostatic repulsion in the EDL (also see Fig. 3a). We have also considered a limiting proton current case where no more than 10% of the bulk concentration of H+ is allowed to accumulate at the OHP and the protons get consumed via the catalytic reactions (S14) and (S15) in the ESI.† Adding the flux of protons at the catalyst surface leads to the pH profiles for all current densities to overlap and a pH value of 8 is obtained at the OHP with a maximum value of ∼9.7 beyond the EDL (Fig. S5 in ESI†). The current attributed to the H+ flux for H2 and CO production is <0.5% of the total current density for all cases considered.
Numerous studies of CO2ER systems have shown a strong correlation between pH of the electrolyte in the vicinity of the catalyst (or the so-called local pH) and the overall performance, especially the catalyst selectivity.27,46–52 Our results demonstrate that the EDL leads to pH and OH− concentration profiles which do not monotonically increase towards the catalyst surface but in fact, become considerably diminished in the immediate vicinity of the OHP up to a distance of ∼5 nm. Since the OH− concentration is depleted from the EDL region, the pH at the OHP at high applied potentials will have a stronger dependence on the rate of H+ consumption in catalytic processes than the total current density. Therefore, we believe that there is a strong need to explicitly define what is meant by the term ‘local’ in the context of pH and concentrations of solution species when discussing mechanistic insights and relative performance of CO2ER systems.
In addition, Fig. 5 shows the extent of the deviation of homogeneous reactions (6)–(8) from equilibrium at steady-state as defined by the eqn (S11)–(S13) in the ESI.† The buffer reaction of CO2 to HCO3− (reaction (8)) is too slow to reach equilibrium and is deficient of HCO3− in the entire Nernst domain. Therefore even though the concentration of OH− rises due to CO2ER, the competing rates of diffusion and reaction kinetics imply that CO2 is still present in excess in reaction (8). This is in line to what has been shown previously using spectroscopic measurements.53 The HCO3− to CO32− buffer reaction (reaction (7)) remains in equilibrium in the entire domain outside the EDL which is expected considering that ka1 is 6 order of magnitudes bigger than kb1. The water-dissociation reaction (reaction (6)) also deviates from its equilibrium due to competing reaction and mass transport rates. It should be noted that the results shown in Fig. 5 remain qualitatively similar even if a reaction-diffusion model is considered. The dramatic variation of the pH profile as a function of distance from the OHP (Fig. 4c) as well as the deviation of the buffer reactions from their equilibrium are important factors that should be considered in experimental studies aiming to measure pH in CO2ER systems using for e.g. spectroscopic techniques.54
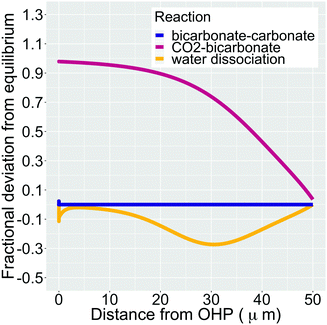 | ||
| Fig. 5 Fractional deviation from equilibrium for reactions (6)–(8) in the simulation domain. The data shown is for a total current density of 1 mA cm−2, a CO faradaic efficiency of 0.8 and a potential of −0.32 V vs. PZC at the OHP. We have removed the deviation values for the initial 1 nm from the OHP since the formation of the EDL wildly distorts the species concentrations. | ||
3.3 Influence of cation size
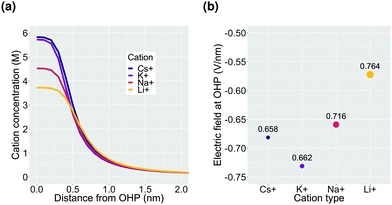
Finally, we consider the effect of changing the type of cation in the electrolyte solution. We compare Cs+, K+, Na+ and Li+ while keeping the composition of the other species in the bulk electrolyte the same.In the context of the GMPNP simulations, the cations (i) differ in terms of their solvated size (ai in eqn (10)) and the hydration number of each ion (wi in eqn (12)) (the values of both parameters for each cation can be found in the ESI†). The trend of solvated sizes of the cations in an aqueous solution follows the order Cs+ < K+ < Na+ < Li+ which is the inverse of the trend for the neutral atoms due to difference in the hydration properties amongst the alkali metal cations.55,56 Fig. S6 in the ESI† shows an illustration of the effect of cations with different sizes on the concentration at the steric limit and the thickness of the EDL. This can be used to understand the difference in concentration profiles of the cations in the EDL as shown in Fig. 6a, with Cs+ being the smallest solvated cation reaching the highest concentration at the OHP followed very closely by K+ with a similar solvated size, followed by Na+ and Li+ in that order. The resulting trend in the electric field strength at the OHP is shown in Fig. 6b.
Despite reaching a higher concentration at the OHP and therefore a higher charge density, the electric field strength for Cs+ is found to be weaker as compared to K+. This is due to the fact that Cs+ polarizes fewer water molecules compared to the other alkali metal cations and therefore the drop in relative permittivity of the solution at the OHP is smaller based on the eqn (12) (see Fig. S7a, ESI†). Multiple experimental results have shown Cs+ to benefit the activation of CO2 relative to other cation types.2,39,41,42,44 The electric field strength close to the cathode surface in the presence of the cations has been regarded as an important factor leading to the observed experimental results owing to the interaction of the field with the adsorbed polar reactive species.2,3,12,42 However, based on our results, we believe that the observed improvement in the reduction of CO2 in the presence of Cs+ cannot be understood solely on the basis of electric field strength. The specific ion interactions of the cation with the surrounding water and the CO2, as well as with the charged metal surface, also need to be taken into account.
4 Discussion
The reaction environment of the CO2 electrochemical reduction process is highly complex with several coupled phenomena operating at vastly varying length and time scales that incorporate important degrees of freedom for the overall system performance. A multi-scale approach is therefore essential in order for computational simulations to effectively develop the understanding of such a reaction system to compliment the experimental efforts in the area.Ab initio calculations of the double layer suffer from several limitations that lead to unfeasible computational costs which can be circumvented in the continuum treatment of the double layer.57–59 In addition, the results derived using a continuum approach such as the GMPNP can provide valuable inputs to atomistic quantum mechanical models by defining the steady-state environment under which reaction energetics need to be studied.12,60 However, the continuum treatment of the electrolyte system does not capture effects pertaining to ion specificity which can potentially play a role at molecular length scales and concentrations relevant in the EDL for highly charged surfaces such as in the case of CO2ER.61–64 The Bjerrum length (lB = e2/4πεrε0kBT, 0.7 nm at room temperature) defines the length scale at which the electrostatic interaction between two charged species is comparable to the thermal energy kBT. The relative permittivity of the electrolyte can decrease drastically in the EDL where the electric field strength is high (Fig. S2, ESI†).31,32 This will lead to an increase in the Bjerrum length indicating a prevalence of ion-specific effects. A promising approach to account for particle correlations in EDLs uses density functional theory (DFT) to estimate excess chemical potentials of species at equilibrium which can be used as an input to continuum models such as PNP to study transport.65,66 In addition, our results represent the nature of the double layer in the absence of specific short-range electrostatic interactions between the electrode surface and the solution species. The presence of specific adsorption can add significant complexity to the EDL description as it can influence the potential at the PZC, the balance of charge between the metal surface and the double layer and consequently the potential and concentration profiles at a given applied potential.60,67 There is a need to develop computational frameworks applicable to practical CO2 electrocatalytic systems with high surface charge densities, multiple components, long-range concentration gradients and specific adsorption that correct the mean-field continuum dynamics of the double-layer in a computationally and numerically tractable manner.
In addition to theoretical challenges, a more practical challenge arises from solving the (GM)PNP system of partial difference equations numerically at operating potentials. The Galerkin finite element method is found to be unstable for typical values of applied potentials unless a very fine time and space discretization is used to resolve the EDL region. The SUPG method was used in this study to stabilize the PNP system as described in Section 2.3. However, there is still a need to develop stabilization techniques suited for the modified version of the Nernst–Planck equation with a non-linear volume exclusion term added. The development of better stabilization techniques will go a long way in making the application of the GMPNP system more feasible to a wider array of operating conditions for electrocatalytic systems of relevance.
5 Conclusions
Our results establish the importance of electrostatic forces and volume exclusion in the determination of the reaction environment for CO2 electrocatalysis. The electrical double layer formed as a consequence will be highly influential for the access of the catalyst to the reactive species, both CO2 and H+, and will therefore play a role in the activity as well as selectivity of the process.The defining characteristic of the EDL is the screening of the charge density on the cathode surface with solvated cations in the electrolyte and a concomitant repulsion of anions away from the surface. The nature of the cation therefore plays an important role in determining the structure of the EDL, the strength of electric field, the differential capacitance and the extent of the polarization of solvent molecules. The operating potentials of practical CO2ER and other electrocatalytic systems imply that the cations in the EDL will reach their steric limit close to the electrode. This closed-pack nature of the EDL is expected to have significant implications for the energetics of the reactive and non-reactive processes relevant to CO2ER. The local reaction environment of CO2 electrocatalysis is therefore formed by the double layer and more research effort is needed to develop a stronger understanding of the region spanning the first 5–10 nm from the catalyst surface.
As all catalysts of practical relevance to CO2ER have a nano and meso structure, the effect of mass transport is expected to be even more complex and significant in the presence of nanometer scale pores and confinements.1,68 Nanopores and channels with sizes less than twice the potential screening length can have overlapping double layers which can lead to interesting effects due to selective ion enrichment and depletion with several practical applications.61,69 Nanostructuring is therefore a very important tool to influence the reaction environment and thus the performance of the catalyst. Unlike a planar surface, the distribution of charge density over a structured surface will be non-uniform and will lead to a varying double layer structure across the catalyst. Application of models such as the GMPNP in higher dimensions can then be very useful to study such phenomena. Gas diffusion electrode (GDE) based CO2ER systems employing nanostructured catalyst layers and significantly shorter diffusion length of CO2 have achieved considerably higher current densities and enhanced selectivity through better mass transport.5,6 Electrified porous catalysts therefore are a very practically relevant class of systems where continuum modeling approach similar to the one presented here can play an important role.
In conclusion, the continuum treatment of the GMPNP equations provides a computationally tractable method to model the reaction environment of CO2ER close to highly charged surfaces, although with certain limitations. We believe that our approach can provide a qualitatively sound starting point for further theoretical as well as experimental investigations while bridging some of the gap between quantum mechanical surface reactivity studies and mass transport of species from the bulk solution in electrocatalytic systems.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project received funding from NWO via the VIDI grant (WAS and DB). The authors thank Mike Radersma, Dr Recep Kas and Dr Nathan Nesbitt for their valuable discussions during the course of this research. The authors thank NWO for access to SURFsara HPC facilities and Dr Caspar van Leeuwen at SURFsara for HPC technical support.References
- G. O. Larrazábal, A. J. Martín and J. Pérez-Ramírez, J. Phys. Chem. Lett., 2017, 8, 3933–3944 CrossRef PubMed.
- J. Resasco, L. D. Chen, E. Clark, C. Tsai, C. Hahn, T. F. Jaramillo, K. Chan and A. T. Bell, J. Am. Chem. Soc., 2017, 139, 11277–11287 CrossRef CAS PubMed.
- M. Liu, Y. Pang, B. Zhang, P. De Luna, O. Voznyy, J. Xu, X. Zheng, C. T. Dinh, F. Fan, C. Cao, F. P. G. de Arquer, T. S. Safaei, A. Mepham, A. Klinkova, E. Kumacheva, T. Filleter, D. Sinton, S. O. Kelley and E. H. Sargent, Nature, 2016, 537, 382 CrossRef CAS PubMed.
- M. G. Kibria, J. P. Edwards, C. M. Gabardo, C.-T. Dinh, A. Seifitokaldani, D. Sinton and E. H. Sargent, Adv. Mater., 2019, 1807166 CrossRef PubMed.
- T. Burdyny and W. A. Smith, Energy Environ. Sci., 2019, 12, 1442–1453 RSC.
- C.-T. Dinh, T. Burdyny, M. G. Kibria, A. Seifitokaldani, C. M. Gabardo, F. P. Garca de Arquer, A. Kiani, J. P. Edwards, P. De Luna, O. S. Bushuyev, C. Zou, R. Quintero-Bermudez, Y. Pang, D. Sinton and E. H. Sargent, Science, 2018, 360, 783–787 CrossRef CAS PubMed.
- N. Gupta, M. Gattrell and B. MacDougall, J. Appl. Electrochem., 2006, 36, 161–172 CrossRef CAS.
- D. Raciti, M. Mao and C. Wang, Nanotechnology, 2018, 29, 044001 CrossRef PubMed.
- H. Hashiba, L.-C. Weng, Y. Chen, H. K. Sato, S. Yotsuhashi, C. Xiang and A. Z. Weber, J. Phys. Chem. C, 2018, 122, 3719–3726 CrossRef CAS.
- C. Delacourt, P. L. Ridgway and J. Newman, J. Electrochem. Soc., 2010, 157, B1902–B1910 CrossRef CAS.
- S. Suter and S. Haussener, Energy Environ. Sci., 2019, 12, 1668–1678 RSC.
- S. Ringe, E. L. Clark, J. Resasco, A. Walton, B. Seger, A. T. Bell and K. Chan, Energy Environ. Sci., 2019 10.1039/C9EE01341E.
- M. S. Kilic, M. Z. Bazant and A. Ajdari, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 021503 CrossRef PubMed.
- M. Gouy, J. Phys. Theor. Appl., 1910, 9, 457–468 CrossRef.
- D. L. Chapman, London, Edinburgh Dublin Philos. Mag. J. Sci., 1913, 25, 475–481 CrossRef.
- J. Newman and K. E. Thomas-Alyea, Electrochemical Systems, John Wiley & Sons, 3rd edn, 2004 Search PubMed.
- J. Lyklema, Fundamentals of interface and colloid science. Volume 2: Solid-liquid interfaces. With special contributions by A. de Keizer, B. H. Bijsterbosch, G. J. Fleer and M. A. Cohen Stuart, Academic Press, 1995.
- M. S. Kilic, M. Z. Bazant and A. Ajdari, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 021502 CrossRef PubMed.
- L. Pilon, H. Wang and A. d. Entremont, J. Electrochem. Soc., 2015, 162, A5158–A5178 CrossRef CAS.
- H. Wang, A. Thiele and L. Pilon, J. Phys. Chem. C, 2013, 117, 18286–18297 CrossRef CAS.
- M. Z. Bazant, M. S. Kilic, B. D. Storey and A. Ajdari, Adv. Colloid Interface Sci., 2009, 152, 48–88 CrossRef CAS PubMed.
- I. Borukhov, D. Andelman and H. Orland, Phys. Rev. Lett., 1997, 79, 435–438 CrossRef CAS.
- A. Iglic and V. Kralj-Iglic, Electrotecnical Rev., 1994, 61, 127–133 Search PubMed.
- O. Stern, Z. Elektrochem. Angew. Phys. Chem., 1924, 30, 508–516 CAS.
- H. Helmholtz, Ann. Phys., 1879, 243, 337–382 CrossRef.
- S. Weisenberger and A. Schumpe, AIChE J., 1996, 42, 298–300 CrossRef CAS.
- T. Burdyny, P. J. Graham, Y. Pang, C.-T. Dinh, M. Liu, E. H. Sargent and D. Sinton, ACS Sustainable Chem. Eng., 2017, 5, 4031–4040 CrossRef CAS.
- S. Trasatti and E. Lust, in The Potential of Zero Charge, ed. R. E. White, J. O. Bockris and B. E. Conway, Springer US, Boston, MA, 1999, pp. 1–215 Search PubMed.
- J. B. Hasted, D. M. Ritson and C. H. Collie, J. Chem. Phys., 1948, 16, 1–21 CrossRef CAS.
- J. O. Bockris and A. K. Reddy, Modern Electrochemistry, Springer US, 1998, 2nd edn, vol. 1 Search PubMed.
- F. Booth, J. Chem. Phys., 1951, 19, 391–394 CrossRef CAS.
- A. J. Appleby, in Electron Transfer Reactions With and Without Ion Transfer, ed. B. E. Conway, C. G. Vayenas, R. E. White and M. E. Gamboa-Adelco, Springer US, Boston, MA, 2005, pp. 175–301 Search PubMed.
- M. S. Alnæs, J. Blechta, J. Hake, A. Johansson, B. Kehlet, A. Logg, C. Richardson, J. Ring, M. E. Rognes and G. N. Wells, Archive of Numerical Software, 2015, 3, 9–23 Search PubMed.
- A. Logg, K.-A. Mardal and G. N. Wells, et al., Automated Solution of Differential Equations by the Finite Element Method, Springer, 2012 Search PubMed.
- J. H. Chaudhry, J. Comer, A. Aksimentiev and L. N. Olson, Commun. Comput. Phys., 2014, 15, 93–125 CrossRef PubMed.
- P. B. Bochev, M. D. Gunzburger and J. N. Shadid, Comput. Methods Appl. Mech. Eng., 2004, 193, 2301–2323 CrossRef.
- T. J. Hughes, L. P. Franca and G. M. Hulbert, Comput. Methods Appl. Mech. Eng., 1989, 73, 173–189 CrossRef.
- L. P. Franca, S. L. Frey and T. J. Hughes, Comput. Methods Appl. Mech. Eng., 1992, 95, 253–276 CrossRef.
- M. R. Singh, Y. Kwon, Y. Lum, J. W. Ager and A. T. Bell, J. Am. Chem. Soc., 2016, 138, 13006–13012 CrossRef CAS.
- C. X. Zhao, Y. F. Bu, W. Gao and Q. Jiang, J. Phys. Chem. C, 2017, 121, 19767–19773 CrossRef CAS.
- C. M. Gunathunge, V. J. Ovalle and M. M. Waegele, Phys. Chem. Chem. Phys., 2017, 19, 30166–30172 RSC.
- A. Murata and Y. Hori, Bull. Chem. Soc. Jpn., 1991, 64, 123–127 CrossRef CAS.
- L. D. Chen, M. Urushihara, K. Chan and J. K. Nørskov, ACS Catal., 2016, 6, 7133–7139 CrossRef CAS.
- M. R. Thorsona, K. I. Siila and P. J. A. Kenis, J. Electrochem. Soc., 2013, 160, F69–F74 CrossRef.
- Y. Hori, in Electrochemical CO2 Reduction on Metal Electrodes, ed. C. G. Vayenas, R. E. White and M. E. Gamboa-Aldeco, Springer New York, New York, NY, 2008, pp. 89–189 Search PubMed.
- M. Ma, K. Djanashvili and W. A. Smith, Angew. Chem., Int. Ed., 2016, 55, 6680–6684 CrossRef CAS PubMed.
- S. Lee, S. Hong and J. Lee, Catal. Today, 2017, 288, 11–17 CrossRef CAS.
- R. Kas, R. Kortlever, H. Yilmaz, M. T. M. Koper and G. Mul, ChemElectroChem, 2015, 2, 354–358 CrossRef CAS.
- M. Ma, B. J. Trześniewski, J. Xie and W. A. Smith, Angew. Chem., Int. Ed., 2016, 55, 9748–9752 CrossRef CAS PubMed.
- A. S. Varela, M. Kroschel, T. Reier and P. Strasser, Catal. Today, 2016, 260, 8–13 CrossRef CAS.
- K. J. P. Schouten, E. P. Gallent and M. T. Koper, J. Electroanal. Chem., 2014, 716, 53–57 CrossRef CAS.
- Y. Hori, A. Murata and R. Takahashi, J. Chem. Soc., Faraday Trans. 1, 1989, 85, 2309–2326 RSC.
- M. Dunwell, X. Yang, B. P. Setzler, J. Anibal, Y. Yan and B. Xu, ACS Catal., 2018, 8, 3999–4008 CrossRef CAS.
- O. Ayemoba and A. Cuesta, ACS Appl. Mater. Interfaces, 2017, 9, 27377–27382 CrossRef CAS PubMed.
- E. R. Nightingale, J. Phys. Chem., 1959, 63, 1381–1387 CrossRef CAS.
- J. O. Bockris and P. P. S. Saluja, J. Phys. Chem., 1972, 76, 2140–2151 CrossRef CAS.
- Computational Catalysis, ed. A. Asthagiri and M. J. Janik, The Royal Society of Chemistry, 2014, pp. 116–156 Search PubMed.
- J. A. Gauthier, S. Ringe, C. F. Dickens, A. J. Garza, A. T. Bell, M. Head-Gordon, J. K. Nørskov and K. Chan, ACS Catal., 2019, 9, 920–931 CrossRef CAS.
- F. Nattino, M. Truscott, N. Marzari and O. Andreussi, J. Chem. Phys., 2019, 150, 041722 CrossRef PubMed.
- A. Baskin and D. Prendergast, J. Electrochem. Soc., 2017, 164, E3438–E3447 CrossRef CAS.
- L. Bocquet and E. Charlaix, Chem. Soc. Rev., 2010, 39, 1073–1095 RSC.
- W. Kunz, P. L. Nostro and B. Ninham, Curr. Opin. Colloid Interface Sci., 2004, 9, 1–18 CrossRef CAS.
- B. W. Ninham and V. Yaminsky, Langmuir, 1997, 13, 2097–2108 CrossRef CAS.
- P. Attard, Electrolytes and the Electric Double Layer, John Wiley & Sons, Ltd, 2007, pp. 1–159 Search PubMed.
- D. Gillespie, W. Nonner and R. S. Eisenberg, J. Phys.: Condens. Matter, 2002, 14, 12129–12145 CrossRef CAS.
- A. Voukadinova, M. Valiskó and D. Gillespie, Phys. Rev. E, 2018, 98, 012116 CrossRef CAS PubMed.
- A. Bard and L. Faulkner, Electrochemical Methods: Fundamentals and Applications, John Wiley & Sons, Inc., 2001, vol. 6 Search PubMed.
- J. H. Bae, J.-H. Han and T. D. Chung, Phys. Chem. Chem. Phys., 2012, 14, 448–463 RSC.
- R. B. Schoch, J. Han and P. Renaud, Rev. Mod. Phys., 2008, 80, 839–883 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Supporting modeling details, parameter values and simulation results. See DOI: 10.1039/c9ee02485a |
| This journal is © The Royal Society of Chemistry 2019 |