Stable and tunable phosphonic acid dipole layer for band edge engineering of photoelectrochemical and photovoltaic heterojunction devices

Abstract

A key challenge for photoelectrochemical water splitting is that high performance semiconductors are not stable in aqueous electrolytes, necessitating corrosion protection layers such as TiO₂. In the best case, the protection layer would also serve as the heterojunction partner, minimizing complexity and thereby cost. However, the bands of most high performance semiconductors are poorly aligned with TiO₂, limiting the photovoltage. Here, we describe a method to overcome this limitation through the placement of a tunable dipole layer at the interface of the p- and n-type materials, shifting the relative band positions to enable an increased photovoltage. The introduction of a phosphonic acid (PA, H₃PO₃) layer increases the photovoltage of TiO₂-protected Si, Sb₂Se₃, and Cu₂O photocathodes. The dipole effect scales with PA surface coverage, and gives even larger shifts when multilayers are employed. By varying the thickness from submonolayer to multilayer (up to 2 nm), we are able to tune the photovoltage of p-Si/TiO₂ over a range of 400 mV.

---

Broader context

While usage of solar energy offers many benefits, one of its main limitations for large scale implementation is that solar irradiation varies strongly with day/night and summer/winter cycles. Efficient storage of solar energy is therefore of crucial importance, with one possibility being to convert solar energy into chemical energy, for example in the form of H₂ obtained from splitting water (2H₂O → 2H₂ + O₂). Water splitting could be achieved by coupling photovoltaic (PV) cells to an electrolyzer or, in a more direct way, in a photoelectrochemical (PEC) cell, which absorbs sunlight and, instead of generating electricity, uses the solar energy to drive a chemical reaction. PEC cells are operated in direct contact with corrosive electrolytes and measures have to be taken to protect the otherwise unstable materials. Finding suitable protection strategies is an open challenge, since not only the stability is important, but also the energetics of the protective materials have to be matched with the photoabsorbing semiconductor. This study presents a general method to tune the band alignment between photoabsorbers and one of the most promising protective materials, TiO₂, which makes otherwise unfavorable material combinations more efficient.

The maximum possible photovoltage of photoelectrochemical (PEC) cells as well as heterojunction-based photovoltaic (PV) devices is determined by the band alignment of the involved materials. In traditional PEC, the maximum photovoltage is set by the difference of the Fermi level of the semiconductor and the redox potential of the solution, while in PV the maximum theoretical photovoltage is set by the difference of the Fermi levels of the p- and n-type materials. Furthermore, large discontinuities (i.e. spikes) in the conduction band have to be avoided to assure an unhindered flow of the photo-excited electrons through the junction. Optimizing band alignments at semiconductor heterointerfaces is a key challenge in the development of new technologies for PEC and PV applications.¹ Strategies to improve the band alignments include graded interfaces,² introduction of buffer layers,^3,4 doping of the electron acceptor material⁵ as well as interface and bulk defect engineering.^6,7 However, most of these solutions are specific for a particular materials combination. An elegant way to tune the band alignment in a more general fashion is by adding a dipole layer at the junction interface, which results in an increase of band bending, minimizing recombination losses at the interface.⁸

The interface dipole strategy has been successfully demonstrated in the fields of organic PV,^9–12 perovskite PV^13,14 and quantum dot PV, utilizing self-assembled monolayers (SAMs) of carboxylic- and phosphonic acids.^15–17

In traditional PEC, the dipole layer is added at the semiconductor/electrolyte interface, which usually leads to very limited stability and only a small voltage increase due to shielding of the dipole by the electrolyte.^18–21 In order to compete with commercially well-established PV coupled with electrolyzers, PEC systems have to be stable for years, likely in extreme pH electrolytes.²² Thus, corrosion protection layers have been investigated, using chemically stable materials such as TiO₂.²³ The use of overlayers in PEC systems creates a “buried junction”, which functions much like a PV heterojunction, and therefore strategies to improve the performance of buried junction PEC cells are directly translatable to PV devices.

TiO₂ is a good candidate for a protective overlayer due its chemical stability over a wide range of pH, and it has been shown to protect photoanodes as well as photocathodes.²³ In the best case, TiO₂ would also serve as the heterojunction partner, minimizing the number of layers in the device (i.e. the complexity) and therefore the cost. However, the band alignment of most high performance photoabsorbers (such as Si) with TiO₂ is unfavorable. Thus, a dipole induced band shifting can give a better band alignment, increased photovoltage and therefore higher efficiency from these otherwise unfavorable photoabsorber/protective layer pairs.

We sought to find a dipole strategy for PEC water splitting that fulfills the following requirements: utilizes cheap and abundant materials; enables a large, tunable photovoltage increase; exhibits high stability; and is generally applicable to many different photoabsorber materials. Here, we report our strategy fulfilling the above requirements and serving as a proof of concept using p-Si as a well-behaved model photoabsorber, which would in a next step be replaced by emerging thin film materials. There is also a large body of literature on dipole modification of Si to tune its electronic properties, but those works chemically modify the Si directly and the obtained results are not transferrable to other photoabsorbing substrates.^24–28

A 0.5 nm Al₂O₃ anchoring layer allows us to use different photoabsorbers with no changes in the dipole binding, since the dipole is deposited onto the anchoring layer and not directly onto the photoabsorber. After assessing several oxide materials (Fig. S1 and S2, ESI†), we found that Al₂O₃ performed best as anchoring layer and is straight-forward to deposit homogeneously in well-defined thicknesses by atomic layer deposition (ALD). Phosphonic acid (PA, H₃PO₃) serves as the dipole layer. In contrast to previous work using SAMs, we chose to use the spin coating technique to deposit the dipole layer which allowed us to tune the thickness of the layer without being restricted to a monolayer as maximal surface coverage. Upon screening of different phosphonic acids with different thicknesses (ranging from sub-monolayer to multilayers) in our system, the largest dipole effect was obtained using 1–2 nm of PA, where photovoltage shifts of close to 400 mV were obtained for the p-Si/TiO₂ heterojunction. TiO₂ was used as heterojunction partner and protective layer.

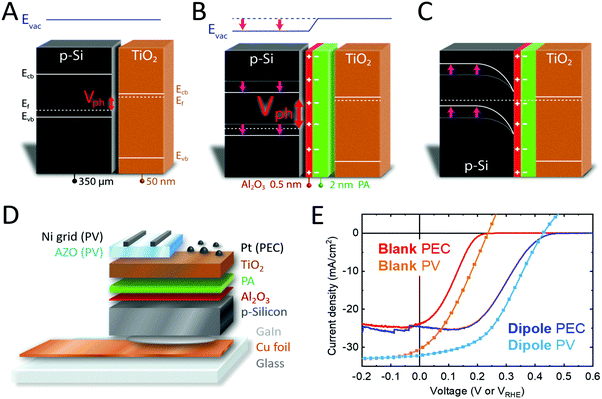
Water splitting electrodes were fabricated by depositing a platinum catalyst on the TiO₂ surface. Additionally, we fabricated PV cells by sputtering a transparent conducting oxide (TCO) front contact on top of the TiO₂. Qualitative band diagrams of p-Si/n-TiO₂ as well as p-Si/anchor layer/PA/n-TiO₂ are shown in Fig. 1A–C. The effect of the dipole is represented as a step in the vacuum energy (E_vac), shifting the bands of p- and n-type layers relative to each other, and resulting in an increased band bending and photovoltage (V_ph). Fig. S3 (ESI†) shows band diagrams in flat band condition, in equilibrium and under illumination for both p-Si/n-TiO₂ and p-Si/anchor layer/PA/n-TiO₂. The PA modification strategy was also extended to other emerging photocathodes like Sb₂Se₃ and Cu₂O resulting in improvements in the onset potential, demonstrating the universal applicability of our approach.

Fig. 1 (A and B) Band diagrams of p-Si/n-TiO₂ and p-Si/anchor layer/PA/n-TiO₂ in flat band condition, and (C) in equilibrium, showing the increased band bending that is obtained with a dipole layer. The dipole layer induces a shift in the band edge, represented by a step in the vacuum energy level (E_vac), and therefore higher photovoltage (V_ph) can be obtained. Due to the high doping of TiO₂, band bending in the TiO₂ was omitted. (D) Device architecture of the PV and PEC cells used in this study. (E) Current density–Voltage plots of PV and PEC cells made from p-Si/n-TiO₂ well as p-Si/anchor layer/PA/n-TiO₂. PEC measurements in 1 M H₂SO₄ and 1 sun illumination, PV measurements under 1 sun illumination. The small current fluctuations in the blue trace (and other J–V curves in this paper) are attributed to the formation and release of hydrogen bubbles on the device surface.

Band edge engineering at p-Si/n-TiO₂ heterojunctions

The schematic structure of the dipole modified PEC and PV cells is shown in Fig. 1D. Detailed experimental methods can be found in the ESI.† Briefly, thin Al₂O₃ layers were deposited by ALD onto etched p-Si wafers, followed by spin coating of phosphonic acid (PA). The samples were then annealed at 120 °C in air and thoroughly rinsed with ethanol, resulting in PA layers of 0.5–2 nm thickness depending on the PA concentration used for spin coating (as determined by ellipsometry). The presence of PA on the surface was confirmed by XPS, with phosphorus core level emissions occurring at binding energies of 134.2, 135.0 and 192.0 eV (P 2p_3/2, P 2p_1/2, P 2s), which are in good agreement with literature reference values (Fig. S4, ESI†).²⁹ SEM-EDX and AFM showed that the morphology of the samples did not change upon PA modification, since PA is deposited as a flat and homogeneous film. A weak phosphorus signal was detected in EDX measurement in a concentration close to the detection limit of the device (0.2–0.3 at%) (Fig. S5 and S6, ESI†). The anchoring of PA is only stable under acidic conditions. Therefore, a pH 11 solution was used to fully remove the PA layer from the substrate and the resulting PA solution was analyzed with high resolution ESI-MS, showing that PA did not undergo chemical changes during annealing and was still present as H₃PO₃ (Fig. S7, ESI†). PA diffraction peaks were not observed in XRD measurements due to the very thin nature of the PA layer.

In a next step, n-TiO₂ was deposited on p-Si/Al₂O₃/PA samples by ALD. We have previously shown that ∼50 nm of ALD-TiO₂ is sufficient to minimize the chance of a pinhole over larger areas (1 cm²),³⁰ thus 50 nm TiO₂ was used in this work. PEC devices were then fabricated by sputtering 1 nm of Pt as hydrogen evolving catalyst,³¹ and PV cells were fabricated by sputtering 200 nm aluminum-doped zinc oxide (AZO) followed by a 4 μm Ni grid as a front contact.³²Fig. 1E shows current density–voltage plots for p-Si/n-TiO₂ PEC cells and PV devices. By introducing an anchor layer and a PA layer at the interface of the p-Si and n-TiO₂, the J–V curves are shifted to higher potentials by 200 mV (Fig. 1E, blue traces). This shift leads to an increased V_oc and a higher fill factor (FF), and a power conversion efficiency (PCE) increase by more than 100% (figures of merit for PEC and PV in Tables S1 and S2, ESI†). The measured J_sc values are confirmed by the external quantum efficiency (EQE) spectra, giving an integrated current density of 31.6 mA cm⁻² (Fig. S8, ESI†) for the solar cells. p-Si/TiO₂ PEC devices have been reported in the literature and hardly exceed photovoltages of 200 mV, in agreement with our blank samples lacking the dipole stack.^28,33 The high photovoltage that we obtain with the p-Si/Al₂O₃/PA/TiO₂ heterojunction can usually only be obtained with homojunction Si.

We attribute the increased photovoltages in the PA modified devices to a dipole effect caused by the covalent binding of the PA layer onto the anchor layer metal oxide (in most cases Al₂O₃, which gives the highest performance devices, but TiO₂ and Ga₂O₃ and even native SiO₂ showed the same band shifting behavior; Fig. S1, ESI†). These anchor layers were grown by ALD and are naturally OH terminated.³⁴ Replacement of the hydroxyl groups by phosphonate groups, which are more electron withdrawing, gives a surface dipole that results in a downward shift of the substrate bands. The dipole magnitude increases linearly with increasing surface coverage, as more and more electron donating hydroxyl groups are replaced by electron withdrawing phosphonate groups (Fig. S9, ESI†).

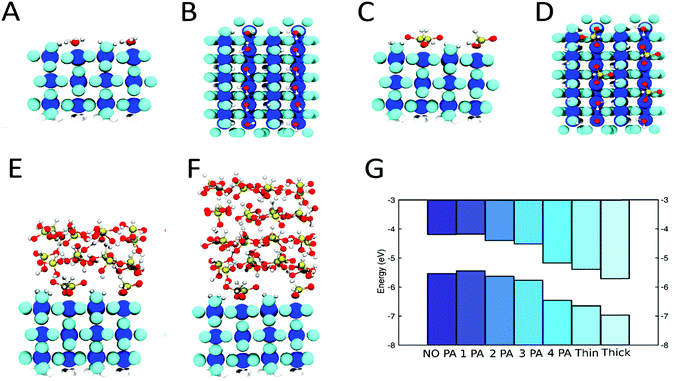
DFT simulations have been employed to model the anchor layer/PA interface. A variety of different binding modes of PA to TiO₂ were proposed in the literature, ranging from monodentate³⁵ to bidentate.^36,37 An analysis of the adsorption modes of one PA molecule on a specific bulk-like TiO₂ slab, where the PA molecules are mirrored on the bottom side to avoid spurious dipole effects, results in the bidentate B2 mode as the most stable one (Fig. 2 and Fig. S10, ESI†). The TiO₂ anchor layer that was used in a subset of devices has been modeled with a three layers thick rutile TiO₂(110) slab, where the surface has been terminated with hydroxyl groups³⁸ while the bottom side has been passivated with hydrogens. The presence of OH groups on ALD grown TiO₂ surfaces is evident from the ALD growth mechanism and was also demonstrated experimentally.^34,39,40

Fig. 2 Optimized configurations of hydroxylated TiO₂ (A and B) and TiO₂/PA with maximum PA coverage (C and D), TiO₂ with a thin PA multilayer (E) and thick PA multilayer (F). Color code: blue atoms represent Ti, cyan atoms the O of TiO₂, red is for O, gold for P and white for H. All TiO₂ atoms are enlarged for clarity purposes. (G) Bands alignment (top: conduction band, bottom: valence band) for different coverages of PA on TiO₂, namely from left to right: fully hydroxylated TiO₂, TiO₂ with 1, 2, 3 and 4 PA molecules adsorbed on top as well as TiO₂ with a thin and thick PA multilayer. The bands are shifted downwards with increasing PA coverage.

Increasing PA surface coverage was modeled by sequentially placing additional PA molecules onto the hydroxylated TiO₂ until a full PA monolayer coverage was obtained (Fig. 2C and D). To model our experimental findings of up to 2 nm thick PA layers, we started with a TiO₂ substrate with full PA monolayer coverage and added a crystalline PA layer,⁴¹ which was slightly strained to match the TiO₂ substrate and then equilibrated for a few picoseconds at 300 K with ab initio molecular dynamics simulations. Two and four layers of PA were added on top of the first PA monolayer to simulate PA layer thicknesses of approximately 1 and 2 nm (Fig. 2E and F).

Fig. 2G shows the calculated band structures with increasing PA coverage, where the band alignment has been obtained from macroscopic-averaged wavefunction values (Computational details in ESI†). The bands are shifted to more negative energy values on the vacuum scale (or to more positive values on the RHE scale) as more PA molecules are adsorbed on TiO₂(110). In our simulations, the shift increases even more, as we go from a full PA monolayer to a multilayer, which is in good agreement with our experimental results. The origin of this multilayer effect seems to arise from the restructuring at the interface of the PA that is covalently bound to the TiO₂ with the annealed PA layer. The magnitude of the calculated band shift is larger than the experimentally determined V_onset shift since surface states of the photoabsorber are expected to limit the obtainable shift as discussed below. Furthermore, in real devices, the electrolyte or the TiO₂ protection layer may shield and therefore reduce the observed shift. Those factors were not accounted for in our calculations. Nevertheless, we conclude that a three layer thick TiO₂(110) slab is an appropriate model for the amorphous TiO₂ anchor layers obtained by ALD and the qualitative results (direction of the dipole as well as the trend with increasing PA surface coverage) can be extended to other metal oxide anchor layers.

In addition to DFT calculations, several experimental results support the dipole hypothesis. XPS measurements revealed that PA modification of p-Si/Al₂O₃ leads to an increase in band bending (i.e. shifting of the band edge). Core level emissions corresponding to the Al₂O₃ anchor layer (Al 2p) as well as the native SiO₂ layer (Si 2p) exhibit a much stronger shift in binding energies than the core level emission associated with pure Si, indicating an increase in band bending on the order of 0.5 eV in the surface region of the PA modified p-Si/Al₂O₃ sample (Fig. S11, ESI†).

We also carried out the PA modification experiment on n-type silicon as well as p–n junction silicon. It has been demonstrated that relatively thick (>100 nm) ALD TiO₂ layers coated with a nickel catalyst are indeed conductive for photo-generated holes by an underlying n-type silicon photoabsorber.⁴² As expected, the samples fabricated with n-type silicon also exhibit a band shift leading to a later V_onset and decreased V_oc by 200–250 mV (Fig. S12 and S13, ESI†). On the other hand, when p–n silicon was coated with PA, we did not observe any change in V_oc or V_onset, since the photovoltage is generated inside the p-Si/n-Si homojunction and not affected by a dipole layer stacked outside that junction (Fig. S14 and S15, ESI†). The finding that a PA layer shifts the onset potentials to more positive values on p-Si/TiO₂ photocathode as well as n-Si/TiO₂ photoanode but does not affect the pn-Si/TiO₂ photocathode strongly supports the dipole hypothesis.

We note that the dipole as drawn in Fig. 1B and Fig. S9 (ESI†) is pointing in the opposite direction of the molecular gas phase dipole of PA. In our devices the dipole is rather formed by a difference in electron withdrawing/donating behavior of phosphonate as compared to hydroxyl surface termination of the anchor layer, and the gas phase dipole of the PA appears to be one out of multiple minor factors influencing the magnitude of the observed shift.⁴³ Therefore, substituted phosphonic acids on an anchor layer should also give a similar dipole as PA despite having substantially different gas phase dipole moments. This hypothesis was tested by fabricating PEC devices with fluorophosphonic acid (dipole moment = −1.1 D), phosphoric acid (0.0 D), hydroxybenzylphosphonic acid (+4.8 D), methylphosphonic acid (+0.6 D) instead of PA (−0.3 D). All of these samples showed an increased photovoltage as compared to a blank sample without dipole layer (Fig. S16, ESI†).

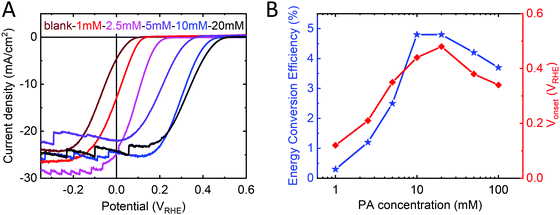
In agreement with the DFT calculations, we found that the increase in V_oc in p-Si/Al₂O₃/PA/TiO₂ samples scaled with PA thickness and thus with PA concentration used in the spin coating step. The dipole magnitude increases even more as we go from a full monolayer to a multilayer (2 nm PA ≈ 4–5 monolayers). Exploiting PA thickness dependence, we were able to fine tune the V_onset from +0.07 V_RHE up to +0.48 V_RHE over a range of 410 mV (Fig. 3A). A maximum V_onset shift of 410 mV was obtained with PA concentrations of 20 mM (giving rise to a ∼2 nm thick layer, as measured by ellipsometry). Thicker PA layers affect the series resistance of the device, leading to a decrease in the performance for PA concentrations greater than 50 mM. Samples made with PA concentrations of 10 and 20 mM (1.5–2 nm thick) showed the highest performance with good V_onset increase while retaining low series resistance (Fig. 3B).

Fig. 3 (A) Current density–voltage plots of PEC devices with the structure p-Si/Al₂O₃/PA/TiO₂/Pt with different PA concentrations used for spin coating of the dipole layer (maroon: no dipole layer; black: 20 mM PA). Linear sweeps were recorded in 1 M H₂SO₄ and 1 sun illumination at scan speed of 10 mV s⁻¹. (B) Dependence of energy conversion efficiency and onset potential (V_onset) on the PA concentration used to make the dipole layer.

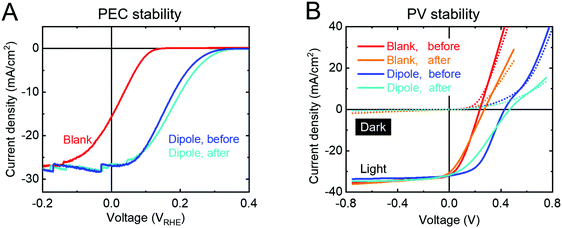
Our measurements show that the PA layer is not stable in direct contact with the electrolyte (Fig. S17, ESI†) and even changes its morphology when kept unprotected in air for more than a day (presumably due to a slow dewetting process, Fig. S18, ESI†). However, when protected from the electrolyte by a TiO₂ overlayer, the PA layer does not limit the stability of the device. The V_onset shift is stable for more than 2 h in 1 M H₂SO₄, under 1 sun illumination and at 0 V_RHE (Fig. 4A). The J–V curve after stability measurement even shows a small increase in photovoltage for both types of devices (PEC and PV). After prolonged illumination, both the blank sample as well as the dipole-modified sample start to degrade and gradually lose their performance. This phenomenon has been previously demonstrated and is attributed to detachment of the Pt catalyst particles followed by TiO₂ corrosion as soon as the accumulated electrons cannot be transferred into the electrolyte and degrade the TiO₂ instead.⁴⁴

Fig. 4 (A) Current density–voltage curves of a p-Si/Al₂O₃/PA/TiO₂/Pt sample before (blue) and after (light blue) a 2 hour chronoamperometry measurement at 0 V_RHE in 1 M H₂SO₄ under 1 sun illumination. A linear sweep measurement of the blank sample p-Si/TiO₂/Pt (red) is also included. (B) Current density–voltage plots of PV cells in the dark (dotted lines) and under 1 sun illumination (solid lines) before and after heat soaking at 80 °C and 1 sun illumination with max power point tracking for 6 days in N₂ atmosphere.

The stability of the PV devices was tested by keeping them at 80 °C under 1 sun illumination at the maximum power point for 6 days (Fig. 4B). After 6 days of this treatment, all devices (with and without dipole) showed a V_oc increase by 40 mV, unchanged J_sc and smaller FF. Obviously, the dark currents (dotted lines, Fig. 4B) of all samples decreased upon stability measurements, indicating an increased series resistance that causes the FF decreases under illumination. There are numerous possible reasons for such an increase in the series resistance (e.g. front- and back contacts). Fig. S19 (ESI†) shows how the figures of merit develop over time during the stability measurements and indicate that all major changes take place in the first few hours of the measurement before reaching a very stable equilibrium state. One of these stabilization processes even leads to a slightly increased V_oc, but since this effect is also observed in the blank p-Si/TiO₂ samples, it is not directly related to the dipole layer and was not further investigated in this study. S-Shaped J–V curves have been observed in several solar cell device types like OPV and CIGS.^45,46 Such behavior can be explained by the mismatch of the bands at a heterojunction, which may indicate that we have reached the limit of V_oc maximation for this heterojunction. We can conclude, however, that the dipole layer is not limiting the stability of the device.

The built-in voltage of the p-Si/n-TiO₂ PV cells was determined using Mott–Schottky analysis with data obtained from electrical impedance spectroscopy. The p-type doping of the silicon wafer is evident from the plot of the inverse of the squared space charge capacitance (1/C²) versus applied potential (Fig. 5). It is observed that the PA dipole layer shifts the flat band potential (E_FB) of the device from 0.22 V to 0.49 V, which is in good agreement with the increased V_oc (Fig. 1E). A very similar difference in E_FB was also observed when bare ALD-TiO₂ on FTO glass was modified with a PA layer, with and without protection by a second (very thin, 2 nm) TiO₂ layer. Those samples showed an E_F shift of 200–300 mV upon PA modification, depending upon whether a second TiO₂ layer was employed, which partially shielded the dipole effect of the PA and led to smaller E_FB shifts (see Fig. S20, ESI† for discussion).

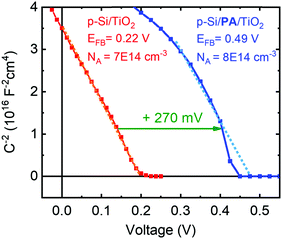Fig. 5 Mott–Schottky analysis of p-Si/TiO₂ and p-Si/Al₂O₃/PA/TiO₂ PV cells obtained from impedance measurements in the dark. Experimental and fitting details are given in the ESI.† The measured doping densities match with the resistivity data provided by the manufacturer.

Improvement of emerging material thin film devices

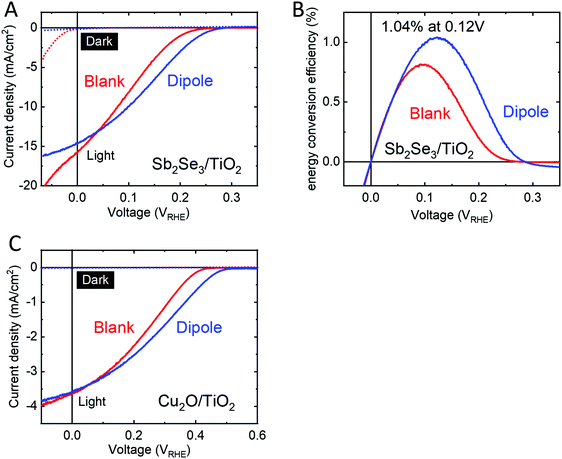
We sought to demonstrate the versatility of this dipole approach by applying it to emerging thin film materials. Two potential candidates under study in our group, Sb₂Se₃ and Cu₂O, showed an improved performance and onset potential when a dipole layer was spin coated onto the photoabsorber prior to deposition of the protecting layer and n-type heterojunction partner, TiO₂ (Fig. 6). Sb₂Se₃ has shown high efficiencies in PV (9.2%)⁴⁷ and our group has reported very high PEC current densities of 16 mA cm⁻² using Sb₂Se₃ with MoS_x catalyst for hydrogen evolution.⁴⁸ However, energy conversion efficiencies are limited by poor photovoltages. Modifying Sb₂Se₃ with a thin TiO₂ anchor layer and PA dipole layer followed by protection with 50 nm ALD TiO₂ increased the photovoltage by 40 mV as compared to the blank sample without the dipole layer (Fig. 6A) resulting in Sb₂Se₃ devices reaching a thermodynamically-based energy conversion efficiency over 1% (Fig. 6B) with onsets comparable to the very best reports in the literature.^49–51 Furthermore, the large dark current observed in the Sb₂Se₃/TiO₂ device is suppressed when a dipole layer is utilized (Fig. 6A, dotted lines).

Fig. 6 (A) Current density–voltage plots of Sb₂Se₃/TiO₂ (red) and Sb₂Se₃/TiO₂/PA/TiO₂ (blue). Linear sweeps were recorded in 1 M H₂SO₄ at a scan speed of 10 mV s⁻¹ in the dark (dotted) and under 1 sun illumination (solid). (B) Energy conversion efficiency of the same devices. (C) Current–voltage plots of Cu₂O/TiO₂ (red) and Cu₂O/TiO₂/PA/TiO₂ (blue). Linear sweeps were recorded in 1 M phosphate solution at pH 7 at a scan rate of 10 mV s⁻¹ in the dark (dotted) and under 1 sun illumination (solid).

For cuprous oxide,⁵² we spin coated PA onto electrodeposited Cu₂O covered with a 1 nm TiO₂ anchor layer and protected the PA with 50 nm ALD TiO₂. These samples showed a photovoltage increase by 70 mV as compared to the blank samples without PA layers. V_onset of the blank samples (0.4 V_RHE) are in line with values reported for p-Cu₂O/TiO₂ heterojunction PEC cells,^53,54 while V_onset of our dipole modified samples (0.5 V_RHE) sets a new record photovoltage for this heterojunction in PEC water splitting.

It should be noted that the choice of the anchor layer and PA spin coating conditions require optimization for each substrate. In the p-Si/n-TiO₂ system, we found that Al₂O₃ is the ideal anchor layer while Sb₂Se₃ and Cu₂O worked best with TiO₂ as anchor layer. We hypothesize that more large band gap metal oxide materials could serve this purpose and for some materials even the native oxide layer forming on the semiconductor surface could serve as an anchor layer. As an example, Fig. S1 (ESI†) compares the influence of different anchor layers (Al₂O₃, Ga₂O₃, TiO₂, native SiO₂) on the performance of p-Si/anchor layer/PA/n-TiO₂ devices. Furthermore, the behavior of PA during the spin coating process is strongly influenced by the surface morphology of the substrate. Using relatively high PA concentrations of 10–20 mM were ideal to form a nanometer thick PA film on perfectly flat Si substrate, giving large photovoltage improvement while still maintaining a low series resistance. On the other hand, for Sb₂Se₃ as well as Cu₂O, both of which feature a rougher surface, high PA concentrations gave very resistive devices and therefore decreased performance as compared to blank samples. For those materials the ideal PA thickness was obtained using a concentration of 1–2 mM PA giving a large photovoltage shift and low series resistance.

It should also be emphasized that for some substrates the photovoltage is limited by Fermi level pinning due to a high density of surface states within the band gap of the material. In those cases the photovoltage is independent of the band alignment with the heterojunction partner and also a dipole (for example the PA layer reported herein) will not lead to an increased photovoltage.⁵⁵ Therefore, if the anchor layer itself does not passivate the surface states well enough, additional steps are required to passivate the surface states before a dipole layer is added. In a few cases partial Fermi level pinning was also reported and those substrates would show an increased photovoltage upon addition of a dipole layer, but the increase is expected to be much smaller than in an unpinned system and we assume this to be the reason for the smaller V_onset shifts observed for Cu₂O and Sb₂Se₃ substrates as compared to p-Si.⁵⁶ To unravel whether the lack of a photovoltage increase can be attributed to a very weak dipole or to Fermi level pinning, work function measurements (by ultraviolet photoelectron spectroscopy (UPS) or Kelvin probe force microscopy (KPFM)) can be used to clarify the presence or absence of a dipole, since the dipole has an effect on the work function even if the Fermi level is pinned and is therefore “invisible” in (photo)electrochemical measurements.⁵⁵

Conclusion

We have shown that inorganic, molecular phosphonic acid layers can be used as interface dipole layers to increase the photovoltage of several heterojunctions employed for photoelectrochemical (PEC) water splitting. The strategy was developed on a p-Si/n-TiO₂ system, where TiO₂ functioned as both the heterojunction partner and as a corrosion protective layer, enabling us to fabricate PV cells and PEC cells by only exchanging the front contact/catalyst. A large increase in photovoltage was observed (+200 mV), with excellent stability, which was not limited by the dipole layer in both the PV and PEC devices. The PA layer thickness depends on the PA concentration used in spin coating and enables the fine-tuning of the band shift in a range of 0–400 mV. DFT calculations and experimental methods (XPS, electrochemical impedance) were employed to support our hypothesis that the dipole is formed at the anchor layer/PA interface by replacing the natural OH surface termination by functional groups with different electron donating/withdrawing behavior. Furthermore, a PA multilayer increases the dipole even more than a monolayer, due to some slight structural changes at the anchor layer/PA interface induced by the PA network. Insertion of a PA layer in Sb₂Se₃/TiO₂ and Cu₂O/TiO₂ allowed us to increase the photovoltage by 40 and 70 mV, respectively, demonstrating the versatility of our approach.

Author contributions

R. W. J. and S. D. T. conceived the project, directed the experiments and analyzed the data. R. W. J. fabricated the samples, carried out electrochemical and SEM measurements and wrote the manuscript. J. L. fabricated and tested the PV devices. T. Musso performed the DFT calculations, T. Musso, M. J. and J. H. planned the DFT calculations and analyzed the results. S. S. performed XPS and AFM measurements. R. R. P. provided the Sb₂Se₃ substrates and W. C. synthesized the Cu₂O samples. J. S. performed XRD measurements. T. Moehl assisted with EIS measurements. L. S. assisted with the characterization of the devices. All authors contributed to data analysis, read and commented on the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was funded by the Swiss National Science Foundation, AP Energy Grant # PYAPP2 160586, and the University of Zurich Research Priority Program (URPP) LightChEC. Sebastian Siol acknowledges funding from COST project IZCNZ0-174856 C16.0075, in the COST Action MP1407 (e-MINDS). For computing resources, we thank the Swiss National Supercomputer Centre (CSCS) under the projects ID s657 and uzh1. The authors acknowledge the assistance and support of the Center for Microscopy and Image Analysis at the University of Zurich for help with SEM characterization as well as the Mass Spectrometry service at University of Zurich for HR-ESI-MS measurements. We also want to thank Dr. Claudia Cancellieri for her help with AFM measurements, and Prof. Jürg Osterwalder and Dr Yaroslav E. Romanyuk for valuable discussions.

References

1. W. Jaegermann, A. Klein and T. Mayer, Adv. Mater., 2009, 21, 4196–4206.
2. J. Fritsche, A. Klein and W. Jaegermann, Adv. Eng. Mater., 2005, 7, 914–920.
3. C.-H. M. Chuang, P. R. Brown, V. Bulović and M. G. Bawendi, Nat. Mater., 2014, 13, 796–801.
4. T. Minami, Y. Nishi and T. Miyata, Appl. Phys. Express, 2013, 6, 044101.
5. S. E. Shaheen, W. J. Mitchell, M. F. A. M. van Hest, R. T. Collins, D. C. Olson, M. S. White and D. S. Ginley, Adv. Funct. Mater., 2006, 17, 264–269.
6. S. Siol, J. C. Hellmann, S. D. Tilley, M. Graetzel, J. Morasch, J. Deuermeier, W. Jaegermann and A. Klein, ACS Appl. Mater. Interfaces, 2016, 8, 21824–21831.
7. X. Yan, Q. Liang, S. Cao, Y. Zhang, Z. Kang and X. Liao, Nano Energy, 2016, 24, 25–31.
8. R. E. Brandt, M. Young, H. H. Park, A. Dameron, D. Chua, Y. S. Lee, G. Teeter, R. G. Gordon and T. Buonassisi, Appl. Phys. Lett., 2014, 105, 263901.
9. S. Khodabakhsh, B. M. Sanderson, J. Nelson, T. S. Jones, J. S. Kim, J. H. Park, J. H. Lee, J. Jo, D. Kim, K. Cho, J. S. Kim, J. H. Park, J. H. Lee, J. Jo and D. Kim, Adv. Funct. Mater., 2006, 16, 95–100.
10. C. Goh, S. R. Scully and M. D. McGehee, J. Appl. Phys., 2007, 101, 1–12.
11. J. S. Kim, J. H. Park, J. H. Lee, J. Jo, D. Y. Kim and K. Cho, Appl. Phys. Lett., 2007, 91, 1–4.
12. H. Ma, H.-L. Yip, F. Huang and A. K.-Y. Jen, Adv. Funct. Mater., 2010, 20, 1371–1388.
13. L. Zuo, Z. Gu, T. Ye, W. Fu, G. Wu, H. Li and H. Chen, J. Am. Chem. Soc., 2015, 137, 2674–2679.
14. Y. C. Shih, L. Y. Wang, H. C. Hsieh and K. F. Lin, J. Mater. Chem. A, 2015, 3, 9133–9136.
15. G. H. Kim, F. P. García De Arquer, Y. J. Yoon, X. Lan, M. Liu, O. Voznyy, Z. Yang, F. Fan, A. H. Ip, P. Kanjanaboos, S. Hoogland, J. Y. Kim and E. H. Sargent, Nano Lett., 2015, 15, 7691–7696.
16. R. Azmi, S. Y. Nam, S. Sinaga, S. H. Oh, T. K. Ahn, S. C. Yoon, I. H. Jung and S. Y. Jang, Nano Energy, 2017, 39, 355–362.
17. R. Azmi, H. Aqoma, W. T. Hadmojo, J. M. Yun, S. Yoon, K. Kim, Y. R. Do, S. H. Oh and S. Y. Jang, Adv. Energy Mater., 2016, 6, 1–10.
18. U. Koldemir, J. L. Braid, A. Morgenstern, M. Eberhart, R. T. Collins, D. C. Olson and A. Sellinger, J. Phys. Chem. Lett., 2015, 6, 2269–2276.
19. B. A. MacLeod, K. X. Steirer, J. L. Young, U. Koldemir, A. Sellinger, J. A. Turner, T. G. Deutsch and D. C. Olson, ACS Appl. Mater. Interfaces, 2015, 7, 11346–11350.
20. W. A. Smith, I. D. Sharp, N. C. Strandwitz and J. Bisquert, Energy Environ. Sci., 2015, 8, 2851–2862.
21. J. B. Rivest, G. Li, I. D. Sharp and D. J. Milliron, J. Phys. Chem. Lett., 2014, 1–5.
22. R. Sathre, C. D. Scown, W. R. Morrow, J. C. Stevens, I. D. Sharp, J. W. Ager, K. Walczak, F. A. Houle and J. B. Greenblatt, Energy Environ. Sci., 2014, 7, 3264–3278.
23. D. Bae, B. Seger, P. C. K. Vesborg, O. Hansen and I. Chorkendorff, Chem. Soc. Rev., 2017, 46, 1933–1954.
24. R. Cohen, N. Zenou, D. Cahen and S. Yitzchaik, Chem. Phys. Lett., 1997, 279, 270–274.
25. A. Vilan, O. Yaffe, A. Biller, A. Salomon, A. Kahn and D. Cahen, Adv. Mater., 2010, 22, 140–159.
26. N. T. Plymale, A. A. Ramachandran, A. Lim, B. S. Brunschwig and N. S. Lewis, J. Phys. Chem. C, 2016, 120, 14157–14169.
27. D. C. Gleason-Rohrer, B. S. Brunschwig and N. S. Lewis, J. Phys. Chem. C, 2013, 117, 18031–18042.
28. J. Seo, H. J. Kim, R. T. Pekarek and M. J. Rose, J. Am. Chem. Soc., 2015, 137, 3173–3176.
29. C. J. P. Alexander, V. Naumkin, A. Kraut-Vass and S. W. Gaarenstroom, NIST X-ray Photoelectron Spectroscopy Database, Gaithersburg MD, 20899, 2012.
30. T. Moehl, J. Suh, L. Sévery, R. Wick-Joliat and S. D. Tilley, ACS Appl. Mater. Interfaces, 2017, 9, 43614–43622.
31. W. Septina, R. R. Prabhakar, R. Wick, T. Moehl and S. D. Tilley, Chem. Mater., 2017, 29, 1735–1743.
32. J. Löckinger, S. Nishiwaki, T. P. Weiss, B. Bissig, Y. E. Romanyuk, S. Buecheler and A. N. Tiwari, Sol. Energy Mater. Sol. Cells, 2018, 174, 397–404.
33. S. Li, P. Zhang, X. Song and L. Gao, ACS Appl. Mater. Interfaces, 2015, 7, 18560–18565.
34. K. Kukli, A. Aidla, J. Aarik, M. Schuisky, A. Hårsta, M. Ritala and M. Leskelä, Langmuir, 2000, 16, 8122–8128.
35. M. Nilsing, S. Lunell, P. Persson and L. Ojamäe, Surf. Sci., 2005, 582, 49–60.
36. M. Wagstaffe, A. G. Thomas, M. J. Jackman, M. Torres-Molina, K. L. Syres and K. Handrup, J. Phys. Chem. C, 2016, 120, 1693–1700.
37. R. Luschtinetz, A. F. Oliveira, J. Frenzel, J. Joswig, G. Seifert and H. A. Duarte, Surf. Sci., 2008, 602, 1347–1359.
38. J. Scaranto and S. Giorgianni, Mol. Phys., 2008, 106, 2425–2430.
39. S. Haukka, E. L. Lakomaa, O. Jylha, J. Vilhunen and S. Hornytzkyj, Langmuir, 1993, 9, 3497–3506.
40. A. C. Bronneberg, C. Höhn and R. Van De Krol, J. Phys. Chem. C, 2017, 121, 5531–5538.
41. K. A. Persson, D. Skinner, W. Chen, S. Cholia, G. Hautier, D. Gunter, S. P. Ong, S. Dacek, W. D. Richards, A. Jain and G. Ceder, APL Mater., 2013, 1, 011002.
42. S. Hu, M. R. Shaner, J. A. Beardslee, M. Lichterman, B. S. Brunschwig and N. S. Lewis, Science, 2014, 344, 1005–1009.
43. S. Rühle, M. Greenshtein, S. G. Chen, A. Merson, H. Pizem, C. S. Sukenik, D. Cahen and A. Zaban, J. Phys. Chem. B, 2005, 109, 18907–18913.
44. W. Cui, W. Niu, R. Wick-Joliat, T. Moehl and S. D. Tilley, Chem. Sci., 2018, 9, 6062–6067.
45. W. Tress, K. Leo and M. Riede, Adv. Funct. Mater., 2011, 21, 2140–2149.
46. B. Ecker, H.-J. Egelhaaf, R. Steim, J. Parisi and E. von Hauff, J. Phys. Chem. C, 2012, 116, 16333–16337.
47. Z. Li, X. Liang, G. Li, H. Liu, H. Zhang, J. Guo, J. Chen, K. Shen, X. San, W. Yu, R. E. I. Schropp and Y. Mai, Nat. Commun., 2019, 10, 125.
48. R. R. Prabhakar, W. Septina, S. Siol, T. Moehl, R. Wick-Joliat and S. D. Tilley, J. Mater. Chem. A, 2017, 5, 23139–23145.
49. W. Yang, S. Lee, H. C. Kwon, J. Tan, H. Lee, J. Park, Y. Oh, H. Choi and J. Moon, ACS Nano, 2018, 12, 11088–11097.
50. W. Yang, J. Ahn, Y. Oh, J. Tan, H. Lee, J. Park, H. C. Kwon, J. Kim, W. Jo, J. Kim and J. Moon, Adv. Energy Mater., 2018, 8, 1–11.
51. H. Lee, W. Yang, J. Tan, Y. Oh, J. Park and J. Moon, ACS Energy Lett., 2019, 995–1003.
52. R. Wick and S. D. Tilley, J. Phys. Chem. C, 2015, 119, 26243–26257.
53. W. Siripala, A. Ivanovskaya, T. F. Jaramillo, S. Baeck and E. W. McFarland, Sol. Energy Mater. Sol. Cells, 2003, 77, 229–237.
54. J. Choi, J. T. Song, H. S. Jang, M.-J. Choi, D. M. Sim, S. Yim, H. Lim, Y. S. Jung and J. Oh, Electron. Mater. Lett., 2017, 13, 57–65.
55. B. S. Simpkins, S. Hong, R. Stine, A. J. Mäkinen, N. D. Theodore, M. A. Mastro, C. R. Eddy and P. E. Pehrsson, J. Phys. D: Appl. Phys., 2010, 43, 015303.
56. C. Gong, L. Colombo, R. M. Wallace and K. Cho, Nano Lett., 2014, 14, 1714–1720.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ee00748b

---